第五章对流扩散问题(一维稳态对流扩散问题)

合集下载

第五章——对流-扩散问题的有限体积法

混合格式兼具中心差分格式和迎风差分格式的优点，具有守恒性、有界性和迁移性，其缺点是按 Taylor级数展开后截断误差为一阶，精度不高
第五章对流-扩散问题的有限体积法
边界条件处理：
第五章对流-扩散问题的有限体积法
上机课：高速流计算
第五章对流-扩散问题的有限体积法
一维稳态对流-扩散问题的有限体积法举例：考虑一维无源项的稳态对流-扩散问题：（核心区的稳态能量方程） d d d d ( u ) ( ) ( u ) 0 dx dx dx dx
第五章对流-扩散问题的有限体积法
W
uw
w
P
x
xwp
ue
e
E
d d d ( u ) ( ) dx dx dx
P点中心差分
d ( u ) 0 dx
x pe
xWP
xPE
d d ( uA ) e ( uA ) w (A ) e (A ) w dx dx
设： F u
D x
w e De 有： Fw ( u) w Fe ( u ) e Dw xWP xPE
aPP aWW aEE
第五章对流-扩散问题的有限体积法
当速度较大时，采用中心差分格式处理边界值，下游边界条件对数值计算法
离散格式的性质：（1）在数学上，一个离散格式必须要引起很小的误差才能收敛于精确解，即要求离散格式必须稳定或网格必须满足稳定性条件。（2）在物理上，离散格式所计算出的解必须要具有物理意义，对于得到物理上不真实的解的离散方程，其数学上精度再高也没有价值
FeE FwP De (E P ) Dw (P W )
[(Dw ) ( De Fw ) ( Fe Fw )]P DwW ( De Fw )E

对流扩散问题有限体积法

流体仿真与应用第八讲二、对流-扩散问题的有限体积法◆中心差分格式（例子）节点增加到20个结果◆离散格式的性质在数学上，一个离散格式必须要引起很小的误差（包括离散误差和舍入误差）才能收敛于精确解，即要求离散格式必须要稳定或网格必须满足稳定性条件。

在物理上，离散格式所计算出的解必须要有物理意义，对于得到物理上不真实的解的离散方程，其数学上精度再高也没有价值。

通常，离散方程的误差都是因离散而引起，当网格步长无限小时，各种误差都会消失。

然而，在实际计算中，考虑到经济性（计算时间和所占的内存）都只能用有限个控制容积进行离散。

因此，格式需要满足一定的物理性质，计算结果才能令人满意。

主要的物理性质包括：守恒性、有界性和迁移性。

◆离散格式的性质——守恒性满足守恒性的离散方程不仅使计算结果与原问题在物理上保持一致，而且还可以使对任意体积（由许多个控制容积构成的计算区域）的计算结果具有对计算区域取单个控制容积上的格式所估计的误差。

◆离散格式的性质——迁移性③当Pe 为有限大小时，对流和扩散同时影响一个节点的上、下游相邻节点。

随着Pe 的增加，下游受的影响逐渐增大，而上游受的影响逐渐变小。

①，即纯扩散，无对流。

②，即纯对流，无扩散。

0=Pe ∞=Pe◆迎风格式迎风格式（Upwind Differencing Scheme ）在确定控制容积界面上的值时就考虑了流动的方向性，其思想为：在控制容积界面上对流项的取上游节点处的值，称之为第二类迎风格式。

中心差分格式的缺点是，它不能识别流动的方向，控制容积界面上的值取相邻上、下游节点的平均值。

当对流作用较强时，这样的处理就与其物理特征（某点的值受上游的影响，而不受下游的影响）不一致了。

φφφ◆迎风格式◆迎风格式在控制容积界面上对流项的取其上游节点处的值EW →φWw φφ=Pe φφ=()()W P w P E e W w P e D D F F φφφφφφ−−−=−()()[]()Ee W w w P w e e w w D F D F F D F D φφφ++=−+++WE →Pw φφ=Ee φφ=()()[]()Ee e W w Pw e e e w F D D F F F D D φφφ−+=−+−+◆迎风格式通用形式WW E E P P a a a φφφ+=()w e E W P F F a a a −++=EW →ww W F D a +=eE D a =W E →w W D a =ee E F D a −=◆迎风格式的特点迎风格式满足守恒性。

哈尔滨工业大学计算传热学第五章对流-扩散方程的离散格式-2013

而
aPP aEE aWW
Fe Fw exp( Pw ) aE , aW exp( Pe ) 1 exp( Pw ) 1
(D)
aP aE aW (Fe Fw )
区别就在函数 aE和aW
aE De
Pe aE De exp( Pe ) 1
aE Pe De
该格式计算量比指数小，且指数格式的解差别很小。
§ 5-3
为了在讨论中引入 PE 记
通用表达式
x
i
J*
i+1 i+1/2
x
1 界面i+ 上的值可以用界面两侧节点值表示 2
J * Bi Ai 1 （y）
系数A和B的性质的讨论 (1)当 i i 1 时，扩散量=0， J *完全由对流造成，即
即
aPP aEE aW W
显然不论那种格式，仅仅是 A(| P |) 表达式的区别。
A( P )
A(|P |)
中心 1 0.5 | P | 迎风 1 混合 [| 0,1 0.5 | P | |] 指数 | P | [exp(| P |) 1]
1.0
迎风
指数乘方
乘方 | 0, (1 0.1| P |)5 |
中心
混合
P
§ 5-4
原始的假扩散概念
关于假扩散的讨论
一维非稳态对流方程（纯对流,没有扩散）
u t x
显示迎风差分格式
in1 in
t
u
in in 1
x
, o(x, t )
将上式在（i，n）点做Taylar级数展开，保留二阶。
上述若对任何成立，必得
B( P ) A( P ) A( P ) B( P )

CFD理论对流项与扩散项

CFD理论对流项与扩散项《数值计算》导读：介绍离散方程中对流项及扩散项的物理特性，分析离散方程的迁移性。

01物理过程从物理过程的角度，对流与扩散现象在传递信息或扰动方面的特性有很大的区别。

扩散是由于分子的不规则热运动所致，分子不规则热运动对空间不同方向几率都是一样，因此扩散过程可以把发生在某一地点上的扰动的影响向各个方向传递。

对流是流体微团的定向运动，具有强烈的方向性。

在对流作用下，某一地点扰动的影响只能向其下游方向传递而不会逆向传播。

在离散过程中，对流和扩散的物理特性可以在各自的离散格式中体现出来。

02扩散项的中心差分扩散项的离散格式要求能够满足将扰动向四周均匀传递的特性。

这里，我们以一维非稳态扩散方程为例：其中心差分的显示格式：采用离散扰动分析法来确定上式传递扰动的特性。

假设开始的物理量的场已经均匀化，即处处相等，且假定其值为零；从时刻开始，在节点突然有一个扰动，而其余各点的扰动都为零，如下图所示。

将上诉的中心差分格式应用于时层的的各个节点。

对于节点：其中：，可以得到：对于节点：其中：，可以得到：对于节点：如果取，则时层的扰动到时刻变成下图所示： :显然时刻发生在节点的扰动已均匀向四周传递。

因此扩散项的中心差分格式具有使扰动均匀地向四周传递的特性，并且具有守恒性。

03对流项的差分格式首先要提到迁移性，如果某种离散格式仅能使扰动沿着流动方向传递，则说明此格式具有迁移特性。

我们以一维纯对流方程的非守恒形式为例：运用离散扰动分析法。

中心差分格式将中心差分格式运用于上式：采用第二节类似的方法，对于节点在时层：而在点处：可以看出，点的扰动可以同时向相反的两个方向传递，所以对流项的中心差分具有迁移特性。

迎风差分格式迎风差分格式的基本思想是迎着来流(即上游)去获取信息以构造的离散格式。

本文采用Taylor展开法中迎风差分的构造方法。

上式为点一阶导数的向后或向前差分，因为只有一阶截差，因而称为一阶迎风格式。

对流扩散方程clank

对流扩散方程clank标题：对流扩散方程的概述引言概述：对流扩散方程是数学中常见的描述物质传输过程的方程。

它在众多领域中都有广泛的应用，如流体力学、热传导、质量传输等。

本文将从五个大点出发，详细阐述对流扩散方程的相关内容。

正文内容：1. 对流扩散方程的基本概念1.1 对流扩散方程的定义1.2 对流扩散方程的一般形式1.3 对流扩散方程的物理意义2. 对流项与扩散项的影响2.1 对流项的作用2.2 扩散项的作用2.3 对流项与扩散项的相互作用3. 对流扩散方程的解析解与数值解3.1 解析解的求解方法3.2 数值解的求解方法3.3 解析解与数值解的比较4. 对流扩散方程的边界条件和初值条件4.1 边界条件的选择与影响4.2 初值条件的确定与影响4.3 边界条件和初值条件的耦合效应5. 对流扩散方程的应用领域5.1 流体力学中的应用5.2 热传导中的应用5.3 质量传输中的应用总结：对流扩散方程是描述物质传输过程的重要方程，其基本概念包括方程的定义、形式和物理意义。

对流项和扩散项是方程中的两个关键因素，它们分别对物质传输起到对流和扩散的作用，并且相互作用影响着传输过程。

对流扩散方程的求解可以采用解析解和数值解两种方法，它们各有优劣，需要根据具体情况选择。

边界条件和初值条件是方程求解中必要的条件，它们的选择与确定对结果有重要影响。

对流扩散方程在流体力学、热传导和质量传输等领域都有广泛应用，它为我们理解和解决实际问题提供了重要的数学工具。

总之，对流扩散方程是一个复杂而重要的数学方程，它在物质传输过程中起着关键作用。

深入理解和研究对流扩散方程，对于解决实际问题具有重要意义。

一维对流扩散问题例题含吸附作用

一维对流扩散问题例题含吸附作用一维对流扩散问题是描述物质在一维空间中传输的数学模型。

吸附作用是指物质在传输过程中与固体表面发生相互作用，被固体吸附的现象。

下面是一个关于一维对流扩散问题含吸附作用的例题：假设有一根长度为L的管道，管道内充满了某种气体。

气体沿管道的方向发生对流传输和扩散，同时在管道壁上发生吸附作用。

已知管道的吸附速率常数为k，气体的对流速度为u，扩散系数为D。

求解以下问题：1. 假设管道内初始时刻气体浓度均匀分布，求解在稳态情况下管道内吸附物质的分布。

2. 假设管道内初始时刻气体浓度为C0，求解在稳态情况下管道内气体浓度随时间和位置的变化。

解答：1. 在稳态情况下，管道内吸附物质的分布可以通过解一维扩散方程和吸附方程的组合得到。

扩散方程为：∂C/∂t = D * ∂²C/∂x²吸附方程为：∂θ/∂t = -k * θ其中，C是气体浓度，θ是吸附物质的分布，t是时间，x是空间位置。

根据稳态条件，扩散方程右侧为0，可以得到：∂²C/∂x² = 0对扩散方程积分两次得到：C(x) = Ax + B再根据吸附方程，可以得到：θ(t) = Ce^(-kt)其中A、B和C是待定系数，可以利用边界条件来确定。

边界条件可以是在管道起始端和末端的浓度值或者通量值。

求解稳态问题时，通常会假设管道起始端浓度已知，末端处的吸附物质浓度为零。

2. 在稳态情况下，气体浓度随时间和位置的变化可以通过解一维扩散方程得到。

扩散方程为：∂C/∂t = D * ∂²C/∂x²根据稳态条件，扩散方程右侧为0，可以得到：∂²C/∂x² = 0对扩散方程积分一次得到：∂C/∂x = A再次积分得到：C(x) = Ax + B其中A和B是待定系数，根据边界条件可以确定A和B的值。

边界条件可以是在管道起始端和末端的浓度值或者通量值。

通过上述方法，可以求解一维对流扩散问题含吸附作用的例题。

第五章对流扩散问题(假扩散)

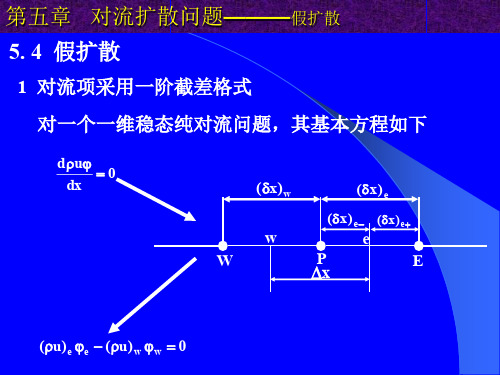
该问题的数值解如下：
1 n i
u t n u t n (1 ) i i 1 x x
MUD : du d ux d (( ) ) dx dx 2 dx
第五章对流扩散问题———假扩散
由图可以看出，在区间 P 2 ，中心差分格式预报的 P 值优于迎风格式的预报值。对比这两种格式，其扩散项的处理是完全相同的，所不同的仅仅是对流项的处理上，在中心差分格式中对流项的差分格式具有二阶精度，而在迎风格式中对流项的差分格式只具有一阶精度。在区间 P 2 ，两种格式预报 P值所表现出的差异性恰恰是这两种格式精度不同的体现。观察上图，迎风格式所预报的 P值具有该高不高和该低不低的特点，这一特点正是由一阶精度迎风格式所引起的扩散系数为 ux / 2 的假扩散项造成的。也反映了假扩散项的影响。
n n ux ut 2 n ( ) i u( ) i (1 )( 2 ) i O( x 2 , t 2 ) t x 2 x x
由此可以看出，我们前边得到的差分方程所逼近的是一个非稳态对流扩散问题，而非原型问题所要求的非稳态对流问题。
第五章对流扩散问题———假扩散
1 n (1 P
ut n ut n ) P W x x
用编号法表示
1 n i
1 n , n 在点 (i, n) i i 1
u t n u t n (1 ) i i 1 x x
做Taylor展开
n n u 2 n 1 2 n ( ) i u( ) i ( 2 ) i x ( 2 ) i t O( x 2 , t 2 ) t x 2 x 2! t
第五章对流扩散问题———假扩散
将 i 1 和 i 1 台劳级数展开代入

第五章对流扩散问题(引言)

第五章对流扩散问题 ———引言
u j ( ) S t x j x j x j
典型的对流扩散问题在这四项中，通过上一章的学习，我们已经知道时间
项、扩散项和源项如何来处理。所以，本章我们研究
对流扩散问题的重点是在其对流项的处理上，即对流项存在的情况下，如何保证正系数准则得到遵守。
aN Dn
Ft aT Dt 2
P Vol P ( Fe Fw Fn Fs Ft Fb ) Vol P (S p ) P t
n n P P Vol P b (S C )P Vol P t
第五章对流扩散问题 ———引言导致正系数准则不满足的三种可能原因
边界问题
源项负线化问题差分方程如何求解问题正系数问题
不论什么过程的数值计算中，均存在这些问题
尚未解决
为此，我们先来回顾以下所谓的正系数问题
第五章
对流扩散问题 ———引言
含时间项、对流项、扩散项和源项的热物理过程控制方程的通用形式的差分方程，如下(在时间方向上，我们采用全隐格式)：
aP P
第五章对流扩散问题 ———引言正系数准则问题是由输运方程中的对流项引起的
同时解决这两个问题，将会使我们的解决过程变得十分复杂和混乱
压力梯度项的特殊性问题
是由动量方程中的压力梯度项的
第五章对流扩散问题 ———引言注意到这两个问题并不互成因果关系，即正系数问题只要有流动就存在，但与流动的起因却没有关系。因此，可以分开来解决它们。为此，我们完全可以在一个已知流动过程的基础上来讨论正系数问题，即无须一定要求解流动问题，从而可以避免压力梯度项的特殊性问题的引入。

(参考资料)一维对流扩散方程的数值解法

一维对流扩散方程的数值解法对流-扩散方程是守恒定律控制方程的一种模型方程，它既是能量方程的表示形式，同时也可以认为是把压力梯度项隐含到了源项中去的动量方程的代表。

因此，以对流-扩散方程为例，来研究数值求解偏微分方程的相容性、收敛性和稳定性具有代表性的意义。

1 数学模型本作业从最简单的模型方程，即一维、稳态、无源项的对流扩散方程出发，方程如下： 22, 02f f fU D x t x x∂∂∂+=≤≤∂∂∂ (1)初始条件 (),0sin(2)f x t A kx π==(2)解析解()()()224,sin 2Dk tf x t eA k x Ut ππ-=-(3)式中，1,0.05,0.5,1U D A k ====函数(3)描述的是一个衰减波的图像，如图1所示t=0 t=0.5 t=1图1 函数()()()224,sin 2Dk tf x t ek x Ut ππ-=- 的图像（U=1，D=0.05，k=1）2 数值解法2.1 数值误差分析在网格点(),i n 上差分方程的数值解ni f 偏离该点上相应的偏微分方程的精确解(),f i n 的值，称为网格节点上的数值误差。

当取定网格节点数21N =时，观察差分方程的解与微分方程的解在不同时间步长下的趋近程度，其中时间步长分别取值0.05,0.025,0.0125,0.0005t ∆=。

（a ）21,0.05N t =∆= （b ）21,0.025N t =∆=（c ）21,0.0125N t =∆= （d ）201,0.0005N t =∆=图2 数值误差随步长的变化情况从图2的(a)~(d)可以定性的看出，数值误差与步长的大小有关。

在满足稳定性条件的前提下，数值误差随着时间步长的减小而减小，同时，图（d ）表示增大网格的分辨率也有助于减小网格误差。

为了对数值误差有一个定量的认识，接下来取定时间步长为0.0005t ∆=，分别算出11,21,41,61,81,101,121,161N =时，指标E =1所示。

《对流扩散方程》课件

环境科学
描述污染物在大气、水体等环境介质中的扩散、输移和归宿。
在环境科学中，对流扩散方程用于模拟污染物在大气、水体等环境介质中的扩散、输移和归宿过
程。
在环境保护、污染治理等领域，对流扩散方程具有重要的应用价
值。
化学反应动力学
描述化学反应在流体或固定床反应器中的传递和反应过程。
在化学反应动力学中，对流扩散方程用于模拟化学反应在流体或固定床反应器中的
初始条件
指定在求解开始时刻的解的性质，如常数、函数等。
03 对流扩散方程的应用
流体动力学
01
描述流体在运动状态下的物质传递和扩散现象。
02
在流体动力学中，对流扩散方程用于模拟流体中的物质传递过
程，如温度、浓度、速度等。
在航空航天、船舶、汽车等领域的流体动力学分析中，对流扩
03
散方程被广泛应用。
应用于多尺度问题
研究对流扩散方程在多尺度问题中的应用，如微纳尺度流动、大气污染扩散等。
探索新的应用领域
将该方程应用于其他领域，如生物医学、环境科学等。
与其他领域的交叉研究
与流体动力学结合
研究对流扩散方程与流体动力学之间的相互作用和影响，探索更深入的物理机制。
与偏微分方程理论的交叉
将对流扩散方程的研究与偏微分方程理论相结合，推动数学理论的发展。
02
03
有限体积法
将连续的求解域离散化为有限个小的体积，在每个体积上近似函数，将微分方程转化为代方程进行求解。
有限差分法
向前差分法
将微分方程中的导数项用前一步的函数值近似代替，得到向前差分方程。
向后差分法
将微分方程中的导数项用后一步的函数值近似代替，得到向后差分方程。

一维对流扩散方程的数值解法

因此，以对流-扩散方程为例，来研究数值求解偏微分方程的相容性、收敛性和稳定性具有代表性的意义。

当取定网格节点数21N =时，观察差分方程的解与微分方程的解在不同时间步长下的趋近程度，其中时间步长分别取值0.05,0.025,0.0125,0.0005t ∆=。

在满足稳定性条件的前提下，数值误差随着时间步长的减小而减小，同时，图（d ）表示增大网格的分辨率也有助于减小网格误差。

为了对数值误差有一个定量的认识，接下来取定时间步长为0.0005t ∆=，分别算出11,21,41,61,81,101,121,161N =时，指标E =1所示。

电化学基本原理与应用-第5章

第5章液相传质过程与浓差极化主要内容5.1 液相传质方式与基本方程5.2 平面电极上的稳态扩散传质过程5.3 浓差极化动力学方程5.4 电迁移对稳态扩散的影响液相传质过程是电极过程中必不可少的过程，涉及反应物离子向电极表面的传质过程以及生成物向溶液本体的传质过程。

由于电极过程中传质过程速度的缓慢而引起的电极极化现象为“浓差极化”。

本章将介绍液相传质过程中的规律以及浓差极化控制的电极过程的动力学方程。

为了简单，在讨论浓差极化时，假设电子转移速度很快，远远大于液相传质速度。

5.1 液相传质方式与基本方程5.1 液相传质方式与基本方程5.1.1 液相传质的三种方式5.1.2 三种液相传质的比较5.1.3 液相传质的基本方程5.1.1 液相传质的三种方式（1）对流溶液中物质的粒子随着流动的液体一起运动，此时液体与离子之间没有相对运动，这种传质方式叫对流。

包括：自然对流（温度差、密度差等），强制对流（搅拌等）。

对流可以增加单位时间内到达电极表面的粒子数目。

采用对流流量πc,i 来描述溶液中i离子的对流传质速度。

πc,i ：粒子i 在单位时间、垂直于运动方向的单位截面积上流过的量，单位(mol •m -2•s -1) ；v x ：与电极表面垂直方向上的液体的流速,单位（m •s -1）;c i ：为i 离子的浓度，单位（mol •m -3）。

ix i c c v •=,π（2）电迁移当所研究的粒子带有电荷（即为离子）时，在电场力的作用下，将引起带电粒子迁移。

电迁移作用引起的所研究粒子的传质速。

度为πe,i显然：当研究对象（反应物或生成物）不带电荷时，如为中性分子，则不存在电迁移。

（3）扩散当溶液中某一组分存在浓度差，即在不同区域内某组份的浓度不同时，该组份将自发的从高浓度区域向低浓度区域移动，这种液相传质运动叫扩散。

稳态扩散时，即扩散区域内各点浓度不随时间而变化，这时可用Fick第一定律计算扩散速度。

（3）传质发生的区域电极表面附近的液层可以分为双电层区、扩散层区、对流区。

第五章对流扩散问题(多维对流扩散问题)

n 1 P
U P x VP y ) S P
xx yy 2 A x 2 B y g
A 0.5 RU P , B 0.5 RVP , R n 1 g (P P ) SP t
第三章对流扩散问题———多维对流扩散问题
给线化的方程配置边界条件
R n 1 ( C nb nb C P P C P S P ) t n 1 P ( 1 C P R / t )
8
第三章对流扩散问题———多维对流扩散问题如果把上式中的h和k改为x和y，则就获得了以前边所配一类边界条件下对流扩散问题的精确解
R n 1 ( Cnb ( x, y ) nb CP ( x, y ) P C P ( x, y )S P ) t n 1 ( x , y ) (1 C P ( x, y )R / t )
De Dw 1, W 50, Fe Fw 4 Ds Dn 1, Fs Fn 4 E 200, S 50, N 200,
则，
a E 1 4 / 2 1 a W 1 4 / 2 3 a N 1 4 / 2 1 a S 1 4 / 2 3 a P 1 3 1 3 4
分离变量法
R n 1 ( C nb nb C P P C P S P ) t n 1 P ( 1 C P R / t )
8
第三章对流扩散问题———多维对流扩散问题其中，
CEC exp( Ah ) exp(Ah ) PB , C WC PB 2 cosh( Ah ) 2 cosh( Ah ) exp(Ah Bk ) (1 PA PB ) 4 cosh( Ah ) cosh( Bk ) exp(Ah Bk ) (1 PA PB ) 4 cosh( Ah ) cosh( Bk )

一维稳态对流问题解析解法

一维稳态对流问题解析解法《一维稳态对流问题解析解法》对流问题是流体力学中重要的研究内容之一，涉及流体在多种条件下的运动和传递问题。

在一维稳态对流问题中，我们研究流体在只与时间无关的情况下的运动状态。

解析解法是一种基于数学分析的解决问题的方法，通过使用数学模型和方程式，推导出解析解，即能够准确描述问题的解。

对于一维稳态对流问题，解析解法可以提供流体的各种流动参数的精确计算结果。

在解析解法中，我们首先需要建立流场的控制方程。

一维稳态对流问题中，常见的方程有质量守恒方程、动量守恒方程和能量守恒方程。

这些方程描述了流体在流动过程中质量、动量和能量的守恒关系，是解析解法的基础。

通过对这些方程进行数学分析和推导，我们可以得到关于流体速度、压力和温度等的微分方程。

接下来，我们需要根据边界条件和初值条件，对这些微分方程进行求解。

根据问题的不同，我们可以使用分析方法、数值方法或者近似方法来求解方程。

解析解法最大的优点是能够提供精确的解，对于一维稳态对流问题，可以得到流场中各个物理量的精确值，有效地指导实际问题的分析和解决。

例如，我们可以计算出流体速度和压力分布的解析解，从而准确预测流体的流动方向和速度分布，为管道设计和流体输送等问题提供理论依据。

此外，解析解法也有一定的局限性。

对于复杂的流体流动问题，方程的解析解往往很难求得，甚至不可行。

这时候，我们可以借助数值模拟和实验方法来获得近似解。

总的来说，一维稳态对流问题解析解法是一种重要且有效的流体力学分析方法。

它通过建立数学模型和方程式，推导出精确的流动参数解析解，为实际问题的研究和解决提供重要指导。

在实际应用中，我们可以结合其他方法，如数值模拟和实验方法，综合分析和解决流体对流问题，以得到更全面和准确的结果。

第五章对流-扩散方程的离散格式

令 F u ，D （扩导）则上式可变为： x
aP P aE E aW W
aE 1 1 De Fe aW Dw Fw 2 2
式⑴
a p aE aW
在数值计算中，若连续性方程始终得到满足，aP仍为相邻各系数的和。aE, aW包括了扩散与对流作用的影响。
对于坐标系I，C位于界面之后，而D位于界面之前，于是： J * B( P )C A( P ) D 对于坐标系II，D位于界面之后，而C 位于界面之前，于是：
J B( P ) D A( P )C
*

由于
J J
*
*'
C [ B( P ) A( P )] D [ A( P ) B( P )]
动量方程的压力梯度项处理涉及到压力与速度的耦合问题。
5.1.1 对流项离散格式的重要性对流项离散格式是否合适将会影响： ⑴ 数值解的准确性（假扩散误差）； ⑵ 数值解的稳定性； ⑶ 数值解的经济性。
5.1.2 构造对流项离散格式的两种方式
1、Taylor展开方式对于节点上的一阶导数给出其相应的离散方式，如表5-1。
aW (i 1) a E (i) 1 1 (1 P ) (1 P ) P D D 2 2
迎风差分(FUD)：
aW Dw Fw ,0 Dw 1 Pw ,0
aE De Fe ,0 De 1 Pe ,0
exp( Pe ) 1
Fe ；
Fw exp( Pw ) aW exp( Pw ) 1
aP aE aW ( Fe Fw )
5.3.4 乘方格式(Power-law scheme)

数值传热第五章课件2陶文铨

主讲陶文铨西安交通大学能源与动力工程学院热流中心CFD-NHT-EHT CENTER2010年10月18日, 西安数值传热学第五章对流扩散方程的离散格式(2)对流项离散格式的重要性及两种离散方式5.5.1假扩散的含义与成因5.5.2一阶截差格式引起严重假扩散举例1.本来的含义2.扩充的含义3.Taylor 展开法的分析5.5关于假扩散的讨论5.5.3网格倾斜交叉引起的计算误差5.5.4 非常数源项引起的假扩散5.5.5 两个名例以一维非稳态纯对流过程为例俩分析，其中有两n nφφ2(,O x φΔΔ其中关于时间的二阶导数项可做如下变化：时才没有这部分的计算误差。

2. 扩充的含义现有文献中常常将较大的计算误差都称为假扩散，大致有以下几项原因：(1) 一阶导数的一阶截差格式；(2) 流动方向与网格线呈倾斜交叉；(3) 离散格式未计及非常数源项的影响。

5.5.2一阶截差格式引起严重假扩散举例1.一维稳态对流扩散问题对流项用FUD，扩散项用CD，当Pe较大时，数值计算结果严重偏离精确解。

Physically plausible solution纯对流传递纯对流传递由离散方程：1n−1此时只有对流，没有扩散！时则有严重假扩散！0.8C =0.8C =当时，产生了严重的扩散作此种误差称为流向假扩散Γ≠Γ气流01. 设UE对P 控制容积，有2. 设控制容积，此时：计算误差纯对流传递三个对流问题的归纳这就是假扩散纯对流传递3)网格倾斜交叉引起的计算误差E冷热流体之间产生了温度均匀化的过程，即交叉5.5.5 已知流场计算温度场232(1),2(1)u y x v x y =−=−−参考解xT严重假扩散2) Leonard细高方腔中的自然对流换热5.6.1采用高阶格式克服流向假扩散5.6可以克服或减轻假扩散的格式与方法5.2.2 克服、减轻交叉假扩散的方法1. 采用二阶迎风2.采用三阶迎风3. 采用QUICK 格式1. 采用有效扩散系数2.采用自适应网格4. 采用SGSD 格式可以克服或减轻假扩散的格式与方法相当于界面上的中心差分)W WWxφ+Δ如型线上凹，则(2) FVM向上游取两点定义界面插值2.采用三阶迎风展开定义－一阶导数的三阶偏差分格式3. 采用定义－界面的插值在中心差分基础上考虑曲中心差分插值率修正？需要满足两个条件：插值的正确修正：相邻(2)0W PE φφφ−+<型线下凹8Cur −对e-界面u e 小于零时，取,,W P φφφu e 大于零时，取怎样相邻的三点?QUICK(2)e φφ=1/2w i φφ−=有：4. 采用CD条件稳定，但没有二阶假扩散；二阶迎风绝对稳定，组合起来，但是：如何确定值，特别是如何由计算结果来5. 高阶格式实施中的问题f u f计算边界：固o2) 代数方程的求解：等时，5.6.2用减小扩散系采用自适应网格（以减轻流5.7 对流-扩散方程离散形式稳定性分析5.7.1 数值计算中常见的三种不稳定性5.7.2 分析对流项格式不稳定性的“符号不变原则”5.7.3 稳定性分析结果讨论5.7.4 对流项格式问题讨论小结2.“符号不变”原则的基本思想3. “符号不变”原则的实施步骤4. “符号不变”原则的实施例子1. 研究背景扩散方程离散形式稳定性分析也会产生振荡的解，称为对流项离散格式的不稳态定性，研究目的是，找出产生振荡的临界Peclet 数。

第五章对流扩散方程的数值方法

5.2.3 一阶迎风格式
• 1.积分离散和格式推演
d (u)
dx

d dx

d
dx

( u )e
(u)w

d
dx
e

d
dx
w
采用迎风思想：从来流上游方向找依赖区
在界面e上,若 ue 0,则e P;若 ue 0,则e E ; 在界面w上,若 uw 0,则w W ;若 uw 0,则w P
第五章对流扩散方程的数值方法
胡茂彬
/~humaobin/ humaobin@
对流扩散方程求解难点
• 对流项：流动有方向性，并且有精度、稳定性和计算耗时方面的要求
• 压力梯度项：压力没有方向性的，采用中心差分符合物理意义，但会带来误差累积的问题 [留待第六章解决]
界面流量
• 引入符号 • 对流：
a1, a2 max(a1, a2 )
(u)e Fee P Fe,0 E Fe,0 , (u)w Fww W Fw,0 P Fw,0
• 扩散：

• 精度差：某些国际学术刊物已对该格式提出限制 • 在对流很强时，扩散效应已经很弱，迎风格式过
渡估算了扩散作用
5.2.4 指数格式
• 1．指数格式推演，根据精确解表达式
0 exp(ux / ) 1 exp(Pe x / L) 1 L 0 exp(uL / ) 1 exp(Pe) 1
0 L
exp(Pe) 1
界面上通量
Jw

Fw

W

W P

一维对流扩散方程的稳定性条件推导

一维稳态对流扩散方程稳定性条件的推导姓名：班级：硕5015学号：2015/12/15证明：一维稳态对流扩散方程：22ux xφφρ∂∂=Γ∂∂采用控制容积积分法，对上图P控制的容积作积分，取分段线性型线，对均分网格可得下列离散方程：()()()()()()()() 11112222e w e wP E We w e ww we eu u u u x x x xφρρφρφρδδδδ⎡⎤⎡⎤⎡⎤ΓΓΓΓ+-+=-++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦记：()()()()1122e wP e wwea u ux xρρδδΓΓ=+-+()()12eE eea uxρδΓ=-()()12wW wwa uxρδΓ=+定义通过界面的流量uρ记为F,界面上单位面积扩散阻力的倒数xδΓ记为D,则原式简化为：P P E E W Wa a aφφφ=+12E e ea D F=-12W w wa D F=+()P E W e wa a a F F=++-令u xFPe Dρδ==Γ则1111222E WPPe Peφφφ⎛⎫⎛⎫-++⎪ ⎪⎝⎭⎝⎭=当Pe 大于2以后，数值解出现了异常；P φ小于其左右邻点之值，在无源项情况下是不可能的。

因为当2Pe >时系数12E e e a DF =-小于零，即右边点的通过对流及扩散作用对中间点所产生的影响是负的，这会导致物理上产生不真实的解，所以2u x Pe ρδ=≤Γ证毕。

第五章扩散

第五章习题集锦1问题式(5－1)是一维形式的扩散第一定律，请写出三维形式的扩散第一定律。

()CCCJ D i j k x y z ∂∂∂=-++∂∂∂2问题请举出上坡扩散的具体例子。

提示：参考“相互作用参数”的相关内容。

注意与调幅分解联系 Fe －C －Si ；原子的偏聚；……3问题请分别在液态和气态中，举出下坡扩散的具体例子。

墨水滴入静止的水中；熔炼中的除气、提纯等4问题夏天铺设柏油马路，沥青味从外面进入教室。

请问沥青的味道主要通过扩散进入教室的吗？不是，沥青气味是通过对流进入教室的气体液体中物质流动方式：对流+扩散，固体中只有扩散5问题氧气与氮气的平均自由程约为0.055m μ与0.06m μ。

这两个数据与门窗通常的缝隙比小很多。

假定门窗缝隙经过细致加工后达到上述尺寸精度，问关紧门窗在房间里睡觉会出现什么问题？为什么？气体分子：相邻两次碰撞之间的平均距离，即称为分子的平均自由程。

门缝小于O 与N 的自由程，无法进入室内，……6问题 1.()B x μ化学势的一维形式?。

请写出B 原子化学势的三维形式。

2. B 原子化学势的数学性质是标量还是矢量？扩散通量J 呢（矢量）？如果它们的数学性质存在差异，写成等式?是不是会引起矛盾？7问题讲义中写到：“气体中的扩散都是下坡扩散，因为气体的0Ω≈”，为什么气体的0Ω≈？气体分子的平均自由程比较大，原子间距离太远问题讲义中说：“若Ω非常大且温度不是特别高，则内能项起决定作用，此时1x 的化学势高于2x ，因此B 原子由低浓度的1x 处向2x 处扩散，即上坡扩散”。

1.自己给定数据，用数据具体说明化学势的高低；2.结合固溶体三种微观状态的理论分析，解释为什么此时低浓度向高浓度扩散。

Ω＞＞0，内能决定作用，同类原子A-A 更易于聚集，因此倾向偏聚，偏聚处A 原子浓度较其他区域高，而A 原子仍向该区域聚集，因此是上坡扩散。

8问题规则溶液模型的()2B B B 1ln GC Z k T C μ=+-Ω+中，没有考虑应变能。