哈工大信号与系统实验电气学院
哈工大随机信号实验报告

H a r b i n I n s t i t u t e o f T e c h n o l o g y实验报告课程名称:随机信号分析院系:电信学院班级: 1205201 姓名:学号:指导教师:郑薇实验时间: 2014年 11月哈尔滨工业大学实验一 各种分布随机数的产生一、 实验目的在很多系统仿真的过程中,需要产生不同分布的随机变量。
利用计算机可以很方便地产生不同分布的随机变量,各种分布的随机变量的基础是均匀分布的随机变量。
有了均匀分布的随机变量,就可以用函数变换等方法得到其他分布的随机变量。
二、 实验内容产生均匀分布的随机数、高斯分布的随机数和其它分布的随机数。
三、 实验原理1. 均匀分布随机数的产生原理产生伪随机数的一种实用方法是同余法,它利用同余运算递推产生伪随机数序列。
最简单的方法是加同余法)(m od 1M c y y n n +=+My x n n 11++=为了保证产生的伪随机数能在[0,1]内均匀分布,需要M 为正整数,此外常数c 和初值y0亦为正整数。
加同余法虽然简单,但产生的伪随机数效果不好。
另一种同余法为乘同余法,它需要两次乘法才能产生一个[0,1]上均匀分布的随机数)(m od 1M ay y nn =+M y x n n 11++=式中,a 为正整数。
用加法和乘法完成递推运算的称为混合同余法,即)(m od 1M c ay y n n +=+My x n n 11++=用混合同余法产生的伪随机数具有较好的特性,一些程序库中都有成熟的程序供选择。
常用的计算语言如Basic 、C 和Matlab 都有产生均匀分布随机数的函数可以调用,只是用各种编程语言对应的函数产生的均匀分布随机数的范围不同,有的函数可能还需要提供种子或初始化。
Matlab 提供的函数rand()可以产生一个在[0,1]区间分布的随机数,rand(2,4)则可以产生一个在[0,1]区间分布的随机数矩阵,矩阵为2行4列。
哈工大电气学院仪器科学与技术

哈工大电气学院仪器科学与技术自动化测试与控制系简介哈尔滨工业大学自动化测试与控制系仪器科学与技术学科创建于1955年,在苏联专家的帮助下,以前苏联人才培养模式培养出国内第一批精密仪器专业研生和本科生,这批学生均成为我国该学科领域的学术带头人和技术带头人。
该学科现为国家重点一级学科, 1998年成为全国首批按一级学科培养和授予博士学位的学科点,同年被批准建立仪器科学与技术博士后流动站。
本学科在2001-2003年间全国一级学科整体水平评估中,全国排名第二, 2004-2006年间全国一级学科整体水平评估中,全国排名第三。
本学科具有较高的学术声誉和影响力。
本学科始终瞄准国际高科技前沿和国家重大需求,针对航天和国防尖端技术的前沿科学问题和关键技术问题,开展科学研究与工程关键技术研究,形成了以航天、航空、尖端与先进装备制造、微电子与信息装备制造为背景,以精密/超精密测量技术与仪器、自动化综合测试与控制技术、光电信息技术与系统为主要特色的科学研究方向,取得了以国家技术发明奖一等奖为标志的一批重大科研成果。
近三年累计科研经费超过2.6亿元。
此外,还申请国际发明专利和中国发明专利150余项,已获授权70余项;近年来完成国防航天重点预研和工程项目与国家自然科学基金项目近百项。
本学科由四个研究所、五个研究室及一个基础课教研室组成。
现有教授32人,副教授36人,其中博士生导师28硕士生导师53人。
本学科不仅在科学研究与工程关键技术研究上取得了较突出的成果,还在研究生培养方面取得了突出的成绩,共有4人获得全国百名优秀博士学位论文奖,2人获得全国百名优秀博士学位论文提名奖。
硕士研究生就业去向:国内各科研院所、国企、外企、各大公司、技术开发类企业,以及国家机关等单位,或去国内外高校攻读博士学位。
电气工程及自动化学院已走过17年的风雨路程,作为哈工大的重要组成部分,在教学与科研工作上始终处于校内的前列,并取得了令人瞩目的成绩。
哈工大数字逻辑电路与系统实验报告

哈工大数字逻辑电路与系统实验报告引言本实验旨在通过对数字逻辑电路与系统的学习与实践,加深对数字逻辑电路原理和应用的理解,掌握数字逻辑电路实验的设计与调试方法。
本报告将详细介绍实验步骤、实验结果以及实验心得体会。
实验目的1.掌握基本的数字逻辑电路设计方法;2.熟悉数字逻辑电路的布线和调试方法;3.学会使用EDA软件进行数字逻辑电路的仿真和验证。
实验器材•FPGA开发板•EDA软件实验过程实验一:逻辑门的基本控制本实验采用FPGA开发板进行实验,以下是逻辑门的基本控制步骤:1.打开EDA软件,新建工程;2.选择FPGA开发板型号,并进行相应配置;3.在原理图设计界面上,依次放置与门、或门、非门和异或门,并连接输入输出引脚;4.面向测试向量实现逻辑门的控制和数据输入;5.运行仿真并进行调试。
实验二:数字逻辑电路实现本实验以4位全加器为例,进行数字逻辑电路的实现,以下是实验步骤:1.打开EDA软件,新建工程;2.选择FPGA开发板型号,并进行相应配置;3.在原理图设计界面上,放置输入引脚、逻辑门和输出引脚,并进行连接;4.根据全加器的真值表,设置输入信号,实现加法运算;5.运行仿真并进行调试。
实验三:数字逻辑电路的串联与并联本实验旨在通过对数字逻辑电路的串联与并联实现,加深对逻辑门的理解与应用。
以下是实验步骤:1.打开EDA软件,新建工程;2.选择FPGA开发板型号,并进行相应配置;3.在原理图设计界面上,放置多个逻辑门,并设置输入输出引脚;4.进行逻辑门的串联与并联连接;5.根据逻辑门的真值表,设置输入信号,进行运算;6.运行仿真并进行调试。
实验结果经过实验测试,实验结果如下:1.实验一:逻辑门的基本控制–与门的功能得到实现;–或门的功能得到实现;–非门的功能得到实现;–异或门的功能得到实现。
2.实验二:数字逻辑电路实现–4位全加器的功能得到实现;–正确进行了加法运算。
3.实验三:数字逻辑电路的串联与并联–逻辑门的串联与并联功能得到实现;–通过逻辑门的串联与并联,实现了复杂的逻辑运算。
(精编)哈工大通信原理实验报告

(精编)哈工大通信原理实验报告H a r b i n I n s t i t u t e o f T e c h n o l o g y通信原理实验报告课程名称:通信原理院系:电子与信息工程学院班级:姓名:学号:指导教师:倪洁实验时间:2015年12月哈尔滨工业大学实验二帧同步信号提取实验一、实验目的1.了解帧同步的提取过程。
2.了解同步保护原理。
3.掌握假同步,漏同步,捕捉动态和维持态的概念。
二、实验原理时分复用通信系统,为了正确的传输信息,必须在信息码流中插入一定数量的帧同步码,帧同步码应具有良好的识别特性。
本实验系统帧长为24比特,划分三个时隙,每个时隙长度8比特,在每帧的第一时隙的第2至第8码元插入七位巴克码作为同步吗。
第9至24比特传输两路数据脉冲。
帧结构为:X11100101010101011001100,首位为无定义位。
本实验模块由信号源,巴克码识别器和帧同步保护电路三部分构成,信号源提供时钟脉冲和数字基带脉冲,巴克码识别器包裹移位寄存器、相加器和判决器。
其余部分完成同步保护功能。
三、实验内容1.观察帧同步码无错误时帧同步器的维持状态。
2.观察帧同步码有一位错误时帧同步器的维持态和捕捉态3.观察帧同步器假同步现象和同步保护器。
四、实验步骤1.开关K301接2.3脚。
K302接1.2脚。
2.接通电源,按下按键K1,K2,K300,使电路工作。
3.观察同步器的同步状态将信号源中的SW001,SW002,SW003设置为11110010,10101010,11001100(其中第2-8位为帧同步码),SW301设置为1110,示波器1通道接TP303,2通道接TP302,TP304,TP305,TP306,观察上述信号波形,使帧同步码(SW001的2-8位)措一位,重新做上述观察,此时除了TP303外,个点波形不变,说明同步状态仍在维持。
4.观察同步器的失步状态。
关闭电源,断开K302,在开电源(三个发光二极管全亮)。
哈尔滨工业大学电子与信息工程学院2012学年秋学期研究生助教岗聘任公示名单
12B905015
B
通信电子线路
赵雅琴、陈浩、侯成宇
60/24
谷献模
10B907009
A
通信电子线路
赵雅琴、陈浩、侯成宇
60/24
陈蒙
11S005042
C
13
通信电子线路
赵雅琴、陈浩、侯成宇
60/24
陈美航
11S005098
C
通信电子线路
赵雅琴、陈浩、侯成宇
60/24
张亚非
11S005013
C
通信电子线路
吴群、孟繁义、秦月梅
40/6
李宛露
11S005005
C
24
通信电子线路实验
赵雅琴
24
吴龙文
12S105034
C
25
电磁兼容原理与技术
张狂
32
周长飞
12S105024
D
26
交换技术
王学东、叶亮
28
李斌
11S105012
D
27
光纤通信
张文彬、吴玮
30
邱昕
11B905021
C
12B905010
B
卫星定位导航原理与应用
孟维晓、迟永钢
36/4
邹德岳
11B905006
A
6
通信原理I
于启月、赵洪林
60/12
郑艺
11S005069
C
7
通信原理II
苏雁泳、刘春刚
60/12
杨堃
11S105013
C
通信原理I
于启月、赵洪林
60/12
赵莹
11S105041
C
信号与系统3.5

2F(2ω)
缩
π
τ
ω
−τ O
τ t
τ
τ
ω
f(2t) 缩 1 缩 展
τ /2
O
4π
1 F(ω / 2) 2
展
4π
−τ / 4 O τ / 4 t
−
τ
τ
ω
11
时域中的压缩(扩展)等于频域中的扩展(压缩) 时域中的压缩(扩展)等于频域中的扩展(压缩)
哈尔滨工业大学(威海)信息与电气工程学院 通信工程系 哈尔滨工业大学(威海)
解
Qe
−at
2a ↔ 2 a + ω2
a=1
1 −t 1 ∴ e ↔ 2 1+ ω2
1 1 − −ω −ω ∴ 2 ↔ 2π e = πe t +1 2
9
哈尔滨工业大学(威海)信息与电气工程学院 通信工程系 哈尔滨工业大学(威海)
信号与系统
4. 尺度变换性
时间波形的扩展和压缩, 时间波形的扩展和压缩,将影响频谱的波形 a为实常数
信号与系统
信号与系统 例 尺度变换变换后语音信号的变化
f(t)
0.5 0.4 0.3 0.2 0.1 0 -0.1 -0.2 -0.3 -0.4 -0.5 0
f(2t)
f(t/2)
f (t)
f (1.5t)
f (0.5t)
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
一段语音信号( 对了 对了” 一段语音信号(“对了”) 。抽样频率 =22050Hz
1 ω f (t) ↔ F(ω) 则 f (at) ↔ F( ) a a
哈工大电路实验答案【电工学实验】
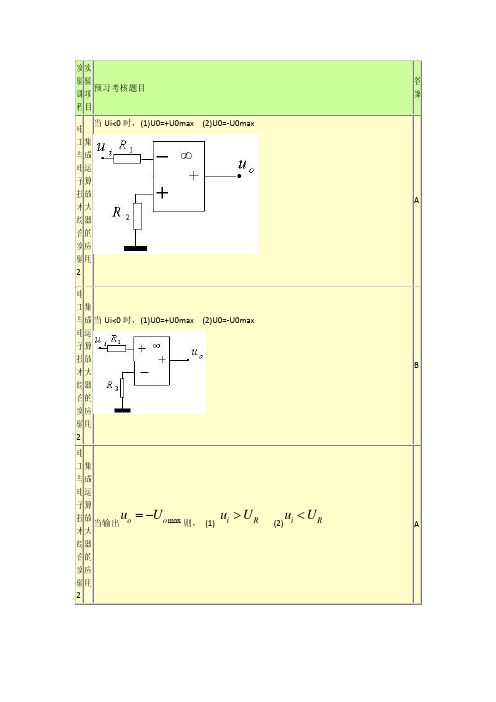
集成运算放大器的应用当Ui<0时,(1)U0=+U0max (2)U0=-U0maxA集成运算放大器的应用当Ui<0时,(1)U0=+U0max (2)U0=-U0maxB集成运算放大器的应用电路如图,改变Ui可使U0发生变化,当U0由正电压跃变为负电压时的Ui值和U0由负电压跃变为正电压时的Ui值:B集成运算放大器的应用电路如图:A大器的应用集成运算放大器的应用电路如图:A集成运算放大器的应用电路如图:B集成运算放大器的应用电路如图:B集成运算放大器的应用电路如图.当和相位相同时,则A )(1ωjU∙)(2ωjU∙组合逻辑电路及其应用当ui=A,则1) u0=A,2)B组合逻辑电路及其应用当ui=A,则1) u0=A,2)B组合逻辑电路及其应用当ui=A,则1) u0=A,2)BAuo=Auo=Auo=其应用组合逻辑电路及其应用当ui=A,则1) u0=A,2)B组合逻辑电路及其应用当ui=A,则1) u0=A,2)AAuo=Auo=触发器及时序逻辑电路电路如图,已知A=1,JK触发器的功能是A序逻辑电路触发器及时序逻辑电路当M=1时为几进制A与电子技直流直流电路下图的开路电压UOC的测定方法中,哪个是正确的。
A直流电路下图中电源的等效内阻RO的测定方法中,哪个是正确的。
A交流电路如图,当输入的交流信号U1的幅值一定时,输入信号的频率越高,输出电压的幅值A交流电路如图,当输入的交流信号Ui的幅值一定时,输入信号的频率越高,则输出电压的幅值B交流电路当电源电压一定,电路发生谐振时,则电路中的电流IA路交流电路在电感元件电路中,在相位上A集成运算放A 大器的应用集成运算放B 大器的应用集成运算放A 大器的应用集成运算放B 大器的应用集成运算放A 大器的应用集成运算放B 大器的应用集成运算放A 大器的应用集成运算放A 大器的应用集成运算放C 大器的应用集成运算放B 大器的应用集成运算放B 大器的应用集成运算放C 大器的应用集成运算放C 大器的应用集成运算放A 大器的应用集成运算放A 大器的应用集成运算放B 大器的应用集成运算放A 大器的应用集成运算放A 大器的应用集成运算放A 大器的应用集成运算放B 大器的应用触发器及时序逻辑电路电路如图,已知A=1,JK触发器的功能是A触发器及时序逻辑电路当74LS161的输出状态为1111时,再来一个计数脉冲,则下一个状态为B触发器及时序逻辑电路当M=1时为几进制A电路网络的频率特性一阶RC低通滤波器实验电路图是:A电路网络的频率特性一阶RC高通滤波器实验电路图是:B的频率特性电路网A 络的频率特性。
哈工大电气培养方案【精选】

电气工程及其自动化专业本科生培养方案一、培养目标本专业培养具备电气工程领域相关的基础理论、专业技术和实践能力,具有宽广的自然科学基础和良好的人文素养,富于创新精神,能在电机与电器、电力系统、工业自动化以及电气装备制造等领域从事科学研究、工程设计、系统运行、试验分析、管理等工作的宽口径、复合型高级工程技术人才,以及具有国际竞争力的高水平研究型精英人才或工程领军人才。
二、培养要求本专业学生主要学习电路、电磁场、电子技术基础、计算机技术、信号分析与处理、通信与网络技术、电机学、自动控制理论和电力电子技术等方面基础理论和专业知识,接受电工、电子、信息、控制及计算机技术方面的基本训练,掌握解决电气工程领域中的装备设计与制造、系统分析与运行及控制的基本能力。
毕业生应当具备以下几方面的知识和能力:1.掌握较扎实的高等数学和大学物理等自然科学基础知识,具有较好的人文社会科学和管理科学基础,具有一定的外语国际交流和运用能力;2.系统地掌握电气工程学科的基础理论和基本知识,主要包括电工理论、电子技术、信息处理、控制理论、计算机软硬件基本原理与应用等;3.掌握电气工程相关的系统分析方法、设计方法和实验技术;4.具有本专业领域内至少一个专业方向(电机、电力系统、工业自动化和电器)的专业知识和技能,了解本专业学科前沿的发展趋势;5.具有较强的适应能力,具备一定的科学研究、技术开发和组织管理能力;6.具有较好的工程实践动手能力和计算机应用能力,能综合运用所学知识分析和解决本领域工程问题;7.掌握其他的一些技能,如信息技术获取,组织管理,团队合作,持续的知识学习等。
三、主干学科电气工程。
四、专业主干课程C语言程序设计、机械学基础、电路、模拟电子技术基础、数字电子技术基础、电磁场、电机学、自动控制理论、嵌入式系统原理及应用、仿真技术与应用、电力电子技术、信号与系统、工业通信与网络技术。
五、修业年限、授予学位及毕业学分要求修业年限:四年。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 常用连续时间信号的实现1 实验目的 (1) 了解连续时间信号的特点; (2) 掌握连续时间信号表示的方法; (3) 熟悉MATLAB 基本绘图命令的应用。
2 实验原理 (1) 信号的定义:信号是带有信息的随时间变化的物理量或物理现象。
(2) 信号的描述:时域法和频域法。
(3) 信号的分类:信号的分类方法很多,可以从不同角度对信号进行分类。
在信号与系统分析中,根据信号与自变量的特性,信号可分为确定信号与随机信号,周期信号与非周期信号,连续时间信号与离散时间信号,能量信号与功率信号,时限与频限信号,物理可实现信号。
3 涉及的MATLAB 函数 (1) 正弦信号; (2) 指数信号; (3) 单位冲激信号; (4) 单位阶跃信号; (5) 抽样信号。
4 实验内容与方法参考给出的程序并观察产生的信号,并通过改变相关参数(例如频率,周期,幅值,相位,显示时间段等),进一步熟悉这些工程实际与理论研究中常用信号的特征。
5 实验要求 (1) 在MATLAB 中输入程序,验证实验结果,并将实验结果存入指定存储区。
(2) 要求通过对验证性实验的练习,自行编制完整的程序,实现以下几种信号的模拟,并得出实验结果。
(1)()(),010f t t t ε==取~ (2)()(),010f t t t t ε==取~(3)2()5e 5e ,010ttf t t --=-=取~ (4)()cos100cos 2000,=00.2f t t t t =+取~(5)0.5()4ecos ,=010t f t t t π-=取~(3)在实验报告中写出完整的自编程序,并给出实验结果。
6 实验结果(1)()(),010f t t t ε==取~t=-1:0.01:10;程序和输出如下y=heaviside(t); plot(t,y);axis([-1,10,-0.1,1.2])-11234567891000.20.40.60.81(3)2()5e 5e,010ttf t t --=-=取~程序和输出如下A=5;a=-1;b=-2; t=0:0.001:10;ft=A*exp(a*t)-A*exp(b*t); plot(t,ft)0123456789100.20.40.60.811.21.4(4)()cos100cos 2000,=00.2f t t t t =+取~程序和输出如下A=100;B=2000; t=0:0.001:0.2;ft=cos(A*t)+cos(B*t); plot(t,ft)00.020.040.060.080.10.120.140.160.180.2-2-1.5-1-0.500.511.52实验二常用LTI系统的频域分析1.实验目的(1)掌握连续时间信号傅里叶变换和傅里叶反变换的实现方法以及傅里叶变换的特性实现方法;(2)了解傅立叶变换的特点及其应用;(3)掌握MATLAB相关函数的调用格式及作用;(4)掌握傅里叶变化的数值计算方法以及绘制信号频谱图的方法;(5)能够应用MATLAB对系统进行频域分析。
2.实验原理(1)傅里叶级数的三角函数形式(2)傅立叶级数的指数形式(3)非周期信号的傅里叶变换3.涉及的MATLAB函数(1)fourier函数;(2)ifourier函数;(3)quad8函数;(4)quad1函数;(5)freds函数;4.实验内容与方法周期信号的傅里叶级数MATLAB实现;利用MATLAB画出下图所示的周期三角波信号的频谱。
5. 实验要求(1)在MATLAB中输入程序,验证实验结果,并将实验结果存入指定存储区。
(2)在实验报告中写出完整的自编程序,并给出实验结果。
6. 实验结果 实验程序如下%三角波脉冲信号的傅里叶级数实现 N=10;n1=-N:-1;c1=-4*j*sin(n1*pi/2)/pi^2./n1.^2; c0=0;n2=1:N;c2=-4*j*sin(n2*pi/2)/pi^2./n2.^2; cn=[c1 c0 c2];n=-N:N;subplot 211;stem(n,abs(cn));ylabel('Cn 的幅度'); subplot 212;stem(n,angle(cn));ylabel('Cn 的相位'); xlabel('\omega/\omega_0')输出频谱如下-10-8-6-4-224681000.10.20.30.40.5C n 的幅度-10-8-6-4-20246810-2-1012C n 的相位ω/ω0实验三 连续LTI 系统的复频域分析1. 实验目的(1)掌握连续时间信号拉普拉斯变换和拉普拉斯反变换的实现方法以及拉普拉斯变换的特性实现方法; (2)了解拉普拉斯变换的特点及其应用;(3)掌握MATLAB 相关函数的调用格式及作用; (4)能够应用MATLAB 对系统进行复频域分析。
2. 实验原理(1)拉普拉斯变换(2)拉普拉斯的收敛域(3)拉普拉斯反变换计算方法 (4)微分方程的拉普拉斯变换解法 (5)系统函数H (s ) 3. 涉及的MATLAB 函数 (1)residue 函数 (2)laplace 函数 (3)i laplace 函数 (4)ezplot 函数 (5)roots 函数 4. 实验内容与方法已知连续时间信号()sin()()f t t t ε=,求出该信号的拉普拉斯变换,并用MATLAB 绘制拉普拉斯变换的曲面图。
5. 实验要求(1)在MATLAB 中输入程序,验证实验结果,并将实验结果存入指定存储区。
(2)在实验报告中写出完整的自编程序,并给出实验结果。
6. 实验结果 程序如下%绘制单边正弦信号拉普拉斯变换曲面图程序 clf;a=-0.5:0.08:0.5; b=-1.99:0.08:1.99; [a,b]=meshgrid(a,b); d=ones(size(a)); c=a+i*b;c=c.*c; c=c+d; c=1./c; c=abs(c); mesh(a,b,c); surf(a,b,c);axis([-0.5,0.5,-2,2,0,15]);title('单边正弦信号拉普拉斯变换曲面图'); colormap(hsv);输出结果如下-0.50.5-2-112051015单边正弦信号拉普拉斯变换曲面图实验四离散时间信号的卷积和1 实验目的(1)熟悉离散时间信号卷积的定义和表示以及卷积的结果;(2)掌握利用计算机进行离散时间信号卷积运算的原理和方法;(3)熟悉离散时间信号的相关计算方法;(4)熟悉离散时间信号卷积运算函数dconv的应用。
2 实验原理(1)卷积的定义;(2)卷积计算的几何解法;(3)卷积积分的应用。
3 涉及的MATLAB函数(1)dconv函数;(2)conv函数。
4实验内容与方法(1)用MATLAB计算两个离散序列的卷积和,并绘制它们的时域波形;(2)用MATLAB图解法计算两个离散序列的卷积和。
5 实验要求(1)在MATLAB中输入程序,验证实验结果,并将实验结果存入指定存储区域。
(2)要求通过对验证性实验的练习,自行编制完整的程序,实现以下几种情况的模拟,并得出实验结果。
已知序列1为, 05[]0,n nh n≤≤⎧=⎨⎩其他,序列2为1, 05[]0,nf n≤≤⎧=⎨⎩其他,分别计算和绘出下列信号的图形:①1[][][]y n f n h n=*;②2[][][5]y n f n h n=*+(3)在实验报告中写出完整的自编程序,并给出实验结果。
6. 实验结果程序和输出如下1.计算法①f1 = [0 1 2 3 4 5];k1= [0 1 2 3 4 5];f2 = [1 1 1 1 1 1];k2= [0 1 2 3 4 5];f = conv(f1,f2)k0=k1(1)+k2(1);k3=length(f1)+length(f2)-2;k=k0:k0+k3subplot 221stem(k1,f1)title('f1(k)')xlabel('k')ylabel('f1(k)')subplot 222stem(k2,f2)title('f2(k)')xlabel('k')ylabel('f2(k)')subplot 223stem(k,f)title('f(k)=f1(k)*f2(k)')xlabel('k')ylabel('f(k)')h=get(gca,'position');h(3)=2.3*h(3);set(gca,'position',h)f =0 1 3 6 10 15 15 14 12 9 5 k =0 1 2 3 4 5 6 7 8 9 100246246f1(k)kf 1(k )02460.51f2(k)kf 2(k )01234567891051015f(k)=f1(k)*f2(k)kf (k )②f1 = [0 1 2 3 4 5]; k1= [-5 -4 -3 -2 -1 0]; f2 = [1 1 1 1 1 1]; k2= [0 1 2 3 4 5]; f = conv(f1,f2) k0=k1(1)+k2(1);k3=length(f1)+length(f2)-2; k=k0:k0+k3 subplot 221 stem(k1,f1) title('f1(k)') xlabel('k') ylabel('f1(k)') subplot 222 stem(k2,f2) title('f2(k)') xlabel('k') ylabel('f2(k)') subplot 223 stem(k,f)title('f(k)=f1(k)*f2(k)') xlabel('k') ylabel('f(k)')h=get(gca,'position'); h(3)=2.3*h(3);set(gca,'position',h) f =0 1 3 6 10 15 15 14 12 9 5 k =-5 -4 -3 -2 -1 0 1 2 3 4 5-6-4-200246f1(k)kf 1(k )02460.51f2(k)kf 2(k )-5-4-3-2-1012345051015f(k)=f1(k)*f2(k)kf (k )2.图解法 ①n=[-10:10];x=[0 0 0 0 0 0 0 0 0 0 0 1 2 3 4 5 0 0 0 0 0] h=[0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0] subplot 321;stem(n,x,' *k'); subplot 322;stem(n,h,'k'); n1=fliplr(-n);h1=fliplr(h);subplot 323;stem(n,x,' *k');hold on;stem(n1,h1,'k'); h2=[0,h1];h2(length(h2)) = [];n2 = n1;subplot 324;stem(n,x,' *k');hold on;stem(n2,h2,'k'); h3=[0,h2];h3(length(h3)) = [];n3 = n2;subplot 325;stem(n,x,' *k');hold on;stem(n3,h3,'k');n4=-n;nmin=min(n1)-max(n4);nmax=max(n1)-min(n4);n=nmin:nmax;y=conv(x,h)subplot 326;stem(n,y,'.k');-10-55100246-10-551000.51-10-55100246-10-55100246-10-55100246-20-101020051015②n=[-10:10];x=[0 0 0 0 0 0 1 2 3 4 5 0 0 0 0 0 0 0 0 0 0] h=[0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0] subplot 321;stem(n,x,' *k'); subplot 322;stem(n,h,'k'); n1=fliplr(-n);h1=fliplr(h);subplot 323;stem(n,x,' *k');hold on;stem(n1,h1,'k'); h2=[0,h1];h2(length(h2)) = [];n2 = n1;subplot 324;stem(n,x,' *k');hold on;stem(n2,h2,'k'); h3=[0,h2];h3(length(h3)) = [];n3 = n2;subplot 325;stem(n,x,' *k');hold on;stem(n3,h3,'k');n4=-n;nmin=min(n1)-max(n4);nmax=max(n1)-min(n4);n=nmin:nmax; y=conv(x,h)subplot 326;stem(n,y,'.k');-10-55100246-10-551000.51-10-55100246-10-55100246-10-55100246-20-101020051015实验五 常用LTI 系统的频域分析1. 实验目的(1) 熟悉离散LTI 系统在典型激励信号下的响应及其特征; (2) 掌握用卷积法计算离散时间系统的零状态响应; (3) 掌握MATLAB 相关函数的调用格式及其作用; (4) 通过该实验,掌握应用MATLAB 对系统进行频域分析基本方法。
