哈工大张晔信号与系统第五六七章作业答案
通信信号分析与处理知到章节答案智慧树2023年哈尔滨工业大学

通信信号分析与处理知到章节测试答案智慧树2023年最新哈尔滨工业大学第一章测试1.概率是衡量一个事件发生可能性大小的数量指标,其值介于-1和1之间。
()参考答案:错2.随机试验E的可能结果称为样本,不可再分的事件称为基本事件,所有基本事件的集合称为样本空间。
()参考答案:对3.样本空间的完备性是指样本空间必须包含随机试验的所有可能的基本结果。
()参考答案:对4.对随机试验而言,样本空间给出它的所有可能的试验结果,事件描述了所关心的具体情况,而概率给出每一事件发生的概率,则(样本空间,事件,概率)称为概率空间。
()参考答案:错5.如果我们把某事件看成“结果”,把产生这个事件的条件看成是导致这个结果的可能的“原因”,则可以形象地把全概率公式看为“由结果推原因”;而贝叶斯公式则恰好相反,其作用在于“由原因推结果”。
()参考答案:错6.()表示事件发生的频繁程度,而()表示事件发生的可能性,如果试验次数足够多,那么()具有稳定性,且趋近于事件()。
上述内容的空格中依次填入()参考答案:频率,概率,频率,概率7.相应于概率对应的概率空间,条件概率对应()。
参考答案:条件概率空间8.对于随机变量X和Y,存在()参考答案:对于任意常数c和b,有E[cX+bY]=cE[X]+bE[Y]9.有许多随机变量,它们是由()的随机变量的综合影响所形成的,而其中每个因素作用都很小,这种随机变量往往服从或近似服从正态分布,或者说它的极限分布是正态分布。
参考答案:大量的互相独立10.下列说法错误的是()参考答案:两个随机变量的相关系数不能是负数。
第二章测试1.严平稳随机过程一定是宽平稳随机过程,但宽平稳随机过程不一定是严平稳随机过程。
()参考答案:错2.当随机过程同时满足数学期望为常数和自相关函数只与时间间隔有关时,称该随机过程为宽平稳随机过程。
()参考答案:错3.随机过程的自相关函数和协方差函数为偶函数。
()参考答案:错4.相关时间越大,这说明随机过程随时间变化越缓慢。
信号与系统课后习题与解答第七章

15- 分别绘出以下各序列的图形)()21()()1(n u n x n = )(2)()2(n u n x n =)()21()()3(n u n x n -= )()2()()4(n u n x n -=)1(2)()5(1-=-n u n x n )()21()()6(1n u n x n -=解)()1(n x 序列的图形如图5-1(a)所示。
)()2(n x 序列的图形如图5-1(b)所示。
)()3(n x 序列的图形如图5-1(c)所示。
)()4(n x 序列的图形如图5-1(d)所示。
)()5(n x 序列的图形如图5-1(e)所示。
(b)图5-1(a)(f)(e)(d)25- 分别绘出以下各序列的图形)()()1(n nu n x = )()()2(n nu n x --= )(2)()3(n u n x n -= )()21()()4(n u n x n --=)()21()()5(n u n x n --= )1()21()()6(1+=+n u n x n解) 序列的图形如图5-2(b)所示。
x()2(n 序列的图形如图5-2(c)所示。
x))3(n(x 序列的图形如图5-2(d)所示。
)4(n())5(n 序列的图形如图5-2(e)所示。
x()x 序列的图形如图5-2(f)所示。
())6(n(b)图5-2(c)(f)(e)(d)8-(a)35- 分别绘出以下各序列的图形)5sin()()1(πn n x =)510cos()()2(ππ-=n n x)5sin()65()()3(πn n x n =解)()1(n x 序列的图形如图5-3(a)所示。
)()2(n x 序列的图形如图5-3(b)所示。
)()3(n x 序列的图形如图5-3(c)所示。
图5-3(a)45- 判断以下各序列是否是周期性的,如果是周期性的,试确定其周期。
)873sin()()1(ππ-=n A n x)8()()2(π-=ne n x j解)1(因为3147322==πππw 是有理数,所以)(n x 是周期性的,且周期为14。
哈工大数字电子技术基础习题册2010-答案6-7章

哈工大数字电子技术基础习题册2010-答案6-7章第6章触发器【6-1】已知由与非门构成的基本RS触发器的直接置“0”端和直接置“1”端的输入波形如图6.1所示,试画出触发器Q端和Q端的波形。
R d SdQQ图 6.1解:基本RS触发器Q端和Q端的波形可按真值表确定,要注意的是,当dR和d S同时为“0”时,Q端和Q端都等于“1”。
d R和d S同时撤消,即同时变为“1”时,Q端和Q端的状态不定。
见图6.1(b)所示,图中Q端和Q端的最右侧的虚线表示状态不定。
R dS dQQ不定状态图6.1(b)题6-1答案的波形图【6-2】触发器电路如图6.2(a)所示,在图(b)中画出电路的输出端波形,设触发器初态为“0”。
QdS dQQR(a) (b)图6.2解:此题是由或非门构成的RS 触发器,工作原理与由与非门构成的基本RS 触发器一样,只不过此电路对输入触发信号是高电平有效。
参照题6-1的求解方法,即可画出输出端的波形,见图6.2(c)。
d S dQR 不定状态图6.2(c)【6-3】试画出图6.3所示的电路,在给定输入时钟作用下的输出波形,设触发器的初态为“0”。
“CPYZCP图 6.3解:见图6.3(b)所示,此电路可获得双相时钟。
Q Q CP Y Z图6.3(b)【6-4】分析图6.4所示电路,列出真值表,写出特性方程,说明其逻辑功能。
Q图6.4解:1.真值表(CP =0时,保持;CP =1时,如下表)D n Q n Q n+1 0 0 0 0 1 0 1 0 1 1 1 12.特性方程Q n+1=D n3.该电路为锁存器(时钟型D 触发器)。
CP =0时,不接收D 的数据;CP =1时,把数据锁存,但该电路有空翻。
【6-5】试画出在图6.5所示输入波形的作用下,上升和下降边沿JK 触发器的输出波形。
设触发器的初态为“0”。
CP J K图 6.5解:见图6.5(b)所示。
CP J KJ K QQ图6.5(b)【6-6】试画出图P6.6(a)所示电路,在图6.6(b)给定输入下的Q 端波形,设触发器初态为“0”。
信号系统课后习题答案

信号系统课后习题答案2-7 试计算下列结果。
(1) t δ( t - 1 )(2) ?∞∞--t t t d )1(δ(3) ?∞--0d )()3πcos(t t t δω (4) ?+---003d )(e t t t δ解 (1) t δ( t - 1 ) = δ( t - 1 )(2) 1d )1(d )1(=-=-??∞∞-∞∞-t t t t t δδ(3) 21d )()3πcos(d )()3πcos(00=-=-??∞∞--t t t t t δδω (4) 1d )(d )(e d )(e 00003003===-+-+-+---t t t t t t t t δδδ2-5 设有题2-6图⽰信号f ( t ),对(a)写出f ' ( t )的表达式,对(b)写出f " ( t )的表达式,并分别画出它们的波形。
题2-6图解 (a)20,2f ' ( t ) = δ( t - 2 ), t = 2-2δ( t - 4 ), t = 4(b) f " ( t ) = 2δ( t ) - 2δ( t - 1 ) - 2δ( t - 3 ) + 2δ( t - 4 )图p2-63-11 试求下列卷积。
(a) δ( t ) * 2(b) ε( t + 3 ) * ε( t - 5 ) (c) t e -t ?ε( t ) * δ' ( t )解 (a) 由δ( t )的特点,故δ( t ) * 2 = 2(b) 按定义ε( t + 3 ) * ε( t - 5 ) = ?∞∞---+ττετεd )5()3(t考虑到τ < -3时,ε( τ + 3 ) = 0;τ > t -5时,ε( t -τ - 5 ) = 0,故ε( t + 3 ) * ε( t - 5 ) =2,2d 53>-=?--t t t τ也可以利⽤迟延性质计算该卷积。
信号与系统第六章习题答案

第六章 离散系统的Z域分析 6.1学习重点 1、离散信号z 域分析法—z变换,深刻理解其定义、收敛域以及基本性质;会根据z变换的定义以及性质求常用序列的z变换;理解z变换与拉普拉斯变换的关系。
2、熟练应用幂级数展开法、部分分式法及留数法,求z 反变换。
3、离散系统z 域分析法,求解零输入响应、零状态响应以及全响应。
4、z 域系统函数()z H 及其应用。
5、离散系统的稳定性。
6、离散时间系统的z 域模拟图。
7、用MATLAB 进行离散系统的Z 域分析。
6.2 教材习题同步解析 6.1 求下列序列的z 变换,并说明其收敛域。
(1)n 31,0≥n (2)n−−31,0≥n(3)nn−+ 3121,0≥n (4)4cos πn ,0≥n(5)+42sin ππn ,0≥n 【知识点窍】本题考察z 变换的定义式 【逻辑推理】对于有始序列离散信号[]n f 其z 变换的定义式为()[]∑∞=−=0n nzn f z F解:(1)该序列可看作[]n nε31()[][]∑∑∞=−∞=− == =010313131n n n nn n z z n n Z z F εε对该级数,当1311<−z ,即31>z 时,级数收敛,并有 ()13331111−=−=−z zz z F其收敛域为z 平面上半经31=z 的圆外区域 (2)该序列可看作[]()[]n n nnεε331−=−−()()[][]()[]()∑∑∞=−∞=−−=−=−=010333n nn nnnzzn n Z z F εε对该级数,当131<−−z ,即3>z 时,级数收敛,并有()()33111+=−−=−z zz z F 其收敛域为z 平面上半经3=z 的圆外区域(3)该序列可看作[][]n n nn n n εε+ = + −3213121()[][]()∑∑∑∞=−∞=−∞=−+ =+ = + =01010*********n nn n n nn n n n z z z n n Z z F εε对该级数,当1211<−z 且131<−z ,即3>z 时,级数收敛,并有 ()3122311211111−+−=−+−=−−z zz z z zz F 其收敛域为z 平面上半经3=z 的圆外区域(4)该序列可看作[]n n επ4cos()[]∑∑∑∑∞=−−∞=−−∞=−∞=−+=+== =0140140440*******cos 4cos n nj n nj nn j j n n z e z e z e e z n n n Z z F πππππεπ对该级数,当114<−ze j π且114<−−zejπ,即1>z 时,级数收敛,并有()122214cos 24cos 21112111212222441414+−−=+−−=−+−=−×+−×=−−−−z z zz z z z z e z z e z z z eze z F j j j j ππππππ其收敛域为z 平面上半经1=z 的圆外区域 (5)该序列可看作[][][]n n n n n n n n εππεππππεππ+=+= +2cos 2sin 222sin 4cos 2cos 4sin 42sin()[]()122212212212cos 22cos 2212cos 22sin 222cos 222sin 222cos 2sin 222222222200++=+++=+−−++−=+=+=∑∑∞=−∞=−z z z z z z z z z z z z z z z n z n n n n Z z F n nn n ππππππεππ 其收敛域为z 平面上半经1=z 的圆外区域 6.2 已知[]1↔n δ,[]a z z n a n −↔ε,[]()21−↔z z n n ε, 试利用z 变换的性质求下列序列的z 变换。
信号与系统课后答案第六章作业答案
⋅
2⎤⎥⎦
⋅
u
(n
−
3)
=
2⋅
( −1)n
⎡2 ⎢⎣ k =0
( −1)− k
⎤ ⎥⎦
⋅
u
(n
−
3)
∑ y
f
(3)
=
2
⋅
(
−1)3
⎡ ⎢⎣
k
2 =0
(
−1)−k
⎤ ⎥⎦
=
2
⋅
( −1)
⋅
(1
−1
+
1)
=
−2
∑ y
f
(4)
=
2
⋅
(
−1)4
⎡ ⎢⎣
k
2 =0
(
−1)−k⎤ ⎥⎦=2⋅(1)
⋅
(1
−1
+
1)
-1
对应时刻点相乘后累加得 y(1) = 4 。 由于 f1(n) 和 f2 (n) 为有限序列,故该题可采用数乘法进行计算:
11112 2 2 2 ↑ 1 1 1 1 −1 −1 −1 ↑
−1 −1 −1 −1 − 2 − 2 −2 −2 −1 −1 −1 −1 − 2 − 2 −2 −2 −1 −1 −1 −1 − 2 − 2 −2 −2
u
(
n
+
4)
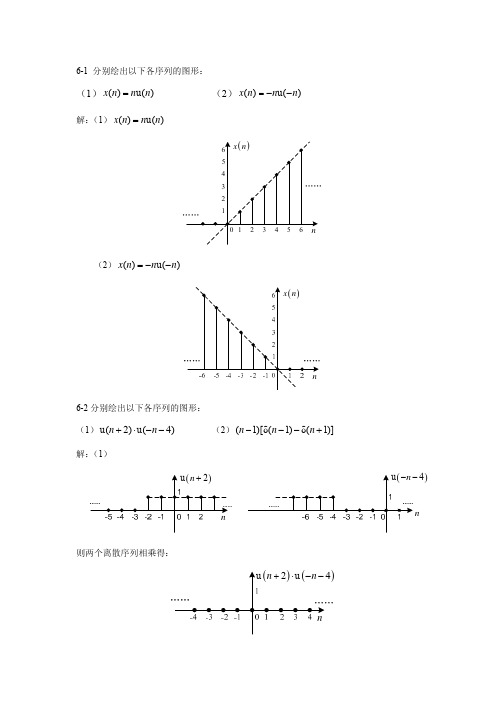
(4)利用卷积的性质( f (n) *δ(n − m) = f (n − m) )可得:
nu(n) * δ(n + 3) = nu(n) n=n+3 = (n + 3) u(n + 3)
6-7 如题图 6-4 所示,如果 y(n) = f1(n) * f2 (n) ,则试求 y(−2)、y(0)、y(1) 的值。
信号与系统第三版 第六章习题答案

2 t 2
cos
2 2
t ]u (t )
6.13 一个因果LTI系统的频率响应为:
5 jw 7 H ( jw) ( jw 4)[( jw) 2 jw 1]
(a) 求该系统的冲激响应
(b) 试确定由一阶系统和二阶系统构成的串联型结构 (c)试确定由一阶系统和二阶系统构成的串联型结构 解:(a) 5 jw 7 1 jw 2
I 2 (w) 2 jw H ( jw) E (w) 8 jw 3
(b) 对H(jw)作反傅立叶变换可得h(t)
2 jw 1 H ( jw) 8 jw 3 4
h(t ) F 1{H ( jw)}
3 32 3 jw 8 3t 1 3 8 (t ) e u (t ) 4 32
(b) 对H(jw)作反傅立叶变换可得h(t)
3 3 3( jw 3) 2 H ( jw) 2 ( jw 2)( jw 4) ( jw 2) jw 4
3 2t h(t ) F {H ( jw)} (e e 4t )u (t ) 2 (c) 3( jw 3) 3 jw 9 Y ( w) H ( jw) 2 ( jw 2)( jw 4) ( jw) 6 jw 8 X ( w)
1 X ( w) ( jw 2) 2
Y (w) H ( jw) X (w)
2 Y ( w) 3 ( jw 2) ( jw 4)
1 1 4 2 3 ( jw 2) ( jw 2) ( jw 2) ( jw 4) 1 4 1 2
1 2t 1 2t 1 2 2t 1 4t y (t ) F {Y ( w)} ( e te t e e )u (t ) 4 2 2 4 2 2 ( jw ) 2 (c) H ( jw) ( jw) 2 2 jw 1
信号与系统第七章课后答案
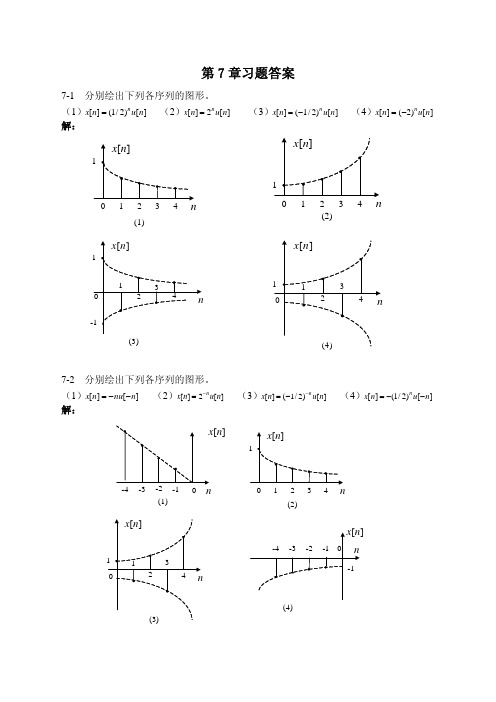
7-1 分别绘出下列各序列的图形。 (2)x[n] 2n u[n] (3)x[n] (1/ 2)n u[n] (4)x[n] (2) n u[ n] (1)x[n] (1/ 2)n u[n] 解:
x[ n ]
1
x[n]
1
0 1 2 (1) 3 4
n
0
1
2 3 (2)
x[n]
1
x[n]
-4
-3
-2 (1)
-1
0
n
0
1
2 (2)
3
4
n
x[n]
-4 1 0 1 2 3 4 -3 -2 -1 0
x[n] n
-1
n
(4)
(3)
7-3
分别绘出下列各序列的图形。 (2) x[n] cos
n 10 5
n (1) x[n] sin 5
1 z2 X (z) ( 1 1 2 z 1 )( 1 2 z 1 ) ( z 1 2 )( z 2 ) X (z) z 1 4 z ( z 1 2 )( z 2 ) 3( z 1 2 ) 3( z 2 )
X (z)
z 4z 3( z 1 2 ) 3 ( z 2 )
N
)
由于 x[n] 、 h[n] 均为因果序列,因此 y[n] 亦为因果序列,根据移位性质可求得
y [ n ] Z 1 [Y ( z )]
1 1 (1 a n 1 ) u [ n ] (1 a n 1 N ) u [ n N ] 1 a 1 a
7-24 计算下列序列的傅里叶变换。
(2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时
Rs
n二十时
ng
2onauin.mn
10元10f W5到ㄨ t
n 1 specs 10元 ócw 5 玐合
则原
rltnltws5ntxiiiiz.FM
mi
下以时 求输出波形
2元
原 州w
沁王
Iólwn
㖄
画E 删图幅渔 IE 吲二三
jmnitl
2
1
丽 2mg
-
人
-
vn
ii
runner
iii
em tent cuts x eun
D
tztyanliwyenj
3ylnDtzyin.y
ccn
八8
只知输入信号与样相响应如 图
pan
4
in hui
i
则和用周8祥法
htn
4
i
人
1
n
5
狐州2 n 二水m 加 n_n
的 心
八
n
1
j
2
1
g
4
2
1
z
i
8
8
4 8
2
1
4
2
1
1
N
8
4 8
4 8
2
利用H127 则可以直接求美分方积
2 22
Hit 1127
则可知 Fsu
I
ǛFCWHRW
iFM
言 品 ócw_nwciiw
li 州前
采样25 得到4096个采样序列
刚fmax 40961.4104
则f
赢 22fm
nmx AESay
竿
利用
Csi
t
则
2
nu
uicyo
则分别求并联后阻抗
火
簵
二
品
同理 R2
p.su 1
君袖 磊 1 咖 啊
则以 以
二
点到
拉 RISCH十月 R2512⺾
一
140几万 十 nlócwtsoon 1400㕴 101W
0lmao
800元
nzgtólw
140几到 十二 Ólwt 4 on
1400
抽样后 经111w
40 140几到 进行冲激
则El 以 R 以FCW
HM ulttqoom uct.to元
然后依据 的不同 几次
Ran To Eun
m l mu 7 oonrlw
RISCH
unylpzscz.tl
MSGtl RisCity
R
HRzslz.Xpnscatgtp.mn
则Hljw jWCIRR.tn
则合
111⻔以1为
RHM
wnstjwczmmtjwlz.BR
qwj Wt
it
则 彘
My
蕊
eetkzwscwontslltwsllon.tl 侍立叶
zcoslwontgtzwslwonty.cm looms
0
两边同时进行Z交他
X
社
zym ZYlzjtzyoj zylzixlzl.z
EIzj zyzwj
1 Xlz
2z
22
心
z_z.dz
z2 z 2
xzyz2
Yxcn 二主 n 2 Ulm
Xltkxxcniz
二
至
前2
Yzscz
二
HE 加
Zzcz1
山
二三大川
Thing
july
则wm
一定混耳
Witwig
IN
EHWHEzmn
E3们
以北 2 比3 若无失夏则wcnwztW3
叫 心 叫琴 器吓 告 则为同期但是同期为䛓的某个整倍
e 靔 域 则比一 则 下乲 16元 则为同期
z sun e 将 州
菲
3 xcn e 玔 te in 分别看2个的日期 㗟 i
第2个 乲 元 不是同期高列
㗊 e
1000
以000
然后通过H
以外 HMRlugziglwioogtgcwtloog.gl
gunny
以000
1000
tgcwt
1
2
7
y.l.eu
Has 5 时 FO.IS时为抽样函数 求EM
原 Utgoip F1以 言 my Pin
plug ME rlw.ms
则将1 以 心州转化为须域即可 沁 们十吨叫 15元
2101 wtwomtoiw zozgtzlnwtwomtoiw
2101Wtwonstoiw.mn
zozu.IO
cwttoast 0 W600元
4
2 ócwt800到十ólw 40元 01Wtaoomtócw was
一
金高 uwnwy
抽样的得方叶
减 让梁 熙
则利用pm 冮以可知 抽样后的 函700 ztzniócwt soon 14omg
ycnty
fycnty
jycujxlzlzyzyz
xln.tn 2 Xln
则 ycnriycn n jyen.is
画模拟图
cn
加
D
3
D
细
2X M 2
1⺕
i
火则
娰
1
xcnn
国
回
1
回 sycm
xcn 7 xcn
传递图画差分方程
1利用
则
HE
2 1
2 Z 2
xzmlz
从而
X
2
ziycn ytzycny.lyin
wmne
lp.cm 7 on Mwtwm
则加上器上ayz
系统函数
型 costnot 头HAD
atg.sn 以先进行乘法运算 装
cost
只
Hang
以为
以
则
先对 2个时域做乘积
ehiyz
sinn eix e
Cloy
iyzjznபைடு நூலகம்.WS
Simm
it
以 wscootg Sag.eie.no
乺
mi
9 切 1000片 e 100017 ùglmoogtgcwt
凖
0cw
15nDPCWFzn.IN
turn 207
In w_w my
in
唦十元也叫15元 ócw 15列木 些 W
进
zouzniznnwjtnloiwtliwgthW
l5wyxnw.no n_n
二亢
下
以
则
220 W_W几到十二 0 W 15 n_n nzytócw 15 n_n
HIM二
结 占步器
两者相来 in
0
Ruin 点 Íólwnws
然后求和二三⻆脉冲信号可以看成矩形的卷积 Ǚsǎc竿
0
须
则两者抽样后 请可知 FSCWFFCts gs 言知网心 竺砍竿 点击ólunw
高吉saiicwnwsD
i
冲激的抽样序列为 0后 切
以
-
i
ir
b 同期涌波的脉冲序列
fnfoltióltnīs 则二fun ownÉxólwnw
2 二六
4
n
n
1005
xcn
cos
5
6
品 二 空 则合为 i 和书信即可
壳
4
年
li
N 62
22m
1 加小
加以
鵼
加以
第i
h
1
0
i 狄州
I2
21
0
i
则
3
i
1
3
ivb.li
no
I
zum
alum
aoxy
bycry
by灬
则
axcm
画模拟图
aoxcn
zum
bi yl n ⻔
boyin
灬
阶
一
DI ETTI
27In
