哈工大信号与系统第三章术后作业答案张晔
通信信号分析与处理知到章节答案智慧树2023年哈尔滨工业大学

通信信号分析与处理知到章节测试答案智慧树2023年最新哈尔滨工业大学第一章测试1.概率是衡量一个事件发生可能性大小的数量指标,其值介于-1和1之间。
()参考答案:错2.随机试验E的可能结果称为样本,不可再分的事件称为基本事件,所有基本事件的集合称为样本空间。
()参考答案:对3.样本空间的完备性是指样本空间必须包含随机试验的所有可能的基本结果。
()参考答案:对4.对随机试验而言,样本空间给出它的所有可能的试验结果,事件描述了所关心的具体情况,而概率给出每一事件发生的概率,则(样本空间,事件,概率)称为概率空间。
()参考答案:错5.如果我们把某事件看成“结果”,把产生这个事件的条件看成是导致这个结果的可能的“原因”,则可以形象地把全概率公式看为“由结果推原因”;而贝叶斯公式则恰好相反,其作用在于“由原因推结果”。
()参考答案:错6.()表示事件发生的频繁程度,而()表示事件发生的可能性,如果试验次数足够多,那么()具有稳定性,且趋近于事件()。
上述内容的空格中依次填入()参考答案:频率,概率,频率,概率7.相应于概率对应的概率空间,条件概率对应()。
参考答案:条件概率空间8.对于随机变量X和Y,存在()参考答案:对于任意常数c和b,有E[cX+bY]=cE[X]+bE[Y]9.有许多随机变量,它们是由()的随机变量的综合影响所形成的,而其中每个因素作用都很小,这种随机变量往往服从或近似服从正态分布,或者说它的极限分布是正态分布。
参考答案:大量的互相独立10.下列说法错误的是()参考答案:两个随机变量的相关系数不能是负数。
第二章测试1.严平稳随机过程一定是宽平稳随机过程,但宽平稳随机过程不一定是严平稳随机过程。
()参考答案:错2.当随机过程同时满足数学期望为常数和自相关函数只与时间间隔有关时,称该随机过程为宽平稳随机过程。
()参考答案:错3.随机过程的自相关函数和协方差函数为偶函数。
()参考答案:错4.相关时间越大,这说明随机过程随时间变化越缓慢。
信号系统(第3版)习题解答

文档《信号与系统》(第3版)习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t)表示将f ( t )波形展宽。
](a) 2 f ( t - 2 ) (b) f ( 2t )(c) f ( 2t)(d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S RS LS C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T == )()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
信号系统习题解答_3版_徐天成_南理工老师留的平时作业题

信号系统习题解答_3版_徐天成_南理工老师留的平时作业题信号系统习题解答_3版_徐天成_南理工老师留的平时作业题第2章习题答案 2-1 绘出下列各时间函数的波形图1 2 3 45 6解2-5 已知波形如图题2-5所示试画出下列信号的波形图图题2-53 5 解2-6 已知波形如图题2-6所示试画出下列信号的波形图图题2-64 6解2-7 计算下列各式1 2 3 4 5 6 7 8 910 11 12 解 1 原式2 原式3 原式4 原式5 原式6 原式7 原式8 原式9 原式10 原式11 原式12 原式2-8 画出图题2-8所示各信号的偶分量和奇分量的波形图题2-8解 bc已知求的表达式并画出的波形图解2-13 已知的波形如图题2-13所示求和并分别画出和的波形图图题2-13解2-14 对下列函数进行积分运算并画出积分后的波形图1 2 3解23第3章习题答案3-1 已知周期矩形脉冲信号的重复频率脉宽幅度如图题3-1所示用可变中心频率的选频回路能否从该周期矩形脉冲信号中选取出512205080及频率分量来要求画出图题3-1所示信号的频谱图图题3-1解频谱图为从频谱图看出可选出52080kHz的频率分量3-3 求图题3-3 所示周期锯齿信号指数形式的傅里叶级数并大致画出频谱图图题3-3解在一个周期0T1内的表达式为傅氏级数为频谱图为3-4 求图题3-4 所示半波余弦信号的傅里叶级数若大致画出幅度谱图题3-4解由于是偶函数所以展开式中只有余弦分量故傅氏级数中另由图可知有直流分量在一个周期内的表达式为其中所以的三角形式的傅里叶级数为3-6 利用信号的对称性定性判断图题3-6中各周期信号的傅里叶级数中所含有的频率分量图题3-6解 a 为偶函数及奇谐函数傅氏级数中只包含奇次谐波的余弦分量b 为奇函数及奇谐函数傅氏级数中只包含奇次谐波的正弦分量c 为偶谐函数而且若将直流分量12去除后为奇函数所以傅氏级数中只包含直流以及偶次谐波的正弦分量d 为奇函数傅氏级数中只包含正弦分量e 为偶函数及偶谐函数傅氏级数中只包含直流以及偶次谐波的余弦分量f 为奇谐函数傅氏级数中只包含奇次谐波分量3-7 已知周期函数前四分之一周期的波形如图题3-7所示根据下列各种情况的要求画出在一个周期的波形1是偶函数只含有直流分量和偶次谐波分量2是偶函数只含有奇次谐波分量3是偶函数含有直流分量偶次和奇次谐波分量解1由画出在内的波形由在内的波形及是偶谐函数它在内的波形与它在内的波形相同它在内的波形与它在内的波形相同根据上述分析可画出在内的波形按上述类似的方法可画出2和3233-8 求图题3-8 所示半波余弦脉冲的傅里叶变换并画出频谱图图题3-8解法一按定义求由于是偶函数所以化简得解法二利用卷积定理求设则于是而故的频谱是将矩形脉冲的频谱分别向左右移动幅度乘以后叠加的结果3-10 求图题3-10所示的傅里叶逆变换图题3-10解ab3-13 求函数的傅里叶变换解利用对偶性求因为所以令则即F3-15 对图题3-15所示波形若已知利用傅里叶变换的性质求图中和的傅里叶变换图题3-15解已知F3-21 已知三角脉冲信号如图题3-21 a 所示试利用有关性质求图题3-21 b 中的的傅里叶变换图题3-21解设F则F而FF3-23 利用傅里叶变换的微分与积分特性求图题3-23所示信号的傅里叶变换图题3-23解33-25 若已知利用傅里叶变换的性质求下列信号的傅里叶变换 2 4 5解2FF4F5FF3-29 根据附录B中给出的频谱公式粗略地估计图题3-29所示各脉冲的频带宽度图中时间单位为图题3 -29解a若时间单位为则频带为MHz即250KHzb若时间单位为则频带为MHz即250KHzd若时间单位为则频带为1 MHzf频若时间单位为则带为MHz即500KHz 3-32 周期矩形脉冲信号如图题3-32所示 1求的指数形式的傅里叶级数并画出频谱图 2求的傅里叶变换并画出频谱图图题3-32解 1指数形式的傅里叶级数为频谱图如下图所示图中2F频谱图为3-33 求下列函数的拉氏变换设1 46 8解14683-35 求下列函数的拉氏变换注意阶跃函数的跳变时间 1 2 3 解1233-39 求下列函数的单边拉普拉斯逆变换 3 4 7解3473-40 试利用拉氏变换的时域卷积定理求下列拉氏变换的原函数1解所以3-43 分别求下列函数的逆变换之初值和终值 1 3 解13第4章习题答案4-2 已知系统微分方程相应的齐次方程为 1试求两系统的零输入响应并粗略画出波形解124-3 给定系统微分方程起始状态及激励信号分别如下试判断系统在起始点是否发生跳变并据此写出的值123解 1因为方程在t 0时存在冲激作用则起始点会发生跳变设得a 32因为方程在t 0时存在冲激作用则起始点会发生跳变设得a 053因为方程在t 0时存在冲激和冲激偶作用则起始点会发生跳变设4-4 给定系统微分方程为若激励信号与起始状态为以下二种情况时分别求它们的全响应并指出其零输入响应零状态响应自由响应和强迫响应各分量应注意在起始点是否发生跳变12解1齐次解特解完全解因为方程在t 0时存在冲激作用则起始点会发生跳变设得a 1则完全解设零输入响应为则自由响应强迫响应152微分方程右边为原方程为由上述微分方程可知t 0后方程右边没有输入因此系统没有强迫响应完全响应和自由响应相同零输入和零状态响应的形式均为齐次解形式且零输入响应同1为零状态响应的形式为设得a 1则4-6 一线性时不变系统在相同的起始状态下当输入为时全响应为当输入为2时全响应为求输入为4时的全响应解系统的零状态响应为当输入为4x t 时系统的全响应为4-7 系统的微分方程由下列各式描述分别求系统的冲激响应与阶跃响应1解1首先求阶跃响应原方程变为方程右边没有冲激作用则起始点不会发生跳变特征方程齐次解特解B,05则代入初始值系统的阶跃响应为系统的冲激响应为4-12 一线性时不变系统当激励信号为时全响应为当激励信号为时全响应为求系统的冲激响应两种激励下起始状态相同解式 1 –式 2 得上式求导设代入上式方程两边函数相等4-13 试求下列各函数与的卷积13解134-14 对图题4-14所示的各组信号求二信号的卷积并绘出的波形解a4-15 已知分别求和画出和的波形并比较二者的区别解4-16 对图题4-16所示的各组信号求二信号的卷积并绘出的波形图题4-16 解d4-17 图题4-17所示系统是由几个子系统组合而成的各子系统的冲激响应分别为试求总系统的冲激响应并画出的波形图题4-17解第5章习题答案5-1 图题5-1所示RC电路中当t 0时开关S闭合求输出信号输入信号分别为以下几种情况1 3 4图题5-1解1345-3 电路如图题5-3所示当t 0时电路元件无储能当t 0时开关闭合求电压的表达式并画出的波形图题5-3解电流源电流为5-6 系统的微分方程为初始状态为若激励为1试用拉氏变换分析法求全响应2分别求零输入响应和零状态响应然后叠加得全响应解5-7 电路如图题5-7所示已知当t 0时开关S打开电路已达稳态设当t 0时开关S闭合求时的和图题5-7解5-10 当F s 的一阶极点落于图题5-10所示s平面中各方框所处位置时画出对应的f t 的波形填入方框中图中给出了示例此例极点实部为正波形是增长振荡解画图5-12 求图题5-12所示各网络的电压转移函数在s平面画出其零极点分布若激励信号为冲激函数 t 求响应并画出波形图题5-12解 ac5-14 写出图题5-14所示各梯形网络的电压转移函数在s平面示出其零极点分布图题5-14解 ab零极点图与a相同略d零点为0 4阶极点为5-15 已知策动点阻抗函数分别为下列各式试画出对应的电路图 1 2 34 5 6解即电路中电流源作为激励信号而电路中的电压作为响应信号 1 2 3 4 5 6 5-19 已知系统的阶跃响应为为使其零状态响应为求激励信号解5-20 某系统的起始状态一定已知输入时全响应为输入时全响应为试求输入时的全响应解5-24 如图题5-24所示电路已知激励信号为求响应并指出响应中的强迫分量自由分量暂态分量与稳态分量各分量题图5-24解所以响应为是自由响应是强迫响应是暂态响应稳态响应为05-29 给定的零极点分布如图题5-29所示令s沿j 轴移动由矢量因子之变化分析频响特性粗略绘出幅频与相频特性曲线解abcdef5-30 若的零极点如图题5-30所示试讨论它们分别是哪种滤波网络低通高通带通带阻并绘出各自的幅频特性曲线解abcdefgh5-35 图题5-35所示格形网络写出电压转移函数设在s平面画出H s 零极点分布图指出是否为全通网络在网络参数满足什么条件下才能构成全通网络题图5-35解极点为零点为当网络参数满足时系统为全通系统5-37 求图题5-37所示各流图的增益图题5-37解b5-38 试绘出下列微分方程描述的系统直接形式的模拟框图或信号流图2解25-39 用级联形式和并联形式模拟上题的系统并画出方框图解2和系统的级联形式的方框图为系统的并联形式的方框图为或用各自的信号流图表示为级联并联5-41 图题5-41所示反馈电路中是受控源 1求电压转移函数 2k满足什么条件时系统稳定图题5-41解1而所以2要使系统稳定对于二阶系统只要分母多项式各次系数非负即k 3第6章习题答案6-1 已知现用的时间间隔对其进行理想采样 1画出的波形图 2求并画出频谱图解12FF6-2 已知三角脉冲信号的频谱见附录B求图题6-2中各脉冲被冲激采样后信号的频谱并大致画出频谱图采样间隔图题6-2解ab6-3 确定下列信号的奈奎斯特采样率与奈奎斯特间隔 1 2 3 4解1F所以的最高角频率为这样奈奎斯特取样率为或奈奎斯特间隔2由于信号自乘频带展宽一倍3与叠加最高频率同4 由于的最高角频率为而的最高角频率展宽一倍即又的最高角频率为所以的最高角频率为这样6-4 已知某系统如图题6-4所示输入信号理想低通滤波器的频响特性为 1求并画出频谱图2画出的频谱图3求输出的表达式解123根据F以及F可得6-5 已知带限信号的频谱函数如图题6-5 a 所示试画出当通过图题6-5 b 所示系统时在系统中ABCD各点信号的频谱图图题6-5 b 中两个理想滤波器的频响特性分别为图题6-5解6-6 对于图64-6所示的抑制载波调幅信号的频谱由于的偶对称性使在和左右对称利用此特点可以只发送如图题6-6所示的信号的频谱称为单边带信号以节省频带试证明在接收端用同步解调的方法可以恢复原信号证明同步解调就是使单边带信号在时域上乘以在频域上则是与卷积幅度上乘以卷积结果如下图所示从此图可以看到卷积结果得到了原信号和一载频为的单边带信号再利用一低通滤波器滤除载频为的单边带信号后就得到了原信号6-12 电路如图题6-12所示写出系统频率响应特性为得到无失真传输元件参数应满足什么关系图题6-12解由电路图得可见为了得到无失真传输应有也即这样所以满足无失真传输的条件6-14 一个理想低通滤波器的网络函数为其幅频特性与相频特性如图题6-14所示试证明此滤波器对于和的响应是相同的图题6-14证明设则因为式中所以因此故两者响应一样即F6-18 图题6-18所示系统中为理想低通特性即 1若为单位阶跃信号写出的表达式2若写出的表达式解1由图知直接加在滤波器上的信号是因为而理想低通滤波器的阶跃响应为所以响应为2若则因此的频带范围限制在内最高频率又的截止频率故对是无失真传输从而有第7章习题答案7-1 分别绘出下列各序列的图形1 2 3 4解7-2 分别绘出下列各序列的图形1 2 3 4解7-3 分别绘出下列各序列的图形1 2解7-5 序列x[n]如图题7-5所示把x[n]表示为 [n]的加权与延迟之线性组合图题7-5解7-7 求下列序列的z变换X z 并注明收敛域绘出X z 的零极点图1u[n] [n] 4 u[n] u[n8] 5 [n] [n2]解7-8 求双边序列的变换标明收敛域及绘出零极点图7-11 画出X z 的零极点图三种收敛域下哪种情况对应左边序列哪种情况对应右边序列哪种情况对应双边序列并求各对应序列2 2 05 305 2解1 当时为右边序列2 当时为左边序列3 当时为双边序列7-13 已知X z1确定与X z 有关的收敛域可能有几种情况画出各自的收敛域图2求以上各种收敛域3以上序列中哪一种存在傅氏变换1收敛域可能有三种情况2对应的序列分别为3序列的收敛域包括单位圆所以此序列存在傅氏变换7-14 已知X z 若收敛域分别为1 2和2 3两种情况求对应的逆变换7-21 利用卷积定理求y[n] x[n] h[n]已知3x[n] RN[n] u[n] u[nN]h[n] anu[n]0 a 1解3根据卷积定理得由于均为因果序列因此亦为因果序列根据移位性质可求得7-24 计算下列序列的傅里叶变换n] 3 [42n] 解第8章习题答案8-2 列出图题8-2所示系统的差分方程指出其阶次图题8-2解二阶8-3 列出图题8-3所示系统的差分方程已知边界条件y[1] 0分别求以下输入序列时的输出y[n]并绘出其图形用逐次迭代方法求1 2 图题8-3 解1 28-7 求解下列差分方程的完全解1 2解1方程齐次解为特解为代入原方程完全响应为代入得2方程齐次解为特解为代入原方程完全响应为代入得8-12 用单边变换解下列差分方程y[n] 01y[n1] 002y[n2] 10u[n]y[1] 4y[2] 62y[n] 09y[n1] 005 u[n]y[1] 1 3y[n] 2y[n1] n2 u[n]y[0] 1解 2差分方程两边同时进行z变换3由差分方程得差分方程两边同时进行z变换8-13 若描述某线性时不变系统的差分方程为y[n] y[n 1] 2y[n 2]x[n] 2x[n 2]已知y[1] 2y[2] 12x[n] u[n]求系统的零输入响应和零状态响应解差分方程两边同时进行Z变换8-16 对于差分方程yy[n 1] x[n]所表示的离散系统1求系统函数H z 及单位样值响应h并说明系统的稳定性2若系统起始状态为零 10 u[n]求系统的响应y系统的收敛域不包括单位圆所以不稳定8-19 因果系统的系统函数H z 如下试说明这些系统是否稳定1 2 3 4解1收敛域为包括单位圆所以稳定2收敛域为不包括单位圆所以不稳定3收敛域为不包括单位圆所以不稳定4收敛域为不包括单位圆所以不稳定8-20 已知系统函数H z 分别在 10及05 10两种收敛域情况下系统的单位样值响应并说明系统的稳定性与因果性系统是因果不稳定的系统是非因果稳定的8-21 建立图题8-21所示各系统的差分方程并求单位样值响应h[n] 图题8-21解ab8-23 如下各序列中x[n]是系统的激励序列h[n]是线性时不变系统的单位样值响应分别求出各响应y[n]画出y[n]的图形用卷积方法1x[n] h[n]如图题8-23 a 所示 2x[n] h[n]如图题8-23 b 所示 3且图题8-23解1238-24 已知线性时不变系统的单位样值响应h[n]和输入x[n]分别如下所示求输出序列y[n]并绘出y[n]的图形1 3解138-25 图题8-25所示的系统包括两个级联的线性时不变系统它们的单位样值响应分别为h1[n]和h2[n]已知令1按下式求y[n]y[n] x[n] h1[n] h2[n] 2按下式求y[n]y[n] x[n] h1[n] h2[n] 注以上两种方法的结果应该相同卷积结合律解128-27 用计算机对测量的随机数据进行平均处理当收到一个测量数据后计算机就把这一次输入数据与前三次输入数据进行平均试求这一运算过程的频率响应则本次与前三次数据的平均值为对上式进行z变换得8-28 利z平面零极点作图法画出下列系统函数所对应系统的幅1H z 2H z 3H z解 1238-29 已知横向数字滤波器的结构如图题示试以M 8为例写出差分方2求系统函数H z 3求单位样值响应h4画出H z 的零极点图5粗略画出系统的幅频特性图题8-29解7阶为保证系统稳定设 1则零极点图如下8-36 由下列差分方程画出离散系统的结构图求系统函数H z 及单位样值响应hy[n] 6y[n 1] x [n] 2y[n] x[n] 5x[n 1]8x[n 2]3y[n] 3y[n 1] 3y[n 2] y[n 3] x [n]4y[n] 5y[n 1] 6y[n 2] x [n] 3x[n 2]解8-37 已知某离散系统的系统函数为H z m为常数1写出对应的差分方程 2画出该系统的结构图3求系统的频率响应特性并画出m 0 05 1三种情况下系统的幅频特性与相频特性曲线28-38 画出系统函数H z 所表示的系统的级联和并联形式结构图 2并联形式第9章习题答案9-1 建立图题9-1所示电路的状态方程图题9-1解b9-2 建立图题-2所示电路的状态方程若指定输出为 R2上的电压图题9-2 解b9-4 将图题-4 a 所示系统画成流图形式并列写系统的状态方程和输出方程9-4解a9-5 系统为如图题9-5所示的方框图试列写状态方程和输出方程图题9-5 解9-7 给定系统的状态方程和起始条件为求解该系统9-10 系统的状态方程和输出方程为且已知 1 0 1 2 0 1x t u t1求系统函数矩阵H s 2求输出y t 解9-12 一离散系统如图题-12所示1当输入x[n] [n]时求 1[n] 2[n]和h[n]2列系统的差分方程129-13 系统的状态方程和输出方程为已知1画出模拟框图和信号流图2求系统函数Hz 3求解1231tf1t 321tf2t 105tf3t 11π2π图题3-7tS t图题4-140 t 1 2 1t s 1 0 t 2 4 1 t s 2tS t 312ab4 3ab4 -1153-3-5tv2 t 0 jtv2 t 0jjajci tv t 1F 1Hi tv t 1 1Hi tv t 1F1Hi t v t 1 1Fi t v t 1 1H1Fi t v t 1 1HjH j 0jH j 0jH j1jH j1jH j1jH j1jH j 0低通滤波器jH j 0带通滤波器jH j 0高通滤波器jH j 0带通滤波器带通滤波器jj 0j 0H j 0带阻滤波器jj 1j 1 j 2j 2H j 02高通滤波器jj 0j 0H j 0带阻滤波器jj 1j 1 j 2 j 2H j21s 1 s 1 3s 1322XsYs1s 1 s 1 s 1 32XsYs321s 1 s 12s 1112XsYs1s 1 s 1111s 12Xs2Yss 1 s 1 s 1112XsYs2s 1 s 111s 12XsYs21t图题6-4 图题6-6 02 0 2 0 m2 0 m 2 0F1 j 图题6-18 12Re zjIm z 14Re zjIm z 1272Re z jIm z jIm z 122Re z 2z 2Re z jIm z 12z 12Re z jIm z 12 z 2 jIm z Re z 图题8-25 Re z jIm z 0051ωωH ejω 223Re z jIm z051ω223ωH ejω 0ω-05 01Re z jIm z H ejω ω320571Re z jIm z x [n] 213y [n] -58x [n] y[n] x[n] y [n] 3 -3x[n] y[n] -35-6mx[n] y[n] ω 1ωφ ωa 0223π2πω13ππ6-π6 π2πωφ ωb 05π2πωωφ ω π2ππ2-π2 0c 3-5102-5x[n] y[n] 2 x[n] y[n] 2 -5图题9-12。
信号与系统张晔版第三章ppt

Signals and Systems
Fourier是法国大革命时期的数学家,他在频谱分析领域做有卓越的 贡献。
在当时,拿破仑时代,科学界流行一种哲学:世界是由“基元”组 成的,任何一种物质只是基元的加权代数和。基元是什么?
运动是物质的一种存在形态,也应该具有一种相同的特性,即运动
/
2
sin(n1t
)dt
T1 T1 /
2
sin(n1t
)dt
4
n
0
n为奇数 n为偶数
信号分解为:
f
(t)
4
sin
1t
1 3
sin
31t
1 5
sin
51t
n分别取1、3、5、7、9、…→
结论:项数越多(加入了高频信息), 近似误差越小,边沿更陡峭(边沿有丰富 高频信息)。
选多少项取决于应用要求!
哈尔滨工业大学图象与信息技术研究所
Signals and Systems
3.1.1 三角形式的傅立叶级数
分解线性组合形式:
f
(t)
a0 2
[an
n1
cos(n1t) bn
sin(n1t)]
下面转到如何计算傅立叶级数的系数?
a0
2 T1
t0 T1 f (t)dt
t0
2
an T1
t0 T1 t0
想象脉宽趋于零? 哈尔滨工业大学图象与信息技术研究所
Signals and Systems
3.2.2 周期锯齿脉冲信号
因为是奇函数,可求得: a0 0
an 0
(1)n1 E bn n
哈工大移动通信课后作业答案

第一章1.答:所谓单工通信是指双方电台交替地进行收信和发信。
单工通信常用于点到点通信,待机时,单工制工作方式双方设备的接收机均处于接听状态,其中A方需要通话时,先按下“按—讲”开关,关闭接收机,由B方接收;B方发话时也将按下“按—讲”开关,关闭接收机,由A方接收,从而实现双向通信。
这种工作方式收发信机可以使用同一副天线,而不需要天线共用器,设备简单,功耗小,但操作不方便。
在使用过程中,往往会出现通话断续现象。
双工通信是指通信双方,收发信机均同时工作,即任一方讲话时,都可以听到对方的语音,没有“按—讲”开关,双方通话像室内电话通话一样。
但是采用这种方式,在使用过程中,不管是否发话,发射机总是工作的,故电能消耗大。
2.答:蜂窝网使用两种双工制式,频分双工(FDD)和时分双工(TDD)。
FDD利用两个不同的频率来区分收发信道。
即对于发送和接收两种信号,采用不同频率进行传输。
TDD利用同一频率但不同的时间段来区分收发信道。
即对于发送和接收两种信号,采用不同的时间(时隙)进行传输。
TDD双工方式的工作特点使TDD具有如下优势:能够灵活配置频率,使用FDD系统不易使用的零散频段;可以通过调整上下行的时隙转换点,提高下行的时隙比例,能够很好地支持非对称业务;具有上下行信道一致性,基站的接收和发送可以共用射频单元,降低了设备成本;接受上下行数据时,不要需要收发隔离器,只需要一个开关即可,降低了设备的复杂度;具有上下行信道互惠性,能够更好地采用传输预处理技术,能有效地降低移动终端的处理复杂性。
但是,TDD双工方式相较于FDD,也存在明显的不足:快衰落对TDD系统具有更大的影响,TDD支持用户的移动速率不高,通常只能达到FDD移动台的一半甚至更低;TDD系统收发信道同频,无法借助频率选择性进行干扰隔离,系统内和系统间存在干扰;需要更复杂的网络规划和优化技术。
3.答:20世纪70年代中期,随着民用移动通信用户数量的增加,业务范围的扩大,有限的频谱供给与可用信道数要求递增之间的矛盾日益尖锐。
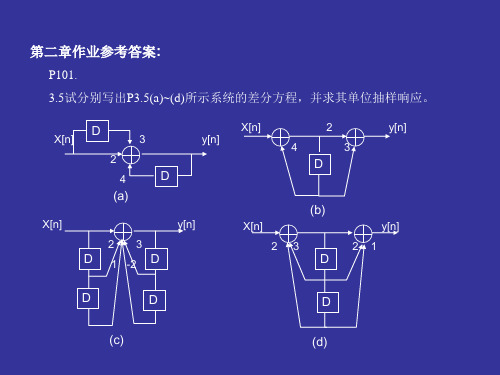
北理工-信号与系统-第三版-第三章-作业参考答案
k
| u[k ] | ,有界
是非稳定系统
(e) 显然n<0时,h[n]=0,所以是因果系统;
k
| h[k ] | | u[k ] / n | ,无界
k
是非稳定系统
(f) 显然n<0时,h[n]=0,所以是因果系统;
| h[k ] |
(d)
y[n] x[n] h[n]
k
[k n ] [n k n ]
1 2
[n n1 n2 ]
3.11在LTI离散时间系统中 已知x[n]=u[n]时的零状态响应(单位阶跃响应)为s[n],求单位抽样响应h[n]; 已知h[n],求s[n].
y[n] - 4y[n-1] =2x[n]+3x[n-1];
令x[n]=δ[n],则有 h[n] – 4h[n-1] =2 δ[n]+3 δ[n-1];当n<0时,h[n]=0,得h[0]=2,h[1]=11,
特征方程为 λ-4=0, 得λ=4,
h[n]=c(4)nu[n],由h[1]=4c=11,c=11/4得 h[n]=(11/4)(4)nu[n-1]=11 (4)n-1u[n-1],考虑h[0]=2=2 δ[n],得 h[n]=2 δ[n]+11 (4)n-1u[n-1]。(n>0的解) (b).据图有同(a)一样的结果…。 (c).据图 y[n]=3y[n-1]- 2y[n-2]+ x[n]+2x[n-1]+x[n-2] ,即差分方程为 y[n] -3y[n-1]+2y[n-2] = x[n]+2x[n-1]+x[n-2], 先求
信号与系统课后习题与解答第三章
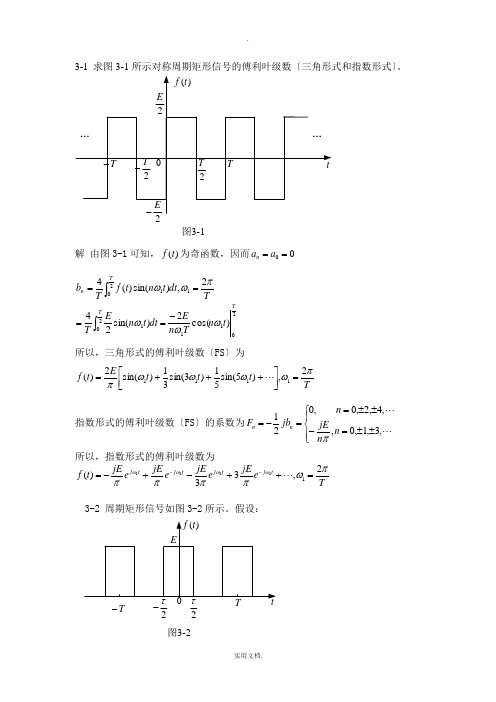
3-1 求图3-1所示对称周期矩形信号的傅利叶级数〔三角形式和指数形式〕。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数〔FS 〕为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数〔FS 〕的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
假设:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数〔FS 〕的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n那么的指数形式的傅利叶级数〔FS 〕为∑∑∞-∞=∞-∞=⎪⎭⎫⎝⎛==n tjn n tjn ne n Sa TE eF t f 112)(1ωωτωτ 其直流分量为T E n Sa T E F n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω 将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 假设周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:〔1〕)(1t f 的谱线间隔和带宽〔第一零点位置〕,频率单位以kHz 表示; 〔2〕)(2t f 的谱线间隔和带宽; 〔3〕)(1t f 与)(2t f 的基波幅度之比; 〔4〕)(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统第三章习题答案

=2 T
T +t0 t0
f
t
cos nω0tdt
∫ ( ) bn
=
2 T
T+t0 t0
f
t
sin
nω0 tdt
n = 1,2,L n = 1,2,L
信号指数型为:
∞
∑ ( ) f t =
F e jnω0t n
n= −∞
Fn = Fn e jϕ n
96
∫ ( ) Fn
=
1 T
f t0 +T
+L
∑ =
a0 2
+
∞
(an
n=1
cos nω 0t
+ bn
sin
nω 0t)
式中 a0 , an , bn 称为傅里叶系数,分别代表了信号 f (t ) 的直流分量,余弦分量和正经弦分量的振荡幅度,
其值分别由下式确定:
∫ ( ) a0
=
2 T
f T + t0
t0
t dt
∫ ( ) an
4 T
π
2 cos t cos ntdt
0
=
2 T
π
∫2
0
[cos(n
+ 1)t
+
cos(n
− 1)t ]dt
( ) =
2 T
n
1 +
1
sin
π
2(n +
1)
+
1 sin n −1
π
2(n −
1)
=
−
n2
2 −1π
cos
nπ 2
该信号的三角傅里叶级数为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
fltnzlults
因为是
bniif.c EJ.siunwndttjErsincnwtsdt
品
奇
这是咋求的
求锯⻮信号
ftkocnejnmtcniiffme
则⼴哻f
则fits品蕊ei哔世这是利⽤指数表示
求三⻆函数形式下的⽐⼆ffctldt.FI ff aniiffmcoscnwtgdtiifl ttEjcoscnwtydttf
奇㷒依然为奇则为0⼆if Ewscnwtdt
2
元ㄨ103kHz 6.128X 2X
106t
1间隔ME
巺⼆
㗟s
不
4112X1066.28106带
亮13乺烈烈6
nfzxi
14三
次诮波11
批
t 10⽐红__
2.12Et E 4
i 1
l
Cni
Èf
fme atdt
fcne atdttffze.at dt
其中a
in
⼆
弦
表
ǏF
试⻦扣与fun的傅⽴叶变换Fifn Film
fit Alum ut沙井控ult.int坷
同样将fun表示⼀下⼆是cult ultt t Al ul ti Ultt
则Fl funk Ftw ejwto
詏
们对于la 来说原因为三⻆以及余弦之积
inn
则n 01wtionjtoiw zuScilE 2对于⼼来说
原⼆Sin 5元
右侧的相当于则
Sachi ii nl ócw 5元-01W 5到vi
vre
怎么看
出来的h
t
利⽤时域积分把原函
看成积分原⽐⽐出⼀吐动de
no 个
吢
砟⼼ólug
201W e iwi name
Íjm
jw
⼆⽆以costing tisinihg
znwilosciugtisin int
器
nom
aunt jw
求的傅⾥叶变换
利⽤傅⾥叶变换的定义式求
FlwkfofneiTltftl
tgeiwtdt.tt
cu.int Fxi Ei
j w W2
t恐器加⼀兜
圜篮圝噬部
⼆品ceiwte Mtice2N.ie可以应leine
全部转化为⼼sin之形成三吉xzcoswth.zwszwtfw.zsinz.ru
为了求得⽴叶级则要利⽤原tniiFocwilninw.F4
从⽽cnet.to cnn.in代⼊上式中
则代⼊到了覃⽴叶级数的公式中funÍcneimt
⼀
H
求⼼的傅⾥叶交换则Rcntawhn HIM⼆舙⽅站1jhntl 然后求输⼊信号的得主叶交换
在⼀个周期内P fltsejwtdt in哭⼏
⼆T T teiwtdt
iwlteiwt jeiwtsi
Eiji
M
n D 求
fun
的傅⽴叶级数90i hits dtf.li
灬
i
1
第⼀次分布积分⼜弄错
了duty
卡twsnwitdt ijtwscnw ndt lnwdwscnwnliw.co scnwtsi ǜǐ⼆声n.dz cost 哔_sinc 哔⼆
前
2
11
叮
n
华
⼆则no 时
IAN
则An 有加上
n 为偶iq ⼥终900
则
⼈品
㹷
n 为
奇
彘
流i
iwiwiwj.ws
对fun 进⾏傉⽴叶
交他fun
为奇函数
外
an sc.no
求dni ǐ
Ǖ
sincnwmdt.lu 笇
d n ⾔Ǖs in
2
巺七d t ⾔ǜ
则所
求即为flat fun 不⽤合求i
i
i n
t
1
11
11
1
1
i
i
n
n
n
n
i
i
i
i。
