单元2资金等值计算
第二章第二节资金的等值计算13春

(2)利率
• 概念
简称利率,是一定时期内(一年、半年、 月、季度,即一个计息周期)利息总额与本金 (借贷金额)的比率 。 利率=期利息(I1) *100% 本金(P) 利率是单位本金经过一个计息周期后的增殖额。 (年利率、半年利率、月利率,……)
利息的计算-单利/复利
引入: 现在存入100元,存期3年,每年计息 一次,年利率10%,计算第1年、第2年的 利息。 第一年的利息=100×10%=10 第二年的利息= 已产生的利息 10元是否计息
20 18 16 14 12 10 8 6 4 2 0 0 5 10 15 20 25 30 年数
单利 复利
本利和
6.名义利率和实际利率
(1)名义利率(Nominal Interest Rate) 问题提出 在技术经济分析中,复利计算通常以年为计息 周期。但在实际经济活动中,计息周期有年、半 年、季、月等多种,这样出现了不同计息周期的 利率换算问题。 如:按月计算利息,且其月利率为1%,通常 称为“年利率12%,每月计息一次”。这个年利率 12%称为“名义利率”。
名义年利率:一年的利息额是按单利计算的;
实际年利率:一年的利息额是按复利计算的;
当一年中多次计息时(即m>1时),两者产生差异;
二、资金等值
资金的时间价值引发的问题:
2000
0 1 2 3 4 5
3000
5000
-不能直接比较不同时间点的资金的价值大小。 -需要利用等值换算,将不同时点的资金换算到同 一时点进行比较。
r m i lim (1 ) 1 m m r e 1
若名义年利率为12%,以下各种情况下,实际 年利率等于多少?
按年计息,m=1 按半年计息,m=2 按季度计息,m=4
第2章 资金等值计算

例 2-2 下面是 A、B 两方案的现金流量图。在其它条件都相
8
同,不考虑通货膨胀和风险因素的情况下,哪个方案较优?(单 位:万元)
8
6 4 2 0 1 2 3 4 0 1 2 3 4 2 4 6
8
12
A 方案
12
B 方案
图 2—2
A、 B 两方案的现金流量图
请思考:(1)不同时点上(第 1 和第 4 年)相同数额的资金(8)在价值上是 否相等? (2)一笔资金的价值,除了与其数额有关,是否还与其他因素有关? (3)发生在不同时点上的资金能否直接相加减?
1.资金等值计算——即利用资金等值的概念,把在一个时点 上发生的资金换算成另一时点上的等值金额的过程。
2.资金等值的影响要素
在不考虑通货膨胀和风险影响的情况下,资金等值的 影响要素是:
(1)资金金额
(2)资金发生的时间 (3)利率(折现率,在这种情况下,利率可以被看作是资金的增殖率)
.
F
3.几个关键术语
F3=13310(元);F4=14641(元);F5=16105(元)
∴在复利利率为10%的情况下,我存入银行的10000元
与5 笔发生在不同时点上的资金等值。
请思考:在10%的复利利率下,为了获得16105元钱, (1)我在5年前应存入多少钱呢? (2)我在4年前应存入多少钱呢
该10000元还可以与:
胀货币贬值所造成损失的补偿。 (3)风险因素的影响,即资金的时间价值中,还包含着因冒一定风险 而投资,所获得的高于平均利润的额外利润,即风险价值。
资金时间价值(或增殖率)的大小是较难恰当地估计的。
但是资金时间价值的计算方法与银行复利计算方法是相同的。
02资金等值计算

资金等值计算/2.1资金时间价值 第2章 资金等值计算/2.1资金时间价值
例题: 例题: 今借款1000元,年名义利率是 %,每月计息一 %,每月计息一 今借款 元 年名义利率是12%, 则一年后应还多少本利和? 次,则一年后应还多少本利和? 解1: i = ( 1+ r/ m ) m - 1=(1+12% / 12)12-1 :
本利和 (元)
偿还额 (元)
1080
0
1166.40 0
1166.40*8%=93.31 1259.71 0 2 1259.71*8%=100.7 1360.49 1360.49 77
资金等值计算/2.1资金时间价值 第2章 资金等值计算/2.1资金时间价值 2.1.6 周期利率、名义利率与实际利率 周期利率、
资金等值计算/2.1资金时间价值 第2章 资金等值计算/2.1资金时间价值 2.1.5 利息的计算方法
• 计息周期:计算利息的时间单位 。计息周期通常有年、半年、季、月、周和日 计息周期: 计息周期通常有年、半年、
等,相应的利率有年利率、半年利率、季利率、月利率、周利率和日利率等。 相应的利率有年利率、半年利率、季利率、月利率、周利率和日利率等。 •单利法:在各计息周期内,只用本金生息,利息不生息的计息方式,即“利不 单利法:在各计息周期内,只用本金生息,利息不生息的计息方式, 单利法 生利”。 生利” F = P ( 1+ n · i ) 元存入银行, 例:将100元存入银行,利率假设为 元存入银行 利率假设为10%,一年后、两年后、三年后的终值是多 ,一年后、两年后、 少?(单利计算) ?(单利计算) 单利计算 一年后: )=110(元) 一年后:100×(1+10%)= × )= ( 两年后: )=120(元) 两年后:100×(1+10%×2)= × × )= ( 三年后: )=130(元) 三年后:100×(1+10%×3)= × × )= (
第二章资金等值基本计算公式

解:A =F(A/F,i ,n)
=100 × (A/F,10% ,35) = 100 × 0.00369=0.369(万元)
3、等额支付现值(分期等付现值)公式
问题:工程项目经济评价中,常需要求一系列等额资金的年效益或年费
用的现值,属于折现法的一种。 即已知A,求P
P 1 2
i
n A
(1 i ) 1 P A n i (1 i )
0 A 1 A 2 A 3 A n-1 A n
F = ?
(1 i )n -1 FA i
F=A (F/A,i ,n)
等额支付终值因子
复利计算公式—等额多次支付公式 等额支付终值公式
例题: 某人每年年末存入银行1万元。 存款利率3%(复利),10年后的 本利和为多少 ?
复利计算公式—等额多次支付公式
P=F/(1+i)
0
1
2
n-1
n
=F(P/F,i,n)
一次支付现值因子
back
复利计算公式—一次支付公式 2、一次支付现值公式
例题:
某人希望10年后有50万元买房子。
按6%的年利率,他现在应该存入银行
多少钱?(复利)
复利计算公式—一次支付公式 2、一次支付现值公式
步骤:1. 画现金流量图
p 6% 50万元
值)F。 资金流程图如图所示。其计算公式推导过程如下:
第一年年末偿付A,至第n年年末可得终值 0 1 2 A i F n
F1 A(1 i )
n 1
第二年年末偿付A,至第n年年末可得终值
F1 A(1 i) n2
第n-1年年末可得终值: Fn 1 A(1 i ) n ( n 1) A(1 i )
资金等值计算公式详解4篇

资金等值计算公式详解4篇以下是网友分享的关于资金等值计算公式详解的资料4篇,希望对您有所帮助,就爱阅读感谢您的支持。
篇13.资金等值计算公式在考虑资金时间价值的前提下,在一定的利率条件下,不同时点、不同金额的资金在价值上是等效的,称为资金等值。
资金等值概念的建立是工程经济方案比选的理论基础。
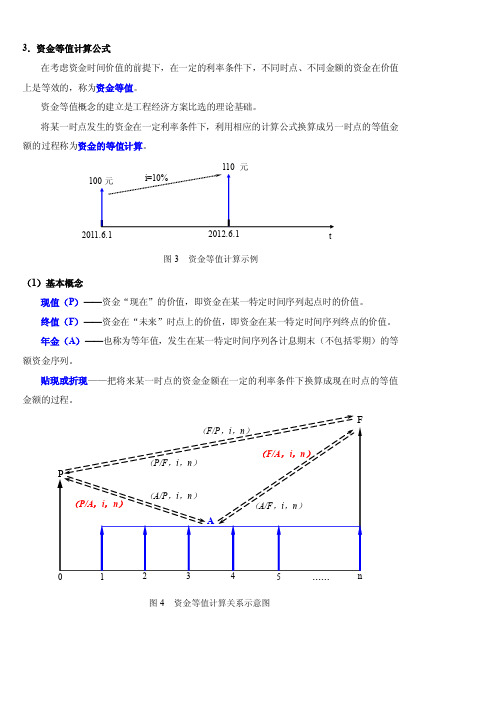
将某一时点发生的资金在一定利率条件下,利用相应的计算公式换算成另一时点的等值金额的过程称为资金的等值计算。
图3 资金等值计算示例t(1)基本概念现值(P )——资金“现在”的价值,即资金在某一特定时间序列起点时的价值。
终值(F )——资金在“未来”时点上的价值,即资金在某一特定时间序列终点的价值。
年金(A )——也称为等年值,发生在某一特定时间序列各计息期末(不包括零期)的等额资金序列。
贴现或折现——把将来某一时点的资金金额在一定的利率条件下换算成现在时点的等值金额的过程。
图4 资金等值计算关系示意图(2)资金等值基本计算公式篇2资金的价值等值计算公式如何应用A 年金, 发生在( 或折算为) 某一特定时间序列各计息期末(不包括零期) 的等额资金序列的价值。
1. 终值计算( 已知A, 求F)等额支付系列现金流量的终值为:[(1+i )n -1]/i年称为等额支付系列终值系数或年金终值系数, 用符号(F/A,i ,n) 表示。
公式又可写成:F=A(F/A,i ,n) 。
例:若10 年内,每年末存1000 元,年利率8%, 问10 年末本利和为多少?解: 由公式得:=1000×[(1+8%)10-1]/8%=144872. 偿债基金计算( 已知F, 求A)偿债基金计算式为:i/ [(1+i )n -1]称为等额支付系列偿债基金系数,用符号(A /F,i ,n) 表示。
则公式又可写成:A=F(A /F,i ,n)例:欲在 5 年终了时获得10000 元,若每年存款金额相等,年利率为10%, 则每年末需存款多少?解: 由公式(1Z101013-16) 得:=10000×10%/ [(1+10%)5-1]=1638 元3. 现值计算( 已知A, 求P)[(1+i )n -1]/i(1+i )n 称为等额支付系列现值系数或年金现值系数, 用符号(P/A,i ,n) 表示。
第二章 资金的时间价值与等值计算 第三节

A
A
A
…………
A
A
0 1
234源自n-1nt(年)P=?
等额支付现值计算现金流量图
思路:由一次支付终值公式及等额支付终值公 式进行推导。
等额支付现值因子或 等额支付现值系数
(P/A,i,n)
P=A(P/A,i,n)
2、计算例题 若己知某企业欲购买一台设备,每年收益 40万元,该设备可用15年,不计残值。折 现 率i=7%,试计算该设备各年收益的现值。
A=P×(A/P,i,n) =50×0.1168 =5.84(万元)
五、等差多次支付公式 (一)等差支付终值公式(已知G求F) 1.若每年年末向银行存款,存款额分别为:0、 G、2G、3G、…、(n-2)G、(n-1)G,存款 利率为i,求n年后的本利和F.
等差支付终值计算现金流量图
❖ 思路:利用F=P(1+i)n
思路:将各年末的A值按一次支付终值公式 , 折算到n年年末,然后求和 :
F=A(1+i)n-1+A(1+i)n+…+A(1+i)2+A(1+i)1+A =A〔(1+i)n-1+(1+i)n+…+(1+i)2+(1+i)1+1〕
等比数列求和公式 等额支付终值因子或 等额年金终值系数
(F/A,i,n)
几何(等比)序列现值计算现金流量图
1 = F ( P / F , i , n) ❖ 思路:利用一次支付现值公式 P = F n (1 + i)
(二)几何(等比)序列终值公式 现假定第一年末的费用为Q,则第二年末至 第n年末的费用分别为:Q(1+j),Q(1+j)2,…, Q(1+j)n-1 ,折现率为i,求终值F。
资金等值计算公式
3.资金等值计算公式在考虑资金时间价值的前提下,在一定的利率条件下,不同时点、不同金额的资金在价值上是等效的,称为资金等值。
资金等值概念的建立是工程经济方案比选的理论基础。
将某一时点发生的资金在一定利率条件下,利用相应的计算公式换算成另一时点的等值金额的过程称为资金的等值计算。
(1)基本概念现值(P )——资金“现在”的价值,即资金在某一特定时间序列起点时的价值。
终值(F )——资金在“未来”时点上的价值,即资金在某一特定时间序列终点的价值。
年金(A )——也称为等年值,发生在某一特定时间序列各计息期末(不包括零期)的等额资金序列。
贴现或折现——把将来某一时点的资金金额在一定的利率条件下换算成现在时点的等值金额的过程。
2011.6.1t图3 资金等值计算示例图4 资金等值计算关系示意图(2)资金等值基本计算公式文,wen,从玄从爻。
天地万物的信息产生出来的现象、纹路、轨迹,描绘出了阴阳二气在事物中的运行轨迹和原理。
故文即为符。
上古之时,符文一体。
古者伏羲氏之王天下也,始画八卦,造书契,以代结绳(爻)之政,由是文籍生焉。
--《尚书序》依类象形,故谓之文。
其后形声相益,即谓之字。
--《说文》序》仓颉造书,形立谓之文,声具谓之字。
--《古今通论》(1) 象形。
甲骨文此字象纹理纵横交错形。
"文"是汉字的一个部首。
本义:花纹;纹理。
(2) 同本义[figure;veins]文,英语念为:text、article等,从字面意思上就可以理解为文章、文字,与古今中外的各个文学著作中出现的各种文字字形密不可分。
古有甲骨文、金文、小篆等,今有宋体、楷体等,都在这一方面突出了"文"的重要性。
古今中外,人们对于"文"都有自己不同的认知,从大的方面来讲,它可以用于表示一个民族的文化历史,从小的方面来说它可用于用于表示单独的一个"文"字,可用于表示一段话,也可用于人物的姓氏。
第二章_资金等值计算本1总结

i=8%
0 1 2 3 9
10
8000
8000
8000
8000
8000
(1 i ) n 1 F A i
F=A×(F/A,i ,n)
= 8000×(F/A,8% ,10)
=8000 ×14.487 = 115892(元)
例2 某单位在大学设立奖学金,每年年 末存入银行2万元,若存款利率为3%。第5年 末可得款多少?
25 26 27 A=? 59
解:A =F×(A/F,i ,n) =100 × (A/F,10% ,59-25+1) = 100 × 0.00369=0.369(万元)
某厂欲积累一笔福利基金,用于3年后建 造职工俱乐部。此项投资总额为200万元,设 利率为5%,问每年末至少要等额存多少钱?
i A F n 1 i 1 F A / F ,5%,3 200 0.31721 63.442(万元)
200 1 4 400
200 2
200
300
3
时间
注意
第一年年末的时刻点同时也表示第二年年初
(三)一次支付(一次收付、整付、整收)
整付:分析期内,只有一次现金流量发生 现值P与将来值(终值)F之间的换算 现金流量模型: F
0 P
0 1 2
1
2
0 1
n
n- 1 n
2
n- 1 n
P(现值)
F(将来值)
F=500 i=12% 0 1 2 3 A=? 5
解:A =F×(A/F,i ,n) =500 × (A/F,12% ,5) = 500 × 0.15741=78.70(万元)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
投资的狭义概念是指为实 现某建设项目而预先垫付的资 金。对于一般的工业投资项目 来说,总投资包括建设投资和 生产经营所需要的资金、建设 期的借款利息。
工程经济学中的常用的投 资是投资的狭义概念。
2.1.2 现金流量图
2.现金流入:指一个系统内在某一时点上流入系 统的资金或货币量,如销售收入等。
资金的时间价值是商品经济中的普遍现象,资金 之所以具有时间价值,是基于以下两个原因:
l (1)从社会再生产的过程来讲,对于投资者或生 产者,其当前拥有的资金能够立即用于投资并在 将来获取利润,而将来才可取得的资金则无法用 于当前的投资,因此也就无法得到相应的收益。
l (2)从流通的角度来讲,对于消费者或出资者, 其拥有的资金一旦用于投资,就不能再用于消费 。消费的推迟是一种福利损失,资金的时间价值 体现了对牺牲现期消费的损失所应作出的必要补 偿。
【例】某人现借得本金2000元,1年后付息180元
【解】
年利率=180/2000×100%=9%。
利率的高低由如下因素决定:
①利率的高低首先取决于社会平均利润的高低, 并随之变动。
②在平均利润率不变的情况下,利率高低取决于 金融市场上的借款资本的供求情况。
③借出资本要承担一定的风险,而风险的大小也 影响利率的高低。
单元2资金等值计算
2014年中行利率
单元2资金等值计算
中国人民银行决定,自2015年3月1日起下调金融机构人民币贷款和存款基准利率。金融机 构一年期贷款基准利率下调0.25个百分点至5.35%;一年期存款基准利率下调0.25 个百分点至2.5%,同时结合推进利率市场化改革,将金融机构存款利率浮动区间 的上限由存款基准利率的1.2倍调整为1.3倍;其他各档次存贷款基准利率及个人 住房公积金存贷款利率相应调整。
3.净现金流量 = 现金流入 - 现金流出 4.现金流量:各个时点上实际的资金流出或资金 流入(现金流入、现金流出及净现金流量的统称 )
现金流入
现金流出
时间轴
二、现金流量图
l 所谓现金流量图,就是一种描述现金流量作为时间函数的 图形,即把项目经济系统的资金流量绘入一时间坐标图中 ,表示出各项资金流入、流出与相应的对应关系,它能表 示资金在不同时间点上流入与流出的情况。
单元2资金等值计算
2020/11/13
单元2资金等值计算
项目1 资金的时间价值概述
2.1.1.资金的时间价值的含义及意义 1.资金的时间价值的概念
不同时间发生的等额资金在价值上的差别,就称为资金的 时间价值。资金的价值随时间推移而变化。(1)通货膨胀 ;(2)承担风险;(3)货币增值:投资,储蓄。(社会 平均利润率) 2.资金具有时间价值的内涵 ➢资金在生产与交换过程中由于有劳动者的劳动使之产生 了增值 ➢资金的时间价值是对放弃现时消费的必要补偿。
➢风险
➢通货膨胀
资金的时间价值
l 货币的作用体现在流通中,货币作为社会生产资 金参与再生产的过程中即会得到增值、带来利润 。 我们常说的“时间就是金钱”,是指资金在生产 经营及其循环、周转过程中,随着时间的变化而 产生的增值。
1.资金时间价值的概念: 是指资金在生产和流通过程中随着时间推移而产 生的增值。
某银行的三个月定期存款利息是1.91%, 那么存100元三个月定期,到期的利息是 1.91元??。
单元2资金等值计算
(2)利率
利率就是在一个计息周期内所得利息额与本金之比, 一般以百分数(%)表示。 根据计息周期的不同,一 般有年利率、季利率、月利率等 利率=单位时间内所得的利息额/本金×100%
在市场经济的条件下,资金增值有两种主要方式:一种 是将现有资金存入银行,可以取得利息;一种是将现有 资金用于生产建设,可以取得利润。
单元2资金等值计算
(1)利息
在借贷过程中,债务人支付给债权人超过原借 贷款金额(原借贷款金额常称作本金)的部分, 就是利息
利息=目前应付(应收)的总金额-本金
本金 + 利息 = 本利和
④
⑤借出资本的期限长短对利率也有重大影响。
(3)利息和利率在技术经济活动中的作用
①影响社会投资的多少。 ②影响社会资金的供给量。 ③利率是调节经济政策的工具。
我国银行存款利率的变化
(1)一年定期存款利率变化 (2)所有存款方案利率变化
单元2资金等值计算
2014年
2014年
单元2资金等值计算
2014年各大银行利率
资金时间价值在经济计算中的作用
考察一笔资金的价值时
数量? 时间?
考虑资金时间价值 ???
静态的 计算方法
动态的 计算方法
单元2资金等值计算
2.资金时间价值的计算方法
l 衡量资金时间价值的尺度有两种: l 其一为绝对尺度,即利息、盈利或收益; l 其二为相对尺度,即利率、盈利率或收益率。
资金时间价值的表现形式
P + I = Fn
从本质上看,利息是由贷款产生的利润的一种再分 配。 在工程经济学中,利息是指占用资金所付出的代 价或者是放弃现期消费所得的补偿。
存款利息=存款本金×存款利率×存款期限 根据存款期限的不同,存款利息也有年息 、月息和日息之分。应当注意,一般银行 公布的存款利率都是年利率的,存款利息 不是简单的本金乘以利率,还要结合存款 期限。
l 现金流量图包括三大要素:大小、流向、时间点。 l 其中: l 大小表示资金数额, l 流向指项目的现金流入或流出,
2.2.1 资金的时间价值
资金的时间价值存在的条件有两个: 一是将货币投入生产或流通领域,使货币转化为资金, 从而产生的增值(称为利润或收益); 二是货币借贷关系的存在,货币的所有权及使用权的分 离。比如把资金存入银行或向银行借贷所得到或付出的 增值额(称为利息)。
3.影响资金使用的因素
➢投资收益率
单元2资金等值计算
2.1.2 现金流量图
一、基本概念
1.现金流出:指一个系统内在某一时点上流出系统 的资金或货币量,如投资、费用等。
投资的广义概念是指有目的的经济行 为,泛指企业的一切资金分配与运用行为, 是企业为了获取所期望的报酬而投入某项 计划的资源,所投入的资源包括资金,也包 括人力、技术或信息等其它资源。
