江苏省无锡市滨湖区中学八年级数学上册《44近似数》教学案
苏科版数学八年级上册教学设计《4-4近似数》

苏科版数学八年级上册教学设计《4-4近似数》一. 教材分析《4-4近似数》这一节内容是苏科版数学八年级上册的教学内容,主要让学生了解和掌握近似数的概念、求法以及应用。
通过这一节的学习,学生能够理解近似数在实际生活中的意义,提高他们解决实际问题的能力。
二. 学情分析学生在学习这一节内容之前,已经掌握了实数、分数和小数等基础知识,具备了一定的逻辑思维能力。
但对于近似数的概念和求法可能还比较陌生,需要通过实例和练习来逐步理解和掌握。
三. 教学目标1.让学生了解近似数的概念,理解近似数在实际生活中的意义。
2.让学生掌握近似数的求法,能够运用近似数解决实际问题。
3.培养学生的逻辑思维能力和合作交流能力。
四. 教学重难点1.近似数的概念和求法。
2.近似数在实际生活中的应用。
五. 教学方法采用问题驱动法、实例教学法和合作交流法,通过引导学生思考、讨论和操作,让学生在实践中掌握近似数的概念和求法。
六. 教学准备1.准备相关的实例和练习题。
2.准备多媒体教学设备,如投影仪、电脑等。
七. 教学过程1.导入(5分钟)通过生活中的实例,如称重、测量身高等,引导学生思考近似数的概念和作用。
让学生意识到近似数在实际生活中的重要性。
2.呈现(15分钟)呈现近似数的定义和求法,通过讲解和示例,让学生理解和掌握近似数的概念。
同时,引导学生思考如何运用近似数解决实际问题。
3.操练(10分钟)让学生分组进行练习,运用近似数解决实际问题。
教师巡回指导,解答学生的疑问,并给予反馈。
4.巩固(5分钟)选取一些典型的练习题,让学生独立完成,巩固对近似数的理解和掌握。
教师及时给予解答和反馈。
5.拓展(10分钟)引导学生思考近似数在科学研究和工程应用中的作用,如天气预报、建筑设计等。
让学生了解近似数在其他领域的应用。
6.小结(5分钟)对本节课的内容进行总结,强调近似数的概念和求法,以及近似数在实际生活中的意义。
7.家庭作业(5分钟)布置相关的练习题,让学生巩固所学内容。
苏科版数学八年级上册4.4 近似数 学案

八年级数学—§4.4近似数学案姓名班级等第1、预习书本第107-108页,掌握近似数概念,按精确度的要求用四舍五入法取近似数,正确说出一个近似数的精确度2、预习检测:(1)八年级(1)班有50名学生;(2)小明测得数学课本的长21cm(3)今天的气温是25℃;(4)中国的国土面积为960万平方公里。
以上4个数据中,中的数据为准确数,中的数据为近似数。
例1、下列各数,哪些是近似数?哪些是准确数?2000年第五次人口普查表明,我国大约有13亿人口;绿化队今年植树约2万棵;小明到书店买了10本书;一次数学测验中,有2人得了100分;某区在校中学生近75万人;1米等于100厘米;小明称得体重为38千克;现在的气温是-2℃例2、用四舍五入法,按括号的要求取近似值0.85419(精确到千分位) 87.6(精确到个位)54810(精确到千位) 4.27×105(精确到万位)3、课堂练习:1、下面给出的四个数据中是近似数的有()①张明的身高是160.0cm ②一间教室有面积是30m2③初一(1)班有48人④俄罗斯的陆地面积是1707.9万千米A、1个B、2个C、3个D、4个2、用四舍五入法,按要求对下列各数取近似值:(1)1102.5亿(精确到亿);(2)0.00291 (精确到万分位);(3) 0.06328(精确到0.01)(4) 7.9122(精确到个位)(5)47155(精确到百位)3、下面由四舍五入得到的近似数,各精确到哪一位?(1)1.23 (2)0.04060 (3)2000(4)1.69万 (5)5108.24、张华用最小刻度单位是毫米的直尺测量一本书的长度,他量得的数据是9.58cm ,其中( )A.9和5是精确的,8是估计的B.9是精确的,5和8是估计的C.9、5和8都是精确的D.9、5和8都是估计的。
4.4近似数-苏科版八年级数学上册教案

4.4 近似数-苏科版八年级数学上册教案本节课目标1.学习什么是近似数。
2.学习使用近似数进行计算。
3.学习近似数的正确使用方法。
教学内容何为近似数近似数是指在一定精度范围内正确的数值表达。
近似数解决的问题是,当数学运算的结果因为计算机精度问题而输入不了精度时,需要使用近似值来进行计算。
如何使用近似数进行计算使用近似数进行计算的步骤如下:1.把被计算数改写成符合近似数精度的数值。
2.以计算符合近似数精度的数值所需的运算符进行计算。
3.以计算出的数作为结果,并在最后加上误差范围。
在使用针对近似数的计算机程序进行计算时,可以忽略第三步,因为计算机会自动计算最终误差范围。
近似数的正确使用方法近似值的正确使用方法有以下几点:1.必须说明近似数的误差范围。
2.必须在算术运算中明确使用近似数。
3.必须根据实际问题中的需求选择合适的近似数。
4.必须掌握保留位数规则和四舍五入规则。
5.必须知晓计算结果误差的重要性,不可随便忽略计算误差。
教学步骤1.引入本节课目标,并解释何为近似数。
2.学生默写一句话回答问题:“何为近似数?”3.告诉学生本节课将学习如何使用近似数进行计算。
4.介绍使用近似数计算的步骤。
5.举例说明如何使用近似数进行计算。
6.解释使用近似数的正确方法,并给学生完成练习。
7.学生在课下根据实际问题使用并计算近似数,以强化本节课学习内容。
教学重点1.理解何为近似数。
2.掌握使用近似数进行计算的步骤。
3.掌握近似数的正确使用方法。
教学难点1.如何正确使用近似数完成计算。
2.近似数误差略,如何减小偏差。
参考文献1.苏科版八年级数学上册。
2.吴家春,《近似数在数值计算中的应用》。
4.4近似数-苏科版八年级数学上册教案

4.4 近似数-苏科版八年级数学上册教案教学目标1.掌握求近似数的方法;2.能够判断近似数的误差;3.能够应用近似数解决实际问题。
教学重点1.求近似数的方法;2.判断近似数的误差。
教学难点1.近似数误差的判断。
教学步骤第一步:导入新知教师可以在黑板上写下以下内容:•近似数:指比某一数更接近它的数;•近似数的计算有以下两个步骤:先找到与原数最接近的整十、或整百、或整千数,然后估算差值(单位在以原数最接近的数为基数的位数)。
•近似数误差是指近似数和原数之间的差值。
第二步:概念讲解教师可以上课讲解或者教师会让学生互动、合作,让学生自由探究得出概念。
第三步:例题解析通过例题,让学生加深对近似数和近似数误差的理解。
可以通过小组合作等形式,带领学生一步步分析每个例题并求解。
第四步:学生练习每个学生在分组合作或独立完成练习。
第五步:讲解重难点老师将在课堂上处理一些学生不容易理解的重点、难点问题,并让学生做练习题时注意。
第六步:巩固练习课后学生可以完成指定作业,让学生巩固并理解更深入。
第七步:板书设计可以根据这节课教学的内容和重难点设计板书,便于学生复习时可以回到课堂上。
求近似数的步骤•找到距离原数最近的整十、整百或整千数,用这个整数来作为估算值;•估算这个整数与原数之间的差,以此来得到近似数。
判断近似数的误差•精确度:近似数与原数之间丝毫没有差别;•化整为零法;•保留几位有效数字。
总结通过本节课的学习,学生理解了近似数的含义、求近似数的方法和判断近似数的误差,加深了对这些知识点的了解和掌握。
让学生明白,近似数作为实际问题中常用的解法,时刻保持警惕,把握近似数的精度与误差,更好地解决实际问题。
参考文献1.苏科版八年级数学上册教材;2.陈志民. (2009). 近似数的学习和测试. 数学课程导刊, (05), 104-104.。
八年级数学上册4_4近似数学案无答案新版苏科版

课题:4.4 近似数学习目标: 姓名:1.了解近似数的概念,体会近似数的意义及其在生活中的作用;2.能说出一个近似数的精准度,能依照要求用四舍五入的方式取一个数的近似数.学习进程:一.【情景创设】(1)班级中的人数是不是是精准数?全世界有40亿人收看了北京奥运会揭幕式的电视转播.那个地址40亿是精准数吗?(2)生活中,有些数据是准确的,有些是近似的,你能举例说明吗?二.【问题探讨】问题1:以下实际问题中显现的数,哪些是准确值,哪些是近似数?(1)某同窗的身高1.58米 (2)中国有31个省级行政单位(3)北京市大约有1300万人口 (4)那座山高出海平面3875米问题2:探讨如何确信近似数取一个数的近似值有多种方式,四舍五入是最经常使用的一种方式.用四舍五入法取一个数的近似数时,四舍五入到哪一名,就说那个近似数精准到哪一名.例如,圆周率=3.1415926…取π≈3,确实是精准到个位(或精准到1),取π≈3.1,确实是精准到十分位(或精准到0.1),取π≈3.14,确实是精准到百分位(或精准到0.01),取π≈3.142,确实是精准到千分位(或精准到0.001).问题3:小亮的体重为43.954kg,请按以下要求别离取近似值:(1)精准到1kg (2)精准到0.1kg (3)精准到0.01kg问题4:用四舍五入法,按要求对以下各数取近似值,并用科学记数法表示.2(3)0.000077nm (精准到0.00001nm )问题5:以下各数是由四舍五入取得的近似数,指出它们别离精准到哪一名.(1)3.6万 (2)8千 (3)0.41万(4)41079.3⨯ (5)610040.5⨯ (6)2.40问题6:依照括号里的要求用四舍五入法对以下各数取近似数0.34482(精准到百分位) 1.5046(精准到0.01)603400(精准到千位) 0.0697(精准到千分位)2.953(保留一名小数) 2.953(保留整数)三.【变式拓展】问题7:数a 用四舍五入法求得的近似数为1.8;数b 用四舍五入法求得的近似数为1.80,a 、b 是不是表示同一个数,什么缘故?变式:近似数m ≈3.3,求m 的取值范围.问题8:探讨.(1)成功农场养鸡35467只,一个个体户养鸡13530只(四舍五入到十位),光明农场养鸡64800只(四舍五入到百位),要比较他们养鸡的多少,成功农场养鸡数应四舍五入到哪一名数时,误差会少些.(2)张娟和李敏在讨论问题. 张娟:若是你把7498近似到千位数,你就会取得7000.李敏:不,我有另外一种解答方式,能够取得不同的答案.第一将7498近似到百位得7500,接着把7500近似到千位,就取得8000. 张娟:……你如何评判张娟和李敏的说法呢?四.【总结提升】1.用四舍五入法求得的近似数时应注意什么?2.把一个较大数取近似数且精准到较高位时需要用到什么?五. 【课堂反馈】六. 【课后作业】(选做题)。
苏科版八年级数学上册教案《4.4近似数》

《4.4近似数》本节课是苏科版八年级上册第四章最后一个单元,近似数的概念学生虽然没有接触过,但在日常生活中是很多的。
通过学生对生活事例的调查和直观描述,不仅让学生了解近似数,同时也让学生体会生活中处处有数学,从而体现数学学习的有用性,激发学生学习数学的兴趣。
求近似数、四舍五入法的教学,一方面为学习—求较大数的近似数(省略万或亿后面的尾数)、求积的近似值、求商的近似值以及为除法试商等内容做好知识上的铺垫;另一方面通过数学小知识的学习,让学生知道我国是世界上最早使用四舍五入法进行计算的国家,以此激发学生的民族自豪感,提高学好数学的热情。
【知识与能力目标】了解近似数的概念,并按要求取近似数.【过程与方法目标】经历对实际问题的探究过程,体会用近似数字刻画现实问题的思想.【情感态度价值观目标】在独立思考的基础上,积极参与对数学问题的讨论,并敢于表现自己,丰富学习数学的成功体验,激发对空间与图形的好奇心.【教学重点】了解近似数、精确度的意义,能根据具体要求取近似数.【教学难点】近似数的意义,按实际需要取近似数.教师准备:课件、多媒体;学生准备:练习本;一、导入新课对于参加同一个会议的人数,有两个报道.一个报道说:“会议秘书处宣布,参加今天会议的有513人.”另一报道说:“约有5百人参加了今天的会议.”问题2:在这些数据中,哪些是与实际接近的?哪些数据是与实际完全符合的?二、新课学习1、得出概念问题1:根据我们预习的结果,上述的4个问题中,是准确数,是不能准确反映实际情况的。
这些数只是一个大概的数,我们给它取个名字叫做。
问题2:你能列举出生活中哪些是准确数,哪些用到近似数吗?问题3:七年级的实际学生数为224,与第2个问题相比较,误差是。
问题4:为什么会产生这个误差?近似数与准确数的接近程度,用精确度表示。
524精确到个位,而约5百精确到位。
2、尝试解决问题问题5:按四舍五入对圆周率取得的近似数精确到哪一位?π≈3(精确到位)π≈3.1(精确到0.1或叫做精确到位)π≈3.14(精确到或叫做精确到位)π≈3.142(精确到或叫做精确到位)练习:教材P46页练习问题6:在表示近似数的方法有和。
苏科版数学八年级上册教案-4.4 近似数
近似数教学设计二、探讨如何确定近似数取一个数的近似值有多种方法,四舍五入是最常用的一种方法.用四舍五入法取一个数的近似数时,四舍五入到哪一位,就说这个近似数精确到哪一位.例如,圆周率=3.1415926…取π≈3,就是精确到个位(或精确到1),取π≈3.1,就是精确到十分位(或精确到0.1),取π≈3.14,就是精确到百分位(或精确到0.01),取π≈3.142,就是精确到千分位(或精确到0.001).三、例题教学:在明白如何确定近似数的基础上进行具体数字分析.写出:圆周率=3.1415926…取π≈3,就是精确到个位(或精确到1),取π≈3.1,就是精确到十分位(或精确到0.1),取π≈3.14,就是精确到百分位(或精确到0.01),取π≈3.142,就是精确到千分位(或精确到0.001).通过具体实例探索如何根据精确度确定近似数的值。
取一个数的近似值有多种方法,四舍五入是最常用的一种方法.用四舍五入法取一个数的近似数时,四舍五入到哪一位,就说这个近似数精确到哪一位。
例 1 小亮用天平称得罐头的质量为2.026kg,按下列要求取近似值.(1)精确到0.01kg;(2)精确到0.1kg;(3)精确到1kg.例2 用四舍五入法,按要求对下列各数取近似值,并用科学记数法表示.(1)地球上七大洲的面积约为149 480 000 (km)2(精确到10 000 000(km)2);(2)某人一天饮水1 890mL (精确到1 000mL);(3)人的眼睛可以看见的红光的波长为0.000 077cm (精确到0.000 01 cm).请与同学交流讨论.学生体验。
按照精确度确定近似数的值。
按照精确度确定近似数的值,由于本例有一定难度,可讨论完成。
按四舍五入取近似数时,应提醒学生不能随便将小数点后面的0去掉,比如例1第(2)题。
按四舍五入取近似数.通过讨论使学生理解使用科学记数法记数,不仅便于记一些较大(小)的数,而且易于表示近似数。
新苏科版初中数学八年级上册4.4近似数公开课优质课教学设计
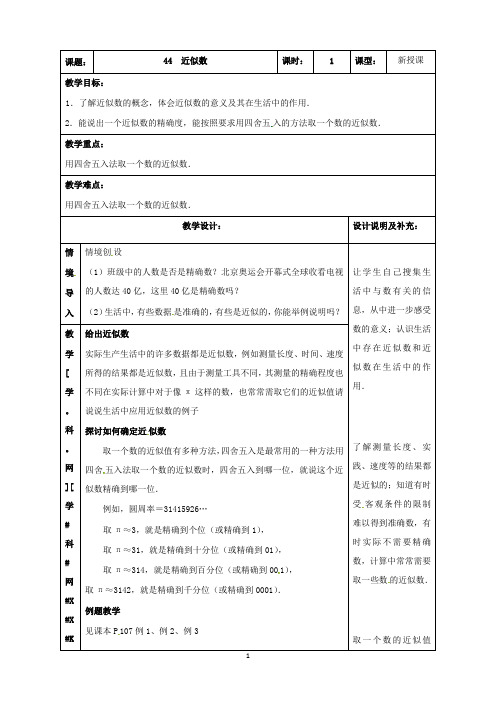
取π≈3,就是精确到个位(或精确到1),
取π≈31,就是精确到十分位(或精确到01),
取π≈314,就是精确到百分位(或精确到00 1),
取π≈3142,就是精确到千分位(或精确到0001).
例题教学
见课本P 107例1、例2、例3
课堂练习
课本108-109页练习1、2.
教
学[学。科。网][学#科#网#X#X#K]
过
程
给出近似数
实际生产生活中的许多数据都是近似数,例如测量长度、时间、速度所得的结果都是近似数,且由于测量工具不同,其测量的精确程度也不同在实际计算中对于像π这样的数,也常常需取它们的近似值请说说生活中应用近似数的例子
探讨如何确定近 似数
取一个数的近似值有多种方法,四舍五入是最常用的一种方法用四舍 五入法取一个数的近似数时,四舍五入到哪一位,就说这个近似数精确到哪一位.
取一个数的近似值有多种方法,四舍五入是最常用的一种方法用四舍五入法取一个数的近似数时,四舍五入到哪一位,就说这 个近似数精确到哪一位.
按四舍五入取近似数时,应提醒学生不能随便将小数点后面的0去掉,比如例1第(2)题.
按四舍五入取近似数通过讨论使学生理解使用科学记数法记数,不仅便于记一些较大(小)的数,而且易于表示近似 数.
(1)班级中的人数是否是精确数?北京奥运会开幕式全球收看电视的人数达40亿,这里40亿是精确数吗?
(2)生活中,有些数据 是准确的,有些是近似的,你能举例说明吗?
让学生自己搜集生活中与数有关的信息,从中进一步感受数的意义;认识生活中存在近似数和近似数在生活中的作用.
了解测量长度、实践、速度等的结果都是近似的;知道有时受 客观条件的限制难以得到准确数,有时实际不需要精确数,计算中常常需要取一些数 的近似数.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课型:新授课
学习目标(重点)
1.了解近似数的概念,体会近似数的意义及在生活中的作用;
2.能说出一个近似数的精确度,能按照要求用四舍五入的方法取一个数的近似数.
课后续助:
一、填空题
1.近似数0.4062精确到 位.
2.π=3.1415926…精确到千分位的近似数是 .
3.5.47×105精确到 位.
4.近似数1.69万精确到 位.
5.2.40万精确到__________位.
6.(1)近似数1.8×105
精确到 位.
7.某厂2004年的产值约为2000万元,约是1998年的6.8倍(其中2000万精确到哪一位? .
8.我国人口约为13亿人,其中13亿精确到 位.
9.小明的体重约为51.51千克,如果精确到10千克,其结果为 千克;
如果精确到1千克,其结果为 千克;如果精确到0.1千克,其结果为 千克.
二、用四舍五入法,把下列各数按括号内的要求取近似值.
三、解答题
计算:⑴3+2-3(保留两个有效数字) ⑵23
(精确到0.01)
复习巩固作业
一、填空题
1.49
的平方根______;0.216的立方根______的平方根__ ;的立方根_____. 2.算术平方根等于它本身的数有________,立方根等于本身的数有________.
3.如果0)6(42=++-y x ,则=+y x ________.
4.如果21a -和5a -是一个数m 的平方根,则.__________,==m a
5.03|2|=-+-y x ,则______=xy .
6. 33-的绝对值是 .
7.若a 、b 互为相反数,c 、d 互为负倒数,则______3=++cd b a .
8.下列实数(1)3.1415926 .
(2)0.3 22
(3)7 (5)(6)2
π (7)0.3030030003...
其中无理数有________,有理数有________.(填序号) 9._____2516=±
;_____814=-;_____8
333=;_____643=--. 10.比较大小: 5-______6-;14.3_______π; 213-______ 21.
二、解答题
1.求下列各式中x 的值
2(1)16490x -=;
2(2)(1)25x -=; 3(3)(2)8x =-; 3(4)(3)27x --=.
2.若8-a +(b+27)2=0,则求3a +3b .
3 =2,求2x +5的算术平方根.。
