特征选择法与蚁群算法简介
蚁群算法内容简介

蚁群算法内容简介蚁群算法(ant colony optimization, ACO),又称蚂蚁算法,是一种用来在图中寻找优化路径的机率型算法群算法是由意大利学者Dorigo等人于20世纪90年代初期通过模拟自然界中蚂蚁集体寻经的行为而提出的一种基于种群的启发式随机搜索算法,蚁群算法具有并行性、鲁棒性、正反馈性等特点。
蚁群算法最早成功应用于解决著名的旅行商问题以及二次分配问题、车间任务调度问题、图的着色问题、网络路由等许多复杂的组合问题。
蚁群算法是一种模拟进化算法,初步的研究表明该算法具有许多优良的性质.针对PID控制器参数优化设计问题,将蚁群算法设计的结果与遗传算法设计的结果进行了比较,数值仿真结果表明,蚁群算法具有一种新的模拟进化优化方法的有效性和应用价值。
随着人们对效益的要求越来越高,人们发现组合优化的各种方法,但在一些复杂度比较高的问题上,一些传统的方法显示了他的限制,列如计算量上升太快,时间复杂度很高,这就需要一些新的方法来解决这些问题,从而有效地克服传统蚁群算法中容易陷入局部最优解和收敛速度慢的现象。
蚁群系统(Ant Colony System),这种算法是目前国内外启发式算法中的研究热点和前沿课题,被成功地运用于旅行商问题的求解,蚁群算法在求解复杂优化问题方面具有很大的优越性和广阔的前景。
但是,根据观察实验发现,蚁群中的多个蚂蚁的运动是随机的,在扩散范围较大时,在较短时间内很难找出一条较好的路径,在算法实现的过程中容易出现停滞现象和收敛速度慢现象。
在这种弊端的情况下,学者们提出了一种自适应蚁群算法,通过自适应地调整运行过程中的挥发因子来改变路径中信息素浓度,从而有效地克服传统蚁群算法中容易陷入局部最优解和收敛速度慢的现象。
下面是一些最常用的变异蚁群算法精英蚂蚁系统全局最优解决方案在每个迭代以及其他所有的蚂蚁的沉积信息素。
最大最小蚂蚁系统(MMAS)添加的最大和最小的信息素量[ τmax ,τmin ],只有全局最佳或迭代最好的巡逻沉积的信息素。
特征选择中的基于蚁群算法的方法研究

特征选择中的基于蚁群算法的方法研究特征选择是机器学习和数据挖掘领域的一个重要研究方向,它的主要目的是从原始数据中选择最相关和具有重要意义的特征,以提高模型的性能和准确性。
近年来,蚁群算法作为一种新型的优化算法,被广泛应用于特征选择中。
本文将从蚁群算法的原理和特征选择的意义出发,介绍基于蚁群算法的特征选择方法的研究现状、优缺点及发展趋势。
第一章绪论1.1 研究背景特征选择是机器学习和数据挖掘中一个重要的预处理步骤。
随着数据量的不断增大和特征维度的增加,特征选择变得越来越重要,因为有效的特征选择可以提高模型的性能,降低计算资源的消耗。
目前已经有许多特征选择方法被提出和应用,其中基于蚁群算法的方法成为研究的热点之一。
1.2 研究目的和意义蚁群算法是一种模拟蚂蚁觅食行为的优化算法,其具有全局搜索和局部优化的能力。
将蚁群算法应用于特征选择中,可以有效地解决特征选择问题,提高模型的准确性和泛化能力。
因此,本文旨在研究基于蚁群算法的特征选择方法,探讨其在实际应用中的优势和不足。
第二章蚁群算法的原理2.1 蚁群算法的基本思想蚁群算法是一种模拟蚂蚁觅食行为的启发式算法,其基本思想是通过模拟蚂蚁在搜索和发现食物过程中的行为与能力,寻找到最优解或次优解。
蚂蚁以信息素作为交流和引导的方式,信息素的浓度会影响蚂蚁的选择行为,从而达到优化的目的。
2.2 蚁群算法的优势和不足蚁群算法具有以下优势:全局搜索能力强、适应性强、具有一定的局部优化能力、对问题的约束条件不敏感。
然而,蚁群算法也存在不足之处,比如收敛速度慢、易陷入局部最优、参数设置对算法性能影响较大等。
第三章基于蚁群算法的特征选择方法3.1 特征选择的概念和常用方法特征选择的目标是从原始数据中选择出最相关和具有重要意义的特征。
常用的特征选择方法包括过滤式方法、包裹式方法和嵌入式方法。
这些方法根据不同的准则和算法原理,在特征选择过程中起到不同的作用。
3.2 基于蚁群算法的特征选择方法基于蚁群算法的特征选择方法可以分为两类:基于启发式信息素模型的方法和基于蚁群搜索的方法。
蚁群算法及案例分析精选全文

群在选择下一条路径的时
候并不是完全盲目的,而是
按一定的算法规律有意识
地寻找最短路径
自然界蚁群不具有记忆的
能力,它们的选路凭借外
激素,或者道路的残留信
息来选择,更多地体现正
反馈的过程
人工蚁群和自然界蚁群的相似之处在于,两者优先选择的都
是含“外激素”浓度较大的路径; 两者的工作单元(蚂蚁)都
正反馈、较强的鲁棒性、全
局性、普遍性
局部搜索能力较弱,易出现
停滞和局部收敛、收敛速度
慢等问题
优良的分布式并行计算机制
长时间花费在解的构造上,
导致搜索时间过长
Hale Waihona Puke 易于与其他方法相结合算法最先基于离散问题,不
能直接解决连续优化问题
蚁群算法的
特点
蚁群算法的特点及应用领域
由于蚁群算法对图的对称性以
及目标函数无特殊要求,因此
L_ave=zeros(NC_max,1);
%各代路线的平均长度
while NC<=NC_max
%停止条件之一:达到最大迭代次数
% 第二步:将m只蚂蚁放到n个城市上
Randpos=[];
for i=1:(ceil(m/n))
Randpos=[Randpos,randperm(n)];
end
Tabu(:,1)=(Randpos(1,1:m))';
scatter(C(:,1),C(:,2));
L(i)=L(i)+D(R(1),R(n));
hold on
end
plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)])
蚁群算法原理简介

蚁群算法主要有以下三个特点:
(1).正反馈,使得该算法可以较快的发现较好解。
(2).分布式,易于并行实现。 (3).启发式搜索,反映了搜索中的先验性、确定性因素的强度。
(4).鲁棒性强,不易受某个个体影响。
基本蚁群原理
A
2 食物
蚁穴
3 B
1
基本蚁群原理
ijt ijt P t is is J
k ij s
k
转移概率
(i )
启发函数t 1时刻信息素累积量
本次迭代信息素增量
t 1 (1 ) t
ij
ij
k ij
ij
k 1
m
k
蚂蚁k释放的信息素
Q
L
k
最
优
路
径
改进蚁群算法
蚁群算法:又称蚂蚁算法,是一种用来在图中寻找优化路径的概率型算 法。它由Marco Dorigo于1992年在他的博士论文中提出,其灵感来源于 蚂蚁在寻找食物过程中发现路径的行为。
蚁群算法特点
蚁群算法主要用来解决路径规划等离散优化问题,比如旅行商问题、指 派问题、调度问题等
机器学习中的特征选择方法研究综述

机器学习中的特征选择方法研究综述简介:在机器学习领域,特征选择是一项重要的任务,旨在从原始数据中选择出对于解决问题最具有代表性和预测能力的特征子集。
特征选择方法能够改善模型性能、减少计算复杂性并提高模型解释性。
本文将综述机器学习中常用的特征选择方法,并对其优点、缺点和应用范围进行评估和讨论。
特征选择方法的分类:特征选择方法可以分为三大类:过滤式、包裹式和嵌入式方法。
1. 过滤式方法:过滤式方法独立于任何学习算法,通过对特征进行评估和排序,然后根据排名选择最佳特征子集。
常用的过滤式方法包括相关系数、互信息、卡方检验等。
(1) 相关系数:相关系数是评估特征与目标变量之间线性关系强弱的一种方法。
常用的相关系数包括皮尔逊相关系数和斯皮尔曼相关系数。
优点是简单且易于计算,但仅能检测线性关系,对于非线性关系效果较差。
(2) 互信息:互信息是评估特征与目标变量之间信息量共享程度的一种方法。
互信息能够发现非线性关系,但对于高维数据计算复杂度较高。
(3) 卡方检验:卡方检验适用于特征与目标变量均为分类变量的情况。
它衡量了特征与目标变量之间的依赖性。
然而,在特征之间存在相关性时,卡方检验容易选择冗余特征。
过滤式方法适用于数据集维度较高的情况,计算速度快,但无法考虑特征间的相互影响。
2. 包裹式方法:包裹式方法直接使用学习算法对特征子集进行评估,通常使用启发式搜索算法(如遗传算法、蚁群算法等)来找到最佳特征子集。
包裹式方法的优点是考虑了特征间的相互作用,但计算复杂度高,易受算法选择和数据噪声的影响。
(1) 遗传算法:遗传算法是一种模拟生物进化过程的优化算法。
在特征选择中,遗传算法通过使用编码表示特征子集,通过选择、交叉和变异等操作来搜索最佳特征子集。
遗传算法能够有效避免包裹式方法中特征间的相互影响,但计算复杂度高。
(2) 蚁群算法:蚁群算法是一种基于模拟蚁群觅食行为的优化算法。
在特征选择中,蚁群算法通过模拟蚂蚁在搜索空间中的移动来寻找最佳特征子集。
蚁群算法概述

蚁群算法概述一、蚁群算法蚁群算法(ant colony optimization, ACO),又称蚂蚁算法,是一种用来寻找最优解决方案的机率型技术。
它由Marco Dorigo于1992年在他的博士论文中引入,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。
蚂蚁在路径上前进时会根据前边走过的蚂蚁所留下的分泌物选择其要走的路径。
其选择一条路径的概率与该路径上分泌物的强度成正比。
因此,由大量蚂蚁组成的群体的集体行为实际上构成一种学习信息的正反馈现象:某一条路径走过的蚂蚁越多,后面的蚂蚁选择该路径的可能性就越大。
蚂蚁的个体间通过这种信息的交流寻求通向食物的最短路径。
蚁群算法就是根据这一特点,通过模仿蚂蚁的行为,从而实现寻优。
这种算法有别于传统编程模式,其优势在于,避免了冗长的编程和筹划,程序本身是基于一定规则的随机运行来寻找最佳配置。
也就是说,当程序最开始找到目标的时候,路径几乎不可能是最优的,甚至可能是包含了无数错误的选择而极度冗长的。
但是,程序可以通过蚂蚁寻找食物的时候的信息素原理,不断地去修正原来的路线,使整个路线越来越短,也就是说,程序执行的时间越长,所获得的路径就越可能接近最优路径。
这看起来很类似与我们所见的由无数例子进行归纳概括形成最佳路径的过程。
实际上好似是程序的一个自我学习的过程。
3、人工蚂蚁和真实蚂蚁的异同ACO是一种基于群体的、用于求解复杂优化问题的通用搜索技术。
与真实蚂蚁通过外激素的留存/跟随行为进行间接通讯相似,ACO中一群简单的人工蚂蚁(主体)通过信息素(一种分布式的数字信息,与真实蚂蚁释放的外激素相对应)进行间接通讯,并利用该信息和与问题相关的启发式信息逐步构造问题的解。
人工蚂蚁具有双重特性:一方面,他们是真实蚂蚁的抽象,具有真实蚂蚁的特性,另一方面,他们还有一些在真实蚂蚁中找不到的特性,这些新的特性,使人工蚂蚁在解决实际优化问题时,具有更好地搜索较好解的能力。
人工蚂蚁与真实蚂蚁的相同点为:1.都是一群相互协作的个体。
蚁群算法——精选推荐
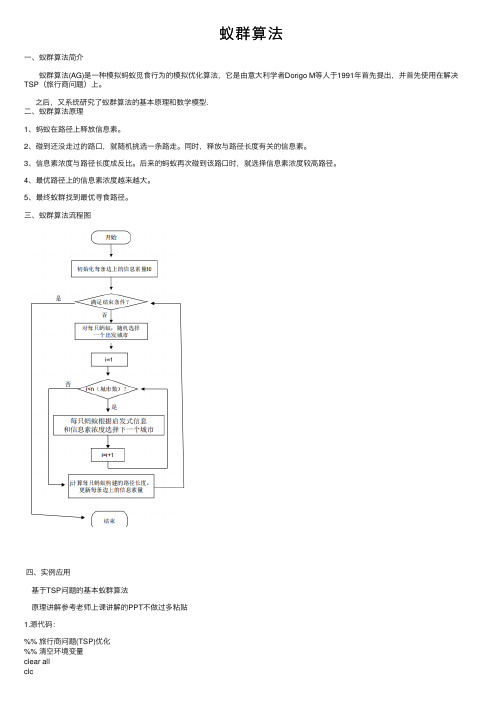
蚁群算法⼀、蚁群算法简介 蚁群算法(AG)是⼀种模拟蚂蚁觅⾷⾏为的模拟优化算法,它是由意⼤利学者Dorigo M等⼈于1991年⾸先提出,并⾸先使⽤在解决TSP(旅⾏商问题)上。
之后,⼜系统研究了蚁群算法的基本原理和数学模型.⼆、蚁群算法原理1、蚂蚁在路径上释放信息素。
2、碰到还没⾛过的路⼝,就随机挑选⼀条路⾛。
同时,释放与路径长度有关的信息素。
3、信息素浓度与路径长度成反⽐。
后来的蚂蚁再次碰到该路⼝时,就选择信息素浓度较⾼路径。
4、最优路径上的信息素浓度越来越⼤。
5、最终蚁群找到最优寻⾷路径。
三、蚁群算法流程图四、实例应⽤基于TSP问题的基本蚁群算法原理讲解参考⽼师上课讲解的PPT不做过多粘贴1.源代码:%% 旅⾏商问题(TSP)优化%% 清空环境变量clear allclc%% 导⼊数据citys = ceil(rand(50,2)*50000)%load newcitys.mat%% 计算城市间相互距离fprintf('Computing Distance Matrix... \n');n = size(citys,1);D = zeros(n,n);for i = 1:nfor j = 1:nif i ~= jD(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));elseD(i,j) = 1e-4;endendend%% 初始化参数fprintf('Initializing Parameters... \n');m = 50; % 蚂蚁数量alpha = 1; % 信息素重要程度因⼦beta = 5; % 启发函数重要程度因⼦rho = 0.05; % 信息素挥发因⼦Q = 1; % 常系数Eta = 1./D; % 启发函数Tau = ones(n,n); % 信息素矩阵Table = zeros(m,n); % 路径记录表iter = 1; % 迭代次数初值iter_max = 150; % 最⼤迭代次数Route_best = zeros(iter_max,n); % 各代最佳路径Length_best = zeros(iter_max,1); % 各代最佳路径的长度Length_ave = zeros(iter_max,1); % 各代路径的平均长度%% 迭代寻找最佳路径figure;while iter <= iter_maxfprintf('迭代第%d次\n',iter);% 随机产⽣各个蚂蚁的起点城市start = zeros(m,1);for i = 1:mtemp = randperm(n);start(i) = temp(1);endTable(:,1) = start;% 构建解空间citys_index = 1:n;% 逐个蚂蚁路径选择for i = 1:m% 逐个城市路径选择for j = 2:ntabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)allow_index = ~ismember(citys_index,tabu);allow = citys_index(allow_index); % 待访问的城市集合P = allow;% 计算城市间转移概率for k = 1:length(allow)P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta; endP = P/sum(P);% 轮盘赌法选择下⼀个访问城市Pc = cumsum(P);target_index = find(Pc >= rand);target = allow(target_index(1));Table(i,j) = target;endend% 计算各个蚂蚁的路径距离Length = zeros(m,1);for i = 1:mRoute = Table(i,:);for j = 1:(n - 1)Length(i) = Length(i) + D(Route(j),Route(j + 1));endLength(i) = Length(i) + D(Route(n),Route(1));end% 计算最短路径距离及平均距离if iter == 1[min_Length,min_index] = min(Length);Length_best(iter) = min_Length;Length_ave(iter) = mean(Length);Route_best(iter,:) = Table(min_index,:);else[min_Length,min_index] = min(Length);Length_best(iter) = min(Length_best(iter - 1),min_Length);Length_ave(iter) = mean(Length);if Length_best(iter) == min_LengthRoute_best(iter,:) = Table(min_index,:);elseRoute_best(iter,:) = Route_best((iter-1),:);endend% 更新信息素Delta_Tau = zeros(n,n);% 逐个蚂蚁计算for i = 1:m% 逐个城市计算for j = 1:(n - 1)Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); endDelta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); endTau = (1-rho) * Tau + Delta_Tau;% 迭代次数加1,清空路径记录表% figure;%最佳路径的迭代变化过程[Shortest_Length,index] = min(Length_best(1:iter));Shortest_Route = Route_best(index,:);plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');pause(0.3);iter = iter + 1;Table = zeros(m,n);% endend%% 结果显⽰[Shortest_Length,index] = min(Length_best);Shortest_Route = Route_best(index,:);disp(['最短距离:' num2str(Shortest_Length)]);disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);%% 绘图figure(1)plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');grid onfor i = 1:size(citys,1)text(citys(i,1),citys(i,2),[' ' num2str(i)]);endtext(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');xlabel('城市位置横坐标')ylabel('城市位置纵坐标')title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])figure(2)plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')legend('最短距离','平均距离')xlabel('迭代次数')ylabel('距离')title('各代最短距离与平均距离对⽐')运⾏结果:利⽤函数citys = ceil(rand(50,2)*50000) 随机产⽣五⼗个城市坐标2.研究信息素重要程度因⼦alpha, 启发函数重要程度因⼦beta,信息素挥发因⼦rho对结果的影响为了保证变量唯⼀我重新设置五⼗个城市信息进⾏实验在原来设值运⾏结果:实验结果可知当迭代到120次趋于稳定2.1 alpha值对实验结果影响(1)当alpha=4时运⾏结果实验结果可知当迭代到48次左右趋于稳定(2)当alpha=8时运⾏结果:有图可知迭代40次左右趋于稳定,搜索性较⼩(3)当alpha= 0.5运⾏结果:有图可知迭代到140次左右趋于稳定(4)当alpha=0.2时运⾏结果:结果趋于110次左右稳定所以如果信息素因⼦值设置过⼤,则容易使随机搜索性减弱;其值过⼩容易过早陷⼊局部最优2.2 beta值对实验影响(1)当 beta=8时运⾏结果结果迭代75次左右趋于稳定(2)当 beta=1时运⾏结果:结果迭代130次左右趋于稳定所以beta如果值设置过⼤,虽然收敛速度加快,但是易陷⼊局部最优;其值过⼩,蚁群易陷⼊纯粹的随机搜索,很难找到最优解2.3 rho值对实验结果影响(1)当rho=3时运⾏结果:结果迭代75次左右趋于稳定(2)当rho=0.05运⾏结果:结果迭代125次左右趋于稳定所以如果rho取值过⼤时,容易影响随机性和全局最优性;反之,收敛速度降低总结:蚁群算法对于参数的敏感程度较⾼,参数设置的好,算法的结果也就好,参数设置的不好则运⾏结果也就不好,所以通常得到的只是局部最优解。
昆虫群体行为学中的蚁群算法

昆虫群体行为学中的蚁群算法随着社会的发展和科技的不断进步,人们日常的各种活动都离不开计算机和信息技术的支持,人工智能、机器学习已经成为重要的研究领域。
而昆虫群体行为学中的蚁群算法也成为了这个领域中的热门算法之一。
本文将结合案例深入剖析蚁群算法的工作原理及其应用。
一、蚁群算法概述蚁群算法,又称蚁群优化算法,是一种基于群体智能的优化算法,源于自然界中蚂蚁生活方式的模拟。
自然界中蚂蚁以信息的方式寻找到食物和家,形成了一套完整的优化流程。
在这个过程中,蚂蚁会不断地散发信息素,当有蚂蚁发现了食物或者家后,会回到巢穴,散发出一种信息素,可以引起其他蚂蚁的注意。
一段时间过后,信息素会消失,这样就可以避免信息过时。
蚂蚁就利用这样的方式,在一片茫茫草地中快速找到食物和家。
而蚁群算法就是对这种生物的生命周期进行了模拟。
蚁群算法主要基于以下两大原理:正反馈和负反馈。
正反馈指的是蚂蚁在寻找食物和家的过程中,距离食物和家越近,越有可能被其他蚂蚁选择。
因此,经过一段时间的搜寻,食物或家附近的信息素浓度就会越来越高,吸引越来越多的蚂蚁。
负反馈指的是信息素的挥发时间有限,如果蚂蚁在搜寻过程中进入了死路,无法找到食物或家,很快就会失去它们的踪迹,寻找其它的目标。
二、蚁群算法的原理蚁群算法是一种基于贪心策略和启发式搜索的算法。
贪心策略是指在局部最优解的情况下选择全局最优解。
而启发式搜索则是通过评估函数进行深度优先或广度优先的搜索。
蚁群算法将这两种方法相结合,将其运用到求解优化问题的任务中。
在蚁群算法中,人们把寻优问题抽象成一个图论问题,称之为图。
设有m个蚂蚁在图中寻找最短路径,并假设每个蚂蚁可以移动的来源于强化自身链接的信息素来对图进行搜索,并通过蚁群算法来不断优化搜索的结果。
蚁群算法的核心在于挥发函数(Evaporation Rate)和信息素覆盖(Pheromone Coverage),通过这两个函数控制信息素在搜索过程中的流动和新建,在搜索过程中提高发现最优解的概率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简介
什么叫特征选择?
经典的特征选择方法是从多个特征中选取一些特 征,这个方法可以说包括特征选择和特征提取两个方 面。特征提取广义上指的是一种变换,将处于高维空 间的样本通过映射或变换的方式转换到低维空间,达 到降维的目的;特征选择指从一组特征中去除冗余或 不相关的特征来降维。这两者常联合使用,一般先通 过变换将高维特征空间映射成低维特征空间,然后再 去除冗余和不相关的特征来进一步达到降维的目的。
简介
提高测试数据 更低的虚警率 为什么要用特征选择算法 ? 的效率
获取最优特 征组合
减少系统计 算时间 更高的检测率
简介
特征选择的步骤
原始特征集
不 满 意 特 征 组 合 通过特征算法
产生特征集
评估子集
子集优劣
停止准则
满意特 征组合
结果验证
特征选择分类
根据特征子集形成方式分类:
特征选择分类
根据特征集合的评价策略方式分类:
• 信息素的更新方式有2种,一是挥发,也就是所有路径上的信息素以一定的 比率进行减少,模拟自然蚁群的信息素随时间挥发的过程;二是增强,给评 价值“好”(有蚂蚁走过)的边增加信息素。 • 蚂蚁向下一个目标的运动是通过一个随机原则来实现的,也就是运用当前所 在节点存储的信息,计算出下一步可达节点的概率,并按此概率实现一步移 动,逐此往复,越来越接近最优解。 • 蚂蚁在寻找过程中,或者找到一个解后,会评估该解或解的一部分的优化程 度,并把评价信息保存在相关连接的信息素中。
粒子群算法
• 粒子群算法:
也称粒子群优化算法(Particle Swarm Optimization,PSO),是由Eberhart 博士和
kennedy 博士提出,源于对鸟群捕食的行为研究 。该算法最初是受到飞鸟集群活动的规律 性启发,进而利用群体智能建立的一个简化模型。这个算法基于迭代的优化算法。粒子群
简化的蚂蚁寻食过程
蚂蚁从A点出发,速度相同,食物在D点,可能随机选择路线ABD或ACD。 假设初始时每条分配路线一只蚂蚁,每个时间单位行走一步, 本图为经过9 个时间单位时的情形:走ABD的蚂蚁到达终点,而走ACD的蚂蚁刚好走到C 点,为一半路程。
简化的蚂蚁寻食过程
本图为从开始算起,经过18个时间单位时的情形:走ABD的蚂蚁到达终点后 得到食物又返回了起点A,而走ACD的蚂蚁刚好走到D点。
1 k 1
m
信息素更新的作用
信息素挥发(evaporation)信息素痕迹的挥发过程是每个连接上的信
•
息素痕迹的浓度自动逐渐减弱的过程,这个挥发过程主要用于避 免算法过
快地向局部最优区域集中,有助于搜索区域的扩展。 • 信息素增强(reinforcement)增强过程是蚁群优化算法中可选的部分,
简化的蚂蚁寻食过程
• 假设蚂蚁每经过一处所留下的信息素为一个单位,则经过36个时间单位后, 所有开始一起出发的蚂蚁都经过不同路径从D点取得了食物,此时ABD的路 线往返了2趟,每一处的信息素为4个单位,而ACD的路线往返了一趟,每 一处的信息素为2个单位,其比值为2:1。 • 寻找食物的过程继续进行,则按信息素的指导,蚁群在ABD路线上增派一 只蚂蚁(共2只),而ACD路线上仍然为一只蚂蚁。再经过36个时间单位后, 两条线路上的信息素单位积累为12(4+4*2)和4(2*2),比值为3:1。 • 若按以上规则继续,蚁群在ABD路线上再增派一只蚂蚁(共3只), 而 ACD路线上仍然为一只蚂蚁。再经过36个时间单位后,两条线路上的信息 素单位积累为24(4+4*2+4*3)和6(2*3),比值为4:1。 • 若继续进行,则按信息素的指导,最终所有的蚂蚁会放弃ACD路线而选择 ABD路线。
蚁群优化算法基本流程
t (i, j ) h (i, j ) , if j J k (i) pk (i, j ) t (i, u ) h (i, u ) uJ k (i ) 0, otherwise
为了模拟蚂蚁在较短路径上留下更多的信息素,当所有蚂蚁到达终点时,必须把各路径 的信息素浓度重新更新一次,信息素的更新也分为两个步骤: (1)每一轮过后,问题空间中的所有路径上的信息素都会发生蒸发
的每个个体都代表优化问题的候选解,每个粒子具有位置x和速度v两个特征,位置代表候
选解的值,速度用于决定粒子在搜素空间迭代的位移。粒子对应的目标函数值作为粒子的 适应度f,候选解的优劣程度由该适应度决定。
粒子群算法
• 基于粒子群优化算法的特征选择的算法步骤如下:
(1)粒子群初始化。 (2)对粒子群每个粒子计算适应值,适应值与最优解的距离直接有关。 (3)种群根据适应值进行复制。 (4)如果终止条件满足的话,就停止,否则转步骤(2)。
(2)所有的蚂蚁根据自己构建的路径长度在它们本轮经过的边上释放信息素 路径构建 信息素更新
t (i, j ) (1 ) t (i, j ) t k (i, j),
(Ck ) , if (i, j ) R k t k (i, j ) otherwise 0,
蚁群算法起源
• 蚂蚁在运动过程中, 能够在它所经过的路径上留下外激素,而且蚂蚁在运 动过程中能够感知外激素的存在及其强度,并以此指导自己的运动方向, 蚂蚁 倾向于朝着外激素强度高的方向移动. • 由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象: 某一路 径上走过的蚂蚁越多,则后来者选择该路径的概率就越大. 蚂蚁个体之间就是 通过这种信息的交流达到搜索食物的目的。
蚁群优化算法基本流程
t (i, j ) h (i, j ) , if j J k (i) pk (i, j ) t (i, u ) h (i, u ) uJ k (i ) 0, otherwise
• 对于每只蚂蚁k,路径记忆向量Rk按照访问顺序记录了所有k已经经过的城市 序号。设蚂蚁k当前所在城市为i,则其选择城市j作为下一个访问对象的概率 如上式。Jk(i)表示从城市i可以直接到达的、且又不在蚂蚁访问过的城市序列 Rk中的城市集合。h(i, j)是一个启发式信息(信息素浓度变量),通常由 h (i, j)=1/dij直接计算。t(i, j)表示边(i, j)上的信息素量。
遗传算法
• 遗传算法的基本运算过程如下:
(1)初始化:设置进化代数计数器t=0,设置最大进化代数T,随机生成M个个体作为初始 群体P(0)。 (2)个体评价:计算群体P(t)中各个个体的适应度。 (3)选择运算:将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或 通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基 础上的。 (4)交叉运算:将交叉算子作用于群体。遗传算法中起核心作用的就是交叉算子。 (5)变异运算:将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值 作变动。 群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。 (6)终止条件判断:若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出, 终止计算。
简化的蚂蚁寻食过程
• 基于以上蚁群寻找食物时的最优路径选择问题,可以构造人工蚁 群,来解决最优化问题,如TSP问题。 • 人工蚁群中把具有简单功能的工作单元看作蚂蚁。二者的相似之 处在于都是优先选择信息素浓度大的路径。较短路径的信息素浓 度高,所以能够最终被所有蚂蚁选择,也就是最终的优化结果。 • 人工蚁群和自然蚁群的区别:人工蚁群有一定的记忆能力,能够 记忆已经访问过的节点; • 人工蚁群选择下一条路径的时候是按一定算法规律有意识地寻找 最短路径,而不是盲目的。例如在TSP问题中,可以预先知道当 前城市到下一个目的地的距离。
称为离线更新方式(还有在线更新方式)。这种方式可以实现 由单个蚂蚁 无法实现的集中行动。基本蚁群算法的离线更新方式是 在蚁群中的m只蚂 蚁全部完成n城市的访问后,统一对残留信息进行更新处理。
TSP问题的蚁群优化算法伪代码
for each edge set t0 = m/Cnn (initial pheromone value ) while not stop for each ant k randomly choose an initial city for i = 1 to n choose next city j with probability compute the length Ck of the tour constructed by the kth ant for each edge update the pheromone value print result
TSP举例
四个城市的TSP问题,距离矩阵和城市图示如下:
假设共m=3只蚂蚁,参数α =1,β=2,ρ =0.5
A
3
1 2
2
D
4
C
•步骤1
5
B
3 1 2 3 5 4 W dij 1 5 2 2 4 2
首先使用贪婪算法得到路径的(ACDBA), 则Cnn =1+2+4+3=10,求得τ 0 =m/Cnn =0.3。 初始化所有边上的信息素含量。
蚁群算法起源
• 20世纪50年代中期创立了仿生学,人们从生物进化的机理中受到启发。 提出了许多用以解决复杂优化问题的新方法,如进化规划、进化策略、 遗传算法等,这些算法成功地解决了一些 实际问题。
• 1991年意大利米兰理学院M. Dorigo提出Ant System, 用于求解TSP等组合优化问题。 • 1995年Gramdardella和Dorigo提出Ant-Q算法, 建立了AS和Q-learning的联系。 • 1996年二人又提出Ant Colony System
基于滤波(Filter)评价策略的特征选择算法。
基于嵌入式(Wrapper)评价策略的特征选择算法。
