第二章1_矩估计和极大似然估计(课堂PPT)
合集下载
矩法估计PPT课件

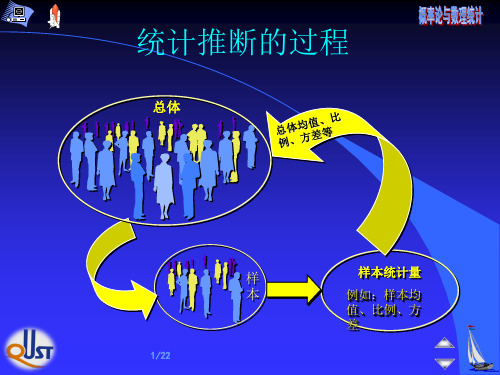
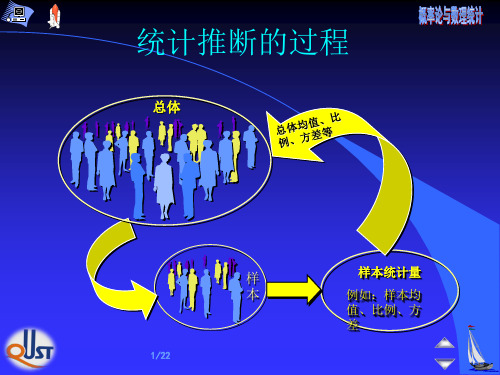
设总体的分布函数形式已知, 但它的一个或 多个参数为未知, 借助于总体的一个样本来估计总 体未知参数称为点估计问题.
点 估 计 问 题 就 是 要 构 造 一 个 适 当 的 统 计 量
ˆ(1,2,L,n),用 它 的 观 察 值 ˆ(x1,x2,L,xn) 来 估 计 未 知 参 数 .
ˆ(1 ,2 ,L ,n )称 为 的 估 计 量 . 通 称 估 计 ,
ˆ ( x 1 ,x 2 ,L ,x n ) 称 为 的 估 计 值 . 简 记 为 ˆ.
.
5
二、估计量的求法
由于估计量是样本的函数, 是随机变量, 故 对不同的样本值, 得到的参数值往往不同, 求估 计量的问题是关键问题.
点估计的求法: (两种) 矩估计法和极大似然估计法.
.
6
一、 矩估计法 它是基于一种简单的“替换” 思想建立起来的一种估计方法 . 是英国统计学家K.皮尔逊最早提出的 . 其基本思想是用样本矩估计总体矩 .
.
19
例 6 .设 X 在 [ 0 , ] 上 均 匀 分 布 , 求 的 矩 法 估 计 量 并 确 定
是 否 为 无 偏 估 计 量 ?
1
解 : f(x,)
0x, 0
( 列 1) 方矩 程法 :2 估 =0计 X : E X 0 x 1 其 dx 它 2 解 方 程 : ˆ = 2 X 即 为 的 矩 法 估 计 量 。
112X312X7
2 13X232X5
都是EX的无偏估计,并问哪一个比较有效?
解 E 1 E ( 1 2 X 3 1 2 X 7 ) 1 2 E X 3 1 2 E X 7 E X
E 2 E ( 1 3 X 2 2 3 X 5 ) 1 3 E X 3 2 3 E X 5 E X
点 估 计 问 题 就 是 要 构 造 一 个 适 当 的 统 计 量
ˆ(1,2,L,n),用 它 的 观 察 值 ˆ(x1,x2,L,xn) 来 估 计 未 知 参 数 .
ˆ(1 ,2 ,L ,n )称 为 的 估 计 量 . 通 称 估 计 ,
ˆ ( x 1 ,x 2 ,L ,x n ) 称 为 的 估 计 值 . 简 记 为 ˆ.
.
5
二、估计量的求法
由于估计量是样本的函数, 是随机变量, 故 对不同的样本值, 得到的参数值往往不同, 求估 计量的问题是关键问题.
点估计的求法: (两种) 矩估计法和极大似然估计法.
.
6
一、 矩估计法 它是基于一种简单的“替换” 思想建立起来的一种估计方法 . 是英国统计学家K.皮尔逊最早提出的 . 其基本思想是用样本矩估计总体矩 .
.
19
例 6 .设 X 在 [ 0 , ] 上 均 匀 分 布 , 求 的 矩 法 估 计 量 并 确 定
是 否 为 无 偏 估 计 量 ?
1
解 : f(x,)
0x, 0
( 列 1) 方矩 程法 :2 估 =0计 X : E X 0 x 1 其 dx 它 2 解 方 程 : ˆ = 2 X 即 为 的 矩 法 估 计 量 。
112X312X7
2 13X232X5
都是EX的无偏估计,并问哪一个比较有效?
解 E 1 E ( 1 2 X 3 1 2 X 7 ) 1 2 E X 3 1 2 E X 7 E X
E 2 E ( 1 3 X 2 2 3 X 5 ) 1 3 E X 3 2 3 E X 5 E X
1矩估计和极大似然估计
16/22
设总体 X 的分布函数中含 k 个未知参数
1 , 2 , k .
步骤一:记总体 X 的 m 阶原点矩 E(Xm)为 am , m =1,2,„,k. 一般地, am (m =1, 2, „, K) 是总体分布 故, 中参数或参数向量 (1, 2, „, k) 的函数。 am (m=1, 2, „, k) 应记成: am(1,2,…,k), m =1, 2, „, k.
13/22
例3:设总体X的均值为,方差为2,求 和 2 的矩估计。
解:由
E(X) , 2 2 2 E(X ) .
^ X, 即 ^ n 2 1 2 2 X i X . n i 1
14/22
即
ˆ X, ˆ2 1 n 2 (Xi X ) . n i 1
依样本对参数θ 做出估计,或估计参数 θ 的 某个已知函数 g(θ ) 。 这类问题称为参数估计。 参数估计包括:点估计和区间估计。
4/22
为估计参数 µ ,需要构造适当的统计量 T( X1, X2 , „ , Xn ), 一旦当有了样本,就将样本值代入到该统计 量中,算出一个值作为 µ的估计, 称该计算 值为 µ的一个点估计。
故,均值,方差2的矩估计为
ˆ X, 即 n 1 2 1 n 2 2 S . ˆ ( X X ) i n n i 1
15/22
如:正态总体N( , 2) 中 和2的矩估计为
ˆ X, ˆ2 1 n 2 ( X X ) . i n i 1
19/22
又如:若总体 X∼ U(a, b),求a, b的矩估计。
解:列出方程组
ˆ, E( X ) 2 ˆ Var ( X ) .
矩估计和极大似然估计
^ 2
1 n
n i1
Xi2
2
X .
14/22
即
ˆ X ,
ˆ 2
1 n
n i 1
(Xi
X )2.
故,均值,方差2的矩估计为
ˆ ˆ
X, 2 1
n
n
(X
i1
i
X )2
即
n 1S2. n
15/22
如:正态总体N(, 2) 中和2的矩估计为
)2
i1 2
(2 ) e , 2
n 2
1
2
2
n i1
( xi )2
对数似然函数为
ln
L(,
2
)
n 2
ln( 2
)
n 2
ln
2
1
2
2
n
( xi
i1
)2,
35/22
似然方程组为
ln L(, 2 ) 1 2
ln L(, 2 )
X1, X2 , … , Xn . 依样本对参数θ 做出估计,或估计参数θ 的 某个已知函数 g(θ ) 。 这类问题称为参数估计。
参数估计包括:点估计和区间估计。
4/22
为估计参数 µ,需要构造适当的统计量 T( X1, X2 , … , Xn ),
一旦当有了样本,就将样本值代入到该统计 量中,算出一个值作为µ的估计, 称该计算 值为 µ的一个点估计。
7/22
总体 k 阶原点矩 ak E(X k ),
样本 k 阶原点距
Ak
1 n
概率论与数理统计课件 L5.2参数的最大似然估计与矩估计

§52 参数的最大似然估计与矩估计
一、最大似然估计 二、矩估计
1
一、最大似然估计
1 最大似然法的基本思想 在已经得到试验结果的情况下 我们应该寻找使这个
结果出现的可能性最大的那个作为真的估计
2
一、最大似然估计
1 最大似然法的基本思想
设(X1 Xn)为来自总体X的样本 X的分布类型已知
但参数未知Θ
解 先求平均寿命EX即的最大似然估计量
似然函数为
ln
L(
)
nln
1
n
i1
xi
求得似然函数的驻点为0 x 故ˆ X 是的最大似然估计量
从而平均寿命的最大似然估计值为 x 172.7
11
例5.8 设某种型号的电子元件的寿命X(以小时计)的密
度函数为
f
(x, )
1
x
e
(x
0)
,θ未知且θ>0,现得样本值为
解 EX 2DX 故
xi
x
2 0
1 n
n
(xi
i1
x)2
可以断定0,
2 0
是最大值点
从而ˆ X
与ˆ
2
1 n
n
(
i1
X
i
X
)2
分别为与 2 的最大似然估计量
ˆ
x
与ˆ
2
1 n
n
(xi
i1
x)2
分
别为与2的最大似然估计值
8
最大似然估计的不变性 如果ˆ 是的最大似然估计 ug()是的函数且存在单值
反函数h(u) 那么g(ˆ) 是 g()的最大似然估计
20 (X1 Xn)为来自X的样本 (x1 xn)为样本值 试求 与 2的最大似然估计
一、最大似然估计 二、矩估计
1
一、最大似然估计
1 最大似然法的基本思想 在已经得到试验结果的情况下 我们应该寻找使这个
结果出现的可能性最大的那个作为真的估计
2
一、最大似然估计
1 最大似然法的基本思想
设(X1 Xn)为来自总体X的样本 X的分布类型已知
但参数未知Θ
解 先求平均寿命EX即的最大似然估计量
似然函数为
ln
L(
)
nln
1
n
i1
xi
求得似然函数的驻点为0 x 故ˆ X 是的最大似然估计量
从而平均寿命的最大似然估计值为 x 172.7
11
例5.8 设某种型号的电子元件的寿命X(以小时计)的密
度函数为
f
(x, )
1
x
e
(x
0)
,θ未知且θ>0,现得样本值为
解 EX 2DX 故
xi
x
2 0
1 n
n
(xi
i1
x)2
可以断定0,
2 0
是最大值点
从而ˆ X
与ˆ
2
1 n
n
(
i1
X
i
X
)2
分别为与 2 的最大似然估计量
ˆ
x
与ˆ
2
1 n
n
(xi
i1
x)2
分
别为与2的最大似然估计值
8
最大似然估计的不变性 如果ˆ 是的最大似然估计 ug()是的函数且存在单值
反函数h(u) 那么g(ˆ) 是 g()的最大似然估计
20 (X1 Xn)为来自X的样本 (x1 xn)为样本值 试求 与 2的最大似然估计
矩估计和极大似然估计 58页PPT文档共60页

矩估计和极大似ቤተ መጻሕፍቲ ባይዱ估计 58页 PPT文档
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
矩估计和极大似然估计PPT课件

(2). 把样本的联合概率函数中的自变量看成
已知常数, 参数θ 看成自变量, 得到似然 函数 L(θ );
(3). 求似然函数 L(θ) 的最大值点 (常常转化 为求ln L(θ)的最大值点) ,即θ的MLE;
(4). 在最大值点的表达式中,代入样本值, 就得参数 θ 的极大似然估计。
第30页/共45页
i1
i
X )2
即
n 1S2. n
第13页/共45页
如:正态总体N(, 2) 中和2的矩估计为
ˆ X ,
ˆ 2
1 n
n
(X i
i 1
X )2.
第14页/共45页
设总体 X 的分布函数中含 k 个未知参数
1,2 ,k .
步骤一:记总体X的m阶原点矩 E(Xm)为am ,
m =1,2,…,k. 一般地, am (m=1, 2,…, K) 是总体分布
Xn,要去估计未知参数θ 。
一种直观的想法是:哪个参数(多个参数 时是哪组参数) 使得现在的出现的可能性 (概 率) 最大,哪个参数(或哪组参数)就作为参数 的估计。这就是 极大似然估计原理。 如果
L(ˆ) max L( ).
θ 可能变化空间,
称为参数空间。
称 ˆ为θ 的极大似然估计 (MLE)。
若θ 是向量,上述似然方程需用似然方程组
代替 。
ln ln
L(1,2
1 L(1,2
,,k ,,k
) )
0, 0,
2
ln
L(1,2
,,k
)
0
k
● 用上述方法求参数的极大似然估计有时行不
通,这时要用极大似然原理来求 。
第32页/共45页
例2:某机器生产的金属杆用于汽车刹车系统,
已知常数, 参数θ 看成自变量, 得到似然 函数 L(θ );
(3). 求似然函数 L(θ) 的最大值点 (常常转化 为求ln L(θ)的最大值点) ,即θ的MLE;
(4). 在最大值点的表达式中,代入样本值, 就得参数 θ 的极大似然估计。
第30页/共45页
i1
i
X )2
即
n 1S2. n
第13页/共45页
如:正态总体N(, 2) 中和2的矩估计为
ˆ X ,
ˆ 2
1 n
n
(X i
i 1
X )2.
第14页/共45页
设总体 X 的分布函数中含 k 个未知参数
1,2 ,k .
步骤一:记总体X的m阶原点矩 E(Xm)为am ,
m =1,2,…,k. 一般地, am (m=1, 2,…, K) 是总体分布
Xn,要去估计未知参数θ 。
一种直观的想法是:哪个参数(多个参数 时是哪组参数) 使得现在的出现的可能性 (概 率) 最大,哪个参数(或哪组参数)就作为参数 的估计。这就是 极大似然估计原理。 如果
L(ˆ) max L( ).
θ 可能变化空间,
称为参数空间。
称 ˆ为θ 的极大似然估计 (MLE)。
若θ 是向量,上述似然方程需用似然方程组
代替 。
ln ln
L(1,2
1 L(1,2
,,k ,,k
) )
0, 0,
2
ln
L(1,2
,,k
)
0
k
● 用上述方法求参数的极大似然估计有时行不
通,这时要用极大似然原理来求 。
第32页/共45页
例2:某机器生产的金属杆用于汽车刹车系统,
极大似然估计.ppt

d dL( ) 0要容易
d
2、用上述求导方法求参数的MLE有时行不通,这时 要用极大似然估计原理来求 .
例1 设ξ1,ξ2,…, ξn是取自母体 ξ~b(1, p) 的一个子样,
求参数p的极大似然估计.
0 1分布
解:的概率函数为: P( x) px (1 p)1x ( x 0,1)
n
(1)似然函数 : L( p; x1,, xn ) pxi (1 p)1xi
§6.2 极大似然估计
(maximum likelihood estimate 简记为MLE或ML估计)
极大似然估计是在母体类型已知条件下使用的一 种参数估计方法 .
它首先是由德国数学家高斯在1821年提出的 , 费歇在1922年重新发现了这一方法,并首先研究了 这种方法的一些性质 .
极大似然原理:
i 1
n
n
xi
n xi
pi1 (1 p) i1
( xi 0,1)
n
n
(2)ln L ( xi )ln p (n xi )ln(1 p)
i 1
i 1
令
d
ln L dp
n
(
i 1
xi
)
1 p
(n
n
i 1
xi
)
1
1
p
0
(3) pˆ L
1 n
n i 1
xi
x
pˆ L
pˆ L是p的一致无偏估计量
解:该母体ξ服从两点分布:
ξ0 1 P 1-p p 因此,出现此子样的可能性的大小,是概率
P(1 1,2 1,3 0,4 1,5 1) 子样的联合分布列 P(1 1)P(2 1)P(3 0)P(4 1)P(5 1) p p (1 p) p p p4(1 p)记为 L( p)
d
2、用上述求导方法求参数的MLE有时行不通,这时 要用极大似然估计原理来求 .
例1 设ξ1,ξ2,…, ξn是取自母体 ξ~b(1, p) 的一个子样,
求参数p的极大似然估计.
0 1分布
解:的概率函数为: P( x) px (1 p)1x ( x 0,1)
n
(1)似然函数 : L( p; x1,, xn ) pxi (1 p)1xi
§6.2 极大似然估计
(maximum likelihood estimate 简记为MLE或ML估计)
极大似然估计是在母体类型已知条件下使用的一 种参数估计方法 .
它首先是由德国数学家高斯在1821年提出的 , 费歇在1922年重新发现了这一方法,并首先研究了 这种方法的一些性质 .
极大似然原理:
i 1
n
n
xi
n xi
pi1 (1 p) i1
( xi 0,1)
n
n
(2)ln L ( xi )ln p (n xi )ln(1 p)
i 1
i 1
令
d
ln L dp
n
(
i 1
xi
)
1 p
(n
n
i 1
xi
)
1
1
p
0
(3) pˆ L
1 n
n i 1
xi
x
pˆ L
pˆ L是p的一致无偏估计量
解:该母体ξ服从两点分布:
ξ0 1 P 1-p p 因此,出现此子样的可能性的大小,是概率
P(1 1,2 1,3 0,4 1,5 1) 子样的联合分布列 P(1 1)P(2 1)P(3 0)P(4 1)P(5 1) p p (1 p) p p p4(1 p)记为 L( p)
矩估计和极大似然估计

参数估计的方法
估计方法
点估计
矩估计法 顺序统计量法 最大似然法 最小二乘法
1/22
区间估计
参数的点估计
1. 矩法估计 2. 极大似然估计
2/22
参数估计问题的一般提法 设总体X的分布函数为F( x, θ ),其中θ 为未知参数或参数向量,现从该总体中抽样, 得到样本
X1, X2 , … , Xn . 依样本对参数θ 做出估计,或估计参数θ 的 某个已知函数 g(θ ) 。 这类问题称为参数估计。
设分布律 P{X k} f (x; ), 为待估参数, ,
(其中 是 可能的取值范围)
X1,
X2 ,
,
X
是来自总体
n
X
的样本,
n
则 X1, X 2,L , X n 的联合分布律为 f (xi ; ). i 1
2. 最大似然估计法
1.设总体X为离散型随机变量,它的分布律为
P{X x} f (x, )
θ 2 (θ )2,
11/22
令
2
( )2
X,
1 n
n i1
X i2.
用样本矩 估计总体矩
得
ˆ
1 n
n
i1
X
2 i
nX
2
1
n
n i1
(Xi
X
)2
,
ˆ X
1
n
n i1
(Xi
X )2
.
ˆ, ˆ 为参数 , 的矩估计。
12/22
例3:设总体X的均值为,方差为2,求和 2 的矩估计。
解: 先求总体的均值和2阶原点矩。
E( X ) x 1 e(x) d x
0
估计方法
点估计
矩估计法 顺序统计量法 最大似然法 最小二乘法
1/22
区间估计
参数的点估计
1. 矩法估计 2. 极大似然估计
2/22
参数估计问题的一般提法 设总体X的分布函数为F( x, θ ),其中θ 为未知参数或参数向量,现从该总体中抽样, 得到样本
X1, X2 , … , Xn . 依样本对参数θ 做出估计,或估计参数θ 的 某个已知函数 g(θ ) 。 这类问题称为参数估计。
设分布律 P{X k} f (x; ), 为待估参数, ,
(其中 是 可能的取值范围)
X1,
X2 ,
,
X
是来自总体
n
X
的样本,
n
则 X1, X 2,L , X n 的联合分布律为 f (xi ; ). i 1
2. 最大似然估计法
1.设总体X为离散型随机变量,它的分布律为
P{X x} f (x, )
θ 2 (θ )2,
11/22
令
2
( )2
X,
1 n
n i1
X i2.
用样本矩 估计总体矩
得
ˆ
1 n
n
i1
X
2 i
nX
2
1
n
n i1
(Xi
X
)2
,
ˆ X
1
n
n i1
(Xi
X )2
.
ˆ, ˆ 为参数 , 的矩估计。
12/22
例3:设总体X的均值为,方差为2,求和 2 的矩估计。
解: 先求总体的均值和2阶原点矩。
E( X ) x 1 e(x) d x
0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二阶原点矩
EX 2 x2
1
x
e dx
1
x
2e
x
dx
2(3)
2
2
2
0
2020/4/26
15
EX 用 A2
1 n
n i 1
X i2替换
2即
得的矩估计量为
A2
1 n
n i 1
X
2 i
2 2
ˆ
11 2n
n i 1
X
2 i
A2 / 2 ,
0
解法二
E
X
x
1
x
e dx
1
x
一个或多个未知参数:1,2, ,k
设 X1, X2,…, Xn为总体的一个样本 构造 k 个统计量:
1( X1, X 2 , , X n ) 2 ( X1, X 2 , , X n )
随机变量
2020/4/26
k ( X1, X 2 , , X n )
5
当测得一组样本值(x1, x2,…, xn)时,代入上述 统计量,即可得到 k 个数:
1
n 1
n i 1
(Xi
X )2
S2
是无偏矩估计
注: 矩估计不唯一
2020/4/26
8
事实上,按矩法原理,令
X
1 n
n i 1
Xi
ˆ
A2
1 n
n i 1
Xi2是E(X2 )的估计
ˆ X
ˆ 2 E( X 2 ) E 2 ( X ) A2 ˆ 2
1 n
n i1
X
2 i
X
2
1 n
n i 1
1. 矩方法
方法
用样本的 k 阶矩作为总体的 k 阶矩的 估计量, 建立含待估计参数的方程, 从而可解出待估计参数
2020/4/26
7
一般地,不论总体服从什么分布,总体期望 与方差 2 存在,则根据矩估计法它们的
矩估计量分别为
ˆ
1 n
n i1
Xi
X
ˆ 2
1 n
n i 1
(Xi
X )2
Sn2
(Xi
X
)2
Sn2
2020/4/26
9
设待估计的参数为1,2 , ,k
设总体的 r 阶矩存在,记为
E( X r ) r (1, 2 , , k )
设 X1, X2,…, Xn为一样本,样本的 r 阶矩为
令
Br
1 n
n i 1
X
r i
r (1,2 ,
, k
)
1 n
n i1
X
r i
r 1,2, , k
2020/4/26
18
2、极大似然函数法
先看一个简单的例子: 某位同学与一位猎人一起外出打猎,一只
野兔从前方窜过.只听到一声枪响,野兔应声 倒下.如果要你推测,是谁打中的呢?你会如 何想呢?
你就会想,只发一枪便打中,猎人命中的 概率一般大于这位同学命中的概率.看来这 一枪是猎人射中的.
ˆ1(x1, x2 , , xn )
ˆ2 (x1, x2 , , xn )
数值
ˆk (x1, x2 , , xn )
称数ˆ1,ˆ2 , ,ˆk 为未知参数1,2 , ,k 的估计值
对应的统计量为未知参数1,2 , ,k 的估计量
问题 如何构造统计量?
2020/4/26
6
二.点估计的方法
1、矩方法;(矩估计) 2、极大似然函数法(极大似然估计).
第二章 参数估计
2020/4/26
1
统计 推断 的 基本 问题
参数估 计问题
点估计 区间估 计
假设检 验问题
2020/4/26
2
什么是参数估计?
参数是刻画总体某方面的概率特性的数量.
当这个数量是未知的时候,从总体抽出一个 样本,用某种方法对这个未知参数进行估计 就是参数估计.
例如,X ~N ( , 2),
1 n
n i 1
Xi
X
ˆ X 为的矩估计量,
1 X
ˆ x
1 x
为的矩估计值.
2020/4/26
14
例3 设总体X的概率密度为
f (x, )
1
x
e ,
2
求的矩估计量 ˆ
x ,
0
解法一 虽然 f (x中, )仅含有一个参数,但
因
EX
x
1
x
e dx 0
2
不含,不能由此解出,需继续求总体的
x e dx (2)
2
0
即 E|X|
1 n
用 n i1 X i
替换
EX
即得的另一矩估计量为
ˆ 1
n
n i 1
Xi
2020/4/26
16
• 矩估计的优点 – 不依赖总体的分布,简便易行 – 只要n充分大,精确度也很高。
• 矩估计的缺点 – 矩估计的精度较差; – 要求总体的某个k阶矩存在; – 要求未知参数能写为总体的原点矩的函数形 式
ˆ2 ˆ2 (x1, x2 , , xn )
——未知参数1,2, ,k
的矩估计值
ˆ 2020/4/2k6 ˆk ( x1, x2 , , xn )
11
例1 有一批零件,其长度X~N(,2),现从 中任取4件,测的长度(单位:mm)为 12.6,13.4,12.8,13.2。试估计和2的值。
解: 由
f
( x;
)Leabharlann x 1 ,0,0 x 1 其它
X1,X2,,Xn为来自于总体X的样本,x1,x2, ,xn 为样本值,求参数的矩估计。
解: 先求总体矩
1
1
E( X ) x x 1dx x dx
x 1 1
0
0
1 0 1
解之: E( X )
1 E(X )
2020/4/26
13
令
A1
2020/4/26
17
注意:
1. 总体不一定存在适当阶的矩。
例 考虑Cauchy分布,其密度函数为
f ( x, )
1
, x ,
(1 ( x )2 )
其各阶矩均不存在。
2. 对相同的参数 q( ),存在多个矩估计。
例如,考虑总体是参数为 的Poisson分布,
既是总体的均值,又是总体的方差。
x 1 (12.6 13.4 12.8 13.2) 13 4
s2 1 [(12.6 13)2 (13.4 13)2 (12.8 13)2 4 1 (13.2 13)2 ] 0.133
得和2的估计值分别为13(mm)和 0.133(mm)2
2020/4/26
12
例2 设总体X的概率密度为
—— 含未知参数 1,2, ,k 的方程组
2020/4/26
10
解方程组,得 k 个统计量:
ˆ1( X1, X 2 , , X n )
ˆ2 ( X1, X 2 , , X n )
——未知参数1,2, ,k
的矩估计量
ˆk ( X1, X 2 , , X n )
代入一组样本值得k个数:
ˆ1 ˆ1(x1, x2 , , xn )
若, 2未知,通过构造样本的函数, 给出它
们的估计值或取值范围就是参数估计的内容.
点估计 区间估计
2020/4/26
3
参数估计的类型
点估计 —— 估计未知参数的值
区间估计—— 估计未知参数的取值范围, 使得这个范围包含未知参数 真值的概率为给定的值.
2020/4/26
4
第一节 参数的点估计
一、点估计的思想方法 设总体X 的分布函数的形式已知,但它含有
