数字逻辑设计习题参考答案 (第2,3章)
数字逻辑与数字系统设计第2-3章客观题
（）1、数字电路又称为开关电路、逻辑电路。
答案：正确（）2、二极管、三极管、场效应管是常用的开关元件。
答案：正确（）3、最基本的逻辑关系是：与、或、非。
答案：正确（）4、高电平用0表示，低电平用1表示，称为正逻辑。
答案：错误（）5、TTL型门电路比CMS型门电路开关速度快。
答案：正确（）6、逻辑表达式是逻辑函数常用的表示方法。
答案：正确（）7、用真值表表示逻辑函数，缺乏直观性。
答案：错误（）8、逻辑图是最接近实际的电路图。
答案：正确（）9、由真值表得到的逻辑函数一般都要经过化简。
答案：正确（）10、组合电路的特点是：任意时刻的输出与电路的原状态有关。
答案：错误（）11、1+A＝1答案：正确（）12、AB+A＝A（）13、将实际问题转换成逻辑问题第一步是要先写出逻辑函数表达式。
答案：错误14、异或函数与同或函数在逻辑上互为反函数。
（对）每个最小项都是各变量相“与”构成的，即n个变量的最小项含有n个因子。
（对）15、因为逻辑表达式A+B+AB=A+B成立，所以AB=0成立。
（错）16、逻辑函数F=A B+A B+B C+B C已是最简与或表达式。
（错）17、利用约束项化简时，将全部约束项都画入卡诺图，可得到函数的最简形式。
（错）18、卡诺图中为1的方格均表示逻辑函数的一个最小项。
（对）19、在逻辑运算中，“与”逻辑的符号级别最高。
（错）20、标准与或式和最简与或式的概念相同。
（对）21、数字电路中用“1”和“0”分别表示两种状态，二者无大小之分。
（对）22、格雷码具有任何相邻码只有一位码元不同的特性。
（对）23、所有的集成逻辑门，其输入端子均为两个或两个以上。
（错）24、根据逻辑功能可知，异或门的反是同或门。
（对）25、逻辑门电路是数字逻辑电路中的最基本单元。
（对）26、TTL和CMOS两种集成电路与非门，其闲置输入端都可以悬空处理。
（错）27、74LS系列产品是TTL集成电路的主流，应用最为广泛。
数字逻辑第二章课后答案
2-1
2-2
均可以作为反相器使用。
与非门：
或非门：
异或门：
2-3 1
Y V
CMOS 与非门的一个输入端通过电阻接地，相当于该输入端输入低电平，输出Y1是高电平。
2Y V
CMOS 或非门的一个输入端通过电阻接高电平与直接接高电平是一样的，输出Y2是低电平。
V 3
Y V 低电平有效的三态门的使能端EN 接高电平，则Y3为高阻态。
4
Y V
与或非门的一个与门输入全为高电平，则输出Y4是低电平。
2-4
E D C B A Y ⋅⋅⋅⋅=1 E D C B A Y ++++=2
))((3F E D C B A Y ++++=
F E D C B A Y ⋅⋅+⋅⋅=4 2-5
当1=EN ，T1`和T2截止，Y=Z （高阻）。
当0=EN ，T1`导通，A A Y ==。
2-7
（1）忽略所有门电路的传输延迟时间，除去开始的一小段时间，与非门的两个输入端总有一个是低电平，输出一直为高电平。
（2）考虑每个门都有传输延迟时间。
假设1级门的传输延迟时间为tpd ，则与非门的两个输入端的输入信号变化实际上并不是同时的。
信号A 经过两级门的传输延迟，比信号B 要晚2tpd 时间到达与非门的输入端。
因此，将出现,在短暂时间里，两个输入端的输入信号都是高电平的情况，输出电压波形出现毛刺。
《数字逻辑》第3章习题答案
题
【3-1】填空： (1) 逻辑代数中有三种最基本运算： 与 、 或 和 非 ，在此基础上又派生出五种基本运算， 分别为 与非 、 或非 、 异或 、 同或 、和 与或非 。 (2) 与运算的法则可概述为：有 0 出 0 ，全 1 出 1 ；类似地，或运算的法则为 有”1”出”1”， 全”0”出”0” 。 (3) 摩根定理表示为： A B = A B ； A B = A B 。 (4) 函数表达式 Y= AB C D ，则其对偶式为 Y ' = ( A B)C D 。 积的形式结果应为 M ( 0,1,2,4,5,8,9,10)。 (5) 函数式 F=AB+BC+CD 写成最小项之和的形式结果应为 m ((3,6,7,11,12,13,14,15))， 写成最大项之
0 0 1 1 1 1
1 1 0 0 1 1
0 1 0 1 0 1
1 1 0 0 1 0
【3-8】写出下列函数的反函数 F ，并将其化成最简与或式。 (1) F1 ( A D )( B C D)( AB C ) (2) F2 ( A B )( BCD E )( B C E )(C A) (3) F3 A B C A D (4) F4 ( A B)C ( B C ) D 解： (1) F1 AD C (2) F2 AB A C E (3) F3 AB AC A D (4) F4 BC C D ABD A B C 【3-9】用对偶规则，写出下列函数的对偶式 F ，再将 F 化为最简与或式。 (1) F1 AB B C A C (2) F2 A B C D (3) F3 ( A C )( B C D)( A B D) ABC (4) F4 ( A B )( A C )( B C )(C D) (5) F5 AB C CD BD C 解：题中各函数对偶函数的最简与或式如下： (1) F1 A BC AB C (2) F2 A B D A C D (3) F3 AC A BD (4) F4 A BC B C CD (5) F5 ABC D (6) F6 AB C D 【3-10】已知逻辑函数 F A B C , G=A⊙B⊙C，试用代数法证明： F G 。 解：
数字逻辑设计习题参考答案 (第2章)
数字逻辑设计习题册班级：学号：姓名：哈尔滨工业大学（威海）计算机科学与技术学院体系结构教研室第2章 逻辑代数基础2—1 填空1．摩根定理表示为：=⋅B A ＿B A +＿＿；=+B A ＿B A ⋅＿＿。
2. 函数表达式D C AB Y ++=，则其对偶式为='Y ＿D C B A ⋅⋅+)(＿＿＿＿＿＿＿。
3．根据反演规则，若C D C B A Y +++=，则=Y C D C B A ⋅++)(。
4．函数式CD BC AB F ++=写成最小项之和的形式结果为()15,14,113,12,11,7,6,3∑m ，写成最大项之积的形式结果为)10,9,8,5,4,2,1,0(∏M。
5. （33.33）10 =（100001.0101 ）2 =（ 41.2 ）8 =（ 21.5 ）162—2 证明1．证明公式()()A BC A B A C +=++成立。
2．证明此公式B A B A A +=+成立。
3．证明此公式)()()()()(C A B A C B C A B A +⋅+=+⋅+⋅+成立。
左边 (由分配律得)右边BCA BCB C A BC BA AC AA C A B A +=+++=+++=++)1())((BA A AB B B A B A B A AB AB B A B A AB BA B B A +=+++=+++=++=++=)()()(ACBC A B C A AC B C A C B B A ++=+⋅+=+⋅+⋅+=)()()()()(ACBC A B BC A B AC A A ++=+++=4. 证明此公式1))(((=+++⋅++C B D B A C B D C C B A 成立。
左边5.证明此公式D C D C B A D AC D C B D C A ⊕=+++⊕)(成立。
左边2—3 用代数法化简下列各式 1．B A BC A F +=1 2．D C A ABD CD B A F ++=2F 1 F 23．CD D AC ABC C A F +++=3 F 34．)()(4C B A C B A C B A F ++⋅++⋅++=F 41))((0))((=+++=+++⋅=C B D B A C B C B D B A C B D C C B A DC DC BD C D C D C A D C B D C A D AC D C A D C B D C A D AC A B D C D C A D AC B A B D C D C A ⊕=++=⊕++⊕=+++⊕=+++⊕=+++⊕=)()()()()()()(1=++++=B A C B A ADC B C B AD C B C B AD =+=++=)()(CDA CDC B C A CD AC AB C A D A C B C A D D A C BC C A +=+++=+++=+++=+++=)()()()()(CB AC B C B A A C A C B A C A C B A +=++=++=+++=)()(x y x y x =+⋅+)()(5．C DE C BE CD B B A AC F ++++=5F 56．C B A AD C B A CD AB F ++++=6F 67．D BC A BD A BD CD B B A C A F +++++=7F 78. D D C C A B A F +++=8F 8 1=++++=D D C C A B A9. D AC D C A D C B D C D C A F ++++=)(9F 9CE B AC CE D B B AC C E D B AC B AC C E D B C A B AC C E D B D B C B B A AC C E D B D C B B A AC ++=+++=+++=++++=++++=+++++=)()()(DC B A AD B C AB AD D C B C AB AD A A C B D C AB +++=++++=++++=+++++=)()(1)()()()()(=++++=+++++=+++++=+++++=+++++=+++++=A CD B BD A C A A CD B BD B B A C A A CD B B A D A B C A A CD B B A BD D B A C A A BD CD B B A D B C A BD A BD CD B B A D BC C A DC D C D C B D C D C D C D C A D C B D C D C A +=++=++++=)()(10.D B AB C D B AB F +++++=10(y x y x x +=+)2—4用卡诺图化简下列各式1．C B A AB C B F ++=1 2．C B BC B A F ++=2F 1ABC += F 2B A +=3．C B C B C A C A F +++=3F 3C B B A C A ++=4．D C A C B AD C D C A ABD ABC F +++++=4D A F +=4111111111111AB CD0001111000011110D B AB C DB ABCD B AB ++=++⋅⋅=5．D B A AC C B A F ++=5 6．C B A AD C B A D C AB F ++++=6AC D B B A F ++=5 A C B DC F ++=6 7．D BC A BD A CD B B A C A F +F 7=18．D B D B C A C A F +++=8D)⊙(B C)⊙(8⋅=+++=A D C B A ABCD D C B A D C B A F11111111AB CD 00011110000111109．D C B A D AC D C B D C A F +++⊕=)(9D C D C F +=9 10. ))((10C AB B A F ++=C B C A F +=1011. C B AC D C A B A F +++=11AC C B B A F ++=1112．∑=mC B A P )7,6,5,2,1,0(),,(1AC C B B A P ++=2 13．=D C B A P )14,11,10,9,8,7,6,4,3,2,1,0(),,,(2D C C A D A B P +++=2 14．∑=mD C B A P )15,14,13,12,10,9,8,6,4,1,0(),,,(3D A D B C B AB D C P ++++=315. ∑=m D C B A P )15,14,13,11,9,7,6,5,3,1(),,,(4F 15=D+BC2—5 用卡诺图化简下列带有约束条件的逻辑函数 1．∑∑+=d mD C B A P )15,14,13,2,1,0()12,11,9,8,6,3(),,,(1CD A D B C A P ++=1 2．∑∑+=d mD C B A P )15,14,13,10,9,8()12,11,6,5,4,3,2,0(),,,(2C B C BD P ++=23．D C B A D C B A D C A P ++++=3， 约束：0=+AC ABD C B D C A D C A P ++=34．CD B A CD B A P +=4， 约束：A B C D 为互相排斥的一组变量，即在任何情况下它们之中不可能两个同时为1。
数字逻辑课后答案第二章
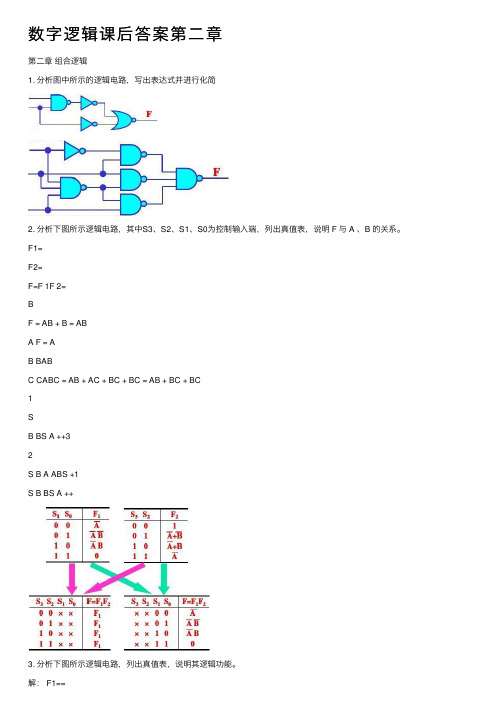
数字逻辑课后答案第⼆章第⼆章组合逻辑1. 分析图中所⽰的逻辑电路，写出表达式并进⾏化简2. 分析下图所⽰逻辑电路，其中S3、S2、S1、S0为控制输⼊端，列出真值表，说明 F 与 A 、B 的关系。
F1=F2=F=F 1F 2=BF = AB + B = ABA F = AB BABC CABC = AB + AC + BC + BC = AB + BC + BC1SB BS A ++32S B A ABS +1S B BS A ++3. 分析下图所⽰逻辑电路，列出真值表，说明其逻辑功能。
解： F1==真值表如下：当B ≠C 时， F1=A 当B=C=1时， F1=A 当B=C=0时， F1=0裁判判决电路，A 为主裁判，在A 同意的前提下，只要有⼀位副裁判（B ，C ）同意，成绩就有效。
F2=真值表如下：CB BC A C AB C B A +++ABCC B A ABC C B A C B A +⊕=++)(A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 100000111AC BC AB C A C B B A ++=++当A 、B 、C 三个变量中有两个及两个以上同时为“1”时，F2 = 1 。
4.图所⽰为数据总线上的⼀种判零电路，写出F 的逻辑表达式，说明该电路的逻辑功能。
解：F=只有当变量A0~A15全为0时，F = 1；否则，F = 0。
因此，电路的功能是判断变量是否全部为逻辑“0”。
5. 分析下图所⽰逻辑电路，列出真值表，说明其逻辑功能解：因此，这是⼀个四选⼀的选择器。
6. 下图所⽰为两种⼗进制数代码转换器，输⼊为余三码，输出为什么代码？解：A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1000011111514131211109876543210A A A A A A A A A A A A A A A A +++301201101001X A A X A A X A A X A A F +++=这是⼀个余三码⾄8421 BCD 码转换的电路7. 下图是⼀个受 M 控制的4位⼆进制码和格雷码的相互转换电路。
数字逻辑课后习题答案
第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制491100016153110101651271111111177635100111101111737.493111.11117.7479.4310011001.0110111231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010101211110161751011100921340.100110.593750.4610111147570110113153.将下列十进制数转换成8421BCD码1997=000110011001011165.312=01100101.0011000100103.1416=0011.00010100000101100.9475=0.10010100011101014.列出真值表，写出X的真值表达式A B C X00000010010001111000101111011111X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时：A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时：A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时：A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1)(A⊕B)⊕C=A⊕(B⊕C)A B C(A⊕B)⊕C A⊕(B⊕C)0000000111010110110010011101001100011111所以由真值表得证。
（2）A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C00011001000100001111100001011111011111007.证明下列等式（1）A+A B=A+B 证明：左边=A+A B=A(B+B )+A B =AB+A B +A B =AB+A B +AB+A B =A+B =右边(2)ABC+A B C+AB C =AB+AC 证明：左边=ABC+A B C+AB C=ABC+A B C+AB C +ABC =AC(B+B )+AB(C+C )=AB+AC =右边（3）E D C CD A C B A A )(++++=A+CD+E证明：左边=ED C CD A C B A A )(++++=A+CD+A B C +CDE =A+CD+CD E =A+CD+E =右边（4）C B A C B A B A ++=CB C A B A ++证明：左边=CB AC B A B A ++=C B A C AB C B A B A +++)(=C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式(1)F=A+ABC+A C B +CB+C B =A+BC+C B (2)F＝(A+B+C )(A+B+C)=(A+B)+C C =A+B (3)F＝ABC D +ABD+BC D +ABCD+B C =AB+BC+BD (4)F=C AB C B BC A AC +++=BC(5)F=)()()()(B A B A B A B A ++++＝B A 9.将下列函数展开为最小项表达式(1)F(A,B,C)=Σ(1,4,5,6,7)(2)F(A,B,C,D)=Σ(4,5,6,7,9,12,14)10.用卡诺图化简下列各式（1）CAB C B BC A AC F +++=0 ABC00 01 11 1011111化简得F=C(2)CB A D A B A DC AB CD B A F++++=111111AB CD 00 01 11 1000011110化简得F=DA B A +（3）F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)1111111111ABCD 00 01 11 1000011110化简得F=DBC D C A BC A C B D C ++++(4)F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)Φ1ΦΦ1ΦΦ1Φ1AB CD 00 01 11 1000011110化简得F=ACAD B A ++11.利用与非门实现下列函数，并画出逻辑图。
数字逻辑第3章答案
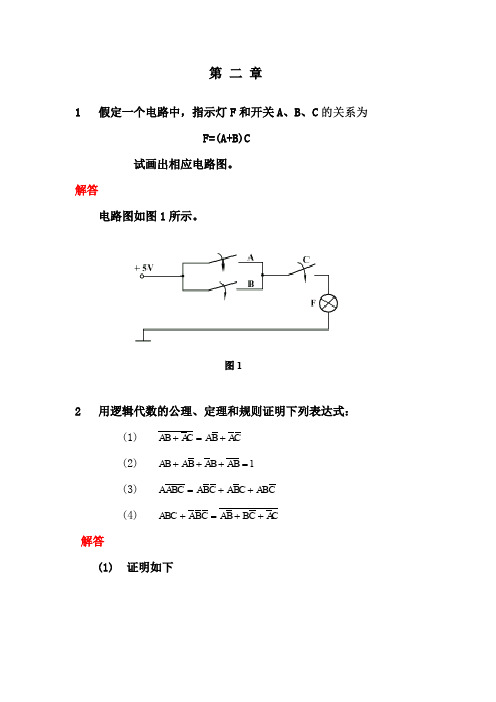
F， A B[(C D)E G]
5 (1) 如果已知 X + Y 和 X + Z 的逻辑值相同,那么 Y 和 Z 的逻
辑值一定相同。正确吗?为什么? (2) 如果已知 XY 和 XZ 的逻辑值相同,那么那么 Y 和 Z 的逻辑值
一定相同。正确吗?为什么? (3)如果已知 X + Y 和 X + Z 的逻辑值相同,且 XY 和 XZ 的逻辑
(1) F(A, B,C, D) BD AD CD CD ACD ABD
(2) F(A, B,C, D) (AB AB) C (AB AB) C
解答
G(A, B,C, D) AB BC AC (A B C) ABC
(1) 当 b a 时，令 a=1,b=0 能得到最简“与-或”表达式： F BC CD ACD （3 项）
(2) 当 a=1,b=1 时，能得到最简的“与-或”表达式：
F BC CD AC （3 项）
11 用列表法化简逻辑函数
F(A, B,C, D) m(0,2,3,5,7,8,10,11,13,15)
10
0
0
01 0 0 1 1
1
1
10 0 0 1 1
1
1
11 0 1 0 1
0
0
4 求下列函数的反函数和对偶函数： (1) F AB AB
(2) F A B A C C DE E
(3) F (A B)(C DAC)
(4) F A B CD E G
值相同，那么 Y = Z。正确吗?为什么? (4) 如果已知 X+Y 和 X·Y 的逻辑值相同,那么 X 和 Y 的逻辑值
数字逻辑与数字系统设计习题参考答案
input a,b,c,d;
output f;
reg f;
always @(a or b or c or d)
case({a,b,c,d})
4'b0011: f<=1'b1;
4'b0100: f<=1'b1;
4'b0101: f<=1'b1;
4'b1010: f<=1'b1;
W=∑m(5,6,7,8,9)+∑d(10,11,12,13,14,15)
X=∑m(1,2,3,4,9)+∑d(10,11,12,13,14,15)
Y=∑m(0,3,4,7,8)+∑d(10,11,12,13,14,15)
Z=∑m(0,2,4,6,8)+∑d(10,11,12,13,14,15)
用卡诺图化简得：
[104-97]补=01101000+10011111=00000111, 104-97=(00000111)2=7
(2)(-125)10=(-1111101)2[-1111101]补=10000011
(79)10=(01001111)2[01001111]补=01001111
[-125+79]补=10000011+01001111=11010010，-125+79=(-0101110)2=-46
(5)F=∑m(1,2,3,4,5,6)
(6)F=∑m(4,7,8,11)
2.9解：
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
或=
数字逻辑电路与系统设计习题答案
第1章习题及解答1.1 将下列二进制数转换为等值的十进制数。
（1）（11011）2 （2）（10010111）2（3）（1101101）2 （4）（11111111）2（5）（0.1001）2（6）（0.0111）2（7）（11.001）2（8）（101011.11001）2题1.1 解：（1）（11011）2 =（27）10 （2）（10010111）2 =（151）10（3）（1101101）2 =（109）10 （4）（11111111）2 =（255）10（5）（0.1001）2 =（0.5625）10（6）（0.0111）2 =（0.4375）10（7）（11.001）2=（3.125）10（8）（101011.11001）2 =（43.78125）10 1.3 将下列二进制数转换为等值的十六进制数和八进制数。
（1）（1010111）2 （2）（110111011）2（3）（10110.011010）2 （4）（101100.110011）2题1.3 解：（1）（1010111）2 =（57）16 =（127）8（2）（110011010）2 =（19A）16 =（632）8（3）（10110.111010）2 =（16.E8）16 =（26.72）8（4）（101100.01100001）2 =（2C.61）16 =（54.302）81.5 将下列十进制数表示为8421BCD码。
（1）（43）10 （2）（95.12）10（3）（67.58）10 （4）（932.1）10题1.5 解：（1）（43）10 =（01000011）8421BCD（2）（95.12）10 =（10010101.00010010）8421BCD（3）（67.58）10 =（01100111.01011000）8421BCD（4）（932.1）10 =（100100110010.0001）8421BCD1.7 将下列有符号的十进制数表示成补码形式的有符号二进制数。
数字设计-原理与实践(第四版)课后习题答案
第1 章习题参考答案:1-6 一个电路含有一个2 输入与门（AND2），其每个输入/输出端上都连接了一个反相器；画出该电路的逻辑图，写出其真值表；能否将该电路简化解：电路图和真值表如下：由真值表可以看出，该电路与一个2 输入或门（OR2）相同。
第2 章习题参考答案:将下面的八进制数转换成二进制数和十六进制数。
(a) 12348=1 010 011 1002=29C16(b) 1746378=1 111 100 110 011 1112=F99F16(c) 3655178=11 110 101 101 001 1112=1EB4F16(d) =10 101 011 101 011 010 0012=ABAD116(e) =111 100 011 0012=(f) =100 101 011 001 100 111 12=将下面的十六进制数转换为二进制数和八进制数。
(a) 102316=1 0000 0010 00112=100438(b) 7E6A16=111 1110 0110 10102=771528(c) ABCD16=1010 1011 1100 11012=1257158(d) C35016=1100 0011 0101 00002=1415208(e)=1001 1110 10102=(f)=1101 1110 1010 1110 1110 11112=将下面的数转换成十进制数。
(a) =107 (b) 1740038=63491 (c) 2=183(d) = (e)= (f)F3A516=62373(g) 120103=138 (h) AB3D16=43837 (i) 71568=3694(j) =完成下面的数制转换。
(a) 125= 1 111 1012 (b) 3489= 66418 (c) 209= 11 010 0012(d) 9714= 227628 (e) 132= 10 000 1002 (f) 23851= 5D2B16(g) 727= 104025 (h) 57190=DF6616 (i) 1435=26338(j) 65113=FE5916将下面的二进制数相加，指出所有的进位：(a) S：1001101 C：100100(b) S: 1010001 C: 1011100(c) S: 0 C: 0(d) S: C:利用减法而不是加法重复训练题，指出所有的借位而不是进位：(a) D：011 001 B：110000 (b) D：111 101 B：1110000(c) D： B：00111000 (d) D：1101101 B：写出下面每个十进制数的8 位符号－数值，二进制补码，二进制反码表示。
数字逻辑与系统设计习题(1-3)
第1章习题一．单选题：1．以下代码中为恒权码的是（ ）。
A ）余3循环码B ）5211码C ）余3码D ）右移码2．一位八进制数可以用（ ）位二进制数来表示。
A ）1B ）2C ）3D ）43．十进制数43用8421BCD 码表示为（ ）A ）10011B ）0100 0011C ）1000011D ）100114．A + BC =（ ）A ）AB + AC B ）ABC C ）(A +B)(A + C)D ）BC5．在函数L(A,B,C,D) = AB + CD 的真值表中，L=1的状态有（ ）A ）2个B ）4个C ）6个D ）7个6．已知两输入逻辑变量AB 和输出结果Y 的真值表如下表，则AB 的逻辑关系为（ ）A ）同或B ）异或C ）与非D ）或非 7．利用约束项化简逻辑函数时，约束项应看成（ ） A ）1B ）2C ）能使圈组大的看成1，其它看成0D ）无所谓8．当逻辑函数有 n 个变量时，共有（ ）组变量取值组合A ）nB ）2nC ）n 2D ）2n9．利用卡诺图化简逻辑函数时,8个相邻的最小项可消去（ ）个变量。
A ）1B ）2C ）3D ）410．下面的卡诺图化简,应画（ ）个包围圈。
A ）2B ）3C ）4D ）511．卡诺图中，变量的取值按（ ）规律排列。
A ）Ascii 码B ）8421BCD 码C ）余3码D ）循环码12．4变量逻辑函数的真值表，表中的输入变量的取值应有（ ）种。
A ）2B ）4C ）8D ）1613．TTL 逻辑电路是以( )为基础的集成电路A ）三极管B ）二极管C ）场效应管D ）晶闸管14．CMOS 逻辑电路是以( )为基础的集成电路A ）三极管B ）NMOS 管C ）PMOS 管D ）NMOS 管和PMOS 管二．判断题：1．十进制数(64.5)10与(40.8)16等值。
（ ）2．在任一输入为1的情况下,"或非"运算的结果是逻辑0。
《数字逻辑-应用与设计》部分习题参考答案
6.4d 激励表达式： T1=F1+F3’F2’ T2=F2+F3’F1’x1’+F3’x1x2’x3+F3’F2’F1’x3’ T3=F3F2’+F2F1+F1x1’+F1x3’
十进制 +12 -12 +9.5 -22.5
+19.75 -17.25
以 1 为基的补码 01100 10011 01001.1
1 01001.0 10011.11 101110.10
以 2 为基的补码 01100 10100 01001.1
1 01001.1 10011.11 101110.11
Made by HeYuchu&QinPiqi
5.b 略(见课本附录 B-奇数号习题参考答案)
6.1c 激励表达式：
S3=F2F1’x S2=F3’F1x+F3F1’x S1=F1’x+F2F1’+F3x R3=F3 R2=x’+F3’F1’ R1=F3’F2’F1+F1x’
6.1d 激励表达式：
R1=F1 R2=F2 R3=F1’ S1=F3’F2’F1’ S2=F3’F2’F1’x1’+F3’F2’F1’x3’+F3’F2’x1x2’x3 S3=F2F1+F1x1’+F1x2+F1x3’
or=A’B+A’C=(A+B’)’+(A+C’)’=[(A+B’)(A+C’)]’ f. (A’B’)’(CD’)’=(A’B’+CD’)’=(A+B)’+(C’+D)’ g. W+Q=(W’Q’)’ h. (A+B+C)D=(AD+BD+CD)=(A’+D’)’+(B’+D’)’+(C’+D’)’ i. (AB’+C’D+EF)’=[(A’+B)’+(C+D’)’+(E’+F’)’]’=(A’+B)(C+D’)(E’+F’) j. [(A+B)’+C’]’=(A’B’+C’)’=(A’B’)’C=(A+B)C
数字逻辑与数字系统设计习题参考答案
数字逻辑与数字系统设计第1章习题解答1.3 (1)86 (2)219 (3)106.25 (4)0.6875 1.4 (1)101111 (2)1001000 (3)100001l.11 (4)0.1011.5 (1)(117)10=(165)8=(1110101)2=(75)16(2)(3452)10=(6574)8=(110101111100)2=(D7C)16(3)(23768.6875)10=(56330.54)8=(101110011011000.1011)2=(5CD8.B)16(4)(0.625)10=(0.5)8=(0.101)2=(0.A)161.6 (1)(117)8=(1001111)2=(79)10(2)(7456)8=(111100101110)2=(3886)10(3)(23765.64)8=(10 0111 1111 0101.1101)2=(10229.8125)10(4)(0.746)8=(0.11111)2=(0.96875)101.7 (1) (9A)16=(10011010)2=(154)10(2) (3CF6)16=(11110011110110)2=(15606)10(3) (7FFE.6)16=(111111*********.011)2=(32766.375)10(4) (0.C4)16=(0.110001)2=(0.765625)101-8 (1)(125)10=(000100100101)8421BCD(2)(7342)10=(0111001101000010)8421BCD(3)(2018.49)10=(0010000000011000.01001001)8421BCD(4)(0.785)10=(0.011110000101)8421BCD1.9(1)(106)10=(1101010)2原码=反码=补码=01101010(2)(-98)10=(-1100010)2 原码=11100010反码=10011101补码=11100011(3)(-123)10=(-1111011)2 原码=11111011反码=10000101补码=11111011(4)(-0.8125)10=(-0.1101)2 原码=1.1101000反码=1.0010111补码=1.00110001.10(1)(104)10=(1101000)2 [1101000]补=01101000(-97)10=(-1100001)2 [-1100001]补=1001111110000011+ 0100111111010010 01101000+ 1001111100000111[104-97]补=01101000+10011111=00000111, 104-97=(00000111)2=7 (2) (-125)10=(-1111101)2[-1111101]补=10000011(79)10=(01001111)2[01001111]补=01001111[-125+79]补=10000011+01001111=11010010，-125+79=(-0101110)2=-46 (3) (120)10=(1111000)2[01111000]补=01111000(-67)10=(-1000011)2[-1000011]补=10111101[120-67]补=10000011+01001111=00110101，-125+79=(00110101)2=53 (4) (-87)10=(-1010111)2[-1010111]补=10101001(12)10=(1100)2[1100]补=00001100[-87+12]补=10101001+00001100=10110101，-125+79=(-1001011)2=-7501111000 + 101111010011010110101001 + 0000110010110101第2章 习题解答2.3 解：根据逻辑图可直接写出逻辑表达式：(a) F=C B B A +；(b) F=C A C B B A解：设3个输入变量分别为A 、B 、C ，输出为F ，按题意，其中有奇数个为1，则输出F ＝1，因此可写出其逻辑表达式为F=ABC C B A C B A C B A +++。
数字逻辑课后习题答案（科学出版社_第五版）
第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表，写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时：A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时：A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时：A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
（2）A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式（1）A+A B=A+B证明：左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明：左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B)+AB(C+C)=AB+AC=右边（3）EDCCDACBAA)(++++=A+CD+E证明：左边=EDCCDACBAA)(++++=A+CD+A B C+CD E=A+CD+CD E=A+CD+E=右边（4）C B A C B A B A ++=CB C A B A ++证明：左边=CB AC B A B A ++=CB AC AB C B A B A +++)(=C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式(1) F=A+ABC+A C B +CB+C B = A+BC+C B(2) F ＝(A+B+C )(A+B+C) = (A+B)+C C = A+B(3) F ＝ABC D +ABD+BC D +ABCD+B C = AB+BC+BD(4) F=C AB C B BC A AC +++= BC(5) F=)()()()(B A B A B A B A ++++＝BA 9.将下列函数展开为最小项表达式(1) F(A,B,C) = Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14)10.用卡诺图化简下列各式（1）CAB C B BC A AC F +++=0ABC00 01 11 1011111化简得F=C(2)CB A D A B A DC AB CD B A F++++=111111ABCD 00 01 11 1000011110化简得F=DA B A +（3） F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)1111111111AB CD 00 01 11 1000011110化简得F=DBC D C A BC A C B D C ++++(4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)Φ1ΦΦ1ΦΦ1Φ1AB CD 00 01 11 1000011110化简得F=ACAD B A ++11.利用与非门实现下列函数，并画出逻辑图。
数字逻辑设计基础答案 (第1-13章)
=（5.75）10
[题 2-3] 将下列二进制数转换成八进制数和十六进制数 （1） （1010001101）2 （3） （0.11100011）2 （2） （110110001.11001）2 （4） （1001101.110011）2
解：将二进制数转换为八进制或十六进制的方法是：以小数点为中心，分别向左、右按 3 位一组转换为八进制， 或按 4 位一组转换为十六进制， 最后不满 3 位或 4 位的需补 0 组成， 将每组以对应等值的八进制数或十六进制数代替。 （1） （1010001101）2 =（1215）8 =（28D）16 （2） （110110001.11001）2 =（661.62）8 =（1B1.C8）16 （3） （0.11100011）2 =（0.706）8 =（0.E3）16 （4） （1001101.110011）2 =（115.63）8 =（）16 [题 2-4] 将下列十六进制数转换成二进制数、八进制数和十进制数 （1） （4E8.3）16 （3） （0.CD2）16 解： （1） （4E8.3）16 =（10011101000.0011）2 =（2350.14）8 = （1256.1875）10 （2） （AB4.0C1）16 =（101010110100.000011000001）2 =（5264.03401）8 = （2740.004147690625）10 （3） （0.CD2）16 =（0.110011010010）2 =（0.6322）8 = （0.80126953125）10 （4） （AF1.D1）16 =（101011110001. 11010001）2 =（4361.642）8 =（2289.81640625）10 （2） （AB4.0C1）16 （4） （AF1.D1）16
数字逻辑课后答案 第三章
第三章 时序逻辑1.写出触发器的次态方程，并根据已给波形画出输出 Q 的波形。
解：2. 说明由RS 触发器组成的防抖动电路的工作原理，画出对应输入输出波形解：3. 已知JK 信号如图，请画出负边沿JK 触发器的输出波形（设触发器的初态为0）1)(1=+++=+c b a Qa cb Q nn4. 写出下图所示个触发器次态方程，指出CP 脉冲到来时，触发器置“1”的条件。
解：（1），若使触发器置“1”，则A 、B 取值相异。
（2），若使触发器置“1”，则A 、B 、C 、D 取值为奇数个1。
5.写出各触发器的次态方程，并按所给的CP 信号，画出各触发器的输出波形（设初态为0）解：6. 设计实现8位数据的串行→并行转换器。
B A B A D +=DC B A K J ⊕⊕⊕==Q AQ B Q D Q C Q E Q F Q7. 分析下图所示同步计数电路解：先写出激励方程，然后求得状态方程状态图如下：该计数器是五进制计数器，可以自启动。
8. 作出状态转移表和状态图，确定其输出序列。
解：求得状态方程如下故输出序列为：000119. 用D 触发器构成按循环码(000→001→011→111→101→100→000)规律工作的六进制同步计数器解：先列出真值表，然后求得激励方程PS NS 输出N0 0 0 0 0 1 00 0 1 0 1 1 0 0 1 1 1 1 1 0 1 1 1 1 0 1 0 1 0 1 1 0 0 0 1 0 0 0 0 0 1化简得：逻辑电路图如下：n Q 2n Q 1n Q 012+n Q 11+n Q 10+n Q n n n nn n n n n n nnQ Q Q Q Q Q Q Q Q Q Q Q Z 121002*********+==+==+++nnn nnn nnnn QQ Q D QQ Q D QQ Q Q D 121211121122+====+==+++10. 用D 触发器设计3位二进制加法计数器，并画出波形图。
在线网课《数字逻辑(山东联盟-烟台大学)》课后章节测试答案全文
可编辑修改精选全文完整版绪论单元测试1【多选题】(5分)计算机的五大组成部分是（）、（）、（）、输入设备和输出设备。
A.控制器B.运算器C.硬盘D.存储器2【判断题】(5分)数字逻辑课程是计算机专业的一门学习硬件电路的专业基础课。
A.错B.对3【判断题】(5分)计算机的运算器是能够完成算术和逻辑运算的部件，逻辑运算比如与运算。
A.错B.对第一章测试1【单选题】(10分)与二进制数1101011.011对应的十六进制数为（）A.53.3B.73.3C.6B.3D.6B.62【单选题】(10分)与二进制数101.011等值的十进制数是（）A.5.175B.5.375C.3.625D.5.6753【单选题】(10分)（17）10对应的二进制数是（）A.10011B.101111C.10110D.100014【判断题】(10分)数字电路中用“1”和“0”分别表示两种状态,二者通常无大小之分A.错B.对5【判断题】(10分)格雷码具有任何相邻码只有一位码元不同的特性A.对B.错6【多选题】(20分)以下代码中为无权码的为()A.余三码B.C.5421BCD码D.8421BCD码7【单选题】(10分)十进制数25用8421BCD码表示为（）A.00100101B.11010C.11001D.101018【单选题】(10分)BCD码1001对应的余3BCD码是（）A.B.1100C.1000D.10109【单选题】(10分)8421BCD码001001010100转换成十进制数为（）A.252B.1250C.1124D.254第二章测试1【单选题】(5分)在何种输入情况下，“或非”运算的结果是逻辑0A.任一输入为0，其他输入为1B.全部输入是0C.全部输入是1D.任一输入为12【单选题】(5分)一个两输入端的门电路，当输入为1和0时，输出不是1的门是（）A.或门B.异或门C.与非门D.或非门3【多选题】(10分)求一个逻辑函数F的对偶式，可将F中的（）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
数字逻辑设计习题册班级：学号：姓名：哈尔滨工业大学（威海）计算机科学与技术学院体系结构教研室第2章 逻辑代数基础2—1 填空1．摩根定理表示为：=⋅B A ＿B A +＿＿；=+B A ＿B A ⋅＿＿。
2. 函数表达式D C AB Y ++=，则其对偶式为='Y ＿D C B A ⋅⋅+)(＿＿＿＿＿＿＿。
3．根据反演规则，若C D C B A Y +++=，则=Y C D C B A ⋅++)(。
4．函数式CD BC AB F ++=写成最小项之和的形式结果为()15,14,113,12,11,7,6,3∑m ，写成最大项之积的形式结果为)10,9,8,5,4,2,1,0(∏M。
5. （33.33）10 =（100001.0101 ）2 =（ 41.2 ）8 =（ 21.5 ）162—2 证明1．证明公式()()A BC A B A C +=++成立。
2．证明此公式B A B A A +=+成立。
3．证明此公式)()()()()(C A B A C B C A B A +⋅+=+⋅+⋅+成立。
左边 (由分配律得)右边BCA BCB C A BC BA AC AA C A B A +=+++=+++=++)1())((BA A AB B B A B A B A AB AB B A B A AB BA B B A +=+++=+++=++=++=)()()(ACBC A B C A AC B C A C B B A ++=+⋅+=+⋅+⋅+=)()()()()(ACBC A B BC A B AC A A ++=+++=4. 证明此公式1))(((=+++⋅++C B D B A C B D C C B A 成立。
左边5.证明此公式D C D C B A D AC D C B D C A ⊕=+++⊕)(成立。
左边2—3 用代数法化简下列各式 1．B A BC A F +=1 2．D C A ABD CD B A F ++=2F 1 F 23．CD D AC ABC C A F +++=3 F 34．)()(4C B A C B A C B A F ++⋅++⋅++=F 41))((0))((=+++=+++⋅=C B D B A C B C B D B A C B D C C B A DC DC BD C D C D C A D C B D C A D AC D C A D C B D C A D AC A B D C D C A D AC B A B D C D C A ⊕=++=⊕++⊕=+++⊕=+++⊕=+++⊕=)()()()()()()(1=++++=B A C B A ADC B C B AD C B C B AD =+=++=)()(CDA CDC B C A CD AC AB C A D A C B C A D D A C BC C A +=+++=+++=+++=+++=)()()()()(CB AC B C B A A C A C B A C A C B A +=++=++=+++=)()(x y x y x =+⋅+)()(5．C DE C BE CD B B A AC F ++++=5F 56．C B A AD C B A CD AB F ++++=6F 67．D BC A BD A BD CD B B A C A F +++++=7F 78. D D C C A B A F +++=8F 8 1=++++=D D C C A B A9. D AC D C A D C B D C D C A F ++++=)(9F 9CE B AC CE D B B AC C E D B AC B AC C E D B C A B AC C E D B D B C B B A AC C E D B D C B B A AC ++=+++=+++=++++=++++=+++++=)()()(DC B A AD B C AB AD D C B C AB AD A A C B D C AB +++=++++=++++=+++++=)()(1)()()()()(=++++=+++++=+++++=+++++=+++++=+++++=A CD B BD A C A A CD B BD B B A C A A CD B B A D A B C A A CD B B A BD D B A C A A BD CD B B A D B C A BD A BD CD B B A D BC C A DC D C D C B D C D C D C D C A D C B D C D C A +=++=++++=)()(10.D B AB C D B AB F +++++=10(y x y x x +=+)2—4用卡诺图化简下列各式1．C B A AB C B F ++=1 2．C B BC B A F ++=2F 1ABC += F 2B A +=3．C B C B C A C A F +++=3F 3C B B A C A ++=4．D C A C B AD C D C A ABD ABC F +++++=4D A F +=4111111111111AB CD0001111000011110D B AB C DB ABCD B AB ++=++⋅⋅=5．D B A AC C B A F ++=5 6．C B A AD C B A D C AB F ++++=6AC D B B A F ++=5 A C B DC F ++=6 7．D BC A BD A CD B B A C A F +F 7=18．D B D B C A C A F +++=8D)⊙(B C)⊙(8⋅=+++=A D C B A ABCD D C B A D C B A F11111111AB CD 00011110000111109．D C B A D AC D C B D C A F +++⊕=)(9D C D C F +=9 10. ))((10C AB B A F ++=C B C A F +=1011. C B AC D C A B A F +++=11AC C B B A F ++=1112．∑=mC B A P )7,6,5,2,1,0(),,(1AC C B B A P ++=2 13．=D C B A P )14,11,10,9,8,7,6,4,3,2,1,0(),,,(2D C C A D A B P +++=2 14．∑=mD C B A P )15,14,13,12,10,9,8,6,4,1,0(),,,(3D A D B C B AB D C P ++++=315. ∑=m D C B A P )15,14,13,11,9,7,6,5,3,1(),,,(4F 15=D+BC2—5 用卡诺图化简下列带有约束条件的逻辑函数 1．∑∑+=d mD C B A P )15,14,13,2,1,0()12,11,9,8,6,3(),,,(1CD A D B C A P ++=1 2．∑∑+=d mD C B A P )15,14,13,10,9,8()12,11,6,5,4,3,2,0(),,,(2C B C BD P ++=23．D C B A D C B A D C A P ++++=3， 约束：0=+AC ABD C B D C A D C A P ++=34．CD B A CD B A P +=4， 约束：A B C D 为互相排斥的一组变量，即在任何情况下它们之中不可能两个同时为1。
P4=A+B 5. D C A C B A D C B A P ++⊕=)(5，且0=+CD ABAC D A B P ++=5第3章 集成逻辑门电路3—1 选择填空1．由TTL 门组成的电路如图3.1-1所示，已知它们的输入低电平电流为m A 6.1iL =I ，输入高电平电流为μA 40iH =I 。
试问：当1==B A 时，1G 的＿灌＿（拉，灌）电流为＿3.2mA ＿＿；0=A 时，1G 的＿拉＿（拉，灌）电流为＿160＿A μ。
对于与非门 灌电流（低电平输入电流）看门数；拉电流看端数 2．图3.1-2中示出了某门电路的特性曲线，试据此确定它的下列参数：输出高电平=OH U ＿3V ＿＿；输出低电平=OL U ＿0.3V ＿＿；输入低电平电流=iL I ＿-1.4mA ＿＿；输入高电平电流=iH I ＿＿0.02mA ＿；阈值电平=T U ＿1.5V ＿＿；开门电平=ON U ＿1.5V ＿＿；关门电平=OFF U ＿1.5V＿＿；低电平噪声容限=NL U ＿1.2V ＿＿；高电平噪声容限=NH U ＿1.5V ＿＿；最大灌电流OLMax I =＿15mA ＿＿。
3．TTL 门电路输入端悬空时，应视为＿高＿＿；（高电平，低电平，不定）此时如用万用表测量其电压，读数约为＿1.4V ＿＿（3.5V ，0V ，1.4V ）。
AB图3.1-1u i33.0u OH30)mA (i i 4.1-mA02.0i u u OL3.0图 3.1-24．CT74，CT74H ，CT74S ，CT74LS 四个系列的TTL 集成电路，其中功耗最小的为＿CT74LS ＿＿；速度最快的为＿CT74S ＿＿；综合性能指标最好的为＿＿CT74LS ＿。
5．集电极开路门（OC ）门在使用时须在＿输出与电源＿＿之间接一电阻（输出与地，输出与输入，输出与电源）。
6．CMOS 门电路的特点：静态功耗＿极低＿＿（很大，极低）；而动态功耗随着工作频率的提高而＿＿增加＿（增加，减小，不变）；输入电阻＿高＿＿（很大，很小）；噪声容限＿高＿＿（高，低，等）于TTL 门电路。
3—2 图3.2各电路中凡是能实现非功能的要打√，否则打×。
图3.2-1为TTL 门电路，图3.2-2为CMOS 门电路。
3—3 由CMOS 传输门和反相器构成的电路如图3.3（a ）所示，试画出在图3.3（b ）波形作用下的输出O U 的波形（V 10i1=U ，V 5i2=U ）UUoU i2CttCO U V 10V 10图3.3（a ）图3.3（b）AV B图3.2-1图3.2-23—4有两个相同型号的TTL 与非门，对它们进行测试的结果如下：(1) 甲的开门电平为1.4V ，乙的开门电平为1.5V ； (2) 甲的关门电平为1.0V ，乙的关门电平为0.9V 。
试问在输入相同高电平时，哪个抗干扰能力强?在输入相同低电平时，哪个抗干扰能力强?答:在输入相同高电平时，甲的抗干扰能力强。
因为开门电平愈小，在输入高电平时的抗干扰能力愈强。