最优估计大作业1.
最优化方法大作业答案

1.用薄钢板制造一体积5m 3,长度不小于4m ,无上盖的货箱,要求钢板耗量最小。
确定货箱的长x 1、宽x 2和高x 3。
试列出问题的数学模型。
解:min 32312122x x x x x x z ++= s.t 5321=x x x 41≥x 0,,321≥x x x2.将下面的线性规划问题表示为标准型并用单纯形法求解max f=x 1+2x 2+x 3s .t .2x 1+x 2-x 3≤2 -2x 1+x 2-5x 3≥-6 4x 1+x 2+x 3≤6 x i ≥0 i=1,2,3 解:先化标准形:Min 321x x x z -+=224321=+-+x x x x 6525321=++-x x x x646321=+++x x x x列成表格:121610011460105122001112-----可见此表已具备1°,2°,3°三个特点,可采用单纯形法。
首先从底行中选元素-1,由2/2,6/2,6/4最小者决定选第一行第一列的元素2,标以记号,迭代一次得121210231040116201002121211--------再从底行中选元素-2/3,和第二列正元素1/2,迭代一次得12123230210231040116201002121211-------再从底行中选元素-3,和第二列正元素2,迭代一次得4233410120280114042001112---再迭代一次得1023021062210231010213000421021013--选取最优解:01=x 42=x 23=x3. 试用DFP 变尺度法求解下列无约束优化问题。
min f (X )=4(x 1-5)2+(x 2-6)2取初始点X=(8,9)T ,梯度精度ε=0.01。
解:取IH=0,初始点()TX 9,8=2221)6()5(4)(-+-=x x x f⎥⎦⎤⎢⎣⎡--=∇122408)(21x x x f⎪⎪⎭⎫⎝⎛=∇624)()0(xfTx f d )6,24()()0()0(--=-∇=)0(0)0()1(dxxα+=T)69,248(00αα--=])669()5248(4min[)(min 2020)0(0)0(--+--⨯=+αααdxf 0)6()63(2)24()2458(8)(00)0(0)0(=-⨯-+-⨯--=+ααααd d xdf13077.0130170≈=α⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛--⨯+⎪⎪⎭⎫ ⎝⎛=21538.886153.462413077.098)1(x⎪⎪⎭⎫⎝⎛-=∇43077.410784.1)()1(xf进行第二次迭代:⎥⎦⎤⎢⎣⎡--=-=78463.013848.31)0()1(xxδ⎥⎦⎤⎢⎣⎡--=∇-∇=56924.110783.25)()(1)0()1(xf xf γ101011011101γγγγγδδδH HH H H TTTT-+=03172.8011=γδT86614.6321101==γγγγH T⎥⎦⎤⎢⎣⎡=61561.046249.246249.285005.911Tδδ⎥⎦⎤⎢⎣⎡==46249.240022.3940022.3940363.630110110TTHH γγγγ所以:⎪⎪⎭⎫⎝⎛--=0038.103149.003149.012695.01H⎪⎪⎭⎫⎝⎛-⨯⎪⎪⎭⎫⎝⎛---=∇-=43076.410784.10038.103149.003149.012695.0)()1(1)1(xf H d⎪⎪⎭⎫⎝⎛-=48248.428018.0令 )1(1)1()2(dx x α+=利用)()1()1(=+ααd dxdf ,求得49423.01=α,所以⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫⎝⎛=+=21538.213848.021538.886152.449423.0)1()1()2(dxx⎪⎪⎭⎫ ⎝⎛=65因)()2(=∇xf ,于是停,)2(x 即为最优解。
北航最优化大作业

北航最优化大作业1.引言旅行商问题(Traveling Salesman Problem,TSP)是一种经典的组合优化问题,目标是找到一条路径,使得旅行商从起点出发,途经所有城市一次后返回起点,并且总路径长度最短。
TSP问题具有NP-hard的特性,寻找最优解是一个非常具有挑战性的任务。
本文将基于禁忌算法,探讨TSP问题的求解方法。
2.禁忌算法简介禁忌算法是一种基于局部的元启发式算法,通过在过程中禁止一定的动作来跳出局部最优解,以期望获得更好的全局最优解。
算法通过引入禁忌表和禁忌长度等机制,避免过程中陷入局部最优解。
3.TSP问题的数学建模假设有n个城市,城市之间的距离可以表示为一个n×n的距离矩阵D。
TSP问题的目标可以定义为:min ∑_(i=1)^n ∑_(j=1)^(n) D_ij*x_ijs.t. ∑_(i=1)^n x_ij=1,∑_(j=1)^n x_ij=1,∀i ≠ jx_ij∈{0,1}, 1≤i,j≤n其中x_ij表示城市i与城市j之间的路径是否存在,1表示存在,0表示不存在。
4.禁忌算法在TSP问题中的应用(1)初始化选取一个起始解x,计算其路径长度f(x)。
将x设为当前解x_best,将f(x)设为当前解的最优值f_best。
(2)选择邻域解选择当前解的一个邻域解x',使得x'与x只有一个位置上的交换。
通过随机选择两个位置,进行交换操作。
(3)禁忌判断如果邻域解x'的路径长度f(x')小于当前解的最优值f_best,则更新f_best为f(x'),并将x'设为新的当前解。
否则,比较x'与当前解的禁忌情况。
(4)禁忌更新如果x'未在禁忌表中,或者禁忌表中对应的禁忌周期已过,则将x'设为新的当前解。
否则,选择一个路径长度较短的邻域解x'',即使其路径长度f(x'')大于f_best。
北航最优化大作业
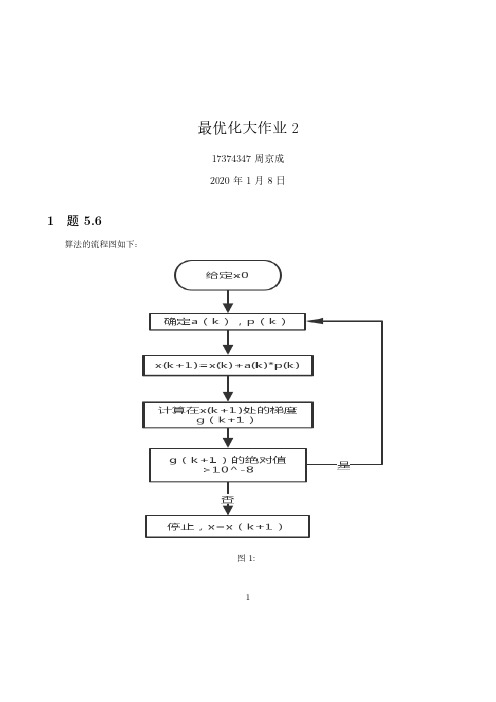
图 18: 前两行为迭代点 xk, 后面一行为梯度的 2 范数,显然,前两行行都趋于无穷大,发散,梯度的 2 范数 趋于 13.4536(从 matlab 变量表格中得到)。 4: 初始点 x(0) = (10, 20)T 前两行为迭代点 xk, 后面一行为梯度的 2 范数,显然,前两行行都趋于无穷大,发散,梯度的 2 范数 趋于 13.4536(从 matlab 变量表格中得到)。
33
图 57: 7、9、11、13 迭代停止测试。
当 n=50 时,解 x*=[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1] 判断矩阵:
图 58: 可以发现,没有发现负曲率的情况,第 1 和第 2 次的迭代到了边界,第 4、6、8、10、12、14、16 次 迭代到了边界。
▽f (x) = g = −400x1(x2 − x21) + 2x1 − 2
200(x2 − x21)
[
]
▽2f (x) = G = 1200x21 − 400x2 + 2 −400x1
−400x1
200
14
4.1 最速下降法
代码和流程图:
图 33:
图 34: 15
4.1.1 初始点为 (1.2,1.2)
++
)
x1 + x12 − 100
x11
x1
−
50 1
−
x2
−10 − µ(
++
)
x1 + x2 − 100 x2 −x1 + 50 + x2
最优化方法与应用大作业(一)最速下降法

最优化方法与应用大作业(一)
---最速下降法部分:
1.问题描述:
用梯度下降法求解以下优化问题
min f(x)=(x1+10*x2)^2+5(x3-x4)^2+(x2-2*x3)^4+10*(x1-x4)^4
2.编程感想:
该算法需要计算Hesse矩阵,C语言在向量运算时没有Matlab方便,所以手工完成了理论计算,再输入,破坏了程序的移植性。
同时,实验表明当初始值离理想点较远且精度要求较高时,最速下降法的收敛速率极慢,迭代几乎不可能完成,这对初值的选取提出了一定限制。
3.结果分析:
编译界面(Mac os X,Xcode环境)
输入参数(设定为(0.1,0.2,0.3,0.4)):
结果(此处列出每次迭代结果)。
明显的看到,最速下降法的收敛较慢,最终结果接近理论值(F(0,0,0,0)=0)所以该结果可以满意。
4.算法代码见下页
西安电子科技大学电子工程学院020951
李骏昊02095005。
最优化方法大作业模板
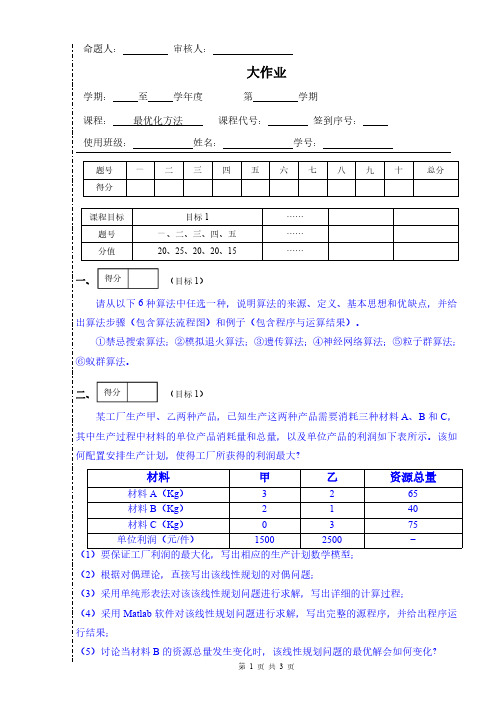
命题人:审核人:大作业学期:至学年度第学期课程:最优化方法课程代号:签到序号:使用班级:姓名:学号:题号一二三四五六七八九十总分得分一、(目标1)请从以下6种算法中任选一种,说明算法的来源、定义、基本思想和优缺点,并给出算法步骤(包含算法流程图)和例子(包含程序与运算结果)。
①禁忌搜索算法;②模拟退火算法;③遗传算法;④神经网络算法;⑤粒子群算法;⑥蚁群算法。
二、(目标1)某工厂生产甲、乙两种产品,已知生产这两种产品需要消耗三种材料A 、B 和C ,其中生产过程中材料的单位产品消耗量和总量,以及单位产品的利润如下表所示。
该如何配置安排生产计划,使得工厂所获得的利润最大?材料甲乙资源总量材料A (Kg )3265材料B (Kg )2140材料C (Kg )0375单位利润(元/件)15002500-(1)要保证工厂利润的最大化,写出相应的生产计划数学模型;(2)根据对偶理论,直接写出该线性规划的对偶问题;(3)采用单纯形表法对该该线性规划问题进行求解,写出详细的计算过程;(4)采用Matlab 软件对该线性规划问题进行求解,写出完整的源程序,并给出程序运行结果;(5)讨论当材料B 的资源总量发生变化时,该线性规划问题的最优解会如何变化?课程目标目标1……题号一、二、三、四、五……分值20、25、20、20、15……得分得分三、(目标1)求解下列无约束非线性规划问题(1)采用黄金分割法求解:min 4()24f x x x =++。
初始区间为[-1.0],精度为ε=10-4。
(要求:采用黄金分割法进行Matlab 编程求解,写出源程序,并给出运行结果,列出迭代过程的数据表格)(2)采用阻尼牛顿法求解:222121212min (,)4f x x x x x x =+-。
分别取两个初始点:x A =(1,1)T ,x B =(3,4)T 。
(要求:采用阻尼牛顿法进行Matlab 编程求解,并给出运行结果,列出迭代过程的数据表格)四、(目标1)求解下列约束非线性规划问题:22112212121212min ()23532..00f x x x x x x x x x x x s t x x =-+--+≤⎧⎪-≤⎪⎨≥⎪⎪≥⎩(1)采用罚函数法进行求解,需写出具体计算过程;(2)采用二次规划方法进行求解,需写出具体计算过程,并进行MATLAB 编程,写出源程序和运算结果;五、(目标1)(1)某商店在未来的4个月里,准备利用它的一个仓库来专门经营某种商品,仓库的最大容量为1000单位,而且该商店每月只能出卖仓库现有的货。
西电最优化上机报告(大作业)

上机报告一.最速下降法算法简述:1.在本例中,先将最速下降方向变量赋一个值,使其二范数满足大于ε的迭代条件,进入循环。
2.将函数的一阶导数化简,存在一个矩阵,将其hesse矩阵存在另一个矩阵。
依照公式求出α,进而求出下一任迭代的矩阵初值。
循环内设置一个计数功能的变量,统计迭代次数。
3.求其方向导数的二范数,进行判别,若小于ε,则跳出循环,否则将继续迭代。
4.显示最优解,终止条件,最小函数值。
心得体会:最速下降法的精髓,无疑是求梯度,然后利用梯度和hesse矩阵综合计算,求解下一个当前最优解。
但是,要求函数是严格的凸函数,结合严格凸函数的大致图像,这就给初值的选取提供了一点参考。
例如在本例中,由于含有两个变量的二次方之和,结合大致图像,想当然的,初值的选取应当在原点附近;又因为变量的二次方之和后面,还减去了变量的一次形式和一次混合积,所以初值的选取应该再向第一象限倾斜。
综合以上考量,第一次选取(1,1)作为初值,判别精度方面,取到千分位,暂定为0.001。
运行以后,结果显示迭代了25次,最优解为(3.9995,1.9996),终止条件为5.4592e-04,目标函数为-8.0000。
这个结果已经相当接近笔算结果。
整体的运行也比较流畅,运算速度也比较快。
第二次取值,决定保留判别精度不变,将初值再适当向第一象限倾斜,取(2,2)作为初值,运行后,显示只迭代了11次!最优结果显示(3.9996,1.9997),终止条件为3.6204e-04,最优解-8.0000。
可见,最优结果更接近理想值,终止条件也变小了,最关键的是,迭代次数减少至第一次的一半以下!这说明以上初选取的方向是对的!第三次再进行初值细化,判别精度仍然不变,初值取(3,3)。
结果令人兴奋,只迭代了四次!最优解已经显示为(4.0000,2.0000),终止条件为2.4952e-04,目标函数-8.0000。
第四次,判别精度不变,取初值(4,4)。
最优化理论和算法: 大作业(一)

最优化理论和算法:大作业(一)简介:这个大作业的主要目的是在Matlab下自己编写单纯形法算法来求解标准型线性规划问题:min c T xs.t.Ax=bx≥0其中b≥0,A是m×n(m≤n)的矩阵。
假设A的秩是m.特别的,A并不一定包含单位矩阵。
按照要求编写下列小程序。
程序(一):实现单步单纯形法程序格式:function[istatus,iB,iN,xB]=simplex_step(A,b,c,iB,iN,xB)%实现一步单纯形法%输入参数:%A-(n,m)系数矩阵%b-(m,1)(正)右端向量%c-(n,1)目标函数系数%iB-(1,m)整数向量记录当前基本变量的指标数%iN-(1,n-m)整数向量记录当前非基本变量的指标数%xB-(m,1)向量代表当前基本变量的值%输出参数:%istatus-整数标记单纯形法执行状态%istatus=0正常单纯形法步完成% istatus=32问题无界% istatus=-1找到最优基本可行解%iB-(1,m)整数向量记录运行单纯形法之后的基本变量的指标数%iN-(1,n-m)整数向量记录运行单纯形法之后的非基本变量的指标数%xB-(m,1)向量记录运行单纯形法之后的基本变量的值注:该程序不考虑退化情形。
程序(二):利用两步法中的第一步来求解一个初始基本可行解程序格式:function[istatus,iB,iN,xB]=simplex_init(A,b)%实现两步法中的第一步来求解一个初始基本可行解,通过求解下面的问题:%min y_1+...+y_m%s.t.Ax+y=b%x>=0,y>=0%A是m x n矩阵。
%输入参数:%A-(n,m)系数矩阵%b-(m,1)正的右端向量%输出参数:%istatus-整数标记初始化状态% istatus=1找到原问题的一个基本可行解% istatus=4问题可行域是空集% istatus=16初始化过程失败%iB-(1,m)整数向量记录运行初始化之后的基本变量的指标数(对应原问题)%iN-(1,n-m)整数向量记录运行初始化之后的非基本变量的指标数(对应原问题)%xB-(m,1)向量记录运行初始化之后的基本变量的值(对应原问题)注:为了简单化程序,若初始化过程找到的初始基本可行解包含某些人工变量y j,设置istatus=16(初始化失败)。
最优化方法大作业

发动机空燃比控制器引言:我主要从事自动化相关研究。
这里介绍我曾经接触过的发动机空燃比控制器设计中的优化问题。
发动机空燃比控制器设计中的最优化问题AFR =afm m && (1)空燃比由方程(1)定义,在发动机运行过程中如果控制AFR 稳定在14.7可以获得最好的动力性能和排放性能。
如果假设进入气缸的空气流量am &可以由相关单元检测得到,则可以通过控制进入气缸的燃油流量f m &来实现空燃比的精确控制。
由于实际发动机的燃油喷嘴并不是直接对气缸喷燃油,而是通过进气歧管喷燃油,这么做会在进气歧管壁上液化形成油膜,因此不仅是喷嘴喷出的未液化部分燃油会进入气缸,油膜蒸发部分燃油也会进入气缸,如方程(2)。
这样如何更好的喷射燃油成为了一个问题。
1110101122211ττττ⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎣⎦⎢⎥⎣⎦f ff v X x x u x x X x y =x && (2)其中12、,==ff fv x m x m &&=f y m &,=fi u m &这里面,表示油膜蒸发量ff m &、fvm &表示为液化部分燃油、fim &表示喷嘴喷射的燃油,在τf 、τv 、X 都已知的情况下,由现代控制理论知识,根据系统的增广状态空间模型方程(3)00000011011011114.70ττττ⎡⎤⎡⎤-⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥=-+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎡⎤=⎢⎥⎣⎦⎣⎦ff v v a X X u +q q m y q x x x &&& (3)其中()014.7⎰taq =y -m&。
由极点配置方法,只要设计控制器方程(4),就可以使得y 无差的跟踪阶跃输入,那么y 也能较好的跟踪AFR *am /&。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最优估计大作业姓名:李海宝学号:S314040186导师:刘胜专业:控制科学与工程模糊逻辑卡尔曼滤波器在智能AUV导航系统中的自适应调整摘要本论文基于全球定位系统(GPS)和几个惯性导航系统(INS)传感器描述了对于自主水下航行器(AUV)应用的一种智能导航系统的执行过程。
本论文建议将简单卡尔曼滤波器(SKF)和扩展卡尔曼滤波器(EKF)一前一后地用于融合INS 传感器的数据并将它们与GPS数据结合到一起。
传感器噪声特性里潜在的变化会引起SKF和EKF的初始统计假定的调整,本论文针对这一问题着重突出了模糊逻辑方法的使用。
当这种算法包含实际传感器噪特性的时候,SKF和EKF只能维持他们的稳定性和性能,因此我们认为这种自适应机制同SKF与EKF一样有必要。
此外,在提高导航系统的可靠性融合过程期间,故障检测和信号恢复算法也需在此要讨论。
本论文建议的这种算法用于使真实的实验数据生效,这些数据都是从Plymouth大学和Cranfield大学所做的一系列AUV实验(运行低成本的锤头式AUV)中获得的。
关键词:自主水下航行器;导航;传感器融合;卡尔曼滤波器;扩展卡尔曼滤波器;模糊逻辑1.引言对于以科学、军事、商业为目的应用,如海洋勘察、搜索未爆弹药和电缆跟踪检查,AUV的发展需要相应导航系统的发展。
这样的系统提供航行器位置和姿态的数据是很有必要的。
在这样的系统中对精度的要求是最重要的:错误的位置和姿态数据会导致收集数据的一个毫无意义的解释,或者甚至AUV的一个灾难性故障。
越来越多来自整个世界的研究团队正利用INS和GPS来研发组合导航系统。
然而,他们的工作中几乎都没有明确几个INS传感器融合的本质要求,这些传感器用于确保用户保持精度或甚至用来防止在与GPS融合之前导航系统这部分的完全失败。
例如,金赛和惠特科姆(2003)使用一个切换机制来防止INS的完全失败。
虽然这个方法简单易行,但是可能不适合用于维持一个确定的精度等级。
出于多传感器数据融合和集成的目的,几种估计方法在过去就已经被使用过。
为此,SKF/EKF和它们的变形在过去就已经是流行的方法,并且一直到现在都对开发算法感兴趣。
然而,在设计SKF/EKF过程中,一个显著的困难经常会被描绘成缺少过程协方差矩阵(Q)和测量噪声协方差矩阵(P)的先验知识。
在大多数实际应用中,这些矩阵都是初步估计的甚至是未知的。
这里的问题就是,对于SKF/EKF估计算法的过程和测量噪声最优性来说,先验信息的品质与设置是紧密结合的。
研究表明未充分知道先验滤波器的统计会降低滤波器状态估计的精度或者会给它们的估计引入偏差。
此外,不正确的先验信息会导致滤波器的实际发散。
上面提到,具有固定矩阵R和或矩阵Q的传统SKF/EKF应该被一个自适应估计方程替代,这一问题可能有争议,该问题在下一部分作讨论。
2.卡尔曼滤波算法的自适应优化在过去的几年里,在自适应卡尔曼滤波这一领域里,仅仅能找到少数出版物包含这一类文献。
提出自适应卡尔曼滤波的两个主要方法分别是多模型自适应估计(MMAE)和创新自适应估计(IAE)。
尽管这些方法的执行方式都很不一样,但是它们都共享了同一概念—使用包含于更新序列的新的统计信息。
在这两种情况下,采样时间k时刻对应的值是被滤波器接收的真实测量值和它的估计(预测)值之间的差值。
预测测量值是滤波器预测状态通过测量设计矩阵到测量空间的投影。
由于新的测量值,更新代表了滤波器可获得的额外信息。
不同于先验信息的统计数据的出现将第一次出现在更新向量中。
由于这个原因,更新序列代表了在新的观测器里的信息内容,它也被认为是对于自适应滤波器最有关联的信息资源。
在MMAE这一方法中,一堆卡尔曼滤波器在一个不同的统计滤波信息矩阵(即Q和R)的模型下并行运行或用门控算法运行。
在IAE这一方法中Q和R矩阵自适应随时间变化的测量值。
在本文中,IAE方法外加采用运用启发式方法的隶属函数的模糊逻辑技术常常用于SKF和EKF两者的R矩阵。
本文使用一系列来自锤头式AUV实验的实验数据来执行所提出的算法。
2.1模糊简单卡尔曼滤波器在这一部分中,呈现了基于采用模糊逻辑准则调整R矩阵的SKF的自适应体制的在线更新。
选择模糊逻辑主要是因为其简单性。
这激发了被证实出现在文献里该话题的兴趣。
本节将提出模糊逻辑简单卡尔曼滤波器(FSKF),在第四部分讨论的模糊逻辑扩展卡尔曼滤波器(FEKF)是基于使用协方差匹配技术的IAE方法。
该技术背后的基本思想是使更新序列协方差的实际值去匹配理论值。
定义实际协方差为通过在一个M尺寸的运动估计窗口里求平均值而得的样本协方差的近似值。
其中是在估计窗口里的第一个采样点。
做一个经验性的实验来选择M尺寸的窗口。
该实验发现对于在公式(1)里的移动窗口的合适尺寸是15。
更新序列的理论协方差被定义为使用协方差匹配技术的自适应算法的逻辑可以被定性描述如下。
如果实际协方差值能被观测,这个值是在被理论预测的范围内而且它的差值非常接近零,这就表明协方差几乎完美匹配而且仅有一个小的变化需要依靠R矩阵来做。
如果实际协方差大于理论值,那么R矩阵的值应该减小。
相反,如果小于,那么R矩阵的值应该增加。
这种调整机制把它自身用于处理使用基于这种规则的模糊逻辑方法。
如果<发生前面的>那么<随之发生的>,(3)这里的前因与后果分别是,这里的与输入和输出变量,和是模糊设置参数。
图1 (a)和(b)的隶属函数为实现上述运用模糊逻辑方法的协方差匹配技术,定义一个叫做的新变量用于检测和之间的差异。
需要注意的是,在这个特殊应用中,和被约束成对角矩阵。
以下三种模糊规则被用来使用:图2(a)和(b)的隶属函数如果<>那么<不变>,(4)如果<>那么<减少>,(5)如果<>那么<增加>,(6)因此R是根据下式作调整,(7)其中是加上或减去每个时刻的R。
这里的是模糊推理系统(FIS)的输入,是输出。
在上述自适应理论的基础上,可以用的三个模糊设置来执行FIS。
N=负,N=零和N=正。
对于,模糊集被指定为I=增加,M=不变和D=减少。
这些用启发式方法设计的模糊集的隶属函数显示在图1中。
2.2传感器故障诊断和恢复算法除了自适应程序,该FSKF已配备了传感器故障诊断和恢复算法。
该算法背后的基本思想是对于传感器而言的真实值的幅值和它的理论值必须无任何偏差在1附近。
但是如果一个短暂的或持续的错误出现在测量数据中,这个值就会突然增加。
出于这一目的,变量被定义为(8)因此,如果值大于或者等于阈值(α)那么会宣布一个短暂的错误和分配给一个0值。
如果仍然大于一个瞬时时刻的阈值α,那么会宣布一个持续的错误和分配给一个值乘以随机值。
从实验中发现,好的α值是1.2。
2.3 模糊逻辑观测器为了监测FSKF的性能,这里使用了叫做模糊逻辑观测器(FLO)的另一个FIS。
FLO分配了信心的量或程度记为。
这个数字在(0-1)区间内用于FSKF的状态估计。
用两个输入和的值来实现FLO。
我们发现这些变量的隶属函数使用了启发式方法产生一个对于的非对称形状和对于的对称形状如图2所示。
表1 基于FLO模糊规则隶属函数的模糊标签:Z=零,S=小和L=大。
为输出?定义了三个模糊个体分别被标记为G=好,AV=平均和P=坏,值分别为1,0.5和0。
FLO基本启发式理论如下:如果和的值接近0,那么FSKF几乎完美工作,FSKF的状态估计被设定在1附近的一个量。
相反,如果这两值中一个或者两个远离0而增加,那么意味着FSKF性能退化而FLO设定一个接近0的量。
表1给出了每个FLO完整的模糊规则库。
3INS传感器数据融合在这一部分中,将FSKF算法运用到锤头式AUV的线性模型中。
图3(a)显示了在实验舱里进行泄漏测试和压舱之前的潜行器,图3(b)在航向系统辨识实验期间的潜行器。
潜行器舵输入被来自上位机的用户通过脐带电缆发送出去。
图3锤头式AUV:(a)泄漏测试和压舱前和(b)系统辨识实验期间因此,在实际中它对于那个特异性实验是以一个半自治模型行驶的。
电缆的牵制效应被认为是不可忽略的。
在潜行器面板上的电子罗盘和惯性测量单元(IMU)用于捕捉相应的响应。
来自实验数据的线性离散状态空间模型的系统矩阵A,输入矩阵B和输出向量H分别为A=[0 1;-0.98312 1.9831],B=[-0.00.1961 -0.0036115],H=[1 0]。
假定该模型能足够准确的呈现潜行器的力度变化,由于这个原因,该模型在给定输入之后产生的任意输出都可以认为是一个实际输出值。
这个假设也促使了该模型输出作为在测量FSKF算法性能的一个参考使用。
为了测试FSKF算法,将来自电子罗盘和IMU(图5)的真实数据作为图4中输入的响应和两个模拟数据集融合到一起。
为了产生模拟数据,图6(a)和(b)里的噪声分别简单的添加到电子罗盘和IMU真实数据里。
图4舵输入图5实际电子罗盘和IMU输出会导致具有图6中所显示特性的噪声的一个可能实时场景就是第二个电子罗盘的位置紧靠螺旋桨直流电机,电机内部温度会随着时间变化而增加从而影响传感器的环境温度。
相似的情况也会发生在当第二个IMU紧靠着前面水上划艇步进电机,而最初内部温度较高过段时间稳定下来的时候。
这种特定的情形会导致如图6中显示的噪声特性。
初始状态的情形是,和。
对于每个传感器来说R的实际值假设是未知的,但是它的初始值被选为。
仿真结果将在下一部分展示。
图6(a)增加噪声谱给电子罗盘数据和(b)给IMU数据3.1仿真结果图7和8是仿真结果显,示了通过电子罗盘和IMU观测的锤头式AUV的响应,而图9和图10分别由传感器3和4观测到的,它们分别是添加了均匀噪声且随时间增加或减小的前置传感器的输出。
图7(a)过程,测量,估计偏航角输出(b)电子罗盘的测量与偏航角误差图8(a)过程,测量,估计偏航角输出(b)IMU的测量与偏航角误差图9(a)过程,测量,估计偏航角输出(b)传感器3的测量与偏航角误差图10(a)过程,测量,估计偏航角输出(b)传感器4的测量与偏航角误差图7和8是通过从传感器直接测量所产生的误差等级作比较,来显示用FSKF 算法的改善性。
除了在误差等级方面的改善,图9和10也显示了所提出的算法是如何检测到传感器内瞬时性和持久性错误(看2.2部分)并做出合适的恢复。
为了融合估计偏航角,这里采用了重心法:这里的是第i个FSKF的输出(i=1,2,3,4),而是k时刻的各自的量。
图11显示了实际偏航角和融合估计偏航角的比较。
很明显,通过比较图11和图7-10,融合估计偏航角可以取得改善。
最后,采用以下工作指标作为比较目的:这里的是偏航角的实际值,是测量值,是k时刻和采样点n的估计值(表2)。
