新人教版九年级数学上册第24章试卷及 答案解析
九年级数学上册第二十四章圆测试卷1新人教版附答案

九年级数学上册第二十四章圆测试卷1新人教版附答案一、选择题1.用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是()A.2cm B.3cm C.4cm D.4cm2.如图,边长为40cm的等边三角形硬纸片,小明剪下与边BC相切的扇形AEF,切点为D,点E、F分别在AB、AC上,做成圆锥形圣诞帽,(重叠部分忽略不计),则圆锥形圣诞帽的底面圆形半径是()A.cm B.cm C.cm D.cm3.如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(接缝忽略不计),则这个纸帽的高是()A.cmB.2cm C.3cm D.4cm4.已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是()A.20πcm2B.20cm2C.40πcm2D.40cm25.已知某几何体的三视图(单位:cm),则这个圆锥的侧面积等于()A.12πcm2B.15πcm2C.24πcm2D.30πcm26.如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为()A.10cm2B.10πcm2C.20cm2D.20πcm27.一个圆锥的底面半径是6cm,其侧面展开图为半圆,则圆锥的母线长为()A.9cm B.12cm C.15cm D.18cm8.圆锥体的底面半径为2,侧面积为8π,则其侧面展开图的圆心角为()A.90°B.120°C.150°D.180°9.如图,某同学用一扇形纸板为一个玩偶制作一个圆锥形帽子,已知扇形半径OA=13cm,扇形的弧长为10πcm,那么这个圆锥形帽子的高是()cm.(不考虑接缝)A.5B.12C.13D.1410.若一个圆锥的主视图是腰长为5,底边长为6的等腰三角形,则该圆锥的侧面积是()A.15πB.20πC.24πD.30π11.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为()A.1.5B.2C.2.5D.312.圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是()A.6πB.8πC.12πD.16π13.一个立体图形的三视图如图,根据图中数据求得这个立体图形的侧面积为()A.12πB.15πC.18πD.24π14.已知圆锥的母线长为3,底面的半径为2,则圆锥的侧面积是()A.4πB.6πC.10πD.12π15.如图,圆锥的侧面展开图是半径为3,圆心角为90°的扇形,则该圆锥的底面周长为()A.πB.πC.D.16.一个圆锥的侧面展开图是半径为R的半圆,则该圆锥的高是()A.R B.C.D.17.一个几何体的三视图如图所示,这个几何体的侧面积为()A.2πcm2B.4πcm2C.8πcm2D.16πcm218.底面半径为4,高为3的圆锥的侧面积是()A.12πB.15πC.20πD.36π二、填空题19.一个圆锥形漏斗,某同学用三角波测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为.20.在△ABC纸板中,AB=3cm,BC=4cm,AC=5cm,将△ABC纸板以AB所在直线为轴旋转一周,则所形成的几何体的侧面积为cm2(结果用含π的式子表示).21.一个底面直径是80cm,母线长为90cm的圆锥的侧面展开图的圆心角的度数为.22.圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为cm2.23.一个底面直径为10cm,母线长为15cm的圆锥,它的侧面展开图圆心角是度.24.已知圆锥的底面半径为3,母线长为8,则圆锥的侧面积等于.25.若圆锥的侧面展开图的弧长为24πcm,则此圆锥底面的半径为cm.26.用一个圆心角为240°半径为6的扇形做一个圆锥的侧面,则这个圆锥底面半径为.27.用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,则这个圆锥底面圆的周长为.28.如图,如果从半径为3cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径是cm.29.用圆心角是216°,半径是5cm的扇形围成一个圆锥体的侧面(接缝处不重叠),则这个圆锥体的高是cm.30.若圆锥的轴截面是一个边长为4的等边三角形,则这个圆锥的侧面展开后所得到的扇形的圆心角的度数是.参考答案与试题解析一、选择题1.用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是()A.2cm B.3cm C.4cm D.4cm【考点】圆锥的计算.【分析】先利用弧长公式得到圆心角为120°,半径为6cm的扇形的弧长=4π,根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,则可计算出圆锥的底面圆的半径为2,然后根据勾股定理可计算出圆锥的高.【解答】解:∵圆心角为120°,半径为6cm的扇形的弧长==4π,∴圆锥的底面圆的周长为4π,∴圆锥的底面圆的半径为2,∴这个纸帽的高==4(cm).故选C.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,扇形的半径等于圆锥的母线长.也考查了弧长公式和勾股定理.2.如图,边长为40cm的等边三角形硬纸片,小明剪下与边BC相切的扇形AEF,切点为D,点E、F分别在AB、AC上,做成圆锥形圣诞帽,(重叠部分忽略不计),则圆锥形圣诞帽的底面圆形半径是()A.cm B.cm C.cm D.cm【考点】圆锥的计算.【专题】计算题.【分析】连结AD,如图,根据切线的性质得AD⊥BC,再根据等边三角形的性质得∠BAC=∠B=60°,BD=BC=20,所以AD=BD=20,设圆锥形圣诞帽的底面圆形半径为rcm,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=,再解方程即可.【解答】解:连结AD,如图,∵边BC相切于扇形AEF,切点为D,∴AD⊥BC,∵△ABC为等边三角形,∴∠BAC=∠B=60°,BD=BC=×40=20,∴AD=BD=20,设圆锥形圣诞帽的底面圆形半径为rcm,∴2πr=,解得r=(cm),即圆锥形圣诞帽的底面圆形半径为cm.故选A.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.3.如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(接缝忽略不计),则这个纸帽的高是()A.cmB.2cm C.3cm D.4cm【考点】圆锥的计算.【分析】先利用弧长公式得到圆心角为120°,半径为6cm的扇形的弧长=4π,根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,则可计算出圆锥的底面圆的半径为2,然后根据勾股定理可计算出圆锥的高.【解答】解:∵圆心角为120°,半径为6cm的扇形的弧长==4π,∴圆锥的底面圆的周长为4π,∴圆锥的底面圆的半径为2,∴这个纸帽的高==4(cm).故选D.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,扇形的半径等于圆锥的母线长.也考查了弧长公式和勾股定理.4.已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是()A.20πcm2B.20cm2C.40πcm2D.40cm2【考点】圆锥的计算.【专题】计算题.【分析】圆锥的侧面积=底面周长×母线长÷2,把相应数值代入即可求解.【解答】解:圆锥的侧面积=2π×4×5÷2=20π.故选:A.【点评】本题考查了圆锥的计算,解题的关键是弄清圆锥的侧面积的计算方法,特别是圆锥的底面周长等于圆锥的侧面扇形的弧长.5.已知某几何体的三视图(单位:cm),则这个圆锥的侧面积等于()A.12πcm2B.15πcm2C.24πcm2D.30πcm2【考点】圆锥的计算.【专题】计算题.【分析】俯视图为圆的只有圆锥,圆柱,球,根据主视图和左视图都是三角形可得到此几何体为圆锥,那么侧面积=底面周长×母线长÷2.【解答】解:∵底面半径为3,高为4,∴圆锥母线长为5,∴侧面积=2πrR÷2=15πcm2.故选:B.【点评】由该三视图中的数据确定圆锥的底面直径和高是解本题的关键;本题体现了数形结合的数学思想,注意圆锥的高,母线长,底面半径组成直角三角形.6.如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为()A.10cm2B.10πcm2C.20cm2D.20πcm2【考点】圆锥的计算.【专题】数形结合.【分析】圆锥的侧面积=底面周长×母线长÷2.【解答】解:圆锥的侧面积=2π×2×5÷2=10π.故选:B.【点评】本题考查了圆锥的计算,解题的关键是知道圆锥的侧面积的计算方法.7.一个圆锥的底面半径是6cm,其侧面展开图为半圆,则圆锥的母线长为()A.9cm B.12cm C.15cm D.18cm【考点】圆锥的计算.【专题】计算题.【分析】圆锥的母线长=圆锥的底面周长×.【解答】解:圆锥的母线长=2×π×6×=12cm,故选:B.【点评】本题考查圆锥的母线长的求法,注意利用圆锥的弧长等于底面周长这个知识点.8.圆锥体的底面半径为2,侧面积为8π,则其侧面展开图的圆心角为()A.90°B.120°C.150°D.180°【考点】圆锥的计算.【专题】计算题.【分析】设圆锥的侧面展开图的圆心角为n°,母线长为R,先根据锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式得到•2π•2•R=8π,解得R=4,然后根据弧长公式得到=2•2π,再解关于n的方程即可.【解答】解:设圆锥的侧面展开图的圆心角为n°,母线长为R,根据题意得•2π•2•R=8π,解得R=4,所以=2•2π,解得n=180,即圆锥的侧面展开图的圆心角为180°.故选:D.【点评】本题考查了圆锥的计算:锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.9.如图,某同学用一扇形纸板为一个玩偶制作一个圆锥形帽子,已知扇形半径OA=13cm,扇形的弧长为10πcm,那么这个圆锥形帽子的高是()cm.(不考虑接缝)A.5B.12C.13D.14【考点】圆锥的计算.【专题】几何图形问题.【分析】首先求得圆锥的底面半径,然后利用勾股定理求得圆锥的高即可.【解答】解:先求底面圆的半径,即2πr=10π,r=5cm,∵扇形的半径13cm,∴圆锥的高==12cm.故选:B.【点评】此题主要考查圆锥的侧面展开图和勾股定理的应用,牢记有关公式是解答本题的关键,难度不大.10.若一个圆锥的主视图是腰长为5,底边长为6的等腰三角形,则该圆锥的侧面积是()A.15πB.20πC.24πD.30π【考点】圆锥的计算;简单几何体的三视图.【专题】计算题.【分析】根据圆锥的主视图得到圆锥的底面圆的半径为3,母线长为5,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.【解答】解:根据题意得圆锥的底面圆的半径为3,母线长为5,所以这个圆锥的侧面积=•5•2π•3=15π.故选:A.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图.11.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为()A.1.5B.2C.2.5D.3【考点】圆锥的计算.【专题】计算题.【分析】半径为6的半圆的弧长是6π,圆锥的底面周长等于侧面展开图的扇形弧长,因而圆锥的底面周长是6π,然后利用弧长公式计算.【解答】解:设圆锥的底面半径是r,半径为6的半圆的弧长是6π,则得到2πr=6π,解得:r=3,这个圆锥的底面半径是3.故选:D.【点评】本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.12.圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是()A.6πB.8πC.12πD.16π【考点】圆锥的计算.【专题】计算题.【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.【解答】解:此圆锥的侧面积=•4•2π•2=8π.故选:B.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.13.一个立体图形的三视图如图,根据图中数据求得这个立体图形的侧面积为()A.12πB.15πC.18πD.24π【考点】圆锥的计算;由三视图判断几何体.【分析】从主视图以及左视图都为一个三角形,俯视图为一个圆形看,可以确定这个几何体为一个圆锥,由三视图可知圆锥的底面半径为3,高为4,故母线长为5,据此可以求得其侧面积.【解答】解:由三视图可知圆锥的底面半径为3,高为4,所以母线长为5,所以侧面积为πrl=3×5π=15π,故选:B.【点评】本题主要考查了由三视图确定几何体和求圆锥的侧面积.牢记公式是解题的关键,难度不大.14.已知圆锥的母线长为3,底面的半径为2,则圆锥的侧面积是()A.4πB.6πC.10πD.12π【考点】圆锥的计算.【专题】计算题.【分析】根据锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算即可.【解答】解:圆锥的侧面积=•2π•2•3=6π.故选:B.【点评】本题考查了圆锥的计算:锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.15.如图,圆锥的侧面展开图是半径为3,圆心角为90°的扇形,则该圆锥的底面周长为()A.πB.πC.D.【考点】圆锥的计算.【专题】计算题.【分析】根据圆锥侧面展开扇形的弧长等于底面圆的周长,可以求出底面圆的半径,从而求得圆锥的底面周长.【解答】解:设底面圆的半径为r,则:2πr==π.∴r=,∴圆锥的底面周长为,故选:B.【点评】本题考查的是弧长的计算,利用弧长公式求出弧长,然后根据扇形弧长与圆锥底面半径的关系求出底面圆的半径.16.一个圆锥的侧面展开图是半径为R的半圆,则该圆锥的高是()A.R B.C.D.【考点】圆锥的计算.【分析】根据侧面展开图的弧长等于圆锥的底面周长,即可求得底面周长,进而即可求得底面的半径长,然后表示出圆锥的高即可.【解答】解:圆锥的底面周长是:πR;设圆锥的底面半径是r,则2πr=πR.解得:r=R.由勾股定理得到圆锥的高为=,故选:D.【点评】本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.17.一个几何体的三视图如图所示,这个几何体的侧面积为()A.2πcm2B.4πcm2C.8πcm2D.16πcm2【考点】圆锥的计算;由三视图判断几何体.【专题】几何图形问题.【分析】俯视图为圆的只有圆锥,圆柱,球,根据主视图和左视图都是三角形可得到此几何体为圆锥,那么侧面积=底面周长×母线长÷2.【解答】解:此几何体为圆锥;∵半径为1,圆锥母线长为4,∴侧面积=2πrR÷2=2π×1×4÷2=4π;故选:B.【点评】本题考查了圆锥的计算,该三视图中的数据确定圆锥的底面直径和高是解本题的关键;本题体现了数形结合的数学思想,注意圆锥的高,母线长,底面半径组成直角三角形.18.底面半径为4,高为3的圆锥的侧面积是()A.12πB.15πC.20πD.36π【考点】圆锥的计算.【专题】计算题.【分析】首先根据底面半径和高利用勾股定理求得母线长,然后直接利用圆锥的侧面积公式代入求出即可.【解答】解:∵圆锥的底面半径为4,高为3,∴母线长为5,∴圆锥的侧面积为:πrl=π×4×5=20π,故选:C.【点评】本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键.二、填空题19.一个圆锥形漏斗,某同学用三角波测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为15π.【考点】圆锥的计算.【专题】计算题.【分析】根据图中数据得到圆锥的高为4,底面圆的半径为3,则根据勾股定理计算出母线长为5,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.【解答】解:圆锥的母线长==5,所以该圆锥形漏斗的侧面积=•2π•3•5=15π.故答案为15π.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.20.在△ABC纸板中,AB=3cm,BC=4cm,AC=5cm,将△ABC纸板以AB所在直线为轴旋转一周,则所形成的几何体的侧面积为20πcm2(结果用含π的式子表示).【考点】圆锥的计算;点、线、面、体;勾股定理的逆定理.【分析】易得此几何体为圆锥,那么圆锥的侧面积=底面周长×母线长÷2.【解答】解:∵在△ABC中,AB=3,BC=4,AC=5,∴△ABC为直角三角形,∴底面周长=8π,侧面积=×8π×5=20πcm2.故答案为:20π.【点评】本题考查了圆锥的计算,以及勾股定理的逆定理,利用圆的周长公式和扇形面积公式求解.21.一个底面直径是80cm,母线长为90cm的圆锥的侧面展开图的圆心角的度数为160°.【考点】圆锥的计算.【专题】计算题.【分析】根据圆锥的底面直径求得圆锥的侧面展开扇形的弧长,再利用告诉的母线长求得圆锥的侧面展开扇形的面积,再利用扇形的另一种面积的计算方法求得圆锥的侧面展开图的圆心角即可.【解答】解:∵圆锥的底面直径是80cm,∴圆锥的侧面展开扇形的弧长为:πd=80π,∵母线长90cm,∴圆锥的侧面展开扇形的面积为:lr=×80π×90=3600π,∴=3600π,解得:n=160.故答案为:160°.【点评】本题考查了圆锥的有关计算,解决此类题目的关键是明确圆锥的侧面展开扇形与圆锥的关系.22.圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为60πcm2.【考点】圆锥的计算.【专题】计算题.【分析】圆锥的侧面积=π×底面半径×母线长,把相应数值代入即可求解.【解答】解:圆锥的侧面积=π×6×10=60πcm2.【点评】本题考查圆锥侧面积公式的运用,掌握公式是关键.23.一个底面直径为10cm,母线长为15cm的圆锥,它的侧面展开图圆心角是120度.【考点】圆锥的计算.【专题】计算题.【分析】利用底面周长=展开图的弧长可得.【解答】解:∵底面直径为10cm,∴底面周长为10π,根据题意得10π=,解得n=120.故答案为:120.【点评】考查了圆锥的计算,解答本题的关键是有确定底面周长=展开图的弧长这个等量关系,然后由扇形的弧长公式和圆的周长公式求值.24.已知圆锥的底面半径为3,母线长为8,则圆锥的侧面积等于24π.【考点】圆锥的计算.【专题】计算题.【分析】圆锥的侧面积=底面周长×母线长÷2,把相应数值代入即可求解.【解答】解:圆锥的侧面积=2π×3×8÷2=24π,故答案为:24π.【点评】本题考查圆锥的侧面积的求法,牢记公式是解答本题的关键,难度不大.25.若圆锥的侧面展开图的弧长为24πcm,则此圆锥底面的半径为12cm.【考点】圆锥的计算.【分析】利用扇形的弧长等于圆锥的底面周长列出等式求得圆锥的底面半径即可.【解答】解:设圆锥的底面半径为r,∵圆锥的侧面展开图的弧长为24πcm,∴2πr=24π,解得:r=12,故答案为:12.【点评】本题考查了圆锥的计算,解题的关键是牢记扇形的弧长等于圆锥的底面周长.26.用一个圆心角为240°半径为6的扇形做一个圆锥的侧面,则这个圆锥底面半径为4.【考点】圆锥的计算.【专题】计算题.【分析】易得扇形的弧长,除以2π即为圆锥的底面半径.【解答】解:∵扇形的弧长==8π,∴圆锥的底面半径为8π÷2π=4.故答案为:4.【点评】考查了扇形的弧长公式;圆的周长公式;用到的知识点为:圆锥的弧长等于底面周长.27.用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,则这个圆锥底面圆的周长为π.【考点】圆锥的计算.【分析】根据圆锥的底面周长即为圆锥的侧面展开扇形的弧长求解.【解答】解:圆锥的底面圆的周长=π,故答案为:π.【点评】本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.28.如图,如果从半径为3cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径是2cm.【考点】圆锥的计算.【专题】几何图形问题.【分析】易求得扇形的弧长,除以2π即为圆锥的底面半径.【解答】解:扇形的弧长为:=4πcm,圆锥的底面半径为:4π÷2π=2cm,故答案为:2.【点评】考查了扇形的弧长公式,圆的周长公式,用到的知识点为:圆锥的弧长等于底面周长.29.用圆心角是216°,半径是5cm的扇形围成一个圆锥体的侧面(接缝处不重叠),则这个圆锥体的高是4cm.【考点】圆锥的计算.【分析】设圆锥底面的圆的半径为r,利用圆锥的侧面展开图为一扇形得到2πr=,解得r=3,然后根据勾股定理计算这个圆锥的高.【解答】解:设圆锥底面的圆的半径为r,根据题意得2πr=,解得r=3,所以这个圆锥的高==4(cm).故答案为:4.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.30.若圆锥的轴截面是一个边长为4的等边三角形,则这个圆锥的侧面展开后所得到的扇形的圆心角的度数是180°.【考点】圆锥的计算.【专题】计算题.【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长得到扇形的弧长为4π,扇形的半径为4,再根据弧长公式求解.【解答】解:∵轴截面是一个边长为4的等边三角形,∴母线长为4,圆锥底面直径为4,∴底面周长为4π,即扇形弧长为4π.设这个圆锥的侧面展开后所得到的扇形的圆心角的度数为n,根据题意得4π=,解得n=180°.故答案为:180°.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.。
2023-2024学年第一学期人教版九年级数学上册第24章复习测试卷附答案

2023-2024学年第一学期九年级数学上册第24章【圆】复习测试卷一、选择题:1.一圆形玻璃被打碎后,其中四块碎片如图所示,若选择其中一块碎片带到商店,配制与原来大小一样的圆形玻璃,不能选择的是()A.①B.②C.③D.④2.如图,⊙O 的半径长为10cm,弦AB=16cm,则圆心O 到弦AB 的距离为()A.4cm B.5cm C.6cmD.7cm 3.如图所示,已知四边形ABDC 是圆内接四边形,∠1=112°,则∠CDE=()A.56°B.68°C.66°D.58°4.如图,AB 与⊙O 相切于点A,BO 与⊙O 相交于点C,点D 是优弧AC 上一点,∠CDA=27°,则∠B 的大小是()A.27°B.34°C.36°D.54°5.如图,O 是锐角三角形ABC 的外接圆,OD AB OE BC OF AC ⊥⊥⊥,,,垂足分别为D,E,F,连接DE,EF,FD.若 6.5DE DF ABC += ,的周长为21,则EF 的长为()A.8B.4C.3.5D.36.如图,⊙O 是四边形ABCD 的内切圆,切点依次是E、F、G、H,下列结论一定正确的有()个①AF=BG ②CG=CH ③AB+CD=AD+BC ④BG<CG.A.1B.2C.3D.47.一个长为4cm,宽为3cm 的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板左上角一点A 位置的变化为A→A 1→A 2,其中第二次翻滚被面上一小木块挡住,使木板与桌面成30°的角,则点A 滚到A 2位置时共走过的路径长为()A.7π2cm B.23π6cm C.4π3cm D.5π2cm 8.如图,O 是ABC 的外接圆,弦BD 交AC 于点E,AE DE =,BC CE =,过点O 作OF AC ⊥于点F,延长FO 交BE 于点G,若3DE =,2EG =,则AB 的长为()A.43B.7C.8D.459.如图,AB 是O 的直径,弦CD 与AB 垂直,垂足为点E,连接OC 并延长交O 于点F ,30CDB ∠=︒,3CD =,则图中阴影部分的面积为()A.π332-B.2π33C.4π33-D.2π23-二、填空题:10.已知正六边形的边心距为32,则这个正六边形的周长为.11.点P 到O 上一点A 的距离PA 的最大值是18cm ,PA 的最小值为8cm ,则O的半径为.12.如图,公园内有一个半径为20米的圆形草坪,A ,B 是圆上的点,O 为圆心,120AOB ∠=︒,从A 到B 只有路AB ,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB .通过计算可知,这些市民其实仅仅少走了步(假设1步为0.5米,结果保留整数).(参考数据:1.732π≈,取3.142)13.如图,在O 中,直径AB 与弦CD 交于点 2E AC BD=,.连接AD ,过点B 的切线与AD 的延长线交于点F .若68AFB ∠=︒,则DEB ∠=°.14.如图,Rt ABC 中,60C ∠=︒,斜边4BC =,以边AB 为直径在ABC 另一侧作半圆,点P 为半圆上一点,将半圆沿AP 所在直线翻折,翻折后的AP 与BC 边相切于点D ,与AB 边相交于点E ,则BE 的长为.15.如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b 进行无滑动滚动,使半圆的直径与直线b 重合为止,则圆心O 运动路径的长度等于.三、解答题:16.如图,在⊙O 中,弦AB、CD 的延长线交于点P,且DA=DP.求证:BC=BP.17.如图,边长为1的正方形ABCD 的边AB 是⊙O 的直径,CF 是⊙O 的切线,E 为切点,F 点在AD 上,BE 是⊙O 的弦,求△CDF 的面积.18.已知O 的直径为10,四边形ABDC 内接于O ,AD 平分CAB ∠.(1)如图1,若BC 为O 的直径,求BD 的长;(2)如图2,若120BDC ∠=︒,求BD 的长.19.如图,已知AC 是⊙O 的直径,B 为⊙O 上一点,D 为 BC的中点,过D 作EF∥BC 交AB 的延长线于点E,交AC 的延长线于点F.(Ⅰ)求证:EF 为⊙O 的切线;(Ⅱ)若AB=2,∠BDC=2∠A,求 BC 的长.20.如图,等边三角形ABC 内接于O ,D 是 BC上一动点,连接AD ,BD ,CD ,延长DC 到点E ,使CE BD =,连接AE .(1)求证:ADE 是等边三角形;(2)填空:①若1BD =,2CD =,则AD 的长为;②当BAD ∠的度数为时,四边形OBDC 为菱形.参考答案:1.C 2.C 3.A 4.C 5.B 6.B 7.B 8.B 9.B 10.611.5cm 或13cm12.1513.6614.3-15.5π16.证明:∵DA=DP,∴∠P=∠A.又∵∠C=∠A,∴∠P=∠C.∴BC=BP.17.解:设AF=x,∵四边形ABCD 是正方形,∴∠DAB=90°,∴DA⊥AB,∴AD 是圆的切线,∵CF 是⊙O 的切线,E 为切点,∴EF=AF=x,∴FD=1﹣x,∴CF=CE+EF=CB+EF=1+x.∴在Rt△CDF 中由勾股定理得到:CF 2=CD 2+DF 2,即(1+x)2=1+(1﹣x)2,解得x=14,∴DF=1﹣x=34,∴S △CDF =12×1×34=38.18.(1)解:∵AD 平分CAB ∠,∴CAD BAD ∠=∠,∴ CD BD =,∴CD BD =,∵BC 为O 的直径,O 的直径为10,∴1090BC BDC ∠==︒,,∴BDC 为等腰直角三角形,∴2BD BC ==;(2)解:如图所示,连接OB OD ,,∵四边形ABDC 内接于O ,120BDC ∠=︒,∴18060BAC BDC ∠=︒-∠=︒,∵AD 平分CAB ∠,∴1302CAD BAD BAC ∠=∠=∠=︒,∴260BOD BAD ∠=∠=︒,又∵OB OD =,∴BOD 是等边三角形,∴11052BD OB ==⨯=.19.解:(1)连接OD,OB,∵D 为BC 的中点,∴∠BOD=∠COD,∵OB=OC,∴OD⊥BC,∴∠OGC=90°,∵EF∥BC,∴∠ODF=∠OGC=90°,即OD⊥EF,∵OD 是⊙O 的半径,∴EF 是⊙O 的切线;(2)∵四边形ABDC 是⊙O 的内接四边形,∴∠A+∠BDC=180°,又∵∠BDC=2∠A,∴∠A=60°,∵OA=OB,∴△OAB 等边三角形,∵OB=AB=2,又∵∠BOC=2∠A=120°,∴EC=12024=1803ππ⨯⨯20.(1)证明:∵△ABC 是等边三角形,∴AB=AC=BC,∠ABC=∠ACB=∠BAC=60°,∵∠CBD 与∠CAD 是 CD 所对的圆周角,∴∠CBD=∠CAD,同理可得:∠ABC=∠ADC=60°,∵∠ACE=∠CAD+∠ADC,∴∠ACE=∠ABC+∠CBD=∠ABD,在△ABD 和△ACE 中,AB ACABD ACE BD CE=⎧⎪∠=∠⎨⎪=⎩,∴△ABD≌△ACE,∴AD=AE,∴△ADE 是等边三角形(2)8;30°①∵BD=CE=1,DE=CD+CE,CD=2,∴DE=3,∵△ADE 是等边三角形,∴AD=DE=3.故答案为:3;②如图,连接OB、OC,∵∠BAC 和∠BOC 分别是 BC 所对的圆周角和圆心角,∴∠BOC=2∠BAC=120°,∵OB=OC,∴∠OCB=30°,∵四边形OBDC 为菱形,∵∠BAD和∠BCD都是 BD所对的圆周角,∴∠BAD=∠BCD=30°,的度数为30°时,四边形OBDC为菱形.∴当BAD故答案为:30°。
人教版数学九年级上册第24章《圆》单元培优练习题卷(含解析)

《圆》单元培优练习卷一.选择题1.面积为6π,圆心角为60°的扇形的半径为()A.2 B.3 C.6 D.92.如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为()A.60°B.50°C.40°D.20°3.如图:已知AB是⊙O的直径,点C在⊙O上,点D在半径OA上(不与点O,A重合).若∠COA=60°,∠CDO=70°,∠ACD的度数是()A.60°B.50°C.30°D.10°4.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则劣弧AC的长是()A.4πB.2πC.πD.5.如图,直角三角形ABC的内切圆分别与AB、BC相切于D点、E点,根据图中标示的长度与角度,求AD的长度为何?()A.B.C.D.6.如图物体由两个圆锥组成.其主视图中,∠A=90°,∠ABC=105°,若上面圆锥的侧面积为1,则下面圆锥的侧面积为()A.2 B.C.D.7.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=16,∠BAC=∠BOD,则⊙O 的半径为()A.4B.8 C.10 D.68.如图,CD是⊙O的切线,点C在直径的延长线上,若BD=AD,AC=3,CD=()A.1 B.1.5 C.2 D.2.59.如图,四边形ABCD为⊙O的内接四边形,∠AOC=110°,则∠ADC=()A.55°B.110°C.125°D.70°10.如图,在菱形ABCD中,AC与BD交于点O,BD=CD,以点D为圆心,BD长为半径作,若AC=6,则图中阴影部分的面积是()A.2π﹣3B.2π+3C.π﹣D.π+11.如图,AB是⊙O的弦,作OC⊥OA交⊙O的切线BC于点C,交AB于点D.已知∠OAB=20°,则∠OCB的度数为()A.20°B.30°C.40°D.50°12.如图,四边形ABCD中,CD∥AB,E是对角线AC上一点,DE=EC,以AE为直径的⊙O 与边CD相切于点D,点B在⊙O上,连接BD,若DE=4,则BD的长为()A.4 B.4C.8 D.813.在正六边形ABCDEF中,若边长为3,则正六边形ABCDEF的边心距为.14.Rt△ABC中,∠ACB=90°,CD为AB边上的高,P为AC的中点,连接P D,BC=6,DP =4.O为边BA上一点,以O为圆心,OB为半径作⊙O,当⊙O与△PDC的一边所在直线相切时,⊙O的半径等于.15.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=42°,则∠CAD=16.如图,在Rt△ABC中,∠C=90°,∠B=30°,其中AC=2,以AC为直径的⊙O交AB 于点D,则圆周角∠A所对的弧长为(用含π的代数式表示)17.如图,在△ABC中,∠ABC=90°,∠ACB=30°,BC=2,BC是半圆O的直径,则图中阴影部分的面积为.18.如图,在边长为2的菱形ABCD中,∠B=45°,以点A为圆心的扇形FAG与菱形的边BC相切于点E,则图中的弧长是.19.如图,△ABC是⊙O的内接三角形,AB为⊙O直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连接BD.(1)求证:∠BAD=∠CBD;(2)若∠AEB=125°,求的长(结果保留π).20.如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点D,与AC交于点E,延长CD、BA相交于点F,∠ADF的平分线交AF于点G.(1)求证:DG∥CA;(2)求证:AD=ID;(3)若DE=4,BE=5,求BI的长.21.如图,在矩形ABCD中,以BC边为直径作半圆O,OE⊥OA交CD边于点E,对角线AC与半圆O的另一个交点为P,连接AE.(1)求证:AE是半圆O的切线;(2)若PA=2,PC=4,求AE的长.22.如图,AB为⊙O的直径,且AB=4,点C是上的一动点(不与A,B重合),过点B作⊙O的切线交AC的延长线于点D,点E是BD的中点,连接EC.(1)求证:EC是⊙O的切线;(2)当∠D=30°时,求阴影部分面积.23.已知AB是⊙O的直径,C,D是⊙O上AB同侧的两点,∠BAC=25°(Ⅰ)如图①,若OD⊥AB,求∠ABC和∠ODC的大小;(Ⅱ)如图②,过点C作⊙O的切线,交AB延长线于点E,若OD∥EC,求∠ACD的大小.24.如图,以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点D,过点D作⊙O的切线与BC交于点E,弦DM与AB垂直,垂足为H.(1)求证:E为BC的中点;(2)若⊙O的面积为12π,两个三角形△AHD和△BMH的外接圆面积之比为3,求△DEC的内切圆面积S1和四边形OBED的外接圆面积S2的比.参考答案一.选择题1.解:设扇形的半径为r.由题意:=6π,∴r2=36,∵r>0,∴r=6,故选:C.2.解:连接AD,∵AB为⊙O的直径,∴∠ADB=90°.∵∠BCD=40°,∴∠A=∠BCD=40°,∴∠ABD=90°﹣40°=50°.故选:B.3.解:∵OA=OC,∠COA=60°,∴△ACO为等边三角形,∴∠CAD=60°,又∵∠CDO=70°,∴∠ACD=∠CDO﹣∠CAD=10°.故选:D.4.解:∵四边形ABCD为圆O的内接四边形,∴∠B+∠D=180°,∵∠B=135°,∴∠D=45°,∵∠AOC=2∠D,∴∠AOC=90°,则l==2π,故选:B.5.解:设AD=x,∵直角三角形ABC的内切圆分别与AB、BC相切于D点、E点,∴BD=BE=1,∴AB=x+1,AC=AD+CE=x+4,在Rt△ABC中,(x+1)2+52=(x+4)2,解得x=,即AD的长度为.故选:D.6.解:∵∠A=90°,AB=AD,∴△ABD为等腰直角三角形,∴∠ABD=45°,BD=AB,∵∠ABC=105°,∴∠CBD=60°,而CB=CD,∴△CBD为等边三角形,∴BC=BD=AB,∵上面圆锥与下面圆锥的底面相同,∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB:CB,∴下面圆锥的侧面积=×1=.故选:D.7.解:∵∠BAC=∠BOD,∴,∴AB⊥CD,∵AE=CD=16,∴DE=CD=8,设OD=r,则OE=AE﹣r=16﹣r,在Rt△ODE中,OD=r,DE=8,OE=16﹣r,∵OD2=DE2+OE2,即r2=82+(16﹣r)2,解得r=10.故选:C.8.解:∵CD是⊙O的切线,∴∠CDB=∠CAD,又∠C=∠C,∴△CDB∽△CAD,∴==,即=,解得,CD=2,故选:C.9.解:由圆周角定理得,∠B=∠AOC=55°,∵四边形ABCD为⊙O的内接四边形,∴∠ADC=180°﹣∠B=125°,故选:C.10.解:∵在菱形ABCD中,AC与BD交于点O,BD=CD,AC=6,∴AC⊥BD,OC=3,BD=CD=BC,BD=2OB,∴△BCD是等边三角形,∴∠BDC=60°,OB=,∴BD=2,∴图中阴影部分的面积是:S阴=S扇形CDB﹣S△CDB=﹣×2×3=2π﹣3,故选:A.11.解:连接OB,∵BC是⊙O的切线,∴∠OBC=90°,∵OA=OB,∴∠OAB=∠OBA=20°,∴∠DBC=70°,∵∠AOC=90°,∴∠ODA=∠BDC=70°,∴∠OCB=40°,故选:C.12.解:如图,连接OD,设⊙O的半径为r,∵⊙O与边CD相切于点D,∴OD⊥CD,∴∠ODC=90°,即∠3+∠ODE=90°,∵AE为直径,∴∠ADE=90°,∴∠ODA+∠ODE=90°,∴∠ODA=∠3,而∠ODA=∠1,∴∠1=∠3,∵ED=EC=4,∴∠2=∠3,∴∠1=∠2,∵AB∥CD,∴∠2=∠CAB,∴∠1=∠CAB∴=,∴AE⊥BD,∵∠1=∠2,DF⊥AC,∴AF=CF,∴CF=﹣4=r﹣2,∵∠DEF=∠AED,∠DFE=∠ADE,∴△EDF∽△EAD,∴DE:EA=EF:DE,即4:2r=(r﹣2):4,整理得r2﹣2r﹣8=0,解得r=﹣2(舍去)或r=4,∴EF=r﹣2=2,在Rt△DEF中,DF==2,∴DB=2DF=4.故选:B.二.填空题(共6小题)13.解:如图,设正六边形ABCDEF的中心为O,连接OA,OB,则△OAB是等边三角形,过O作OH⊥AB于H,∴∠AOH=30°,∴OH=AO=,故答案为:.14.解:∵∠ADC=90°,P是AC中点,∴AC=2DP=8,又∵BC=6,∴AB=10,则CD===,∴BD==,如图1,若⊙O与CD相切,则⊙O的半径r=BD=;如图2,若⊙O与CP相切,则BO=OE=r,AO=10﹣r,由OE⊥AC知OE∥BC,∴△AOE∽△ABC,∴=,即=,解得r=;如图3,若⊙O与DP所在直线相切,切点F,则OF⊥DP,即∠OFD=∠ACB=90°,OB=OF=r,∴OD=BD﹣BO=﹣r,∵∠ODF=∠ADP=∠A,∴△ODF∽△BAC,∴=,即=,解得r=;综上,当⊙O与△PDC的一边所在直线相切时,⊙O的半径等于或或,故答案为:或或.15.解:连接OC,OD,如图所示.∵∠CAB=42°,∴∠COB=84°.∵=,∴∠COD=(180°﹣∠COB)=48°,∴∠CAD=∠COD=24°.故答案为:24°.16.解:连接OD,在Rt△ABC中,∠C=90°,∠B=30°,∴∠A=60°,∴∠COD=2∠A=120°,∵AC=2,∴圆周角∠A所对的弧长为:=,故答案为:.17.解:如图,连接OF.S阴=(S扇形OFC﹣S△OFC)+(S△ABC﹣S△OFC﹣S扇形OBF)=﹣•×+×2×﹣××﹣=﹣+﹣=+,故答案为: +.18.解:连接AE,如图,∵以点A为圆心的扇形FAG与菱形的边BC相切于点E,∴AE⊥BC,在Rt△ABE中,∵AB=2,∠B=45°,∴∠BAE=45°,AE=AB=×2=2,∵四边形ABCD为菱形,∴AD∥BC,∴∠DAE=∠BEA=90°,∴的弧长==π.故答案为π.三.解答题(共6小题)19.(1)证明:∵AD平分∠BAC,∴∠CAD=∠BAD,∵∠CAD=∠CBD,∴∠BAD=∠CBD;(2)解:连接OD,∵∠AEB=125°,∴∠AEC=55°,∵AB为⊙O直径,∴∠ACE=90°,∴∠CAE=35°,∴∠DAB=∠CAE=35°,∴∠BOD=2∠BAD=70°,∴的长==π.20.(1)证明:∵点I是△ABC的内心,∴∠2=∠7,∵DG平分∠ADF,∴∠1=∠ADF,∵∠ADF=∠ABC,∴∠1=∠2,∵∠3=∠2,∴∠1=∠3,∴DG∥AC;(2)证明:∵点I是△ABC的内心,∴∠5=∠6,∵∠4=∠7+∠5=∠3+∠6,即∠4=∠DAI,∴DA=DI;(3)解:∵∠3=∠7,∠AED=∠BAD,∴△DAE∽△DBA,∴AD:DB=DE:DA,即AD:9=4:AD,∴AD=6,∴DI=6,∴BI=BD﹣DI=9﹣6=3.21.(1)证明:∵在矩形ABCD中,∠ABO=∠OCE=90°,∵OE⊥OA,∴∠AOE=90°,∴∠BAO+∠AOB=∠AOB+∠COE=90°,∴∠BAO=∠COE,∴△ABO∽△OCE,∴=,∵OB=OC,∴,∵∠ABO=∠AOE=90°,∴△ABO∽△AOE,∴∠BAO=∠OAE,过O作OF⊥AE于F,∴∠ABO=∠AFO=90°,在△ABO与△AFO中,,∴△ABO≌△AFO(AAS),∴OF=OB,∴AE是半圆O的切线;(2)解:连接PF,FC,FO并延长交⊙O于G,则∠G=∠ACF,∠G+∠PFG=90°,∵AF是⊙O的切线,∴∠AFG+∠PFG=90°,∴∠AFP=∠G=∠ACF,∵∠FAP=∠A CF,∴△AFP∽△ACF,∴=,∴AF2=AP•AC,∴AF==2,∴AB=AF=2,∵AC=6,∴BC==2,∴AO==3,∵△ABO∽△AOE,∴,∴=,∴AE=3.22.解:(1)如图,连接BC,OC,OE,∵AB为⊙O的直径,∴∠ACB=90°,在Rt△BDC中,∵BE=ED,∴DE=EC=BE,∵OC=OB,OE=OE,∴△OCE≌△OBE(SSS),∴∠OCE=∠OBE,∵BD是⊙O的切线,∴∠ABD=90°,∴∠OCE=∠ABD=90°,∵OC为半径,∴EC是⊙O的切线;(2)∵OA=OB,BE=DE,∴AD∥OE,∴∠D=∠OEB,∵∠D=30°,∴∠OEB=30°,∠EOB=60°,∴∠BOC=120°,∵AB=4,∴OB=2,∴.∴四边形OBEC的面积为2S△OBE=2×=12,∴阴影部分面积为S四边形OBEC ﹣S扇形BOC=12﹣=12﹣4π.23.解:(Ⅰ)连接OC,∵AB是⊙O的直径,∴∠ACB=90°,∵∠BAC=25°,∴∠ABC=65°,∵OD⊥AB,∴∠AOD=90°,∴∠ACD=∠AOD==45°,∵OA=OC,∴∠OAC=∠OCA=25°,∴∠OCD=∠OCA+∠ACD=70°,∵OD=OC,∴∠ODC=∠OCD=70°;(Ⅱ)连接OC,∵EC是⊙O的切线,∴OC⊥EC,∴∠OCE=90°,∵∠BAC=25°,∴∠COE=2∠BAC=50°,∴∠OEC=40°,∵OD∥CE,∴∠AOD=∠COE=40°,∴∠ACD=AOD=20°.24.解:(1)连接BD、OE,∵AB是直径,则∠ADB=90°=∠A DO+∠ODB,∵DE是切线,∴∠ODE=90°=∠EDB+∠BDO,∴∠EDB=∠ADO=∠CAB,∵∠ABC=90°,即BC是圆的切线,∴∠DBC=∠CAB,∴∠EDB=∠EBD,则∠BDC=90°,∴E为BC的中点;(2)△AHD和△BMH的外接圆面积之比为3,则两个三角形的外接圆的直径分别为AD、BM,∴AD:BM=,而△ADH∽△MBH,∴DH:BH=,则DH=HM,∴HM:BH=,∴∠BMH=30°=∠BAC,∴∠C=60°,E是直角三角形的中线,∴DE=CE,∴△DEC为等边三角形,⊙O的面积:12π=(AB)2π,则AB=4,∠CAB=30°,∴BD=2,BC=4,AC=8,而OE=AC=4,四边形OBED的外接圆面积S2=π(2)2=4π,等边三角形△DEC边长为2,则其内切圆的半径为:,面积为,故△DEC的内切圆面积S1和四边形O BED的外接圆面积S2的比为:.。
人教版九年级上册第24章数学圆单元测试卷(含答案)(6)

人教版九年级上册第24章数学圆单元测试卷(含答案)(6)一、选择题(每题3分,共30分) 1.下列说法中不正确的是( )A .圆是轴对称图形B .三点确定一个圆C .半径相等的两个圆是等圆D .每个圆都有无数条对称轴2.若⊙O 的面积为25π,在同一平面内有一个点P ,且点P 到圆心O 的距离为4.9,则点P 与⊙O 的位置关系为( ) A .点P 在⊙O 外 B .点P 在⊙O 上 C .点P 在⊙O 内D .无法确定3.如图,⊙O 是△ABC 的外接圆,∠BOC =120°,则∠BAC 的度数是( )A .70°B .60°C .50°D .30°(第3题) (第4题) (第5题) (第6题)4.如图所示,⊙O 的半径为13,弦AB 的长度是24,ON ⊥AB ,垂足为点N ,则ON =( ) A .5B .7C .9D .115.如图,在Rt △ABC 中,∠C =90°,AC =4,BC =7,点D 在边BC 上,CD =3,⊙A 的半径长为3,⊙D 与⊙A 相交,且点B 在⊙D 外,那么⊙D 的半径长r 的取值范围是( ) A .1<r <4B .2<r <4C .1<r <8D .2<r <86.如图,四边形ABCD 内接于⊙O ,F 是CD ︵上一点,且DF ︵=BC ︵,连接CF 并延长交AD 的延长线于点E ,连接AC .若∠ABC =105°,∠BAC =25°,则∠E 的度数为( ) A .45°B .50°C .55°D .60°7.如图,⊙O 与矩形ABCD 的边相切于点E ,F ,G ,点P 是EFG ︵上一点,则∠P的度数是( )A .45°B .60°C .30°D .无法确定8.如图,在△ABC 中,∠ACB =90°,∠ABC =30°,AB =2.将△ABC 绕直角顶点C逆时针旋转60°得△A ′B ′C ,则点B 转过的路径长为( ) A.π3B.3π3C.2π3D .π(第7题) (第8题) (第10题)9.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( ) A .60°B .90°C .120°D .180°10.如图,正六边形A 1B 1C 1D 1E 1F 1的边长为2,正六边形A 2B 2C 2D 2E 2F 2的外接圆与正六边形A 1B 1C 1D 1E 1F 1的各边相切,正六边形A 3B 3C 3D 3E 3F 3的外接圆与正六边形A 2B 2C 2D 2E 2F 2的各边相切……按这样的规律进行下去,正六边形A 10B 10C 10D 10E 10F 10的边长为( ) A.24329B.81329C.8129D.81328二、填空题(每题3分,共30分)11.如图,在圆内接四边形ABCD 中,若∠A ,∠B ,∠C 的度数之比为4∶3∶5,则∠D 的度数是________.(第11题) (第12题) (第13题) (第14题)12.如图,PA ,PB 是⊙O 的切线,切点分别为A ,B ,若OA =2,∠P =60°,则AB︵的长为________.13.如图,⊙O 中,AB ︵=AC ︵,∠BAC =50°,则∠AEC 的度数为________.14.如图,AB 是⊙O 的直径,BD ,CD 分别是过⊙O 上点B ,C 的切线,且∠BDC=110°.连接AC ,则∠A 的度数是________.15.一元钱硬币的直径约为24 mm ,则用它能完全覆盖住的正六边形的边长最大不能超过________mm.16.如图,在⊙O 的内接五边形ABCDE 中,∠CAD =35°,则∠B +∠E =________°. 17.一个圆锥形漏斗,某同学用三角板测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为________.(第16题) (第17题) (第18题) (第19题)18.如图,AC ⊥BC ,AC =BC =4,以BC 长为直径作半圆,圆心为点O .以点C 为圆心,BC 长为半径作弧AB ,过点O 作AC 的平行线交两弧于点D ,E ,则阴影部分的面积是________.19.如图,AB 是⊙O 的一条弦,点C 是⊙O 上一动点,且∠ACB =30°,点E ,F分别是AC ,BC 的中点,直线EF 与⊙O 交于G ,H 两点,若⊙O 的半径是7,则GE +F H 的最大值是________.(第20题)20.如图所示,在⊙O 中,C ,D 分别是OA ,OB 的中点,MC ⊥AB ,ND ⊥AB ,M ,N 在⊙O 上.下列结论:①MC =ND ;②AM ︵=MN ︵=NB ︵;③四边形MCDN 是正方形;④MN =12AB ,其中正确的结论是________.(填序号)三、解答题(21、22题每题8分,23、24题每题10分,其余每题12分,共60分)21.如图,AB 是圆O 的直径,CD 为弦,AB ⊥CD ,垂足为H ,连接BC 、BD . (1)求证:BC =BD ;(2)已知CD =6,O H =2,求圆O 的半径长.(第21题)22.“不在同一条直线上的三个点确定一个圆”.请你判断平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)是否可以确定一个圆.23.如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,恰有AB=AC.(1)求证:AB是⊙O的切线;(2)若PC=25,OA=5,求⊙O的半径.(第23题)24.如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,CD=CE.(1)求证:OA=OB;(2)已知AB=43,OA=4,求阴影部分的面积.(第24题)25.如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.(1)求桥拱的半径.(2)现有一艘宽60米,顶部截面为长方形且高出水面9米的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.(第25题)26.已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.(1)当直线CD与半圆O相切时,如图①,连接OC,求∠DOC的度数;(2)当直线CD与半圆O相交时,如图②,设另一交点为E,连接AE,OC,若AE∥OC.①试猜想AE与OD的数量关系,并说明理由;②求∠ODC的度数.(第26题)答案一、1.B 2.C 3.B 4.A 5.B 6.B7.A 点拨:连接OE ,OG ,易得OE ⊥AB ,OG ⊥AD .∵四边形ABCD 是矩形,∴∠A =90°,∴∠EOG =90°,∴∠P =12∠EOG =45°.8.B 点拨:∵∠ACB =90°,∠ABC =30°,AB =2,∴AC =12AB =1.∴BC =AB 2-AC 2=22-12= 3.∴点B 转过的路径长为60π·3180=3π3.9.C10.D 点拨:∵正六边形A 1B 1C 1D 1E 1F 1的边长为2=(3)1-121-2,∴正六边形A 2B 2C 2D 2E 2F 2的外接圆的半径为3,则正六边形A 2B 2C 2D 2E 2F 2的边长为3=(3)2-122-2,同理,正六边形A 3B 3C 3D 3E 3F 3的边长为32=(3)3-123-2,…,正六边形A n B n C n D n E n F n 的边长为(3)n -12n -2,则当n =10时,正六边形A 10B 10C 10D 10E 10F 10的边长为(3)10-1210-2=(3)8·328=34·328=81328,故选D. 二、11.120° 12.43π 13.65° 14.35° 15.1216.215 点拨:∵A ,B ,C ,D 四点共圆,∴∠B +∠ADC =180°.又∵A ,C ,D ,E 四点共圆,∴∠E +∠ACD =180°.∴∠ACD +∠ADC +∠B +∠E =360°.∵∠ACD +∠ADC =180°-35°=145°,∴∠B +∠E =360°-145°=215°. 17.15π 18.53π-23 19.10.520.①②④ 点拨:连接OM ,ON ,易证Rt △OMC ≌Rt △OND .可得MC =ND ,故①正确.在Rt △MOC 中,CO =12MO .得∠CMO =30°,所以∠MOC =60°.易得∠MOC =∠NOD =∠MON =60°,所以A M ︵=M N ︵=NB ︵.故②正确.易得CD =12AB =OA =OM ,因为MC <OM ,所以MC <CD .所以四边形MCDN 不是正方形.故③错误.易得MN =CD =12AB ,故④正确.三、21.(1)证明:∵AB 是圆O 的直径,CD 为弦,AB ⊥CD ,∴BC ︵=BD ︵,∴BC =BD .(第21题)(2)解:如图,连接OC .∵AB 是圆O 的直径,CD 为弦,AB ⊥CD ,CD =6, ∴CH =3,∴OC =OH 2+CH 2=22+32=13,即圆O 的半径长为13.22.解:设经过A ,B 两点的直线对应的函数解析式为y =kx +b .∵A (2,3),B (-3,-7), ∴⎩⎨⎧2k +b =3,-3k +b =-7.解得⎩⎨⎧k =2,b =-1.∴经过A ,B 两点的直线对应的函数解析式为y =2x -1. 当x =5时,y =2×5-1=9≠11, ∴点C (5,11)不在直线AB 上, 即A ,B ,C 三点不在同一条直线上.∴平面直角坐标系内的三个点A (2,3),B (-3,-7),C (5,11)可以确定一个圆.23.(1)证明:如图,连接OB .∵OA ⊥l , ∴∠PAC =90°, ∴∠APC +∠ACP =90°. ∵AB =AC ,OB =OP ,∴∠ABC =∠ACB ,∠OBP =∠OPB . ∵∠BPO =∠APC ,∴∠ABC +∠OBP =90°,即∠OBA =90°, ∴OB ⊥AB , ∴AB 是⊙O 的切线.(第23题)(2)解:设⊙O 的半径为r ,则AP =5-r ,OB =r . 在Rt △OBA 中,AB 2=OA 2-OB 2=52-r 2, 在Rt △APC 中,AC 2=PC 2-AP 2=(25)2-(5-r )2. ∵AB =AC ,∴52-r 2=(25)2-(5-r )2, 解得r =3,即⊙O 的半径为3. 24.(1)证明:连接OC .∵AB 与⊙O 相切于点C , ∴OC ⊥AB . ∵CD =CE , ∴∠AOC =∠BOC . 在△AOC 和△BOC 中,⎩⎨⎧∠AOC =∠BOC ,OC =OC ,∠ACO =∠BCO =90°,∴△AOC ≌△BOC ,∴OA =OB .(2)解:∵△AOC ≌△BOC ,∴AC =BC =12AB =2 3.∵OB =OA =4,且△OCB 是直角三角形,∴根据勾股定理,得OC =OB 2-BC 2=2,∴OC =12OB ,∴∠B =30°, ∴∠BOC =60°.∴S 阴影=S △BOC -S 扇形COE =12×2×23-60π×22360=23-23π. 25.解:(1)如图,设点E 是桥拱所在圆的圆心.过点E 作EF ⊥AB 于点F ,延长EF 交⊙E 于点C ,连接AE , 则CF =20米.由垂径定理知,F 是AB 的中点,∴AF =FB =12AB =40米.设圆的半径是r ,由勾股定理,得AE 2=AF 2+EF 2=AF2+(CE-CF)2,即r2=402+(r-20)2.解得r=50米.∴桥拱的半径为50米.(第25题)(2)这艘轮船能顺利通过.理由如下:如图,设MN=60米,MN∥AB,EC与MN的交点为D,连接EM,易知DE⊥MN,∴MD=30米,∴DE=E M2-D M2=502-302=40(米).∵EF=EC-CF=50-20=30(米),∴DF=DE-EF=40-30=10(米).∵10米>9米,∴这艘轮船能顺利通过.26.解:(1)∵直线CD与半圆O相切,∴∠OCD=90°.∵OC=OA,CD=OA,∴OC=CD,∴∠DOC=∠ODC=45°,即∠DOC的度数是45°.(2)①AE=OD.理由如下:如图,连接OE.∵OC=OA,CD=OA,∴OC=CD,∴∠COD=∠CDO.∵AE∥OC,∴∠EAD=∠COD,∴∠EAD=∠CDO,∴AE=DE.∵OA=OE,OC=CD,∴∠DOE=2∠EAD,∠OCE=2∠CDO,∴∠DOE=∠OCE.∵OC=OE,∴∠DEO=∠OCE,∴∠DOE=∠DEO,∴OD=DE,∴AE=OD.②由①得,∠DOE=∠DEO=2∠ODC. ∵∠DOE+∠DEO+∠ODC=180°,∴2∠ODC+2∠ODC+∠ODC=180°,∴∠ODC=36°.(第26题)人教版数学九年级上册第二十四章《圆》培优单元测试卷(含解析)一.选择题1.如图,圆锥的底面半径为1,母线长为3,则侧面积为()A.2πB.3πC.6πD.8π2.如图,AB为⊙O的直径,P为弦BC上的点,∠ABC=30°,过点P作PD⊥OP交⊙O于点D,过点D作DE∥BC交AB的延长线于点E.若点C恰好是的中点,BE=6,则PC的长是()A.6﹣8 B.3﹣3 C.2 D.12﹣63.如图,已知⊙O的内接正六边形ABCDEF的边长为6,则弧BC的长为()A.2πB.3πC.4πD.π4.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆柱形木材的直径是多少?”如图所示,请根据所学知识计算:圆柱形木材的直径AC是()A.13寸B.20寸C.26寸D.28寸5.如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于()A.55°B.70°C.110°D.125°6.如图,在Rt△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为D、E、F,若BF=2,AF=3,则△ABC的面积是()A.6 B.7 C.7D.127.如图,正方形ABCD内接于圆O,AB=4,则图中阴影部分的面积是()A.4π﹣16 B.8π﹣16 C.16π﹣32 D.32π﹣168.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H.若AE=3,则EG的长为()A.B.C.D.9.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.将半径为5的“等边扇形”围成一个圆锥,则圆锥的侧面积为()A.B.πC.50 D.50π10.如图,点C为△ABD外接圆上的一点(点C不在上,且不与点B,D重合),且∠ACB=∠ABD=45°,若BC=8,CD=4,则AC的长为()A.8.5 B.5C.4D.11.在△ABC中,∠C=90°,∠A=30°,AB=12,将△ABC绕点B按逆时针方向旋转60°,直角边AC扫过的面积等于()A.24πB.20πC.18πD.6π12.如图,矩形ABCD中,BC=2,C D=1,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为()A.B.C.D.二.填空题13.若一个圆锥的底面圆的周长是5πcm,母线长是6cm,则该圆锥的侧面展开图的圆心角度数是.14.如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,连接DE,过点D作DF⊥AC于点F.若AB=6,∠CDF=15°,则阴影部分的面积是.15.如图,已知AB是⊙O的弦,C是的中点,联结OA,AC,如果∠OAB=20°,那么∠CAB 的度数是.16.如图,用等分圆的方法,在半径为OA的圆中,画出了如图所示的四叶幸运草,若OA=2,则四叶幸运草的周长是.17.半径为6的扇形的面积为12π,则该扇形的圆心角为°.18.如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B 在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为.三.解答题19.如图,⊙O与△ABC的AC边相切于点C,与AB、BC边分别交于点D、E,DE∥OA,CE是⊙O的直径.(1)求证:AB是⊙O的切线;(2)若BD=4,EC=6,求AC的长.20.如图,AB是⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E.(1)试判断直线DE与⊙O的位置关系,并说明理由;(2)若⊙O的半径为2,∠BAC=60°,求线段EF的长.21.如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦AD,BC相交于点E.(1)求证:=;(2)若CE=1,EB=3,求⊙O的半径;(3)在(2)的条件下,过点C作⊙O的切线,交BA的延长线于点P,过点P作PQ∥CB 交⊙O于F,Q两点(点F在线段PQ上),求PQ的长.22.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积是多少?23.已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=60°,求证:AH=AO.(初二)24.如图,AB是半圆O的直径,C是半圆上一点,=,DH⊥AB于点H,AC分别交BD、DH于E、F.(1)已知AB=10,AD=6,求AH.(2)求证:DF=EF25.已知:如图,在△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E为的中点.(1)求证:∠ACD=∠DEC;(2)延长DE、CB交于点P,若PB=BO,DE=2,求PE的长.参考答案一.选择题1.解:圆锥的侧面积=×2π×1×3=3π,故选:B .2.解:连接OD ,交CB 于点F ,连接BD ,∵=,∴∠DBC =∠ABC =30°,∴∠ABD =60°,∵OB =OD ,∴△OBD 是等边三角形,∴OD ⊥FB ,∴OF =DF ,∴BF ∥DE ,∴OB =BE =6∴CF =FB =OB •cos30°=6×=3,在Rt △POD 中,OF =DF ,∴PF =DO =3(直角三角形斜边上的中线,等于斜边的一半),∴CP =CF ﹣PF =3﹣3. 故选:B .3.解:∵ABCDEF 为正六边形,∴∠COB =360°×=60°,∴△OBC 是等边三角形,∴OB =OC =BC =6,弧BC的长为=2π.故选:A.4.解:设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r﹣1,OA=r,则有r2=52+(r﹣1)2,解得r=13,∴⊙O的直径为26寸,故选:C.5.解:连接OA,OB,∵PA,PB是⊙O的切线,∴PA⊥OA,PB⊥OB,∵∠ACB=55°,∴∠AOB=110°,∴∠APB=360°﹣90°﹣90°﹣110°=70°.故选:B.6.解:连接DO,EO,∵⊙O 是△ABC 的内切圆,切点分别为D ,E ,F ,∴OE ⊥AC ,OD ⊥BC ,CD =CE ,BD =BF =3,AF =AE =4又∵∠C =90°,∴四边形OECD 是矩形,又∵EO =DO ,∴矩形OECD 是正方形,设EO =x ,则EC =CD =x ,在Rt △ABC 中BC 2+AC 2=AB 2故(x +2)2+(x +3)2=52,解得:x =1,∴BC =3,AC =4,∴S △ABC =×3×4=6,故选:A .7.解:连接OA 、OB ,∵四边形ABCD 是正方形,∴∠AOB =90°,∠OAB =45°,∴OA =AB cos45°=4×=2,所以阴影部分的面积=S ⊙O ﹣S 正方形ABCD =π×(2)2﹣4×4=8π﹣16. 故选:B .8.解:如图,连接AC、BD、OF,,设⊙O的半径是r,则OF=OA=r,∵AO是∠EAF的平分线,∴∠OAF=60°÷2=30°,AC⊥EF,EG=EF=∵OA=OF,∴∠OFA=∠OAF=30°,∴∠COF=30°+30°=60°,∴FI=r•sin60°=r,∴EF=r×2=r=AE=3,∴r=∴OI=,∴CI=OC﹣OI=,∵EF⊥AC,∠BCA=45°∴∠IGC=∠BCI=45°∴CI=GI=∴EG=EI﹣GI=故选:B.9.解:圆锥的侧面积=•5•5=.故选:A.10.解:延长CD到E,使得DE=BC,连接AE,如右图所示,∵∠ACB=∠ABD=45°,∠ACB=∠ADB,∴∠ADB=45°,∴∠BAD=90°,AB=AD,∵四边形ABCD是圆内接四边形,∠ADE+∠ADC=180°,∴∠ADC+∠ABC=180°,∴∠ABC=∠ADE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠BAC=∠DAE,∵∠BAC+∠CAD=∠BAD=90°,∴∠DAE+∠CAD=90°,∴∠CAE=90°,∵ACD=45°,BC=DE=8,CD=4,∴∠ACE=45°,CE=12,∴AC=AE=6,故选:D.11.解:∵在△ABC中,∠C=90°,∠A=30°,AB=12,∴BC=AB=6,∠ABC=60°,=﹣=﹣=18π.∴S阴影故选:C.12.解:连接OE交BD于F,如图,∵以AD为直径的半圆O与BC相切于点E,∴OE⊥BC,∵四边形ABCD为矩形,OA=OD=1,而CD =1,∴四边形ODCE 和四边形ABEO 都是正方形,∴BE =1,∠DOE =∠BEO =90°∵∠BFE =∠DFO , OD =BE ,∴△ODF ≌△EBF (AAS ),∴S △ODF =S △EBF ,∴阴影部分的面积=S 扇形EOD ==.故选:C .二.填空题(共6小题)13.解:∵圆锥的底面圆的周长是5πcm ,∴圆锥的侧面展开扇形的弧长为5πcm ,∴=5π,解得:n =150故答案为150°.14.解:连接OE ,∵∠CDF =15°,∠C =75°,∴∠OAE =30°=∠OEA ,∴∠AOE =120°,S △OAE =AE ×OE sin ∠OEA =×2×OE ×cos ∠OEA ×OE sin ∠OEA =,S 阴影部分=S 扇形OAE ﹣S △OAE =×π×32﹣=3π﹣.故答案3π﹣.15.解:连接OC交AB于E.∵C是的中点,∴OC⊥AB,∴∠AEO=90°,∵∠BAO=20°,∴∠AOE=70°,∵OA=OC,∴∠OAC=∠C=55°,∴∠CAB=∠OAC﹣∠OAB=35°,故答案为35°.16.解:由题意得:四叶幸运草的周长为4个半圆的弧长=2个圆的周长,连接AB、BC、CD、AD,则四边形ABCD是正方形,连接OB,如图所示:则正方形ABCD的对角线=2OA=4,O A⊥OB,OA=OB=2,∴AB=2,过点O作ON⊥AB于N,则NA=AB=,∴圆的半径为,∴四叶幸运草的周长=2×2π×=4π;故答案为:4π.17.解:设该扇形的圆心角为n2,则=12π,解得:n=120,故答案为:120.18.解:连接OC并延长,交⊙C上一点P,以O为圆心,以OP为半径作⊙O,交x轴于A、B,此时AB的长度最大,∵C(3,4),∴OC==5,∵以点C为圆心的圆与y轴相切.∴⊙C的半径为3,∴OP=OA=OB=8,∵AB是直径,∴∠APB=90°,∴AB长度的最大值为16,故答案为16.三.解答题(共7小题)19.(1)证明:连接OD、CD,∵CE是⊙O的直径,∴∠EDC=90°,∵DE∥OA,∴OA⊥CD,∴OA垂直平分CD,∴OD=OC,∴OD=OE,∴∠OED=∠ODE,∵DE∥OA,∴∠ODE=∠AOD,∠DEO=∠AOC,∴∠AOD=∠AOC,∵AC是切线,∴∠ACB=90°,在△AOD和△AOC中∴△AOD≌△AOC(SAS),∴∠ADO=∠ACB=90°,∵OD是半径,∴AB是⊙O的切线;(2)解:连接OD,CD,∵BD是⊙O切线,∴∠ODB=90°,∴∠BDE+∠ODE=90°,∵CE是⊙O的直径,∴∠CDE=90°,∴∠ODC+∠ODE=90°,∴∠BDE=∠ODC,∵OC=OD,∴∠OCD=∠ODC,∴∠BDE=∠OCD,∵∠B=∠B,∴△BDE∽△BCD,∴∴BD2=BE•BC,设BE=x,∵BD=4,EC=6,∴42=x(x+6),解得x=2或x=﹣8(舍去),∴BE=2,∴BC=BE+EC=8,∵AD、AC是⊙O的切线,设AD=AC=y,在Rt△ABC中,AB2=AC2+BC2,∴(4+y)2=y2+82,解得y=6,∴AC=6,故AC的长为6.20.解:(1)直线DE与⊙O相切,连结OD.∵AD平分∠BAC,∴∠OAD=∠CAD,∵OA=OD,∴∠OAD=∠ODA,∴∠ODA=∠CAD,∴OD∥AC,∵DE⊥AC,即∠AED=90°,∴∠ODE=90°,即DE⊥OD,∴DE是⊙O的切线;(2)过O作OG⊥AF于G,∴AF=2AG,∵∠BAC=60°,OA=2,∴AG=OA=1,∴AF=2,∴四边形AODF是菱形,∴DF∥OA,DF=OA=2,∴∠EFD=∠BAC=60°,∴EF=DF=1.21.证明:(1)∵OC=OB∴∠OBC=∠OCB∵O C∥BD∴∠OCB=∠CBD∴∠OBC=∠CBD∴(2)连接AC,∵CE=1,EB=3,∴BC=4∵∴∠CAD=∠ABC,且∠ACB=∠ACB ∴△ACE∽△BCA∴∴AC2=CB•CE=4×1∴AC=2,∵AB是直径∴∠ACB=90°∴AB==2∴⊙O的半径为(3)如图,过点O作OH⊥FQ于点H,连接OQ,∵PC是⊙O切线,∴∠PCO=90°,且∠ACB=90°∴∠PCA=∠BCO=∠CBO,且∠CPB=∠CPA∴△APC∽△CPB∴∴PC=2PA,PC2=PA•PB∴4PA2=PA×(PA+2)∴PA=∴PO=∵PQ∥BC∴∠CBA=∠BPQ,且∠PHO=∠ACB=90°∴△PHO∽△BCA∴即∴PH=,OH=∴HQ==∴PQ=PH+HQ=22.解:过O点作OE⊥CD于E,∵AB为⊙O的切线,∴∠ABO=90°,∵∠A=30°,∴∠AOB=60°,∴∠COD=120°,∠OCD=∠ODC=30°,∵⊙O的半径为2,∴OE=1,CE=DE=,∴CD=2,∴图中阴影部分的面积=﹣2×1=﹣23.证明:(1)过O作OF⊥AC,于F,则F为AC的中点,连接CH,取CH中点N,连接FN,MN,则FN∥AD,AH=2FN,MN∥BE,∵AD⊥BC,OM⊥BC,BE⊥AC,OF⊥AC,∴OM∥AD,BE∥OF,∵M为BC中点,N为CH中点,∴MN∥BE,∴OM∥FN,MN∥OF,∴四边形OMNF是平行四边形,∴OM=FN,∵AH=2FN,∴AH=2OM.(2)证明:连接OB,OC,∵∠BAC=60°,∴∠BOC=120°,∴∠BOM=60°,∴∠OBM=30°,∴OB=2OM=AH=AO,即AH=AO.24.(1)解:∵AB是⊙O的直径,∴∠ADB=90°,∵DH⊥AB,∴∠DHA=∠ADB=90°,又∵∠DAB=∠HAD,∴△DAB∽△HAD,∴=即=,∴AH=3.6.(2)证明:∵=,∴∠DAC=∠DBA,∵DH⊥AB,∴∠FDE+∠B=90°,∵∠ADB=90°,∴∠DEF+∠DAC=90°,∴∠DEF=∠DEF,∴DF=EF.25.(1)证明:∵BC是⊙O的直径,∴∠BDC=90°,∴∠BCD+∠B=90°,∵∠ACB=90°,∴∠BCD+∠ACD=90°,∴∠ACD=∠B,∵∠DEC=∠B,∴∠ACD=∠DEC.(2)证明:连结OE∵E为BD弧的中点.∴∠DCE=∠BCE,∵OC=OE,∴∠BCE=∠OEC,∴∠DCE=∠OEC,∴OE∥CD,∴△POE∽△PCD,∴=,∵PB=BO,DE=2∴PB=BO=OC∴==,∴=,∴PE=4.人教版数学九年级上册第24章《圆》单元综合练习卷(含详细答案)一.选择题1.已知圆内接四边形ABCD中,∠A:∠B:∠C=1:2:3,则∠D的大小是()A.45°B.60°C.90°D.135°2.如图,AB,AC分别是⊙O的直径和弦,OD⊥AC于点D,连接BD,BC,且AB=10,AC=8,则BD的长为()A.2B.4 C.2D.4.83.下列说法正确的是()A.菱形的对角线垂直且相等B.到线段两端点距离相等的点,在线段的垂直平分线上C.点到直线的距离就是点到直线的垂线段D.过三点确定一个圆4.已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是()A.60πcm2B.65πcm2C.120πcm2D.130πcm25.如图,已知钝角△ABC内接于⊙O,且⊙O的半径为5,连接OA,若∠OAC=∠ABC,则AC 的长为()A.5B.C.5D.86.如图,在△ABC中,AB=4,AC=2,BC=5,点I为△ABC的内心,将∠BAC平移,使其顶点与点I重合,则图中阴影部分的周长为()A.4 B.5 C.6 D.77.如图,将一块直角三角板△ABC(其中∠ACB=90°,∠CAB=30°)绕点B顺时针旋转120°后得Rt△MBN,已知这块三角板的最短边长为3,则图中阴影部分的面积()A.B.9πC.9π﹣D.8.如图,点A,B,C,D都在半径为3的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为()A.B.3C.3 D.29.边长相等的正方形与正六边形按如图方式拼接在一起,则∠ABC的度数为()A.10°B.15°C.20°D.30°10.如图,在⊙O的内接正六边形ABCDEF中,OA=2,以点C为圆心,AC长为半径画弧,恰好经过点E,得到,连接CE,OE,则图中阴影部分的面积为()A.﹣4B.2π﹣2C.﹣3D.﹣211.如图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=28°,则∠ACB的度数是()A.28°B.30°C.31°D.32°12.如图,已知正六边形ABCDEF的边长为,点G,H,I,J,K,L依次在正六边形的六条边上,且AG=BH=CI=DJ=EK=FL,顺次连结G,I,K,和H,J,L,则图中阴影部分的周长C的取值范围为()A.6≤C≤6B.3≤C≤3C.3≤C≤6 D.3≤C≤6二.填空题13.已知圆锥底面圆的半径为5,高为12,则圆锥的侧面积为(结果保留π).14.如图,点A,B,C,D是⊙O上的四个点,点B是弧AC的中点,如果∠ABC=70°,那∠ADB=.15.如图,MN为⊙O的直径,MN=10,AB为⊙O的弦,已知MN⊥AB于点P,AB=8,现要作⊙O的另一条弦CD,使得CD=6且CD∥AB,则PC的长度为.16.如图,AB是⊙O的直径,点C、D在⊙O上,若∠DCB=110°,则∠AED=.17.如图,AB是⊙O的直径,点C、D在⊙O上,∠AOC=70°,AD∥OC,则∠ABD=.18.如图,在平面直角坐标系中,⊙O的半径为5,弦AB的长为6,过O作OC⊥AB于点C,⊙O内一点D的坐标为(﹣2,1),当弦AB绕O点顺时针旋转时,点D到AB的距离的最小值是.三.解答题19.已知等边△ABC内接于⊙O,D为弧BC的中点,连接DB、DC,过C作AB的平行线,交BD的延长线于点E.(1)求证:CE与⊙O相切;(2)若AB长为6,求CE长.20.如图,AB是⊙O的直径,弦CD与AB交于点E,过点B的切线BP与CD的延长线交于点P,连接OC,CB.(1)求证:AE•EB=CE•ED;(2)若⊙O的半径为3,OE=2BE,=,求线段DE和PE的长.21.如图,△ABC内接于⊙O,∠ACB=60°,BD是⊙O的直径,点P是BD延长线上一点,且PA是⊙O的切线.(1)求证:AP=AB;(2)若PD=,求⊙O的直径.22.如图所示,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC至点D,使CD=AC,连接AD交⊙O于点E,连接BE、CE,BE交AC于点F.(1)求证:CE=AE;(2)填空:①当∠ABC=时,四边形AOCE是菱形;②若AE=,AB=,则DE的长为.23.如图,已知AB为⊙O的直径,C为⊙O上异于A、B的一点,过C点的切线于BA的延长线交于D点,E为CD上一点,连EA并延长交⊙O于H,F为EH上一点,且EF=CE,C F 交延长线交⊙O于G.(1)求证:弧AG=弧GH;(2)若E为DC的中点,sim∠CDO=,AH=2,求⊙O的半径.24.在等边△ABC中,BC=8,以AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.(1)求证:DF为⊙O的切线.(2)求弧DE的长度;(3)求EF的长.25.如图,△ACB内接于圆O,AB为直径,CD⊥AB与点D,E为圆外一点,EO⊥AB,与BC 交于点G,与圆O交于点F,连接EC,且EG=EC.(1)求证:EC是圆O的切线;(2)当∠ABC=22.5°时,连接CF,①求证:AC=CF;②若AD=1,求线段FG的长.参考答案一.选择题1.解:∵四边形ABCD为圆的内接四边形,∴∠A:∠B:∠C:∠D=1:2:3:2,而∠B+∠D=180°,∴∠D=×180°=90°.故选:C.2.解:∵AB为直径,∴∠ACB=90°,∴BC===3,∵OD⊥AC,∴CD=AD=AC=4,在Rt△CBD中,BD==2.故选:C.3.解:A、菱形的对角线垂直但不一定相等,故错误;B、到线段两端点距离相等的点,在线段的垂直平分线上,正确;C、点到直线的距离就是点到直线的垂线段的长度,故错误;D、过不在同一直线上的三点确定一个圆,故错误,故选:B.4.解:这个圆锥的侧面积=×2π×5×13=65π(cm2).故选:B.5.解:连接OC,如图,设∠OAC=α,则∠OAC=∠ABC=α,∠AOC=2∠ABC=2α,∵OA=OC,∴∠OCA=∠OAC=α,∴α+2α+α=180°,解得α=45°,∴∠AOC=90°,∴△AOC为等腰直角三角形,∴AC=OA=5.故选:A.6.解:连接BI、CI,如图所示:∵点I为△ABC的内心,∴BI平分∠ABC,∴∠ABI=∠CBI,由平移得:AB∥DI,∴∠ABI=∠BID,∴∠CBI=∠BID,∴BD=DI,同理可得:C E=EI,∴△DIE的周长=DE+DI+EI=DE+BD+CE=BC=5,即图中阴影部分的周长为5,故选:B.7.解:∵∠ACB=90°,∠CAB=30°,BC=3,∴AB=2BC=6,∴AC===3,∵O、H分别为AB、AC的中点,∴OB=AB=3,CH=AC=,在Rt△BCH中,BH==,∵旋转角度为120°,∴阴影部分的面积=﹣=π.故选:A.8.【解答】解:OA交BC于E,如图,∵OA⊥BC,∴=,CE=BE,∴∠AOB=2∠CDA=2×30°=60°,在Rt△OBE中,OE=OB=,∴BE=OE=,∴BC=2BE=3.故选:B.9.解:由题意得:正六边形的每个内角都等于120°,正方形的每个内角都等于90°,故∠BAC=360°﹣120°﹣90°=150°,∵AB=AC,∴∠ABC=∠ACB==15°.故选:B.10.解:连接OB、OC、OD,S 扇形CAE ==2π,S △AOC ==,S △BOC ==,S 扇形OBD ==,∴S 阴影=S 扇形OBD ﹣2S △BOC +S 扇形CAE ﹣2S △AOC =﹣2+2π﹣2=﹣4; 故选:A .11.解:连接OB ,如图,∵AB 为切线,∴OB ⊥AB ,∴∠ABO =90°,∴∠AOB =90°﹣∠A =90°﹣28°=62°,∴∠ACB =∠AOB =31°.故选:C .12.解:根据对称性可知,△GKI ,△HLJ 是等边三角形.阴影部分是正六边形,边长为GK的.∵GK 的最大值为2,GK 的最小值为3,∴阴影部分的正六边形的边长的最大值为,最小值为1,∴图中阴影部分的周长C 的取值范围为:4≤C ≤6.故选:C.二.填空题(共6小题)13.解:∵圆锥的底面半径为5,高为12,∴圆锥的母线长为13,∴它的侧面积=π×13×5=65π,故答案为:65π.14.解:∵四边形ABCD内接于⊙O,∴∠ABC+∠ADC=180°,∴∠ADC=180°﹣70°=110°.∵点B是弧AC的中点,∴弧AB=弧BC.∴∠ADB=∠BDC.∴∠ADB=∠ADC=×110°=55°.故答案为55°.15.解:当AB、CD在圆心O的两侧时,如图,连接OA、OC,∵AB∥CD,MN⊥AB,∴AP=AB=4,MN⊥CD,∴CQ=CD=3,在Rt△OAP中,OP==3,同理:OQ=4,则PQ=OQ+OP=7,∴PC===,当AB、CD在圆心O的同侧时,PQ=OQ﹣OP=1,∴PC===;故答案为:或.16.解:连接BE,如图,∵AB是⊙O的直径,∴∠AEB=90°,∵∠DEB+∠DCB=180°,∴∠DEB=180°﹣110°=70°,∴∠AED=∠AEB﹣∠DEB=90°﹣70°=20°.故答案为20°17.解:∵AD∥OC,∴∠BAD=∠AOC=70°,∵AB是⊙O的直径,∴∠D=90°,∴∠ABD=90°﹣70°=20°.故答案为20°.18.解:连接OB,如图所示:∵OC⊥AB,∴BC=AB=3,由勾股定理得,OC===4,当OD⊥AB时,点D到AB的距离的最小,由勾股定理得,OD==,∴点D到AB的距离的最小值为:4﹣,故答案为:4﹣.三.解答题(共7小题)19.(1)证明:连接OC,OB,∵△ABC是等边三角形,∴∠A=∠A BC=60°,∵AB∥CE,∴∠BCE=∠ABC=60°,∵OB=OC,∴∠OBC=∠OCB=30°,∴∠OCE=∠OCB+∠BCE=30°+60°=90°,∴CE与⊙O相切;(2)∵四边形ABDC是圆的内接四边形,∴∠A+∠BDC=180°,∴∠BDC=120°,∵D为弧BC的中点,∴∠DBC=∠BCD=30°,∴∠BEC=180°﹣∠EBC﹣∠BCE=90°,∵AB=BC=6,∴.20.(1)证明:连接AC、BD,如图,∵∠CAE=∠CDB,∠ACE=∠BDE,∴△ACE∽△BDE,∴AE:DE=CE:BE,∴AE•EB=CE•ED;(2)∵OE+BE=3,OE=2BE,∴OE=2,BE=1,∴AE=5,∴CE•DE=5×1=5,∵=,∴CE=DE,∴DE•DE=5,解得DE=,∴CE=3.∵PB为切线,∴PB2=PD•PC,而PB2=PE2﹣BE2,∴PD•PC=PE2﹣BE2,即(PE﹣)(PE+3)=PE2﹣1,∴PE=321.(1)证明:连接OA,如图,∵∠AOB=2∠ACB=2×60°=120°,而OA=OB,∴∠OAB=∠OBA=30°,∠AOP=60°,∵PA是⊙O的切线,∴OA⊥PA,∴∠OAP=90°,∴∠P=90°﹣60°=30°,∴∠ABP=∠P,∴AB=AP;(2)解:设⊙O的半径为r,在Rt△OPA中,∵∠P=30°,∴OP=2OA,即r+=2r,解得r=,∴⊙O的直径为2.22.证明(1)∵AB=AC,AC=CD∴∠ABC=∠ACB,∠CAD=∠D∵∠ACB=∠CAD+∠D=2∠CAD∴∠ABC=∠ACB=2∠CAD∵∠CAD=∠EBC,且∠ABC=∠ABE+∠EBC∴∠ABE=∠EBC=∠CAD,∵∠ABE=∠ACE∴∠CAD=∠ACE∴CE=AE(2)①当∠ABC=60°时,四边形AOCE是菱形;理由如下:如图,连接OE。
初中数学人教版九年级上册第24章《圆》测试卷解析及答案-九上24

∴AC⊥OC,·······················(2分)
又∵OC是圆O的半径,···················(1分)
∴AC与圆O相切;
(2)在Rt△AOC中,∠A=30°,AC=6,
∴AO=2CO························(1分)
∴BC=BF=3 .························(1分)
在△ADF中,∠DAB=∠AFD=45°,
∴EF=ED=1.························(1分)
∴AB=5·························(1分)
∴AC= = ··················(1分)
∴圆O半径的长 。···················(2分)
21.(本小题满分10分)
(1)(-2, 0)·······················(2分)
(2)连接AC、AD、CD,
·················(1分)
圆D的半径长= ,···············(1分)
AC= ,····················(1分)
1.选择题
1.B
【考点】直线与圆的位置关系
【分析】若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
【解答】解:圆的直径为10cm,则圆的半径为5cm,
由圆心到直线的距离等于圆的半径,则直线和圆相切.
故选:B
2.B
【考点】圆锥的计算
【分析】利用勾股定理易得圆锥的底面半径,那么圆锥的侧面积=π×底面半径×母线长,把相关数值代入即可求解。
人教版 九年级上册数学 第24章质量检测(含答案)
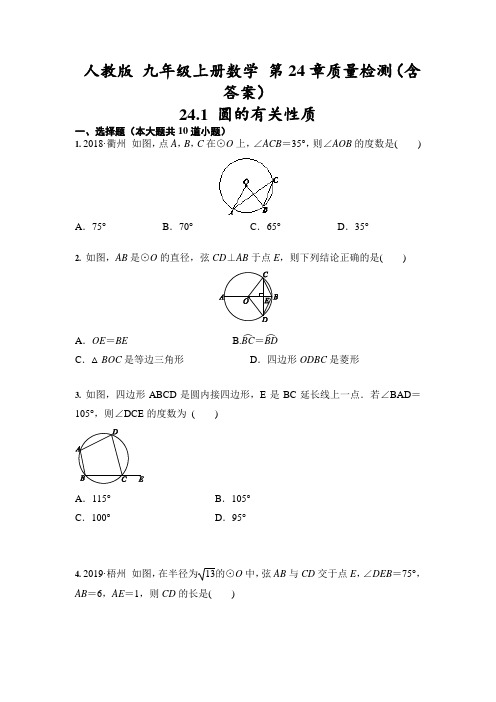
人教版 九年级上册数学 第24章质量检测(含答案)24.1 圆的有关性质一、选择题(本大题共10道小题) 1. 2018·衢州 如图,点A ,B ,C 在⊙O 上,∠ACB =35°,则∠AOB 的度数是( )A .75°B .70°C .65°D .35°2. 如图,AB是⊙O 的直径,弦CD ⊥AB 于点E ,则下列结论正确的是( )A .OE =BEB.BC ︵=BD ︵C .△BOC 是等边三角形D .四边形ODBC 是菱形3. 如图,四边形ABCD 是圆内接四边形,E 是BC 延长线上一点.若∠BAD =105°,则∠DCE 的度数为 ( )A .115°B .105°C .100°D .95°4. 2019·梧州如图,在半径为13的⊙O 中,弦AB 与CD 交于点E ,∠DEB =75°,AB =6,AE =1,则CD 的长是( )A .2 6B .2 10C .2 11D .4 35. (2019•广元)如图,AB ,AC分别是⊙O 的直径和弦,OD AC ⊥于点D ,连接BD ,BC ,且10AB =,8AC =,则BD 的长为A .25B .4C .213D .4.86.如图,⊙O 的半径为4,△ABC 是⊙O 的内接三角形,连接OB 、OC ,若∠BAC 与∠BOC 互补,则弦BC 的长为( ) A . 3 3 B . 4 3 C . 5 3 D . 6 37. 如图,△ABC 的内心为I ,连接AI 并延长交△ABC 的外接圆于点D ,则线段DI 与DB 的关系是( )A .DI =DB B .DI >DBC .DI <DBD .不确定如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD 的延长线上,则∠CDE的度数为( )A.56°B.62°C.68°D.78°9. 如图,AB是⊙O的直径,点C,D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD的度数为()A.70°B.60°C.50°D.40°10. 2019·武汉京山期中在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB为6分米,如果再注入一些油后,油面宽变为8分米,则油面AB上升()A.1分米B.4分米C.3分米D.1分米或7分米二、填空题(本大题共7道小题)11. 如图,C,D两点在以AB为直径的圆上,AB=2,∠ACD=30°,则AD=________.12. 如图所示,动点C在⊙O的弦AB上运动,AB=23,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为________.13. 如图,在⊙O中,半径OA垂直于弦BC,点D在圆上,且∠ADC=30°,则∠AOB的度数为________.14. 如图,以△ABC的边BC为直径的⊙O分别交AB,AC于点D,E,连接OD,OE.若∠A=65°,则∠DOE=________°.15. 如图,在⊙O中,BD为⊙O的直径,弦AD的长为3,AB的长为4,AC平分∠DAB,则弦CD的长为________.16. 将量角器按图所示的方式放置在三角形纸片上,使顶点C在半圆上,点A,B 的读数分别为100°,150°,则∠ACB的大小为________°.17. 如图,四边形ABCD 内接于⊙O ,AB 为⊙O 的直径,C 为弧BD 的中点.若∠DAB =40°,则∠ABC =________°.三、解答题(本大题共4道小题)18. 如图,在△ABC 中,∠C =90°,D 是BC 边上一点,以BD 为直径的⊙O 经过AB 的中点E ,交AD 的延长线于点F ,连接EF. (1)求证:∠1=∠F ;(2)若AC =4,EF =2 5,求CD 的长.19.如图,已知⊙O 上依次有A ,B ,C ,D 四个点,AD ︵=BC ︵,连接AB ,AD ,BD ,延长AB 到点E ,使BE =AB ,连接EC ,F 是EC 的中点,连接BF.求证:BF =12BD.20. 如图,在⊙O 中,AB ︵=2AC ︵,AD ⊥OC于点D.求证:AB =2AD.21. 2018·牡丹江如图,在⊙O 中,AB ︵=2AC ︵,AD ⊥OC 于点D .求证:AB =2AD .人教版 九年级数学 24.1 圆的有关性质 同步训练-答案一、选择题(本大题共10道小题) 1. 【答案】B2. 【答案】B[解析] AB 是⊙O 的直径,弦CD ⊥AB 于点E ,由垂径定理可以得到CE =DE ,BC ︵=BD ︵,AC ︵=AD ︵.但并不一定能得到OE =BE ,OC =BC ,从而A ,C ,D 选项都是错误的.故选B.3. 【答案】B4. 【答案】C5. 【答案】C【解析】∵AB 为直径,∴90ACB ∠=︒,∴22221086BC AB AC =-=-=, ∵OD AC ⊥,∴142CD AD AC ===, 在Rt CBD △中,2246213BD =+=.故选C .6.【答案】B【解析】如解图,延长CO 交⊙O 于点A ′,连接A ′B .设∠BAC =α,则∠BOC =2∠BAC=2α,∵∠BAC +∠BOC =180°,∴α+2α=180°,∴α=60°.∴∠BA ′C =∠BAC =60°,∵CA ′为直径,∴∠A ′BC =90°,则在Rt △A ′BC 中,BC =A ′C ·sin ∠BA ′C=2×4×32=4 3.7. 【答案】A[解析] 连接BI ,如图.∵△ABC 的内心为I , ∴∠1=∠2,∠5=∠6. ∵∠3=∠1, ∴∠3=∠2.∵∠4=∠2+∠6,∠DBI =∠3+∠5, ∴∠4=∠DBI ,∴DI =DB. 故选A.8. 【答案】C[解析] ∵点I 是△ABC 的内心,∴∠BAC =2∠IAC ,∠ACB =2∠ICA . ∵∠AIC =124°,∴∠B =180°-(∠BAC +∠ACB )=180°-2(∠IAC +∠ICA )=180°-2(180°-∠AIC )=68°.又四边形ABCD 内接于⊙O , ∴∠CDE =∠B =68°.9. 【答案】D[解析] ∵∠BOC =110°,∴∠AOC =70°.∵AD ∥OC ,∴∠A =∠AOC =70°.∵OA =OD ,∴∠D =∠A =70°.在△OAD 中,∠AOD =180°-(∠A +∠D)=40°.10. 【答案】D二、填空题(本大题共7道小题)11. 【答案】1[解析] ∵AB 为⊙O 的直径,∴∠ADB =90°. ∵∠B =∠ACD =30°, ∴AD =12AB =12×2=1.12. 【答案】3 [解析] 如图,连接OD ,过点O 作OH ⊥AB 于点H ,则AH =BH=12AB = 3.∵CD ⊥OC ,∴CD =OD 2-OC 2.∵OD 为⊙O 的半径,∴当OC 最小时,CD 最大.当点C 运动到点H 时,OC 最小,此时CD =BH =3,即CD 的最大值为 3.13. 【答案】60°[解析] ∵OA ⊥BC ,∴AB ︵=AC ︵,∴∠AOB =2∠ADC.∵∠ADC=30°,∴∠AOB =60°.14. 【答案】50[解析] 由三角形的内角和定理,得∠B +∠C =180°-∠A .再由OB =OD =OC =OE ,得到∠BDO =∠B ,∠CEO =∠C .在等腰三角形BOD 和等腰三角形COE 中,∠DOB +∠EOC =180°-2∠B +180°-2∠C =360°-2(∠B +∠C )=360°-2(180°-∠A )=2∠A ,所以∠DOE =180°-2∠A =50°.15. 【答案】52 2 [解析] ∵BD 为⊙O 的直径,∴∠DAB =∠DCB =90°. ∵AD =3,AB =4,∴BD =5.又∵AC 平分∠DAB ,∴∠DAC =∠BAC =45°, ∴∠DBC =∠DAC =45°,∠CDB =∠BAC =45°, 从而CD =CB ,∴CD =52 2.16. 【答案】25[解析] 设量角器的中心为O ,由题意可得∠AOB =150°-100°=50°,所以∠ACB =12∠AOB =25°.17. 【答案】70[解析] 如图,连接AC.∵AB 为⊙O 的直径,∴∠ACB =90°.∵C为弧BD 的中点,∴∠CAB =12∠DAB =20°, ∴∠ABC =70°.三、解答题(本大题共4道小题)18. 【答案】解:(1)证明:如图,连接DE. ∵BD 是⊙O 的直径, ∴∠DEB =90°,即DE ⊥AB. 又∵E 是AB 的中点, ∴AD =BD ,∴∠1=∠B. 又∵∠B =∠F ,∴∠1=∠F.(2)∵∠1=∠F ,∴AE =EF =2 5, ∴AB =2AE =4 5.在Rt △ABC 中,∵AC =4,∠C =90°, ∴BC =AB2-AC2=8. 设CD =x ,则AD =BD =8-x. 在Rt △ACD 中,∵∠C =90°,∴AC2+CD2=AD2,即42+x2=(8-x)2, 解得x =3,即CD =3.19. 【答案】证明:连接AC.∵AB =BE ,F 是EC 的中点, ∴BF 是△EAC 的中位线, ∴BF =12AC. ∵AD ︵=BC ︵,∴AD ︵+AB ︵=BC ︵+AB ︵,即BD ︵=AC ︵, ∴BD =AC ,∴BF =12BD.20. 【答案】证明:如图,延长AD 交⊙O 于点E.∵OC ⊥AD ,∴AE ︵=2AC ︵,AE =2AD. ∵AB ︵=2AC ︵,∴AE ︵=AB ︵,∴AB =AE ,∴AB =2AD.21. 【答案】证明:如图,延长AD 交⊙O 于点E , ∵OC ⊥AD ,∴AE ︵=2AC ︵,AE =2AD . ∵AB ︵=2AC ︵,∴AE ︵=AB ︵, ∴AB =AE ,∴AB =2AD .24.2 点和圆、直线和圆的位置关系一、选择题(本大题共10道小题)1. 下列直线中,一定是圆的切线的是()A .与圆有公共点的直线B .垂直于圆的半径的直线C .到圆心的距离等于半径的直线D .经过圆的直径一端的直线2. 下列说法中,正确的是()A .垂直于半径的直线是圆的切线B .经过半径的外端且垂直于这条半径的直线是圆的切线C .经过半径的端点且垂直于这条半径的直线是圆的切线D .到圆心的距离等于直径的直线是圆的切线3. 如图,P是⊙O 外一点,OP 交⊙O 于点A ,OA =AP .甲、乙两人想作一条经过点P 且与⊙O 相切的直线,其作法如下:甲:以点A 为圆心,AP 长为半径画弧,交⊙O 于点B ,则直线BP 即为所求. 乙:过点A 作直线MN ⊥OP ,以点O 为圆心,OP 长为半径画弧,交射线AM 于点B ,连接OB ,交⊙O 于点C ,直线CP 即为所求. 对于甲、乙两人的作法,下列判断正确的是( )A .甲正确,乙错误B .乙正确,甲错误C .两人都正确D .两人都错误4. 已知⊙O的半径为5 cm,圆心O到直线l的距离为5 cm,则直线l与⊙O的位置关系为()A.相交B.相切C.相离D.无法确定5. 如图,AB为⊙O的切线,切点为A,连接AO,BO,BO与⊙O交于点C,延长BO与⊙O交于点D,连接AD.若∠ABO=36°,则∠ADC的度数为()A.54°B.36°C.32°D.27°6. 如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是()A.DE=DO B.AB=ACC.CD=DB D.AC∥OD7.如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠A OD的度数为( )A. 70°B. 35°C.20°D. 40°8. 2020·黄石模拟如图,在平面直角坐标系中,A(-2,2),B(8,2),C(6,6),点P为△ABC的外接圆的圆心,将△ABC绕点O逆时针旋转90°,点P的对应点P′的坐标为()A.(-2,3) B.(-3,2)C.(2,-3) D.(3,-2)9. 如图,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在⊙O外、⊙O内、⊙O上,则原点O的位置应该在()图A.点A与点B之间靠近点AB.点A与点B之间靠近点BC.点B与点C之间靠近点BD.点B与点C之间靠近点C10. 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值为()A.5 B.4 2 C.4.75 D.4.8二、填空题(本大题共7道小题)11. 如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是__________.12. 如图,∠APB =30°,⊙O 的半径为1 cm ,圆心O 在直线PB 上,OP =3 cm ,若⊙O 沿BP 方向移动,当⊙O 与直线PA 相切时,圆心O 移动的距离为__________.13. 如图,半圆的圆心O 与坐标原点重合,半圆的半径为1,直线l 的解析式为y =x +t .若直线l 与半圆只有一个公共点,则t 的取值范围是________.14. 如图,⊙O 的半径为1,正方形ABCD 的对角线长为6,OA =4.若将⊙O 绕点A 按顺时针方向旋转360°,则在旋转的过程中,⊙O 与正方形ABCD 的边只有一个公共点的情况一共出现( )A .3次B .4次C .5次D .6次15. 如图所示,在半圆O 中,AB 是直径,D是半圆O 上一点,C 是AD ︵的中点,CE ⊥AB 于点E ,过点D 的切线交EC 的延长线于点G ,连接AD ,分别交CE ,CB 于点P ,Q ,连接AC ,有下列结论:①∠BAD =∠ABC ;②GP =GD ;③点P 是△ACQ 的外心.其中正确的结论是________(只需填写序号).如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为________.17. 如图,⊙M的圆心为M(-2,2),半径为2,直线AB过点A(0,-2),B(2,0),则⊙M关于y轴对称的⊙M′与直线AB的位置关系是________.三、解答题(本大题共4道小题)18. 如图,点O在∠APB的平分线上,⊙O与P A相切于点C.求证:直线PB与⊙O相切.19.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,P是CD的延长线上一点,且AP=AC.(1)求证:P A是⊙O的切线;(2)若PD=5,求⊙O的直径.20. 在Rt△ABC中,∠C=90°,AB=13,AC=5.(1)以点A为圆心,4为半径的⊙A与直线BC的位置关系是________;(2)以点B为圆心的⊙B与直线AC相交,求⊙B的半径r的取值范围;(3)以点C为圆心,R为半径的⊙C与直线AB相切,求R的值.21. 如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.求证:直线DM是⊙O的切线.人教版九年级数学24.2 点和圆、直线和圆的位置关系同步训练-答案一、选择题(本大题共10道小题)1. 【答案】C2. 【答案】B3. 【答案】C[解析] 对于甲的作法:连接OB ,如图①.∵OA =AP ,∴OP 为⊙A 的直径, ∴∠OBP =90°,即OB ⊥PB , ∴PB 为⊙O 的切线,∴甲的作法正确.对于乙的作法:如图②,∵MN ⊥OP ,∴∠OAB =90°.在△OAB 和△OCP 中,⎩⎨⎧OA =OC ,∠AOB =∠COP ,OB =OP ,∴△OAB ≌△OCP ,∴∠OAB =∠OCP =90°,即OC ⊥PC , ∴PC 为⊙O 的切线, ∴乙的作法正确.4. 【答案】B5. 【答案】D[解析] ∵AB 为⊙O 的切线,∴∠OAB =90°.∵∠ABO =36°,∴∠AOB =90°-∠ABO =54°. ∴∠ADC =12∠AOB =27°.故选D.6. 【答案】A7.【答案】D 【解析】∵AB 是⊙O 的直径,AC 切⊙O 于点A ,∴∠BAC =90°,∵∠C =70°,∴∠B=20°,∴∠AOD=∠B+∠BDO=2∠B=2×20°=40°.8. 【答案】A9. 【答案】C[解析] 如图.10. 【答案】D[解析] 如图,设PQ的中点为F,⊙F与AB 的切点为D,连接FD,FC,CD.∵AB=10,AC=8,BC=6,∴∠ACB=90°,∴PQ为⊙F的直径.∵⊙F与AB相切,∴FD⊥AB,FC+FD=PQ,而FC+FD≥CD,∴当CD为Rt△ABC的斜边AB上的高且点F在CD上时,PQ有最小值,为CD 的长,即CD为⊙F的直径.∵S△ABC =12BC·AC=12CD·AB,∴CD=4.8.故PQ的最小值为4.8.二、填空题(本大题共7道小题)11. 【答案】3<r<5[解析] 连接BD.在Rt△ABD中,AB=4,AD=3,则BD=32+42=5.由题图可知3<r<5.12. 【答案】1 cm或5 cm[解析] 当⊙O与直线PA相切时,点O到直线PA的距离为1 cm.∵∠APB=30°,∴PO=2 cm,∴圆心O移动的距离为3-2=1(cm)或3+2=5(cm).13. 【答案】t=2或-1≤t<1[解析] 若直线与半圆只有一个公共点,则有两种情况:直线和半圆相切于点C或从直线过点A开始到直线过点B结束(不包括直线过点A).直线y=x+t与x轴所形成的锐角是45°.当点O 到直线l 的距离OC =1时,直线l 与半圆O 相切,设直线l 与y 轴交于点D ,则OD =2,即t = 2.当直线过点A 时,把A (-1,0)代入直线l 的解析式,得t =y -x =1. 当直线过点B 时,把B (1,0)代入直线l 的解析式,得t =y -x =-1. 即当t =2或-1≤t <1时,直线和半圆只有一个公共点. 故答案为t =2或-1≤t <1.14. 【答案】B[解析] ∵正方形ABCD 的对角线长为6,∴它的边长为3 2.如图,⊙O 与正方形ABCD 的边AB ,AD 只有一个公共点的情况各有1次,与边BC ,CD 只有一个公共点的情况各有1次,∴在旋转的过程中,⊙O 与正方形ABCD 的边只有一个公共点的情况一共出现4次.15. 【答案】②③[解析] ∵在半圆O 中,AB 是直径,D 是半圆O 上一点,C 是AD ︵的中点,∴AC ︵=DC ︵,但不一定等于DB ︵,∴∠BAD 与∠ABC 不一定相等,故①错误. 如图,连接OD ,则OD ⊥GD ,∠OAD =∠ODA .∵∠ODA +∠GDP =90°,∠OAD +∠GPD =∠OAD +∠APE =90°,∴∠GPD =∠GDP ,∴GP =GD ,故②正确. 补全⊙O ,延长CE 交⊙O 于点F . ∵CE ⊥AB ,∴A 为FC ︵的中点,即AF ︵=AC ︵. 又∵C 为AD ︵的中点,∴CD ︵=AC ︵,∴AF ︵=CD ︵, ∴∠CAP =∠ACP ,∴AP =CP . ∵AB 为⊙O 的直径,∴∠ACQ =90°,∴∠ACP +∠PCQ =90°,∠CAP +∠PQC =90°, ∴∠PCQ =∠PQC ,∴PC =PQ ,∴AP =PQ ,即P 为Rt △ACQ 的斜边AQ 的中点,∴点P为Rt△ACQ的外心,故③正确.16. 【答案】3或4 3[解析] 如图①,当⊙P与CD边相切时,设PC=PM=x. 在Rt△PBM中,∵PM2=BM2+BP2,∴x2=42+(8-x)2,∴x=5,∴PC=5,∴BP=BC-PC=8-5=3.如图②,当⊙P与AD边相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形,∴PM=PK=CD=2BM,∴BM=4,PM=8,在Rt△PBM中,BP=82-42=4 3.综上所述,BP的长为3或4 3.17. 【答案】相交[解析] ∵⊙M的圆心为M(-2,2),则⊙M关于y轴对称的⊙M′的圆心为M′(2,2).因为M′B=2>点M′到直线AB的距离,所以直线AB与⊙M′相交.三、解答题(本大题共4道小题)18. 【答案】证明:如图,连接OC,过点O作OD⊥PB于点D.∵⊙O与P A相切于点C,∴OC⊥P A.∵点O在∠APB的平分线上,OC⊥P A,OD⊥PB,∴OD=OC,∴直线PB与⊙O相切.19. 【答案】解:(1)证明:如图,连接OA.∵∠B=60°,∴∠AOC=2∠B=120°.又∵OA=OC,∴∠OAC=∠OCA=30°.又∵AP=AC,∴∠P=∠OCA=30°,∴∠OAP=∠AOC-∠P=90°,∴OA⊥P A.又∵OA是⊙O的半径,∴P A是⊙O的切线.(2)在Rt△OAP中,∵∠P=30°,∴PO=2OA=OD+PD.又∵OA=OD,∴PD=OD=OA.∵PD=5,∴2OA=2PD=2 5,∴⊙O的直径为2 5.20. 【答案】解:(1)∵AC ⊥BC ,而AC >4,∴以点A 为圆心,4为半径的⊙A 与直线BC 相离.故答案为相离.(2)BC =AB 2-AC 2=12.∵BC ⊥AC ,∴当⊙B 的半径大于BC 的长时,以点B 为圆心的⊙B 与直线AC 相交,即r >12.(3)如图,过点C 作CD ⊥AB 于点D .∵12CD ·AB =12AC ·BC ,∴CD =5×1213=6013.即当R =6013时,以点C 为圆心,R 为半径的⊙C 与直线AB 相切.21. 【答案】证明:如图,作直径DG ,连接BG .∵点E 是△ABC 的内心,∴AD 平分∠BAC ,∴∠BAD =∠DAC.∵∠G =∠BAD ,∠BDM =∠DAC ,∴∠BDM =∠G .∵DG 为⊙O 的直径,∴∠GBD =90°,∴∠G +∠BDG =90°,∴∠BDM +∠BDG =90°,即∠MDG =90°.又∵OD 是⊙O 的半径,∴直线DM 是⊙O 的切线.24.3正多边形和圆一.选择题1.下面说法正确的个数有()①若m>n,则ma2>nb2;②由三条线段首尾顺次相接所组成的图形叫做三角形;③有两个角互余的三角形一定是直角三角形;④各边都相等的多边形是正多边形;⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形一定是钝角三角形.A.1 个B.2 个C.3 个D.4 个2.下列说法,错误的是()A.为了解一种灯泡的使用寿命,宜采用普查的方法B.一元二次方程3x2﹣2x﹣1=0有两个不相等的实数根C.一次函数y=﹣3x+2的图象经过第一、二、四象限D.正六边形每个内角的度数是外角度数的2倍3.如图,正五边形ABCDE内接于⊙O,点P是劣弧上一点(点P不与点C 重合),则∠CPD=()A.45°B.36°C.35°D.30°4.如图,用若n个全等的正五边形按如下方式拼接可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为24°,图中所示的是前3个正五边形的拼接情况,拼接一圈后,中间会形成一个正多边形,则n的值为()A.5 B.6 C.8 D.105.如图,五边形ABCDE是⊙O的内接正五边形,则正五边形中心角∠COD的度数是()A.60°B.36°C.76°D.72°6.如图,正方形ABCD和正三角形AEF内接于⊙O,DC、BC交EF于G、H,若正方形ABCD的边长是4,则GH的长度为()A.2B.4﹣C.D.﹣7.如图,⊙O是正八边形ABCDEFGH的外接圆,则下列结论:①弧DF的度数为90°;②AE=DF;③S正八边形ABCDEFGH=AEDF.其中所有正确结论的序号是()A.①②B.①③C.②③D.①②③8.如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则的值为()A.B.C.D.29.如图,正五边形ABCDE与正三角形AMN都是⊙O的内接多边形,若连接BM,则∠MBC的度数是()A.12°B.15°C.30°D.48°10.如图,在由边长相同的7个正六边形组成的网格中,点A,B在格点上.再选择一个格点C,使△ABC是以AB为腰的等腰三角形,符合点C条件的格点个数是()A.1 B.2 C.3 D.4二.填空题11.正六边形的边长为2,则边心距为.12.如图,正方形ABCD内接于⊙O,若⊙O的半径是1,则正方形的边长是.13.中心角为36°的正多边形边数为.14.如图,正五边形ABCDE内接于圆O,P为弧DE上的一点(点P不与点D、E重合),则∠CPD的度数为.15.如图1,将一个正三角形绕其中心最少旋转60°,所得图形与原图的重叠部分是正六边形;如图2,将一个正方形绕其中心最少旋转45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转°,所得图形与原图的重叠部分是正多边形.在图2中,若正方形的边长为4,则所得正八边形的面积为.三.解答题16.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)求证:△ABC是等边三角形.(2)若⊙O的半径为2,求等边△ABC的边心距.17.如图,以△ABC的一边AC为直径的⊙O交AB边于点D,E是⊙O上一点,连接DE,∠E=∠B.(1)求证:BC是⊙O的切线;(2)若∠E=45°,AC=4,求⊙O的内接正四边形的边长.18.如图,实线部分是由正方形,正五边形和正六边形叠放在一起形成的,其中正方形和正六边形的边长相同,求图中∠MON的度数.19.中心为O的正六边形ABCDEF的半径为6cm,点P,Q同时分别从A,D 两点出发,以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间为t(s).(1)求证:四边形PBQE为平行四边形;(2)求矩形PBQE的面积与正六边形ABCDEF的面积之比.参考答案与试题解析一.选择题1.【解答】解:①若m>n,则ma2>nb2,当a=0时错误;故不符合题意;②由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形,故不符合题意;③有两个角互余的三角形一定是直角三角形,故符合题意;④各边都相等,各角也相等的多边形是正多边形,故不符合题意.⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形是钝角三角形或直角三角形,故不符合题意;故选:A.2.【解答】解:A、为了解一种灯泡的使用寿命,此调查具有破坏性,宜采用抽查的方法;故此选项符合题意;B、一元二次方程3x2﹣2x﹣1=0有两个不相等的实数根;故此选项不符合题意;C、一次函数y=﹣3x+2的图象经过第一、二、四象限;故此选项不符合题意;D、正六边形每个内角的度数是外角度数的2倍;故此选项不符合题意;故选:A.3.【解答】解:如图,连接OC,OD,∵ABCDE是正五边形,∴∠COD==72°,∴∠CPD=∠COD=36°,故选:B.4.【解答】解:∵正五边形的每个内角为:=108°,∴组成的正多边形的每个内角为:360°﹣2×108°﹣24°=120°,∵n个全等的正五边形拼接可以拼成一个环状,中间会形成一个正多边形,∴组成的正多边形为正n边形,则=120°,解得:n=6,故选:B.5.【解答】解:∵五边形ABCDE是⊙O的内接正五边形,∴五边形ABCDE的中心角∠COD的度数为=72°,故选:D.6.【解答】解:连接AC交EF于M,连接OF,∵四边形ABCD是正方形,∴∠B=90°,∴AC是⊙O的直径,∴△ACD是等腰直角三角形,∴AC=AD=4,∴OA=OC=2,∵△AEF是等边三角形,∴AM⊥EF,∠OFM=30°,∴OM=OF=,∴CM=,∴∠ACD=45°,∠CMG=90°,∴∠CGM=45°,∴△CGH是等腰直角三角形,∴GH=2CM=2.故选:A.7.【解答】解:设圆心为O ,连接OD ,OF , ∵∠DOE =∠EOF ==45°,∴∠DOF =90°,∴弧DF 的度数为90°,∴①正确;∵∠DOF =90°,OD =OF ,∴2OD 2=DF 2,∴OD =, ∵AE =2OD ,∴AE =DF ,∴②正确;∵S 四边形ODEF =DFOE ,∴S 正八边形ABCDEFGH =4S 四边形ODEF =2DFOE , ∵OE =AE ,∴S 正八边形ABCDEFGH =AEDF ,∴③正确;故选:D .8.【解答】解:如图,连接AC、BD、OF,设⊙O的半径是r,则OF=r,∵AO是∠EAF的平分线,∴∠OAF=60°÷2=30°,∵OA=OF,∴∠OF A=∠OAF=30°,∴∠COF=30°+30°=60°,∴FI=r sin60°=r,∴EF=r×2=r,∵AO=2OI,∴OI=r,CI=r﹣r=r,∴==,∴GH=BD=r,∴==.故选:C.9.【解答】解:连接OA、OC.∵五边形ABCDE是正五边形,∴∠AOB==72°,∴∠AOC=72°×2=144°,∵△AMN是正三角形,∴∠AOM==120°,∴∠COM=∠AOC﹣∠AOM=144°﹣120°=24°,∴∠MBC=∠COM=×24°=12°.故选:A.10.【解答】解:AB的长等于六边形的边长+最长对角线的长,据此可以确定共有2个点C,位置如图,故选:B.二.填空题(共5小题)11.【解答】解:如图所示:连接OA、OB,作OC⊥AB于C,则∠OCA=90°,AC=BC=AB=1,∠AOB=60°,∴∠AOC=30°,∴OC=AC=;故答案为:.12.【解答】解:连接OB,OC,则OC=OB=1,∠BOC=90°,在Rt△BOC中,BC==.∴正方形的边长是,故答案为:.13.【解答】解:由题意可得:∵360°÷36°=10,∴它的边数是10.故答案为10.14.【解答】解:如图,连接OC,OD.∵ABCDE是正五边形,∴∠COD==72°,∴∠CPD=∠COD=36°,故答案为:36°.15.【解答】解:如图2所示:将一个正三角形绕其中心最少旋转60°,所得图形与原图的重叠部分是正六边形;将一个正方形绕其中心最少旋转45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转,所得图形与原图的重叠部分是正多边形.在图2中,由题意得:PM=MN=NQ,AM=AP=BN=BQ,则MN=PM=AM,∵AM+MN+BN=AB=4,∴AM+AM+AM=4,解得:AM=4﹣2,则所得正八边形的面积为4×4﹣4××(4﹣2)2=32﹣32;故答案为:(),32﹣32.三.解答题(共4小题)16.【解答】(1)证明:在⊙O中,∵∠BAC与∠CPB是对的圆周角,∠ABC与∠APC是所对的圆周角,∴∠BAC=∠CPB,∠ABC=∠APC,又∵∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC为等边三角形;(2)过O作OD⊥BC于D,连接OB,则∠OBD=30°,∠ODB=90°,∵OB=2,∴OD=1,∴等边△ABC的边心距为1.17.【解答】解:(1)证明:连接CD,∵AC为直径,∴∠ADC=90°,∵∠E=∠ACD,∠E=∠B.∴∠ACD=∠B,∴∠ACD+∠CAD=∠B+∠CAD=90°,∴∠ACB=90°,∴BC是⊙O的切线;(2)如图,连接OD、CE,若∠E=45°,则∠AOD=90°,∵AC=4,∴OA=OD=2,∴AD=2.∴⊙O的内接正四边形的边长为AD的长为2.18.【解答】解:由正方形、正五边形和正六边形的性质得,∠AOM=108°,∠OBC=120°,∠NBC=90°,∴∠AOB=×120°=60°,∠MOB=108°﹣60°=48°,∴∠OBN=360°﹣120°﹣90°=150°,∴∠NOB=×(180°﹣150°)=15°,∴∠MON=33°.19.【解答】(1)证明:∵六边形ABCDEF是正六边形,∴AB=BC=CD=DE=EF=F A,∠A=∠ABC=∠C=∠D=∠DEF=∠F,∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,∴AP=DQ=t,PF=QC=6﹣t,在△ABP和△DEQ中,,∴△ABP≌△DEQ(SAS),∴BP=EQ,同理可证PE=QB,∴四边形PEQB为平行四边形.(2)解:连接BE、OA,则∠AOB==60°,∵OA=OB,∴△AOB是等边三角形,∴AB=OA=6,BE=2OB=12,当t=0时,点P与A重合,Q与D重合,四边形PBQE即为四边形ABDE,如图1所示:则∠EAF=∠AEF=30°,∴∠BAE=120°﹣30°=90°,∴此时四边形ABDE是矩形,即四边形PBQE是矩形.当t=6时,点P与F重合,Q与C重合,四边形PBQE即为四边形FBCE,如图2所示:同法可知∠BFE=90°,此时四边形PBQE是矩形.综上所述,t=0s或6s时,四边形PBQE是矩形,∴AE==6,∴矩形PBQE的面积=矩形ABDE的面积=AB×AE=6×6=36;∵正六边形ABCDEF的面积=6△AOB的面积=6×矩形ABDE的面积=6××36:24.4《弧长和扇形面积》一.选择题1.已知一个扇形的弧长为3π,所含的圆心角为120°,则半径为()A.9B.3C.D.2.一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为()A.cm B.cm C.3cm D.cm3.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为()A.B.C.4D.2+4.如图,P A、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则的长为()A.πB.πC.D.5.如图,在扇形OAB中,∠AOB=90°,半径OA=6,将扇形OAB沿过点A的直线折叠,点O恰好落在弧AB上的点O'处,折痕交OB于点C,则弧O'B的长是()A.πB.πC.2πD.3π6.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为()A.175πcm2B.350πcm2C.πcm2D.150πcm27.如图,蒙古包可近似地看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25πm2,圆柱高为3m,圆锥高为2m的蒙古包,则需要毛毡的面积是()A.(30+5)πm2B.40πm2C.(30+5)πm2D.55πm28.如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为()A.3B.6C.3πD.6π9.如图,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3,则它们之间的关系是()A.S1<S2<S3B.S2<S1<S3C.S1<S3<S2D.S3<S2<S1 10.已知一个圆心角为270°扇形工件,未搬动前如图所示,A、B两点触地放置,搬动时,先将扇形以B为圆心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当A、B两点再次触地时停止,半圆的直径为6m,则圆心O所经过的路线长是()m.(结果用含π的式子表示)A.6πB.8πC.10πD.12π二.填空题11.一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是度.12.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则的长为.13.如图,圆锥的母线长为10cm,高为8cm,则该圆锥的侧面展开图(扇形)的弧长为cm.(结果用π表示)14.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为cm.15.如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中的长是cm(计算结果保留π).16.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D.若OA=2,则阴影部分的面积为.三.解答题17.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.(1)求证:AE=ED;(2)若AB=10,∠CBD=36°,求的长.18.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.(1)求证:BE=CE;(2)若AB=6,∠BAC=54°,求劣弧的长.19.如图,在平面直角坐标系xOy中,以原点O为旋转中心,将△AOB顺时针旋转90°得到△A'OB',其中点A'与点A对应,点B'与点B对应.如果A(﹣4,0),B(﹣1,2).请回答:(1)点B'的坐标为.(2)点A经过的路径的长度为π.(友情提示:已经有π)20.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为2,求图中阴影部分的面积.21.如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2,∠DP A=45°.(1)求⊙O的半径;(2)求图中阴影部分的面积.22.如图,在正方形网格中建立平面直角坐标系,一条圆弧经过网格点A(0,8)、B(﹣8,8)、C(﹣12,4),请在网格图中进行如下操作:(1)若该圆弧所在圆的圆心为D,则D点坐标为;(2)连接AD、CD,则⊙D的半径长为(保留根号).∠ADC的度数为°;(3)若扇形ADC是一个圆锥的侧面展开图,求该圆锥的底面圆的半径长.(结果保留根号)参考答案一.选择题1.解:设半径为r,∵扇形的弧长为3π,所含的圆心角为120°,∴=3π,∴r=,故选:C.2.解:设此圆锥的底面半径为r,根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得:2πr=,r=cm.3.解:如图:BC=AB=AC=1,∠BCB′=120°,∴B点从开始至结束所走过的路径长度为2×弧BB′=2×=,故选:B.4.解:∵P A、PB是⊙O的切线,∴∠OBP=∠OAP=90°,在四边形APBO中,∠P=60°,∴∠AOB=120°,∵OA=2,∴的长l==π,故选:C.5.解:连接OO′,∴OO′=OA,∵将扇形OAB沿过点A的直线折叠,点O恰好落在弧AB上的点O'处,∴OA=O′A,∴△AOO′是等边三角形,∴∠AOO′=60°,∵∠AOB=90°,∴∠BOO′=30°,∴的长==π,故选:B.6.解:∵AB=25,BD=15,∴AD=10,∴S贴纸=2×(﹣)=2×175π故选:B.7.解:设底面圆的半径为R,则πR2=25π,解得R=5,圆锥的母线长==,所以圆锥的侧面积=•2π•5•=5π;圆柱的侧面积=2π•5•3=30π,所以需要毛毡的面积=(30π+5π)m2.故选:A.8.解:∵圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,∴2πr=×2π×10,解得r=6.故选:B.9.解:作OD⊥BC交BC与点D,∵∠COA=60°,∴∠COB=120°,则∠COD=60°.∴S扇形AOC=;S扇形BOC=.在三角形OCD中,∠OCD=30°,∴OD=,CD=,BC=R,∴S△OBC=,S弓形==,>>,∴S2<S1<S3.故选:B.10.解:∠AOB=360°﹣270°=90°,则∠ABO=45°,则∠OBC=45°,O旋转的长度是:2×=π,O移动的距离是:=π,则圆心O所经过的路线长是:π+π=6π.故选:A.二.填空题11.解:根据l===11π,解得:n=110,故答案为:110.12.解:∵ABCDEF为正六边形,∴∠AOB=360°×=60°,的长为=.故答案为:.13.解:设底面圆的半径为rcm,由勾股定理得:r==6,∴2πr=2π×6=12π,故答案为:12π.14.解:圆锥的底面周长=2π×2=4πcm,设圆锥的母线长为R,则:=4π,解得R=6.故答案为:6.15.解:∵圆锥的高h为12cm,OA=13cm,∴圆锥的底面半径为=5cm,∴圆锥的底面周长为10πcm,∴扇形AOC中的长是10πcm,故答案为:10π.16.解:连接OE、AE,∵点C为OA的中点,∴∠CEO=30°,∠EOC=60°,∴△AEO为等边三角形,∴S扇形AOE==π,∴S阴影=S扇形AOB﹣S扇形COD﹣(S扇形AOE﹣S△COE)=﹣﹣(π﹣×1×)=π﹣π+=+.故答案为:+.三.解答题17.证明:(1)∵AB是⊙O的直径,∴∠ADB=90°,∵OC∥BD,∴∠AEO=∠ADB=90°,即OC⊥AD,∴AE=ED;(2)∵OC⊥AD,∴,∴∠ABC=∠CBD=36°,∴∠AOC=2∠ABC=2×36°=72°,∴.18.(1)证明:如图,连接AE.∵AB是圆O的直径,∴∠AEB=90°,即AE⊥BC.又∵AB=AC,∴AE是边BC上的中线,∴BE=CE;(2)解:∵AB=6,∴OA=3.又∵OA=OD,∠BAC=54°,∴∠AOD=180°﹣2×54°=72°,∴的长为:=.19.解:如图所示:∵A(﹣4,0),B(﹣1,2).∴A'的坐标为(0,4),B'的坐标为(2,1),∴OA=OA'=4,∴点A经过的路径的长度==2π.20.(1)证明:连接OC.∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.∵OA=OC,∴∠2=∠A=30°.∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.即OC⊥CD,∴CD是⊙O的切线.(2)解:∵∠A=30°,∴∠1=2∠A=60°.∴S扇形BOC=.在Rt△OCD中,.∴.∴图中阴影部分的面积为:.21.解:(1)连接OF,∵直径AB⊥DE,∴CE=DE=1.∵DE平分AO,∴CO=AO=OE.设CO=x,则OE=2x.由勾股定理得:12+x2=(2x)2.x=.∴OE=2x=.即⊙O的半径为.(2)在Rt△DCP中,∵∠DPC=45°,∴∠D=90°﹣45°=45°.∴∠EOF=2∠D=90°.∴S扇形OEF==π.∵∠EOF=2∠D=90°,OE=OF=S Rt△OEF==.∴S阴影=S扇形OEF﹣S Rt△OEF=π﹣.22.解:(1)点D的坐标为(﹣4,0);(2)如图,AD==4,即⊙D的半径长为4;∵AD=CD=4,AC==4,∴AD2+DC2=AC2,∴△ACD为直角三角形,∠ADC的度数为90°;故答案为(﹣4,0);4;90;(3)设该圆锥的底面圆的半径长为r,根据题意得2πr=,解得r=,即该圆锥的底面圆的半径长为.。
第24章 圆 人教版数学九年级上册单元测试卷(含答案)

第二十四章 圆一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)1.(2022·北京通州区期末)如图,若OA⊥OB,则∠C=( )A.22.5°B.67.5°C.90°D.45°(第1题) (第2题)2.(2022·江苏镇江润州区段考改编)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是( )A.3B.4C.5D.63.(2021·江苏常熟期中)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(-3,0),B(-1,2),C(3,2),则△ABC的外心的坐标是( )A.(1,-2)B.(0,0)C.(1,-1)D.(0,-1)(第3题) (第4题)4.(2021·山东寿光期中)如图,若正方形ABCD的边长为6,则其外接圆半径OA与内切圆半径OE的比值为( )A.3B.2C.2D.35.(2022·湖北十堰期末)如图,点A,B,C,D都在☉O上,OA⊥BC,∠OBC=40°,则∠ADC 的度数为( ) A.40° B.30° C.25° D.50°6.(2022·浙江金华期中改编)如图,☉O 与正六边形OABCDE 的边OA ,OE 分别交于点F ,G ,点M 为劣弧FG 的中点.连接FM ,GM ,若FM=22,则☉O 的半径为( )A.2B.6C.22D.26(第6题) (第7题)7.(2022·浙江宁波江北区期末)如图,AB 是半圆O 的直径,C ,D 是半圆上两点,连接CA ,CD ,AD.若∠ADC=120°,BC=1,则BC 的长为( )A.π3B.π4C.π6D.2π38.(2022·江苏镇江期中)简易直尺、含60°角的直角三角板和量角器如图摆放(无重叠部分),A 为三角板与直尺的交点,B 为量角器与直尺的接触点,C 为量角器与三角板的接触点.若点A 处刻度为4,点B 处刻度为6,则该量角器的直径长为( )A.2B.23C.4D.439.如图,四边形ABCD 内接于☉O ,AD ∥BC ,直线EF 是☉O 的切线,B 是切点.若∠C=80°,∠ADB=54°,则∠CBF=( )A.45°B.46°C.54°D.60°10.如图(1),AB是半圆O的直径,点C是半圆O上异于A,B的一点,连接AC,BC.点P从点A出发,沿A→C→B以1 cm/s的速度运动到点B.图(2)是点P运动时,△PAB 的面积y(cm2)随时间x(s)变化的图象,则点D的横坐标为( )A.a+2B.2C.a+3D.3二、填空题(共5小题,每小题3分,共15分)11.(2022·山东济南天桥区期末)如图,☉A,☉B,☉C两两相离,且半径都为2,则图中阴影部分的面积之和为 .(结果保留π)(第11题) (第12题)12.(2022·江苏苏州姑苏区期中)如图,A,B,C,D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为 .13.(2022·河北唐山期末改编)如图,△ABC内接于☉O,过点A作直线EF,已知∠B=∠EAC,根据弦AB的位置变化,试探究直线EF与☉O的位置关系.甲:如图(1),当弦AB过点O时,EF与☉O相切;乙:如图(2),当弦AB不过点O时,EF也与☉O相切.你认为 的判断正确.14.新风向关注数学文化在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为☉O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,则直径AB的长为 寸.(第14题) (第15题)15.如图,已知四边形ABCD是边长为4的正方形,以AB为直径向正方形内作半圆,P为半圆上一动点(不与点A,B重合),当PA= 时,△PAD为等腰三角形.三、解答题(共6小题,共55分)16.(7分)(2022·北京四中期中改编)某游乐园的摩天轮采用了国内首创的横梁结构,如图,摩天轮半径为44 m,中心O距离地面56 m,匀速运行一圈的时间为18 min.由于受到周边建筑物的影响,乘客与地面之间超过一定距离时,可视为最佳观赏位置.已知在运行的一圈里最佳观赏时长为12 min,求最佳观赏位置与地面的最小距离(即BD的长).17.(8分)(2021·浙江温州模拟)如图,已知AB是☉O的直径,弦CD⊥AB于点E,点M 是☉O上一动点,∠M=∠D,连接BC.(1)判断BC与MD的位置关系,并说明理由;(2)若MD恰好经过圆心O,求∠D的度数.18.(8分)(2022·山东临沂期末)如图,AB为☉O的直径,AC,DC为弦,∠ACD=60°,P 为AB延长线上的点,连接PD,∠APD=30°.(1)求证:DP是☉O的切线.(2)若☉O的半径为2,求图中阴影部分的面积.19.(10分)[与特殊平行四边形综合](2021·河南驻马店二模)如图,已知☉O的直径AB=2,C是AB上一个动点(不与点A,B重合),切线DC交AB的延长线于点D,连接AC,BC,OC.(1)请添加一个条件使△BAC≌△ODC,并说明理由.(2)若点C关于直线AB的对称点为E.①当AD= 时,四边形OCDE为正方形.②当∠CDB= °时,四边形ACDE为菱形.20.(10分)新风向探究性试题如图,已知AB是☉O的直径,BC与☉O相切于点B,CD 与☉O相切于点D,连接AD,OC.(1)求证:AD∥OC.(2)小聪与小明在做这个题目的时候,对∠CDA+∠AOC的值进行了探究:小聪说,∠CDA+∠AOC的值是一个固定值;小明说,∠CDA+∠AOC的值随∠A的度数的变化而变化.若∠CDA+∠AOC的值为y,∠A的度数为x,你认为他们之中谁的说法正确?若小聪的说法正确,请求出y;若小明的说法正确,请求出y与x之间的关系.21.(12分)新风向探究性试题【问题呈现】阿基米德折弦定理:如图(1),AB和BC是☉O的两条弦(即折线ABC是☉O的一条折弦),BC>AB,M是ABC的中点,则从点M 向BC作垂线,垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的过程. 图(1) 图(2) 图(3) 图(4)证明:如图(2),在CD上截取CG=AB,连接MA,MB,MC和MG.∵M是ABC的中点,∴MA=MC.①∵∠A=∠C,②∴△MAB≌△MCG,∴MB=MG.又MD⊥BC,∴BD=DG,∴CD=CG+DG=AB+BD,即CD=AB+BD.根据证明过程,分别写出步骤①,②的理由:① .② .【理解运用】在图(1)中,若AB=4,BC=6,则BD= .【变式探究】如图(3),AB,BC是☉O的两条弦,点M是AC的中点,MD⊥BC于点D,请写出CD,DB,BA之间存在的数量关系: .【实践应用】如图(4),△ABC内接于☉O,BC是☉O的直径,点D为圆周上一动点,满足∠DAC=45°.若AB=6,☉O的半径为5,求AD的长.第二十四章 圆·B卷1.D ∵OA⊥OB,∴∠AOB=90°,∴∠C=12∠AOB=【技巧】同圆中,同弧所对的圆周角等于圆心角的一半45°.2.B 连接BD,由勾股定理可得BD=AB2+AD2=42+32=5,由题意可知,3<r<5,因此只有B选项符合.3.A 如图,∵三角形的外心到三角形三个顶点的距离相等,∴线段BC,AB的垂直平分线的交点即为外心P,由图可知,点P的坐标为(1,-2).4.B 由题意结合题图可知,内切圆直径等于正方形边长,则OE=3.由正方形的性质可得OA=32,则OAOE =323=2.5.C ∵OA ⊥BC ,∴AC =AB .∵∠OBC=40°,∴∠AOB=50°,∴∠ADC=12∠AOB=12×50°=25°.6.C 连接OM ,由题意知∠FOG=120°.∵点M 为劣弧FG 的中点,∴∠FOM=60°.∵OM=OF ,∴△OFM 是等边三角形,∴OM=OF=FM=22,则☉O 的半径为22,故选C .7.A 如图,连接OC.∵∠ADC=120°,∴∠ABC=60°.∵OB=OC ,∴△OBC 为等边三角形,∴∠COB=60°,OB=OC=BC=1,∴BC 的长=60π·1180=π3.8.D 如图,添加点D ,连接OA ,OB ,由题意得AB=6-4=2,∵∠CAD=60°,∴∠BAC=120°.∵AB 与半圆O 相切于点B ,AC 与半圆O 相切于C ,∴∠BAO=60°,∠AOB=30°,∴OA=2AB=4,∴OB=OA 2-AB 2=42-22=23,∴量角器的直径长为43.9.B 如图,连接OD ,OB ,则∠BOD=2∠C=160°.∵OB=OD ,∴∠OBD=180°―160°2=10°.∵四边形ABCD 内接于☉O ,∴∠A=180°-∠C=100°.∵AD ∥BC ,∴∠A+∠ABC=180°,∴∠ABC=80°.在△ABD 中,∠ADB=54°,∴∠ABD=180°-54°-100°=26°,∴∠OBC=80°-26°-10°=44°.∵EF 是☉O 的切线,∴∠OBF=90°,∴∠CBF=90°-∠OBC=90°-44°=46°.故选B .∵AD ∥BC ,∴∠ADB+∠BDC+∠C=180°.∵∠C=80°,∠ADB=54°,∴∠BDC=46°.∵∠CBF 是弦切角,∴∠CBF=∠BDC=46°.(弦切角定理:弦切角的度数等于它所夹的弧所对的圆心角度数的一半,等于它所夹的弧所对的圆周角度数)10.A 从题图(2)看,当x=a 时,y 取得最大值a ,此时点P 运动到点C 处,即AC=a.∵∠ACB=90°,∴y=12×AC×BC=12BC×a=a ,解得BC=2.当点P 运动到点B 处时,y=0,即AC+BC=OD ,∵AC+BC=a+2,∴点D 的横坐标为a+2.11.2π 因为∠A+∠B+∠C=180°,所以阴影部分的面积之和等于半径为2的半圆的面积,为2π.12.10 如图,连接OA ,OB ,由题意知点A ,B ,C ,D 在以点O 为圆心,OA 的长为半径的同一个圆上.∵∠ADB=18°,∴∠AOB=2∠ADB=36°,∴这个正多边形的边数=360°÷36°=10.13.甲、乙 题图(1)中,∵AB 是☉O 的直径,∴∠C=90°,∴∠B+∠CAB=90°.∵∠EAC=∠B ,∴∠EAC+∠CAB=90°,∴EF ⊥AB.∵OA 是半径,∴EF 是☉O 的切线,故甲的判断正确.如图,作直径AM ,连接CM ,则∠ACM=90°,∠B=∠M.∵∠EAC=∠B ,∴∠EAC=∠M.∵∠CAM+∠M=90°,∴∠CAM+∠EAC=90°,∴EF 是☉O 的切线,故乙的判断正确.14.26 连接OC.∵CD ⊥AB ,AB 为☉O 的直径,CD=10,∴CE=12CD=5. 设OC=OA=x ,则OE=x-1.由勾股定理得OE 2+CE 2=OC 2,即(x-1)2+52=x 2,解得x=13,∴AB=26寸.15.22或85516.【参考答案】由题意得AB⊥OM,BO=44,×360°=120°,∠AOB=18―1218∴∠BOC=60°,∠OBC=30°,∴OC=1OB=22.2∵中心O距离地面56 m,∴OM=56,∴CM=OM-OC=34,∴BD=34 m,故最佳观赏位置与地面的最小距离为34 m.(7分) 17.【参考答案】(1)BC∥MD.(1分)理由:∵∠MBC=∠D,∠M=∠D,∴∠M=∠MBC,∴BC∥MD.(4分) (2)∵AB是☉O的直径,CD⊥AB于点E,∴∠D+∠EOD=90°.(6分)∵MD过圆心O,∴∠BOD=2∠M=2∠D,∴∠D+2∠D=90°,∴∠D=30°.(8分) 18.【参考答案】(1)证明:如图,连接OD.∵∠ACD=60°,∴∠AOD=120°,∴∠BOD=60°.∵∠APD=30°,∴∠ODP=90°,即PD⊥OD.∵OD是半径,∴PD是☉O的切线.(4分)(2)∵在Rt △POD 中,OD=2,∠OPD=30°,∴OP=4.由勾股定理得PD=23.∴S 阴影部分=S △POD -S扇形ODB =12×2×23-60π·22360=23-2π3.(8分)19.【参考答案】(1)添加条件∠A=30°.(1分)理由:∵AB 是☉O 的直径,∴∠ACB=90°.∵DC 是☉O 的切线,∴∠DCO=90°,∴∠ACB=∠DCO.(3分)∵OA=OC ,∴∠A=∠OCA=30°,∴∠BOC=60°.∵OC=OB ,∴△BOC 是等边三角形,∴BC=OC ,∠ABC=∠DOC=60°,∴△BAC ≌△ODC (ASA).(6分)或添加条件BC=1.(1分)∵AB 是☉O 的直径,∴∠ACB=90°.∵DC 是☉O 的切线,∴∠DCO=90°,∴∠ACB=∠DCO.(3分)∵OC=OB=12AB=1=BC ,∴△BOC 是等边三角形,∴∠ABC=∠DOC=60°,∴△BAC ≌△ODC (ASA).(6分)(答案不唯一,正确即可给分)(2)①2+1(8分)解法提示:∵AB=2,∴OA=OC=1.连接OE ,DE ,若四边形OCDE 是正方形,则△OCD 是等腰直角三角形,易得OD=2,∴AD=OD+OA=2+1.②30(10分)解法提示:∵DC 是☉O 的切线,∴∠DCO=90°,∴∠COD=90°-∠CDB.∵OC=OA ,∴∠CAB=12∠COD=90°―∠CDB2.连接AE ,若四边形ACDE 是菱形,则CA=CD ,∴∠CAB=∠CDB ,即90°―∠CDB2=∠CDB ,解得∠CDB=30°,∴当∠CDB=30°时,四边形ACDE 是菱形.20.【思路导图】(1)连接ODRt △ODC ≌Rt △OBC →∠DOC=∠BOC →∠DAO=∠BOC →AD ∥CO【参考答案】(1)如图,连接OD.(1分)∵BC 与☉O 相切于点B ,CD 与☉O 相切于点D ,∴∠ODC=∠OBC=90°.(2分)在Rt △ODC 和Rt △OBC 中,OD =OB ,OC =OC ,∴Rt △ODC ≌Rt △OBC ,∴∠DOC=∠BOC.(4分)∵∠DAO=12∠DOB ,∴∠DAO=∠BOC ,∴AD ∥CO.(5分)(2)小聪的说法正确.(6分)∵∠CDA+∠AOC=y ,∠A=x ,∴∠ODC+∠ODA+∠AOC=y ,∠ODA=∠OAD=x.∵∠ODC=90°,∴90°+x+∠AOC=y.由(1)得AD ∥CO ,∴∠OAD+∠AOC=180°,即x+∠AOC=180°,∴y=90°+x+∠AOC=90°+180°=270°.(10分)21.【参考答案】【问题呈现】①在同圆中,如果两条弧相等,那么它们所对的弦相等②同弧所对的圆周角相等(4分)【理解运用】1(6分)解法提示:∵CD=AB+BD ,∴CD=12(AB+BC )=12×(4+6)=5,∴BD=BC-CD=6-5=1.【变式探究】DB=AB+CD(8分)解法提示:如图,在DB 上截取BG=BA ,连接MA ,MB ,MC ,MG.∵M 是AC 的中点,∴AM=MC ,∠MBA=∠MBG.又MB=MB ,∴△MAB ≌△MGB ,∴MA=MG ,∴MC=MG.又DM ⊥BC ,∴DC=DG ,∴AB+DC=BG+DG ,即DB=AB+CD.【实践应用】∵BC是☉O的直径,∴∠BAC=90°.∵AB=6,☉O的半径为5,∴易得AC=8.(分类讨论思想)如图,连接AD,当∠DAC=45°时,有两种情况.①∠D1AC=45°,则D1是BC的中点.过点D1作D1G1⊥AC于点G1,则CG1+AB=AG1.∴AG1=1(6+8)=7,∴AD1=72.2②∠D2AC=45°,过点D2作D2G2⊥AC于点G2,同理易得CG2=AB+AG2,∴CG2=7,AG2=1,∴AD2=2.综上,AD的长为72或2.(12分)。
人教版九年级数学上册第24章 圆单元测试及答案解析-优质新版

第二十四章圆单元测试一、单选题(共10题;共30分)1、如图,⊙O是△ABC的外接圆,已知∠ABO=50°,则∠ACB的大小为()A、40°B、30°C、45°D、50°2、下列说法:①平分弦的直径垂直于弦;②三点确定一个圆;③相等的圆心角所对的弧相等;④垂直于半径的直线是圆的切线;⑤三角形的内心到三条边的距离相等。
其中不正确的有()个。
A、1B、2C、3D、43、如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是()A、80°B、100°C、60°D、40°4、已知Rt△ACB,∠ACB=90°,I为内心,CI交AB于D,BD=,AD=,则S△ACB=()A、12B、6C、3D、7.55、如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为()A、B、C、D、6、如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F,∠E=α,∠F=β,则∠A=()A、α+βB、C、180﹣α﹣βD、7、如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是()A、2B、2+C、2D、2+8、如图,已知AB是⊙O的直径,∠CAB=50°,则∠D的度数为()A、20°B、40°C、50°D、70°9、已知A、B、C三点在⊙O上,且AB是⊙O内接正三角形的边长,AC是⊙O内接正方形的边长,则∠BAC的度数为()A、15°或105°B、75°或15°C、75°D、105°10、如图,在⊙O中,∠ABC=52°,则∠AOC等于()A、52°B、80°C、90°D、104°二、填空题(共8题;共25分)11、如图,⊙O是ABC的外接圆,OCB=40°,则A的度数等于________°.12、如图,已知半圆O的直径AB=4,沿它的一条弦折叠.若折叠后的圆弧与直径AB相切于点D,且AD:DB=3:1,则折痕EF的长________ .13、如图,若∠1=∠2,那么与 ________相等.(填一定、一定不、不一定)14、如图,AB是半圆O的直径,点C、D是半圆O的三等分点,若弦CD=2,则图中阴影部分的面积为________.15、已知扇形的圆心角为150°,它所对应的弧长20πcm,则此扇形的半径是________ cm,面积是________ cm2.16、如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD=________.17、若一个圆锥的侧面积是它底面积的2倍,则这个圆锥的侧面展开图的圆心角是________.18、已知一圆锥的底面半径为1cm,母线长为4cm,则它的侧面积为________cm2(结果保留π).三、解答题(共5题;共35分)19、已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.(1)求证:直线EF是⊙O的切线;(2)当直线DF与⊙O相切时,求⊙O的半径.20、【阅读材料】已知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切圆O的半径为r,连接OA,OB,OC,△ABC被划分为三个小三角形.∵S=S△OBC+S△OAC+S△OAB=BC•r+AC•r+AB•r=ar+br+cr=(a+b+c)r.∴r= .(1)【类比推理】如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;(2)【理解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC各边分别相切于D、E和F,已知AD=3,BD=2,求r的值.21、如图,公路MN与公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否受到噪音影响?说明理由;如果受影响,且知拖拉机的速度为18km/h,那么学校受影响的时间是多少秒?22、如图,已知矩形ABCD的边AB=3cm、BC=4cm,以点A为圆心,4cm为半径作⊙A,则点B、C、D与⊙A怎样的位置关系.23、已知圆的半径为R,试求圆内接正三角形、正四边形、正六边形的边长之比.四、综合题(共1题;共10分)24、(2017•襄阳)如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.(1)求证:EF是⊙O的切线;(2)若DE=1,BC=2,求劣弧的长l.答案解析一、单选题1、【答案】 A【考点】圆周角定理【解析】【分析】根据等边对等角及圆周角定理求角即可.【解答】∵OA=OB∴∠OAB=∠OBA=50°∴∠AOB=80°∴∠ACB=40°.故选A.【点评】此题综合运用了等边对等角、三角形的内角和定理以及圆周角定理2、【答案】 D【考点】垂径定理,确定圆的条件,三角形的内切圆与内心【解析】【解答】①中被平分的弦是直径时,不一定垂直,故错误;②不在同一条直线上的三个点才能确定一个圆,故错误;③应强调在同圆或等圆中,否则错误;④中垂直于半径,还必须经过半径的外端的直线才是圆的切线,故错误;⑤三角形的内心是三角形三个角平分线的交点,所以到三条边的距离相等,故正确;综上所述,①、②、③、④错误。
