6A-SX-0000001 天河区2018-2019学年第一学期期末水平测试六年数学试卷
每日一学:广东省广州市天河区2018-2019学年六年级上学期数学期末考试试卷_压轴题解答

每日一学:广东省广州市天河区2018-2019学年六年级上学期数学期末考试试卷_压轴题解答
答案广东省广州市天河区2018-2019学年六年级上学期数学期末考试试卷_压轴题
~~ 第1题 ~~
(2019天河.六上期末) 这是一张机器人的行走路线图.
(1) 机器人从出发站出发,向偏°方向,行走m 可以到达A 站.
(2) 机器人最终目的地是C 站.C
站位于B 站南偏东30°、距离B 站15m 的位置上.请你在图上标出C 站的位置.(3) 如果机器人的行走速度控制在 米/秒,那么行完全程需要分钟.
考点: 根据方向和距离描述路线图;~~ 第2题 ~~
(2019天河
.六上期末) 如图,四个圆的半径都为3cm ,圆心分别在四边形的四个顶点上,则阴影部分的面积为________cm . (π取3.14
)~~ 第3题 ~~
(2019天河.六上期末) 甲、乙、丙三名小朋友用相同的正方形手工纸剪成圆形,甲剪了一个最大的扇形,乙剪了一最大的圆,丙剪了四个最大的圆.(如图)三个人中对手工纸的利用率情况是( )
A . 甲最高
B . 乙最高
C . 丙最高
D . 三人相同
广东省广州市天河区2018-2019学年六年级上学期数学期末考试试卷_压轴题解答
~~ 第1题 ~~
答案:2
解析:
~~ 第2题 ~~
答案:
解析:
~~ 第3题 ~~
答案:D
解析:。
2018-2019学年天河区高一上学期数学期末考

天河区2018-2019年第一学期期末联考试题高一数学一、选择题:本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集{1,2,3,4}U =,集合{}1,3S =,{}4T =,则()U S T ⋃等于( ).A .{}2,4B .{}4C .∅D .{1,34},2. 已知向量(),1a x =,()1,2b =-,若//a b ,则a b +=( ).A .1,12⎛⎫- ⎪⎝⎭B .1,12⎛⎫⎪⎝⎭C .()3,1-D .()3,13. 已知函数2log ,0()3,0xx x f x x >⎧⎪=⎨≤⎪⎩,则14f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值是( ).A .19-B .9-C .19D .94. 设2513a ⎛⎫= ⎪⎝⎭,432b =,21log 3c =,则( ).A .b a c <<B .a b c <<C .b c a <<D .c a b <<5. 函数()ln 26f x x x =+-的零点一定位于下列哪个区间( ).A .()1,2B .()2,3C .()3,4D .()5,66. 已知角α的终边经过点(4,3)P -,则tan 4πα⎛⎫+ ⎪⎝⎭的值等于( ).A .17-B .17C .37D .477. 已知函数()()sin (,0,0,)2f x A x x R A πωϕωϕ=+∈>><的图象(部分)如图所示,则()f x 的解析式是( ).第2页,共23页A .()2sin 6f x x ππ⎛⎫=+ ⎪⎝⎭B .()2sin 26f x x ππ⎛⎫=+ ⎪⎝⎭C .()2sin 3f x x ππ⎛⎫=+ ⎪⎝⎭D .()2sin 23f x x ππ⎛⎫=+ ⎪⎝⎭8. 若两个非零向量a ,b 满足22b a ==,23a b +=,则a ,b 的夹角是( ).A .6πB .3π C .2π D .π9. 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积12=⨯(弦⨯矢+矢2),弧田(如图)由圆弧和其所对弦围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为23π,弧长为4π米的弧,按上述经公式计算)173.,所得弧田面积约是( ).A .16平方米B .18平方米C .20平方米D .25平方米10.偶函数()()f x x R ∈满足:()()520f f -==,且在区间[]0,3与[)3,+∞上分别递减和递增,则不等式()0x f x ⋅<的解集为( ). A .()()(),52,25,-∞-⋃-⋃+∞B .()()(),52,02,5-∞-⋃-⋃C .()()522,5--⋃.D .()()()5,20,25,--⋃⋃+∞11. 已知锐角α满足cos cos24παα⎛⎫-= ⎪⎝⎭,则tan2α=( ).AB .CD.12.如图,在平行四边形ABCD 中,M 、N 分别为AB 、AD 上的点,且45AM AB =,23AN AD =,连接AC 、MN 交于P 点,若AP AC λ=,则λ的值为( ).A .35B .37C .411D .413. 二、填空题:本大题共4小题,每小题5分,共20分.13.函数()()lg 1f x x =+的定义域是______.14.已知()1cos 3θπ+=-,则sin 22πθ⎛⎫+= ⎪⎝⎭______.15.已知函数(),0ln ,0x e x f x x x ⎧≤=⎨>⎩,()()g x f x x a =++,若()g x 存在2个零点,则实数a 取值范围是______.16.函数()2sin 23f x x π⎛⎫=- ⎪⎝⎭的图象为C ,如下结论中正确的是______.①图象C 关于直线1112x π=对称; ②图象C 关于点2,03π⎛⎫⎪⎝⎭对称; ③函数()f x 在区间5,1212ππ⎛⎫- ⎪⎝⎭内是增函数;④由2sin2y x =图象向右平移3π个单位长度可以得到图象C . 三、解答题:本大题共6小题,满分70分.解答应写出文字说明,证明过程或演算步骤. 17.已知向量()1,0a =,()1,1b =.(1)若22c =,且c b ⊥,求向量c 的坐标;(2)2AB a b =-,BC a mb =+,且A 、B 、C 三点共线,求实数m 的值.第4页,共23页18.已知函数()21mx n f x x +=+是定义在R 上的奇函数,且()225f =. (1)求函数()f x 的解析式;(2)判断函数()f x 在区间()0,1上的单调性,并用定义法证明.19.已知函数()2sin 26x f x π⎛⎫=+ ⎪⎝⎭.(1)求函数()f x 的最小正周期及单调递减区间;(2)先列表,并用描点法作出函数()f x 在[]0,4π上的简图.20.某家庭进行理财投资,根据长期收益率市场预测,投资债券类稳健型产品的收益与投资额成正比,投资股票类风险型产品的收益与投资额的算术平方根成正比.已知两类产品各投资1万元时的收益分别为0125.万元和05.万元,如图:(1)分别写出两类产品的收益(y 万元)与投资额(x 万元)的函数关系;(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,最大收益是多少万元?21.已知()2cos ,1a x =,()3sin cos ,1b x x =+-,函数()f x a b =⋅.(1)求函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值;(2)若()085f x =,0,42x ππ⎡⎤∈⎢⎥⎣⎦,求0cos2x 的值;(3)若函数()y f x ω=在区间2,33ππ⎛⎫⎪⎝⎭上是单调递增函数,求正数ω的取值范围.第6页,共23页22.已知函数()221(0)g x ax ax b a =-++>在区间[]1,1-上有最大值4和最小值0.设()()g x f x x=.(1)求实数a ,b 的值;(2)若不等式()0f x k x -⋅≥在()0,x ∈+∞上恒成立,求实数k 的取值范围;(3)若()2213021xxf k k -+⋅-=-有三个不同的实数解,求实数k 的取值范围.2018-2019学年广东省广州市天河区高一(上)期末数学试卷一、选择题(本大题共12小题,共60分)1. 设全集{1,2,3,4}U =,集合{}1,3S =,{}4T =,则()U S T ⋃等于( ).A .{}2,4B .{}4C .∅D .{1,34},【答案】A【解析】解:全集{1,U =2,3,4},集合{},3S l =,{}4T =, (){}{}{}2,442,4U S T ∴⋃=⋃=.故选:A .利用集合的交、并、补集的混合运算求解.本题考查集合的交、并、补集的混合运算,是基础题,解题时要认真审题. 2. 已知向量(),1a x =,()1,2b =-,若//a b ,则a b +=( ).A .1,12⎛⎫- ⎪⎝⎭B .1,12⎛⎫⎪⎝⎭C .()3,1-D .()3,1【答案】A【解析】解://a b ; 210x ∴--=;12x ∴=-;1,12a ⎛⎫∴=- ⎪⎝⎭;1,12a b ⎛⎫∴+=- ⎪⎝⎭.故选:A .根据//a b 即可得出12x =-,从而得出1,12a ⎛⎫=- ⎪⎝⎭,这样即可求出a b +的坐标.考查平行向量的坐标关系,以及向量坐标的加法运算. 3. 已知函数2log ,0()3,0x x x f x x >⎧⎪=⎨≤⎪⎩,则14f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值是( ). A .19-B .9-C .19D .9第8页,共23页【答案】C【解析】解:函数()2log ,03,0x x xf x x >⎧=≤⎨⎩,211log 244f ⎛⎫∴==- ⎪⎝⎭,()2112349f f f -⎛⎫⎛⎫=-== ⎪ ⎪⎝⎭⎝⎭.故选:C .由已知得211log 244f ⎛⎫==- ⎪⎝⎭,从而()124f f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭,由此能求出结果. 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.4. 设2513a ⎛⎫= ⎪⎝⎭,432b =,21log 3c =,则( ).A .b a c <<B .a b c <<C .b c a <<D .c a b <<【答案】D【解析】解:()2510,13a ⎛⎫=∈ ⎪⎝⎭,4321b =>,21log 03c =<,则c a b <<. 故选:D .利用指数函数与对数函数的单调性即可得出.本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题. 5. 函数()ln 26f x x x =+-的零点一定位于下列哪个区间( ).A .()1,2B .()2,3C .()3,4D .()5,6【答案】B【解析】解:函数()ln 26f x x x =+-()140f =-<, ()2ln240f =-< ()3ln3ln10f =>=,()()230f f ∴<,∴函数的零点在()2,3上,故选:B .要求函数的零点所在的区间,根据所给的函数的解析式,把区间的端点代入函数的解析式进行验算,得到函数的值同0进行比较,在判断出区间两个端点的乘积是否小于0,得到结果.本题考查函数的零点的判定定理,本题解题的关键是做出区间的两个端点的函数值,本题是一个基础题.6. 已知角α的终边经过点()4,3P -,则tan 4πα⎛⎫+ ⎪⎝⎭的值等于( ).A .17-B .17C .37D .47【答案】B【解析】解:角α的终边经过点()4,3P -, 3tan 4α∴=-,则3tan tan1144tan 3471tan tan 144παπαπα+-+⎛⎫+=== ⎪⎝⎭-+. 故选:B .由角α的终边经过点.()4,3P -.,利用任意角的三角函数定义求出tan α的值,然后利用两角和与差的正切函数公式及特殊角的三角函数值化简所求的式子后,将tan α的值代入即可求出值.此题考查了两角和与差的正切函数公式,特殊角的三角函数值,以及任意角的三角函数定义,根据题意得出tan α的值是解本题的关键.7. 已知函数()()sin (,0,0,)2f x A x x R A πωϕωϕ=+∈>><的图象(部分)如图所示,则()f x 的解析式是( ).第10页,共23页A .()2sin 6f x x ππ⎛⎫=+ ⎪⎝⎭B .()2sin 26f x xππ⎛⎫=+ ⎪⎝⎭C .()2sin 3f x x ππ⎛⎫=+ ⎪⎝⎭D .()2sin 23f x x ππ⎛⎫=+ ⎪⎝⎭【答案】A【解析】解:根据图象判断:周期514263T ⎛⎫=⨯-= ⎪⎝⎭,2A =,22πωπ∴==, 12sin 23πϕ⎛⎫+= ⎪⎝⎭,1232k ππϕπ∴+=+,k z ∈, 26k πϕπ∴=+,k z ∈,2πϕ<, 6πϕ∴=.()2sin 6f x x ππ⎛⎫∴=+ ⎪⎝⎭故选:A .根据图象可得周期2T =,2A =,利用周期公式可求ω,利用12sin 23πϕ⎛⎫+= ⎪⎝⎭及ϕ的范围可求ϕ的值,即可确定函数解析式.本题考查了三角函数的图象和性质,考查了由()sin y A x ωϕ=+的部分图象确定其解析式,关键是据图确定参变量的值,属于中档题.8. 若两个非零向量a ,b 满足22b a ==,23a b +=,则a ,b 的夹角是( ).A .6πB .3π C .2π D .π【答案】D【解析】解:根据题意,设a ,b 的夹角是θ, 又由22b a ==,且23a b +=. , 则222(2)449a b a a b b +=+⋅+=, 即()1412cos 169θ+⨯+=, 解可得cos 1θ=-. , 则θπ=; 故选:D .根据题意,设a ,b . 的夹角是θ,由数量积的计算公式可得222(2)449a b a a b b +=+⋅+=,代入数据计算可得cos θ的值,结合的范围,分析可得答案.本题考查向量数量积的计算,关键是掌握由向量的数量积求向量夹角的方法.9.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积12=⨯(弦⨯矢+矢2),弧田(如图)由圆弧和其所对弦围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为23π,弧长为4π米的弧,按上述经公式计算()3173≈.,所得弧田面积约是( ).A .16平方米B .18平方米C .20平方米D .25平方米【答案】C【解析】解:如图,由题意可得:23AOB π∠=,弧长为4π米, 4623OA ππ∴==在Rt AOD 中,可得:3AOD π∠=,6DAO π∠=,116322OD AO ==⨯=, 可得:矢633=-=, 由3sin6333AD AO π=⋅=⨯=,第12页,共23页可得:弦223363AD ==⨯=,所以:弧田面积1(2=弦⨯矢+矢()221)63339345202=⨯+=+≈.平方米. 故选:C .在Rt AOD 中,由题意4OA =,6DAO π∠=,即可求得OD ,AD 的值,根据题意可求矢和弦的值,即可利用公式计算求值得解.本题考查扇形的面积公式,考查学生对题意的理解,考查学生的计算能力,属于中档题.10.偶函数()()f x x R ∈满足:()()520f f -==,且在区间[]0,3与[)3,+∞上分别递减和递增,则不等式()0x f x ⋅<的解集为( ). A .()()(),52,25,-∞-⋃-⋃+∞B .()()(),52,02,5-∞-⋃-⋃C .()()522,5--⋃.D .()()()5,20,25,--⋃⋃+∞【答案】B【解析】解:根据题意,()()000x x f x f x <⎧⋅<⇒>⎨⎩或()00x f x >⎧<⎨⎩,等价于求函数()y f x =的图象在第二、四象限时x 的取值范围.又由偶函数()()f x x R ∈满足()()520f f -==, 则()()()()52520f f f f =-=-==,且()f x 在区间[]0,3与[)3,+∞上分别递减与递增, 其草图为:即()2,5x ∈. 函数图象位于第四象限,()(),52,0x ∈-∞-⋃-函数图象位于第二象限.综上:()0x f x ⋅<的解集为:()()(),52,02,5-∞-⋃-⋃, 故选:B .偶函数关于y 轴对称的性质并结合题中给出函数的单调区间画出函数()f x 的图象,再由()0xf x <得到x 与()f x 异号得出结论本题考查函数的奇偶性与单调性的应用,关键是分析得到函数的图象草图.11. 已知锐角α满足cos cos24παα⎛⎫-= ⎪⎝⎭. ,则tan2α=( ).A .3B .3±C .3D .3±【答案】C【解析】解:锐角α满足cos cos24παα⎛⎫-= ⎪⎝⎭,2222cos sin cos sin αααα∴+=-,2cos sin 2αα∴-=,平方可得11sin22α-=,1sin22α=. cos sin αα>,04πα∴<<,2α∴还是锐角,故23cos21sin 2αα=-=, 则sin23tan2cos2ααα==, 故选:C .由题意利用同角三角函数的基本关系,二倍角公式,求得2cos sin αα-=,1sin22α=,判断 04πα<<,2α还是锐角,再求得cos2α的值,可得tan2α的值.本题主要考查同角三角函数的基本关系,二倍角公式,以及三角函数在各个象限中的符号,属于基础题.12.如图,在平行四边形ABCD 中,M 、N 分别为AB 、AD 上的点,且45AM AB =,23AN AD =,连接AC 、MN 交于P 点,若AP AC λ=,则λ的值为( ).A .35B .37C .411D .413. 【答案】C第14页,共23页【解析】解:45AM AB =,23AN AD =,()53534242AP AC AB AD AM AN AM AN λλλλλ⎛⎫∴==+=+=+ ⎪⎝⎭,三点M ,N ,P 共线. 53142λλ∴+=, 411λ∴=, 故选:C .根据向量的加减的几何意义和三点共线即可求出答案.本题考查了平面向量的线性运算,及三点共线的充要条件,属于中档题.二、填空题(本大题共4小题,共20.0分) 13.函数()()lg 1f x x =+的定义域是______. 【答案】(]1,1- 【解析】解:由题意, 可令1010x x -≥⎧⎨+>⎩,解得11x -<≤,∴函数()()lg 1f x x =+的定义域是(]1,1-故答案为:(]1,1-.由函数的解析式知,对数的真数大于0,偶次根号下非负,易得关于x 的不等式组,解出它的解集即可得到函数的定义域.本题考查求对数函数定义域,解题的关键是理解函数定义域的定义,找出自变量满足的不等式,解出定义域,本题中用到了对数的真数大于是,偶次根号下非负这些限制条件,属于是函数概念考查基本题.14.已知()1cos 3θπ+=-,则sin 22πθ⎛⎫+= ⎪⎝⎭______.【答案】79-【解析】解:()1cos 3θπ+=-,1cos 3θ∴=, 227sin 2cos22cos 11299πθθθ⎛⎫∴+==-=-=- ⎪⎝⎭,故答案为:79-根据诱导公式和二倍角公式即可求出.本题考查了诱导公式和二倍角公式,属于基础题.15.已知函数(),0ln ,0x e x f x x x ⎧≤=⎨>⎩,()()g x f x x a =++,若()g x 存在2个零点,则实数a 取值范围是______. 【答案】[)1,-+∞【解析】解:由()0g x =得()f x x a =--, 作出函数()f x 和y x a =--的图象如图: 当直线y x a =--的截距1a -≤,即1a ≥-时,两个函数的图象都有2个交点, 即函数()g x 存在2个零点, 故实数a 的取值范围是[)1,-+∞, 故答案为:[)1,-+∞.由()0g x =得()f x x a =--,分别作出两个函数的图象,根据图象交点个数与函数零点之间的关系进行转化求解即可.本题主要考查分段函数的应用,利用函数与零点之间的关系转化为两个函数的图象的交点问题是解决本题的关键.16.函数()2sin 23f x x π⎛⎫=- ⎪⎝⎭的图象为C ,如下结论中正确的是______.①图象C 关于直线1112x π=对称;第16页,共23页②图象C 关于点2,03π⎛⎫⎪⎝⎭对称; ③函数()f x 在区间5,1212ππ⎛⎫- ⎪⎝⎭内是增函数;④由2sin2y x =图象向右平移3π个单位长度可以得到图象C . 【答案】①②③【解析】解:函数()2sin 23f x x π⎛⎫=- ⎪⎝⎭,由1132sin 2122f ππ⎛⎫==- ⎪⎝⎭,为最小值,可得图象C 关于直线1112x π=对称,故①正确; 由22sin 03f ππ⎛⎫==⎪⎝⎭,图象C 关于点2,03π⎛⎫ ⎪⎝⎭对称,故②正确; 由5,1212x ππ⎛⎫∈- ⎪⎝⎭,可得2,322x πππ⎛⎫-∈- ⎪⎝⎭,即有()f x 在区间5,1212ππ⎛⎫- ⎪⎝⎭内是增函数,故③正确;由2sin2y x =图象向右平移3π个单位长度可以得到2sin23y x π⎛⎫=- ⎪⎝⎭的图象,故④错误.故答案为:①②③.由正弦函数的对称轴特点可判断①;由正弦函数的对称中心特点可判断②; 由正弦函数的增区间可判断③;由三角函数的图象变换特点可判断④.本题考查三角函数的图象和性质,考查函数的对称性和单调性、图象变换,考查运算能力,属于中档题.三、解答题(本大题共6小题,共70.0分) 17.已知向量()1,0a =,()1,1b =.(1)若22c =,且c b ⊥,求向量c 的坐标;(2)2AB a b =-,BC a mb =+,且A 、B 、C 三点共线,求实数m 的值. 【答案】解:()1设(),c x y =; c b ⊥,且22c =;0c b x y ∴⋅=+=①,228x y +=②;①②联立得,{22x y =-=,或{22x y ==-;()()2,2,2,2c ∴=--或;()()221,1AB a b =-=-,()1,BC a mb m m =+=+;A 、B 、C 三点共线;//AB BC ∴;10m m ∴++=;12m ∴=-.【解析】()1可设(),c x y =,根据c b ⊥及即可得出0x y +=①,228x y +=②,①②联立即可求出x ,y ,22c =即得出向量c 的坐标;()2可先求出()()1,1,1,AB BC m m =-=+,根据A 、B 、C 三点共线可得出//AB BC ,从而得出10m m ++=,解出m 即可.考查向量平行时的坐标关系,向量垂直的充要条件,以及向量坐标的数量积运算.18.已知函数()21mx n f x x +=+是定义在R 上的奇函数,且()225f =. (1)求函数()f x 的解析式;(2)判断函数()f x 在区间()0,1上的单调性,并用定义法证明. 【答案】解:()1根据题意,()225f =函数()21mx n f x x +=+是定义在R 上的奇函数,则()001nf ==,则0n =, 又由,则()2222125m f ==+,解可得1m =, 则()21xf x x =+, ()2由()1的结论,()21xf x x =+在()0,1上为增函数, 证明:1201x x <<<, 则()()()()()()121212122222121211111x x x x x x f x f x x x x x ---=-=++++又由1201x x <<<,第18页,共23页则()120x x -<,()1210x x ->,则有()()120f x f x -<,则函数()f x 在()0,1上为增函数. 【解析】()1根据题意,由奇函数的性质可得()001nf ==,则0n =,又由()2222125m f ==+,解可得m 的值,将m 、n 的值代入函数的解析式,计算可得答案; ()2根据题意,设1201x x <<<,由作差法分析可得答案.本题考查函数的奇偶性与单调性的性质以及应用,涉及单调性的判断,属于基础题.19.已知函数()2sin 26x f x π⎛⎫=+ ⎪⎝⎭.(1)求函数()f x 的最小正周期及单调递减区间;(2)先列表,并用描点法作出函数()f x 在[]0,4π上的简图. 【答案】(本题满分为12分) 解:()()1f x 的最小正周期为2412T ππ==;(4⋯分) 令3222262x k k πππππ+≤+≤+,k Z ∈,解得:284433k x k ππππ+≤≤+,k Z ∈,可得单调递减区间为:284,433k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈. ()2列表如下:连线成图如下:【解析】()1利用正弦函数的图象和性质即可求出()f x 的最小正周期与单调减区间;()2列表如下,作出它在[]0,4π上的简图即可;本题主要考查了五点法作函数()sin y A x ωϕ=+的图象,考查了正弦函数的图象和性质的应用,属于基础题.20.某家庭进行理财投资,根据长期收益率市场预测,投资债券类稳健型产品的收益与投资额成正比,投资股票类风险型产品的收益与投资额的算术平方根成正比.已知两类产品各投资1万元时的收益分别为0125.万元和05.万元,如图:(1)分别写出两类产品的收益(y 万元)与投资额(x 万元)的函数关系;(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,最大收益是多少万元?第20页,共23页【答案】解:(Ⅰ)投资债券类稳健型产品的收益满足函数:(0)y kx x =>, 由题知,当1x =时,0125y =.,则0125k =.,即0125y x =.,投资股票类风险型产品的收益满足函数:0)y k x =>, 由题知,当1x =时,05y =.,则05k =.,即, (Ⅱ)设投资债券类稳健型产品x 万元()020x ≤≤,则投资股票类风险型产品20x -万元,0y =由题知总收益)01250020y x x =+≤≤.,令0t t ≤≤,则220x t =-,()222115101252005(2)38228y t t t t t =-+=-++=--+..,当2t =,即16x =时,3(max y =万元)答:投资债券类稳健型产品16万元,投资股票类风险型产品4万元,此时受益最大为3万元.【解析】(Ⅰ)由投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,结合函数图象,我们可以利用待定系数法来求两种产品的收益与投资的函数关系;(Ⅱ)由(Ⅰ)的结论,我们投资债券类稳健型产品x 万元()020x ≤≤,则投资股票类风险型产品20x -万元.这时可以构造出一个关于收益y 的函数,然后利用求函数最大值的方法进行求解.函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x 取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.21.已知()2cos ,1a x =,()3sin cos ,1b x x =+-,函数()f x a b =⋅.(1)求函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值;(2)若()085f x =,0,42x ππ⎡⎤∈⎢⎥⎣⎦,求0cos2x 的值; (3)若函数()y f x ω=在区间2,33ππ⎛⎫ ⎪⎝⎭上是单调递增函数,求正数ω的取值范围. 【答案】解:()2cos ,1a x =,()3sin cos ,1b x x =+-, ())2cos cos 1f x a b x x x ∴=⋅=+-2cos 2cos 1x x x =+-cos22sin 26x x x π⎛⎫=+=+ ⎪⎝⎭()10,2x π⎡⎤∈⎢⎥⎣⎦, 72666x πππ∴≤+≤, 1sin 2126x π⎛⎫∴-≤+≤ ⎪⎝⎭, ∴函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值2,最小值1-; ()2若()085f x =,则082sin 265x π⎛⎫+= ⎪⎝⎭, 04sin 265x π⎛⎫∴+= ⎪⎝⎭, 0,42x ππ⎡⎤∈⎢⎥⎣⎦, 03cos 265x π⎛⎫∴+=- ⎪⎝⎭,00001cos2cos 22sin 266626x x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫∴=+-=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦314525⎛⎫=-+⨯= ⎪⎝⎭()()32sin 26y f x x πωω⎛⎫==+ ⎪⎝⎭, 令1122262k x k πππωππ-+≤+≤+,k z ∈, 可得,22233k k x ππππωωωω-+≤≤+ 令0k =可得,233x ππωω-≤≤, ()2sin 26y f x x πωω⎛⎫==+ ⎪⎝⎭,在区间2,33ππ⎛⎫ ⎪⎝⎭上是单调递增函数, 233ππω∴≥,解可得,102ω<≤. 【解析】由向量数量积的坐标表示,结合两角和的正弦公式可求()2sin 26f x x π⎛⎫=+ ⎪⎝⎭ ()1由0,2x π⎡⎤∈⎢⎥⎣⎦,结合正弦函数的性质可求函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值及最小值;第22页,共23页()2若()085f x =,可求02sin 26x π⎛⎫+ ⎪⎝⎭,结合同角平方关系可求0cos 26x π⎛⎫+ ⎪⎝⎭,然后由00cos2cos 266x x ππ⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦,利用两角差的余弦公式即可求解 ()3由()2sin 26y f x x πωω⎛⎫==+ ⎪⎝⎭,结合正弦函数的单调性可求单调递增区间,然后与区间2,33ππ⎛⎫ ⎪⎝⎭进行比较可求. 本题主要考查了向量的数量积的运算性质及两角和的余弦公式,正弦函数的性质的灵活应用是求解本题的关键.22.已知函数()221(0)g x ax ax b a =-++>在区间[]1,1-上有最大值4和最小值0.设()()g x f x x =.(1)求实数a ,b 的值;(2)若不等式()0f x k x -⋅≥在()0,x ∈+∞上恒成立,求实数k 的取值范围;(3)若()2213021x x f k k -+⋅-=-有三个不同的实数解,求实数k 的取值范围. 【答案】解:()1函数()2221(1)1g x ax ax b a x b a =-++=-++-,因为0a >,所以()g x 在区间[]1,1-上是减函数,故()1314g a b -=++=,()110g b a =+-=,解得1a =,0b =;()2由()0f x k x -⋅≥即为22210x x kx -+-≥, 即为21(1)k x≤-在0x >恒成立, 由21(1)0x-≥,当且仅当1x =时取得最小值0, 所以k 的取值范围是(],0-∞;()3方程()2213021x k f k k -+⋅-=-可化为: ()()221|2321|120x x k k --+-++=,210x -≠,令21x t -=,则方程化为()()()2231200t k t k t -+++=≠, 方程()2213021k k f k k -+⋅⋅-=-有三个不同的实数解, ∴由21x t =-的图象知,()()()2231200t k t k t -+++=≠,有两个根1t 、2t ,且1201t t <<<或101t <<,21t =.记()()()22312h t t k t k =-+++,则()()012010h k h k =+>⎧⎪=-<⎨⎪⎩,或()()01201023012h k h k k ⎧⎪=+>⎪=-=⎨⎪+⎪<<⎩, 0k ∴>.【解析】()1由函数()2(1)1g x a x b a =-++-,0a >,所以()g x 在区间[]1,1-上是减函数,故()14g -=,()10g =,由此解得a 、b 的值;()2不等式可化为21(1)k x≤-在0x >恒成立,由平方数非负可得不等式右边的最小值,从而求得k 的取值范围;()3方程()()()22213021|2321|12021x x x k f k k k k -+⋅-=⇒--+-++=-,()210x -≠,令21x t -=,则()()()2231200t k t k t -+++=≠,构造函数()()()22312h t t k t k =-+++. ,通过数形结合与等价转化的思想即可求得k 的范围.本题考查二次函数在闭区间上的最值,考查函数恒成立问题问题,考查数形结合与等价转化、函数与方程思想的综合应用,属于难题.。
2018-2019学度广州天河区高一上年末数学试卷(含解析解析).doc.doc

2018-2019学度广州天河区高一上年末数学试卷(含解析解析)注意事项:认真阅读理解,结合历年的真题,总结经验,查找不足!重在审题,多思考,多理解!无论是单选、多选还是论述题,最重要的就是看清题意。
在论述题中,问题大多具有委婉性,尤其是历年真题部分,在给考生较大发挥空间的同时也大大增加了考试难度。
考生要认真阅读题目中提供的有限材料,明确考察要点,最大限度的挖掘材料中的有效信息,建议考生答题时用笔将重点勾画出来,方便反复细读。
只有经过仔细推敲,揣摩命题老师的意图,积极联想知识点,分析答题角度,才能够将考点锁定,明确题意。
【一】选择题1、〔5分〕设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},那么A∩〔∁UB〕=〔〕A、{1,2,5,6}B、{1,2,3,4}C、{2}D、{1}2、〔5分〕直线x﹣y+3=0的倾斜角是〔〕A、30°B、45°C、60°D、150°3、〔5分〕以下函数在其定义域上既是奇函数又是减函数的是〔〕A、f〔x〕=2xB、f〔x〕=log xC、f〔x〕=D、f〔x〕=﹣x|x|4、〔5分〕在长方体ABCD﹣A1B1C1D1中,AB=BC=,AA1=1,那么异面直线AD与BC1所成角为〔〕A、30°B、45°C、60°D、90°5、〔5分〕直线l1的方程为Ax+3y+C=0,直线l2的方程为2x﹣3y+4=0,假设l1与l2的交点在y轴上,那么C的值为〔〕A、4B、﹣4C、±4D、与A有关6、〔5分〕设a=40.1,b=log30.1,c=0.50.1,那么〔〕A、a》b》cB、a》c》bC、b》a》cD、b》c》a7、〔5分〕圆x2+y2+2x﹣2y+2a=0截直线x+y+2=0所得弦长为4,那么实数a的值是〔〕A、﹣4B、﹣3C、﹣2D、﹣18、〔5分〕一个几何体的三视图如下图,那么该几何体的表面积为〔〕A、3πB、4πC、2π+4D、3π+49、〔5分〕函数的零点所在的区间为〔〕A、B、C、D、10、〔5分〕过点A〔3,5〕作圆〔x﹣2〕2+〔y﹣3〕2=1的切线,那么切线的方程为〔〕A、x=3或3x+4y﹣29=0B、y=3或3x+4y﹣29=0C、x=3或3x﹣4y+11=0D、y=3或3x﹣4y+11=011、〔5分〕三棱柱ABC﹣A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,假设该棱柱的体积为,BC=,AC=1,∠ACB=90°,那么此球的体积等于〔〕A、πB、πC、πD、8π12、〔5分〕定义在R上的函数f〔x〕满足:①f〔x〕+f〔2﹣x〕=0;②f〔x ﹣2〕=f〔﹣x〕,③在【﹣1,1】上表达式为f〔x〕=,那么函数f〔x〕与函数g〔x〕=的图象在区间【﹣3,3】上的交点个数为〔〕A、5B、6C、7D、8【二】填空题13、〔5分〕函数y=ln〔1﹣2x〕的定义域是、14、〔5分〕设函数f〔x〕=,那么f〔f〔﹣4〕〕=、15、〔5分〕假设直线〔a+1〕x+ay=0与直线ax+2y=1垂直,那么实数a=、16、〔5分〕α,β是两个平面,m,n是两条直线,那么以下四个结论中,正确的有〔填写所有正确结论的编号〕①假设m∥α,n∥α,那么m∥n;②假设m⊥α,n∥α,那么m⊥n;③假设a∥β,m⊂α,那么m∥β;④假设m⊥n、m⊥α,n∥β,那么α⊥β【三】解答题17、〔10分〕平面内两点A〔8,﹣6〕,B〔2,2〕、〔Ⅰ〕求过点P〔2,﹣3〕且与直线AB平行的直线l的方程;〔Ⅱ〕求线段AB的垂直平分线方程、18、〔12分〕如图,四棱锥P﹣ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点、〔1〕求证:PC∥平面BDE〔2〕求三棱锥P﹣CED的体积、19、〔12分〕函数f〔x〕=2x+2ax〔a为实数〕,且f〔1〕=、〔1〕求函数f〔x〕的解析式;〔2〕判断函数f〔x〕的奇偶性并证明;〔3〕判断函数f〔x〕在区间【0,+∞〕的单调性,并用定义证明、20、〔12分〕如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,CAB=90°,AB=AC=2,AA1=,M为BC的中点,P为侧棱BB1上的动点、〔1〕求证:平面APM⊥平面BB1C1 C;〔2〕试判断直线BC1与AP是否能够垂直、假设能垂直,求PB的长;假设不能垂直,请说明理由、21、〔12分〕半径为的圆C,其圆心在射线y=﹣2x〔x《0〕上,且与直线x +y+1=0相切、〔1〕求圆C的方程;〔2〕从圆C外一点P〔x0,y〕〕向圆引切线PM,M为切点,O为坐标原点,且有|PM|=|PO|,求△PMC面积的最小值,并求此时点P的坐标、22、〔12分〕a∈R,函数f〔x〕=log2〔+a〕、〔1〕假设f〔1〕《2,求实数a的取值范围;〔2〕设函数g〔x〕=f〔x〕﹣log2【〔a﹣4〕x+2a﹣5】,讨论函数g〔x〕的零点个数、2016-2017学年广东省广州市天河区高一〔上〕期末数学试卷参考答案与试题解析【一】选择题1、〔5分〕设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},那么A∩〔∁UB〕=〔〕A、{1,2,5,6}B、{1,2,3,4}C、{2}D、{1}【解答】解:∵全集U={1,2,3,4,5,6},B={2,3,4},∴∁UB={1,5,6},又∵A={1,2},∴A∩〔∁UB〕={1},应选:D、2、〔5分〕直线x﹣y+3=0的倾斜角是〔〕A、30°B、45°C、60°D、150°【解答】解:设直线x﹣y+3=0的倾斜角为θ、由直线x﹣y+3=0化为y=x+3,∴tanθ=,∵θ∈【0,π〕,∴θ=60°、应选C、3、〔5分〕以下函数在其定义域上既是奇函数又是减函数的是〔〕A、f〔x〕=2xB、f〔x〕=log xC、f〔x〕=D、f〔x〕=﹣x|x|【解答】解:对于A,B,非奇非偶函数;对于C,是奇函数,不是定义域上的减函数;对于D,在其定义域上既是奇函数又是减函数,应选:D、4、〔5分〕在长方体ABCD﹣A1B1C1D1中,AB=BC=,AA1=1,那么异面直线AD与BC1所成角为〔〕A、30°B、45°C、60°D、90°【解答】解:如图,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,A〔〕,D〔0,0,0〕,B〔,0〕,C1〔0,,1〕,=〔﹣〕,=〔﹣,0,1〕,设异面直线AD与BC1所成角为θ,那么cosθ===、∴θ=30°、∴异面直线AD与BC1所成角为30°、应选:A、5、〔5分〕直线l1的方程为Ax+3y+C=0,直线l2的方程为2x﹣3y+4=0,假设l1与l2的交点在y轴上,那么C的值为〔〕A、4B、﹣4C、±4D、与A有关【解答】解:直线2x﹣3y+4=0与y轴的交点〔0,〕,代入直线Ax+3y+C=0,可得4+C=0,解得C=﹣4、应选B、6、〔5分〕设a=40.1,b=log30.1,c=0.50.1,那么〔〕A、a》b》cB、a》c》bC、b》a》cD、b》c》a【解答】解:∵a=40.1》1,b=log30.1《0,0《c=0.50.1《1,∴a》c》B、应选:B、7、〔5分〕圆x2+y2+2x﹣2y+2a=0截直线x+y+2=0所得弦长为4,那么实数a的值是〔〕A、﹣4B、﹣3C、﹣2D、﹣1【解答】解:圆x2+y2+2x﹣2y+2a=0即〔x+1〕2+〔y﹣1〕2=2﹣2a,故弦心距d==、再由弦长公式可得2﹣2a=2+4,∴a=﹣2,应选:C、8、〔5分〕一个几何体的三视图如下图,那么该几何体的表面积为〔〕A、3πB、4πC、2π+4D、3π+4【解答】解:由中的三视图可得,该几何体是以俯视图为底面的半圆柱,底面半径为1,高为2,故该几何体的表面积S=2×π+〔2+π〕×2=3π+4,应选:D9、〔5分〕函数的零点所在的区间为〔〕A、B、C、D、【解答】解:函数在〔0,+∞〕上单调递增、因为,,,,所以,所以根据根的存在性定理可知函数的零点所在的区间为、应选D、10、〔5分〕过点A〔3,5〕作圆〔x﹣2〕2+〔y﹣3〕2=1的切线,那么切线的方程为〔〕A、x=3或3x+4y﹣29=0B、y=3或3x+4y﹣29=0C、x=3或3x﹣4y+11=0D、y=3或3x﹣4y+11=0【解答】解:由圆的一般方程可得圆的圆心与半径分别为:〔2,3〕;1,当切线的斜率存在,设切线的斜率为k,那么切线方程为:kx﹣y﹣3k+5=0,由点到直线的距离公式可得:=1解得:k=,所以切线方程为:3x+4y﹣29=0;当切线的斜率不存在时,直线为:x=3,满足圆心〔2,3〕到直线x=3的距离为圆的半径1,x=3也是切线方程;应选A、11、〔5分〕三棱柱ABC﹣A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,假设该棱柱的体积为,BC=,AC=1,∠ACB=90°,那么此球的体积等于〔〕A、πB、πC、πD、8π【解答】解:∵三棱柱ABC﹣A1B1C1的侧棱垂直于底面,棱柱的体积为,BC=,AC=1,∠ACB=90°,∴AA1=∴AA1=2,∵BC=,AC=1,∠ACB=90°,△ABC外接圆的半径R=1,∴外接球的半径为=,∴球的体积等于=π,应选:C、12、〔5分〕定义在R上的函数f〔x〕满足:①f〔x〕+f〔2﹣x〕=0;②f〔x ﹣2〕=f〔﹣x〕,③在【﹣1,1】上表达式为f〔x〕=,那么函数f〔x〕与函数g〔x〕=的图象在区间【﹣3,3】上的交点个数为〔〕A、5B、6C、7D、8【解答】解:由f〔x〕+f〔2﹣x〕=0,可得函数f〔x〕的图象关于点M〔1,0〕对称、由f〔x﹣2〕=f〔﹣x〕,可得函数f〔x〕的图象关于直线x=﹣1对称、又在【﹣1,1】上表达式为f〔x〕=,可得图象:进而得到在区间【﹣3,3】上的图象、画出函数g〔x〕=在区间【﹣3,3】上的图象,其交点个数为6个、应选:B、【二】填空题13、〔5分〕函数y=ln〔1﹣2x〕的定义域是{x|x《}、【解答】解:根据题意:1﹣2x》0∴x《故答案为:{x|x《}14、〔5分〕设函数f〔x〕=,那么f〔f〔﹣4〕〕=3、【解答】解:∵f〔x〕=,∴f〔﹣4〕=〔〕﹣4﹣7=9,f〔f〔﹣4〕〕=f〔9〕==3、故答案为:3、15、〔5分〕假设直线〔a+1〕x+ay=0与直线ax+2y=1垂直,那么实数a=0或﹣3、【解答】解:当a=0时,两条直线方程分别化为:x=0,2y=1,此时两条直线垂直,因此a=0满足条件、当a≠0时,两条直线的斜率分别为﹣,﹣,而﹣•〔﹣〕=﹣1,此时a=﹣3、综上可得:a=0或﹣3、故答案为:0或﹣3、16、〔5分〕α,β是两个平面,m,n是两条直线,那么以下四个结论中,正确的有②③〔填写所有正确结论的编号〕①假设m∥α,n∥α,那么m∥n;②假设m⊥α,n∥α,那么m⊥n;③假设a∥β,m⊂α,那么m∥β;④假设m⊥n、m⊥α,n∥β,那么α⊥β【解答】解:①假设m∥α,n∥α,那么m与n的关系不确定,故错误;②如果m⊥α,n∥α,那么平面α内存在直线l使,m⊥l,n∥l,故m⊥n,故正确;③如果α∥β,m⊂α,那么m与β无公共点,那么m∥β,故正确;④如果m⊥n,m⊥α,n∥β,那么α与β的关系不确定,故错误;故答案为:②③、【三】解答题17、〔10分〕平面内两点A〔8,﹣6〕,B〔2,2〕、〔Ⅰ〕求过点P〔2,﹣3〕且与直线AB平行的直线l的方程;〔Ⅱ〕求线段AB的垂直平分线方程、【解答】解:〔Ⅰ〕因为,…〔2分〕所以由点斜式得直线l的方程4x+3y+1=0…〔4分〕〔Ⅱ〕因为AB的中点坐标为〔5,﹣2〕,AB的垂直平分线斜率为…〔6分〕所以由点斜式得AB的中垂线方程为3x﹣4y﹣23=0…〔8分〕18、〔12分〕如图,四棱锥P﹣ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点、〔1〕求证:PC∥平面BDE〔2〕求三棱锥P﹣CED的体积、【解答】证明:〔1〕连结AC、BD,交于点O,连结OE,∵四棱锥P﹣ABCD的底面是边长为1的正方形,∴O是AC中点,∵E是侧棱PA的中点,∴OE∥PC,∵PC⊄平面BDE,OE⊂平面BDE,∴PC∥平面BDE、解:〔2〕∵四棱锥P﹣ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点,∴PA⊥CD,AD⊥CD,∵PA∩AD=A,∴CD⊥平面PAD,∵S△PDE===,∴三棱锥P﹣CED的体积VP﹣CED =VC﹣PDE===、19、〔12分〕函数f 〔x 〕=2x +2ax 〔a 为实数〕,且f 〔1〕=、 〔1〕求函数f 〔x 〕的解析式;〔2〕判断函数f 〔x 〕的奇偶性并证明;〔3〕判断函数f 〔x 〕在区间【0,+∞〕的单调性,并用定义证明、 【解答】解:〔1〕∵f 〔x 〕=2x +2ax 〔a 为实数〕,且f 〔1〕=、 ∴f 〔1〕=2+2a =、得2a =,即a =﹣1, 那么函数f 〔x 〕的解析式f 〔x 〕=2x +2﹣x ; 〔2〕f 〔﹣x 〕=2﹣x +2x =﹣〔2x ﹣2﹣x 〕=f 〔x 〕, 那么函数f 〔x 〕是偶函数、〔3〕设0≤x 1《x 2,f 〔x 1〕﹣f 〔x 2〕=﹣﹣+=〔﹣〕〔1﹣〕=〔﹣〕,∵y =2x 是增函数,∴﹣《0,当x 》0时,》1,那么﹣1》0,∴f 〔x 1〕﹣f 〔x 2〕《0,即f 〔x 1〕《f 〔x 2〕,函数f 〔x 〕是增函数、20、〔12分〕如图,在三棱柱ABC ﹣A 1B 1C 1中,AA 1⊥底面ABC ,CAB =90°,AB =AC =2,AA 1=,M 为BC 的中点,P 为侧棱BB 1上的动点、 〔1〕求证:平面APM ⊥平面BB 1C 1C ;〔2〕试判断直线BC 1与AP 是否能够垂直、假设能垂直,求PB 的长;假设不能垂直,请说明理由、【解答】证明:〔1〕∵在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,CAB=90°,AB=AC=2,AA1=,M为BC的中点,P为侧棱BB1上的动点、∴AM⊥BC,AM⊥BB1,∵BC∩BB1=B,∴AM⊥平面BB1C1C,∵AM⊂平面APM,∴平面APM⊥平面BB1C1 C、解:〔2〕以A为原点,AC为x轴,AB为y轴,AA1为z轴,建立空间直角坐标系,B〔0,2,0〕,C1〔2,0,〕,A〔0,0,0〕,设BP=t,〔0〕,那么P〔0,2,t〕,=〔2,﹣2,〕,=〔0,2,t〕,假设直线BC1与AP能垂直,那么,解得t=,∵t=》BB1=,∴直线BC1与AP不能垂直、21、〔12分〕半径为的圆C,其圆心在射线y=﹣2x〔x《0〕上,且与直线x +y+1=0相切、〔1〕求圆C的方程;〔2〕从圆C外一点P〔x0,y〕〕向圆引切线PM,M为切点,O为坐标原点,且有|PM|=|PO|,求△PMC面积的最小值,并求此时点P的坐标、【解答】解:〔1〕圆的半径为,设圆心C〔a,﹣2a〕〔a《0〕,∵圆心到直线x+y+1=0的距离d=,∴a=﹣1、∴圆心C〔﹣1,2〕、那么圆的方程为:〔x+1〕2+〔y﹣2〕2=2;〔2〕点P〔x0,y〕,那么PO=,PM=,由|PM|=|PO|,得2x0﹣4y+3=0,PM=PO====、当时,PM=、因此,PM的最小值为、△PMC面积的最小值是:=、此时点P的坐标为〔,〕、22、〔12分〕a∈R,函数f〔x〕=log2〔+a〕、〔1〕假设f〔1〕《2,求实数a的取值范围;〔2〕设函数g〔x〕=f〔x〕﹣log2【〔a﹣4〕x+2a﹣5】,讨论函数g〔x〕的零点个数、【解答】解:〔1〕假设f〔1〕《2,那么log2〔1+a〕《2,即0《1+a《4,解得:a∈〔﹣1,3〕;〔2〕令函数g〔x〕=f〔x〕﹣log2【〔a﹣4〕x+2a﹣5】=0,那么f〔x〕=log2【〔a﹣4〕x+2a﹣5】,即+a=〔a﹣4〕x+2a﹣5,即〔a﹣4〕x2+〔a﹣5〕x﹣1=0,①当a=4时,方程可化为:﹣x﹣1=0,解得:x=﹣1,此时+a=〔a﹣4〕x+2a﹣5=3,满足条件,即a=4时函数g〔x〕有一个零点;②当〔a﹣5〕2+4〔a﹣4〕=0时,a=3,方程可化为:﹣x2﹣2x﹣1=0,解得:x=﹣1,此时+a=〔a﹣4〕x+2a﹣5=2,满足条件,即a=3时函数g〔x〕有一个零点;③当〔a﹣5〕2+4〔a﹣4〕》0时,a≠3,方程有两个根,x=﹣1,或x=,当x=﹣1时,+a=〔a﹣4〕x+2a﹣5=a﹣1,当a》1时,满足条件,当x=时,+a=〔a﹣4〕x+2a﹣5=2a﹣4,当a》2时,满足条件,综上可得:1《a≤2时,函数g〔x〕有一个零点;a》2且a≠3且a≠4时函数g〔x〕有两个零点;。
广州市天河区2018-2019学年第一学期人教版五年级数学上册期末试卷
学校:____________________ _______年_______班 姓名:____________________ 学号:________- - - - - - - - - 密封线 - - - - - - - - - 密封线 - - - - - - - - -2018学年第一学期广州市天河区期末水平测试五年级数学试卷(2019.01)(全卷共7页,满分100分,90分钟完成)题号 一 二 三 总分分数一、 单选题。
(选择正确答案的编号填在括号里)(每小题2分,共20分) 1. 在一个纸箱里装有25个红球,15个篮球,10个黄球和8个白球,它们的形状、大小、质量完全相同。
欢欢从箱子任意摸出一个球,拿到( )的可能性最大?A .黄球 B. 篮球 C. 红球 D. 白球 2. 下面的小数中,( )是循环小数。
① 0.15 ② 3.1415926…… ③ 2.363636363636 ④ 2.4747……A .②④ B. ①③ C. ③④ D. ①④3. 每支铅笔0.2元,买8支需要多少元?正确的列式是( )。
A. 0.2+8B. 8-0.2C. 0.2×8D. 0.2÷8 4. 用方程表示下面的等量关系,正确的是( )。
A . 45加上x 等于80。
用方程表示:45x =80B . x 减去20的差是65。
用方程表示:65-x =20C . x 的9倍是27。
用方程表示:x ÷9=27D . x 除以5的商是90。
x ÷5=905. x =8是下面哪个方程的解?( )。
A .8x =40 B. 70+2x =86 C. 5x -3×2=74 D. 10×(x +11)=916. 母亲的年龄比儿子大25岁,今年母亲的年龄恰好是儿子年龄的3倍,儿子今年多少岁?解:设儿子今年x 岁,依题意列方程,正确的是( )。
A .3x -25-x B. 3x =25 C. 3x -x =25 D. 3x +x =257. 张阿姨家今年种的橘子大丰收。
2018-2019--天河区六年级上学期期末考英语试题复习进程

2018-2019--天河区六年级上学期期末考英语试题2018-2019 6上天河英语期末考试六、词汇归类。
把下列词汇分类,并将其字母编号写在相应的表格内。
(10分)A. Easter B chips C. poor D. tookE. candy E. broken G. jiaozi H . stomachacheI. fever J. Halloween K.came L. Dragon Boat FestivalM. read N. toothache O. simple P. crowdedQ. bought R. headache S. ham T. Chongyang Festival七、单词拼写。
根据示情境(第1-5题)或中文提示(第6-10题),补充完整,每空一词。
(10分)1. My mother asked me to take this m t a day.2.The boy s a f with his parents yesterday.3. When I lived in the countryside, I r a b to school every day.4. During Spring Festival, parents usually give children l m .5. The girl liked to watch TV before, but now she likes to s the I .6. The doctor g me c last Friday.(给…做检查)7. I will m this c after I wake up tomorrow.(挤牛奶)8. In the past, the r in the countryside was very d .(河流很脏)9. At Christmas people like to give e o gifts.(互相)10. Uncle Li says we should drink a l eight glasses of water every day.(至少)八、单项选择。
2018-2019学年广东省广州市天河区六年级(上)期末语文试卷

你好,清凉的山泉!你捧一面明镜,是要我重新梳妆吗?你好,汩汩的溪流!你吟 诵着一首首小诗,是邀我与你唱和吗?你好,飞流的瀑布!你天生的金嗓子,雄浑的男
高音多么有气势。你好,陡峭的悬崖!深深的峡谷衬托着你挺拔的身躯,你高高的额头
上仿佛刻满了智慧……
﹣﹣选自《山中访友》
(1)这段话采用了第几人称的叙述方法?这样写有什么好处?
一篇文章,题目自拟。不少于 400 字。
第 5 页(共 6 页)
2018-2019 学年广东省广州市天河区六年级(上)期末语
文试卷
一、积累与运用. (共 40 分)
参考答案
1. B ;A ; B; A ; 2. B; A ; A ; B ; 二、选择题
3. D ; 4. C; 三、填空题
5. C; D; A ;B ; 6.奥秘;阻挠;严肃;恩赐;眷恋;团聚;苍茫;纯熟;
(1)怅.望
A .zhǎng
B. chàng
(2)扁.舟
A .piān
B. biǎn
(3)憎.恶
A .zèng
B. zēng
(4)塑.料
A .sù
B. suò
2.( 4 分)判断下列各题,说法正确的写“ A ”,错误的写“ B”。 (1)《少年闰土》一文出自鲁迅的小说《狂人日记》 。 (2)诗人杜甫敏锐地抓住雨的特征, 写下了 《春夜喜雨》 这首诗。 诗中没有一个 “喜” 字,
D .虽然太阳离我们太远了,但是看上去只有盘子那么大。 三、填空题
5.( 4 分)朗读下面的句子应分别读出怎样的语气?将正确的答案填写在括号里。 A 、体谅,安慰 B 、担心,祈求 C、伤感,难过 D 、激动,欢喜 (1)波农丁皱着眉头说: “它要离开我们去象冢了。 ”(《最后一头战象》 ) (2)我结结巴巴地说: “哦!您,您就是……” (《一面》)
2018-2019学年广东省广州市天河区高一上学期期末考试数学试题(解析版)

2018-2019学年广东省广州市天河区高一上学期期末考试数学试题(解析版)一、选择题(本大题共12小题,共60.0分)1. 设全集U ={1,2,3,4},集合S ={1,3},T ={4},则(∁U S )∪T 等于( )A. {2,4}B. {4}C. ⌀D. {1,3,4} 【答案】A【解析】解:∵全集U ={1,2,3,4},集合S ={l ,3},T ={4}, ∴(∁U S )∪T ={2,4}∪{4}={2,4}. 故选:A .利用集合的交、并、补集的混合运算求解.本题考查集合的交、并、补集的混合运算,是基础题,解题时要认真审题.2. 已知向量a =(x ,1),b =(1,−2),若a //b ,则a +b =( )A. (12,−1)B. (12,1)C. (3,−1)D. (3,1)【答案】A【解析】解:∵a //b; ∴−2x −1=0; ∴x =−12; ∴a =(−12,1);∴a +b =(12,−1).故选:A .根据a //b 即可得出x =−12,从而得出a =(−12,1),这样即可求出a +b 的坐标. 考查平行向量的坐标关系,以及向量坐标的加法运算. 3.已知函数f (x )= 3x ,x ≤0log 2x ,x >0,则f (f (14))的值是( )A. −19B. −9C. 19D. 9【答案】C【解析】解:∵函数f (x )= 3x ,x ≤0log 2x ,x >0, ∴f (14)=log 214=−2, f (f (14))=f (−2)=3−2=19. 故选:C .由已知得f (14)=log 214=−2,从而f (f (14))=f (−2),由此能求出结果.本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.4. 设a=(13) 25,b=24,c=log213,则()A. b<a<cB. a<b<cC. b<c<aD. c<a<b 【答案】D【解析】解:∵a=(13) 25∈(0,1),b=243>1,c=log213<0,则c<a<b.故选:D.利用指数函数与对数函数的单调性即可得出.本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.5. 函数f(x)=ln x+2x−6的零点一定位于下列哪个区间()A. (1,2)B. (2,3)C. (3,4)D. (5,6)【答案】B【解析】解:∵函数f(x)=ln x+2x−6f(1)=−4<0,f(2)=ln2−4<0f(3)=ln3>ln1=0,∴f(2)f(3)<0,∴函数的零点在(2,3)上,故选:B.要求函数的零点所在的区间,根据所给的函数的解析式,把区间的端点代入函数的解析式进行验算,得到函数的值同0进行比较,在判断出区间两个端点的乘积是否小于0,得到结果.本题考查函数的零点的判定定理,本题解题的关键是做出区间的两个端点的函数值,本题是一个基础题.6. 已知角α的终边经过点P(−4,3),则tan(α+π4)的值等于()A. −17B. 17C. 37D. 47【答案】B【解析】解:∵角α的终边经过点P(−4,3),∴tanα=−34,则tan(α+π4)=tanα+tanπ41−tanαtanπ4=−34+11+3=17.故选:B.由角α的终边经过点P(−4,3),利用任意角的三角函数定义求出tanα的值,然后利用两角和与差的正切函数公式及特殊角的三角函数值化简所求的式子后,将tanα的值代入即可求出值.此题考查了两角和与差的正切函数公式,特殊角的三角函数值,以及任意角的三角函数定义,根据题意得出tanα的值是解本题的关键.7. 已知函数f(x)=A sin(ωx+φ)(x∈R,A>0,ω>0,φ<π2)的图象(部分)如图所示,则f(x)的解析式是()A. f(x)=2sin(πx+π6) B. f(x)=2sin(2πx+π6)C. f(x)=2sin(πx+π3) D. f(x)=2sin(2πx+π3)【答案】A【解析】解:∵根据图象判断:周期T=4×(56−13)=2,A=2,∴ω=2π2=π,∵2sin(13π+φ)=2,∴13π+φ=2kπ+π2,k∈z,∴φ=2kπ+π6,k∈z,∵φ<π2,∴φ=π6.∴f(x)=2sin(πx+π)故选:A.根据图象可得周期T=2,A=2,利用周期公式可求ω,利用2sin(13π+φ)=2及φ的范围可求φ的值,即可确定函数解析式.本题考查了三角函数的图象和性质,考查了由y=A sin(ωx+φ)的部分图象确定其解析式,关键是据图确定参变量的值,属于中档题.8. 若两个非零向量a,b满足b=2 a=2,a+2b=3,则a,b的夹角是()A. π6B. π3C. π2D. π【答案】D【解析】解:根据题意,设a,b的夹角是θ,又由b=2 a=2,且a+2b=3,则(a+2b)2=a2+4a⋅b+4b2=9,即1+4(1×2cosθ)+16=9,解可得cosθ=−1,则θ=π; 故选:D .根据题意,设a ,b 的夹角是θ,由数量积的计算公式可得(a +2b )2=a 2+4a ⋅b +4b 2=9,代入数据计算可得cos θ的值,结合的范围,分析可得答案.本题考查向量数量积的计算,关键是掌握由向量的数量积求向量夹角的方法.9. 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=12×(弦×矢+矢 2),弧田(如图)由圆弧和其所对弦围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为2π3,弧长为4π米的弧,按上述经公式计算( 3≈1.73),所得弧田面积约是( )A. 16平方米B. 18平方米C. 20平方米D. 25平方米【答案】C【解析】解:如图,由题意可得:∠AOB =2π3,弧长为4π米,∴OA =4π2π3=6在Rt △AOD 中,可得:∠AOD =π3,∠DAO =π6,OD =12AO =12×6=3, 可得:矢=6−3=3,由AD =AO ⋅sin π3=6× 32=3 3,可得:弦=2AD =2×3 3=6 3,所以:弧田面积=12(弦×矢+矢 2)=12(6 3×3+32)=9 3+4.5≈20平方米. 故选:C .在Rt △AOD 中,由题意OA =4,∠DAO =π6,即可求得OD ,AD 的值,根据题意可求矢和弦的值,即可利用公式计算求值得解.本题考查扇形的面积公式,考查学生对题意的理解,考查学生的计算能力,属于中档题.10. 偶函数f (x )(x ∈R )满足:f (−5)=f (2)=0,且在区间[0,3]与[3,+∞)上分别递减和递增,则不等式x ⋅f (x )<0的解集为( ) A. (−∞,−5)∪(−2,2)∪(5,+∞) B. (−∞,−5)∪(−2,0)∪(2,5) C. (−5.−2)∪(2,5) D. (−5,−2)∪(0,2)∪(5,+∞) 【答案】B【解析】解:根据题意,x ⋅f (x )<0⇒ f (x )>0x <0或 f (x )<0x >0,等价于求函数y =f (x )的图象在第二、四象限时x 的取值范围.又由偶函数f (x )(x ∈R )满足f (−5)=f (2)=0, 则f (5)=f (−2)=f (−5)=f (2)=0,且f(x)在区间[0,3]与[3,+∞)上分别递减与递增,其草图为:即x∈(2,5)函数图象位于第四象限,x∈(−∞,−5)∪(−2,0)函数图象位于第二象限.综上:x⋅f(x)<0的解集为:(−∞,−5)∪(−2,0)∪(2,5),故选:B.利用偶函数关于y轴对称的性质并结合题中给出函数的单调区间画出函数f(x)的图象,再由xf(x)<0得到x与f(x)异号得出结论本题考查函数的奇偶性与单调性的应用,关键是分析得到函数的图象草图.11. 已知锐角α满足cos(α−π4)=cos2α,则tan2α=()A. 3B. ±3C. 33D. ±33【答案】C【解析】解:∵锐角α满足cos(α−π4)=cos2α,∴22cosα+22sinα=cos2α−sin2α,∴cosα−sinα=22,平方可得1−sin2α=12,sin2α=12.∵cosα>sinα,∴0<α<π4,∴2α还是锐角,故cos2α=22α=32,则tan2α=sin2αcos2α=33,故选:C.由题意利用同角三角函数的基本关系,二倍角公式,求得cosα−sinα=22,sin2α=12,判断0<α<π4,2α还是锐角,再求得cos2α的值,可得tan2α的值.本题主要考查同角三角函数的基本关系,二倍角公式,以及三角函数在各个象限中的符号,属于基础题.12. 如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且AM=45AB,AN=23AD,连接AC、MN交于P点,若AP=λAC,则λ的值为()A. 35B. 37C. 411D. 413【答案】C【解析】解:∵AM=45AB,AN=23AD,连∴AP=λAC=λ(AB+AD)=λ(54AM+32AN)=54λAM+32λAN,∵三点M,N,P共线.∴54λ+32λ=1,∴λ=411,故选:C .根据向量的加减的几何意义和三点共线即可求出答案.本题考查了平面向量的线性运算,及三点共线的充要条件,属于中档题.二、填空题(本大题共4小题,共20.0分)13. 函数f (x )= 1−x +lg(x +1)的定义域是______. 【答案】(−1,1]【解析】解:由题意, 可令 x +1>01−x≥0,解得−1<x ≤1,∴函数f (x )= 1−x +lg(x +1)的定义域是(−1,1] 故答案为:(−1,1].由函数的解析式知,对数的真数大于0,偶次根号下非负,易得关于x 的不等式组,解出它的解集即可得到函数的定义域.本题考查求对数函数定义域,解题的关键是理解函数定义域的定义,找出自变量满足的不等式,解出定义域,本题中用到了对数的真数大于是,偶次根号下非负这些限制条件,属于是函数概念考查基本题.14. 已知cos(θ+π)=−13,则sin(2θ+π2)=______. 【答案】−79【解析】解:∵cos(θ+π)=−13, ∴cos θ=13,∴sin(2θ+π2)=cos2θ=2cos 2θ−1=29−1=−79, 故答案为:−79根据诱导公式和二倍角公式即可求出.本题考查了诱导公式和二倍角公式,属于基础题.15. 已知函数f (x )= ln x ,x >0e x ,x≤0,g (x )=f (x )+x +a ,若g (x )存在2个零点,则实数a 取值范围是______. 【答案】[−1,+∞)【解析】解:由g (x )=0得f (x )=−x −a , 作出函数f (x )和y =−x −a 的图象如图: 当直线y =−x −a 的截距−a ≤1,即a ≥−1时,两个函数的图象都有2个交点, 即函数g (x )存在2个零点,故实数a 的取值范围是[−1,+∞), 故答案为:[−1,+∞).由g (x )=0得f (x )=−x −a ,分别作出两个函数的图象,根据图象交点个数与函数零点之间的关系进行转化求解即可. 本题主要考查分段函数的应用,利用函数与零点之间的关系转化为两个函数的图象的交点问题是解决本题的关键.16. 函数f (x )=2sin(2x −π3)的图象为C ,如下结论中正确的是______.①图象C 关于直线x =11π12对称;②图象C 关于点(2π3,0)对称;③函数f (x )在区间(−π12,5π12)内是增函数;④由y =2sin2x 图象向右平移π3个单位长度可以得到图象C . 【答案】①②③【解析】解:函数f (x )=2sin(2x −π3), 由f (11π12)=2sin3π2=−2,为最小值,可得图象C 关于直线x =11π12对称,故①正确;由f (2π3)=2sin π=0,图象C 关于点(2π3,0)对称,故②正确;由x ∈(−π12,5π12),可得2x −π3∈(−π2,π2),即有f (x )在区间(−π12,5π12)内是增函数, 故③正确;由y =2sin2x 图象向右平移π3个单位长度可以得到y =2sin2(x −π3)的图象,故④错误. 故答案为:①②③.由正弦函数的对称轴特点可判断①;由正弦函数的对称中心特点可判断②; 由正弦函数的增区间可判断③;由三角函数的图象变换特点可判断④.本题考查三角函数的图象和性质,考查函数的对称性和单调性、图象变换,考查运算能力,属于中档题.三、解答题(本大题共6小题,共70.0分)17. 已知向量a =(1,0),b =(1,1).(1)若c =2 2,且c ⊥b ,求向量c的坐标; (2)若AB =2a −b ,BC =a +m b ,且A 、B 、C 三点共线,求实数m 的值. 【答案】解:(1)设c=(x ,y ); ∵c ⊥b ,且c=2 2; ∴c ⋅b =x +y =0①,x 2+y 2=8②;①②联立得, y =2x =−2,或y =−2x =2; ∴c =(−2,2),或(2,−2);(2)AB =2a −b =(1,−1),BC =a +m b =(1+m ,m ); ∵A 、B 、C 三点共线;∴AB //BC ;∴m+1+m=0;∴m=−12.【解析】(1)可设c=(x,y),根据c⊥b及c=22即可得出x+y=0①,x2+y2=8②,①②联立即可求出x,y,即得出向量c的坐标;(2)可先求出AB=(1,−1),BC=(1+m,m),根据A、B、C三点共线可得出AB//BC,从而得出m+1+m=0,解出m即可.考查向量平行时的坐标关系,向量垂直的充要条件,以及向量坐标的数量积运算.18. 已知函数f(x)=mx+n1+x 是定义在R上的奇函数,且f(2)=25.(1)求函数f(x)的解析式;(2)判断函数f(x)在区间(0,1)上的单调性,并用定义法证明.【答案】解:(1)根据题意,函数f(x)=mx+n1+x2是定义在R上的奇函数,则f(0)=n1=0,则n=0,又由f(2)=25,则f(2)=2m1+22=25,解可得m=1,则f(x)=x1+x2,(2)由(1)的结论,f(x)=x1+x在(0,1)上为增函数,证明:0<x1<x2<1,则f(x1)−f(x2)=x11+x12−x21+x22=(x1−x2)(1−x1x2)(1+x12)(1+x22)又由0<x1<x2<1,则(x1−x2)<0,(1−x1x2)>0,则有f(x1)−f(x2)<0,则函数f(x)在(0,1)上为增函数.【解析】(1)根据题意,由奇函数的性质可得f(0)=n1=0,则n=0,又由f(2)=2m1+2=25,解可得m的值,将m、n的值代入函数的解析式,计算可得答案;(2)根据题意,设0<x1<x2<1,由作差法分析可得答案.本题考查函数的奇偶性与单调性的性质以及应用,涉及单调性的判断,属于基础题.19. 已知函数f(x)=2sin(x2+π6).(1)求函数f(x)的最小正周期及单调递减区间;(2)先列表,并用描点法作出函数f(x)在[0,4π]上的简图.【答案】(本题满分为12分)解:(1)f(x)的最小正周期为T=2π12=4π;…(4分)令π2+2kπ≤x2+π6≤3π2+2kπ,k∈Z,解得:2π3+4kπ≤x≤8π3+4kπ,k∈Z,可得单调递减区间为:[2π3+4kπ,8π3+4kπ],k∈Z.(2)列表如下:连线成图如下:【解析】(1)利用正弦函数的图象和性质即可求出f(x)的最小正周期与单调减区间;(2)列表如下,作出它在[0,4π]上的简图即可;本题主要考查了五点法作函数y=A sin(ωx+φ)的图象,考查了正弦函数的图象和性质的应用,属于基础题.20. 某家庭进行理财投资,根据长期收益率市场预测,投资债券类稳健型产品的收益与投资额成正比,投资股票类风险型产品的收益与投资额的算术平方根成正比.已知两类产品各投资1万元时的收益分别为0.125万元和0.5万元,如图:(Ⅰ)分别写出两类产品的收益y(万元)与投资额x(万元)的函数关系;(Ⅱ)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,最大收益是多少万元?【答案】解:(Ⅰ)投资债券类稳健型产品的收益满足函数:y=kx(x>0),由题知,当x=1时,y=0.125,则k=0.125,即y=0.125x,投资股票类风险型产品的收益满足函数:y=k′x(x>0),由题知,当x=1时,y=0.5,则k=0.5,即y=0.5x,(Ⅱ)设投资债券类稳健型产品x万元(0≤x≤20),则投资股票类风险型产品20−x万元,由题知总收益y=0.125x+0.520−x(0≤x≤20),令t=20−x(0≤t≤20),则x=20−t2,y=0.125(20−t2)+0.5t=−18t2+12t+52=−18(t−2)2+3,当t=2,即x=16时,y max=3(万元)答:投资债券类稳健型产品16万元,投资股票类风险型产品4万元,此时受益最大为3万元.【解析】(Ⅰ)由投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,结合函数图象,我们可以利用待定系数法来求两种产品的收益与投资的函数关系;(Ⅱ)由(Ⅰ)的结论,我们投资债券类稳健型产品x万元(0≤x≤20),则投资股票类风险型产品20−x万元.这时可以构造出一个关于收益y的函数,然后利用求函数最大值的方法进行求解.函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.21. 已知a=(2cos x,1),b=(3sin x+cos x,−1),函数f(x)=a⋅b.(1)求函数f(x)在区间[0,π2]上的最大值和最小值;(2)若f(x0)=85,x0∈[π4,π2],求cos2x0的值;(3)若函数y=f(ωx)在区间(π3,2π3)上是单调递增函数,求正数ω的取值范围.【答案】解:∵a=(2cos x,1),b=(3sin x+cos x,−1),∴f(x)=a⋅b=2cos x(3sin x+cos x)−1=23sin x cos x+2cos2x−1=3sin2x+cos2x=2sin(2x+π)(1)∵x∈[0,π2],∴π6≤2x+π6≤7π6,∴−12≤sin(2x+π6)≤1,∴函数f(x)在区间[0,π2]上的最大值2,最小值−1;(2)若f(x0)=85,则2sin(2x0+π6)=85,∴sin(2x0+π6)=45,∵x0∈[π4,π2 ],∴cos(2x0+π6)=−35,∴cos2x0=cos[(2x0+π)−π]=3cos(2x0+π)+1sin(2x0+π)=3×(−3)+1×4=4−33(3)∵y=f(ωx)=2sin(2ωx+π6),令−12π+2kπ≤ωx+π6≤12π+2kπ,k∈z,可得,−2π3ω+2kπω≤x≤π3ω+2kπω令k=0可得,−2π3ω≤x≤π3ω,∵y=f(ωx)=2sin(2ωx+π6),在区间(π3,2π3)上是单调递增函数,∴π3ω≥2π3,解可得,0<ω≤12.【解析】由向量数量积的坐标表示,结合两角和的正弦公式可求f(x)=2sin(2x+π6)(1)由x∈[0,π2],结合正弦函数的性质可求函数f(x)在区间[0,π2]上的最大值及最小值;(2)若f(x0)=85,可求2sin(2x0+π6),结合同角平方关系可求cos(2x0+π6),然后由cos2x0=cos[(2x0+π6)−π6],利用两角差的余弦公式即可求解(3)由y=f(ωx)=2sin(2ωx+π6),结合正弦函数的单调性可求单调递增区间,然后与区间(π3,2π3)进行比较可求.本题主要考查了向量的数量积的运算性质及两角和的余弦公式,正弦函数的性质的灵活应用是求解本题的关键.22. 已知函数g(x)=ax2−2ax+1+b(a>0)在区间[−1,1]上有最大值4和最小值0.设f(x)=g(x)x.(1)求实数a,b的值;(2)若不等式f(x)−k⋅x≥0在x∈(0,+∞)上恒成立,求实数的取值范围;(3)若f( 2x−1 )+k⋅22x−1−3k=0有三个不同的实数解,求实数的取值范围.【答案】解:(1)函数g(x)=ax2−2ax+b+1=a(x−1)2+1+b−a,因为a>0,所以g(x)在区间[−1,1]上是减函数,故g(−1)=3a+b+1=4,g(1)=1+b−a=0,解得a=1,b=0;(2)由f(x)−k⋅x≥0即为x2−2x+1−kx2≥0,即为k≤(1x−1)2在x>0恒成立,由(1x−1)2≥0,当且仅当x=1时取得最小值0,所以的取值范围是(−∞,0];(3)方程f( 2x−1 )+k⋅22−1−3k=0可化为:2x−12−(2+3k) 2x−1 +(1+2k)=0,2x−1 ≠0,令2x−1 =t,则方程化为t 2−(2+3k )t +(1+2k )=0(t ≠0),∵方程f ( 2k −1 )+k ⋅⋅22−1 −3k =0有三个不同的实数解,∴由t = 2x −1 的图象知,t 2−(2+3k )t +(1+2k )=0(t ≠0),有两个根t 1、t 2,且0<t 1<1<t 2或0<t 1<1,t 2=1.记 (t )=t 2−(2+3k )t +(1+2k ),则 (1)=−k <0 (0)=1+2k >0,或 (0)=1+2k >0(1)=−k =00<2+3k 2<1, ∴k >0.【解析】(1)由函数g (x )=a (x −1)2+1+b −a ,a >0,所以g (x )在区间[−1,1]上是减函数,故g (−1)=4,g (1)=0,由此解得a 、b 的值;(2)不等式可化为k ≤(1x −1)2在x >0恒成立,由平方数非负可得不等式右边的最小值,从而求得的取值范围;(3)方程f ( 2x −1 )+k ⋅22−1 −3k =0⇒ 2x −12−(2+3k ) 2x −1 +(1+2k )=0,( 2x −1 ≠0),令2x −1 =t ,则t 2−(2+3k )t +(1+2k )=0(t ≠0),构造函数 (t )=t 2−(2+3k )t +(1+2k ),通过数形结合与等价转化的思想即可求得的范围. 本题考查二次函数在闭区间上的最值,考查函数恒成立问题问题,考查数形结合与等价转化、函数与方程思想的综合应用,属于难题.。
2018~2019学年天河区一年级上学期期末数学试卷答案
3.在多的后面画“√”.
√
4.在少的后面画“√”.
√
第 1页 共 4 页
5.数一数下面各有几个正方体,在正确答案后的里面“√”.
√
√
6.连一连.
7.连一连.
圆柱 正方体 长方体 球 8.数一数,填一填.
(1)把左边 9 个西瓜圈起来. (2)把右数起,把第 11 个西瓜涂上颜色. 9.按顺序填数.
13 12 11 10 9 8 15 16 17 18 19 20
10.2 个十合起来是 20 . 11.17 里面有 1 个十和 7 个一.
第 2页 共 4 页
密封线内不要答题
学校
班级
姓名
考号
考场
密封线内不要答题
12.在空线里填上“ ”、“ ”或“ ”.
3 (>) 0 7 2 (=) 9
10 8 (<)10 2
8 (<) 12 14 3 (>) 9 4+7 (=) 3+8
13.在横线上填上合适的数.
(10) 3 1 3
(5) 1 4
10+(6)=16
7 (2)=5
14.第 3 节和第 10 节车厢之间有_ 6___节车厢.
15.看图列式计算.
16.看图列式计算.
5 +5
10
17.看图列式计算.
9 _4
第 3页 共 4 页
5 (只)
5 + 4 + 3 12
18.看图列式计算.
学校
班级
姓名
考号
考场
密封线内不要答题
1.算一算. 10 4 6 734 055 633 4 6 10 17 8 2 8 10 62 4 9 1 10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
京唐教育©版权所有
(2) 如果 1 个人需要 0.5 米宽的位置就餐,这张餐桌大约能坐多少人?(结果 四舍五入)。
(3) 如果在这张餐桌中央放一个半径 0.5m 的圆形转盘,剩余的面积大约是多 少?(得数保留一位小数)
27. 挖一条水渠,李叔叔每天挖整条水渠的 1 ,王伯伯每天挖的量是李叔叔每天 20
(1) 把扇形统计图中的括号和条形统计图补充完成。 (2) 锻炼时间不超过 1 小时的人数和超过 1 小时的人数比为( ):( )。
-5-
-6-
6A-SX-0000001
26. 当当看一本书,第一天看了全书的 30%,第二天看了全书的1,还剩下 90 页, 4
这本书共有多少页?(5 分)
28. 一个圆形餐桌桌面的直径是 2 米。(π 取 3.14)(9 分) (1) 它的面积是多少平方米?
2
7
(2) (1- 3 ÷ 6) × 10
10 7
13
24. 如右图,已知正方形的周长是 16cm。(π 取 3.14) (1) 求圆的周长。(2 分)
京唐教育©版权所有
(3) 68 ×(3 - 11)
4 34
(4) 5 ÷ 9 + 7 × 4
12 4 12
9
22. 解方程。(每小题 2 分,共 4 分)
(1) 8 ÷ 4 =
9
(4) 2 ÷ 8 =
7 21
(2) 2 × 3 =
95
(5) 11 ÷ 25% =
12
(3) 1.8 ÷ 9 =
7
(6) 6 × (1-30%)=
-3-
-4-
6A-SX-0000001
21. 计算下面各题,怎样简便就怎么计算。(每小题 3 分,共 12 分)
(1) 5 ÷ 15 × 3
25
奇思
25
20
妙想
20
17
A. 明明
B. 淘气
C. 奇思
D. 妙想
-1-
-2-
6A-SX-0000001
9. 下面说法中,正确的有(
)个。
(1) 7 千米可以写成 7%千米 100
(2) 大牛和小牛的头数比是 4:5,表示大牛比小牛少1 。
5
(3) 右图中∠ACB 是圆心角。
(4) 打同一篇稿件,小强用了 10 分钟,小玲用了 12 分
)
人。
16. 144 的1是(
6
),(
)的2是 60.
3
17. 笑笑在操场上从 A 点出发向正东走 30 步,再向正南走 30 步,然后向正西走
30 步到达 B 点,A、B 两点相距(
)步。
18. 淘气用小棒搭房子,他搭 3 间房子
用了 13 根小棒(如右图),像这样
搭 10 间房子要用(
)根小棒。
- - - - - - - - - 密封线 - - - - - - - - - 密封线 - - - - - - - - -
姓名:____________________ 学号:________
6A-SX-0000001
2018 学年第一学期天河区期末水平测试
六年级数学
(全卷共 8 页,满分 100 分,90 分钟完成)
A.
B.
C.
D.
2. 下面的说法正.确.的是(
)。
A.一个数的倒数一定比这个数小。
B. 大圆的圆周率比小圆的圆周率大。
C. 用 110 颗种子做发芽实验,全部发芽,这些种子的发芽率是 110%。
D. 比的前项和后项同时乘或除以相同的数(0 除外),比值不变。
3. 下面四个算式中,计算结果最小的的是( )。
12 月的价格和 10 月比是是涨了还是降了?结论是( )。
A.涨了
B.降了
C. 没涨没降 D. 无法确定
8. 在一场足球比赛中,猛虎队获得一次罚点球的机会,他们准备派四名队员中的
一名去罚点球,下面是这四名队员近期罚点球情况统计。你认为该派(
)
队员去罚点球。
队员
罚球数/个
进球数/个
明明
10Βιβλιοθήκη 9淘气50
)。
3
A. 六(2)班是六(1)班的1
3
B. 六(2)班比六(1)班多1
3
B. 六(2)班比六(1)班少1
3
D. 六(1)班比六(2)班少1
3
7. 东湖小区今年拥有电脑的家庭有 120 户,比去年增加了1,东湖小区去年拥有
4
电脑的家庭是多少户?下面图(
)正确表达了题目的意思。
学校:____________________ _______年_______班
(3) 如果机器人的行走速度控制在6米/秒, 5
那么行完全程需要(
)分钟。
(1 分)
-7-
-8-
A.1×1
62
B. 1 ÷ 3
62
C. 1 × 1 1
6
2
D. 1 ÷ 1
62
4. 把一个平角按照 1:3 分成两个角,这两个角的度数分别是( )。
A. 60゜和 120゜
B. 30゜和 90゜
C. 45゜和 135゜
D. 90゜和 180゜
5. 某种商品 11 月的价格比 10 月降了 10%,12 月的价格比 11 月又涨了 10%,
(1)
27x
=
4 11
(2) x–15% x = 85
(2) 求阴影部分的面积。(3 分)
25. 为开展阳光体育活动,坚持让中小学生“每天锻炼 1 小时”,调查组随机调查 了 600 名学生,调查内容是“每天锻炼的时间”,所得数据制成了以下的扇形 统计图和条形统计图。(5 分)
23. 操作题。(4 分) 请用圆规画一个直径 4cm 的圆,标出圆心和半径,再在圆中画一个圆心角是 45゜的扇形。
钟,小强和小玲打字的速度之比是 6:5.
A. 1
B. 2
C. 3
D. 4
10. 甲、乙、丙三名小朋友用相同的正方形手工纸剪图形,甲剪了一个最大的扇形,
乙煎了一个最大的圆,丙剪了四个最大的圆,如下图。三个人对手工纸的利用
率情况是(
)。
京唐教育©版权所有
15. 六年级同学参加体能测试,有 285 人达标,达标率为 95%,六年级有(
挖的量的2。两人合作,几天能挖完?(5 分) 3
29. 这是一张机器人的行走路线图。
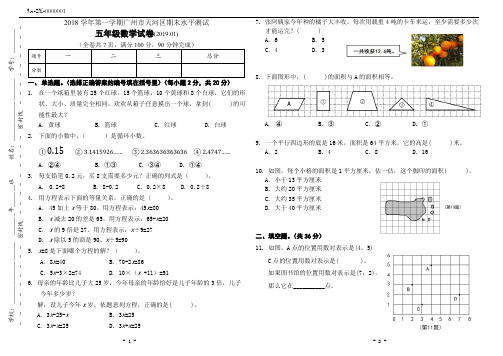
(1) 机器人从出发站出发,向(
)偏
(
)(
) ゜方向,
行走(
)m 可到达 A 站。(2 分)
(2) 机器人最终目的地是 C 站。C 站位于 B 站
南偏东 30゜、距离 B 站 15m 的位置上。
请你在图上标出 C 站的位置。(2 分)
2
(
)。
)米,每份占这条绳子的
14. 在填上 “>”、“<”或“=”。
2× 7
7
3
4
4
5÷1
82
5× 2
8
7÷ 5
7
9
8
9
1 米的5
6
5 米的1
6
19. 如图,四个圆的半径都为 3cm,圆心
分别在四边形的四个顶点上,则阴影
部分的面积为(
)cm2。(π 取 3.14)
三、解答题(共 60 分)
20. 直接写得数。(每小题 1 分,共 6 分)
题号
一
二
三
总分
分数
一、 单选题。(选择正确答案的编号填在括号里)(每小题 2 分,共 20 分) 1. 下面四幅图中,( )的阴影面积占整幅图的 12.5%。
京唐教育©版权所有
6. 植树节六(1)班同学植树 120 棵,___________,六(2)班植树多少棵?
列式为:120×(1-1),那么横线上应该补充的条件是(
A.甲最高
B. 乙最高
C. 丙最高
D. 三人都相同
二、填空题。(除第 14 题除外,每小题 2 分,共 20 分)
11. 把 0.25:1 化成最简整数比是(
6
),比值是(
12. 6:8= (
3
=
)
(
) ÷80 = (
)% = (
)。 ) (填小数)
13. 把一条长5米的绳子平均分成 5 份,每份长(
