BPSK和QPSK调制解调原理及MATLAB程序
BPSK和QPSK调制解调原理及MATLAB程序资料

2.1 PSK调制方式PSK原理介绍(以2-PSK为例)移相键控(PSK)又称为数字相位调制,二进制移相键控记作2PSK。
绝对相移是利用载波的相位(指初相)直接表示数字信号的相移方式。
二进制相移键控中,通常用相位0 和π来分别表示“0”或“1”。
2PSK 已调信号的时域表达式为s2psk(t)=s(t)cosωct, 2PSK移相键控中的基带信号与频移键控和幅度键控是有区别的,频移键控和幅度键控为单极性非归零矩形脉冲序列,移相键控为为双极性数字基带信号,就模拟调制法而言,与产生2ASK 信号的方法比较,只是对s(t)要求不同,因此2PSK 信号可以看作是双极性基带信号作用下的DSB 调幅信号。
在二进制数字调制中,当正弦载波的相位随二进制数字基带信号离散变化时,则产生二进制移相键控(2PSK)信号。
通常用已调信号载波的 0°和 180°分别表示二进制数字基带信号的 1 和 0。
二进制移相键控信号的时域表达式为e2PSK(t)=[nna g(t-nT s)]cosw c t其中, an与2ASK和2FSK时的不同,在2PSK调制中,an应选择双极性。
1, 发送概率为Pan=-1, 发送概率为1-P若g(t)是脉宽为Ts, 高度为1的矩形脉冲时,则有cosωct, 发送概率为Pe2PSK(t)=-cosωct, 发送概率为1-P由上式(6.2-28)可看出,当发送二进制符号1时,已调信号e2PSK(t)取0°相位,发送二进制符号0时,e2PSK(t)取180°相位。
若用φn表示第n个符号的绝对相位,则有0°, 发送 1 符号φn=180°, 发送 0 符号由于在2PSK信号的载波恢复过程中存在着180°的相位模糊,所以2PSK信号的相干解调存在随机的“倒π”现象,从而使得2PSK 方式在实际中很少采用。
为了解决2PSK 信号解调过程的反向工作问题, 提出了二进制差分相位键控(2DPSK),这里不再详述。
基于matlab的QPSK与BPSK信号性能比较仿真

┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊目录第一章概述 (1)第二章QPSK通信系统原理与仿真 (1)2.1 QPSK系统框图介绍 (1)2.2QPSK信号的调制原理 (2)2.2.1QPSK信号产生方法 (2)2.2.2QPSK星座图 (2)2.3QPSK解调原理及误码率分析 (3)2.3.1QPSK解调方法 (3)2.3.2QPSK系统误码率 (3)2.4QPSK信号在AWGN信道下仿真 (4)第三章BPSK通信系统原理与仿真 (4)3.1BPSK信号的调制原理 (4)3.2BPSK解调原理及误码率分析 (4)第四章QPSK与BPSK性能比较 (5)4.1QPSK与BPSK在多信道下比较仿真 (5)4.1.1纵向比较分析 (5)4.1.2横向比较分析 (7)4.2仿真结果分析 (7)4.2.1误码率分析 (7)4.2.2频带利用率比较 (7)附录 (8)代码1 (8)代码2 (8)代码3 (10)代码4 (12)┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊第一章概述QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
它以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接人、移动通信及有线电视系统之中。
BPSK是英文Binary Phase Shift Keying的缩略语简称,意为二相相移键控,是利用偏离相位的复数波浪组合来表现信息键控移相方式的一种。
它使用了基准的正弦波和相位反转的波浪,使一方为0,另一方为1,从而可以同时传送接受2值(1比特)的信息。
本文所研究的QPSK系统与二进制的BPSK系统相比,具有以下特点:1.在传码率相同的情况下,四进制数字调制系统的信息速率是二进制系统的2倍。
2.在相同信息速率条件下,四进制数字调制系统的传码率是二进制系统的1/4倍,这一特点使得四进制码元宽度是二进制码元宽度的2倍,码元宽度的加大,可增加每个码元的能量,也可减小码间串扰的影响。
qpsk、bpsk蒙特卡洛仿真matlab代码

qpsk、bpsk的蒙特卡洛仿真是一种用于测试和验证通信系统性能的重要工具。
通过模拟大量的随机输入数据,并对系统进行多次仿真运算,可以对系统的性能进行全面评估,包括误码率、信噪比要求等。
在matlab中,我们可以通过编写相应的仿真代码来实现qpsk、bpsk 的蒙特卡洛仿真。
下面将分别介绍qpsk和bpsk的蒙特卡洛仿真matlab代码。
一、qpsk的蒙特卡洛仿真matlab代码1. 生成随机的qpsk调制信号我们需要生成一组随机的qpsk调制信号,可以使用randi函数生成随机整数序列,然后将其映射到qpsk符号点上。
2. 添加高斯白噪声在信号传输过程中,会受到各种干扰,其中最主要的干扰之一就是高斯白噪声。
我们可以使用randn函数生成高斯白噪声序列,然后与调制信号相加,模拟信号在传输过程中受到的噪声干扰。
3. 解调和判决接收端需要进行解调和判决操作,将接收到的信号重新映射到qpsk符号点上,并判断接收到的符号与发送的符号是否一致,从而判断是否发生误码。
4. 统计误码率通过多次仿真运算,记录错误判决的次数,从而可以计算出系统的误码率。
二、bpsk的蒙特卡洛仿真matlab代码1. 生成随机的bpsk调制信号与qpsk相似,我们需要先生成一组随机的bpsk调制信号,然后模拟信号传输过程中的噪声干扰。
2. 添加高斯白噪声同样使用randn函数生成高斯白噪声序列,与bpsk调制信号相加。
3. 解调和判决接收端对接收到的信号进行解调和判决,判断接收到的符号是否与发送的符号一致。
4. 统计误码率通过多次仿真运算,记录错误判决的次数,计算系统的误码率。
需要注意的是,在编写matlab代码时,要考虑到信号的长度、仿真次数、信噪比的范围等参数的选择,以及仿真结果的统计分析和可视化呈现。
qpsk、bpsk的蒙特卡洛仿真matlab代码可以通过以上步骤实现。
通过对系统性能进行全面评估,可以帮助工程师优化通信系统设计,提高系统的可靠性和稳定性。
MATLAB_QPSK调制与解调
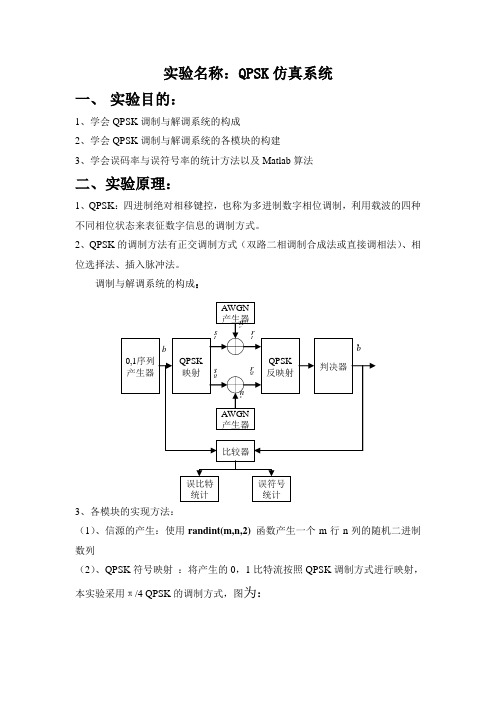
实验名称:QPSK仿真系统一、实验目的:1、学会QPSK调制与解调系统的构成2、学会QPSK调制与解调系统的各模块的构建3、学会误码率与误符号率的统计方法以及Matlab算法二、实验原理:1、QPSK:四进制绝对相移键控,也称为多进制数字相位调制,利用载波的四种不同相位状态来表征数字信息的调制方式。
2、QPSK的调制方法有正交调制方式(双路二相调制合成法或直接调相法)、相位选择法、插入脉冲法。
调制与解调系统的构成:3、各模块的实现方法:(1)、信源的产生:使用randint(m,n,2)函数产生一个m行n列的随机二进制数列(2)、QPSK符号映射:将产生的0,1比特流按照QPSK调制方式进行映射,本实验采用π/4 QPSK的调制方式,图为:(3)、AWGN 信号产生:AWGN 产生器就是产生满足均值为0,方差为1的高斯白噪声。
实验中使用randn(m,n)函数产生一个m 行n 列的高斯噪声序列。
(4)、信号幅度控制:根据AWGN 信道模型,接收信号可以分别表示为α就是当噪声功率归一化为1(0均值,方差为1)时,根据信噪比关系而计算出来的信号平均幅度(5)、QPSK 反映射及判决 :对接收到的信号在4种可能的四种信号向量[(1,0), (0,1), (-1,0), (0,-1)]上投影(即进行点积)。
投影最大的值所对应的信号向量就是所发送信号的符号值,然后恢复出比特流(6)、误码率及误符号率统计:误码率:将检测出来的比特流和发送的原始比特流进行比较,统计出出现错误的比特数误符号率:将检测出来的比特流变成两组,构成符号,和发送端符号映射后的符号流进行比较,只要符号中任错一bit ,就算该符号出错。
统计出现错误的符号数 三、 实验内容:1、调制与解调I I Ir s n α=+Q Q Qr s n α=+22210log 10^10s s n n v SNR SNR v sqrt v v ⎛⎫⎛⎫⎛⎫=⇒=* ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭s v α=clear allclose all% 调制bit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3);bit_Q = bit_in(2:2:1e3);data_I = -2*bit_I+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);end;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=conv(data_I2,xrc)/5.5;data_Q2_rc=conv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;n0=rand(size(t1));I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*sin(2*pi*f1*t1); QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc); QPSK_rc_n0=QPSK_rc+n0;% 解调I_demo=QPSK_rc_n0.*cos(2*pi*f1*t1);Q_demo=QPSK_rc_n0.*sin(2*pi*f1*t1);% 低通滤波I_recover=conv(I_demo,xrc);Q_recover=conv(Q_demo,xrc);I=I_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;% 抽样判决data_recover=[];for i=1:20:10000data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)];end;bit_recover=[];for i=1:20:20000if sum(data_recover(i:i+19))>0data_recover_a(i:i+19)=1;bit_recover=[bit_recover 1];elsedata_recover_a(i:i+19)=-1;bit_recover=[bit_recover -1];endenderror=0;dd = -2*bit_in+1;ddd=[dd'];ddd1=repmat(ddd,20,1);for i=1:2e4ddd2(i)=ddd1(i);endfor i=1:1e3if bit_recover(i)~=ddd(i)error=error+1;endendp=error/1000;figure(1)subplot(2,1,1);plot(t2,ddd2);axis([0 100 -2 2]);title('原序列');subplot(2,1,2);plot(t2,data_recover_a);axis([0 100 -2 2]);title('解调后序列');2、误码率仿真% QPSK误码率分析SNRindB1=0:2:10;SNRindB2=0:0.1:10;for i=1:length(SNRindB1)[pb,ps]=cm_sm32(SNRindB1(i));smld_bit_err_prb(i)=pb;smld_symbol_err_prb(i)=ps;end;for i=1:length(SNRindB2)SNR=exp(SNRindB2(i)*log(10)/10);theo_err_prb(i)=Qfunct(sqrt(2*SNR)); end;title('QPSK误码率分析');semilogy(SNRindB1,smld_bit_err_prb,'*');axis([0 10 10e-8 1]);hold on;% semilogy(SNRindB1,smld_symbol_err_prb,'o'); semilogy(SNRindB2,theo_err_prb);legend('仿真比特误码率','理论比特误码率'); hold off;function[y]=Qfunct(x)y=(1/2)*erfc(x/sqrt(2));function[pb,ps]=cm_sm32(SNRindB)N=10000;E=1;SNR=10^(SNRindB/10);sgma=sqrt(E/SNR)/2;s00=[1 0];s01=[0 1];s11=[-1 0];s10=[0 -1];for i=1:Ntemp=rand;if (temp<0.25)dsource1(i)=0;dsource2(i)=0;elseif (temp<0.5)dsource1(i)=0;dsource2(i)=1;elseif (temp<0.75)dsource1(i)=1;dsource2(i)=0;elsedsource1(i)=1;dsource2(i)=1;end;end;numofsymbolerror=0;numofbiterror=0;for i=1:Nn=sgma*randn(size(s00));if((dsource1(i)==0)&(dsource2(i)==0))r=s00+n;elseif((dsource1(i)==0)&(dsource2(i)==1)) r=s01+n;elseif((dsource1(i)==1)&(dsource2(i)==0)) r=s10+n;elser=s11+n;end;c00=dot(r,s00);c01=dot(r,s01);c10=dot(r,s10);c11=dot(r,s11);c_max=max([c00 c01 c10 c11]);if (c00==c_max)decis1=0;decis2=0;elseif(c01==c_max)decis1=0;decis2=1;elseif(c10==c_max)decis1=1;decis2=0;elsedecis1=1;decis2=1;end;symbolerror=0;if(decis1~=dsource1(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(decis2~=dsource2(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(symbolerror==1)numofsymbolerror=numofsymbolerror+1;end;end;ps=numofsymbolerror/N;pb=numofbiterror/(2*N);3、QPSK在AWGN信道下的仿真close allclcclear allSNR_DB=[0:1:12];sum=1000000;data= randsrc(sum,2,[0 1]);[a1,b1]=find(data(:,1)==0&data(:,2)==0);message(a1)=-1-j;[a2,b2]=find(data(:,1)==0&data(:,2)==1);message(a2)=-1+j;[a3,b3]=find(data(:,1)==1&data(:,2)==0);message(a3)=1-j;[a4,b4]=find(data(:,1)==1&data(:,2)==1);message(a4)=1+j;scatterplot(message)title('B点信号的星座图')A=1;Tb=1;Eb=A*A*Tb;P_signal=Eb/Tb;NO=Eb./(10.^(SNR_DB/10));P_noise=P_signal*NO;sigma=sqrt(P_noise);for Eb_NO_id=1:length(sigma)noise1=sigma(Eb_NO_id)*randn(1,sum);noise2=sigma(Eb_NO_id)*randn(1,sum);receive=message+noise1+noise2*j;resum=0;total=0;m1=find(angle(receive)<=pi/2&angle(receive)>0);remessage(1,m1)=1+j;redata(m1,1)=1;redata(m1,2)=1;m2= find( angle(receive)>pi/2&angle(receive)<=pi);remessage(1,m2)=-1+j;redata(m2,1)=0;redata(m2,2)=1;m3=find( angle(receive)>-pi&angle(receive)<=-pi/2);remessage(1,m3)=-1-j;redata(m3,1)=0;redata(m3,2)=0;m4=find( angle(receive)>-pi/2&angle(receive)<=0);remessage(1,m4)=1-j;redata(m4,1)=1;redata(m4,2)=0;[resum,ratio1]=symerr(data,redata);pbit(Eb_NO_id)=resum/(sum*2);[total,ratio2]=symerr(message,remessage);pe(Eb_NO_id)=total/sum;endscatterplot(receive)title('C点信号的星座图')Pe=1-(1-1/2*erfc(sqrt(10.^(SNR_DB/10)/2))).^2;Pbit=1/2*erfc(sqrt(10.^(SNR_DB/10)/2));figure(3)semilogy(SNR_DB,pe,':s',SNR_DB,Pe,'-*',SNR_DB,pbit,'-o',SNR_DB,Pbit,':+')legend('QPSK仿真误码率','QPSK理论误码率','QPSK仿真误比特率','QPSK理论误比特率',1) xlabel('信噪比/dB')ylabel('概率P')gird on结果:4、QPSK在AWGN信道下的性能检测clear all;%对随机序列产生的方法初始化s = RandStream('mt19937ar','Seed', 5489);RandStream.setDefaultStream(s);s = RandStream('mcg16807', 'Seed',0);RandStream.setDefaultStream(s);N = 10^5; %码元数Eb_N0 = -4:20; %Eb/N0比特信噪比s_data = zeros(1,N);ErrorCount=zeros(1,length(Eb_N0)); %预先分配内存,用于记录错误的码元数for j = 1:length(Eb_N0)p = (2*(rand(1,N)>0.5)-1) + 1i*(2*(rand(1,N)>0.5)-1);s = (1/sqrt(2))*p; %归一化n = 10^(-Eb_N0(j)/40)*1/sqrt(2)*(randn(1,N) + 1i*randn(1,N)); %加性高斯白噪声r = s + n;%解调r_re = real(r); %实部r_im = imag(r); %虚部s_data(r_re < 0 & r_im < 0) = -1 + -1*1i;s_data(r_re >= 0 & r_im > 0) = 1 + 1*1i;s_data(r_re < 0 & r_im >= 0) = -1 + 1*1i;s_data(r_re >= 0 & r_im < 0) = 1 - 1*1i;ErrorCount(j) = size(find(p- s_data),2); %错误的码元数endsim_QPSK = ErrorCount/N;theory_QPSK = erfc(sqrt(0.5*(10.^(Eb_N0/20)))) -(1/4)*(erfc(sqrt(0.5*(10.^(Eb_N0/20))))).^2;close allfiguresemilogy(Eb_N0,theory_QPSK,'b.-');hold onsemilogy(Eb_N0,sim_QPSK,'mx-');axis([-4 20 10^-3 1])grid on。
基于matlab的QPSK与BPSK信号性能比较仿真讲解

┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊目录第一章概述 (2)第二章QPSK通信系统原理与仿真 (2)2.1 QPSK系统框图介绍 (2)2.2 QPSK信号的调制原理 (3)2.2.1 QPSK信号产生方法 (3)2.2.2 QPSK星座图 (4)2.3 QPSK解调原理及误码率分析 (4)2.3.1 QPSK解调方法 (4)2.3.2 QPSK系统误码率 (5)2.4 QPSK信号在AWGN信道下仿真 (5)第三章BPSK通信系统原理与仿真 (6)3.1 BPSK信号的调制原理 (6)3.2 BPSK解调原理及误码率分析 (7)第四章QPSK与BPSK性能比较 (8)4.1 QPSK与BPSK在多信道下比较仿真 (8)4.1.1 纵向比较分析 (8)4.1.2 横向比较分析 (10)4.2 仿真结果分析 (10)4.2.1 误码率分析 (10)4.2.2 频带利用率比较 (10)附录 (11)代码1 (11)代码2 (11)代码3 (14)代码4 (16)┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊第一章概述QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
它以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接人、移动通信及有线电视系统之中。
BPSK是英文Binary Phase Shift Keying的缩略语简称,意为二相相移键控,是利用偏离相位的复数波浪组合来表现信息键控移相方式的一种。
它使用了基准的正弦波和相位反转的波浪,使一方为0,另一方为1,从而可以同时传送接受2值(1比特)的信息。
本文所研究的QPSK系统与二进制的BPSK系统相比,具有以下特点:1.在传码率相同的情况下,四进制数字调制系统的信息速率是二进制系统的2倍。
bpsk调制的matlab程序

题目:BPSK调制的MATLAB程序一、BPSK调制技术介绍BPSK(Binary Phase Shift Keying)调制是一种数字调制技术,它使用两个不同的相位来表示数字比特0和1。
在BPSK调制中,0和1分别映射到正弦波的两种相位,通常为0°和180°。
二、MATLAB程序编写流程在MATLAB中实现BPSK调制的程序主要包括以下几个步骤:1. 生成要调制的数字比特序列2. 将数字比特序列转化为相应的正弦波信号3. 添加高斯白噪声4. 绘制调制后的信号波形图三、MATLAB程序实现下面是一个简单的MATLAB程序,实现了BPSK调制的过程:```matlab生成随机的数字比特序列bitStream = randi([0,1],1,1000);将数字比特序列映射为正弦波信号t = 0:0.01:length(bitStream)-1;t = t/100;carrier = sin(2*pi*t);BPSK调制bpskSignal = (1-2*bitStream).*carrier;添加高斯白噪声noise = 0.1*randn(1,length(bpskSignal)); noisyBpskSignal = bpskSignal + noise;绘制调制后的信号波形图subplot(2,1,1);plot(t,carrier);title('Carrier Signal');xlabel('Time');ylabel('Amplitude');grid on;subplot(2,1,2);plot(t,noisyBpskSignal);title('Noisy BPSK Signal');xlabel('Time');ylabel('Amplitude');grid on;```四、MATLAB程序运行结果分析通过上述程序,我们可以得到BPSK调制后的信号波形图。
QPSK调制与解调在MATLAB平台上的实现

QPSK调制与解调在MATLAB平台上的实现QPSK(Quadrature Phase Shift Keying)是一种常用的调制解调技术,常用于数字通信中。
在QPSK调制中,每个符号代表两个比特,通过将这两个比特与正交信号载波进行调制,实现高效的数据传输。
在这篇文章中,我们将介绍如何在MATLAB平台上实现QPSK调制和解调。
1.QPSK调制首先,我们需要生成待发送的二进制比特序列。
我们可以使用randi 函数生成0和1之间的随机整数序列。
```matlabbits = randi([0,1],1,N);```N表示待发送的比特数。
接下来,我们需要将这个二进制序列转换为QPSK调制符号。
在QPSK 调制中,我们将每两个比特映射到一个复数符号。
将0映射为1+j,将1映射为1-j。
```matlabfor i = 1:2:Nif bits(i) == 0 && bits(i+1) == 0symbols((i+1)/2) = 1 + 1i;elseif bits(i) == 0 && bits(i+1) == 1symbols((i+1)/2) = 1 - 1i;elseif bits(i) == 1 && bits(i+1) == 0symbols((i+1)/2) = -1 + 1i;elseif bits(i) == 1 && bits(i+1) == 1symbols((i+1)/2) = -1 - 1i;endend```最终得到的symbols变量即为QPSK调制后的复数符号序列。
2.QPSK解调首先,我们需要接收到的QPSK信号进行解调,得到复数符号序列。
```matlabsymbols_received = received_signal./carrier; % 将接收到的信号除以载波得到复数符号序列```其中received_signal为接收到的QPSK信号,carrier为发送端使用的载波。
BASK BPSK QPSK MSK调制解调原理以及Matlab代码

目录第一部分仿真的参数设置 (1)第二部分BASK调制与解调 (2)第三部分BPSK调制与解调 (6)第四部分QPSK调制与解调 (10)第五部分MSK调制与解调 (14)第六部分误码率随信噪比变化 (18)参考文献 (20)Matlab代码 (21)BASK (21)BPSK (24)QPSK (27)MSK (31)误码率随着信噪比变化 (35)第一部分仿真的参数设置仿真过程中应用到的参数设置以及相应的解释如表1所示[1]。
表1. 参数设置及其解释第二部分BASK调制与解调BASK调制解调的概要过程如图2.1所示。
图2.1 BASK调制解调原理图首先,信源随机产生1000个二进制(1/0)码并画出其频谱图,如图2.2所示。
图2.2 信源信号的时域波形和频谱图随后,用10Hz的载波频率去调制信源信号完成BASK调制,调制后的时域波形及其频谱如图2.3所示。
可以看到,调制后的频率确搬移到了10Hz处。
图2.3 BASK已调信号的时域波形与频谱图而后,已调信号进入信噪比为20dB的高斯信道。
接收端接收到经过信道信号,其时域波形和频谱如图2.4所示,可以看出分布在整个时间轴上的噪声信号。
图2.4 已调信号经过高斯信道后的时域波形和频谱图接收端接收到信号后,通入BASK解调模块,先乘上载波,获得一个拥有两个频率(10-10;10+10)的信号,其时域波形与频谱图如图2.5所示。
图2.5 BASK解调后的信号时域波形与频谱图而后通入低通滤波器滤除高频载波,时域波形与频谱图如图2.6所示,可以看出此时20Hz处无功率谱密度。
图2.6 通入LPF后的时域波形和频谱图最后将信号进行判决,与信源信号进行对比,如图2.7所示,其误码率为2.14%(如图6.6所示)。
图2.7 信宿恢复信号与信源产生信号波形图对比第三部分BPSK调制与解调BPSK与BASK调制与解调原理基本相同,主要的区别在于信源码是双极性码。
其基本原理如图3.1所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1 PSK调制方式PSK原理介绍(以2-PSK为例)移相键控(PSK)又称为数字相位调制,二进制移相键控记作2PSK。
绝对相移是利用载波的相位(指初相)直接表示数字信号的相移方式。
二进制相移键控中,通常用相位0 和π来分别表示“0”或“1”。
2PSK 已调信号的时域表达式为s2psk(t)=s(t)cosωct, 2PSK移相键控中的基带信号与频移键控和幅度键控是有区别的,频移键控和幅度键控为单极性非归零矩形脉冲序列,移相键控为为双极性数字基带信号,就模拟调制法而言,与产生2ASK 信号的方法比较,只是对s(t)要求不同,因此2PSK 信号可以看作是双极性基带信号作用下的DSB 调幅信号。
在二进制数字调制中,当正弦载波的相位随二进制数字基带信号离散变化时,则产生二进制移相键控(2PSK)信号。
通常用已调信号载波的 0°和 180°分别表示二进制数字基带信号的 1 和 0。
二进制移相键控信号的时域表达式为e2PSK(t)=[nna g(t-nT s)]cosw c t其中, an与2ASK和2FSK时的不同,在2PSK调制中,an应选择双极性。
1, 发送概率为Pan=-1, 发送概率为1-P若g(t)是脉宽为Ts, 高度为1的矩形脉冲时,则有cosωct, 发送概率为Pe2PSK(t)=-cosωct, 发送概率为1-P由上式(6.2-28)可看出,当发送二进制符号1时,已调信号e2PSK(t)取0°相位,发送二进制符号0时,e2PSK(t)取180°相位。
若用φn表示第n个符号的绝对相位,则有0°, 发送 1 符号φn=180°, 发送 0 符号由于在2PSK信号的载波恢复过程中存在着180°的相位模糊,所以2PSK信号的相干解调存在随机的“倒π”现象,从而使得2PSK 方式在实际中很少采用。
为了解决2PSK 信号解调过程的反向工作问题, 提出了二进制差分相位键控(2DPSK),这里不再详述。
2-PSK 调制解调二进制移相键控信号的调制原理:如图9所示。
其中图(a)是采用模拟调制的方法产生2PSK 信号,图(b)是采用数字键控的方法产生2PSK 信号。
解调器原理:如图10所示。
2PSK 信号的解调通常都是采用相干解调, 在相干解调过程中需要用到与接收的2PSK 信号同频同相的相干载波。
(a) 模拟调制产生2PSK 信号(b)数字键控的方法产生2PSK 信号 图 9 2PSK 信号的调制原理图图 102PSK 信号的解调原理图e 2PSK (t)带通滤波器相乘器低通 滤波器抽样 判决器 acde输出定时 脉冲cos(w c t)b乘法器e 2PSK (t)cos(w c t)s(t)码型变换双极性不归零cos(w c t)e 2PSK (t)s(t)开关电路180度移相0度180度10a111bcde图11 2PSK 信号相干解调各点时间波形就键控法来说,用数字基带信号s(t)控制开关电路,选择不同相位的载波输出,这时s(t)为单极性NRZ 或双极性NRZ 脉冲序列信号均可。
当基带信号为0 时候,连通开关0,产生无差别的载波,当所发出的信号为 1 时,既连通开关П改变载波的相位。
在移相键控中还有一种差分移相键,他和普通的移相键控区别在与,差分移相键只有在当前传输的码元和上次传输的码元产生差别时才会产生相位的变化。
移相键控相对与幅度键控和移频键控有着更好的抗干扰性,也更适合于在信道中传输。
QPSK 调制QPSK 信号可以看作两个载波正交2PSK 信号的合成。
用调相法产生QPSK 调制器框图如图12所示,QPSK 的调制器可以看作是由两个BPSK 调制器构成,输入的串行二进制信息序列经过串并变换,变成两路速率减半的序列,电平发生器分别产生双极性的二电平信号I (t )和Q (t ),然后对cosAtω和sinAtω进行调制,相加后即可得到QPSK 信号图12 QPSK 调制器框图QPSK 解调QPSK 信号的解调原理如图3-5的方框图所示。
解调是从已调信号中提取信号的过程,在某种意义上解调是调制的逆过程。
由于QPSK 信号可以看作是两正交2PSK 信号的叠加,故用两路正交的相干载波去解调,这样能电平产生载波发生器电平产生移相90度二进制信息输出QPSK 信号串并转换Q(t)I(t)Acos(wt)Asin(wt)够很容易地分离出这两路正交的2PSK 信号。
相干解调后的两路并行码元a 和b 经过“并/串”转换后成为串行数据输出。
BPSK 调制解调程序%构造载波,产生8个码元,生成已调信号% a=randsrc(1,8,[0:1]);%产生8个随机的二进制数l=linspace(0,2*pi,50);%利用linspace 函数创建数组,2pi 长度取点50个模拟一个码元 f=sin(2*l);%生成载波t=linspace(0,10*pi,400);%定义时轴length 为10pi,取点400个,代表8个码元的总取样点数 out=1:400;%规定已调信号length b=1:400;% 规定基带信号length w=1:400;%规定载波length %生成PSK 信号% for i=1:8if a(i)==0 for j=1:50out(j+50*(i-1))=f(j); %若码元为0则将载波输出 end elsefor j=1:50out(j+50*(i-1))=-f(j); %若码元为1则将载波反相输出 end end end%输出载波和基带信号% for i=1:8 for j=1:50b(j+50*(i-1))=a(i); %b 作为调制信号输出 w(j+50*(i-1))=f(j); %w 作为载波输出s 图3-5 QPSK 信号解调原理方框图endendsubplot(3,3,1),plot(t,b),axis([0 10*pi -0.5 1.2]), xlabel('t'),ylabel('幅度'),title('基带信号');grid on; subplot(3,3,2),plot(t,w),axis([0 10*pi -1.2 1.2]), xlabel('t'),ylabel('幅度'),title('载波'); grid on; subplot(3,3,3),plot(t,out),axis([0 10*pi -1.2 1.2]),xlabel('t'),ylabel('幅度'),title('PSK波形');grid on; %已调信号加入高斯白噪声%noise=awgn(out,80,'measured') ; %产生噪音并加入到已调信号out中,信噪比80 subplot(334);plot(t,noise);ylabel('幅度');title('噪音+信号'); xlabel('t');axis([0 10*pi -1.2 1.2]); grid on;%信号通过BPF%Fs=400; %抽样频率400HZt=(1:400)*10*40/Fs; %时轴步进[b,a]=ellip(4,0.1,40,[10,25]*2/Fs); %设计IIR-BPFsf=filter(b,a,noise); %信号通过该滤波器subplot(335);plot(t,sf); %画出信号通过该BPF的波形xlabel('t'); ylabel('幅度');title('通过BPF后的波形');axis([0 10*pi -1.2 1.2]);grid on;%信号经过相乘器%f=[f f f f f f f f]; %%调整载波函数的长度,与BPF输出函数统一length s=sf.*f;%信号与载波相乘s=(-1).*s;subplot(336);plot(t,s);%画出信号通过该相乘器的波形xlabel('t'); ylabel('幅度');title('通过相乘器后波形');axis([0 10*pi -1 1]);grid on;%信号通过LPF%Fs=400; %抽样频率400HZt=(1:400)*10*pi/Fs; %时轴步进[b,a]=ellip(4,0.1,40,[10]*2/Fs); %设计IIR-LPFsf=filter(b,a,s); %信号通过该滤波器subplot(337);plot(t,sf); %画出信号通过该低通滤波器的波形xlabel('t'); ylabel('幅度');title('通过LPF后的波形');axis([0 10*pi -1 1]);grid on;%抽样判决%b=0.26; %设置判决门限for i=1:8for j=1:50if sf(j+50*(i-1))>bsf(j+50*(i-1))=1; %若sf>判决门限,说明此时码元为1 elsesf(j+50*(i-1))=0; %若sf<判决门限,说明此时码元为0 endendendsubplot(338);plot(t,sf); %画出信号通过抽样判决器的波形xlabel('t'); ylabel('幅度');title('抽样判决后波形');axis([3 10*pi -0.5 1.2]);grid on;QPK调制解调程序(1)调制% 调相法clear allclose allt=[-1:0.01:7-0.01];tt=length(t);x1=ones(1,800);for i=1:ttif (t(i)>=-1 & t(i)<=1) | (t(i)>=5& t(i)<=7);x1(i)=1;else x1(i)=-1;endendt1=[0:0.01:8-0.01];t2=0:0.01:7-0.01;t3=-1:0.01:7.1-0.01;t4=0:0.01:8.1-0.01;tt1=length(t1);x2=ones(1,800);for i=1:tt1if (t1(i)>=0 & t1(i)<=2) | (t1(i)>=4& t1(i)<=8);x2(i)=1;else x2(i)=-1;endendf=0:0.1:1;xrc=0.5+0.5*cos(pi*f);y1=conv(x1,xrc)/5.5;y2=conv(x2,xrc)/5.5;n0=randn(size(t2));f1=1;i=x1.*cos(2*pi*f1*t);q=x2.*sin(2*pi*f1*t1);I=i(101:800);Q=q(1:700);QPSK=sqrt(1/2).*I+sqrt(1/2).*Q;QPSK_n=(sqrt(1/2).*I+sqrt(1/2).*Q)+n0;n1=randn(size(t2));i_rc=y1.*cos(2*pi*f1*t3);q_rc=y2.*sin(2*pi*f1*t4);I_rc=i_rc(101:800);Q_rc=q_rc(1:700);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);QPSK_rc_n1=QPSK_rc+n1;figure(1)subplot(4,1,1);plot(t3,i_rc);axis([-1 8 -1 1]);ylabel('a序列');subplot(4,1,2);plot(t4,q_rc);axis([-1 8 -1 1]);ylabel('b序列');subplot(4,1,3);plot(t2,QPSK_rc);axis([-1 8 -1 1]);ylabel('合成序列'); subplot(4,1,4);plot(t2,QPSK_rc_n1);axis([-1 8 -1 1]);ylabel('加入噪声'); (2)解调% 设定T=1, 不加噪声clear allclose all% 调制bit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3);bit_Q = bit_in(2:2:1e3);data_I = -2*bit_I+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);end;t=0:0.1:1e3-0.1;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=conv(data_I2,xrc)/5.5;data_Q2_rc=conv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*sin(2*pi*f1*t1);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);% 解调I_demo=QPSK_rc.*cos(2*pi*f1*t1);Q_demo=QPSK_rc.*sin(2*pi*f1*t1);I_recover=conv(I_demo,xrc);Q_recover=conv(Q_demo,xrc);I=I_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;data_recover=[];for i=1:20:10000data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)]; end;ddd = -2*bit_in+1;ddd1=repmat(ddd',10,1);for i=1:1e4ddd2(i)=ddd1(i);endfigure(1)subplot(4,1,1);plot(t3,I);axis([0 20 -6 6]); ylabel('解调后奇位');subplot(4,1,2);plot(t3,Q);axis([0 20 -6 6]); ylabel('解调后偶位');subplot(4,1,3);plot(t2,data_recover);axis([0 20 -6 6]); ylabel('解调后序列'); subplot(4,1,4);plot(t,ddd2);axis([0 20 -6 6]); ylabel('原始序列');。
