基于matlab的QPSK与BPSK信号性能比较仿真
BPSK QPSK 8PSK 16QAM等调制方式的性能仿真及频率利用率的对比及分析

引言 (2)1 BPSK QPSK 8PSK 16QAM 调制方式的性能仿真和频率利用率的对比分析 (2)1.1 BPSK QPSK 8PSK 的性能仿真 (2)1.2 16QAM 的性能仿真 (6)2 四种调制方式各自的使用场景 (9)3 能量利用率 (10)3.2 QPSK的能量效率 (10)3.3 8PSK的能量效率 (10)3.4 16QAM的能量效率 (11)结论 (11)参考文献 (11)引言随着信息事业的迅猛发展,对数字信号调制性能上的要求越来越高本文对BPSK QPSK 8PSK 16QAM等调制方式的性能进行仿真及频率利用率的对比及分析,主要对QPSK和16QAM的相关性能进行了阐述。
并对上述四种调制方式各自的使用场景进行总结。
同时分析以上四种方式的能量效率,即每比特能量消耗的对比分析。
1 BPSK QPSK 8PSK 16QAM 调制方式的性能仿真和频率利用率的对比分析1.1 BPSK QPSK 8PSK 的性能仿真BPS K调制方式:所谓BPSK就是根据数字基带信号的两个电平,使载波相位在两个不同的数值之间切换的一种相位调制方法。
在恒参信道条件下,相移键控(BPSK) 与幅移键控( AS K) 和频移键控( F S K) 相比,具有较高的抗噪声干扰性能,且能有效地利用所给定的信道频带,即使在有多径衰落的信道中也有较好的结果,所以BPSK是一种较好的调制方式。
四相相移键控( Q P S K ) 是一种性能优良,应用十分广泛的数字调制方式,它的频带利用率高,是二相相移键控( B P S K) 的2倍。
且Q P S K调制技术的抗干扰性能强,采用相干检测时其误码率性能与B P S K相同。
8PSK,即8 Phase Shift Keying,也就是八相相移键控的意思。
QPSK调制方式中,每个相位包含了2位二进制信息,而8PSK调制方式中,每个相位包含了3位二进制信息,因而编码效率提高了50%,但同时,8PSK的抗扰性比QPSK要低很多。
QPSK通信系统性能分析与MATLAB仿真讲解

QPSK通信系统性能分析与MATLAB仿真讲解QPSK(Quadrature Phase Shift Keying)是一种调制方式,常用于数字通信中的短波通信和卫星通信等场景。
在QPSK通信系统中,将每个二进制位编码为相位不同的信号,通常使用正交载波来实现。
为了分析和评估QPSK通信系统的性能,可以使用MATLAB进行仿真。
下面将具体讲解如何进行QPSK通信系统性能分析和MATLAB仿真。
首先,我们需要定义一些基本参数。
QPSK调制是基于二进制编码的,因此将要发送的数据转换为二进制比特流。
可以使用MATLAB中的函数来生成二进制比特流,如`randi([0,1],1,N)`,其中N是比特流的长度。
在这里,可以自行选择比特流的长度。
接下来,需要将二进制比特流分组为2比特一组,以便编码为相位信息。
可以使用MATLAB中的函数来进行分组,如`reshape(bit_stream,2,length(bit_stream)/2)'`,其中bit_stream是二进制比特流。
这里的重点是要确保二进制比特流的长度为2的倍数。
然后,将每组2比特编码为相位信息。
QPSK调制使用4个相位点来表示4种可能的组合,通常用0、π/2、π和3π/2来表示这些相位点。
可以使用MATLAB中的函数生成这些相位信息,如`phase_data =[0,pi/2,pi,3*pi/2]`。
接下来,通过幅度和相位信息生成QPSK信号。
可以使用MATLAB中的函数来生成QPSK信号,如`qpsk_signal = cos(2*pi*f*t+phase)`,其中f是载波频率,t是时间,phase是相位信息。
然后,添加噪声到QPSK信号中以模拟实际通信环境。
可以使用MATLAB中的函数来添加噪声,如`noisy_signal =awgn(qpsk_signal,SNR)`,其中SNR是信噪比。
最后,解调接收到的信号以恢复原始数据。
可以使用MATLAB中的函数来解调信号,如`received_bits = reshape(received_signal,[],2) > 0`。
BPSK与QPSK调制仿真

BPSK 与QPSK 调制仿真1、BPSK 调制信号仿真BPSK 是二进制相移键控的简称,它利用两种相位来传输二元符号。
其最常用的两种相位是0与π,在第n 时隙,其信号可以表述为:b b nc n c bpsk nT t T n a t f A a t f A S ≤≤-⎩⎨⎧=-==)1(1,2cos 1,2cos ππ即传输码元1时采用与载波同相的正弦波,而传输码元0时采用与载波反相的正弦波。
由于BPSK 调制的本质是相位调制,如果考虑其基带信号时的调制,就相当于在基带信号上再乘以)exp(θj ,本次仿真中传输码元1和0时,θ分别取0和π。
BPSK 信号相位矢量图如图1所示。
图 1 BPSK 信号相位矢量经过理论计算得,BPSK 调制信号在高斯信道下的误比特率为:)2(0N E Q P b b = 根据以上理论,用MATLAB 仿真得BPSK 调制信号在高斯信道下与理论分析结果的误比特率性能比较结果如图2所示。
此次仿真所得误比特率为8次重复检测所得的平均误比特率。
由仿真结果可得仿真出的误比特率与理论误比特率比较接近,仿真较成功。
(注:BPSK 调制时误符号率与误比特率相同,所以仿真结果也相同)图 2 BPSK 调制仿真结果2、QPSK 调制信号仿真QPSK 是四相移键控的简称,它实际上是一种四元数字频带调制方式,它利用4种离散的相位状态传输四元的符号序列。
在第n 时隙,其信号可以表述为:s s n c Q PSK nT t T n t f A S ≤≤-+=)1(),2cos(θπ其中n θ为受调制的相位,其常用的四种相位值有两套,分别为A方式与B 方式,这两种方式的调制信号矢量图如图3所示。
图 3 QPSK 的两套矢量图QPSK 调制实质上是一种正交调制,它等于两路正交的BPSK 的叠加。
以B 方式为例,将四元序列{}n a 的高位比特与低位比特分别排成{}n b 1与{}n b 0序列,那么,QPSK 正是这两个二元序列生成的BPSK信号的正交叠加。
BPSK和QPSK调制解调原理及MATLAB程序

2.1 PSK调制方式PSK原理介绍(以2-PSK为例)移相键控(PSK)又称为数字相位调制,二进制移相键控记作2PSK。
绝对相移是利用载波的相位(指初相)直接表示数字信号的相移方式。
二进制相移键控中,通常用相位0 和π来分别表示“0”或“1”。
2PSK 已调信号的时域表达式为s2psk(t)=s(t)cosωct, 2PSK移相键控中的基带信号与频移键控和幅度键控是有区别的,频移键控和幅度键控为单极性非归零矩形脉冲序列,移相键控为为双极性数字基带信号,就模拟调制法而言,与产生2ASK 信号的方法比较,只是对s(t)要求不同,因此2PSK 信号可以看作是双极性基带信号作用下的DSB 调幅信号。
在二进制数字调制中,当正弦载波的相位随二进制数字基带信号离散变化时,则产生二进制移相键控(2PSK)信号。
通常用已调信号载波的 0°和 180°分别表示二进制数字基带信号的 1 和 0。
二进制移相键控信号的时域表达式为e2PSK(t)=[nna g(t-nT s)]cosw c t其中, an与2ASK和2FSK时的不同,在2PSK调制中,an应选择双极性。
1, 发送概率为Pan=-1, 发送概率为1-P若g(t)是脉宽为Ts, 高度为1的矩形脉冲时,则有cosωct, 发送概率为Pe2PSK(t)=-cosωct, 发送概率为1-P由上式(6.2-28)可看出,当发送二进制符号1时,已调信号e2PSK(t)取0°相位,发送二进制符号0时,e2PSK(t)取180°相位。
若用φn表示第n个符号的绝对相位,则有0°, 发送 1 符号φn=180°, 发送 0 符号由于在2PSK信号的载波恢复过程中存在着180°的相位模糊,所以2PSK信号的相干解调存在随机的“倒π”现象,从而使得2PSK 方式在实际中很少采用。
为了解决2PSK 信号解调过程的反向工作问题, 提出了二进制差分相位键控(2DPSK),这里不再详述。
(完整版)基于matlab的通信系统仿真毕业论文

创新实践报告报告题目:基于matlab的通信系统仿真学院名称:信息工程学院*名:***班级学号:***师:**二O一四年十月十五日目录一、引言 (3)二、仿真分析与测试 (4)2.1 随机信号的生成 (4)2.2信道编译码 (4)2.2.1 卷积码的原理 (4)2.2.2 译码原理 (5)2.3 调制与解调 (5)2.3.1 BPSK的调制原理 (5)2.3.2 BPSK解调原理 (6)2.3.3 QPSK调制与解调 (7)2.4信道 (8)2.4.1 加性高斯白噪声信道 (8)2.4.2 瑞利信道 (8)2.5多径合并 (8)2.5.1 MRC方式 (8)2.5.2 EGC方式 (9)2.6采样判决 (9)2.7理论值与仿真结果的对比 (9)三、系统仿真分析 (11)3.1有信道编码和无信道编码的的性能比较 (11)3.1.1信道编码的仿真 (11)3.1.2有信道编码和无信道编码的比较 (12)3.2 BPSK与QPSK调制方式对通信系统性能的比较 (13)3.2.1调制过程的仿真 (13)3.2.2不同调制方式的误码率分析 (14)3.3高斯信道和瑞利衰落信道下的比较 (15)3.3.1信道加噪仿真 (15)3.3.2不同信道下的误码分析 (15)3.4不同合并方式下的对比 (16)3.4.1 MRC不同信噪比下的误码分析 (16)3.4.2 EGC不同信噪比下的误码分析 (16)3.4.3 MRC、EGC分别在2根、4根天线下的对比 (17)3.5理论数据与仿真数据的区别 (17)四、设计小结 (19)参考文献 (20)一、引言现代社会发展要求通信系统功能越来越强,性能越来越高,构成越来越复杂;另一方面,要求通信系统技术研究和产品开发缩短周期,降低成本,提高水平。
这样尖锐对立的两个方面的要求,只有通过使用强大的计算机辅助分析设计技术和工具才能实现。
在这种迫切的需求之下,MATLAB应运而生。
bpskqpsk的matlab仿真
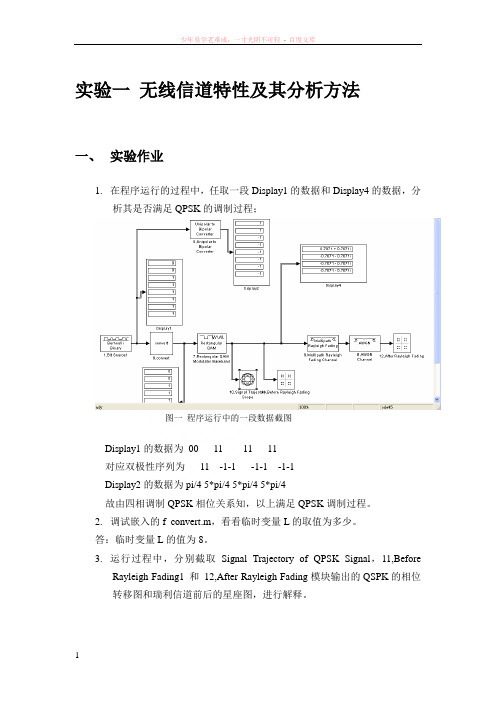
实验一无线信道特性及其分析方法一、实验作业1.在程序运行的过程中,任取一段Display1的数据和Display4的数据,分析其是否满足QPSK的调制过程;图一程序运行中的一段数据截图Display1的数据为00 11 11 11对应双极性序列为11 -1-1 -1-1 -1-1Display2的数据为pi/4 5*pi/4 5*pi/4 5*pi/4故由四相调制QPSK相位关系知,以上满足QPSK调制过程。
2.调试嵌入的f_convert.m,看看临时变量L的取值为多少。
答:临时变量L的值为8。
3.运行过程中,分别截取Signal Trajectory of QPSK Signal,11,BeforeRayleigh Fading1 和12,After Rayleigh Fading模块输出的QSPK的相位转移图和瑞利信道前后的星座图,进行解释。
图二Signal Trajectory of QPSK Signal图三瑞利信道前的星座图图四瑞利信道后的星座图答:QPSK调制相位跳变最大为±pi,最小为±pi/2由图二知仿真满足要求。
图三和图四知,信号通过瑞利信道后星座图出现失真。
因信号受瑞丽信道的干扰在星座图上出现相位和幅度失真,且不同时刻,失真大小不一。
实验二典型通信系统的搭建和分析四、实验作业1.对比Probe1/ Probe2/ Probe3处的数据,说明采用BSPK和QPSK调制前后,比特周期和符号周期之间的关系。
调制前 Probe1: W:16,Tf:[1.6e-005 0]Probe2: W:16,Tf:[1.6e-005 0] QPSKProbe3: W:16,Tf:[1.6e-005 0] BPSKProbe1/2/3处的数据Probe1 W:16 Tf:[1/6e-005 0]Prope2 W:8 Tf[1.6e-005 0]Prope2 W:16 Tf[1.6e-005 0]BPSK调制前后比特周期和符号周期没有变化,且符号周期等于比特周期。
qpsk、bpsk蒙特卡洛仿真matlab代码
qpsk、bpsk的蒙特卡洛仿真是一种用于测试和验证通信系统性能的重要工具。
通过模拟大量的随机输入数据,并对系统进行多次仿真运算,可以对系统的性能进行全面评估,包括误码率、信噪比要求等。
在matlab中,我们可以通过编写相应的仿真代码来实现qpsk、bpsk 的蒙特卡洛仿真。
下面将分别介绍qpsk和bpsk的蒙特卡洛仿真matlab代码。
一、qpsk的蒙特卡洛仿真matlab代码1. 生成随机的qpsk调制信号我们需要生成一组随机的qpsk调制信号,可以使用randi函数生成随机整数序列,然后将其映射到qpsk符号点上。
2. 添加高斯白噪声在信号传输过程中,会受到各种干扰,其中最主要的干扰之一就是高斯白噪声。
我们可以使用randn函数生成高斯白噪声序列,然后与调制信号相加,模拟信号在传输过程中受到的噪声干扰。
3. 解调和判决接收端需要进行解调和判决操作,将接收到的信号重新映射到qpsk符号点上,并判断接收到的符号与发送的符号是否一致,从而判断是否发生误码。
4. 统计误码率通过多次仿真运算,记录错误判决的次数,从而可以计算出系统的误码率。
二、bpsk的蒙特卡洛仿真matlab代码1. 生成随机的bpsk调制信号与qpsk相似,我们需要先生成一组随机的bpsk调制信号,然后模拟信号传输过程中的噪声干扰。
2. 添加高斯白噪声同样使用randn函数生成高斯白噪声序列,与bpsk调制信号相加。
3. 解调和判决接收端对接收到的信号进行解调和判决,判断接收到的符号是否与发送的符号一致。
4. 统计误码率通过多次仿真运算,记录错误判决的次数,计算系统的误码率。
需要注意的是,在编写matlab代码时,要考虑到信号的长度、仿真次数、信噪比的范围等参数的选择,以及仿真结果的统计分析和可视化呈现。
qpsk、bpsk的蒙特卡洛仿真matlab代码可以通过以上步骤实现。
通过对系统性能进行全面评估,可以帮助工程师优化通信系统设计,提高系统的可靠性和稳定性。
基于MATLAB的BPSK调制仿真及性能分析
******************实践教学*******************兰州理工大学计算机与通信学院2015年春季学期通信系统仿真训练课程设计题目:基于MATLAB的BPSK调制仿真及性能分析专业班级:姓名:学号:指导教师:成绩:摘要BPSK是在21世纪的现阶段,数字通信系统是现代通信系统的主流,在社会生活各个方面占据重要地位,调制与解调是一个不可或缺的环节,它大大提高了信号的传输性能和安全性。
BPSK作为数字通信系统中的一种简单、基础的调制解调方法,抗干扰能力强,容易仿真实现。
在了解并掌握了BPSK调制与解调原理后,学习MATLAB仿真软件的使用方法。
本次课程设计为基于MATLAB的BPSK调制仿真。
本次课设着重介绍了算法的实现,并采用MATLAB程序仿真测试了BPSK过程中单极性不归零编码、脉冲成形、PSK调制、信号通过AWGN信道、载波恢复、解调、解码等过程。
关键词:BPSK、调制解调、MATLAB仿真、数字通信系统前言 (3)一、BPSK原理 (4)1.1 MPSK的介绍 (4)1.1.1 MPSK的介绍 (4)1.2 BPSK简介 (5)1.2.1 BPSK的概念及分类 (5)1.3 BPSK信号的产生 (5)1.4 BPSK调制 (5)1.4.1 调制的概念 (5)1.4.2 调制的种类 (6)1.4.3 调制的作用 (6)1.4.4 调制方式 (6)1.4.5 BPSK的调制原理 (7)1.5 BPSK的解调 (8)1.6 高斯噪声 (8)1.6.1 高斯白噪声 (8)二、设计思路 (9)三、设计仿真及分析 (10)3.1 设计仿真 (10)3.2 结果总体分析 (13)总结 (14)参考文献 (15)致谢 (16)数字通信系统使用的最基本的就是PSK,实际上由于交调的存在,大都使用PSK,由于电波主要在自由空间传播,信道参数比较稳定,信道的主要干扰是高斯白噪声,因而可视为恒参信道。
BPSK与QPSK调制解调系统性能仿真
BPSK与QPSK调制解调系统性能仿真比较计算机与信息工程学院****级***班姓名学号指导教师***教授摘要本文利用Systemview系统给我们提供的软件平台,对正弦波数字调制系统的移相键控进行仿真,并进一步对BPSK与DPSK及QPSK进行比较。
我们可以直观实时的观察到信道输出的波形,已调信号功率频谱,相位星座图等变化,误码率曲线,从而分析得到不同调制方式性能差别。
关键词Systemview;BPSK、DPSK、QPSK;功率谱;星座图;误码率;1引言通信系统越来越复杂,System View是适应这种变化的一个动态系统设计、仿真和分析的可视化设计软件,它提供了开发电子系统的模拟和数字工具。
数字相位调制在通信中占有非常重要的地位。
二进制中相对相移DPSK的应用解决了绝对相移BPSK的“倒π”现象,四进制QPSK调制效率高、传输速度快,三者各有其优点。
但在相同信道下传送相同的信息序列性能各自有所不同。
System View仿真将实现基本的BPSK 、DPSK 、QPSK调制解调系统的比较。
输出波形的不同,可对功率谱进行比较,也可反映传输速度。
星座图的观察,也能实现传输速度的分析。
误码率测试,可对系统抗噪声性能比较。
2仿真软件简介2.1 System view简介SystemView是美国ELANIX公司推出的,基于Windows环境下运行的用于系统仿真分析的可视化软件工具,它使用功能模块(Token)去描述程序,无需编写程序即可完成各种系统的设计与仿真,快速地建立和修改系统、访问与调整参数,方便地加入注释。
利用System View,可以构造各种复杂的模拟、数字、数模混合系统,各种多速率系统,因此,它可用于各种线性或非线性控制系统的设计和仿真。
可对线性系统进行拉氏变换和Z变换分析。
用户在进行系统设计时,只需从System View配置的图标库中调出有关图标并进行参数设置,完成图标间的连线,然后运行仿真操作,最终以时域波形、眼图、功率谱等形式给出系统的仿真分析结果。
基于MATLAB的BPSK通信系统仿真
基于MATLAB的BPSK通信系统仿真摘要:BPSK就是数字带通传输系统中一种非常重要的方式。
对于它的研究有助于我们掌握更加复杂的数字通信系统的传输方式。
本文介绍了BPSK的调制原理,以及使用Simulink对其调制过程进行仿真。
Simulink是MATLAB中最重要的组件之一,它向用户提供一个动态系统建模、仿真和综合分析的集成环境,在这种环境中,用户无须写大量的程序,而只要通过简单直观的鼠标操作,选取适当的库模块,就可以构造出复杂的仿真模型。
文章对于Simulink模块的库作了比较详细的介绍,如何进行模块参数的设置也作了说明。
使用Simulink仿真,直观简便,极大地减轻了工作量,简化了复杂的通信过程分析,也极大的方便了我们对于通信系统的研究与掌握。
关键词:BPSK;Simulink;仿真BPSK Communication System Simulation Based on MATAB Abstract:BPSK is the digital transmission system in a very important way. For its research helps us to grasp more complex transmission of a digital communication system. This article introduces the BPSK modulation principle, as well as its modulation process simulation using Simulink. Simulink is one of the most important components in MATLAB, it offers the user a comprehensive analysis of dynamic systems modeling, simulation and integration environments, in this environment, users do not have to write a lot of programs, but merely through simple, intuitive mouse operation, select the appropriate library module, you can construct sophisticated simulation models. Article for a Simulink block library for a more detailed introduction, described how to set module parameters. Using Simulink simulation, intuitive and easy, greatly reducing the workload, simplifying analysis of complex communication process, was also very handy for communication system of research and at our disposal.Key words:BPSK; Simulink; simulation目录1 序言 (1)1.1 数字通信系统研究的背景及意义 (1)1.2 数字通信的应用现状和未来的发展 (1)2 通信的基本知识 (4)2.1通信的基本概念 (4)2.2通信系统的通信过程与原理 (4)2.2.1通信系统的一般模型 (4)2.2.2模拟和数字通信系统 (6)3 BPSK的调制原理 (8)3.1数字调制的基础 (8)3.2 二进制相移键控(BPSK) (9)4 MATLAB的Simulink工具仿真 (11)4.1 MATLAB的简介 (11)4.2 Simulink的主要优点[7] (12)4.3 Simulink的模块库介绍 (12)4.4 Simulink简单模型的建立 (15)4.5 2PSK调制的仿真 (15)4.5.1 键控调制法 (15)4.5.2 模拟调制法 (19)4.6 仿真结果分析 (20)5 结论 (21)参考文献 (22)致谢 (23)1 序言1.1数字通信系统研究的背景及意义古代通信利用自然界的基本规律和人的基础感官(视觉,听觉等)可达性建立通信系统,是人类基于需求的最原始通信方式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊目录第一章概述 (1)第二章QPSK通信系统原理与仿真 (1)2.1 QPSK系统框图介绍 (1)2.2QPSK信号的调制原理 (2)2.2.1QPSK信号产生方法 (2)2.2.2QPSK星座图 (2)2.3QPSK解调原理及误码率分析 (3)2.3.1QPSK解调方法 (3)2.3.2QPSK系统误码率 (3)2.4QPSK信号在AWGN信道下仿真 (4)第三章BPSK通信系统原理与仿真 (4)3.1BPSK信号的调制原理 (4)3.2BPSK解调原理及误码率分析 (4)第四章QPSK与BPSK性能比较 (5)4.1QPSK与BPSK在多信道下比较仿真 (5)4.1.1纵向比较分析 (5)4.1.2横向比较分析 (7)4.2仿真结果分析 (7)4.2.1误码率分析 (7)4.2.2频带利用率比较 (7)附录 (8)代码1 (8)代码2 (8)代码3 (10)代码4 (12)┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊第一章概述QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
它以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接人、移动通信及有线电视系统之中。
BPSK是英文Binary Phase Shift Keying的缩略语简称,意为二相相移键控,是利用偏离相位的复数波浪组合来表现信息键控移相方式的一种。
它使用了基准的正弦波和相位反转的波浪,使一方为0,另一方为1,从而可以同时传送接受2值(1比特)的信息。
本文所研究的QPSK系统与二进制的BPSK系统相比,具有以下特点:1.在传码率相同的情况下,四进制数字调制系统的信息速率是二进制系统的2倍。
2.在相同信息速率条件下,四进制数字调制系统的传码率是二进制系统的1/4倍,这一特点使得四进制码元宽度是二进制码元宽度的2倍,码元宽度的加大,可增加每个码元的能量,也可减小码间串扰的影响。
3.由于四进制码元速率比二进制的降低,所需信道带宽减小。
4.在接收系统输入信噪比相同的条件下,四进制数字调制系统的误码率要高于二进制系统。
5.四进制数字调制系统较二进制系统复杂,常在信息速率要求较高的场合。
基于以上优点,在数字信号的调制方式中QPSK(Quadrature Phase Shift Keying)四相移键控是目前最常用的一种卫星数字信号调制方式,它具有较高的频谱利用率、较强的抗干扰性,在电路上实现也较为简单,因而被WCDMA和CDMA2000等第三代移动通信系统采用。
第二章QPSK通信系统原理与仿真2.1 QPSK系统框图介绍在图2.1的系统中,发送方,QPSK数据源采用随机生成,信源编码采用差分编码,编码后的信号经QPSK调制器,经由发送滤波器进入传输信道。
接收方,信号首先经过相位旋转,再经匹配滤波器解调,经阈值比较得到未解码的接收信号,差分译码后得到接收信号,与信源发送信号相比较,由此得到系统误码率,同时计算系统误码率的理论值,将系统值与理论值进行比较。
对于信道,这里选取的是加性高斯白噪声(Additive White Gaussian Noise)以及多径Rayleigh┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊衰落信道(Multipath Rayleigh Fading Channel)。
图2.1 QPSK系统框图在实验中,选用的是差分码。
差分码又称为相对码,在差分码中利用电平跳变来分别表示1或0,分为传号差分码和空号差分码。
传号差分码:当输入数据为“1”时,编码波型相对于前一码电平产生跳变;输入为“0”时,波型不产生跳变。
空号差分码:当输入数据为“0”时,编码波型相对于前一码电平产生跳变;输入为“1”时,波型不产生跳变。
2.2QPSK信号的调制原理2.2.1QPSK信号产生方法QPSK信号通常由图2.2所示的调相法产生,输入的二进制序列经过一个串/并转换器后分为两路二进制序列,这里假设两路序列为a,b,并通过平衡调制器分别对同相载波及正交载波进行二相调制,得到如图2.3中的虚线矢量。
QPSK信号每个码元含有2比特的信息,如图2.3所示现用ab代表这两个比特。
两个比特有4种组合,即00、01、10和11。
它们和相位之间的关系通常都按格雷码的规律安排,如表2-1所示。
图2.2 调相法产生QPSK信号图2.3 信号矢量2.2.2QPSK星座图在本次系统仿真中使用仿真代码产生QPSK信号星座图,具体代码如附录代码1。
┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊运行得到的信号星座图如图2.4,2.5:表2-1 QPSK编码规则表中k-一组间隔均匀的受调制相位2.3QPSK解调原理及误码率分析2.3.1QPSK解调方法由于QPSK信号可以看作两个正交2PSK信号的叠加,解调框图如图2.6,用相干解调方法,即用两路正交的相干载波,可以很容易的分离出这两路正交的2PSK信号。
解调后的两路基带信号码元a和b,经过并串变换后,成为串行数据输出。
图2.4 A方式信号星座图图2.5 B方式信号星座图2.3.2QPSK系统误码率在QPSK体制中,由其矢量图(图2.7)可以看出,因噪声的影响使接收端解调时发生错误判决,是由于信号矢量的相位发生偏离造成的。
例如,设发送矢量的相位为45,它代表基带信号码元“11”,若因噪声的影响使接收矢量的相位变成135,则将误判为“01”。
当各个发送矢量以等概率出现时,合理的判决门限应该设在和相邻矢量等距离的位置。
在图中对于矢量“11”来说,判决门限应该设在 0和90。
当发送“11”时,接收信号矢量的相位若超出这一范围(图图2.6 QPSK信号解调原理框图图2.7 QPSK噪声容限┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊中阴影区),则将发生错判。
设)(θf为接收矢量(包括信号和噪声)相位的概率密度,则发生错误的概率为:省略计算)(θf和Pe的繁琐过程,直接给出计算结果:上式计算出的是QPSK信号的误码率。
若考虑其误比特率,正交的两路相干解调方法和2PSK 中采用的解调方法一样。
所以其误比特率的计算公式也和2PSK的误码率公式一样。
2.4QPSK信号在AWGN信道下仿真仿真代码见附录代码2。
运行结果如图2.8:图2.8 AWGN环境下QPSK系统的仿真和理论结果由运行结果可以看出,仿真值与理论值基本吻合,误码率值随信噪比增大而下降。
第三章BPSK通信系统原理与仿真3.1BPSK信号的调制原理图3.1 模拟调制方法图3.2 键控调制方法BSPK信号通常有2种调制方式,分别如图3.1、3.2所示。
在2PSK中,通常用初始相位0和p分别表示二进制“1”和“0”。
因此,2PSK信号的时域表达式为式中,nϕ表示第n个符号的绝对相位:因此,上式可以改写为3.2BPSK解调原理及误码率分析BPSK信号的解调器原理方框图3.3和波形图3.4,这里给出的解调框图采用相干解调的接收方法。
图3.3 BPSK信号相干解调框图波形图中,假设相干载波的基准相位与2PSK信号的调制载波的基准相位一致(通常默认为0相位)。
但是,由于在2PSK信号的载波恢复过程中存在着的相位模糊,即恢复的本地载波与┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊所需的相干载波可能同相,也可能反相,这种相位关系的不确定性将会造成解调出的数字基带信号与发送的数字基带信号正好相反,即“1”变为“0”,“0”变为“1”,判决器输出数字信图3.4 相干解调波形示意图号全部出错。
这种现象称为2PSK 方式的“倒π”现象或“反相工作”。
这也是2PSK方式在实际中很少采用的主要原因。
另外,在随机信号码元序列中,信号波形有可能出现长时间连续的正弦波形,致使在接收端无法辨认信号码元的起止时刻。
第四章QPSK与BPSK性能比较4.1QPSK与BPSK在多信道下比较仿真QPSK仿真程序见代码3。
BPSK仿真程序见代码4。
下面对QPSK与BPSK在多信道下的BER-SNR曲线进行横向及纵向的比较,如表4-1所示。
4.1.1纵向比较分析图中依次给出LOS信道、莱斯平坦衰落信道、莱斯频率选择性衰落、瑞利平坦衰落信道、瑞利频率选择性衰落。
比较频率选择性衰落和其相应的平坦衰落,可发现频率选择性衰落比相应的平坦衰落的性能差。
比较莱斯信道和瑞利信道,可发现不存在视距分量的瑞利信道比存在视距分量的任何莱斯信道的性能差。
表4-1 QPSK与BPSK在多信道下性能比较┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊4.1.2横向比较分析相同信道下,BPSK调制的系统误码率小于QPSK调制。
本次仿真过程中,莱斯平坦衰落信道下两者误码率差别显著。
4.2仿真结果分析4.2.1误码率分析由前面介绍的误码率内容可以看出,QPSK判决门限为90,BPSK的判决门限为180。
因此相同系统情况下的误码率BPSK优于QPSK。
4.2.2频带利用率比较在传码率相同的情况下,四进制数字调制系统的信息速率是二进制系统的2倍。
频带利用率公式在相同信号速率的情况下,QPSK和BPSK系统的带宽是相同的,但是由于QPSK每个信号都是四进制的,QPSK每个信号包含2bit信息,所以比特率就是BPSK的两倍,因而其频带利用率即为BPSK的两倍。
BPSK系统理论的频带利用率最大为1,但是在实际的实现中不能达到1,而在QPSK系统中,频带利用率可以超过1。
┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊附录代码1function qpskconstellationA(M)M=4;x=[0:M-1];scatterplot(pskmod(x,M)); % A方式QPSK信号grid on;returnfunction qpskconstellationB(M)M=4;x=[0:M-1];scatterplot(pskmod(x,M,pi/4)); % B方式QPSK信号grid on;return代码2function [x,bits]=random_binary(nbits,nsamples)x=zeros(1,nbits*nsamples);bits=round(rand(1,nbits));for m=1:nbitsfor n=1:nsamplesindex=(m-1)*nsamples+n;x(1,index)=(-1)^bits(m);endendreturnfunction [c,lags]=vxcorr(a,b)%计算a b 的互相关系数,返回C是列向量,长度为ab的长度和减1a=a(:);b=b(:);M=length(a);maxlag=M-1;lags=[-maxlag:maxlag]';A=fft(a,2^nextpow2(2*M-1));%快速傅立叶变换B=fft(b,2^nextpow2(2*M-1));c=ifft(A.*conj(B));%快速傅立叶反变换c=[c(end-maxlag+1:end,1);c(1:maxlag+1,1)];[nr nc]=size(a);if(nr>nc)c=c';lags=lags.';endreturnfunction BER_MC=MCQPSKrun(N,Eb,N0,ChanAtt,TimingBias,TimingJitter,PhaseBias,PhaseJitter) fs=1e+6; % 采样速率SymRate=1e+5; % 信号速率Ts=1/fs; % 采样周期TSym=1/SymRate; % 信号周期SymToSend=N; % 发送信号数ChanBW=4.99e+5; % 带宽MeanCarrierPhaseError=PhaseBias; % 载波相位均值StdCarrierPhaseError=PhaseJitter; % 相位误差标准差MeanSymbolSyncError=TimingBias; % 符号同步误差均值┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊StdSymbolSyncError=TimingJitter; % 符号同步误差标准差ChanGain=10^(-ChanAtt/20); % 信道增益TxBitClock=Ts/2; % 发送机时钟RxBitClock=Ts/2; % 接收机时钟%接收机输入端噪声标准差和信号幅度RxNoiseStd=sqrt((10^((N0-30)/10))*(fs/2));TxSigAmp=sqrt(10^((Eb-30)/10)*SymRate);%分配缓存SampPerSym=fs/SymRate;probe1=zeros((SymToSend+1)*SampPerSym,1);probe1counter=1;probe2=zeros((SymToSend+1)*SampPerSym,1);probe2counter=1;%计已传输信号的个数TxSymSent=1;RxSymDemod=0;%发送和接收数据缓冲区[unused,SourceBitsI]=random_binary(SymToSend,1);[unused,SourceBitsQ]=random_binary(SymToSend,1);%差分编码TxBitsI=SourceBitsI*0;TxBitsQ=SourceBitsQ*0;for k=2:length(TxBitsI)TxBitsI(k)=or(and(not(xor(SourceBitsI(k),SourceBitsQ(k))),xor(SourceBitsI(k),TxBitsI(k-1))),and(xor(SourceBitsI(k),So urceBitsQ(k)),xor(SourceBitsQ(k),TxBitsQ(k-1))));TxBitsQ(k)=or(and(not(xor(SourceBitsI(k),SourceBitsQ(k))),xor(SourceBitsQ(k),TxBitsQ(k-1))),and(xor(SourceBitsI(k) ,SourceBitsQ(k)),xor(SourceBitsI(k),TxBitsI(k-1))));end%产生复信号TxBits=((TxBitsI*2)-1)+(sqrt(-1)*((TxBitsQ*2)-1));RxIntegrator=0; %初始化接收机积分器TxBitClock=2*TSym; %初始化发送机%设计信道滤波器,产生滤波器参数序列[b,a]=butter(2,ChanBW/(fs/2));b=[1];a=[1];[junk,FilterState]=filter(b,a,0);% 开始仿真循环while TxSymSent<SymToSendTxBitClock=TxBitClock+Ts;if TxBitClock>TSymTxSymSent=TxSymSent+1;TxBitClock=mod(TxBitClock,TSym);TxOutput=TxBits(TxSymSent)*TxSigAmp;end%信号经过信道滤波器[Rx,FilterState]=filter(b,a,TxOutput,FilterState);%加高斯白噪声Rx=(ChanGain*Rx)+(RxNoiseStd*(randn(1,1)+sqrt(-1)*randn(1,1)));%基于接收机载波同步误差的相位旋转PhaseRotation=exp(sqrt(-1)*2*pi*(MeanCarrierPhaseError+(randn(1,1)*StdCarrierPhaseError))/360);Rx=Rx*PhaseRotation;probe1(probe1counter)=Rx;probe1counter= probe1counter+1;%更新接收机积分清除器RxIntegrator=RxIntegrator+Rx;probe2(probe2counter)=RxIntegrator;probe2counter= probe2counter+1;%更新接收机时钟,判断是不是适合采样RxBitClock=RxBitClock+Ts;RxTSym=TSym*(1+MeanSymbolSyncError+(StdSymbolSyncError*randn(1,1)));if RxBitClock>RxTSym %解调信号RxSymDemod=RxSymDemod+1;┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊RxBitsI(RxSymDemod)=round(sign(real(RxIntegrator))+1)/2;RxBitsQ(RxSymDemod)=round(sign(imag(RxIntegrator))+1)/2;RxBitClock=RxBitClock-TSym;RxIntegrator=0;endend%差分解码SinkBitsI=SourceBitsI*0;SinkBitsQ=SourceBitsQ*0;for k=2:RxSymDemodSinkBitsI(k)=or(and(not(xor(RxBitsI(k),RxBitsQ(k))),xor(RxBitsI(k),RxBitsI(k-1))),and(xor(RxBitsI(k),RxBitsQ(k)),xor (RxBitsQ(k),RxBitsQ(k-1))));SinkBitsQ(k)=or(and(not(xor(RxBitsI(k),RxBitsQ(k))),xor(RxBitsQ(k),RxBitsQ(k-1))),and(xor(RxBitsI(k),RxBitsQ(k)), xor(RxBitsI(k),RxBitsI(k-1))));end%在输入和输出100字节中寻找最佳时延[C,Lags]=vxcorr(SourceBitsI(10:110),SinkBitsI(10:110));[MaxC,LocMaxC]=max(C);BestLag=Lags(LocMaxC);% 调整时延if BestLag>0SourceBitsI=SourceBitsI(BestLag+1:length(SourceBitsI));SourceBitsQ=SourceBitsQ(BestLag+1:length(SourceBitsQ));elseif BestLag<0SinkBitsI=SinkBitsI(-BestLag+1:length(SinkBitsI));SinkBitsQ=SinkBitsQ(-BestLag+1:length(SinkBitsQ));end%将序列调整成相同长度TotalBits=min(length(SourceBitsI),length(SinkBitsI));TotalBits=TotalBits-20;SourceBitsI=SourceBitsI(10:TotalBits);SourceBitsQ=SourceBitsQ(10:TotalBits);SinkBitsI=SinkBitsI(10:TotalBits);SinkBitsQ=SinkBitsQ(10:TotalBits);Errors=sum(SourceBitsI ~= SinkBitsI)+sum(SourceBitsQ ~= SinkBitsQ);BER_MC=Errors/(2*length(SourceBitsI));returnfunction MCQPSKBEREb=22:0.5:26;N0=-50;ChannelAttenuation=70;EbN0dB=(Eb-ChannelAttenuation)-N0;EbN0=10.^(EbN0dB./10);BER_T=0.5*erfc(sqrt(EbN0));N=round(100./BER_T);BER_MC=zeros(size(Eb));for k=1:length(Eb)BER_MC(k)=MCQPSKrun(N(k),Eb(k),N0,ChannelAttenuation,0,0,0,0);disp(['simulation',num2str(k*100/length(Eb)),'%complate']);endfigure(1);semilogy(EbN0dB,BER_MC,'o',EbN0dB,2*BER_T,'-');xlabel('Eb/N0(dB)');ylabel('bit error rate');legend('MC BER Estimate','Theoretical BER');grid;return代码3function [peideal,pesystem]=qpsk_berest(xx,yy,ebn0db,eb,tb,nbw)%xx为输入序列,yy为输出序列,ebn0db为信噪比,eb为单个信号能力,tb信号周期,nbw噪声带宽[n1 n2]=size(xx);nx=n1*n2;[n3 n4]=size(yy);┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊[n5 n6]=size(ebn0db);neb=n5*n6;%接收机带宽设定为rs/2nbwideal=1/(2*tb*2);for m=1:nebpeideal(m)=0.0; % 初始化pesystem(m)=0.0; % 初始化%计算n0和噪声方差string1=['Eb/N0=',num2str(ebn0db(m))];disp(string1)ebn0(m)=10^(ebn0db(m)/10);n0=eb/ebn0(m); % 噪声功率sigma=sqrt(n0*nbw*2); % 方差sigma1=sqrt(n0*nbwideal*2); % 理想方差b=sqrt(2*eb/tb)/sqrt(sum(abs(xx).^2)/nx);for n=1:nxtheta=angle(xx(n));if(theta<0)theta=theta+2*pi;end%接收信号的相位旋转xxx(n)=b*xx(n)*exp(-i*(theta-(pi/4)));yyy(n)=yy(n)*exp(-i*(theta-(pi/4)));d1=real(xxx(n));d2=imag(xxx(n));d3=real(yyy(n));d4=imag(yyy(n));pe1=q(d1/sigma1)+q(d2/sigma1);pe2=q(d3/sigma)+q(d4/sigma);peideal(m)=peideal(m)+pe1;pesystem(m)=pesystem(m)+pe2;endendpeideal=(1/2)*peideal./nx;pesystem=(1/2)*pesystem./nx;returnfunction QPSKThreeray(p0,p1,p2,delay)NN=256; %发送的信号数tb=0.5; %信号周期fs=16; %每信号的采样数ebn0db=[1:2:14]; %信噪比矢量%产生QPSK信号x=random_binary(NN,fs)+i*random_binary(NN,fs);delay0=0;delay1=0;delay2=delay;%设置瑞利信道gain1=sqrt(p1)*abs(randn(1,NN)+i*randn(1,NN));gain2=sqrt(p2)*abs(randn(1,NN)+i*randn(1,NN));for k=1:NNfor kk=1:fsindex=(k-1)*fs+kk;ggain1(1,index)=gain1(1,k);ggain2(1,index)=gain2(1,k);endendy1=x;for k=1:delay2y2(1,k)=y1(1,k)*sqrt(p0);endfor k=(delay2+1):(NN*fs)y2(1,k)=y1(1,k)*sqrt(p0)+y1(1,k-delay1)*ggain1(1,k)+y1(1,k-delay2)*ggain2(1,k); end%匹配滤波器b=-ones(1,fs);┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊a=1;y=filter(b,a,y2);%应用半解析方法,进行误码率估计。
