有关曲线要素计算
曲线计算公式

一、曲线要素计算已知:JDZH 、JDX 、JDY 、R 、L S1、L S2、L H 、T 、A 1、A 2(L H =L S1+L S2+圆曲线长)1、求ZH 点(或ZY 点)坐标及方位角⎪⎩⎪⎨⎧-=-=-=11sin cos AT JDY ZHY A T JDX ZHX TJDZH ZHZH 2、求HZ 点(或YZ 点)坐标及方位角⎪⎩⎪⎨⎧+=+=+-=22sin cos AT JDY HZY A T JDX HZX L T JDZH HZZH H3、求解切线长T 、外距E 、曲线长L(1)圆曲线⎪⎩⎪⎨⎧=-==180/)1)2/cos(/1()2/tan(απααR L R E R T (2)缓圆曲线 )2/(2/)2/cos(/)(2180/)21()2/tan()(020R l l l Rl l R p R E l R L qp R T s s s HsH H ===⎪⎩⎪⎨⎧-+=+⨯-=+⨯+=ββαπβα时当其中 二、直线上各桩号坐标及方位角计算 已知:ZH 、X 、Y 、A ⎪⎩⎪⎨⎧+=+==-=A L Y DY A L X DX A T ZH DZH L sin cos 三、第一缓和曲线上各桩号点坐标及方位角计算 已知:ZHZH 、ZHX 、ZHY 、A 1、R 、L S1、i (Z+1Y-1) ⎪⎩⎪⎨⎧⨯-+=⨯++=⨯⨯-==-=-=1111121132125cos sin sin cos /180)2/()6/()40/(Ay i A x ZHY DY A y i A x ZHX DX Rl l i A T Rl L y l R L L x ZHZH DZH L s s s π四、圆曲线上各桩号点坐标及方位角计算已知:ZHZH 、ZHX 、ZHY 、A 1、R 、L S1、i (Z+1Y-1)⎪⎩⎪⎨⎧⨯-+=⨯++=⨯+⨯-=⎪⎩⎪⎨⎧=-==++-=-++=--=1111121231110211231111cos sin sin cos /180)/2/(24/240/2/2/24/)]/2/cos(1[240/2/)/2/sin(Ay i A x ZHY DY A y i A x ZHX DX R L R l i A T R l p R l l q R l R l R L R l R y R l l R L R l R x ls ZHZH DZH L s s s s s s s s s s πβ其中五、第二缓和曲线上个桩号坐标及方位角计算 已知:HZZH 、HZX 、HZY 、A2、R 、L S2、i (Z+1Y-1) ⎪⎩⎪⎨⎧⨯--=⨯+-=⨯⨯+==-=-=2222222232225cos sin sin cos /180)2/()6/()40/(Ay i A x HZY DY A y i A x HZX DX Rl l i A T Rl L y l R L L x DZHHZZH L s s s π六、边桩坐标求解 已知:DZH 、X 、Y 、T 、BZJL (Z+Y-)、DLJJ 、N (距中桩距离,左正右负)⎪⎩⎪⎨⎧-=-=+=T N Y BDY T N X BDX T T sin cos α七、纵断面高程计算(1) 直线段上高程计算 已知:直线上任一点桩号(ZH )、高程(H )、纵坡(i ))(*ZH DZH i H DH -+=(2) 竖曲线上高程计算已知:竖曲线起点桩号(ZH )、起点高程(H )、竖曲线半径R 、起点坡度(i )、k (凸曲线+1、凹曲线-1) )2/(2R l k il H DH ZHDZH l ⨯-+=-=注:JDZH 、JDX 、JDY :交点桩号、交点X 、Y 坐标R 、L S1、L S2:半径、缓和曲线1、缓和曲线2LH :缓和曲线1长 +圆曲线长+ 缓和曲线2长 A1、A2:方位角1、方位角2 T :在曲线要素中代表切线长;在坐标计算中代表被求解点的坐标方位角。
曲线要素等计算公式表格

左边桩距 0.000 0.000 0.000 0.000 0.000 0.000 20.900 0.000 20.000 20.000 24.000 24.000 15.000 15.000 23.000
桩号 K716+100.000 K716+100.000 K716+100.000 K716+100.000 K716+100.000 K228+265.899 K718+153.833 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000
Y 519085.088 519082.168 519082.168 519082.168 518738.184 526279.356 526296.381 526308.590 526294.298 524061.827 526332.070 523920.860 523853.932 523855.632 523825.527 523810.141 523821.966 523803.645 523799.102 523779.297 523778.422 523742.714 523685.632 523563.133 523449.901 523451.714 523436.323 523429.087 523392.676 523399.873 523386.237 523388.033 523367.165 523347.919 523329.614
圆曲线要素及计算公式

第二章圆曲线要素及计算公式
如图2-1所示,两相邻直线偏角(线路转向角)为,选定其
图 2-1
连接曲线圆曲线的半径为R,这样,圆曲线和两直线段的切点位置ZY点、YZ点便被确定下来,我们称为对圆曲线相对位置起控制作用的直圆点ZY、圆直点YZ和曲中点QZ为圆曲线三主要点。
我们称R、α以及具体体现三主要点几何位置的切线长T、曲线长L、外矢距E和切曲差(切线长和曲线长之差)D为曲线6要素。
只要知道了曲线6要素,便可于实地测放出圆曲线。
现将圆曲线的元素列下:
:转向角(实地测出)
R:曲率半径(设计给出)
T:切线长(计算得出)
L:曲线长(计算得出)
D:切曲差(计算得出)
偏角是在线路祥测时测放出的,圆曲线半径R是在设计中根据线路的等级以及现场
地形条件等因素选定的,其余要素可根据以下公式计算:。
平曲线的五大要素计算公式

平曲线的五大要素计算公式以下是关于平曲线的五大要素计算公式。
平曲线是指在平面上描述一条曲线的五种基本参数,包括曲线长度、曲线半径、曲线角度、曲线切线和曲线弧度。
下面是这五种要素的计算公式:1.曲线长度(L):曲线长度可以通过计算曲线上的所有坐标点之间的距离来获得。
对于参数方程表示的曲线,曲线长度L可以通过以下公式计算: L=∫(√((dx/dt)²+(dy/dt)²)dt) 其中,(dx/dt)和(dy/dt)分别是曲线在x和y方向上的速度矢量。
2.曲线半径(R):曲线半径表示曲线在某一点处弯曲的程度。
对于圆弧曲线,曲线半径R可以通过以下公式计算: R=(dx²+dy ²)^(1/2)/(1+(dy/dx)²)^(1/2) 其中,(dx,dy)是曲线上的某一点坐标。
3.曲线角度(θ):曲线角度表示曲线在某一点处与x轴的夹角。
对于参数方程表示的曲线,曲线角度θ可以通过以下公式计算: θ=atan2(dy/dx) 其中,(dx,dy)是曲线上的某一点坐标。
4.曲线切线(T):曲线切线表示曲线在某一点处的切线方向。
对于参数方程表示的曲线,曲线切线T可以通过以下公式计算: T=(dx/dt,dy/dt) 其中,(dx/dt)和(dy/dt)分别是曲线在x和y方向上的速度矢量。
5.曲线弧度(α):曲线弧度表示曲线在某一点处沿逆时针方向的旋转程度。
对于圆弧曲线,曲线弧度α可以通过以下公式计算: α=θ 其中,θ是曲线在某一点处与x轴的夹角。
需要注意的是,这些公式适用于平曲线的一般情况。
在实际应用中,根据具体的曲线类型和表示方式,可能需要对公式进行相应的调整。
曲线要素坐标计算
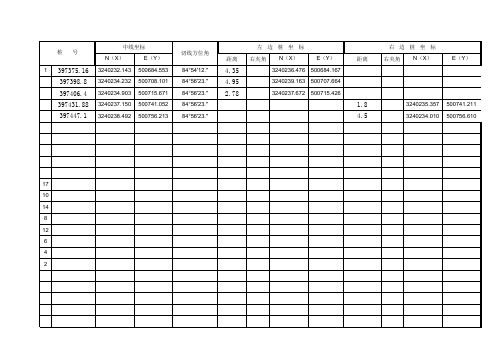
中线坐标
N(X)
E(Y)
切线方位角
距离
左边桩坐标 右夹角 N(X)
E(Y)
距离
右边桩坐标 右夹角 N(X)
E(Y)
1 397375.16 3240232.143 500684.553 84°54′12.″
4.35
3240236.476 500684.167
397398.8 3240234.232 500708.101 84°56′23.″
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号中Leabharlann 坐标切线方位角左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
竖曲线、缓和曲线计算公式
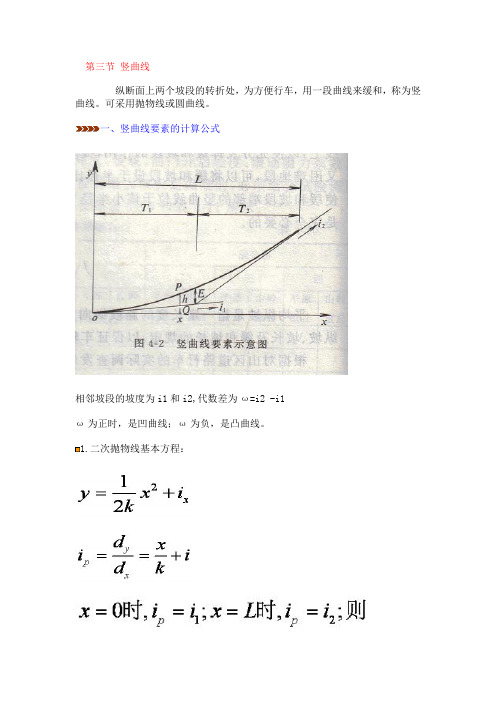
第三节竖曲线纵断面上两个坡段的转折处,为方便行车,用一段曲线来缓和,称为竖曲线。
可采用抛物线或圆曲线。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时,是凹曲线;ω为负,是凸曲线。
1.二次抛物线基本方程:或ω:坡度差(%);L:竖曲线长度;R:竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: (前提:ω很小)L=Rω竖曲线切线长:T=L/2=Rω/2竖曲线上任一点竖距h:竖曲线外距:二、竖曲线最小半径(三个因素)1.缓和冲击对离心加速度加以控制。
ν(m/s)根据经验,a=0.5~0.7m/s2比较合适。
我国取a=0.278,则Rmin=V2/3.6 或Lmin=V2ω/3.62.行驶时间不过短 3s的行程Lmin=V.t/3.6=V/1.23.满足视距的要求分别对凸凹曲线计算。
(一)凸形竖曲线最小半径和最小长度按视距满足要求计算1.当L<ST时,Lmin = 2ST - 4/ω2.当L≥ST时,ST为停车视距。
以上两个公式,第二个公式计算值大,作为有效控制。
按缓和冲击、时间行程和视距要求(视距为最不利情况)计算各行车速度时的最小半径和最小长度,见表4-13。
表中:(1)一般最小半径为极限最小半径的1.5~2倍;(2)竖曲线最小长度为3s行程的长度。
(二)凹曲线最小半径和长度1.夜间行车前灯照射距离要求:1)L<ST2) L≥STL<ST Lmin = 2ST - 26.92/ω (4-14)L≥STω /26.92 (4-15)3s时间行程为有效控制。
例:设ω=2%=0.02;则L=ωR竖曲线最小长度L=V/1.2速度V=120km/h V=40km/h 一般最小半径R凸17000 700一般最小半径R凹6000 700 L凸340 14L凹120 14 例题4-3ω=-0.09 凸形;L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号=k5+030 - T =K4+940起始高程=427.68 - 5%*90=423.18m桩号k5+000处:x1=k5+000-k4+940=60m切线高程=423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程=426.18 - 0.90=425.28m 桩号k5+100处:x2=k5+100-k4+940=160m切线高程=423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m设计高程=431.18 - 6.40=424.78m第一节平面线形概述一、路线路线指路的中心线;路线在水平面上的投影叫路线的平面;路线设计:确定路线空间位置和各部分几何尺寸的工作;可分为平面设计、纵断面设计、横断面设计。
5大桩曲线要素计算 (带公式)
1122.8057
YH 65+491.747
2526966.1620
514499.0642
106°37′48.45″
1122.8057
QZ 65+940.980
2526851.4908
514933.3356
102°57′11.17″
az 12°50′17.05″YH 66+390.213
2526764.9061
线
要
素
表
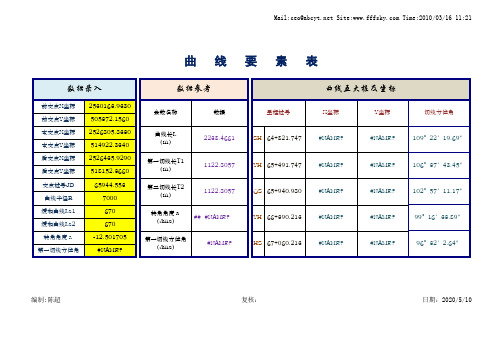
曲线五大桩及坐标
数据参考
参数名称 曲线长L (m) 第一切线长T1 (m) 第二切线长T2 (m) 转角角度a (dms) 第一切线方位角 (dms) 数据 里程桩号
X坐标
Y坐标
切线方位角
2238.4661
ZH 64+821.747
2527178.2703
513863.5970
109°22′19.69″
515374.0670
99°16′33.89″
第一切线方位角 109°22′19.69″
109°22′19.69″
HZ 67+060.213
2526678.0645
516038.3464
96°32′2.64″
编制:陈超
复核:
日期:2013Time:2010/03/16 11:21
曲
数据录入
前交点X坐标 前交点Y坐标 本交点X坐标 本交点Y坐标 后交点X坐标 后交点Y坐标 交点桩号JD 曲线半径R 缓和曲线Ls1 缓和曲线Ls2 转角角度a 2530163.9380 505372.1560 2526805.8330 514922.8340 2526435.9290 518152.3660 65944.553 7000 670 670 -12.501705
曲线要素计算公式

曲线要素计算公式
曲线是数学中的基本概念,是指在平面上由无数个点连接而成的
连续曲线。
曲线具有许多重要的特征,如长度、弧度、曲率等。
而曲线的要素计算就是计算曲线的各种特征值。
下面,我们就来
介绍曲线要素的计算公式,帮助大家更深入地了解曲线的特征和性质。
一、曲线长度的计算公式:
曲线的长度指的是曲线上所有点之间的直线距离总和。
计算公式为:
L = ∫a b √[1+f’(x)²]dx
其中,a和b为曲线上的两个端点,f’(x)表示曲线的导数。
二、曲率的计算公式:
曲率是曲线某一点处曲线的弯曲程度的量度。
计算公式为:
k = |f’’(x)| / [1+f’(x)²]^(3/2)
其中,f’’(x)为曲线的二阶导数。
三、曲线斜率的计算公式:
曲线的斜率是指曲线在某一点处的切线斜率。
计算公式为:
f’(x) = lim Δx→0 [f(x+Δx)−f(x)] / Δx
四、曲线弧度的计算公式:
曲线的弧度是指曲线某一段的弧长对半径的比值。
计算公式为:θ = l / r
其中,l为曲线一段的弧长,r为曲线的半径。
以上就是曲线要素计算公式的详细介绍。
掌握这些公式可以涵盖曲线的多方面特征,并为实际问题的解决提供指导和依据。
