SAS软件与统计应用教程-主成分分析(1)
主成分分析法(1)【可编辑全文】

Fp
Cov(xi , Fj ) Cov(ui1F1 ui2F2 L uipFp , Fj ) uijj
(
xi
,
Fj
)
uij j i
j
uij j i
可见,xi 和 Fj 的相关的密切程度取决于对 应线性组合系数的大小。
五、原始变量被主成分的提取率
前面我们讨论了主成分的贡献率和累计贡献率,他度 量 了 F1 , F2 , …… , Fm 分 别 从 原 始 变 量 X1 , X2,……XP中提取了多少信息。那么X1,X2,……XP 各有多少信息分别F1,F2,……,Fm被提取了。应该用 什 么 指 标 来 度 量 ? 我 们 考 虑 到 当 讨 论 F1 分 别 与 X1 , X2 , ……XP 的 关 系 时 , 可 以 讨 论 F1 分 别 与 X1 , X2,……XP的相关系数,但是由于相关系数有正有负, 所以只有考虑相关系数的平方。
F1
F2
F3
i
i
t
F1
1
F2
0
1
F3
0
0
1
i 0.995 -0.041 0.057
l
Δi -0.056 0.948 -0.124 -0.102 l
t -0.369 -0.282 -0.836 -0.414 -0.112 1
主成分分析是把各变量之间互相关联的复杂 关系进行简化分析的方法。
在社会经济的研究中,为了全面系统的分析 和研究问题,必须考虑许多经济指标,这些指标 能从不同的侧面反映我们所研究的对象的特征, 但在某种程度上存在信息的重叠,具有一定的相 关性。
i
m
j
u2 ij
/
2 i
m
SAS学习系列33.-主成分分析

SAS学习系列33.-主成分分析33. 主成分分析(一)原理一、基本思想主成份分析,是数学上对数据降维的一种方法,是将多个变量转化为少数综合变量(集中了原始变量的大部分信息)的一种多元统计方法。
其主要目的是将变量减少,并使其改变为少数几个相互独立的线性组合形成的新变量(主成份,其方差最大),使得原始资料在这些成份上显示最大的个别差异来。
在所有的线性组合中所选取的F1应该是方差最大的,称为第一主成分。
如果第一主成分不足以代表原来所有指标的信息,再考虑选取第二个线性组合F2, 称为第二主成分。
为了有效地反映原有信息,F1已有的信息就不需要再出现在F2中,用数学语言表达就是要求Cov(F1,F2)=0. 依此类推可以构造出第三、第四、…、第p个主成分。
主成份分析,可以用来综合变量之间的关系,也可用来减少回归分析或聚类分析中的变量数目。
二、基本原理设有n个样品(多元观测值),每个样品观测p项指标(变量):X1,…,X p,得到原始数据资料阵:其中,X i = (x1i,x2i,…,x ni)T,i = 1, …, p.用数据矩阵X的p个列向量(即p个指标向量)X1,…,X p作线性组合,得到综合指标向量:简写成:F i = a1i X1 + a2i X2+…+a pi X p i = 1, …, p限制系数a i = (a1i,a2i,…,a pi)T为单位向量,即且由下列原则决定:(1)F i与F j互不相关,即COV(F i, F j)=a i T∑a i=0,其中∑为X 的协方差矩阵;(2)F1是X1,X2,…,X p的所有满足上述要求的线性组合中方差最大的,即F2是与F1不相关的X1,…,X p所有线性组合中方差最大的,…,F p是与F1,…,F p-1都不相关的X1,…,X p所有线性组合中方差最方向对应。
F1,F2,…,F p可以理解为p维空间中互相垂直的p 个坐标轴。
三、基本步骤1. 计算样品数据协方差矩阵Σ = (s ij)p p,其中2. 求出Σ的特征值及相应的特征向量λ1>λ2>…>λp>0, 及相应的正交化单位特征向量:则X的第i个主成分为F i= a i T X,i=1, …, p.3. 选择主成分在已确定的全部p个主成分中合理选择m个来实现最终的评价分析。
SAS软件应用之主成分分析

本章小节
在大部分实际问题中,变量之间是有一定的相关性的,人们 自然希望找到较少的几个彼此不相关的综合指标尽可能多地 反映原来众多变量的信息。本章介绍了主成分分析的数学模 型、方法步骤以及主成分分析的应用。我们需要一种综合性 的分析方法,既可减少指标变量的个数,又尽量不损失原指 标变量所包含的信息,对资料进行全面的综合分析。主成分 分析正是适应这一要求产生的,是解决这类题的理想工具。 主成份分析的基本思想就是将彼此相关的一组指标变量转化 为彼此独立的一组新的指标变量,并用其中较少的几个新指 标变量就能综合反应原多个指标变量中所包含的主要信息, 符合专业含义。
主成分分析的方法步骤
计算主成分得分 如果标准化指标变量 X 1 , X 2 ,, X k 的第i个主成分是:
Z i liX li1 X 1 li 2 X 2 lik X k xij x j 其中, X ij , j, 1,2,, k sj 是xj的标准化指标变量。那么,第i个主成分可以 转换为原始指标变量的线性组合:
主成分分析的方法步骤
对原始指标数据进行标准化变换:
X ij xij x j sj , j 1,2,, k
将原始数据标准化,然后利用标准化的数据 计算主成分。X为标准化后的数据矩阵,则:
X 11 X X 21 X n1 X 12 X 22 X n2 X 1k X 2k X nk
li1 li 2 lik li1 x1 li 2 x2 lik xk zi x1 x2 xk ( ),i 1,2,, k s1 s2 sk s1 s2 sk
主成分分析的应用
如何正确应用SPSS软件做主成分分析

如何正确应用SPSS软件做主成分分析如何正确应用SPSS软件做主成分分析一、概述主成分分析(Principal Component Analysis, PCA)是一种常用的多变量分析方法,通过将原始变量进行线性组合,得到少数几个新的主成分,用于降低原始变量的维度,并揭示变量之间的结构关系。
SPSS软件是目前主流的数据分析工具之一,本文旨在介绍如何正确应用SPSS软件进行主成分分析。
二、数据准备进行主成分分析前,首先需要将数据导入SPSS软件。
数据应以矩阵形式呈现,每一行代表一个观测对象,每一列代表一个变量。
确保数据清洗完整,并检查是否有缺失值。
若有缺失值,可以选择删除含有缺失值的观测对象,或者使用插补方法填充缺失值。
在数据导入完成后,可以根据需求选择进行标准化操作,以消除不同变量间的量纲差异。
三、主成分分析步骤1. 启动SPSS软件并打开数据文件。
2. 选择"分析"(Analyze)菜单中的"降维"(Dimension Reduction),然后选择"主成分"(Principal Components)。
3. 在"主成分"对话框中,将需要进行主成分分析的变量移动到"变量"框中的右侧。
4. 点击"图"按钮,弹出"主因子图"对话框。
可以选择生成散点图,查看主成分之间的关系。
5. 点击"提取"选项卡,查看提取出的主成分的方差解释比。
6. 可根据需要点击"选项"按钮进行参数设置,如旋转方法、因子得分计算等。
7. 点击"统计"按钮,可以查看每个主成分的特征值以及贡献度。
8. 点击"摘要"按钮,生成主成分分析结果的摘要信息。
四、结果解释与应用主成分分析结果可以通过以下几个方面进行解释与应用:1. 主成分贡献度:通过方差解释比可以判断每个主成分对原始变量的贡献程度。
主成份分析报告(包含sas程序)
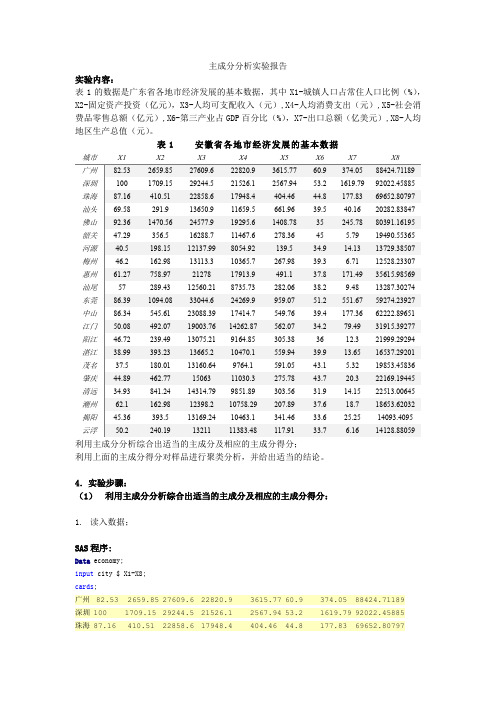
主成分分析实验报告实验内容:表1的数据是广东省各地市经济发展的基本数据,其中X1-城镇人口占常住人口比例(%),X2-固定资产投资(亿元),X3-人均可支配收入(元),X4-人均消费支出(元),X5-社会消费品零售总额(亿元),X6-第三产业占GDP百分比(%),X7-出口总额(亿美元),X8-人均地区生产总值(元)。
表1 安徽省各地市经济发展的基本数据城市X1X2X3X4X5X6X7X8广州82.532659.8527609.622820.93615.7760.9374.0588424.71189深圳1001709.1529244.521526.12567.9453.21619.7992022.45885珠海87.16410.5122858.617948.4404.4644.8177.8369652.80797汕头69.58291.913650.911659.5661.9639.540.1620282.83847佛山92.361470.5624577.919295.61408.7835245.7880391.16195韶关47.29356.516288.711467.6278.3645 5.7919490.55365河源40.5198.1512137.998054.92139.534.914.1313729.38507梅州46.2162.9813113.310365.7267.9839.3 6.7112528.23307惠州61.27758.972127817913.9491.137.8171.4935615.98569汕尾57289.4312560.218735.73282.0638.29.4813287.30274东莞86.391094.0833044.624269.9959.0751.2551.6759274.23927中山86.34545.6123088.3917414.7549.7639.4177.3662222.89651江门50.08492.0719003.7614262.87562.0734.279.4931915.39277阳江46.72239.4913075.219164.85305.383612.321999.29294湛江38.99393.2313665.210470.1559.9439.913.6516537.29201茂名37.5180.0113160.649764.1591.0543.1 5.3219853.45836肇庆44.89462.771506311030.3275.7843.720.322169.19445清远34.93841.2414314.799851.89303.5631.914.1522513.00645潮州62.1162.9812398.210758.29207.8937.618.718653.62032揭阳45.36393.513169.2410463.1341.4633.625.2514093.4095云浮50.2240.191321111383.48117.9133.7 6.1614128.88059利用主成分分析综合出适当的主成分及相应的主成分得分;利用上面的主成分得分对样品进行聚类分析,并给出适当的结论。
SAS软件和统计应用教程(1)PPT课件

-
2
SAS软件与统计应用教程
2.1.1 统计学的基本概念
STAT
1. 总体与样本
总体(population):总体是指所研究对象的全体组成 的集合。
样 本 (sample) : 样 本 是 指 从 总 体 中 抽 取 的 部 分 对 象 (个体)组成的集合。样本中包含个体的个数称为样本 容量。容量为n的样本常用n个随机变量X1,X2,…,Xn 表示,其观测值(样本数据)则表示为x1,...,xn,为 简单起见,有时不加区别。
SAS软件与统计应用教程
STAT
第二章 SAS的描述统计功能
2.1 描述性统计的基本概念 2.2 在SAS中计算统计量 2.3 统计图形
-
1
SAS软件与统计应用教程
STAT
2.1 描述性统计的基本概念
2.1.1 统计学的基本概念 2.1.2 表示数据位置的统计量 2.1.3 表示数据分散程度的统计量 2.1.4 表示数据分布形状的统计量 2.1.5 其它统计量
SAS软件与统计应用教程
2.1.3 表示数据分散程度的统计量
STAT
1. 极差(Range)与半极差(Interquartile range)
极差就是数据中的最大值和最小值之间的差:
极差 = max{xi} – min{xi} 上、下四分位数之差Q3 – Q1称为四分位极差或半极 差,它描述了中间半数观测值的散布情况。
SAS软件与统计应用教程
STAT
2. 峰度(kurtosis)
峰度描述数据向分布尾端散布的趋势。峰度的计算公
式为: K
n (n 1 )
n(x i x )43 (n 1 )2
(n 1 )n ( 2 )n ( 3 )i 1 s (n 2 )n ( 3 )
SPSS进行主成分分析的步骤[图文]
![SPSS进行主成分分析的步骤[图文]](https://img.taocdn.com/s3/m/1b2ef8f4da38376baf1fae83.png)
主成分分析的操作过程原始数据如下(部分)调用因子分析模块(Analyze―Dimension Reduction―Factor),将需要参与分析的各个原始变量放入变量框,如下图所示:单击Descriptives按钮,打开Descriptives次对话框,勾选KMO and Bartlett’s test of sphericity选项(Initial solution选项为系统默认勾选的,保持默认即可),如下图所示,然后点击Continue按钮,回到主对话框:其他的次对话框都保持不变(此时在Extract次对话框中,SPSS已经默认将提取公因子的方法设置为主成分分析法),在主对话框中点OK按钮,执行因子分析,得到的主要结果如下面几张表。
①KMO和Bartlett球形检验结果:KMO为0.635>0.6,说明数据适合做因子分析;Bartlett球形检验的显著性P值为0.000<0.05,亦说明数据适合做因子分析。
②公因子方差表,其展示了变量的共同度,Extraction下面各个共同度的值都大于0.5,说明提取的主成分对于原始变量的解释程度比较高。
本表在主成分分析中用处不大,此处列出来仅供参考。
③总方差分解表如下表。
由下表可以看出,提取了特征值大于1的两个主成分,两个主成分的方差贡献率分别是55.449%和29.771%,累积方差贡献率是85.220%;两个特征值分别是3.327和1.786。
④因子截荷矩阵如下:根据数理统计的相关知识,主成分分析的变换矩阵亦即主成分载荷矩阵U 与因子载荷矩阵A 以及特征值λ的数学关系如下面这个公式:λiiiAU=故可以由这二者通过计算变量来求得主成分载荷矩阵U 。
新建一个SPSS 数据文件,将因子载荷矩阵中的各个载荷值复制进去,如下图所示:计算变量(Transform-Compute Variables )的公式分别如下二张图所示:计算变量得到的两个特征向量U1和U2如下图所示(U1和U2合起来就是主成分载荷矩阵):所以可以得到两个主成分Y1和Y2的表达式如下:Y1=0.456X1+0.401X2+0.428X3+0.490X4+0.380X5+0.253X6Y2=-0.367X1+0.322X2-0.323X3-0.303X4+0.453X5+0.602X6由上面两个表达式,可以通过计算变量来得到Y1、Y2的值。
主成分分析操作步骤

主成分分析操作步骤1)先在spss中录入原始数据。
2)菜单栏上执行【分析】——【降维】——【因子分析】,打开因素分析对话框,将要分析的变量都放入【变量】窗口中。
3)设计分析的统计量点击【描述】:选中“Statistics”中的“原始分析结果”和“相关性矩阵”中的“系数”。
(选中原始分析结果,SPSS自动把原始数据标准差标准化,但不显示出来;选中系数,会显示相关系数矩阵)然后点击“继续”。
点击【抽取】:“方法”里选取“主成分”;“分析”、“输出”、“抽取”均选中各自的第一个选项即可。
点击【旋转】:选取第一个选项“无”。
(当因子分析的抽取方法选择主成分法时,且不进行因子旋转,则其结果即为主成分分析)点击【得分】:选中“保存为变量”,方法中选“回归”;再选中“显示因子得分系数矩阵”。
点击【选项】:选择“按列表排除个案”。
4)结果解读5)A. 相关系数矩阵:是6个变量两两之间的相关系数大小的方阵。
通过相关系数可以看到各个变量之间的相关,进而了解各个变量之间的关系。
相關性矩陣食品衣着燃料住房交通和通讯娱乐教育文化相關食品 1.000 .692 .319 .760 .738 .556 衣着.692 1.000 -.081 .663 .902 .389 燃料.319 -.081 1.000 -.089 -.061 .267 住房.760 .663 -.089 1.000 .831 .387 交通和通讯.738 .902 -.061 .831 1.000 .326 娱乐教育文化.556 .389 .267 .387 .326 1.000B. 共同度:给出了这次主成分分析从原始变量中提取的信息,可以看出交通和通讯最多,而娱乐教育文化损失率最大。
munalities起始擷取食品 1.000 .878衣着 1.000 .825燃料 1.000 .841住房 1.000 .810交通和通讯 1.000 .919娱乐教育文化 1.000 .584擷取方法:主體元件分析。
