Are Large X-ray Clusters at Thermal Equilibrium
Thermal gravitational waves

v12
3kTc . 12
For a core temperature of Tc 10 7 K , the velocity of the particles is of the order of
8 10 5 m / s . For a star of density 200 g / cc 2 10 5 kg / m 3 , the numbeting in these values we get the power of thermal gravitational waves emitted as,
10 9 Watt at a frequency of 1017 Hz . E
2
The flux of thermal gravitational waves from the sun, received at earth is of the order of half a watt. 2. Thermal gravitational waves from compact stars In the case of white dwarfs, the number density is of the order of n1 n2 10 37 m 3 , and the velocity corresponding to the white dwarf temperature of Tc 10 8 K , is of the order of 2 10 6 m / s . The volume of the white dwarf is of the order of 4 1018 m 3 and the frequency corresponding to the temperature Tc 10 8 K is And for a white dwarf,
CVD综述
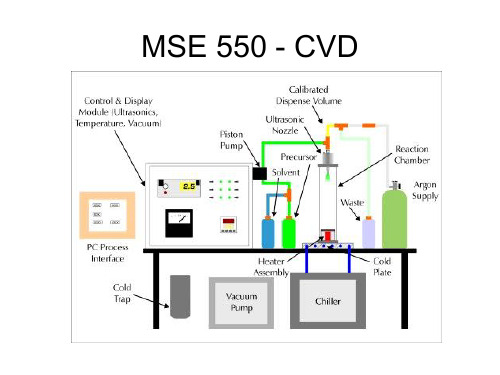
laminar flow: simple case: flow past a plate
near plate velocity = 0 ==> stagnant layer
•
– diffuse gas through stagnant layer to surface mass transport depends on:
fundamental parameters experimental parameters reactant concentration diffusivity boundary layer thickness pressure gas velocity temperature distribution reactor geometry gas properties (viscosity . . .)
Advantages: • high growth rates possible • can deposit materials which are hard to evaporate • good reproducibility • can grow epitaxial films Disadvantages • high temperatures • complex processes • toxic and corrosive gasses
Formation of Low Mass Stars in Elliptical Galaxy Cooling Flows

a r X i v :a s t r o -p h /9907364v 1 26 J u l 1999FORMATION OF LOW MASS STARS IN ELLIPTICAL GALAXYCOOLING FLOWSWilliam G.Mathews 2and Fabrizio Brighenti 2,32University of California Observatories/Lick Observatory,Board of Studies in Astronomy and Astrophysics,University of California,Santa Cruz,CA95064mathews@3Dipartimento di Astronomia,Universit`a di Bologna,viaZamboni 33,Bologna 40126,Italy brighenti@astbo3.bo.astro.itAbstractThermal X-ray emission from cooling flows in ellip-tical galaxies indicates that ∼1M ⊙of hot (T ∼107K)interstellar gas cools each year,accumulating ∼1010M ⊙over a Hubble time.Paradoxically,optical and radio frequency emission from the cooled gas is lacking,indicating that less than ∼10−3of the cooled gas remains.Many have speculated that the cooled gas has formed into relatively invisible low mass stars,particularly in the context of massive cooling flows in galaxy clusters.We focus here on cooling flows in el-liptical galaxies like NGC 4472where the cooled gas is made visible in emission lines from HII regions ionized and heated (T HII ∼104K)by stellar ultraviolet ra-diation.The low filling factor of HII gas requires that the hot gas cools at ∼106cooling sites within several kpc of the galactic center.HII mass slowly increases at each site at ∼10−6M ⊙yr −1until a neutral core develops.Neutral cores are heated (T HI ∼15K)and ionized (x ∼10−6)by thermal X-rays from the entire interstellar cooling flow.We show that the maximum mass of spherical HI cores that become gravitation-ally unstable is only ∼2M ⊙.No star can exceed this mass and fragmentation of collapsing cores produces stars of even lower mass.By this means we establish with some confidence that the hypothesis of low mass star formation is indeed correct –the IMF is bottom heavy,but may be optically luminous.Slightly more massive stars <∼4.5M ⊙can form near the effective ra-dius (r =8.57kpc in NGC 4472)if sufficient masses of interstellar gas cool there,producing a luminous pop-ulation of intermediate mass stars perhaps with radial orbits that may contribute to the stellar H βindex.The degree of ionization in gravitationally collapsing cores is sufficiently low to allow magnetic fields to dis-connect by ambipolar diffusion.Low mass star forma-tion is very efficient,involving ∼106M ⊙of galactic cold gas at any time,in agreement with observed up-per limits on cold gas mass.We discuss the cooling region surrounding a typical cooling site and show that the total X-ray absorption in cold and cooling gas is much less that that indicated by recent X-ray ing a mass dropout scheme consis-tent with X-ray observations and dynamical mass to light ratios,we plot the global H βsurface brightness profile in NGC 4472and compare it with the smaller contribution from HII gas recently ejected from red giant stars.The lifetime of cooled gas at each cooling site,∼105yrs,is too short to permit dust formation and perhaps also gas phase formation of molecules.Subject headings:galaxies:elliptical and lenticular –stars:formation –galaxies:cooling flows –galaxies:interstellar medium –X-rays:galaxies1.INTRODUCTION AND OVER VIEWStrong X-ray emission from luminous elliptical galaxies is clear evidence that the hot interstellar gas they contain is losing energy.Throughout most of the galactic volume,this loss of energy does not result in lower temperatures since the gas is continuously re-heated by compression in the galactic gravitational potential as it slowly moves inward.In this sense the galactic “cooling flow”is a misnomer.Ultimately,however,in the central regions of the flow the gas density becomes large enough for radiative losses to overwhelm dynamical compression and the gas cools catastrophically.For a typical galactic cooling rate,∼1M ⊙per year,the total amount of gas that cools in a massive elliptical over a Hubble time is large,several 1010M ⊙,a few percent of the total stellar mass.Remarkably,the amount of cold gas observed in el-lipticals,either in atomic or molecular form,is many orders of magnitude less than 1010M ⊙(Bregman,Hogg &Roberts 1992).The mass of central black holes in bright ellipticals is also relatively small,typi-cally less than a few 109M ⊙(Magorrian et al.1998),so the cooled gas cannot be in the holes.Soft X-ray absorption has been observed in some galactic cool-ing flows,indicating masses of cold gas comparable to the predicted value,but the quantitative significance or reality of this absorption is unclear at present.In addition to cold gas deposited by cooling flows,it is possible that additional cold,dusty gas is oc-casionally delivered to the centers of ellipticals as aresult of merging with gas-rich companion galaxies. While this is plausible for some gas-rich ellipticals having dusty clouds or lanes,if merging were an im-portant source of cold gas for all massive ellipticals, the merging rate would need to be carefully regulated in order to maintain the small amount of cold gas observed in normal ellipticals.For many years the standard theoretical explana-tion for this shortage of cooled gas is that it has been consumed in forming low mass stars(e.g.Fabian, Nulsen&Canizares1982;Thomas1986;Cowie& Binney1988;Ferland,Fabian,&Johnstone1994). Such young stars must have low masses since neither luminous OB stars nor Type II supernovae have been observed in normal ellipticals.Explaining the disap-pearance of cooled gas by invoking the poorly under-stood physics of star formation may seem contrived and the low stellar mass hypothesis has led to some ridicule.The fate of cooled gas in coolingflows associated with clusters of galaxies has received most of the ob-servational and theoretical attention because of the spectacularly large inferred mass deposition rates,˙M>∼100M⊙yr−1(Fabian1994).In addition to low mass stars,the apparent soft X-ray intrinsic ab-sorption of N∼1021cm−2indicates that∼1010M⊙of cold gas lies within∼100kpc of the cluster cores. Although enormous,this amount of gas would still be only a few percent of the total cooled gas based on the estimated˙M,so low mass stars are still the preferred endstate for most of the cooled cluster gas (Allen&Fabian1997).However,as with elliptical galaxies,this amount of cold gas should in general be detectable in HI or CO emission but has not(O’Dea et al.1994;Ferland,Fabian&Johnstone1994;Vogt &Donahue1995;Puy,Grenacher,&Jetzer1999), amounting to a colossal discrepancy between expec-tation and reality.In the discussion that follows we revisit the prob-lem of cooled gas from the perspective of the galactic coolingflow in NGC4472,a large,well-observed el-liptical galaxy.For relatively nearby ellipticals the threshold for radio detection is much lower and the ratio of observed to predicted cold gas masses is sim-ilar to that of more distant cluster coolingflows;e.g. H2and HI are undetected in NGC4472with an up-per limit107M⊙(Bregman,Roberts&Giovanelli 1988;Braine,Henkel&Wiklind1988),far below the ∼1010M⊙expected.Nevertheless,the intrinsic soft X-ray absorbing column in NGC4472,3×1021cm−2,and its relatively large covering factor indicates cool gas masses far in excess of the radio upper limit.The coolingflow in NGC4472clearly suffers from a minia-ture version of the same coolingflow problems of dis-tant clusterflows.But because of its proximity,there is a large available body of additional observational information for NGC4472that make it a more appro-priate venue to resolve or constrain theoretical possi-bilities for the fate of cooled gas.But the main advantage afforded by large,rela-tively nearby ellipticals emphasized here is that the cooled gas is heated,ionized and therefore illuminated by ultraviolet radiation from highly evolved galactic stars.We argue that the diffuse optical line emission from HII gas at T∼104K distributed across the cen-tral regions of most or all bright ellipticals is a direct tracer of cooled gas deposited by the hot interstellar gas.A simple analysis of this HII gas leads to the con-clusion that hot phase gas is not cooling into a single large cloud of neutral gas,but is cooling at a large number(∼106)of cooling sites located throughout the central regions of NGC4472.The HII gas pro-vides direct observational support for a distributed mass dropout that has been assumed by many authors in the past based on their interpretation of X-ray sur-face brightness profiles(e.g.Thomas1986;Sarazin &Ashe1989).As the mass of HII increases at each cooling site,a neutral core of very low temperature (T≈10−20K)eventually develops.We show that these neutral cores are very weakly ionized and can undergo gravitational collapse even in the presence of maximum strength magneticfields.Evidently this collapse results in local star formation.Another important conclusion from our study of the ionized gas in NGC4472is that only a very small amount,∼1M⊙,of neutral(or molecular)gas can accumulate at each cooling site before it undergoes gravitational collapse.The small mass of collaps-ing neutral cores is an essential requirement for low mass star formation.Previous studies(e.g.Ferland, Fabian&Johnstone1994)have shown that the gas temperature and Jeans mass are small deep within HI or H2gas irradiated by X-rays in cluster coolingflows, but this does not guarantee that massive stars can-not form.For example,the Jeans mass is often very low in Galactic molecular clouds but these clouds are also the birthsites for massive OB stars.The limited mass of cold gas at each cooling site in NGC4472and other similar ellipticals naturally prohibits stars more massive than about1M⊙from forming.The low mass star formation process we propose is also very efficient:the total mass of cold gas at all cooling sites in NGC4472at any time is very small, consistent with observed upper limit of cold gas(< 107M⊙).NGC4472is an excellent galaxy for study-ing this unique star formation process since very lit-tle alien gas or stars have been recently accreted into NGC4472by a merging process.Dusty,and there-fore accreted,gas is confined to within r<∼0.05r e (van Dokkum&Franx1995;Ferrari et al.1999) Afinal advantage of studying cooled gas in ellipti-cals like NGC4472is that the neutral gas formed in the cores of HII regions with temperatures T∼10K, only lasts for a time,<∼105years,that is too short for dust(and possibly many molecules)to form.Al-though dust and molecules are not required for low mass star formation to proceed,these components have complicated previous discussions of coolingflows in clusters of galaxies where,we assume,the cooling process resembles that in NGC4472.One shortcoming of our presentation–as with those of previous authors–is that we cannot reconcile the observed soft X-ray absorption in NGC4472with the small amount of cold gas indicated by null obser-vations of HI and CO emission.We assume,without much justification,that these contradictory observa-tions will be resolved in favor of the radio observations and that the soft X-ray absorption can be interpreted in another way.HII gas in elliptical galaxies can also arise from stellar mass loss which is ionized by hot central stars (planetary nebulae)and galactic UV radiation.We begin our discussion below with an argument that coolingflow dropout,not stellar mass loss,is likely to be the main contributor to internally-produced HII gas mass observed in nearby ellipticals.Then we dis-cuss an elementary model for the HII gas at a typi-cal interstellar cooling site and infer from this a low globalfilling factor for HII gas within the central re-gion of NGC4472.Next we model the cooling of hot gas from∼107to∼104K with a subsonicflow in pressure equilibrium–thisflow is useful in esti-mating the possible contribution of cooling gas to the X-ray absorption.This is followed by a discussion of the temperature,ionization level and gravitational instability of neutral cores at the centers of HII cool-ing site clouds.This part of our presentation fol-lows rather closely several previous discussions,but serves to illustrate that the more spatially concen-trated radiative transfer in spherical geometry still allows low temperatures and low mass star formation within these cores.We then show from observational considerations that magneticfields play little or no role in inhibiting the compression of interstellar gas as it cools from107to104K and from theoretical con-siderations that even the strongest observationally al-lowed magneticfields are unlikely to inhibit thefinal collapse of neutral cores to stellar densities.At the end of our presentation we discuss the effects of galac-tic gravitational forces and stellar collisions on cooling site clouds.Finally,to stimulate further observations of optical emission lines,we present a surface bright-ness map of NGC4472showing all the major com-ponents:stars,X-ray emitting gas,and HII gas from interstellar dropout and stellar ejecta.2.NGC4472:A PROTOTYPICAL ELLIP-TICAL GALAXYFor quantitative estimates in the following discus-sion,we use a specific galaxy,NGC4472,a massive E2 galaxy associated with the Virgo cluster.NGC4472 has been extensively observed at X-ray frequencies with Einstein HRI(Trinchieri,Fabbiano,&Canizares 1986)and with ROSAT HRI and PSPC(Irwin& Sarazin1996).The radial variations of hot gas density and temperature based on these X-ray data are illus-trated in Brighenti&Mathews(1997a).Although the outer region of the X-ray image of NGC4472is distorted,possibly by ram pressure interaction with ambient Virgo gas,the azimuthally averaged radial variation of electron density in NGC4472is typical of other bright ellipticals(Mathews&Brighenti1998).The most likely region for low mass star forma-tion in NGC4472is the volume within∼0.1r e where r e=8.57kpc is the effective or half-light radius at a distance of17Mpc.The gas that cools in NGC4472 cannot all collect at the origin,nor is it likely that most of the cooling occurs at very large galactic radii where the radiative cooling rate(∝n2)is inefficient. Brighenti&Mathews(1999a)have shown that if all the cooled gas accumulates at or near the very cen-ter of the galaxy,r<∼100pc,the remaining uncooled hot gas there is locally compressed and becomes very hot,but this is not observed.Alternatively,if most of the cooling and low mass star formation occurs in 0.1<∼r/r e<∼1,then the extremely close agreement between the total mass inferred from X-ray data and the known stellar mass in this region would be up-set(Brighenti&Mathews1997a).Finally,there isgood evidence from observed gas abundance and tem-perature gradients that hot interstellar gas isflowing inward within∼3r e through the optically bright re-gions of NGC4472(Brighenti&Mathews1999a),so it is unlikely that a significant number of low mass stars could form at r>∼3r e.It is most interesting therefore that HII optical line emission in Hα+[NII] lines is observed just in the region of NGC4472where low mass star formation is most expected,r<∼0.24r e (Macchetto et al.1996).3.SEVERAL SOURCES OF HII GASIn addition to interstellar gas cooling from the hot phase,cold gas is continuously expelled from stars throughout the galaxy as a result of normal stel-lar evolution.The total rate that mass is supplied by a population of old stars in NGC4472is˙M=α∗(t n)M∗t≈1M⊙yr−1where M∗t=7.26×1011 M⊙is the stellar mass in NGC4472andα∗(t n)≈1.7×10−12yr−1is the specific mass loss rate froma single burst of star formation after t n=13Gyrs (Mathews1989).The supply of gas from stars is com-parable to the rate that gas is observed to cool from the hot phase:˙M=(2µm p/5kT)L x,bol≈2.5M⊙yr−1,where m p is the proton mass and L x≈7.2×1041 ergs s−1is the bolometric X-ray luminosity of NGC 4472at a distance of17Mpc.Several lines of evidence suggest that most of the gas lost from stars in ellipticals is dissipatively and conductively heated and rapidly merges with the gen-eral hot interstellar coolingflow.Gas lost from orbit-ing stars inherits stellar velocities which,when dis-sipated in shocks or by thermal conductivity,equili-brates to the virial temperature of the stellar system, T∼1keV.However,the stellar virial temperature is about30percent lower than that of the more exten-sive dark halo.As coolingflow gas slowlyflows in-ward from the halo into the stellar region,it is cooled by∼0.3keV as it mixes with slightly cooler virial-ized gas ejected from local stars(Brighenti&Math-ews1999a).This produces the positive temperature gradients observed within a few r e.In addition,the iron,silicon and other elements supplied by the stars increases the metal abundance in the hot interstellar gas as it slowlyflows toward the galactic center within ∼r e,producing negative abundance gradients(Mat-sushita1997).These observations indicate that most or all of the gas ejected by stars merges with the hot gas phase.For simplicity,in the following discussion we ignore the HII contribution from stellar mass loss, but return to this question in§11.This is contrary to the hypothesis of Thomas(1986)that gas ejected from stars remains largely neutral and collapses into (very)low mass stars without joining the hot phase.The assimilation of stellar ejecta into the hot in-terstellar gas is greatly accelerated by dynamical and thermal processes resulting from the orbital motion of mass-losing stars through the coolingflow(Mathews 1990).Rayleigh-Taylor and other instabilities shred the ejected gas into many tiny cloudlets,greatly in-creasing the surface area presented to the hot cool-ingflow gas and their rapid dissipation by conductive heating.In addition,neutral clumps of gas expelled from stars always have ionized outer layers which are easily ablated and reformed;this results in a rapid and complete disruptive heating of the clump.In con-trast,cold gas produced as gas cools directly from the hot interstellar phase is necessarily formed in the local rest frame of the coolingflow gas so the violent dy-namical instabilities that accompany stellar mass loss are not expected.After∼106years,however,the denser cooling region may begin to fall in the galac-tic gravitationalfield(see§10),possibly leading to some disruption at the cloud boundary(Malagoli et al.1990;Hattori&Habe1990).Assuming that ra-diative cooling from the hot interstellar phase occurs, as gas cools through HII temperatures it is thermally protected by surrounding gas at intermediate tem-peratures(104<T<107K)where the thermal con-ductivity is very low.The global kinematics of the two HII gas components of internal origin are quite different.HII regions produced by stellar ejecta will initially tend to mimic local random and systematic stellar motions while HII gas arising from cooling gas will initially share the velocity of local hot gas.A third source of HII gas in ellipticals are the ion-ized parts of gas acquired in recent merging events such as the small dusty clouds within∼0.05r e of the center of NGC4472(van Dokkum&Franx1995). This gas is spatially disorganized and is dynamically unrelaxed.Dust is another clue of its external ori-gin since gas formed by cooling from the hot phase should be nearly dust-free due to sputtering(Draine &Salpeter1979;Tsai&Mathews1995;1996)and may not have time to grow dust in the gas phase(§7).Our interest here is with the HII component pro-duced as gas cools from the hot phase and we assume that this component dominates the optical line emis-sion in NGC4472.4.THE INVERSE HII REGIONA small cloud of HII gas that has cooled from the hot interstellar medium is photoionized by stellar UV radiation arriving at its outer boundary;this is the inverse geometry of normal HII regions ionized by a central star.We suppose that the HII cloud is spheri-cal and that the electron density n e and temperature T=104K are uniform throughout the HII gas.The spatial uniformity of the HII density is essentially un-affected by small local gravitationalfields due to inter-nal stars,the neutral core in the cloud if one exists, or the HII gas itself.The mass of these HII clouds located at the centers of local cooling sites slowly in-creases with time.Thefirst step in understanding the evolution of HII clouds is to determine the maximum size and mass that can be ionized by stellar UV in the central regions of NGC4472.This size depends on the HII electron density and the mean intensity of galactic UV starlight J uv(r).The intensity of ionizing radiation can be deter-mined by an appropriate integral over the galactic stellar distribution.For this we assume a de Vau-couleurs stellar distribution similar to that in NGC 4472,with an effective radius of r e=8.57kpc and an outer maximum stellar radius of25r e.The stellar density and mass are given to a good approximation byρ∗=ρo(b4r/r e)−0.855exp[−(b4r/r e)1/4]andM(r)=M oγ(8.58,[b4r/r e]1/4)where b=7.66925andγ(a,z)is the incomplete gamma function(Mellier&Mathez1987).If the de Vaucouleurs distribution extends to in-finity,the total mass would be M t=M oΓ(8.58)= 1.6582×104M o where M o=16πρo(r e/b4)3.It is nat-ural to normalize the density coefficientρo tofit the de Vaucouleurs distribution for NGC4472in the re-gion0.1<∼r/r e<∼1where the X-ray and stellar mass determinations agree,i.e.ρo=3.80×10−18gm/cm3. When the stellar distribution is truncated at25r e the total mass6.97×107M⊙is only about1percent less than an infinite stellar distribution having the same ρo.At every radiusx=r/r ein the de Vaucouleurs distribution the mean stellar column density˜J can be found by integrating over solid angle,˜J=1n2αB.The density of HII gas isρ=nMfρwhere fρ= 5µ/(2+µ)=1.20,assumingµ=0.61for the molec-ular weight.The total mass of the Stromgren sphereism s=4n5α3Bwhere m p is the proton mass.Some imprecision is ex-pected since we have ignored those ionizing photons that pass through the HII cloud unabsorbed.How-ever,calculations of the transfer of ionizing radiation in the inverse HII region indicate that Equation(1) is accurate to<∼5percent.Figure2illustrates the radial variation of electron density n e=(ρ/m p)(2+µ)/5µin HII gas(solid line) with galactic radius in NGC4472and the correspond-ing local inverse Stromgren radius r s(long dashed line).Within the radius where Hαis observed in NGC4472,x=r/r e<∼0.24wefind r s≈0.3−0.8 pc,n e≈20−90cm−3,and the mass of a typical Stromgren cloud is m s≈2M⊙.The radial col-umn density in an HII Stromgren cloud is typically N s=n e r s≈1.2×1020cm−2.Hot gas is assumed to be cooling at numerous sites throughout this central region of NGC4472and the cooling is made visible by optical line emission from the HII regions.The mass of any particular HII cloud increases slowly with time,supplied by local cool-ing from the hot gas phase or by dissipative merging of clouds.Presumably,new HII clouds are contin-uously forming from the cooling interstellar gas at newly-formed cooling sites and old sites and associ-ated clouds are disappearing.But we suppose that the mean age of cooling sites is long compared to the time required for typical HII clouds to reach the Stromgren mass;in this case the average cloud can be approximated with Stromgren parameters.Notice also that r s≪r so that even the largest HII clouds are very small compared to their distance to the cen-ter of the galaxy.5.GEOMETRY OF HII AND COLD GASWe propose that most of the extended Balmer line emission in ellipticals arises from a multitude of HII clouds at or near their Stromgren radii.If so,the to-tal volume within clouds occupies only a tiny fraction f F of the galactic volume within the Hα-emitting re-gion of NGC4472,r<∼2kpc.Thefilling factor f F can be estimated by comparing the total volume of HII required to produce the observed Balmer line lu-minosity to the apparent volume from which optical line emission is observed.In most optical observations,such as those of Mac-chetto et al(1996),Hα(6562˚A)is blended with two nearby[NII]lines at6584and6548˚A.The totalflux observed by Macchetto et al.(1996)in all three lines is F lines=17.30×10−14ergs cm−2 s−1.Observations at higher resolution reveal that the F([NII]6584)/F(Hα)≈1.38and F(6584)/F(6548)=bining all these ratios,and adopting CaseB conditions F Hα/F Hβ=2.86,the Hβflux from NGC4472is F Hβ=2.13×10−14ergs cm−2s−1 and the total luminosity from all HII emission is L Hβ=4πD2F Hβ=7.34×1038erg s−1,assuming a distance of D=17Mpc to Virgo.How many dust-free Stromgren clouds are required to produce this total luminosity?The Hβluminosity of a single Stromgren cloud isℓβ,s=n2eǫβ(4π/3)r3s=1.5×1031n2e r3spc ergs s−1 whereǫβ=1.0×10−25erg cm3s−1is the Hβemis-sivity at T=104K.For typical values of n e and r spc(in parsecs)in the central galaxy x<∼0.25,ℓβ≈3−7.5×1033ergs s−1.Therefore,about N cl= 105−106Stromgren clouds are required to account for the Balmer line luminosity observed.The HIIfill-ing factor is found by comparing the volume of all HII gas V cl=L Hβ/ n e 2ǫHβ=2.5×1060cm3(assuming n e =50cm−3)with the total volume of the Hβ-emitting region,V tot=(4/3)π(0.24r e)3=1.1×1066 cm−3.Thefilling factor of HII gas f F=2×10−6is very small,consistent with our proposition that HII emission arises from many small clouds and with ear-lier estimates of f F(Baum1992).If∼1M⊙of hot gas cools each year in NGC4472,then the mass of each cloud will grow quite slowly,∼10−6−10−5M⊙yr−1,requiring t s∼2×105−2×106years to form a typical Stromgren cloud.The total mass of all the HII emitting gas in NGC4472is M II= n Mf F V cl≈1.2×105M⊙,similar to values in the literature but here evaluated using a consistent physical model.A smallfilling factor also implies that each HII cloud is exposed to the unabsorbed stellar UV emis-sion from the entire galaxy,provided the cloud sys-tem is approximately spherical.The“optical depth”for intersecting a Stromgren cloud across the opti-cal line-emitting region within r t=0.24r e isτ=πr2s r t N cl/V tot≈0.006−0.06.Sinceτ≪1the clouds do not shadow each other.In realityτcould be larger (i)if the typical cloud crossection is much less than πr2s(τ∝r−1s)or(ii)if the cloud system were not spherical;a disk-like configuration could result from galactic rotation.In any case,the assumption thateach HII cloud is exposed to the full,unabsorbed stel-lar UV emission is likely to be a reasonably good ap-proximation.Combining previous results,the average column depth that HII gas presents to X-radiation through-out the galactic core,N∼N sτ∼1018−1019cm−2,is much less than the value N∼3×1021cm−2that best fits the observed X-ray continuum(Buote1999).The size that an HII cloud presents to absorbing X-rays is larger than r s since we have ignored the extended cooling region around each cloud with temperatures between106and104K in which X-rays can still be absorbed.This assumption will be justified below.The total mass of HI or H2gas observed in the cen-tral regions of NGC4472,M cold<107M⊙,is another potential source of X-ray absorption.If this mass of cold gas were arranged in a disk of thickness of the X-ray absorbing column N=3×1021cm−2,located in the galactic core and oriented with its symmetry axis along the line of sight,it would have a radius<370 pc,somewhat larger than the faint patch of dust ob-served by van Dokkum&Franx(1996).However a cloud of size370pc obscures only∼0.007of the total X-ray luminosity of NGC4472and would therefore produce negligible X-ray absorption.The true X-ray absorption is very probably much less than3×1021 cm−2.The observation of NGC4472by Buote us-ing the∼4’beam of ASCA also included the nearby gas-rich dwarf irregular galaxy UGC7636(Irwin& Sarazin1996;Irwin,Frayer&Sarazin1997)which may be the source of the X-ray absorbing column at-tributed to NGC4472if its covering factor is suffi-ciently large.Although it seems likely that interstellar magnetic fields are important in the centers of ellipticals(Math-ews&Brighenti1997;Godon,Soker&White1998), it is remarkable that the observed optical line emis-sion does not indicate strongfields in the HII gas. Typical HII densities in bright ellipticals determined from[SII]6716/6731line ratios are∼100−200cm−3 (Heckman et al.1989;Donahue&Voit1997),similar to(or even a bit larger than)the values found here for NGC4472(Figure2).(Unfortunately,we have been unable tofind a determination of the HII density spe-cific to NGC4472.)This suggests that the HII gas density is not being diluted by magnetic support,i.e. B2/8π<2nkT or B<70µG in the HII gas.HII densities of∼100are also supported by comparing the ionization parameter U=n iph/n e for pressure equilibrium HII gas in NGC4472(short dashed line in Figure2)with values that characterize the entire observed line spectrum.Within∼r e in NGC4472log U≈−3.3,very similar to values of U required to reproduce LINER type spectrum typically observed in ellipticals(e.g.Johnstone&Fabian1988);thisprovides an independent check on our HII gas density and J near the center of NGC4472.The apparent absence of magnetic support in the HII gas is interesting since the hot phase gas is re-quired to havefields of at least severalµG at largegalactic radii to explain Faraday depolarization of ra-dio sources and distant quasars(Garrington&Con-way1991).Interstellarfields>∼1µG can be generated in a natural way by stellar seedfields and turbulent dynamo action in the hot gas(Mathews&Brighenti1997).As the gas density increases by∼1000when it cools from the hot phase to HII temperatures,a field of1µG would grow to100µG ifflux is con-served,B∝ρ2/3.The initialfield in the hot gas in r<∼0.24r e would need to be surprisingly small, <∼0.7µG,to evolve into the rather smallfields allowed in HII clouds,B<∼70µG,implied by typical electron densities.Small HIIfields can be understood if localcooling sites form in interstellar regions having lower than averagefields;in pressure balance,lowerfields require higher hot gas densities which cool preferen-tially.Alternatively,it is possible thatfield reconnec-tion has been very efficient during cooling,implying a disorganizedfield and considerable stirring motion during the cooling process.6.COOLING SITE GAS DYNAMICSCooling sites in the hot interstellar gas are initiated in regions of low entropy(i.e.low temperature,high density)which cool preferentially by radiative losses. Entropyfluctuations can be generated by a variety of complex events:stellar mass loss,occasional Type Ia supernovae,sporadic mergers with other nearby (dwarf)galaxies,and differential SNII heating events and outflows that occurred in pregalactic condensa-tions.Due to the complicated nature of these inter-actions,it is difficult to predict the amplitudes and mass scales of the entropy inhomogeneities so the de-tailed nature of the initial cooling process remains unclear.However,once cooling commences,the gas flow toward the cooling site may evolve toward a sim-ple profile provided entropyfluctuations in the hot gas are not too severe over theflow region.We now describe such a model for cooling site。
辐射强度与波长与温度的关系 英文解释

辐射强度与波长与温度的关系英文解释全文共3篇示例,供读者参考篇1Radiation intensity, wavelength, and temperature are closely related in the field of physics. Radiation intensity refers to the amount of energy transferred through electromagnetic waves in a given area. Wavelength, on the other hand, refers to the distance between two consecutive peaks or troughs of a wave. Temperature is a measure of the average kinetic energy of the particles in a substance.The relationship between radiation intensity, wavelength, and temperature can be explained through the black-body radiation law, which states that the total energy radiated by a black body per unit area per unit time is directly proportional to the fourth power of the temperature and inversely proportional to the wavelength to the fifth power. In simpler terms, as the temperature of an object increases, the radiation intensity it emits also increases. Additionally, shorter wavelengths correspond to higher energy levels and thus higher radiation intensity.Another important concept in this relationship is Wien's displacement law, which states that the wavelength at which the intensity of radiation is at its maximum is inversely proportional to the temperature of the object. This means that as the temperature of an object increases, the peak wavelength of radiation emitted by that object shifts to shorter wavelengths.In practical terms, this relationship can be observed in everyday life. For example, when an object such as a stove burner is heated, it begins to emit radiation in the form of infrared light. As the temperature of the burner increases, the intensity of the emitted radiation also increases, and the peak wavelength shifts towards shorter wavelengths. This is why the burner appears red-hot at lower temperatures and blue-white at higher temperatures.Understanding the relationship between radiation intensity, wavelength, and temperature is crucial in various fields such as astronomy, thermodynamics, and materials science. By studying how these parameters interact, scientists and engineers can gain insights into the behavior of objects at different temperatures and wavelengths, leading to advancements in technology and scientific knowledge.篇2The relationship between radiation intensity, wavelength, and temperature is a fundamental concept in physics and plays a key role in understanding the behavior of electromagnetic radiation.Radiation intensity refers to the power per unit area emitted by a source and is typically quantified in terms of watts per square meter. The intensity of radiation is directly proportional to the temperature of the source according to Stefan-Boltzmann Law. This law states that the total energy radiated per unit surface area of a black body is directly proportional to the fourth power of the absolute temperature. In mathematical terms, this relationship can be expressed as:\(I = σT^4\)Where:- I is the radiation intensity,- σ is the Stefan-Boltzmann constant, and- T is the temperature in Kelvin.This relationship demonstrates that as the temperature of a source increases, the radiation intensity emitted by the source also increases. This is why hotter objects appear brighter and emit more radiation than cooler objects.The wavelength of radiation is another important parameter that is related to the temperature of the source. According to Wien's Law, the wavelength of the peak intensity of radiation emitted by a black body is inversely proportional to the temperature of the source. Mathematically, this relationship can be expressed as:\(λ_{max} = \frac{b}{T}\)Where:- \(λ_{max}\) is the wavelength of maximum intensity,- b is Wien's displacement constant, and- T is the temperature in Kelvin.This relationship illustrates that as the temperature of a source increases, the peak wavelength of the radiation it emits shifts to shorter wavelengths. In other words, hotter objects emit radiation that is more blue in color, while cooler objects emit radiation that is more red in color.In conclusion, the intensity and wavelength of radiation emitted by a source are directly influenced by the temperature of the source. Understanding these relationships is crucial for various fields of study, including astrophysics, climate science, and engineering. By studying the interplay between temperature,intensity, and wavelength, scientists can gain insights into the behavior of electromagnetic radiation and its impact on the world around us.篇3Radiation intensity refers to the amount of radiant energy emitted from a source per unit time and unit solid angle. It is dependent on various factors, such as temperature and wavelength. In this article, we will explore the relationship between radiation intensity, wavelength, and temperature.Firstly, let's discuss the relationship between radiation intensity and wavelength. According to Planck's radiation law, the intensity of radiation emitted by a black body is directly proportional to the fourth power of the temperature and inversely proportional to the fourth power of the wavelength. This means that as the temperature of a radiating body increases, the intensity of radiation emitted also increases. However, the intensity decreases as the wavelength of the radiation increases. This relationship is crucial in understanding the spectral distribution of radiation emitted by objects at different temperatures.Next, let's delve into the relationship between radiation intensity and temperature. As mentioned earlier, the intensity of radiation emitted by a black body is directly proportional to the fourth power of the temperature. This relationship is explained by Stefan-Boltzmann's law, which states that the total energy radiated per unit surface area of a black body is directly proportional to the fourth power of its absolute temperature. Therefore, as the temperature of a radiating body increases, the total amount of energy radiated per unit time also increases. This has important implications in various fields, such as astrophysics and material science.In conclusion, the relationship between radiation intensity, wavelength, and temperature is a fundamental aspect of thermal radiation. Understanding these relationships is crucial in predicting the behavior of radiant energy emitted by objects at different temperatures and wavelengths. By studying these relationships, scientists can gain insights into the thermal properties of materials and improve our understanding of the universe.。
HOT GAS IN THE GALAXY WHAT DO WE KNOW FOR SURE

A s t r o p h y s i c a l P l a s m a s : C o d e s , M o d e l s , a n d O b s e r v a t i o n s (M e x i c o C i t y , 25-29 O c t o b e r 1999)E ditors:Jan eArthu r,NancyB rick house,&JoséFra nco RevMexAA (Serie de Conferencias),9,1–5(2000)HOT GAS IN THE GALAXY:WHAT DO WE KNOW FOR SURE?W.T.Sanders Department of Physics,University of Wisconsin-Madison,USA RESUMEN En la d´e cada pasada se lograron grandes avances en nuestra concepci´o n del gas interestelar caliente de la V´ıa L´a ctea.El Diffuse X-ray Spectrometer obtuvo es-pectros del plano gal´a ctico (esto es,de la Burbuja Local),en el rango 0.15–0.28keV,que muestran l´ıneas y mezclas de l´ıneas de emisi´o n.Los espectros confirman que el fondo de rayos-X suaves,en estas energ´ıas,es de origen t´e rmico a aproximadamente 106K,pero el espectro no puede ser bien ajustado con los modelos de emisi´o n de plasma existentes.Los datos del sat´e lite ROSAT ,tanto de muestreo de todo el cielo como de observaciones puntuales,restringen las distancias del gas que emite dentro de la Burbuja Local,el medio interestelar local y el halo.Los datos confirman que la Burbuja Local tiene un tama˜n o de ∼100pc y que el halo gal´a ctico tiene dos componentes de gas caliente;una componente muy inhomog´e nea de 106K y otra componente m´a s caliente,de varios 106K,cuya distribuci´o n es suave y sigue a la es-tructura general de la Galaxia.El sat´e lite ASCA ha detectado emisi´o n de plasmas a m´a s de 107K en la cresta gal´a ctica,en dos regiones del centro gal´a ctico y en el bulbo.M´a s recientemente,el micro calor´ımetro del experimento Wisconsin/Goddard con cohetes observ´o el espectro de la emisi´o n difusa en (l,b )∼(90◦,60◦),con un campo visual de 1sr en el rango espectral 0.1–1keV y con una resoluci´o n de ∼s l´ıneas de O VII y O VIII son detectadas,pero s´o lo se obtienen l´ımites superiores para las l´ıneas esperadas de Fe XVII .ABSTRACT Major advances have been made in the past decade in our knowledge of the hot interstellar gas of our Milky Way galaxy.The Diffuse X-ray Spectrometer obtained spectra in the 0.15–0.28keV range from the Galactic plane (i.e.,from the Local Bubble)that show emission lines and blends.These spectra confirm that the soft X-ray background in this energy range is thermal in origin,at temperature roughly 106K,but the spectra are not well fit by standard plasma emission models.Data fromthe ROSAT satellite,both from the all-sky survey and from pointed observations,have provided constraints on the distances to some of the hot gas emitting regions inthe Local Bubble,the local ISM,and the Galactic halo.These data confirm that thelocal bubble is ∼100pc in size,and they indicate the existence of two independenthot gas components in the Galactic halo:a patchy,localized lower temperaturehalo component near 106K,and a smoother higher temperature halo component atseveral 106K,with a spatial structure reflective of the overall structure of the galaxy.The ASCA satellite has observed emission from hot plasmas at temperatures above107K from the Galactic ridge,from two different galactic center components,andfrom the Galactic bulge.More recently,the Wisconsin/Goddard micro-calorimetersounding rocket payload has observed the spectrum of the diffuse emission from(l,b )∼(90◦,60◦)with a 1sr field of view over the 0.1–1keV spectral range with∼8eV resolution.Lines from O VII and O VIII are clearly seen,but there are onlyupper limits to the expected Fe XVII lines.Key Words:GALAXY:GENERAL —GALAXY:STRUCTURE —ISM:BUBBLES —ISM:GENERAL —X-RAYS:ISM 1A s t r o p h y s i c a l P l a s m a s : C o d e s , M o d e l s , a n d O b s e r v a t i o n s (M e x i c o C i t y , 25-29 O c t o b e r 1999)E d i t o r s : J a n e A r t h u r , N a n c yB r i c k h o u s e , & J o s é F r a n c o2SANDERSWhat I would like to do in this talk is to summarize the observations of diffuse interstellar hot gas—meaning temperatures of order 106K—in our Galaxy.Trying to cover such a broad range of observations means that I probably won’t do a very good job describing any of them,so I apologize in advance and proceed.1.SPATIAL STRUCTUREThe most comprehensive data set we have is that obtained by the ROSAT satellite—both its all-sky survey and its pointed observations.The ROSAT all-sky survey is presented as maps in 3bands,1/4keV,3/4keV,and 1.5keV,in Snowden et al.(1995b,1997).In the 1/4keV band map,we see X-rays characteristically emitted by plasmas with T ∼106K,but interstellar absorption is large,so we can see only out to an N H of a few 1020cm −2,roughly 100–200pc.In the 3/4keV band,we are more sensitive to plasmas at T ∼3×106K,and interstellar absorption is smaller,so we can see out to N H ∼few 1021cm −2,several kpc.In the 1.5keV band we are seeing plasmas with T >107K and we see through almost the entire Galaxy.The different structures that we see in these maps reflect the structure of the Galaxy on those different distance scales.1.1.The 1/4keV BandSome of the bright features visible on the 1/4keV band map have names or are associated with features seen at other wavelengths.A large arc extending from (l,b )∼(30◦,45◦)through (l,b )∼(330◦,75◦)and reaching as far as (l,b )∼(290◦,60◦)is associated with the radio continuum North Polar Spur,which is part of radio Loop I (Berkhuijsen,Haslam,&Salter 1971).This Loop appears coincident with the edge of a superbubble associated with the Scorpius-Centaurus OB associations at a distance of ∼150pc.This is the superbubble nearest to the Local Bubble.Another superbubble,several hundred pc away,is seen in Eridanus,roughly centered at (l,b )∼(205◦,−40◦).It is associated with the cavity generated and heated by the Orion OB stars (Reynolds &Ogden 1979;Snowden et al.1995a;Guo et al.1995).The Monogem Ring (Plucinsky et al.1996),centered at (l,b )∼(205◦,10◦),is thought to be an ancient supernova remnant at a distance of ∼200pc.Also visible on this map are the Cygnus Loop supernova remnant at (l,b )∼(74◦,−9◦),and the Vela supernova remnant (l,b )∼(263◦,−3◦).In the 1/4keV band map,we see that there is emission from all directions,even the Galactic plane where we cannot see farther than ∼100pc.This implies that there is some amount of very local emission.We know from interstellar absorption studies (Sfeir et al.1999)that there is locally a deficiency of neutral material,the local cavity,so inside this local cavity is the natural place to find this local X-ray emission,the Local Bubble.Then there is the question of the bright regions at high Galactic latitudes:are they extensions of the Local Bubble,or are they due to halo or more distant emission shining into the local cavity?A number of shadowing experiments have been done with ROSAT ,in which the X-ray telescope was pointed towards a high latitude H I or molecular cloud and the decrease in X-ray brightness seen toward the cloud was used to constrain foreground and background X-ray emission.One of my favorite shadowing papers is the Snowden et al.(1994)ROSAT observation towards a 300deg 2region in Ursa Major around the direction of the lowest neutral hydrogen column density on the sky,the Lockman Window at (l,b )∼(150◦,52◦).In the 21-cm map of that paper,neutral hydrogen clouds of column density ∼3x 1020cm −2can be seen around (l,b )∼(136◦,53◦)near the Window where the N H drops as low as 0.5x 1020cm −2.The distance to these clouds has been determined by Benjamin et al.(1996)to be ∼350pc.The corresponding ROSAT 1/4keV band X-ray map has the H I contours overlaid.We see X-ray minima on the face of the clouds providing a measure of the Local Bubble contribution in this direction:more than twice as bright as in the Galactic plane,but only 70%of the total 1/4keV band emission in this direction.We also see brighter X-ray emission in directions of lower N H providing a measure of the 1/4keV halo emission.We note the lack of detailed anticorrelation between the H I and the X-ray emission,indicating that the 1/4keV halo emission is patchy on scales of 1◦.In Draco,roughly 30◦away,we see somewhat less bright emission from the Local Bubble,and much brighter 1/4keV halo emission (Burrows &Mendenhall 1991;Snowden et al.1991).But not all clouds give 1/4keV band shadows.MBM 12is a dense low latitude cloud at a distance of 90pc,located just in front of the larger Taurus-Auriga dark cloud complex.It shows little or no 1/4keV shadow (Snowden,McCammon,&Verter 1993),which is consistent with its being at the edge of the Local Bubble,butA s t r o p h y s i c a l P l a s m a s : C o d e s , M o d e l s , a n d O b s e r v a t i o n s (M e x i c o C i t y , 25-29 O c t o b e r 1999)E d i t o r s : J a n e A r t h u r , N a n c yB r i c k h o u s e , & J o s é F r a n c oHOT GAS IN THE GALAXY 3it has a definite 3/4keV shadow that is consistent with little or none (<20%)of the 3/4keV band emission arising from within the Local Bubble.Figures 2and 3in Sanders (1995)give views of the local solar neighborhood from within the plane of the Galaxy and from the north Galactic pole,showing the Sun within the local cavity,filled with the Local Bubble,the nearby Sco-Cen bubble,MBM 12within the local cavity and the Taurus cloud beyond,the UMa lines of sight,the Eridanus superbubble,and the Monogem ring.1.2.The 3/4keV BandAt 3/4keV we again see the Cygnus Loop and Vela supernova remnants and the Eridanus superbubble.The Loop I emission is more pronounced,but towards the direction (l,b )∼(0◦,0◦)much of the emission is likely from the Galactic Bulge.In this band,we now see the Large Magellanic Cloud and the so-called Cygnus Superbubble.We also see clear signs of absorption both along the Galactic plane from galactic longitude ∼330◦through the Galactic center to almost longitude 90◦,and toward the Taurus-Auriga cloud complex in the Galactic anti-center direction.The patchy halo emission seen in 1/4keV is not seen at 3/4keV,but rather at high latitudes we see smooth,nearly isotropic emission with few features.The origin of the 3/4keV band flux is still a mystery.Roughly half of the total high latitude diffuse emission has been resolved into point sources that are almost entirely AGNs (Hasinger et al.1993).Galactic stars may contribute as much as 10%of the apparently diffuse flux (Schmitt &Snowden 1990).The Local Bubble may contribute as much as 30%if the MBM 123/4keV band upper limit on the local emision scales with the 1/4keV band local count rate.An appreciable fraction appears to be coming from a smooth 3/4keV halo that is distinct from the patchy 3/4keV band halo (Wang 1998).A related mystery is why does the competition between the extragalactic and halo components that dominate at high Galactic latitudes and the Galactic components that dominate at low Galactic latitudes not produce a feature somewhere on the map?Why does the stellar and local bubble emission in the plane so exactly fill in the extragalactic emission that is absorbed in the plane?Returning to the Bulge,Park et al.(1997,1998)have presented evidence for an X-ray emitting Galactic Bulge using shadows cast by molecular clouds at distances greater than 3kpc along several lines of sight around (l,b )∼(10◦,0◦)and (l,b )∼(25◦,0◦).Almy et al.(2000)have found similar results toward a molecular cloud ∼2kpc away toward (l,b )∼(337◦,4◦).Snowden et al.(1997)have modeled the Bulge as a cylindrical emission region 5kpc in radius with a 1.9kpc scale height and with all of the N H along the line of sight between us and the emission region.Their Figure 12shows a plot of a cut through this region along Galactic longitude 335◦for both the 3/4keV band and the 1.5keV band.At all points along the cut,the data lie on or above the model,with the excess emission attributed to the Loop I superbubble along the same line of sight.The Bulge surface brightnesses found by these three groups are consistent with one another to within roughly 30%.1.3.The 1.5keV BandAs we turn to the 1.5keV band map,we see that the Galactic features are relatively weaker,and Hasinger et al.(1998)find that the fraction of the background contributed by AGNs is in the 70–80%range.More distant and hotter Galactic gas is not easily studied using ROSAT because of its limited high energy response.Both ASCA (Kaneda et al.1997)and XTE (Valinia &Marshall 1998)have observed the Galactic ridge,a very narrow strip of enhanced harder X-ray emission within 1◦of the Galactic plane towards the inner 60◦of the Galaxy.Both groups discuss this emission as arising from a population of young supernova remnants,but are not able to explain all features of the data satisfactorily.There seem to be two different Galactic ridge components,with different scale heights as well as different temperatures.Valinia &Marshall (1998)use Raymond &Smith models and obtain temperatures ∼3×107K for the ridge plasma.Kaneda et al.(1997)use two NEI plasmas to fit the ASCA data,one plasma with kT ∼0.8keV and far from equilibrium,and the other plasma having kT ∼7keV but close to equilibrium.The hottest diffuse gas seems to be within 0.5◦of the Galactic center where Maeda (1998)used ASCA data to find plasma temperatures in the range of 107−108K.A s t r o p h y s i c a l P l a s m a s : C o d e s , M o d e l s , a n d O b s e r v a t i o n s (M e x i c o C i t y , 25-29 O c t o b e r 1999)E d i t o r s : J a n e A r t h u r , N a n c yB r i c k h o u s e , & J o s é F r a n c o4SANDERS2.SPECTRAL DATAOn the subject of temperature,what do we know about the temperature,composition,or state of equilibrium of the plasmas in the Local Bubble and the Galactic halo?Not all that much,ing band ratios from the ROSAT all sky survey and from University of Wisconsin sounding rockets,and using pulse height fits to UW,ROSAT ,or ASCA data typically give temperatures ∼106K for the Local Bubble and the 1/4keV halo,with some hints of low abundances of Fe (Bloch et al.1990).For the 3/4keV band,typical temperatures are 106.4−6.5K,and for the Galactic Bulge both Park et al.(1997)and Snowden et al.(1997)found T ∼106.6−6.7K.To get higher spectral resolution,we turn to two other instruments,the Diffuse X-ray Spectrometer (DXS)and the X-ray Quantum Calorimeter (XQC).2.1.Diffuse X-Ray SpectrometerDXS is a Bragg crystal spectrometer that flew once on the Space Shuttle and was sensitive over the energy range 150–284eV,essentially the 1/4keV band,with energy resolution that varied from 5–17eV over that range.During its flight,it scanned along the Galactic plane in the longitude interval 150◦<l <300◦.Sanders et al.(1998)give a brief description of the instrument and its calibration.Figure 3of Sanders et al.(1998)shows the DXS data from the interval 220◦<l <250◦along the Galactic plane (the Puppis region),displayed as a function of energy.In this direction,the X-rays that we detect should be X-rays of Local Bubble origin almost entirely.The intensity of the DXS data is in good agreement with that measured in this direction by ROSAT and by the Wisconsin rocket survey.The spectrum shows lines and line blends that indicate that its origin is thermal,but the spectrum is not in agreement with the predictions of a single-temperature plasma in collisional equilibrium,independent of whether the model is Raymond &Smith or MekaL.As discussed in more detail in Sanders et al.(1998),the best fit that was obtained using standard equilibrium models was a modified Raymond &Smith,using line data calculated by Liedahl,with the elemental abundances allowed to float.This fit required reducing the abundances of Fe,Si,and S by factors of 2–3,but the result was still not a good fit (reduced chi-square was ∼2).Several NEI models were also tried,but their fits were no better.A lot of work remains to be done in analyzing these data,in particular not doing global model fitting,but focusing on individual ions and their lines.2.2.The X-ray Quantum CalorimeterThe XQC sounding rocket detector is a micro-calorimeter—a device that is small enough (∼1mm 2)and cold enough (∼60mK)that its heat capacity is so small that the energy of one X-ray photon raises its temperature a measurable amount.This process can be made highly repeatable so that very good energy resolution,a few eV,is obtainable.The detectors flown on the most recent University of Wisconsin/Goddard Space Flight Center sounding rocket flight achieved 4–5eV resolution in the laboratory and ∼8eV resolution in flight.The data in the 0.1–1keV energy range from that most recent XQC flight are shown in the first figure of Stahle,McCammon,&Irwin (1999).The field of view was 1sr,centered on (l,b )∼(90◦,60◦).The intensity of the XQC data is consistent with the ROSAT and UW rocket survey data from this part of the sky.In the spectrum,the lines of O VII at 560–574eV and O VIII at 653eV are clearly visible.Just as clearly,the lines of Fe XVII and Fe XV in the energy range between 727–827eV are not seen.This is consistent with the ASCA results of Gendreau et al.(1995)and Chen,Fabian,&Gendreau (1997),but not with the models having a thermal component at T ∼3×106K used by the Wisconsin group to account for the measured flux in their 3/4keV band (M band).Either the temperature of this component is lower than we thought previously,or the abundance of iron in the emitting plasma is <25%of solar.The spectrum also does not show a strong line or line complex due to Fe IX ,Fe X ,Fe XI at ∼70eV as most models do.This might be an indication of reduced Fe abundance in the Local Bubble,but it is too early to be sure.The data in the Stahle et al.(1999)spectrum are not reliable below about 200eV due to data reduction issues that are still being worked on.Other features of the spectrum are a probable C VI line at 367eV and possibly emission from N VII in the 450–550eV region.A s t r o p h y s i c a l P l a s m a s : C o d e s , M o d e l s , a n d O b s e r v a t i o n s (M e x i c o C i t y , 25-29 O c t o b e r 1999)E d i t o r s : J a n e A r t h u r , N a n c yB r i c k h o u s e , & J o s é F r a n c oHOT GAS IN THE GALAXY 5Clearly there is a lot of work to be done yet to understand and interpret these plications are the large field of view,which makes it more difficult to separate Galactic and extragalactic contributions,and the small number of counts.But the potential for making progress towards understanding the emission from hot gas in the Galaxy in the 0.1–1keV band through analysis of these data is very high.REFERENCESAlmy,R.C.,McCammon,D.,Digel,S.W.,Bronfman,L.,&May,J.2000,ApJ,submittedBenjamin,R.A.,Venn,K.A.,Hiltgen,D.D.,&Sneden,C.1996,ApJ,464,836Berkhuijsen,E.M.,Haslam,C.G.T.,&Salter,C.J.1971,A&A,14,252Bloch,J.J.,Priedhorsky,W.C.,&Smith,B.W.1990,in IAU Colloq.115,High Resolution X-ray Spectroscopy of Cosmic Plasmas,ed.P.Gorenstein &M.Zombeck (Cambridge:Cambridge University Press),160Burrows,D.N.,&Mendenhall,J.A.1991,Nature,351,629Chen,L.-W.,Fabian,A.C.,&Gendreau,K.C.1997,MNRAS,285,449Gendreau,K.C.,et al.1995,PASJ,47,L5Guo,Z.,Burrows,D.N.,Sanders,W.T.,Snowden,S.L.,&Penprase,B.E.1995,ApJ,453,256Hasinger,G.,Burg,R.,Giacconi,R.,Hartner,G.,Schmidt,M.,Truemper,J.,&Zamorani,G.1993,A&A,275,1Hasinger,G.,Burg,R.,Giacconi,R.,Schmidt,M.,Truemper,J.,&Zamorani,G.1998,A&A,329,482Kaneda,H.,Makishima,K.,Yamauchi,S.,Koyama,K.,Matsuzaki,K.,&Yamasaki,N.Y.1997,ApJ,491,638Maeda,Y.1998,Ph.D.Thesis,Kyoto UniversityPark,S.,Finley,J.P.,&Dame,T.M.1998,ApJ,509,203Park,S.,Finley,J.P.,Snowden,S.L,&Dame,T.M.1997,ApJ,476,L77Plucinsky,P.P.,Snowden,S.L.,Aschenbach,B.,Egger,R.,Edgar,R.J.,&McCammon,D.1996,ApJ,463,224Reynolds,R.J.,&Ogden,P.M.1979,ApJ,229,942Sanders,W.T.1995,in ASP Conf.Ser.Vol.80,The Physics of the Interstellar Medium and Intergalactic Medium,A Meeting in Honor of Professor George B.Field,ed.A.Ferrara,C.F.McKee,C.Heiles,&P.R.Shapiro (San Francisco:ASP),498Sanders,W.T.,Edgar,R.J.,Liedahl,D.A.,&Morgenthaler,J.P.1998,in Lecture Notes in Physics 506,IAU Colloq.166,The Local Bubble and Beyond,ed.D.Breitschwerdt,M.J.Freyberg,&J.Truemper (Berlin:Springer-Verlag),83Schmitt,J.H.M.M.,&Snowden,S.L.1990,ApJ,361,207Sfeir,D.M.,Lallement,R.,Crifo,F.,&Welsh,B.Y.1999,A&A,346,785Snowden,S.L.,Burrows,D.N.,Sanders,W.T.,Aschenbach,B.,&Pfeffermann,E.1995a,ApJ,439,399Snowden,S.L.,Egger,R.,Freyberg,M.J.,Plucinsky,P.P.,Schmitt,J.H.M.M.,Truemper,J.,Voges,W.,McCammon,D.,&Sanders,W.T.1997,ApJ,485,125Snowden,S.L.,Freyberg,M.J.,Plucinsky,P.P.,Schmitt,J.H.M.M.,Truemper,J.,Voges,W.,Edgar,R.J.,McCammon,D.,&Sanders,W.T.1995b,ApJ,454,643Snowden,S.L.,Hasinger,G.,Jahoda,K.,Lockman,Felix.J.,McCammon,D.,&Sanders,W.T.1994,ApJ,430,601Snowden,S.L.,McCammon,D.,&Verter,F.1993,ApJ,409,L21Snowden,S.L,Mebold,U.,Hirth,W.,Herbstmeier,U.,&Schmitt,J.H.M.M.1991,Science,252,1529Stahle,C.K.,McCammon,D.,&Irwin,K.D.1999,Physics Today,52,32Valinia,A.,&Marshall,F.E.1998,ApJ,505,134Wang,Q.D.1998,in Lecture Notes in Physics 506,IAU Colloq.166,The Local Bubble and Beyond,ed.D.Breitschwerdt,M.J.Freyberg,&J.Truemper (Berlin:Springer-Verlag),503W.T.Sanders:Department of Physics,University of Wisconsin-Madison,1150University Avenue,Madison,WI 53706,USA (sanders@).。
Accomodating Solar and Atmospheric Neutrino Deficits, Hot Dark Matter, and a Double Beta De

arXiv:hep-ph/9402231v2 9 Feb 1994
−6 2 2 −3 a)Small − angle MSW, ∆m2 ei ∼ 6 × 10 eV , sin 2θei ∼ 7 × 10 ,
2
−6 2 2 b)Large − angle MSW, ∆m2 ei ∼ 9 × 10 eV , sin 2θei ∼ 0.6, −10 eV2 , sin2 2θ ∼ 0.9. c)Vacuum oscillation, ∆m2 ei ei ∼ 10
(1)
Of these, (a) is favored over (b) by the fits to the solar neutrino data [9], and both (b) and (c) are disfavored by information from the neutrino burst from supernova 1987A [11]. B. Atmospheric Neutrino Deficit The second set of experiments indicating non-zero neutrino masses and mixings has to do with atmospheric νµ ’s and νe ’s arising from the decays of π ’s and K ’s and the subsequent decays of secondary muons produced in the final states of the π and K decays. In the underground experiments the νµ and ν ¯µ produce muons and the νe and ν ¯e lead to e± . Observations of µ± and e± indicate a far lower value for νµ and ν ¯µ than suggested by na¨ ıve counting arguments which imply that N (νµ + ν ¯µ ) = 2N (νe + ν ¯e ). More precisely, the ratio of µ events to e-events can be normalized to the ratio of calculated fluxes to reduce flux uncertainties, giving [3] R(µ/e) = 0.60 ± 0.07 ± 0.05 (Kamiokande), = 0.54 ± 0.05 ± 0.12 (IMB), = 0.69 ± 0.19 ± 0.09 (Soudan II). Combining these results with observations of upward going muons by Kamiokande [3], IMB [3], and Baksan [12] and the negative Fr´ ejus [13] and NUSEX [14] results leads to the conclusion [15] that neutrino oscillations can give an explanation of these results, provided
病毒学

6
The Role of Animal Viruses in Understanding the Basic Outlines of Eukaryotic Gene Regulation: The first transcriptional enhancer element (acts in an orientation- and distance-independent fashion) was described in the SV40 genome, as was a distance- and orientation-dependent promoter element observed with the same virus. The transcription factors that bind to the promoter, SP-1, or to the enhancer element, such as AP-1, AP-2, and which are essential to promote transcription along with the basal factors, were first described with SV40. Almost everything we know about the steps of messenger RNA (mRNA) processing began with observations made with viruses. For examples, RNA splicing of new transcripts was first described with the adenoviruses. The signal for polyadenylation in the mRNA was first found using SV40.
Superfluid Friction and Late-time Thermal Evolution of Neutron Stars

Bennett Link1 blink@ Montana State University, Department of Physics, Bozeman MT 59717 ABSTRACT The recent temperature measurements of the two older isolated neutron stars PSR 1929+10 and PSR 0950+08 (ages of 3 × 106 and 2 × 107 yr, respectively) indicate that these objects are heated. A promising candidate heat source is friction between the neutron star crust and the superfluid it is thought to contain. We study the effects of superfluid friction on the long-term thermal and rotational evolution of a neutron star. Differential rotation velocities between the superfluid and the crust (averaged over the inner crust moment of inertia) of ω ¯ ∼ 0.6 rad s−1 for PSR 1929+10 and ∼ 0.02 rad s−1 for PSR 0950+08 would account for their observed temperatures. These differential velocities could be sustained by pinning of superfluid vortices to the inner crust lattice with strengths of ∼ 1 MeV per nucleus. Pinned vortices can creep outward through thermal fluctuations or quantum tunneling. For thermally-activated creep, the coupling between the superfluid and crust is highly sensitive to temperature. If pinning maintains large differential rotation (∼ 10 rad s−1 ), a feedback instability could occur in stars younger than ∼ 105 yr causing oscillations of the temperature and spin-down rate over a period of ∼ 0.3tage . For stars older than ∼ 106 yr, however, vortex creep occurs through quantum tunneling, and the creep velocity is too insensitive to temperature for a thermal-rotational instability to occur. These older stars could be heated through a steady process of superfluid friction. Subject headings: stars: interiors — stars: neutron — stars: evolution — stars: stability — superfluid — dense matter
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a r X i v :a s t r o -p h /9709183v 1 18 S e p 1997ARE LARGE X–RAY CLUSTERS AT THERMAL EQUILIBRIUM ?Jean-Pierre Chi `e zeCEA,DSM/DAPNIA/Service d’Astrophysique,CE SACLAY,F-91191Gif-sur-Yvette,FranceJean-Michel Alimi Laboratoire d’Astrophysique Extragalactique et de Cosmologie,CNRS URA 173,Observatoire de Paris-Meudon,92195Meudon,France Romain Teyssier CEA,DSM/DAPNIA/Service d’Astrophysique,CE SACLAY,F-91191Gif-sur-Yvette,France ABSTRACT We simulate the formation of a large X–ray cluster using a fully 3D hydrodynamical code coupled to a Particle–Mesh scheme which models the dark matter component.We focus on a possible decoupling between electrons and ions temperatures.We then solve the energy transfer equations between electrons,ions and neutrals without assuming thermal equilibrium between the three gases (T e =T i =T n ).We solve self-consistently the chemical equations for an hydrogen/helium primordial plasma without assuming ionization–recombination equilibrium.We find that the electron temperature differs from the true dynamical temperature by 20%at the Virial radius of our simulated cluster.This could lead marginally to an underestimate of the total mass in the outer regions of large X-ray clusters.Subject headings:cosmology:theory –hydrodynamics –X-rays:clusters –methods:numerical1.INTRODUCTIONLarge X-ray clusters are well defined cosmological objects which can provide useful constraints on currently discussed structure formation theories.It is believed that they are composed mainly of dark matter and X-ray emitting gas.The physical conditions of the hot gas are rather mon values for the electrons density range from 10−1cm −3in the core to10−5cm−3in the outer regions.The electrons temperature is about10keV, up to15keV for A2163,the hottest cluster known so far(Arnaud et al.1992).Recently,Markevitch et al.(1996)studied the electrons temperature profile of A2163 using different X-ray experiments.They measured T e≃4keV at a radius corresponding roughly to the Virial radius of the cluster(r200≃2.4Mpc h−1).Using the well known hydrostatic equilibrium equation in order to derive the total mass distribution,they conclude that the total mass distribution is significantly steeper than the X-ray gas distribution.But,as shown by Schindler&Muller(1993)and Evrard,Metzler&Navarro (1996),the hydrostatic equilibrium assumption is unlikely to be true in the low density regions.Moreover,at that radius,the electron density is supposed to be roughly a few10−5 cm−3,and the time-scale for electrons to reach thermodynamical equilibrium with ions is then about4Gyr,comparable to the merger time-scale(Markevitch et al.1996).Therefore, one can ask the following question:in the outer region of A2163and more generally in any large X-ray cluster,is T e=T i?If T e=T i,this could result in additional errors in the mass estimate due to a departure from thermodynamical equilibrium between ions and electrons.In Teyssier,Chi`e ze&Alimi(1997),as afirst approach to this problem,we studied the collapse of a planar density perturbation,usually called a Zel’dovich pancake,of comoving wavelength L=16Mpc h−1.This rather formal case enabled us to test with high resolution 1D simulations our hydrodynamical code which solves a set of collisional processes such as energy exchange,non–equilibrium chemistry,shock heating and electronic conduction.We showed that a large region of the pancake(≃1Mpc h−1)does not recover thermodynamical equilibrium.Only the central part of the pancake recovers within a few percent T e≃T i. The strongest departure from thermodynamical equilibrium was found near the shock front, where T e is one order of magnitude lower than T i.For a real cluster,much higher densities and temperatures than for pancakes are expected in the high temperature,X-ray emitting gas.In this paper,we thus intendto make a quantitative study of the thermodynamical history of the gas during the hierarchical formation of a three-dimensional(3D)X-ray cluster embedded in a standard CDM cosmogony.We solve precisely the energy transfer equations between electrons,ions and neutrals,in order to confirm or infirm the thermodynamical equilibrium assumption.To test the thermodynamical evolution of a realistic X-ray cluster,we have developed a 3D hydrodynamical code,called HYDREL(“HYDrodynamique Euler Lagrange”),coupled to a PM scheme which describes the dark matter component.In section2we describe the physical processes involved in the primordial collisional plasma,the numerical methods we use to simulate the formation of X-ray clusters.and the initial conditions we choose.In section3we present our results,showing that significant departure from thermodynamicalequilibrium can be obtained at a radius r≃r2001.We discuss the general properties of the simulated cluster,which has several average characteristics similar to those of the Coma cluster.Finally,in section4,we discuss possible observational consequences of our work, such as an underestimation of the total mass in the outer regions of large X-ray clusters.2.PHYSICAL AND NUMERICAL METHODSIn this paper,we intend to give a self-consistent description of the thermodynamical evolution of a cluster of galaxy embedded in an Einstein-de Sitter universe.We use the so–called“standard CDM cosmogony”withΩ=1,ΩB=0.1and h=0.5.This scenario is one of the most typical example of the hierarchical clustering picture.We use the Bardeen et al.(1986)power spectrum to generate our initial Gaussian randomfield.In this section, we briefly recall the physical processes that we study here.We also present our numerical algorithm,namely the3D hydrodynamical code HYDREL and wefinally discuss the numerical parameters that we use for the specific realization presented here.2.1.Physical ProcessesThe aim of this paper is to study the effect of several processes which we believe to be relevant in the primordial collisional plasma.We therefore focus on collisional processes and distinguish three thermodynamical species,namely electrons,ions and neutrals.Each specy is supposed to be individually at the local thermodynamical equilibrium(LTE),but we allow T e=T i=T n,where the subscripts design electrons,ions and neutrals respectively. The LTE hypothesis is valid since the“isotropization time-scale”t iso,which drives the distribution function of a given specy to a Maxwellian,is very small,even in the rather extreme conditions found in X-ray clusters.Indeed,from n e≃n i=10−5cm−3and T e≃T i =107K,we can deduce an estimation of t iso≃105yrs for electrons and t iso≃106yrs for ions(Spitzer1962).On the other hand,we outlined in the introduction that the “equipartition time-scale”between electrons and ions was quite long in the outer regions (t ei≥109yrs).We must therefore solve the energy transfer equations between the three thermodynamical species.Note that in the case of X-ray clusters,the neutral component is of weak relevance,since the medium is fully ionized.However,our code was designed for a more general use,and therefore we follow self–consistently all chemical species.For electrons and protons,the internal energy transfer per unit volume and per unit time is due to Coulomb collisions and writes(Spitzer1962)(1)δQm p(kT ei)3/2where T ei is“the reduced temperature”of the two interacting particles andΛep is the Coulomb logarithm.This formula can be applied to other ions with of course a modification due to their different atomic masses and charges(Spitzer1962).We also compute the energy exchange rate between electrons and neutrals,using the classical“hard reflecting sphere”cross-sectionσen≃10−15cm2(Draine&Katz1986).The energy exchange between ions and neutrals which is due to the resonant charge transfer interaction,is derived by using the momentum transfer cross–section of HI–HII presented in Hunter&Kuryan(1977) and Draine(1980).To compute accurate energy exchange rates,we solve the chemical equations without assuming ionization–recombination equilibrium.We consider only6chemical reactions, which are ionization and recombination for HI–HII,for HeI–HeII and for HeII–HeIII.This non–equilibrium approach is important behind shock fronts,where a description using the Saha equation would overestimate the ionization fraction,and would lead to wrong abundances and wrong energy exchange rates.We use the chemical reaction rates presented in Cen(1992).In rich galaxy clusters,the gas temperature ranges from1to10keV.Line cooling is therefore negligible.We only take into account Brehmstrahlung(Mewe et al.1987)and Compton cooling by the Cosmic Background Radiation(Peebles1993).These cooling processes are likely to lower slightly the electrons temperature,and therefore enhance the departure from thermodynamical equilibrium.In Teyssier et al.(1997),we also considered the influence of electronic conduction, assuming no transverse magneticfield.We showed that conduction is effective only in the very low density,outer regions,where a thermal precursor preheats the gas ahead of the shock front(Zel’dovich&Raizer1966).The downstreamflow properties were qualitatively similar to the non conductive case,altough the temperature decoupling between ions and electrons was slightly lowered.This led us to conclude that,even in the assumption of no magneticfield,electronic conduction might have no direct observational consequences.On the other hand,it has been shown that a small magneticfield(≃1µG)does exist in the intracluster medium(Kim et al.1990).Electronic conduction should then be efficently suppressed.We therefore do not consider it in the present paper.The presence of a magneticfield does not affect classical collisional energy exchange, since it is a purely local process.However,a magneticfield has also the well-known effect of introducing various plasma instabilities within the shock structure.These instabilities are believed to be responsible of a rapid,anomalous heating of electrons.Cargill& Papadopoulos(1988)proposed a mechanism for this strong,collisionless heating,based on the Buneman and ion acoustic instabilities.This mechanism justifies why electrons are efficiently heated in young supernovae remnants,an observationnal fact which was unexplained by the classical collisional theory.However,Cargill&Papadopoulos(1988) showed that only12%of the upstream kinetic energy can be converted into electrons thermal energy.Consequently,after the collisionless shock front,complete ions-electrons equipartition still relies on classical collisional processes.In the calculations we present in this paper,altough we neglect the various plasmas instabilities discussed here,we obtain rather low temperature differences,namely T e≥T i/5.This justifies the use of classical collisions theory only.Keeping in mind the physical assumption we just made,let us now summarize the thermodynamical history of the intracluster gas.Ions and neutrals are shock heated through mergers or accretion shock waves.Electrons are less efficiently heated by shocks,as can be shown by hand using the Rankine–Hugoniot discontinuities relations.As a matter of fact, these relations state that a gas with mean molecular weightµis heated by a shock front with velocity D up to a post–shock temperature given by3kT=sec(3)n eThe length of this so–called“equipartition wave”where a significant departure from thermodynamical equilibrium is expected,can be estimated using L ei≃(1/4)t ei D.Under the rather extreme physical conditions encountered in large X-ray clusters,n e≃10−5and D≃1000km s−1,this“equipartition mean free length”is very extended,L ei≃1.4Mpc h−1.Moreover,one clearly sees from equation(3),that the higher is the gas temperature,and the lower is the gas density,the larger is this equipartition region.In Teyssier et al. (1997),we calculated more precisely the size of this region for a pancake of initial comoving wavelength L=16Mpc h−1,and we found L ei≃1Mpc h−1with a total shocked region of 2Mpc h−1.In a fully3D environment,shock waves interact in a very complicated pattern. Hierarchical merging means here that small,low temperature sub–structures merge together,leading to strong shocks propagating in a low density environment,especially in the outer part of X-ray clusters.Consequently,we need a3D hydrodynamical code which self–consistently solves the gas dynamics equations with the different collisional processes previously mentioned.2.2.Numerical SchemesThe choice of our numerical method is dictated by the specific regions of clusters we are interested in.These regions are likely to be far from thermodynamical and chemical equilibrium.First,the low value of the gas density results in rather slow collisional time–scales.Second,these regions are not relaxed,with high bulk velocities and strong shock waves,making non–equilibrium phenomena dominant.We therefore use an Eulerian hydrodynamical code(Kang et al.1994)to simulate the formation of a large cluster of galaxies.Our code,called HYDREL,has been presented in great details for its1D version in Teyssier et al.(1997).We briefly recall here its main characteristics,as well as the specific 3D features.HYDREL is based on an operator splitting algorithm,and solves the different thermo-and hydrodynamical equations in3consecutive steps.Thefirst step,called the gravity step,solves the Poisson equation.It calculates the gravitational potential deduced from the gas and dark matter densityfields.Dark matter particles are displaced during this step with a classical Particle–Mesh(PM)scheme(Hockney&Eastwood1981),developed by Alimi and Scholl(1993)first on Connection Machine,then implemented on Cray–YMP. The equation of motion in this PM code are solved in comoving coordinates and the Green function takes into account aliasing effects and minimizes force’s anisotropies.The time integrator of the PM has however been modified,it is now based on a predictor–corrector scheme.This allows both great accuracy and variable time–stepping which is impossible with the classical Leap–Frog scheme.The second step is the adiabatic hydrodynamical step. It solves the hydrodynamical equations using directional splitting and a staggered mesh. Shock waves are treated using the pseudo–viscosity method(Von Neumann&Richtmyer 1950).We use for that purpose a viscous tensor,and not a viscous pressure.This tensorialformulation(Tscharnuter&Winkler1979;Mihalas&Mihalas1984;Stone&Norman1992; Chi`e ze et al.1997)is of great importance for cosmologicalflows.We therefore recall now the main features of our tensorial pseudo–viscosity in3D.This approach relies on the assumption that dissipation in shock waves is correctly described by the Navier–Stokes equations.For each direction i=1,2,3,we use a diagonal stress tensor,whose coordinatesσi,are proportional to the diagonal terms of the shear tensorσi=P∂x i−1∂x iσi(5)Note that the three components of the pseudo–viscous force differ in general.A viscous pressure,in the contrary,would have been always isotropic.Note also that in case ofan homologousflow(σi=0),there is no dissipation in theflow(Mihalas&Mihalas 1984).A viscous pressure would not have been able to satisfy this fundamental physical requirement.Because shock waves result in a contraction of thefluid elements they cross, the pseudo–viscous force acts only when the following criterion is full-filled∂u i3∇·u<0(6) The hydrodynamical step we describe now is divided in two sub-steps for each direction:first the gas dynamics equations are solved in a Lagrangian way,then we re-map the newflow variables from the perturbed Lagrangian grid to thefixed Eulerian one.The Lagrangian step uses a predictor–corrector time solver,which ensures second order accuracy in time.The Eulerian step uses the Van Leer(1977)advection scheme,which ensures second order accuracy in space.The third step is called the dissipative step.It solves all collisional processes,namely chemical reactions,energy exchange between the three thermodynamical processes and cooling.Because these processes are driven by rather stiffequations,we use for each cell an individual time–stepping.This allows us to compute new energies and abundances with high accuracy without slowing down the whole simulation.Chemical reactions and the other collisional processes are strongly coupled equations.To ensure stability,we solve the system of chemical and thermodynamical equations using the“fully implicit method”.The large hydrodynamical time–step is controlled by the Courant condition, and the small sub–time–steps are controlled by the relative variations of the chemical and thermodynamical variables in each cell.In the case of strong cooling(t cool<t dyn), the pressure can be dramatically underestimated.We therefore impose that during the dissipative step,the total pressure does not vary more than10%.This method works well in general,and allows a very good accuracy in the chemical calculations.However,for large clusters of galaxies,which are the purpose of this paper,cooling is not efficient,due to the high temperature of the intra-cluster gas(T>1keV)and the relatively low–densities that we obtain in our simulation.2.3.Initial ConditionsWe now present the initial conditions that we use to simulate a rich cluster of galaxies embedded in a CDM cosmogony.We use a comoving box size of25Mpc h−1,with periodic boundary conditions.It would have been better to use a larger box,but we have to make a compromise between large scale power and spatial resolution.We made a choice similar to Anninos&Norman(1996),and thus we can compare directly our results to their calculations.We use1283grid points,and the same number of dark matter particles.The numerical force is50%of the true gravitational force at a scale of roughly1.5cells.This gives an effective resolution of300kpc h−1.This corresponds also to the hydrodynamical resolution,as shown by extensive tests(Teyssier et al.1997).We start our simulation at a redshift z i=50.The initial abundances are taken from Peebles(1993)for our chosen valueΩB=0.1.The gas temperature is initially uniform and we use the relation T(z i)=(1+z i)21.37×10−2K,which states that the gas temperature is strongly coupled to the CBR up to z=200,and then evolves adiabatically up to z i.Dark matter particles are initially uniformly distributed on the grid,and then displaced using the Zel’dovich approximation.The initial baryons densityfield is supposed to be equal to the initial Gaussian random densityfield.We impose a3σpeak of length scale4Mpc h−1at the center of the box,using the Hoffman–Ribak(1991)algorithm.We reach thefinal epoch(defined as the epoch when the linear r.m.s.is equal to1at8Mpc h−1)with approximately 350time–steps,controlled by the Courant condition.The energy conservation,as defined by Cen(1992),was less than0.8%during the whole run.3.RESULTSThe cluster we obtained at z=0have average characteristics(mass,size and temperature)similar to those observed for the Coma cluster.We define the cluster center as the cell of maximum X–ray emissivity.We then define the Virial radius r200of the cluster as the radius of the sphere centered on the cluster center and containing a mean over–density¯δ=200.Wefind in this way,r200=1.6Mpc h−1.The total mass embedded in this radius is M200=9.8×1014M⊙h−1.We plot infigure(1)the gas density,temperatures and ionization fraction along a line of sight which crosses the center of the cluster.We can define here three characteristic regions in the vicinity of the cluster:•the cluster itself,which has recovered thermodynamical and chemical equilibrium,•a large non–equilibrium region,where ions and electrons temperatures differsignificantly,•andfinally the cold,unshocked inter–cluster medium.Note that the accretion shock is relatively steep,and that the gas is very quickly ionized.We did not consider here any ionizing background,altough it is strongly suggested by the Gunn–Peterson effect,but ionization by shock waves turned out to be efficient enough,as soon as the intracluster medium is concerned.The equipartition front,where T e gradually reaches T i,has a thickness of approximately1.5Mpc h−1.This non–equilibrium region stands mainly outside the Virial radius of the cluster.The shock front,which marks the beginning of the non–equilibrium region,is located at roughly2r200of the cluster center. The temperature decouling between ions and electrons is maximum just after the shock front,but always greater than T e≃T i/3(except“inside”the shock front).This justifiesa posteriori our assumption that plasma instabilities could be neglected here(see Section2.1).Infigure(2),we plot gray scale images of the dark matter density contrast,the gas density contrast and the electrons and ions temperatures.Note that thefilamentary structures clearly converge towards the cluster.Gas and dark matter isocontours havesimilar elliptical shapes,with axis ratio2:1.They are both relatively smooth.In the contrary,the temperatures isocontours show very complicated patterns,with several shock waves propagating in different directions.Note that the electrons temperature appears much smoother than the ions temperature.The hottest regions are not located in the center of the cluster,but in the outer regions where strong shock heating occurs.This explains why the strongest temperature decoupling is mainly located in the low density, outer regions of the cluster.We plot infigure(3)the spherically averaged density and temperatures profiles.The radius is expressed in units of r200.The most inner point corresponds to our resolution limit in the computation of the gravitational force.Note that gas and dark matter density profiles are both very similar.We show no evidence of core radii in any mass distribution. Moreover,both density profiles are wellfitted by a power lawρ∝r−9/4.This is in good agreement with Anninos&Norman(1996),who studied the influence of numerical effects on gas and dark matter density profiles,using higher resolution simulations.The electrons and ions temperatures profiles show again clearly that a large non–equilibrium region extends from r200/2up to2r200.In order to quantify the error that one observer does between the X-ray temperature T e and the true dynamical temperature T≃(T e+T i)/2,we plot the ratio(T−T e)/T as a function of radius.The maximum departure from thermodynamical equilibrium is located at r200and is about20%.We also calculate the ratio between the bulk kinetic energy and the internal energy of the gas.This ratio is equal to unity at r200, showing that hydrostatic equilibrium is also not recovered in this region.Therefore,the hydrostatic equilibrium assumption and the thermodynamical equilibrium assumption are both valid in the central region of the cluster(r<r200/2),but are both violated in the outer regions of the cluster(r>r200/2).4.CONCLUSIONIn this paper,we studied the formation of a rich X–ray cluster.We found that the total mass embedded in the Virial radius(r200=1.6Mpc h−1)was equal to1015M⊙h−1. We found also that the density profiles of gas and dark matter are both wellfitted by a r−9/4power law.We therefore have similar conclusions than Anninos&Norman(1996), using similar initial conditions.We studied more specifically the thermodynamical history of the intra–cluster gas.We found that a significant decoupling between electrons and ions temperatures occurs between r200/2and the shock front,located roughly at2r200.The maximum departure is found at r200and reaches20%.Therefore,the usual assumption of thermodynamical equilibrium between ions and electrons breaks down in this region.We also checked that the hydrostatic equilibrium assumption was not valid in the outer regions of the simulated cluster.These two errors can both lead to an underestimates of the gravitational mass in the outer regions of X–ray clusters(r≥r200/2).These results could be carefully extrapolated to the case of A2163.As mentioned in the introduction, Markevitch et al.(1996)measured at the Virial radius of A2163a temperature of4keV, which is roughly equal to twice the value we found here for our simulated cluster.This could lead to a thermodynamical decoupling of50%,which means that the(observed)electrons temperature underestimates by a factor of two the true dynamical temperature.Therefore, for A2163,the error in the mass estimate due to a departure from thermodynamical equilibrium could be as large as a factor of two.Further studies are however required to confirm these conclusions,using other types of initial conditions.We would like to thank R.van den Weygaert for providing us the code which generates constrained realizations of Gaussian randomfields(van den Weygaert&Bertschinger1995).REFERENCESAlimi,J.-M.,&Scholl,H.,1993,Int Journal of Mod.Phys.C,4,197.Anninos,P.A.,&Norman,M.L.,1996,ApJ,459,12.Arnaud,M.,Hughes,J.P.,Forman,W.J.,Jones,C.,Lachi`e ze-Ray,M.,Yamashita,K., Hatsukade,I.,1992,ApJ,390,345.Bardeen,J.M.,Bond,J.R.,Kaiser,N.,&Szalay,A.S.,1986,ApJ,300,15.Cargill,P.J.,&Papadopoulos,K.,1988,ApJ,329,L29.Cen,R.Y.,1992,ApJS,78,341.Chi`e ze,J.-P.,Teyssier,R.,&Alimi,J.-M.,1997,ApJ,in press.Draine,B.T.,&Katz,N.,1986,ApJ,306,655.Draine,B.T.,1980,ApJ,246,1045.Evrard,A.E.,Metzler,C.A.&Navarro,J.F.,1996,ApJ,469,494.Hockney,R.W.,&Eastwood,J.W.,1981,“Computer Simulations Using Particles”(New York McGraw-Hill).Hoffman,Y.&Ribak,E.,1991,ApJ,380,5.Hunter,G.,&Kuryan,M.,1977,Proc.Roy.Soc.London,353,575.Kang,H.,Ostriker,J.P.,Cen,R.,Ryu,D.,Hernquist,L.,Evrard,A.E.,Bryan,G.L.,& Norman,M.L.,1994,ApJ,430,83.Kim,K.-T.,Kronberg,P.P.,Dewdney,P.E.,&Landecker,T.L.,1990,ApJ,355,29. Mihalas,D.&Weibel Mihalas,B.,1984,“Foundations of Radiation Hydrodynamics”(Oxford University Press,New York)Markevitch,M,Mushotzky,R,Inoue,H,Yamashita,K,Furuzawa,A.&Tawara,Y.,1996, ApJ,456,437.Mewe,R.,Schrijver,C.J.,Lemen,J.R.,&Bentley,R.D.,1986,A&AS,65,511. Peebles,P.J.E.1993,“Principles of Physical Cosmology”(Princeton University Press). Schindler,S.,&Muller,E.,1993,A&A,272,137.Spitzer,L.,1962,“The Physics of Fully Ionized Gases”(Interscience,New York). Stone,J.M.,&Norman,M.L.,1992,ApJS,80,753.Teyssier,R.,Chi`e ze,J.-P.,&Alimi,J.-M.,1997,submitted to ApJ.Tscharnuter,W.-M.,&Winkler,K.-H.,1979,m.,18,171.Van de Weygaert,R.&Bertschinger,E.,1995,submitted to MNRAS,astro-ph/9507024. Van Leer,B.,1977,put.Phys.,23,276.Von Neumann,J.,&Richtmyer,R.D.,1950,J.Appl.Phys.,21,232.Zel’dovich,Ya.B.,&Raizer,Yu.P.,1966,“Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena”(Academic Press,New York and London).Fig.1.—Gas density in atomic mass per cm3,temperatures:ions(solid line)and electrons (dashed line),abundances of Hydrogen species:fraction of HI(solid line)and HII(dashed line),abundances of Helium species:fraction of HeI(solid line),HeII(dashed line)and HeIII (dotted line).The different quantities are taken along a line of sight which crosses the cluster center.Fig.2.—Upper panels:gray scale images of the gas and dark matter density contrast with 10levels,defined by a constant logarithmic spacing betweenδ=1andδ=103.5.Lower pannels:gray scale images of the electrons and ions temperatures with10levels,defined by a constant logarithmic spacing between T=106K and T=108K.The slice is one-cell width and crosses the cluster center.Fig. 3.—Upper left pannel:spherically averaged density profile for dark matter(solid line)and gas(dashed line)versus the radial distance to the cluster center,in units of r200.The r−9/4power law is also shown as a straight line.Upper right pannel:spherically averaged temperature for electrons(dashed line)and ions(solid line).Lower left pannel: ratio between the bulk kinetic energy and the internal energy of the gas.Lower right pannel: ratio(T i−T e)/(T i+T e)that measures the departure from thermodynamical equilibrium(see text).。
