列主元素Gauss消去法Jacobi迭代法原理及计算方法
Gauss列主元消去法、QR(MATLAB)

Gauss列主元消去法、QR(MATLAB)Gauss列主元消去法是一种线性方程组的求解方法,也称Gauss消去法。
其基本思想是将方程组转化为上三角矩阵,然后通过反向代入求解。
该方法的优点在于计算精度高,求解速度快,但缺点是需要大量的计算,尤其是在矩阵阶数较高时。
具体来讲,Gauss列主元消去法的步骤如下:步骤一:将系数矩阵A进行LU分解,其中L是下三角矩阵、U是上三角矩阵。
设$A=LU$,则原方程组可以写成$LUx=b$。
步骤二:通过初等矩阵左乘系数矩阵A,将每一列的主元变为该列所有元素中绝对值最大的那个元素。
这个过程称为选主元,可以避免计算中的数值不稳定问题。
步骤三:将选主元后的系数矩阵A进行LU分解,得到$L^{'}$、$U^{'}$。
步骤五:通过反向代入求解$U^{'}x=y$,得到$x$的解。
Gauss列主元消去法的实现通常通过矩阵的变换来实现。
对于$n$阶矩阵$A=[a_{ij}]$,通过一系列的行变换,可以将其变为上三角矩阵。
其中的变换可以表示为:$$ R_{i} \leftrightarrow R_{j} $$其中,$R_{i}$和$R_{j}$分别表示矩阵$A$中的第$i$行和第$j$行,$k$是一个非零常数。
这些变换被称为初等行变换。
在MATLAB中,可以使用已经实现好的{\color{blue}\texttt{gauss}}函数来求解线性方程组。
该函数实现的算法是Gauss列主元消去法。
其调用格式为:x = gauss(A,b)其中,$A$是系数矩阵,$b$是结果向量。
函数返回结果向量$x$。
如果$A$或$b$不合法,则函数会返回一个空向量。
除了Gauss列主元消去法,还有一种常用的求解线性方程组的方法是QR分解法。
步骤二:通过正交矩阵左乘系数矩阵$A$,使其变为一个上三角矩阵。
这个过程称为正交相似变换。
步骤三:将$b$进行正交相似变换,得到$Q^{T}b$。
列主元素消去法

列主元素消去法列主元素消去法(Gauss-Jordan 消元法)是一种线性代数中常用的消元方法,用于求解线性方程组的解。
这种方法的基本思想是,将线性方程组的增广矩阵通过一系列的初等变换,化为一个阶梯矩阵或行简化阶梯矩阵,从而得到线性方程组的解。
具体步骤如下:构造增广矩阵,即将系数矩阵和常数矩阵组合成一个矩阵。
将增广矩阵转化为一个上三角矩阵(也叫阶梯矩阵)。
反向消元,将阶梯矩阵转化为一个行简化阶梯矩阵。
根据简化矩阵求解方程组。
这种方法的优点是计算简单、容易理解,且可避免误差的积累。
但是,如果矩阵的规模较大,运算量会很大,计算时间较长。
此时可以使用更高效的算法,如LU分解、QR分解等。
假设有一个 $n$ 个未知量和 $n$ 个方程的线性方程组,可以写成矩阵形式如下:$Ax = b$其中,$A$ 是一个 $n \times n$ 的系数矩阵,$x$ 是一个 $n \times 1$ 的未知量向量,$b$ 是一个 $n \times 1$ 的常数向量。
为了求解 $x$,可以将方程组的增广矩阵表示如下:$\begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} & b_{1} \ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} & b_{2} \ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \ a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn} & b_{n} \end{bmatrix}$ 其中,$a_{ij}$ 表示矩阵的第 $i$ 行第 $j$ 列的元素。
jacobi迭代的原理与公式

jacobi迭代的原理与公式
Jacobi迭代是一种迭代方法,用于求解线性方程组Ax=b。
它的基本原理是将方程组中的每个未知数的值通过迭代逐步逼近最终解。
假设方程组为Ax=b,其中A是一个n×n的矩阵,x和b是n维列向量。
Jacobi迭代的公式为:
x^(k+1) = D^(-1) * (b - (L+U) * x^k)
其中,x^(k+1)表示第k+1次迭代后的x值,x^k表示第k次迭代后的x值,D是A的对角线矩阵,L是A的下三角矩阵,U是A的上三角矩阵。
具体步骤如下:
1. 初始化x^0为一个初始向量。
2. 根据上述公式,计算x^(k+1)。
3. 判断迭代是否收敛。
如果满足收敛条件,停止迭代,得到近似解x^(k+1)。
4. 如果不满足收敛条件,将x^(k+1)作为新的x^k,返回第2步。
Jacobi迭代的收敛条件是矩阵A的谱半径小于1。
如果A是对称正定矩阵,那么Jacobi迭代一定收敛。
总结起来,Jacobi迭代通过不断更新未知数的值,逐步逼近方程组的解。
分别用 jacobi 迭代法和 gauss-seidel 迭代法,求解方程组

分别用 jacobi 迭代法和 gauss-seidel 迭代法,求解方程组【jacobi 迭代法和 gauss-seidel 迭代法分别应用于方程组的求解】1. 引言在数学领域中,方程组的求解一直是一个重要的课题。
为了解决复杂的线性方程组,人们提出了各种迭代方法,其中 jacobi 迭代法和gauss-seidel 迭代法是两种常见的方法。
本文将探讨这两种迭代方法在求解方程组中的应用。
2. jacobi 迭代法的原理和应用jacobi 迭代法是一种基于逐次逼近的迭代方法。
对于线性方程组AX=B,其中 A 是系数矩阵,X 是未知数向量,B 是已知向量。
我们可以通过以下公式进行逐次逼近:X(k+1) = D^(-1)*(B - (L+U)X(k))其中,D、L、U 分别是 A 的对角线、下三角和上三角矩阵。
jacobi 迭代法的优点在于易于理解和实现,但在收敛速度上较慢,需要进行多次迭代才能得到精确解。
在实际应用中,需要根据实际情况选择合适的迭代次数。
3. gauss-seidel 迭代法的原理和应用与 jacobi 迭代法类似,gauss-seidel 迭代法也是一种基于逐次逼近的迭代方法。
不同之处在于,gauss-seidel 迭代法在计算 X(k+1) 时利用了已经得到的 X(k) 的信息,即:X(k+1)_i = (B_i - Σ(A_ij*X(k+1)_j,j≠i))/A_ii这种方式使得 gauss-seidel 迭代法的收敛速度较快,通常比 jacobi 迭代法更快,尤其是对于对角占优的方程组。
4. 分别用 jacobi 迭代法和 gauss-seidel 迭代法求解方程组为了更具体地说明 jacobi 迭代法和 gauss-seidel 迭代法的应用,我们分别用这两种方法来求解以下方程组:2x1 + x2 = 9x1 + 3x2 = 11我们将该方程组写成矩阵形式 AX=B:|2 1| |x1| |9||1 3| * |x2| = |11|我们根据 jacobi 迭代法和 gauss-seidel 迭代法的原理,依次进行迭代计算,直到满足收敛条件。
数值分析1顺序消去法、列主元、列主元Gauss-Jordan消去法

数值分析1顺序消去法、列主元、列主元Gauss-Jordan消去法function x = Gauss (A, b)% 求解方程组的Gauss消去法,调用方法为% x = Gauss (A, b)% 其中% A 为方程组的系数矩阵,b为方程组的右端项% x 为方程组的解[n,m] = size (A); nb = length (b);if n~=merror ('% 系数矩阵必须为方的!');endif m~=nberror ('% b 的维数与方程组的行数不匹配!'); endfor k = 1:n-1% 消元过程for i = k+1:nm = A (i,k)/A(k,k);for j = k+1:nA (i,j) = A (i,j)-m*A (k,j);endb (i) = b (i)-m*b (k);endendx=zeros (size (b));for k = n:-1:1for j = k+1:nb (k) = b (k)-A (k,j)*x (j);endx (k) = b (k)/A(k,k);endendfunction x = Gauss_Elim (A, b)% 求解方程组的列主元Gauss消去法,调用方法为% x = Gauss_Elim (A, b)% 其中% A 为方程组的系数矩阵,b为方程组的右端项% x 为方程组的解[n,m] = size (A); nb = length (b);error ('% 系数矩阵必须为方的!');endif m~=nberror ('% b 的维数与方程组的行数不匹配!');endfor k = 1:n-1% 选主元a_max = 0;for i = k:nif abs (A (i,k))>a_maxa_max = A (i,k); r=i;endendif abs(a_max)<1e-15error ('% 系数矩阵奇异,无法求解方程组!');end% 交换两行if r>kfor j = k:nz=A (k,j); A (k,j)=A (r,j);A (r,j)=z;endz=b (k);b (k)=b (r);b (r)=z;end% 消元过程for i = k+1:nm = A (i,k)/A(k,k);for j = k+1:nA (i,j) = A (i,j)-m*A (k,j);endb (i) = b (i)-m*b (k);endend% 回代过程if abs (A (n,n))<1e-15error ('% 系数矩阵奇异,无法求解方程组!'); endx=zeros (size (b));for k = n:-1:1for j = k+1:nb (k) = b (k)-A (k,j)*x (j);endx (k) = b (k)/A(k,k);endendfunction x = Gauss_Jordan (A, b)% 求解方程组的列主元Gauss-Jordan消去法,调用方法为% x = Gauss_Jordan (A, b)% 其中% A 为方程组的系数矩阵,b为方程组的右端项% x 为方程组的解[n,m] = size (A); nb = length (b);error ('% 系数矩阵必须为方的!');endif m~=nberror ('% b 的维数与方程组的行数不匹配!'); endfor k = 1:n% 选主元a_max = 0;for i = k:nif abs (A (i,k))>a_maxa_max = A (i,k); r=i;endendif abs(a_max)<1e-15error ('% 系数矩阵奇异,无法求解方程组!'); end% 交换两行if r>kfor j = k:nz=A (k,j); A (k,j)=A (r,j);A (r,j)=z;endz=b (k);b (k)=b (r);b (r)=z;end% 消元计算b (k) = b (k)/A(k,k);for j = k+1:nA (k,j) = A (k,j)/A(k,k);endfor i=1:nfor j=k+1:nA (i,j) = A (i,j)-A (i,k)*A (k,j); endb (i)=b (i)-A (i,k)*b (k); endendendx = b; % 输出bend。
数值分析列主元高斯消去法
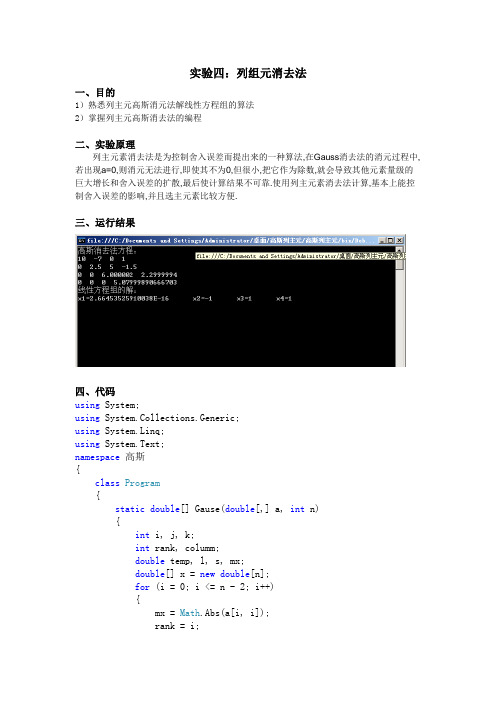
实验四:列组元消去法一、目的1)熟悉列主元高斯消元法解线性方程组的算法2)掌握列主元高斯消去法的编程二、实验原理列主元素消去法是为控制舍入误差而提出来的一种算法,在Gauss消去法的消元过程中,若出现a=0,则消元无法进行,即使其不为0,但很小,把它作为除数,就会导致其他元素量级的巨大增长和舍入误差的扩散,最后使计算结果不可靠.使用列主元素消去法计算,基本上能控制舍入误差的影响,并且选主元素比较方便.三、运行结果四、代码using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace高斯{class Program{static double[] Gause(double[,] a, int n){int i, j, k;int rank, columm;double temp, l, s, mx;double[] x = new double[n];for (i = 0; i <= n - 2; i++){mx = Math.Abs(a[i, i]);rank = i;columm = i;for (j = i + 1; j <= n - 1; j++) //选主元if (Math.Abs(a[j, i]) > mx){mx = Math.Abs(a[j, i]);rank = j;columm = i;}for (k = 0; k <= n; k++) //主元行变换{temp = a[i, k];a[i, k] = a[rank, k];a[rank, k] = temp;} //消元for (j = i + 1; j <= n - 1; j++){l = a[j, i] / a[i, i];for (k = i; k <= n; k++)a[j, k] = a[j, k] - l * a[i, k];}}x[n - 1] = a[n - 1, n] / a[n - 1, n - 1]; //回代方程求解x for (i = n - 2; i >= 0; i--){s = 0;for (j = i + 1; j <= n - 1; j++)s = s + a[i, j] * x[j];x[i] = (a[i, n] - s) / a[i, i];}return x;}static void Main(string[] args){double[,] a = new double[4, 5] { { 10, -7, 0, 1, 8 }, { -3, 2.099999, 6, 2, 5.900001 }, { 5, -1, 5, -1, 5 }, { 2, 1, 0, 2, 1 } };int n = 4;double[] x = new double[n];x = Gause(a, n);Console.WriteLine("高斯消去法方程:");for (int i = 0; i < n; i++){for (int j = 0; j < n; j++)Console.Write(a[i, j].ToString() + " ");Console.WriteLine();}Console.WriteLine("线性方程组的解:");for (int i = 0; i <= n - 1; i++)Console.Write("x" + (i + 1).ToString() + "=" +x[i].ToString() + " ");Console.WriteLine();Console.ReadLine();}}}四、分析通过本次实验的学习,学会根据算法编写基本的相关程序,虽然此次程序模板由老师给予,但认真阅读理解程序有助于今后的学习,再利用计算机中的C语言对高斯列主元消去法可以快速得到线性方程组的解,由简单的线性方程组可以推广到一般n阶线性方程组,这对如何利用高斯列主元消去法解决实际问题有了一定的经验。
运筹学
实验原理
(1)列主元消去法:
Gauss消去法在消元的过程中可能出现的情况,这时消元法将无法进行;即使主元素但很小时,用其作除数,也会导致其他元素数量级的严重增长和舍入误差的扩散。
因此,为了减小误差,每次消元选取系数矩阵的某列中绝对值最大的元素作为主元素。
然后按行使之变到主元位置上,再进行消元计算。
设已完成k-1步消元,即有,利用,确定第k不列主元所在的位置,在交换行和k行后,再进行消元。
根据矩阵理论,交换和k两个方程的位置,相当于再系数矩阵和有段顶上都左乘初等排列矩阵(由减缓单位矩阵I的第k行与第行的到);因此列主元素的消去过程相当于对交换后的新矩阵进行消元,即
同时,右端向量变化为
列主元gauss消去法的矩阵解释为
此外,还有全主元guass消去法和gauss-Jordan消去法等。
但列主元gauss 消去法比全主元guass消去法稳定且工作量少,而gauss-Jordan消去法时高斯消去法的一种修正,消元过程中要消去系数矩阵对角线下方和上方的所有元素。
其计算量大约是次乘法,比gauss消去法计算工作量大。
(2)
(3)jacobi迭代法(又称简单迭代法)
考虑n阶线性代数方程组
其矩阵形式为
设该方程组的系数矩阵A非奇异且,可将A分解为:
其中;
第一题:用列主元消去法解方程组:
第二题:用LU分解法界方程组,其中
第三题:
分别用jacobi迭代法和gauss-seidel迭代法求解方程组:。
jacobi迭代计算式
jacobi迭代计算式Jacobi迭代是一种求解线性方程组的迭代方法。
它可以用于求解大规模的线性方程组,并且具有较好的收敛性和稳定性。
在这篇文章中,我们将介绍Jacobi迭代的原理和应用。
我们来看一下Jacobi迭代的基本原理。
对于一个n阶线性方程组Ax=b,其中A为方阵,b为常向量,Jacobi迭代的基本思想是将方程组转化为x=D^{-1}(b-Rx),其中D为A的对角矩阵,R为A 的非对角矩阵。
然后,我们可以通过不断迭代的方式求解x的近似解。
Jacobi迭代的迭代公式为x^{(k+1)}=D^{-1}(b-Rx^{(k)}),其中x^{(k)}为第k次迭代的近似解,k为迭代次数。
通过不断迭代,我们可以得到x的逼近解。
接下来,我们来看一下Jacobi迭代的应用。
Jacobi迭代广泛应用于科学计算和工程领域,特别是在求解大规模线性方程组时具有一定的优势。
它可以用于求解电力系统潮流计算、结构力学计算、流体力学计算等领域的问题。
例如,在电力系统潮流计算中,Jacobi迭代可以用于求解节点电压和节点功率的关系。
通过迭代计算,可以得到电力系统各个节点的电压和功率的近似值,从而分析电力系统的稳定性和安全性。
Jacobi迭代还可以应用于结构力学计算中的应力分析。
通过迭代计算,可以得到结构体系中各个节点的应力分布情况,从而分析结构的强度和稳定性。
在流体力学计算中,Jacobi迭代可以用于求解流体流动的速度场和压力场。
通过迭代计算,可以得到流体流动过程中各个位置的流速和压力的近似值,从而分析流体流动的规律和特性。
需要注意的是,Jacobi迭代的收敛性和稳定性与矩阵A的特征值有关。
如果矩阵A的特征值分布不合理,Jacobi迭代可能会出现不收敛或收敛速度很慢的情况。
因此,在实际应用中,需要对矩阵A进行合理的预处理,以提高迭代的收敛性和稳定性。
Jacobi迭代是一种求解线性方程组的有效方法。
它具有较好的收敛性和稳定性,并且可以广泛应用于科学计算和工程领域。
Gauss列主消元法与Gauss-Seidel迭代法
Gauss 列主消元法与Gauss-Seidel 迭代法一、实验目的:通过本次实验,学会用Gauss 列主消元法对线性方程组的解的情况进行判断;并且学会利用Gauss-Seidel 迭代法求线性方程组的解。
通过本次实验,加强用Matlab 编程的能力和上机调试能力。
二、实验基本原理:Gauss 列主消元法:根据线性方程组任意交换两个方程的次序,方程组的同解性不变,且解的分量次序也不变。
于是,第k 步在顺序消元法进行之前,从()k A 的第k 列元素()k kk a ,()k k k a 1+,…()k nk a 中选取绝对值最大者,并记录所在行,即()()k ik n i k k k i a a k ≤≤=max ,记k i l =,如果k l ≠,则交换矩阵()()[]k k b A 的第k 行与第l 列所有对应的元素。
然后,再进行第k 步顺序消元算法。
Gauss-Seidel 迭代法:在迭代的每一步计算过程中用()k x 的全部分量来计算()1+k x 的所有分量,进而在计算第i 个分量()1+k i x 时,已经计算出最新的分量()11+k x …()11++k i x 没有被利用。
因而由线性方程组的矩阵形式f x G x J +=(1),任取初始解向量()()()()()Tn x x x x 002010,,, =代入(1)式右端的即可得到迭代格式: ()()()ii i j n i j k j ij k jij i k i a x a x a b x /11111⎪⎪⎭⎫ ⎝⎛--=∑∑-=+=++()n i ,,2,1 =。
三、实验步骤:(一)Gauss 列主消元法:1、编写Gauss 列主消元法以及Gauss 回代法的Matlab 程序。
具体步骤如下:(1)输入A,b(2)计算B=[A b]; n=length(b); RA=rank(A);RB=rank(B);zhica=RB-RA;(3)如果zhica>0,方程组无解如果if RA==RB ,if RA==n ,方程有唯一解且 X=backsub(B(1:n,1:n), B(1:n,n+1));否则RA=RB<n ,方程有无穷多解。
数值分析实验报告
%消元过程
fori=k+1:n
m=A(i,k)/A(k,k);
forj=k+1:n
A(i,j)=A(i,j)-m*A(k,j);
end
b(i)=b(i)-m*b(k);
end
det=det*A(k,k);
end
det=det*A(n,n);
%回代过程
ifabs(A(n,n))<1e-10
flag='failure';return;
*x=(x0,x1….,xn),插值节点
*y=(y0,y1,…,yn);被插函数f(x)在插值节点处的函数值
*t求插值函数Pn(x)在t处的函数值
*返回值 插值函数Pn(x)在t处的函数值
*/
procedureNewton
forj=0to n
d1jyj;
endfor
forj=1to n
fori=j to n
[n,m]=size(A);nb=length(b)
%当方程组行与列的维数不相等时,停止计算,并输出出错信息
ifn~=m
error('The row and columns of matrix A must beepual!');
return;
end
%当方程组与右端项的维数不匹配时,停止计算,并输出错误信息
clear
fprintf('gauss-seidel迭代法')
x1_(1)=0;
x2_(1)=0;
x3_(1)=0;
fori=1:9
x1_(i+1)=7.2+0.1*x2_(i)+0.2*x3_(i);
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 列主元素Gauss 消去法、Jacobi 迭代法原理及计算方法
1. 列主元素Gauss 消去法:
1.1 Gauss 消去法基本原理
设有方程组Ax b =,设A 是可逆矩阵。
高斯消去法的基本思想就是将矩阵的初等行变换作用于方程组的增广矩阵[]B A b = ,将其中的A 变换成一个上三角矩阵,然后求解这个三角形方程组。
1.2 列主元Gauss 消去法计算步骤
将方程组用增广矩阵[]()(1)ij
n n B A b a ⨯+== 表示。
1). 消元过程
对1,2,,1k n =-
(1) 选主元,找{},1,,k i k k n ∈+ 使得 ,max k i k ik k i n
a a ≤≤= (2) 如果,0k i k a =,则矩阵A 奇异,程序结束;否则执行(3)。
(3) 如果k i k ≠,则交换第k 行与第k i 行对应元素位置,k kj i j a a ↔,,,1j k n =+ 。
(4) 消元,对,,i k n = ,计算/,ik ik kk l a a =对1,,1j k n =++ ,计算
.ij ij ik kj a a l a =-
2). 回代过程
(1) 若0,nn a =则矩阵奇异,程序结束;否则执行(2)。
(2) ,1/;n n n nn x a a +=
对1,,2,1i n =- ,计算,11/n i i n ij j ii j i x a a x a +=+⎛⎫=- ⎪⎝⎭
∑
2. Jacobi 迭代法
2.1 Jacobi 迭代法基本原理
Jacobi 迭代法的基本思想是对n 元线性方程组b Ax =,.,n n R b R A ∈∈将其变形为等价方程组f Bx x +=,其中.,,n n n n R x R f R B ∈∈∈⨯B 成为迭代矩阵。
从某一取定的初始向量)0(x 出发,按照一个适当的迭代公式 ,逐次计算出向量f Bx x k k +=+)()1( ( 1,0=k ),使得向量序列}{)(k x 收敛于方程组的精确解.
(1)输入1,,,,)0(=k n x
b A ε,. (2) )(1,1)0()
1(∑≠=-=n j i i j ij i ii
i x a b a x )1,0(n i = (3)判断 ε≤--≤≤)0()1(10max i i n i x x ,若是,输出1)1(2)1(1,,n x x x ,若否,置1+=k k ,
)1()0(i i x x =,)2,1(n i =。
二、 实例
⎪⎩⎪⎨⎧==+=++6018-4-310-7-166********
2121n n n x x x x x x x x x
进行列主元Gauss 消去法和Jacobi 迭代法进行计算(Matlab)
1. 列主元素Gauss 消去法程序及结果
A=[10 4 3;6 16 -7;3 -4 -18];b=[16;-10;60]; %方程参数
Ab=[A,b]; %构造增广矩阵
[m n]=size(Ab); %求增广矩阵维数
x=zeros(m,1); %定义通解0
for i=1:1:m-1
absAb=abs(Ab); %对第i 次的增广矩阵取绝对值
mx=absAb(i,i);p=i;
for j=i+1:1:m
if absAb(j,i)>mx
p=j; %取第i 次的增广矩阵的第i 列后m-i+1 个元素中第一个绝对值最大
的元素所在的位置
end
end
temp=Ab(i,:);Ab(i,:)=Ab(p,:);Ab(p,:)=temp; %交换增广矩阵Ab 的第i 行和第i 列中绝对值最大元素所在行
for k=i+1:1:m
Ab(k,:)=Ab(k,:)+Ab(i,:)*(-Ab(k,i)/Ab(i,i)); %将交换后的增广矩阵Ab 的后m-i 行消
元
end
end
%回带求解
x(m)=Ab(m,n)/Ab(m,m);
for l=m-1:-1:1
x(l)=(Ab(l,n)-Ab(l,1:m)*x)/Ab(l,l);
end
x %显示结果
计算结果(小数点后10位) [3.3738441215, -2.8276089828, -2.1426684280]
format long
A=[10 4 3;6 16 -7;3 -4 -18];b=[16;-10;60]; %方程参数
D=diag(diag(A)); %取矩阵A 的对角线元素构造矩阵D
M=inv(D)*(D-A); %构造矩阵M
evalue=eig(M); %求矩阵M 的的特征值
r=max(abs(evalue)) %求矩阵M 的谱半径,若r<1,则Jacobi 迭代法对于此方程对于任意初始向量都收敛
error=0.000001; %定义终止误差条件
x0=[0;0;0]; %定义初始向量
x1=inv(D)*((D-A)*x0+b); %用迭代法求解
n=1; %用n 记录迭代次数%迭代求解
while max(abs(x1-x0))>error
x0=x1;
x1=inv(D)*((D-A)*x0+b);
n=n+1;
end
x1 %显示结果
n %显示迭代次数
计算结果(小数点后10位) [3.3738443859, -2.8276090662,-2.1426680769],迭代次数17。
3. 结果分析
列主元素Gauss消去法求得的结果是方程组的精确解, Jacobi迭代法的结果为近似解。
本例Jacobi迭代法中error设置为0.000001,其计算迭代次数为17次,计算结果与Gauss消去法计算结果的差为[-0.0000002644, 0.0000000834, -0.0000003511]。
当提高精度时(即减小error值),需要更多的迭代次数(计算时间)。
对于实时测量与分析来说,在达到精度要求情况下,需要尽量提高测量与分析速度。
对于离线数据分析,考虑到数据的实际物理含义,在时间充裕的前提下,提高计算精度要求有利于对数据的处理分析。
