(整理)郁道银主编工程光学(知识点).
工程光学_郁道银_光学习题解答
第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。
解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时，v=1.82 m/s，当光在加拿大树胶中，n=1.526时，v=1.97 m/s，当光在金刚石中，n=2.417时，v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。
解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃（设n=1.5），下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为：(1)其中n2=1, n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径x=179.385mm，所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。
解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。
郁道银工程光学第一章
一个球面有无数光轴
一个透镜有一个光轴
共轴球面系统
物(像)空间 —— 物(像)所在的空间，可从 - ∞到 + ∞
实物(像)空间—— 实物(像)可能存在的空间
虚物(像)空间 —— 虚物(像)可能存在的空间
实物(像)点—— 实际光线的交点(屏上可接收到)
虚物(像)点 —— 光线的延长线的交点(屏上接收不到 , 人眼可感受到)
光 学 系 统 光 学 系 统
(a) 实物成实像
(b) 实物成虚像
光 学 系 统 (c) 虚物成实像
光 学 系 统 (d) 虚物成虚像
发散 发散 会聚
发散
实 物
实 像
实 物
虚 像
会聚
会聚
物像
光束
发散 实 虚
会聚 虚 实
虚 物
实 像
物 像
物像
光束
发散 实
会聚 虚
物
像
虚
实
A
实物成实像
A2
A1
A3
实物成实像
光密介质
光疏介质，即 n n'
sin I ' 不可能大于1，临界情况 I ' 90 ，发生全反射
光从介质射入真空时
真空 介质 真空 介质 真空 介质
大于
全反射临界角
当光恰好发生全反射现象时的入射角叫介质的临界角。
光密介质
光疏介质，即 n n'
临界情况： 折射角I ' 90
微粒说
17世纪
波动说
牛顿 19世纪
惠更斯
泊松
托马斯·杨
菲涅尔
泊松斑 关于光在水中的速度
微粒说：大于光在真空中的速度
工程光学 知识点
郁道银主编工程光学第一章小结（几何光学基本定律与成像概念）1 ）光的直线传播定律：2 ）光的独立传播定律：3 ）反射定律和折射定律（全反射及其应用）：反射定律：即I’’=-I 。
折射定律： n’sinI’=nsinI 。
全反射：当满足 1 、光线从光密介质向光疏介质入射， 2 、入射角大于临界角时，入射到介质上的光会被全部反射回原来的介质中，而没有折射光产生。
sinI m=n’/n ，其中 I m 为临界角。
应用： 1 、用全反射棱镜代替平面反射镜以减少光能损失。
2 、光纤4 ）光路的可逆性5 ）费马原理光从一点传播到另一点，其间无论经历多少次折射和反射，其光程为极值。
6 ）马吕斯定律光线束在各向同性的均匀介质中传播时，始终保持着与波面的正交性，并且入射波面与出射波面对应点之间的光程均为定值。
3 、完善成像条件（ 3 种表述 )1 ）、入射波面为球面波时，出射波面也为球面波；2 ）、入射光束为同心光束时，出射光束也为同心光束；3 ）、物点 A 1 及其像点A k ’ 之间任意二条光路的光程相等。
6 、单个折射面的成像公式（定义、公式、意义）垂轴放大率成像特性：β>0, 成正像，虚实相反；β<0, 成倒像，虚实相同|β|>1, 放大； |β|<1 ，缩小。
第二章小结1 、什么是理想光学系统？任意大的空间中一任意宽的光束都成完善像的理想模型。
2 、共轴理想光学系统的成像性质是什么？（3 大点）1 ）位于光轴上的物点对应的共轭像点也必然位于光轴上；位于过光轴的某一个截面内的物点对应的共轭像点必位于该平面的共轭像面内；同时，过光轴的任意截面成像性质都是相同的4 、无限远的轴上（外）像点的对应物点是什么？物方焦点。
5 、物（像）方焦距的计算公式为何？f’=h/tanU’， h 为平行光线的高度，U’ 为像方孔径角。
6 、物方主平面与像方主平面的关系为何？互为共轭。
光学系统的基点及性质？有何用途？一对主点和主平面，一对焦点和焦平面，称为光学系统的基点和基面。
工程光学郁道银版本,单章整理好的
第三章1．人照镜子时，要想看到自己的全身，问镜子要多长？人离镜子的距离有没有关系？解：镜子的高度为1/2人身高，和前后距离无关。
2、有一双面镜系统，光线平行于其中一个平面镜入射，经两次反射后，出射光线与另一平面镜平行，问两平面镜的夹角为多少？解：OAM M //323211M M N M ⊥∴1''1I I -= 又2''2I I -=∴α同理：1''1I I -=α321M M M ∆中︒=-+-+180)()(1''12''2I I I I α ︒=∴60α答：α角等于60︒。
3、如图3-4所示，设平行光管物镜L 的焦距'f =1000mm ，顶杆离光轴的距离 a =10mm 。
如果推动顶杆使平面镜倾斜，物镜焦点F 的自准直象相对于F 产生了y =2mm 的位移，问平面镜的倾角为多少？顶杆的移动量为多少？解：θ'2f y = rad 001.0100022=⨯=θ Oθx=mm a x 01.0001.010=⨯=⨯=∴θ图3-44、一光学系统由一透镜和平面镜组成，如图3-29所示。
平面镜MM 与透镜光轴垂直交于D 点，透镜前方离平面镜600mm 有一物体AB ，经透镜和平面镜后，所成虚像''A ''B 至平面镜的距离为150mm,且像高为物高的一半，试分析透镜焦距的正负，确定透镜的位置和焦距，并画出光路图。
图3-29 习题4图解： 由于平面镜性质可得''B A 及其位置在平面镜前150mm 处''''B A 为虚像,''B A 为实像则211-=β21'1-==L L β450150600'=-=-L L解得 300-=L 150'=L又 '1L -L 1='1f mmf150'=∴答：透镜焦距为100mm 。
工程光学郁道银版本,单章整理好的
⼯程光学郁道银版本,单章整理好的第四章1、设照相物镜的焦距等于75mm，底⽚尺⼨为5555，求该照相物镜的最⼤视场⾓等于多少？解：第六章7、．设计⼀双胶合消⾊差望远物镜，，采⽤冕牌玻璃K9（，）和⽕⽯玻璃F2（，），若正透镜半径，求：正负透镜的焦距及三个球⾯的曲率半径。
解：2．设照相物镜的焦距等于75mm，底⽚尺⼨为5555，求该照相物镜的最⼤视场⾓等于多少？解：第五章习题⼀个100W的钨丝灯，发出总光通量为，求发光效率为多少?解：2、有⼀聚光镜，（数值孔径），求进⼊系统的能量占全部能量的百分⽐。
解：⽽⼀点周围全部空间的⽴体⾓为3、⼀个的钨丝灯，已知：，该灯与⼀聚光镜联⽤，灯丝中⼼对聚光镜所张的孔径⾓，若设灯丝是各向均匀发光，求1）灯泡总的光通量及进⼊聚光镜的能量；2）求平均发光强度解:4、⼀个的钨丝灯发出的总的光通量为，设各向发光强度相等，求以灯为中⼼，半径分别为：时的球⾯的光照度是多少？解：5、⼀房间，长、宽、⾼分别为：，⼀个发光强度为的灯挂在天花板中⼼，离地⾯，1）求灯正下⽅地板上的光照度；2）在房间⾓落处地板上的光照度。
解：第六章习题1．如果⼀个光学系统的初级⼦午彗差等于焦宽（），则应等于多少？解：2．如果⼀个光学系统的初级球差等于焦深（），则应为多少？解：3．设计⼀双胶合消⾊差望远物镜，，采⽤冕牌玻璃K9（，）和⽕⽯玻璃F2（，），若正透镜半径，求：正负透镜的焦距及三个球⾯的曲率半径。
解：4．指出图6-17中解：第七章1、．⼀个⼈近视程度是D 2-（屈光度），调节范围是D 8，求：（1）远点距离；（2）其近点距离；（3）配戴100度近视镜，求该镜的焦距；（4）戴上该近视镜后，求看清的远点距离；（5）戴上该近视镜后，求看清的近点距离。
解：① 21-==rl R )/1(m∴ m l r5.0-=②P R A -= D A 8= D R 2-=∴D A R P 1082-=--=-=m P l p1.01011-=-==③fD '=1∴m f 1-=' ④D D R R 1-=-=' m l R1-='⑤P R A '-'= D A 8= D R 1-='D A R P 9-=-'=' m l P11.091-=-='2、⼀放⼤镜焦距，通光孔径，眼睛距放⼤镜为50mm ，像距离眼睛在明视距离250mm ，渐晕系数K=50%，试求：（1）视觉放⼤率；（2）线视场；（3）物体的位置。
应用光学 郁道银版的课件 工程光学 (第三节)
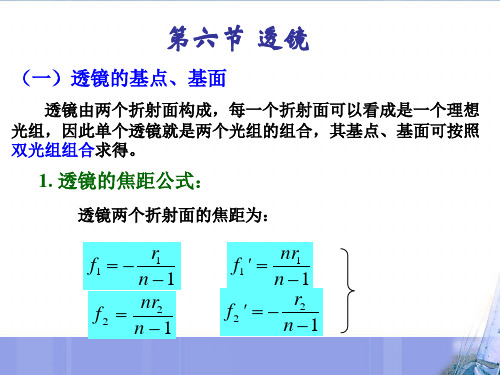
n2' =1
H
F
F1
O1
F'1 F2
O2 F'2
F'
H'
- f1
f 2'
-lF f
-Hl
f '1 D - f2 d
l'F
-f'
lH'
由上图可知 d f1 ' f2
将透镜折射面的焦距公式代入并整理，得：
n(r2 r1) (n 1)d n 1
n1 =1
H1 H'1 n1' =n2 =n H2 H'2
H'
f
-f'
f ' 0 双凸透镜成一发散光组。
（2）平凸透镜
这种透镜的 r1 > 0，r2 ＝∞。
F
F'
由透镜的焦距公式右边的分子、分母同除 r2 。有：
f'
nr1
( n 1) n(1
r1 r2
)( n 1) d r2
当 r2 ＝∞时，上式可以写成：
f ' r1 0 ( n 1)
将此式代入主点位置公式得：
n
1)d
f
若用光焦度形式来表示,可写成:
1 f'
(n
1)( 1
2 )
(n
1)2 n
d1 2
其中：
1
1 r1
2
1 r2
2. 透镜主点（面）和焦点（面）的位 置
将前面得到的焦距和光学间隔公式代入主点位置 公式并整理，得到透镜主点位置公式：
l'H
f ' n 1d nr1
f'
d f '1
工程光学_郁道银_光学习题解答1
第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。
解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时，v=1.82 m/s，当光在加拿大树胶中，n=1.526时，v=1.97 m/s，当光在金刚石中，n=2.417时，v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。
解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃（设n=1.5），下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为：(1)其中n2=1, n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径x=179.385mm，所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。
解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。
工程光学郁道银第七章解读
tg y L y 250
y f l y P' l f P' l
放大镜
f l 250 P' l f
并非常数
y’ ’ y
P’
F’ -l’ f’
放大镜
结 论
f l 250 P' l f
瞳孔 角膜 虹膜
巩膜
网膜 脉络膜 黄斑中心凹
*网膜是眼球的第三层膜，上面布满着感光元素，即锥状细胞和杆状
细胞，锥状细胞直径约5微米，长约35微米；杆状细胞直径约2微米 ，长约60微米。它们在网膜上的分布式不均匀的。在黄斑中心凹处 是锥状细胞的密集区而没有杆状细胞，由中心向外，逐渐相对变化；
8
人眼的构造剖视图
3
已学过：折射定律——单个折射球面——理 想光组——平面系统——光束限制——像差 目的：组成仪器，得到实际应用的光学系统
根据光学基本理论，将光学元件合理组合， 得到光学仪器。 由使用要求决定成像要求，根据成像要求设 计光学系统。 设计过程就是合理的组合过程。
4
§7.1 眼睛及其光学系统
一、眼睛的结构
从光学角度看，眼睛中最主要的是：水晶体、视 网膜和瞳孔。
眼睛和照相机很相似，如果对应起来看：
人眼 ↕ 照相机 水晶体 ↕ ↕ 镜头 视网膜 ↕ 底片 瞳孔
光阑
13
2、眼睛的成像：
人眼是一个类似的摄影系统，角膜相当于一个凸凹镜，前室亦 如此，水晶体相当于一个双凸镜。物点在视网膜上形成一个倒立的 实像，但这一倒像的感觉经神经系统的作用，给人以正像的视觉。 眼睛的物方和像方焦距不相等: f = -17.1mm f ’ =22.8mm 眼睛的调焦范围: -f =14.2~17.1mm f ’ =18.9~22.8mm 瞳孔起着孔径光阑的作用，自动调节进入人眼的光能，它有一 定范围，( 2~8mm)若外界光很强，即使=2mm时仍然使人无法适 应，就很容易使视网膜造成伤害。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
精品文档
精品文档
垂轴放大率成像特性： β>0,成正像，虚实相反；β<0,成倒像，虚实相同 |β|>1,放大；|β|<1，缩小。 轴向放大率结论： 折射球面的轴向放大率恒为正，轴向放大率与垂轴放大率不等。 角放大率：表示折射球面将光束变宽变细的能力；只与共轭点的位置有关，与 光线的孔径角无关。 7 、球面反射镜成像公式
精品文档
第一章小结（几何光学基本定律与成像概念） 1 、光线、波面、光束概念。 光线：在几何光学中，我们通常将发光点发出的光抽象为许许多多携带能量并带
有方向的几何线。 波面：发光点发出的光波向四周传播时，某一时刻其振动位相相同的点所构成的
等相位面称为波阵面，简称波面。 光束：与波面对应所有光线的集合称为光束。 2 、几何光学的基本定律（内容、表达式、现象解释） 1 ）光的直线传播定律：在各向同性的均匀介质中，光是沿着直线传播的。 2 ）光的独立传播定律：不同光源发出的光在空间某点相遇时，彼此互不影
10、理想光学系统两焦距之间的关系？
11、理想光学系统的放大率？（定义、公式、用途、与单个折射面公式的区别 和联系）
精品文档
精品文档
12、理想光学系统的组合公式为何？正切计算法？
13、几种典型的光组组合及其特点（组成、特点和应用）？
精品文档
精品文档
第 三 章 小 结( 平面与平面系统) 1、平面光学元件的种类？作用？（4 种） 平面反射镜，唯一能成完善像的最简单的光学元件，可用于做光杠杆 平行平板，平行平板是个无光焦度的光学元件，不使物体放大或缩小， 反射棱镜，实现折转光路、转像和扫描等功能。 折射棱镜，改变光线的出射角，可用于放大偏转量。 2、平面镜的成像特点和性质？平面镜的旋转特性？ 每一点都能成完善像，并且像与物虚实相反。
精品文档
精品文档
1）沿轴线段(L、L’、r）：规定光线的传播方向自左至右为正方向，以折射面 顶点 O 为原点。
2）垂轴线段(h)：以光轴为基准，在光轴以上为正，以下为负。 3）光线与光轴的夹角(U、U’)：光轴以锐角方向转向光线，顺时针为正，逆时 针为负。 4）光线与法线的夹角(I、I’)：光线以锐角方向转向法线，顺时针为正，逆时针 为负。 5）光轴与法线的夹角(φ )：光轴以锐角方向转向法线，顺时针为正，逆时针为 负。 6）相邻两折射面间隔(d)：由前一面的顶点到后一面的顶点，顺光线方向为 正，逆为负。 5 、单个折射球面的光线光路计算公式（近轴、远轴）
2、共轴理想光学系统的成像性质是什么？（3大点） 1）位于光轴上的物点对应的共轭像点也必然位于光轴上；位于过光轴的某一个 截面内的物点对应的共轭像点必位于该平面的共轭像面内；同时，过光轴的任意截 面成像性质都是相同的 2）垂直于光轴的平面物所成的共轭平面像的几何形状完全与物相似。 3）如果已知两共轭面的位置和放大率，或者一对共轭面的位置和放大率，以及 轴上两对共轭点的位置，则其他一切物点的像点都可以根据这些已知的共轭面和共 轭点来表示。 3、无限远的轴上（外）物点的共轭像点是什么？它发出的光线有何性质？ 像方焦点；它发出的光线都与光轴平行。 4、无限远的轴上（外）像点的对应物点是什么？ 物方焦点。 5、物（像）方焦距的计算公式为何？ f’=h/tanU’，h为平行光线的高度，U’为像方孔径角。 6、物方主平面与像方主平面的关系为何？ 互为共轭。 光学系统的基点及性质？有何用途？ 一对主点和主平面，一对焦点和焦平面，称为光学系统的基点和基面。 一束平行光线经过系统后交于像方焦平面上一点，物方焦平面上一点光源发射
8 、共轴球面系统公式（过渡公式、成像放大率公式） 第二章小结 (理想光学系统) 1、什么是理想光学系统？ 为了系统的讨论物像关系，挖掘出光学系统的基本参量，将物、像与系统件的
精品文档
精品文档
内在关系揭示出来，可暂时抛开光学系统的具体结构（r,d,n），将一般仅在光学系 统的近轴区存在的完善成像，拓展成在任意大的空间中一任意宽的光束都成完善像 的理想模型。简单的说就是物像空间满足“点对应点，直线对应直线，平面对应平 面”的光学系统。
精品文档
精品文档
出的光线经过系统后是一组平行光线。 可用直接表示光学系统，便于推断和计算光路。 7、图解法求像的方法？ （可选择的典型光线和可利用的性质 5条+1条） 8、解析法求像方法为何？（牛顿公式、高斯公式） 1）牛顿公式：
2）高斯公式：
9、由多个光组组成的理想光学系统的成像公式？（过渡公式）
精品文档
精品文档
应用：1、用全反射棱镜代替平面反射镜以减少光能损失。（镀膜平面反射镜只 能反射90%左右的入射光能）2、光纤
折射定律：1、折射光线位于由入射光线和法线所决定的平面内；2、折射角的 正弦和入射角的正弦之比与入射角大小无关，仅由两种介质的性质决定。 n’sinI’=nsinI 。
应用：光纤 4 ）光路的可逆性 光从A点以AB方向沿一路径S传递，最后在D点以CD方向出射，若光从D点以CD 方向入射，必原路径S传递，在A点以AB方向出射，即光线传播是可逆的。 5 ）费马原理 光从一点传播到另一点，其间无论经历多少次折射和反射，其光程为极值。 （光是沿着光程为极值（极大、极小或常量）的路径传播的），也叫“光程极端定 律”。 6 ）马吕斯定律 光线束在各向同性的均匀介质中传播时，始终保持着与波面的正交性，并且入 射波面与出射波面对应点之间的光程均为定值。 折/反射定律、费马原理和马吕斯定律三者中的任意一个均可以视为几何光学的 一个基本定律，而把另外两个作为该基本定律的推论。 3 、完善成像条件（3种表述) 1）、入射波面为球面波时，出射波面也为球面波； 2）、入射光束为同心光束时，出射光束也为同心光束； 3）、物点A1 及其像点Ak ’之间任意二条光路的光程相等。 4 、应用光学中的符号规则（6 条）
响，各光束独立传播。 3 ）反射定律和折射定律（全反射及其应用）： 反射定律：1、位于由入射光线和法线所决定的平面内；2、反射光线和入射光
线位于法线的两侧，且反射角和入射角绝对值相等，符号相反，即I’’=-I。 全反射：当满足1、光线从光密介质向光疏介质入射，2、入射角大于临界角
时，入射到介质上的光会被全部反射回原来的介质中，而没有折射光产生。 sinIm=n’/n，其中mI 为临界角。