北师大版高中数学一轮复习第十二章12.1算法与程序框图word版下载
2021高考数学一轮复习统考第12章算法初步、复数、推理与证明第1讲算法初步学案北师大版

第十二章算法初步、复数、推理与证明第1讲算法初步基础知识整合1.算法的框图及结构(1)算法(2)程序框图的图形.通常,程序框图由程序框和流程线组成,一个或几个程序框的组合表示算法中的一(3)三种基本逻辑结构离不开的11基本结构程序框图步骤n错误!(1)输入语句、输出语句、赋值语句的格式与功能语句一般格式功能输入语句14INPUT“提示内容”;变量输入信息输出语句15PRINT“提示内容”;表达式输出信息赋值语句16变量=表达式17将表达式所代表的值赋给变量①IF-THEN格式②IF-THEN-ELSE格式(3)循环语句的格式及框图①UNTI L语句DO循环体LOOP UNTIL条件②WHILE语句WHILE 条件循环体WEND1.注意区分处理框与输入框,处理框主要是赋值、计算,而输入框只是表示一个算法输入的信息.2.循环结构中必有条件结构,其作用是控制循环进程,避免进入“死循环”,是循环结构必不可少的一部分.3.注意区分当型循环与直到型循环.直到型循环是“先循环,后判断,条件满足时终止循环”,而当型循环则是“先判断,后循环,条件满足时执行循环”.两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反.1.(2019·北京高考)执行如图所示的程序框图,输出的s值为( )A.1 B.2C.3 D.4答案 B解析k=1,s=1;第一次循环:s=2,判断k<3,k=2;第二次循环:s=2,判断k<3,k=3;第三次循环:s=2,判断k=3,故输出2.故选B.2.下列程序段执行后,变量a,b的值分别为( )a=15b=20a=a+bb=a-ba=a-bPRINT a,bA.20,15 B.35,35C.5,5 D.-5,-5答案 A解析a=15,b=20,把a+b赋给a,因此得出a=35,再把a-b赋给b,即b=35-20=15.再把a-b赋给a,此时a=35-15=20,因此最后输出的a,b的值分别为20,15.故选A.3.(2019·武昌调研)执行如图所示的程序框图,如果输入的a 依次为2,2,5时,输出的S 为17,那么在判断框中可以填入( )A .k >nB .k <nC .k ≥nD .k ≤n 答案 A解析 第一次输入a =2,此时S =0×2+2=2,k =0+1=1,不满足k =1>n =2;第二次输入a =2,此时S =2×2+2=6,k =1+1=2,不满足k =2>n =2;第三次输入a =5,此时S =6×2+5=17,k =2+1=3,满足k =3>n =2,循环终止,输出的S =17.故选A.4.(2019·湖南郴州模拟)执行如图所示的程序框图,输出S 的值为12时,k 是( )A .5B .3C .4D .2答案 A解析 模拟执行程序,可得每次循环的结果依次为k =2,k =3,k =4,k =5,大于4,可得S =sin 5π6=12,输出S 的值为12.故选A.5.(2020·锦州摸底)若如图所示的程序框图输出的S 是30,则在判断框中M 表示的“条件”应该是( )A .n ≥3B .n ≥4C .n ≥5D .n ≥6 答案 B解析 第一次循环,n =1,S =2;第二次循环,n =2,S =6;第三次循环,n =3,S =14;第四次循环,n =4,S =30,故选B.6.执行如图所示的程序框图,若输入x 的值为1,则输出n 的值为________.答案 3解析第一次:x=1,x2-4x+3=0≤0.第二次:x=2,n=1,x2-4x+3=-1≤0.第三次:x=3,n=2,x2-4x+3=0≤0.第四次:x=4,n=3,x2-4x+3=3>0,输出n,程序结束.核心考向突破考向一算法的基本结构例 1 (2019·全国卷Ⅲ)执行如图所示的程序框图,如果输入的为0.01,则输出s 的值等于( )A .2-124B .2-125C .2-126D .2-127答案 C 解析=0.01,x =1,s =0,s =0+1=1,x =12,x <不成立; s =1+12,x =14,x <不成立; s =1+12+14,x =18,x <不成立; s =1+12+14+18,x =116,x <不成立; s =1+12+14+18+116,x =132,x <不成立; s =1+12+14+18+116+132,x =164,x <不成立; s =1+12+14+18+116+132+164,x =1128,x <成立,此时输出s=2-126.故选C.利用循环结构表示算法应注意的问题(1)注意是利用当型循环结构,还是直到型循环结构.(2)注意准确选择表示累计的变量.(3)注意在哪一步开始循环,满足什么条件不再执行循环体.[即时训练] 1.(2019·天津高考)阅读右边的程序框图,运行相应的程序,输出S的值为( )A.5B.8C.24D.29答案 B解析i=1,S=0,i不是偶数;第一次循环:S=1,i=2<4;第二次循环:i是偶数,j=1,S=5,i=3<4;第三次循环:i不是偶数,S=8,i=4,满足i≥4,输出S,结果为8.故选B.2.(2020·濮阳模拟)执行如图所示的程序框图(其中b=c mod 10表示b等于c除以10的余数),则输出的b为( )A.2 B.4C.6 D.8答案 D解析a=2,b=8,n=1;c=16,a=8,b=6,n=2;c=48,a=6,b=8,n=3;c =48,a=8,b=8,n=4;c=64,a=8,b=4,n=5;c=32,a=4,b=2,n=6;c=8,a=2,b=8,n=7,…,易知该程序框图中a,b的值以6为周期重复出现.又因为2019=6×336+3,所以当n=2019时,b=8.故选D.精准设计考向,多角度探究突破考向二算法的交汇性问题角度1算法与函数的交汇例2 (2019·潍坊模拟)执行右边的程序框图,如果输出的y值为1,则输入的x值为( )A .0B .eC .0或eD .0或1 答案 C解析 程序对应的函数为y =⎩⎪⎨⎪⎧e x,x ≤0,2-ln x ,x >0.若x ≤0,由y =1,得e x=1,得x =0,满足条件;若x >0,由y =2-ln x =1,得ln x =1,即x =e ,满足条件.综上,输入的x 值为0或e ,故选C.角度2 算法与数列的交汇例3 (2020·西宁模拟)执行如图所示的程序框图,若输入n =10,则输出的S 的值是( )A.910B.1011C.1112D.922答案 B解析 模拟程序的运行,可得程序的功能是利用循环结构计算并输出变量S =11×2+12×3+…+110×11的值, 可得S =11×2+12×3+…+110×11=⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫110-111=1-111=1011.故选B.角度3 算法与统计的交汇例4 (2019·九江联考)图1是随机抽取的15户居民月均用水量(单位:吨)的茎叶图,月均用水量依次记为A 1,A 2,…,A 15,图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图,则输出的n 的值为________.答案7解析由程序框图,知算法的功能是计算15户居民中月均用水量大于2.1的户数,由茎叶图得,在这15户居民中,月均用水量大于2.1的户数为7,故输出的n的值为7.解决算法的交汇性问题的方法循环结构的程序框图与数列、不等式、统计等知识综合是高考命题的一个热点,解决此类问题时应把握三点:一是初始值,即计数变量与累加变量的初始值;二是两个语句,即循环结构中关于计数变量与累加变量的赋值语句;三是一个条件,即循环结束的条件,注意条件与流程线的对应关系.[即时训练] 3.(2020·宁夏银川模拟)执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于( )A .[-6,-2]B .[-5,-1]C .[-4,5]D .[-3,6]答案 D解析 当0≤t ≤2时,S =t -3∈[-3,-1].当-2≤t <0时,2t 2+1∈(1,9],则S ∈(-2,6].综上,当-2≤t ≤2时,S ∈[-3,6],故选D.4.(2019·湖南长沙模拟)如图,给出的是计算1+14+17+…+1100的值的一个程序框图,则图中判断框内的(1)处和执行框中的(2)处应填的语句是( )A .i >100,n =n +1B .i <34,n =n +3C .i >34,n =n +3D .i ≥34,n =n +3答案 C解析 算法的功能是计算1+14+17+…+1100的值,易知1,4,7,…,100成等差数列,公差为3,所以执行框中的(2)处应为n =n +3,令1+(i -1)×3=100,解得i =34,所以终止程序运行的i 值为35,所以判断框内的(1)处应为i >34,故选C.5.在2018~2019赛季NBA 季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如下表:为了对这个队的情况进行分析,此人设计计算σ的算法流程图如图所示(其中x 是这7场比赛的平均得分),求输出的σ的值.解 由题意,知x -=17×(100+104+98+105+97+96+100)=100,由算法流程图可知s =(100-100)2+(104-100)2+(98-100)2+(105-100)2+(97-100)2+(96-100)2+(100-100)2=70.故σ=s7=10. 考向三 基本算法语句例5 (1)(2019·福州质检)下列程序语句的算法功能是( )INPUT a,b,cIF a<b THENa=bEND IFIF a<c THENa=cEND IFPRINT aENDA.输出a,b,c三个数中的最大数B.输出a,b,c三个数中的最小数C.将a,b,c从小到大排列D.将a,b,c从大到小排列答案 A解析由程序语句可知,当比较a,b的大小后,选择较大的数赋给a;当比较a,c的大小后,选择较大的数赋给a,最后输出a,所以此程序的作用是输出a,b,c三个数中的最大数.故选A.(2)运行下面的程序,执行后输出的s的值是( )A.11 B.15C.17 D.19答案 B解析当i=3时,s=7,当i=5时,s=11,当i=7时,s=15,此时不满足“i<6”,所以输出s=15,故选B.基本算法语句应用中需注意的问题(1)赋值号“=”的左、右两边不能对调,A =B 和B =A 的含义及运行结果是不同的. (2)不能利用赋值语句进行代数式的演算(如化简、因式分解等),在赋值语句中的赋值号右边的表达式中每一个“变量”都必须事先赋给确定的值.(3)赋值号与数学中的等号意义不同,比如在数学中式子N =N +1一般是错误的,但在赋值语句中它的作用是将原有的N 的值加上1再赋给变量N ,这样原来的值被“冲”掉.[即时训练] 6.阅读下面的程序:如果上述程序输入的值是51,则运行结果是( ) A .51 B .15 C .105 D .501答案 B解析 因为51÷10=5……1,所以a =5,b =1,x =10×1+5=15.故选B .7.(2019·龙岩质检)如图所示的程序,若最终输出的结果为6364,则在程序中“____?____”处应填入的语句为( )S=0n=2i=1DOS=S+1/nn=2*ni=i+1LOOP UNTIL ?PRINT SENDA.i>=8 B.i>=7C.i<7 D.i<8答案 B解析S=0,n=2,i=1,执行S=12,n=4,i=2;S=12+14=34,n=8,i=3;S=34+18=78,n=16,i=4;S=78+116=1516,n=32,i=5;S=1516+132=3132,n=64,i=6;S=3132+164=6364,n=128,i=7.此时满足题目条件输出的S=6364,∴“?”处应填上i>=7.故选B.(2019·沈阳模拟)程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )A.120 B.84C.56 D.28答案 B解析初始值i=0,n=0,S=0,第一次循环,i=1,n=1,S=1;第二次循环,i=2,n=3,S=4;第三次循环,i=3,n=6,S=10;第四次循环,i=4,n=10,S=20;第五次循环,i=5,n=15,S=35;第六次循环,i=6,n=21,S=56;第七次循环,i=7,n=28,S=84,此时退出循环,输出S=84,故选B.答题启示求解循环结构的程序框图题的“三注意”(1)注意是当型循环结构,还是直到型循环结构;(2)注意选择准确的表示累计的变量;(3)注意在哪一步开始循环,及执行循环体的条件.对点训练“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图所示的程序框图的算法思路就是来源于“欧几里得算法”.执行该程序框图(图中“a MOD b”表示a 除以b的余数),若输入的a,b分别为675,125,则输出的a=()C.50 D.75答案 B解析初始值:a=675,b=125,第一次循环:c=50,a=125,b=50;第二次循环:c=25,a=50,b=25;第三次循环:c=0,a=25,b=0,此时不满足循环条件,退出循环.输出a的值为25,故选B.21。
【走向高考】高考数学总复习 12-1算法与算法框图 课件 北师大版

3.在推理证明的复习中,要准确把握概念,把握好 各种证法的特点和步骤,注意灵活运用. (1)对于合情推理,主要是掌握相关概念,会进行类 比推理,能判断推理的类型. (2) 直接证明与间接证明主要渗透到其他知识板块 中,要注意在复习相应的板块时,培养选择合理证明方法 的能力. 4.熟练准确地进行复数运算是复数学习的重点.
3. 如果执行如图所示的程序框图,那么输出的 k= ( )
A.4 C.6
B.5 D.7
[答案] B
[解析 ] 第一次运行 k= 2,S= 0+ 20= 1; 第二次运行 k= 3, S= 1+ 21= 3; 第三次运行 k= 4, S= 3+ 23= 11; 第四次运行 k= 5, S= 11+ 211>100. 结束循环,输出的 k= 5,故选 B.
1.高考本单元考查的题型主要是选择题和填空题, 分值约在 10~ 15 分之间,属中低档题. 2.重点考查程序框图的“读”或“补”,注重对循 环结构的考查,或与其他知识点相结合的综合考查.
3.预计今后的高考,本单元仍将以程序框图为主, 重点关注程序框图“读”或“补”. 在考查程序框图时经常会与数列、 函数等知识的实际 问题相结合,进一步强化框图问题的实际背景.
(2)流程图形式为
6.循环结构 (1)定义:循环结构是指 从某处开始,按照一定条件,
反复执行处理某步骤的情况. 反复执行的处理步骤称为 循环体.
(2)画循环结构流程图之前,要确定三件事: ①确定循环变量和初始条件; ②确定算法中反复执行的部分,即循环体; ③确定循环的终止条件.
(3)流程图形式为
4.(2011· 福建文,5)阅读下图所示的程序框图,运行 相应的程序,输出的结果是( )
A.3 C.38
2019届一轮复习北师大版理 12.2算法与程序框图 课件(60张)

=2,S=9,S<50⇒x=4,S=73>50,跳出循环,输出 S=73.
栏目 导引
பைடு நூலகம்
第十二章 复数、算法、推理与证明
(2017·高考北京卷)执行如图所示的程序框图,输出的 s 值为 ()
A.2 C.53
B.32 D.85
栏目 导引
第十二章 复数、算法、推理与证明
解析:选 C.运行该程序,k=0,s=1,k<3; k=0+1=1,s=1+1 1=2,k<3; k=1+1=2,s=2+2 1=32,k<3; k=1+2=3,s=32+3 1=53,k=3.输出的 s 值为53.故选 C.
第十二章 复数、算法、推理与证明
(2017·高考全国卷Ⅰ)如图程序框图是为了求出满足 3n
-2n>1 000 的最小偶数 n,那么在 和 两个空白框中,
可以分别填入( )
栏目 导引
第十二章 复数、算法、推理与证明
A.A>1 000 和 n=n+1 B.A>1 000 和 n=n+2 C.A≤1 000 和 n=n+1 D.A≤1 000 和 n=n+2 【解析】 程序框图中 A=3n-2n,故判断框中应填入 A≤1 000,由于初始值 n=0,要求满足 A=3n-2n>1 000 的最小偶数, 故执行框中应填入 n=n+2,选 D. 【答案】 D
语句体 _E__N_D__I_F_ __I_F__条__件__T__H_E__N__
语句体 1 __E_L_S_E___
语句体 2 END IF
栏目 导引
名称
当型
循环
循环 结构
结构 直到 型循
环结
构
第十二章 复数、算法、推理与证明
第12章 算法与程序框图

第一步 投票 第二步 统计票数,如果有一座城市的得票数 超过总票数的一半,那么该城市就获得举办权; 否则将得票数最少的城市淘汰,并转而执行第一步
第三步 输出举办城市
算法步骤 第一步:投票 第二步 统计票数 第三步 输出举办城市
开始 投票
有一座城市的得票数 超过总票数的一半
是
输出该城市为举办城市
P42例5
新课引入
算法是由一系列明确和有限的步骤组成,我们可以用自然语言表示一 个算法,但往往过程复杂,缺乏简洁性,因此必须引入一种使算法表达 的更直观,更准确的方法,这就是今天我们要学习的程序框图。
程序框图基本概念:
程序框图又称流程图,是一种用规定的框、带箭头的线(也称为流程 线或指向线)及文字说明来准确、直观地表示算法的图形。
(2)确切性 算法中的每一个步骤都是确切的,能有效的执行且能得到确定的结果,不能模 棱两可,不存在歧义 (3)可行性(或有效性) 算法的每一个步骤都是可执行的操作,即每一步都可以在有限的时间内完成。 (4)有0个、1个、或多个输入,用于刻画运算对象的初始情况。 (5)有1个或多个输出,用以反映对输入数据加工后的结果,没有输出的算法 是毫无意义的。
结束
将得票数最少 的城市淘汰 否
二、算法的三种基本逻辑结构:
开始 输入n
i=2
①顺序结构 求n除以i的余数r i的值增加1,仍用i表示
③循环结构
i>n-1或r=0?
否
是
是
r=0?
否否
N不是质数
N是质数
②条件结构
结束
算法千差万别,但都是由这 三种基本逻辑结构构成的.
输入n
i=2
求n除以i的余数r
i的值增加1,仍用i表示
12章算法与程序框图

(24,18) (18,6)
(6,12) (6,6)
6就是24和18的最大公约数
循环变量初始化 循环终止条件 循环体
实例四
题意: 某城市对居民的生活用水 实行阶梯式收费,标准为: 每月每户生活用水20m3以 内(含20m3 )为第一级, 按居民生活用水的供水价 格收费;每月每户生活用 水超过20m3且低于或等于 30m3为第二级,超出部分 按供水价格的1.5倍收费; 每月每户生活用水超过 30m3,超过部分按供水价 格的2倍收费,如果该市 居民生活用水的供水价格 为1.24元m3/,另加收城市 附加费用0.06/m3,污水处 理费1.3/m3,水资源费 0.2/m3,请设计一个算法, 输入某户居民某个月的用 水量,输出这个月该户居 民所需缴纳的水费。
当赋予它新的数值,原来的值就被取代。
• 注意: • 1、赋值号左边只能出现变量名,如: x=2,a=b+c,不能出现 2=b, c+1=2 • 2、赋值语句中,只能给一个变量赋值,不能同时给两个变量赋值,如:a=b=5是错误的 。 • 3、赋值号不同于“等号”,赋值号左右可以现现同一个变量,如n=n+1,而等式n=n+1是错误的。 • 4、一个变量可多次赋值,但运算时只跟最后一次赋值相关
题目
起止框 第一步 输入两个数a,b;(输入输出框) 第二步 计算c=a+b;(处理框) 第三步 计算m=c÷2;(处理框) 第四步 输出m;(输入输出框) 起止框
算法
程序框图
实例
起止框
例2: 如图所示程序框图 的功能是( ) A. 求a-b的值 B.求b-a的值 C.求|a-b|的值 D.求 -|a-b|的值
例题
一杯白开水一杯茶水,设计一个算法,将两个怀子中的水对调 ②
2015高考数学(理)一轮复习考点突破课件:12.1算法与程序框图

解决算法语句有三个步骤:首先通读全部语句,
• 把它翻译成数学问题;其次领悟该语句的功能;最后根据语句的功 能运行程序,解决问题.
针对训练 3.(1)(2014· 东北三校模拟)运行如图所示程序的结果为 ( n=10 S=100 DO S=S-n n=n-1 LOOP UNTIL S<=70 PRINT n END )
2
3 解之得,x= (负值舍去); 4 3 综上,输入 x 的值为 . 4 3 【答案】 (1)D (2) 4
• 【归纳提升】 1.解决程序框图问题要注意几个常用变量: • (1)计数变量:用来记录某个事件发生的次数,如i=i+1. • (2)累加变量:用来计算数据之和,如S=S+i. • (3)累乘变量:用来计算数据之积,如p=p×i. • 2 .处理循环结构的框图问题,关键是理解并认请终止循环结构的 条件及循环次数.
1 =2- . k+1
9 当 S= 时,k=4பைடு நூலகம்接着继续计算“k=k+1”,所以 4≤a<5,故 5 选 A. 答案:A
• •
题型三
基本算法语句 (1)(2013· 陕西 ) 根据下列算法语句,当输入 x 为 60 时,输 出y的值为 • ( ) • 输入x;
• A.25 • C.31
B.30 D.61
• (2)(2013·江西)阅读如下程序框图,如果输出i=5,那么在空白矩形 框中应填入的语句为 •( )
• A.S=8*i-2 • C. S=2* i
B.S=2*i-1 D.S=2* i +4
• 【解析】 (1)i=1,S=1;i=2,S=1+2;i=3,S=1+2×(1+2) = 1+ 2+22; i= 4, S=1+ 2×(1+ 2+ 22)= 1+2+ 22+23; „,故 i =10时,S=1+2+22+„+29,故选A. • (2)i=2,S=5;i=3,S<10,排除D;i=4,S=9;i=5,S≥10,排 除A和B,故选C. • 【答案】 (1)A (2)C
北师大版高中数学一轮复习第十二章12.5数学归纳法word版下载

课时作业68 数学归纳法一、选择题1.用数学归纳法证明1+2+…+(2n +1)=(n +1)(2n +1)时,在验证n =1成立时,左边所得的代数式是( ).A .1B .1+3C .1+2+3D .1+2+3+42.用数学归纳法证明不等式1n +1+1n +2+…+12n <1314(n ≥2,n ∈N +)的过程中,由n =k 递推到n =k +1时不等式左边( ).A .增加了一项12(k +1)B .增加了两项12k +1,12k +2C .增加了12k +1和12k +2两项但减少了一项1k +1D .以上各种情况均不对 3.用数学归纳法证明不等式1+12+14+…+12n -1>12764成立时,起始值n 至少应取为( ).A .7B .8C .9D .104.用数学归纳法证明:“(n +1)·(n +2)·…·(n +n )=2n ·1·3·…·(2n -1)”,从“k 到k +1”左端需增乘的代数式为( ).A .2k +1B .2(2k +1) C.2k +1k +1 D.2k +3k +15.在数列{a n }中,a 1=13,且S n =n (2n -1)a n ,通过求a 2,a 3,a 4,猜想a n 的表达式为( ). A.1(n -1)(n +1) B.12n (2n +1) C.1(2n -1)(2n +1) D.1(2n +1)(2n +2)6.设函数f (n )=(2n +9)·3n +1+9,当n ∈N +时,f (n )能被m (m ∈N +)整除,猜想m 的最大值为( ).A .9B .18C .27D .367.对于不等式n 2+n <n +1(n ∈N +),某同学用数学归纳法的证明过程如下:(1)当n =1时,12+1<1+1,不等式成立.(2)假设当n =k (k ∈N +)时,不等式成立,即k 2+k <k +1,则当n =k +1时,(k +1)2+(k +1)=k 2+3k +2<(k 2+3k +2)+(k +2)=(k +2)2=(k +1)+1,∴当n =k +1时,不等式成立,则上述证法( ).A .过程全部正确B .n =1验得不正确C .归纳假设不正确D .从n =k 到n =k +1的推理不正确二、填空题8.用数学归纳法证明“1+a +a 2+…+a n +1=1-a n +21-a(a ≠1,且n ∈N +)”,在验证n =1时,左边计算所得的结果是__________.9.在△ABC 中,不等式1A +1B +1C ≥9π成立;在四边形ABCD 中,不等式1A +1B +1C +1D ≥162π成立;在五边形ABCDE 中,不等式1A +1B +1C +1D +1E ≥253π成立…… 猜想在n 边形A 1A 2…A n 中,有不等式________成立.10.用数学归纳法证明⎝⎛⎭⎫1+13⎝⎛⎭⎫1+15⎝⎛⎭⎫1+17…⎝⎛⎭⎫1+12k -1>2k +12(k >1),则当n =k +1时,左端应乘上__________________________,这个乘上去的代数式共有因式的个数是__________.三、解答题11.设数列{a n}的前n项和为S n,且方程x2-a n x-a n=0有一根为S n-1,n=1,2,3,….(1)求a1,a2;(2)猜想数列{S n}的通项公式,并给出严格的证明.12.(2013届陕西渭南合阳中学月考)已知函数f(n)(n∈N+),满足条件:①f(2)=2,②f(xy)=f(x)·f(y),③f(n)∈N+,④当x>y时,有f(x)>f(y).(1)求f(1),f(3)的值;(2)由f(1),f(2),f(3)的值,猜想f(n)的解析式;(3)证明你猜想的f(n)的解析式的正确性.参考答案一、选择题1.C 解析:左边表示从1开始,连续2n +1个正整数的和,故n =1时,表示1+2+3的和.2.C 解析:当n =k +1时,不等式为1(k +1)+1+1(k +1)+2+…+12(k +1)<1314,∴比当n =k 时增加了12k +1,12k +2项.但最左端少了一项1k +1. 3.B 解析:∵1+12+14+…+127-1=1-⎝⎛⎭⎫1271-12=2-126=27-126=12764, 而1+12+14+ (128)1>12764,故起始值n 至少取8. 4.B 解析:当n =k 时,等式为(k +1)(k +2)·…·(k +k )=2k ×1×3×…×(2k -1), 当n =k +1时,等式为(k +2)(k +3)·…·(k +k )(k +1+k )(k +1+k +1)=2k +1×1×3×…×(2k +1),∴左端增乘(2k +1)(2k +2)k +1=2(2k +1). 5.C 解析:由a 1=13,S n =n (2n -1)a n 求得a 2=115=13×5,a 3=135=15×7,a 4=163=17×9.猜想a n =1(2n -1)(2n +1). 6.D 解析:f (n +1)-f (n )=(2n +11)·3n +2-(2n +9)·3n +1=4(n +6)·3n +1,当n =1时,f (2)-f (1)=4×7×9为最小值,据此可猜想D 正确.7.D 解析:在n =k +1时,没有应用n =k 时的假设,不是数学归纳法.二、填空题8.1+a +a 2 解析:首先观察等式两边的构成情况,它的左边是按a 的升幂顺序排列的,共有n +2项.因此当n =1时,共有3项,应该是1+a +a 2.9.1A 1+1A 2+…+1A n ≥n 2(n -2)π10.⎝⎛⎭⎫1+12k +1⎝⎛⎭⎫1+12k +3·…·⎝⎛⎭⎫1+12k +1-1 2k -1 解析:当n =k 时,⎝⎛⎭⎫1+13⎝⎛⎭⎫1+15·…·⎝ ⎛⎭⎪⎫1+12k -1>2k +12. 当n =k +1时,⎝⎛⎭⎫1+13⎝⎛⎭⎫1+15⎝⎛⎭⎫1+17…⎝ ⎛⎭⎪⎫1+12k -1⎝ ⎛⎭⎪⎫1+12k +1…⎝ ⎛⎭⎪⎫1+12k +1-1>2k +32. ∴左边应乘上⎝ ⎛⎭⎪⎫1+12k +1⎝ ⎛⎭⎪⎫1+12k +3…⎝ ⎛⎭⎪⎫1+12k +1-1,设第一项a 1=2k +1,a n =2k +1-1,d =2,∴n =a n -a 12=2k +1-1-2k -12=2k -1. 三、解答题11.解:(1)当n =1时,x 2-a 1x -a 1=0有一根为S 1-1=a 1-1,于是(a 1-1)2-a 1(a 1-1)-a 1=0,解得a 1=12. 当n =2时,x 2-a 2x -a 2=0有一根为S 2-1=a 2-12, 于是⎝⎛⎭⎫a 2-122-a 2⎝⎛⎭⎫a 2-12-a 2=0,解得a 2=16. (2)由题设知(S n -1)2-a n (S n -1)-a n =0,即S 2n -2S n +1-a n S n =0.当n ≥2时,a n =S n -S n -1,代入上式得S n -1S n -2S n +1=0.(*)由(1)得S 1=a 1=12, S 2=a 1+a 2=12+16=23. 由(*)式可得S 3=34. 由此猜想S n =n n +1,n =1,2,3,…. 下面用数学归纳法证明这个结论.①n =1时已知结论成立.②假设n =k (k ∈N +)时结论成立,即S k =k k +1, 当n =k +1时,由(*)得S k +1=12-S k, 即S k +1=k +1k +2, 故n =k +1时结论也成立.综上,由①,②可知S n =n n +1对所有正整数n 都成立. 12.解:(1)∵f (2)=f (2×1)=f (2)·f (1),又f (2)=2,∴f (1)=1.又∵f (4)=f (2×2)=f (2)·f (2)=4,2=f (2)<f (3)<f (4)=4,且f (3)∈N +.∴f (3)=3.(2)由f (1)=1,f (2)=2,f (3)=3,猜想f (n )=n (n ∈N +).(3)用数学归纳法证明:当n =1时,f (1)=1,函数解析式成立.假设n =k 时,f (k )=k ,函数解析式成立.①若k +1=2m (m ∈N +),f (k +1)=f (2m )=f (2)·f (m )=2m =k +1.②若k +1=2m +1(m ∈N +),f (2m +2)=f [2(m +1)]=f (2)·f (m +1)=2(m +1)=2m +2,2m=f(2m)<f(2m+1)<f(2m+2)=2m+2. ∴f(2m+1)=2m+1=k+1.即当n=k+1时,函数解析式成立.综上可知,f(n)=n(n∈N+)成立.。
【走向高考】高考数学一轮总复习 12-1算法与算法框图课后强化作业 北师大版
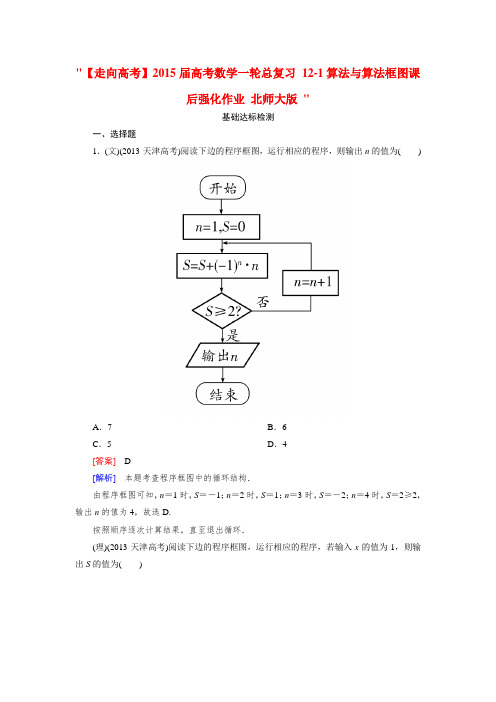
"【走向高考】2015届高考数学一轮总复习12-1算法与算法框图课后强化作业北师大版"基础达标检测一、选择题1.(文)(2013·天津高考)阅读下边的程序框图,运行相应的程序,则输出n的值为()A.7B.6C.5D.4[答案] D[解析]本题考查程序框图中的循环结构.由程序框图可知,n=1时,S=-1;n=2时,S=1;n=3时,S=-2;n=4时,S=2≥2,输出n的值为4,故选D.按照顺序逐次计算结果,直至退出循环.(理)(2013·天津高考)阅读下边的程序框图,运行相应的程序,若输入x的值为1,则输出S的值为()A.64B.73C.512D.585[答案] B[解析]本题考查了程序框图及计算.x=1,S=S+x3=0+13=1;x=2,S=S+x3=1+23=9;x=4,S=S+x3=9+43=9+64=73>50,故输出S.2.(2013·北京高考)执行如图所示的程序框图,输出的S值为()A .1 B.23 C.1321 D.610987[答案] C[解析] 程序运行过程为:i =0,S =1,S =12+12×1+1=23,i =0+1=1,i ≥2不成立;继续下一次循环,S =(23)2+12×23+1=1321,i =1+1=2,由于此时i ≥2成立,故停止循环,输出S 的值1321后结束.3.执行下面的程序框图,如果输入的n 是4,则输出的p 是( )A.8 B.5 C.3 D.2 [答案] C[解析]本小题考查的内容为程序框图中的循环结构.k=1时,p=1,k=2时,p=2,k=3时,p=3.4.执行如图所示的程序框图,输出的S值为()A.2 B.4C.8 D.16[答案] C[解析]当k=0时,满足k<3,因此S=1×20=1;当k=1时,满足k<3,因此S=1×21=2;当k=2时,满足k<3,因此S=2×22=8;当k=3时,不满足k<3,因此输出S=8.5.(文)(2013·江西高考)阅读如下程序框图,如果输出i=4,那么空白的判断框中应填入的条件是()A.S<8 B.S<9C.S<10 D.S<11[答案] B[解析]本题考查了程序框图的循环结构.依据循环要求有i=1,S=0;i=2,S=2×2+1=5;i=3,S=2×3+2=8;i=4,S=2×4+1=9,此时结束循环,故应为S<9.(理)(2013·江西高考)阅读如下程序框图,如果输出i=5,那么在空白矩形框内应填入的语句为()[答案] C[解析]i=2时,i不是奇数,S=2×2+1=5<10,继续循环,i=2+1=3,3是奇数,执行“选项”后,需继续循环,故排除D.当i=4时,i不是奇数,S=2×4+1=9<10,继续循环,i=4+1=5,5是奇数,执行“选项”后,应跳出循环,输出i的值5后结束,但2×5-2=8<10,2×5-1=9<10,都需继续循环,故排除A、B选项,但2×5=10<10不成立,故选C.二、填空题6.如图给出一个算法框图,其作用是输入x的值,输出相应的y值.若要使输入的x 值与输出的y值相等.则这样的x值有________个.[答案] 3[解析] 当x ≤2时,x 2=x ,有x =0或x =1; 当2<x ≤5时,2x -3=x ,有x =3; 当x >5时,x =1x ,x 无解.故可知这样的x 有3个.7.(2013·山东高考)执行下面的程序框图,若输入的ε的值为0.25,则输出的n 的值为________.[答案] 3[解析] 本题考查了程序框图和算法等知识. ε=0.25,F 0=1,F 1=2,n =1,此时F 1=F 0+F 1=1+2=3;F 0=F 1-F 0=3-1=2,n =2,∵1F 1=13≤0.25不成立,进入下一循环,F1=F0+F1=2+3=5,F0=F1-F0=5-2=3,n=3,1F1=15≤0.25成立,输出n=3.三、解答题8.国家法定工作日内,每周工作时间满工作量为40h,每小时工资8元;如因需要加班,则每小时工资为10元.某人在一周内工作时间为x h,但他须交纳个人住房公积金、失业险(这两项费用为每周总收入的10%).试分析算法步骤并画出其净得工资y元的算法的流程图.(注:满工作量外的工作时间为加班)[解析]算法如下:S1输入工作时间x h;S2若x≤40,则y=8x×(1-10%);否则,y=40×8(1-10%)+(x-40)×10(1-10%).S3输出y值.流程图如下:能力强化训练一、选择题1.(文)(2013·新课标Ⅱ)执行下面的程序框图,如果输入的N=4,那么输出的S=()A .1+12+13+14B .1+12+13×2+14×3×2C .1+12+13+14+15D .1+12+13×2+14×3×2+15×4×3×2[答案] B[解析] 本题考查程序框图的循环结构.由程序框图依次可得,输入N =4, K =1,S =0,T =1→T =1,S =1,K =2;2>4否 T =12,S =1+12,K =3;3>4否T =16,S =1+12+13×2,K =4;4>4否T =14×3×2,S =1+12+13×2+14×3×2,K =5;5>4是,输出S =1+12+13×2+14×3×2,故选B.(理)(2013·新课标Ⅱ)执行下面的程序框图,如果输入的N =10,那么输出的S =( )A .1+12+13+…+110B .1+12!+13!+…+110!C .1+12+13+…+111D .1+12!+13!+…+111![答案] B[解析] 当输入N =10时,由于初值k =1,S =0,T =1,故程序运行过程依次为:T =11=1,S =0+1=1,k =1+1=2,此时不满足k >10→T =12=12!,S =1+12!,k =2+1=3,不满足k >10→T =12!3=13!,S =1+12!+13!,k =3+1=4仍不满足k >10,…,直到k =10时,T =19!10=110!,S =1+12!+13!+ (110),k =11,此时满足k >10,结束循环,输出S =1+12!+13!+ (110)后结束. 2.如果执行如图的框图,输入N =5,则输出的数等于()A.54B.45C.65D.56[答案] D[解析] 本题考查了程序框图的有关知识,并且渗透了裂项求和的方法,在解题时要注意首先弄清楚程序框图的功能,然后看限制条件,题目定位是中档题.根据程序框图可知,该程序框图的功能是计算S =11×2+12×3+13×4+…+1k ×(k +1),现在输入的N =5,所以满足条件k <N 的结果为S =11×2+12×3+13×4+14×5+15×6=(1-12)+(12-13)+…+(15-16)=56,故选D. 3.执行如图所示的流程图,若输出的b 的值为16,则图中判断框内①处应填( )A.3B.4C.5D.2[答案] A[解析]按照流程图依次执行:初始a=1,b=1;第一次循环后,b=21=2,a=1+1=2;第二次循环后,b=22=4,a=2+1=3;第三次循环后,b=24=16,a=3+1=4,而此时应输出b的值,故判断框中的条件应为a≤3,故选A.4.(2013·重庆高考)执行如图所示的程序框图,如果输出s=3,那么判断框内应填入的条件是()A .k ≤6B .k ≤7C .k ≤8D .k ≤9 [答案] B[解析] 本题考查程序框图,主要是循环结构的运行问题.依题意,程序框图是计算s =log 23log 34…log k (k +1)的值,当输出s =3时,即log 2(k +1)=3,所以k =7.由k =k +1知,选B.二、填空题5.如图是计算函数y =⎩⎪⎨⎪⎧ ln (-x ) x ≤-20 -2<x ≤32x x >3的值的程序框图,在①、②、③处应分别填入的是____________________.[答案]y=ln(-x),y=2x,y=0[解析]由程序框图所表达的意义知①②③处应分别填入的是y=ln(-x),y=2x,y=0.6.下图是一个算法流程图,则输出的k的值是________.[答案] 5[解析]第一步,当k=1时,k2-5k+4=1-5+4=0;第二步,当k=2时,k2-5k+4=4-10+4=-2<0;第三步,当k=3时,k2-5k+4=9-15+4=-2<0;第四步,当k=4时,k2-5k+4=16-20+4=0;第五步,当k=5时,k2-5k+4=25-25+4>0,结束循环,输出k=5.三、解答题7.用循环语句来书写1+22+32+…+n2>100的最小自然数n的算法,画出算法流程图.[解析]算法如下:第一步:S=0;第二步:n=1;第三步:S=S+n2;第四步:如果S≤100,使n=n+1,并返回第三步,否则输出n-1.相应的流程图如图所示.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业64 算法与程序框图
一、选择题
1.如下框图,当x1=6,x2=9,p=8.5时,x3等于().
A.7 B.8 C.10 D.11
2.(2012江西南昌模拟)若如下程序框图所给的运行结果为S=20,那么判断框中应填入的关于k的条件是().
A.k=9 B.k≤8 C.k<8 D.k>8
3.(2012北京高考)执行如图所示的程序框图,输出的S值为().
A.2 B.4 C.8 D.16
4.阅读如图的程序框图,若输出的S的值等于16,那么在程序框图中的判断框内应填写的条件是().
A.i>5 B.i>6 C.i>7 D.i>8
5.如图是求x1,x2,…,x10的乘积S的程序框图,图中空白框中应填入的内容为().A.S=S·(n+1) B.S=S·x n+1 C.S=S·n D.S=S·x n
6.(2012山东高考)执行下面的程序框图,如果输入a=4,那么输出的n的值为().A.2 B.3 C.4 D.5
7.若下面的程序框图输出的S是126,则①应为().
A.n≤5 B.n≤6 C.n≤7 D.n≤8
二、填空题
8.某程序框图如图所示,则该程序运行后输出的k的值是________.
9. (2012上海十三校联考)根据右面的程序框图,要使得输出的结果在区间[-1,0]上,则输入的x的取值范围是__________.
10.(2012陕西高考改编)下图是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入__________.
三、解答题
11. 已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(x n,y n),…若程序运行中输出的一个数组是(x,-8),求x的值.
12. 程序框图如图,运行此程序,试求输出的b的值.
参考答案
一、选择题
1.B 解析:∵x 1=6,x 2=9, ∴x 1+x 22=6+92=7.5≠8.5, ∴输出的p =x 2+x 32=9+x 32
=8.5, ∴x 3=8.
2.D 解析:据程序框图可得当k =9时,S =11;k =8时,S =11+9=20.
∴应填入“k >8”.
3.C 解析:初始:k =0,S =1,第一次循环:由0<3,得S =1×20=1,k =1; 第二次循环:由1<3得,
S =1×21=2,k =2;
第三次循环:由2<3得,
S =2×22=8,k =3.
经判断此时要跳出循环.因此输出的S 值为8.
4.A
5.D 解析:这里要求的S 是x 1,x 2,…,x 10的乘积,S 从1开始每循环一次就乘以一个xn ,直到符合S =x 1x 2·…·x n 为止,然后跳出循环,输出S .
6.B 解析:由程序框图知,当n =0时,P =1,Q =3;当n =1时,P =5,Q =7;当n =2时,P =21,Q =15,此时n 增加1变为3,满足P >Q ,循环结束,输出n =3.
7.B 解析:程序是计算21+22+…+2n =126,解得n =6,所以判断框内应填“n ≤6”.
二、填空题
8.5 解析:第1次循环:k =3,a =43,b =34;第2次循环:k =4,a =44,b =44; 第3次循环:k =5,a =45,b =54.
此时,满足条件a >b ,循环终止,因此,输出的k 的值是5.
9.⎣⎡⎦⎤2,52 解析:由程序框图可得输出值y =⎩
⎪⎨⎪⎧ x 2, x <0,4-2x ,x ≥0, 若y ∈[-1,0],则
⎩⎪⎨⎪⎧ -1≤x 2≤0,x <0,或⎩⎪⎨⎪⎧
-1≤4-2x ≤0,x ≥0, 解得2≤x ≤52
. 10.q =M M +N 解析:由框图可知M 表示及格人数,N 表示不及格人数,所以q =M M +N
. 三、解答题
11.解:开始n =1,x 1=1,y 1=0→n =3,x 2=3,y 2=-2→n =5,x 3=9,y 3=-4→n =7,x 4=27,y 4=-6→n =9,x 5=81,y 5=-8,则x =81.
12.解:运行程序各次结果分别为i =10,a =1012,b =a =1012;i =9,a =947
,b =a =947;…;i =5,b =a =613;i =4,a =6<613
,b =a =6;i =3,a =7>6,此时程序结束,故输出b 的值为6.。
