复变函数第一章(2)复数的乘幂与方根
合集下载
西安交大西工大 考研备考期末复习 工程数学复变函数 复数与复变函数

z r cos i sin
z rei
三角表达式 指数表达式
说明: z r cos i sin
rei
复变函数
例1.将下列复数写为三角表达式与指数表达式
1)z 12 2i
2)z sin i cos
5
5
3)z 1 cos i sin
0
例2.求证 z1 z2 z1 z2
z2
x22 y22
复变函数
2.复数的运算法则
z1 z2 z2 z1, z1z2 z2 z1
(交换律)
z1 z1
(z2 z3) (z1 (z2 z3 ) (z1z2 )z3
z2
)
z3
(结合律)
z1(z2 z3 ) (z1z2 z1z3 ) (分配律)
复变函数
3.共轭复数
2k
n
其中 k 0,1, , n 1
例2.求 1) 1 i 6
2) 6 1
复变函数
本次课小结 本次课的内容要点
1.复数的概念 2.复数的代数运算 3.复数的几何表示 4.复数的乘幂与方根
作业:习题一 4(4)、8(1,3,6)、11 14(3、4)、16、21(4、6)
复变函数
说明:1) z 0 若z=0,则辐角不定
2) tan y ,即tan Argz y
x
x
3) 多值性 Argz 2k
4) 把满足 的辐角称为辐角主值
记为 arg z
arg z arctan y x
复变函数
arg z arctan y
x
arg z arctan y
x
arg z arctan y x
复变函数
复变函数的理论基础是在十九世纪奠定的,主 要是围绕柯西 、魏尔斯特拉斯和黎曼三人的工作进 行的。
z rei
三角表达式 指数表达式
说明: z r cos i sin
rei
复变函数
例1.将下列复数写为三角表达式与指数表达式
1)z 12 2i
2)z sin i cos
5
5
3)z 1 cos i sin
0
例2.求证 z1 z2 z1 z2
z2
x22 y22
复变函数
2.复数的运算法则
z1 z2 z2 z1, z1z2 z2 z1
(交换律)
z1 z1
(z2 z3) (z1 (z2 z3 ) (z1z2 )z3
z2
)
z3
(结合律)
z1(z2 z3 ) (z1z2 z1z3 ) (分配律)
复变函数
3.共轭复数
2k
n
其中 k 0,1, , n 1
例2.求 1) 1 i 6
2) 6 1
复变函数
本次课小结 本次课的内容要点
1.复数的概念 2.复数的代数运算 3.复数的几何表示 4.复数的乘幂与方根
作业:习题一 4(4)、8(1,3,6)、11 14(3、4)、16、21(4、6)
复变函数
说明:1) z 0 若z=0,则辐角不定
2) tan y ,即tan Argz y
x
x
3) 多值性 Argz 2k
4) 把满足 的辐角称为辐角主值
记为 arg z
arg z arctan y x
复变函数
arg z arctan y
x
arg z arctan y
x
arg z arctan y x
复变函数
复变函数的理论基础是在十九世纪奠定的,主 要是围绕柯西 、魏尔斯特拉斯和黎曼三人的工作进 行的。
复变函数第一章

z1 z1 z2 z2
Arg(
z1 z2
)
Arg
z1
Arg
z2
1、 幂函数
非零复数 z 的 n 次幂
zn rnein rn (cos n i sin n )
其中
zn z n , Arg zn nArg z.
令 r = 1,则得棣莫弗公式
(cos i sin )n cos n i sin n
21
•连续曲线 若实函数 x(t) 和 y(t) 在闭区间[, ]
上连续,则方程组
x x(t),
y
y(t),
( t )
或复数方程 z z(t) x(t) iy(t) ( t )
代表一条平面曲线,称为 z 平面上的连续曲线.
进一步地,若在 t 上,x '(t) 及 y '(t) 存在、
E(C)
线 C 把 z 平面唯一地分成
C、I(C) 及 E(C) 三个点集,
I(C)
它们具有如下性质:
(1)彼此不交;
O
C
x
(2)I(C) 是一个有界区域(称为 C 的内部);
(3)E(C) 是一个无界区域(称为 C 的外部).
25
•单连通区域 设 z 平面上的区域 D, 若在 D 内 无论怎样画简单闭曲线,其内部仍全含于 D, 则称 D 为单连通区域. 非单连通的区域称为多 连通区域.
y
z
v
w
2 O 2 x
4 O 4 u
31
•反函数 假设函数 w=f(z) 的定义域是 z 平面上的 集合 G,值域是 w 平面上的集合 G*. 对 G* 中 的每一个点 w,在 G 中有一个(或至少两个) 点与之相对应,则在 G* 上确定了一个单值(或
(最新整理)复变函数

i z i ( x iy )
y ix
Reiz()3
zrcosirsin
=|z|[cos(Argz)isin(Argz)]
可化为复数的代数表示式.
2021/7/26
29
5 曲线和平面图形的复数方程 引进复数的几何表示,可将平面图形用复数方程 (或不等式)表示;反之,也可由给定的复数方程 (或不等式)来确定它所表示的平面图形。
例1 用复数方程表示: y
4.哈尔滨工业大学建筑工程学院博士导师刘殿魁简介 _..
长期从事弹性波散射与动应力集中问题的研究,并首创分 析弹性波散射与动应力集中的复变函数与保角映射方法, 是经典弹性...《美国应用力学》杂志创刊50周年出版的 特刊中曾著文《固体中的弹性波》,评论:“刘殿魁等人首 创了用于处理特殊类型散射..
2021/7/26
o
x
3. 三角表示法
4. 指数表示法
由xy
r cos 得 r si n
再由 Eule公r 式:
ei cos isin得
zr(co is sin )
z rei
2021/7/26
28
注意: 复数的各种表示法可以相互转化,以适应 不同问题的需要.
(1)已知复数的代数表示式,先求出复数的模和 辐角,即可化为复数的三角表示. (2)已知复数的三角表示式 ,利用
(最新整理)复变函数
2021/7/26
1
课程简介
课程名称 复 变 函 数
Complex Variables
教材 总学时 教师姓名
复变函数 36学时
李雪艳
2021/7/26
2
对 象 复变函数(自变量为复数的函数)
主要任务 研究复变数之间的相互依赖关系,
复变函数第一章(2)复数的乘幂与方根

设w f (z)是定义在D上的复变函数
z x iy, w u iv
则u, v的取值由x, y来确定
u u(x, y) v v(x, y)
w f (z) u(x, y) iv(x, y)
复变函数w
f
(
z)一一对应二元实变函数对uv
注: (1)此公式对于任意整数n都成立。
(2)特别地,当r 1时, (ei )n ein
cos i sin n cos n i sin n 棣莫弗公式.
例1:将cos 3利用cos ,sin表示
解: cos3 Re[cos3 i sin 3 ]
不是区域(不连通)
r2 z0 r1
区域
z2
如果一个区域可以被包含在一个以原点为中心的圆里面, 即存在正数 M,使区域 D的每个点z都满足 |z|<M, 则称 D为 有界的, 否则称为无界的.
|z|>M M
0
1.3.2 曲线
1.简单曲线,简单闭曲线
在数学上, 经常用参数方程来表示各种平面曲线. 如果 x(t)和y(t)是两个连续的实变函数, 则方程组
u(x, v(x,
y) y)
例6 考察函数w z2 令 z x iy, w u iv 则
u iv (x iy)2 x2 y2 i2xy
函数w f (z)所对应的二元实变函数对
u x2 y2, v 2xy
例7 两类常见的复变函数
n次多项式函数 P(z) a0 a1z a2 z 2 an z n
如果在z 平面上函数w f (z)的定义域D内取一点z0 ,
通过w f (z)在w平面上有相应的点w0对应。
复变函数第1章

于是
z1z2 r1 r2 z1 z2 ,
Arg(z1z2 ) Argz1 Argz2. 两个复数乘积的模等于它们的模的乘积; 两 个复数乘积的辐角等于它们的辐角的和.
应该注意的是 Arg(z1z2 ) Argz1 Argz2 中的 加法是集合的加法运算:即将两个集合中所有的
元素相加构成的集合
(3 4) (4 3)i 7 1 i.
2
22
z1 7 1 i. z2 2 2
例 1.2 i1 i, i2 1, i3 i i2 i, i4 i 2 i 2 1, ……
i 4n 1, i4n1 i, i4n2 1, i4n3 i, i4n4 1.
例1.3 设z1, z2是两个复数, 证明
z1 z1 , z2 z2
Arg
z1 z2
Argz1
Argz2
.
两个复数商的模等于它们模的商差.
对给定的复数z, 方程wn=z的解w称为z的n次
方根, 记做
n
z
或
1
zn.
如果
z r(cosq i sinq ), w (cos i sin ),
y .
x
利用直角坐标与极坐标之间的关系
x r cosq , y r sinq ,
复数z=x+yi 可表示为 z r(cosq i sinq ), 称为复
数z的三角表示式. 再利用Euler公式
eiq cosq i sinq ,
复数z=x+yi 又可表示为 z reiq , 称为复数的
指数表示式, 其中r=|z|, q=Argz.
z1 z2 z1z2 2 Re z1 z2 .
证明 因为
z1 z2 z1 z2 z1z2 , 所以由运算规律7,有
复变函数1-3
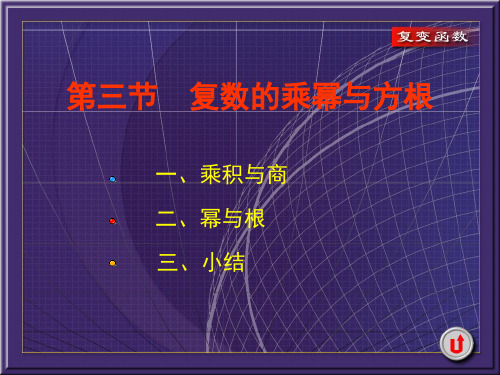
i,
z1 z2
cos
3
6
i
sin
3
6
3 1i. 22
7
二、幂与根
1. n次幂: n 个相同复数 z 的乘积称为z 的 n 次幂,
记作 zn , zn z z z .
n个
对于任何正整数n, 有 zn rn(cosn i sin n ).
如果我们定义
zn
1 zn
,
那么当
幂为负整数时,
求出z的幂.
8
2.棣莫佛公式
当 z 的模 r 1,即 z cos i sin ,
(cos i sin )n cosn i sin n .
棣莫佛公式
3. 方程 wn z 的根 w, 其中 z 为已知复数.
w
n
z
r
1 n
cos
2kπ n
i sin
2kπ n
(k 0,1,2, ,n 1)
w2
o
w0 x
w3
15
三、小结
应熟练掌握复数乘积与商,幂与根的运算. 在各种形式中以三角形式、指数形式最为方便:
z1
z2
r1
r ei(12 ) 2
z2 r e2 i(2 1 )
z1 r1
对于任何正整数n, 有 zn rn(cosn i sin n ).
w
n
z
r
1 n
cos
2kπ
i sin
2kπ
n
n
(k 0,1,2, ,n 1)
放映结束,按Esc退出.
16
i sin(1 2 n )]
r1 r2 rnei(12 n ) .
5
定理二 两个复数的商的模等于它们的模的商; 两 个复数的商的辐角等于被除数与除数的辐角之差.
1.2复数的运算及其几何意义

x1 ) y1 )
参数 t (, ),
上式可以借助复数合并为一个式子,即:
z x(t ) iy(t ) x1 t( x2 x1 ) + i [y1 t( y2 y1 )]. 过z1 , z2的直线方程是: z z(t ) z1 ), 0 t 1.
则将向量OZ1按逆时针方向
•z
y
旋转一个角 2 ,
r • z1
再伸长(缩短)到原来的 r2 倍,
所得向量OZ就表示乘积z1 z2.
1
o
r1
2
•
r2
z2
x
z1z2 r1r2[cos(1 2 ) i sin(1 2 )]
10
可将结论推广到 n 个复数相乘的情况:
设 zk rk (cosk i sink ) rkeik , (k 1,2,, n)
28
cos
π 4
2kπ 4
i sin
π 4
2kπ 4
w3
(k 0,1,2,3).
即 0
1
28
cos
π 16
i
sin
π 16
,
1
1
28
cos
9π 16
i
sin
9π 16
,
2
1
28
cos
17π 16
i
sin
17π 16
,
3
1
28
cos
25π 16
i sin
25π 16
.
15
;
(2) z z;
(3) z z z 2 ;
(4) z z 2 Re(z), z z 2i Im(z).
复数和、差、共轭的几何意义
《复变函数》第1章

实部:x = Re(z) 虚部:y = Im(z)
纯虚数:z = iy ( y ≠ 0 )
2020/7/21
《复变函数》(第四版)
第2页
共轭复数: x iy x iy
z=0 x=y=0
z1= x1 + iy1 , z2= x2 + iy2 , z1 = z2 x1 = x2 , y1 = y2
连接平面上任一点与球面北极的直线段与球面有一个交点, 又在平面上引入一个假想点∞与球面北极对应, 构成扩充复平面 与球面点的一一对应, 即复数与球面上的点的一一对应, 球面称 为复球面.
2020/7/21
《复变函数》(第四版)
第16页
规定: | ∞| = +∞
α≠∞, α + ∞ = ∞ + α = ∞
解: 1) 几何上看 | z + i | = | z -(-i ) | = 2 : 与点-i
的距离为2的点轨迹, 即中心为(-i ),半径为2的圆.
代数推导: 设 z = x + iy
则 | x + (y + 1)i | = 2
(见书P10 图1.5)
x2 + (y + 1)2 = 4
解: 2) | z - 2i | = | z +2 | —— 到点 2i 和-2 距离
复变函数
(第四版)
电子教案
中山大学公共卫生学院 刘素芳 邓卓燊 编写
第一章 复数与复变函数
复变函数——自变量为复数的函数. 复变函数研究的中心对象: 解析函数. 复变函数论又称为解析函数论.
§1 复数及其代数运算
1.复数的概念
i — 虚数单位
i 2 =-1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
w0
) )
w2
x
2 (cos
w3
四个根是内接于中心在原点,半 径为21/8的圆的正方形的四个 顶点.
1.3 平面点集
1.3.1 区域
平面上以 z0为中心, d (任意的正数)为半径的圆: |zz0|<d 内部的点的集合称为z0的邻域, 而称由不等式 0<|zz0|<d 所确定的点集为z0的去心邻域. 设G为一平面点集, z0为G中任意一点. 如果存在z0的一 个邻域, 该邻域内的所有点都属于G, 则称z0为G的内点. 如果G内的每个点都是它的内点, 则称G为开集 平面点集D称为一个区域, 如果它满足下列两个条件: 1) D是一个开集; 2) D是连通的。就是说D中任何两点都可以用完全属于D 的一条折线连接起来.
n
sin n r sin
r , cos n cos , sin n sin
n 2 k , k 0 , 1, 2 ,
n
2 k
n
n
, k 0 , 1,
w
k 0
z
r (cos
r (cos
n
n
r (cos
r (cos
2 ( n 1 )
2n
n
n
i sin
n 2 ( n 1 )
i sin
2 n
) wn 2
i sin
n 2n
n
)
)
w0
z r (cos
n
n
2k
n
n
i sin
2k
n
), k o,1, , n 1
3 i)
Arg (
i
6
6
2 k
i 6 6
6
3 i 2e
(
3 i) 2 6 e
(1 i ) (
5 6
3 i)
(
2) e 2 e
6 i 6 6
5
i
5 4
(
2) 2
6
5
i(
5 4
6 6
)
e
8
1 2
i
4
e
1.2.3 复数的方根(乘幂的逆运算)
设C: z=z(t) (atb)为一条连续曲线, z(a)与z(b)分别为C 的起点与终点. 对于满足 a<t1<b, at2b 的 t1与 t2, 当 t1t2 而有 z(t1)=z(t2) 时, 点 z(t1)称为曲线 C的重点. 没有重点的 连续曲线 C, 称为简单曲线或若尔当(Jardan)曲线. 如果简 单曲线 C的起点与终点闭合, 即 z(a)=z(b) , 则曲线 C 称为 简单闭曲线. z (b )
sin sin
3
)
cos 3 cos 3 cos sin
(1 i ) (
例 2 : 计算
3 i)
2
4
解:
1 i
1 i
3 i 2
Arg ( 1 i )
i
4
2 k
5
i 5 4
2e
(1 i ) ( 2 ) 5 e
例4:
圆环: r1 z z 0 r2
r2
z0
r1
z0
r
区域 不是区域( 不是开集)
S { z | z 1 } { z | z 2 1 }
不是区域(不连通)
如果一个区域可以被包含在一个以原点为中心的圆里面, 即存在正数 M,使区域 D的每个点z都满足 |z|<M, 则称 D为 有界的, 否则称为无界的.
解:
cos 3 Re[cos
3 i sin 3 ]
3
cos 3 i sin 3 (cos i sin )
2
3 k0
c 3 (cos ) ( i sin )
2
k
k
3 k
cos
3
3 cos sin
3
5 6
2
i ( 3 cos
称满足方程
1
w
n
z ( w 0 , n 2 ) 的复数 w 为 z 的 n 次方根,
记作
n
z 或 z n。
设 z r cos i sin , w cos i sin
则
n
w
n
(cos n i sin n )
n
n
cos n r cos ,
注:
n
(1 )复数 z 的 n 次方根共有
n 个。
,
( 2 ) 几何意义:
z 的 n 个值就在以原点为圆心 n 边形的 n 个顶点。
r 为半径的圆内接正
4
例 3: 计算
1 i
1 i 2 (cos
解: 因为 所以
4
4
i sin
4
)
1 i
8
2 (cos 4
2 k 4 i sin
|z|>M M
0
1.3.2 曲线
1.简单曲线,简单闭曲线
在数学上, 经常用参数方程来表示各种平面曲线. 如果 x(t)和y(t)是两个连续的实变函数, 则方程组 x=x(t), y=y(t), (atb) 代表一条平面曲线, 称为连续曲线. 如果令 z(t)=x(t)+iy(t) 则此曲线可用一个方程 z=z(t) (atb) 来代表. 这就是平面曲线的复数表示式.
4
2 k 4 )
( k 0,1,2,3)
即
w0 w1 w2 w3
8 8 8
2 (cos 2 (cos 2 (cos
16 9 16 17 16 25 16
i sin i sin i sin i sin
w1
) )
y
1 i
8
16 9
8
16 17 16 25 16
2 k
n
n
i sin
i sin
n )
2 k
n
)
2 n 2 n
w0
n
k 1,
w1
n
r (cos
2
n
i sin
2
n
w1 (cos
i sin
) w0
)
wn 1 (cos
2
k n 1, w n 1
k n, wn
z (b ) z (a ) z (a )
z ( a ) z (b )
简单,闭
简单,不闭
非简单,不闭
z ( a ) z (b )
非简单,闭
2.光滑曲线,逐段光滑曲线
设曲线 C 的方程为
z ( t ) x ( t ) iy ( t ), ( a t b )
若在区间 [ a,b ] 上, x ' ( t ), y ' ( t ) 连续且不全为零,则称 曲线 C 为光滑曲线。
