浙大 高等土力学讲义3
浙江大学土力学精品课程

不同);
W——滑动土体重,kN/m;
d——滑动土体重心至圆心的水平距离,m。
对饱和粘土坡,在不排水条件下, u 0, f cu和 无关,则式(9.7.1)改写为
Fs
cu Lr Wd
(10.3.2)
上式用于分析饱和粘土坡形成过程和刚竣工时的稳定分析,称为 u 0 法。
10.3 粘性土坡的稳定分析
第10章 土坡稳定分析
10.1 概述 10.2 无粘性土坡的稳定分析 10.3 粘性土坡的稳定分析 10.5 孔隙水压力的估算和抗剪强度指标
的选用 10.6 滑坡的防治和土坡稳定的安全系数
10.1 概述
土坡:具有倾斜坡面的土体形成。 天然土坡:山坡、江河湖海的岸坡等由地质作用形成的土坡。 人工土坡:挖方和填方土坡的统称。 挖方土坡:开挖基坑、路堑和渠道形成的土坡。 填方土坡:填筑堤、坝形成的土坡。 简单土坡:坡底和坡顶水平,并延 伸至无限远的土坡。简单土坡的外 形和各部分名称如图10-l所示。
应取无粘性土覆盖层与其下材料的界面摩擦系数。
图10-4b 有渗流时的土坡稳定分析
10.3 粘性土坡的稳定分析
10.3.1 瑞典圆弧法 瑞典的彼得森(K.E.Petterson, 1915)提出的,故称为瑞典圆弧法。 假定:均质粘性土坡,滑动面为圆弧形(简称滑弧)。 分析模型见图10-5(a),设滑弧圆心在O点,半径为r,对应的圆心角
坡比1:n 1:0.5
1 和 2
(。)
63.43
表10-1
1 (。) 29.5
(。)
2
40
1:0.75 53.13
29
39
1:1.0 45
28
37
1:1.5 33.68
高等土力学课件 03土的强度 3.1 概述

塑性区
图3-2 土中的塑性区
部分土体达到强度(屈服), 地基并不一定破坏。
厚壁筒内压破坏(内压为
面力pi>p0 )
内壁点a与外壁点b必须同时达
到强度线,试样才会破坏-部分
土体达到强度(屈服),并不
一定整体破坏。
弹-完全塑性模型 弹塑性模型计
计算的应力路径
算的应力路径
图3-3 厚壁筒内压扩张的受力与应力路径
强度strength
材料的强度是指材料单元破坏时的 (应力)状态。
f ( ij , kn ) 0
3.1.1 研究历史
c tan f
1.1776年,库仑(Coulomb)公式;
2.1900年,莫尔(Mohr);
3.土的抗剪强度f是作用在其破坏面
上的正应力n的单值函数;
f ( )
f
n
4.现代的强度理论:破坏是应力应变关系的最后 状态:包括在本构关-1 土的几种基本本构关系模型 与应力应变关系曲线
2.土的强度和土体破坏
1) 孤立的土单元,应力状态达到强度=破坏。 2) 土达到屈服不一定达到破坏—对应于什么模型; 3)在土体中,局部土达到强度,不一定引起土体的破坏 3) 渐进破坏:软化-应力转移-过程的持续进行导致土
体最后破坏 4) 崩塌、断裂-以拉伸与倾倒为主的破坏现象。
4.三相组成,固体颗粒之间的液体、气体及液、固、气 间的界面对于土的强度有很大影响:孔隙水压力、吸 力(毛细力)。
5.地质历史造成土强度强烈的多变性、结构性和各向异 性。
6.土强度的这些特点体现在它受内部和外部、微观和宏 观众多因素的影响,成为一个十分复杂的课题。
1. 屈服与强度:
刚塑性
弹-完全 塑性
高等土力学谢定义

高等土力学高等土力学是土木工程领域的一个重要分支,主要研究土壤的力学性质及其在土木工程中的应用。
土力学研究的对象是土壤的物理力学性质和土体在外力作用下的变形和破坏规律,帮助工程师能够正确地选择土壤基础和岩土工程结构设计,确保工程的安全性和可靠性。
土力学基本概念土壤是由固体颗粒、水和空气构成的多相体系,力学性质和结构会随着固体颗粒的类型、粒径和颗粒之间的相互作用、含水量等因素而变化。
土力学研究的基本概念包括以下几个方面:1. 土体力学性质土体的力学性质是指土壤在外力作用下的变形和破坏规律。
它包括土体的弹性性质、塑性性质、强度性质以及变形性质等。
土体在受到外力作用时,会发生弹性、塑性、粘塑性和黏塑性等不同类型的变形,并且会有一定的变形极限和破坏极限。
2. 土体结构土体的结构是指土壤颗粒之间的空隙状态和排列规律。
土壤颗粒之间的接触状态和排列规律会影响土体的力学性质和水力性质。
土体的结构包括颗粒间接触状况、颗粒间的连通性以及孔隙分布和孔隙比等参数。
不同的土体结构对于土体的刚度、渗透性和稳定性会产生重要影响。
3. 土体水力性质土体的水力性质是指土壤中水分的分布和运动规律。
水分含量对土壤的力学性质和稳定状态有重要影响。
土体中的水分可以分为吸附水、毛细水和重力水等不同形式。
高等土力学的应用高等土力学的研究结果将直接应用于土木工程中,确保工程的安全性和可靠性。
以下是高等土力学在工程实践中的一些应用:1. 土壤基础设计土壤基础是土木工程中的重要组成部分,包括建筑物、桥梁、道路等的基础和地基。
通过对土壤岩石的力学性质、结构和水力性质的研究,高等土力学可以对土壤基础进行设计和优化,确保基础的稳定性和承载能力。
2. 土壤侧向力设计土体在侧向力作用下会发生变形和破坏,特别是在边坡、挡墙和隧道施工等工程中。
高等土力学可以通过研究土体的强度性质和侧向变形规律,提供给工程师合理设计和施工,确保工程的稳定性和安全性。
3. 地基处理和加固在某些情况下,土壤的承载力和稳定性不足以满足工程的要求。
高等土力学第一章 课件

高等土力学第一章课件
汇报人:
目录
CONTENTS
01 添加目录标题 03 土的应力与应变
02 土力学基本概念 04 土的强度与稳定性
05 土压力与挡土墙设 计
06 地基承载力与沉降 计算
07 特殊土工程性质与 处理方法
添加章节标题
土力学基本概念
土的气组成的自然体
黄土的工程分类:根据黄土的工程性质,可 以将黄土分为不同的类型,不同类型的黄土 在工程中的处理方法也有所不同。
黄土的处理方法:包括排水固结法、强夯 法、换填法等,这些方法可以有效地改善 黄土的工程性质,提高工程的稳定性和安 全性。
膨胀土工程性质与处理方法
膨胀土的定义与分类
膨胀土的工程性质
膨胀土的膨胀机理
土的应变:土体变形的大小 和方向
土的应力-应变关系曲线:描述 土的应力与应变之间关系的曲 线
土的应力:土体受到的力,包 括压应力、剪应力和弯应力等
土的应力-应变关系特点:非 线性和弹塑性等
土的强度与稳定性
土的强度
土的强度定义:土体抵抗剪切破坏的极限能力 土的强度分类:天然强度、残余强度、有效强度等 影响土强度的因素:土的成分、结构、应力历史、环境条件等 土的强度试验方法:直接剪切试验、三轴压缩试验、无侧限抗压试验等
稳定的能力。
地基承载力的影响 因素:包括土的物 理性质、力学性质、 地质条件、地下水 位、荷载大小和分
布等。
添加标题
添加标题
地基承载力与沉降 计算的关系:地基 承载力是影响建筑 物沉降的重要因素 之一,通过合理的 地基设计和沉降计 算,可以确保建筑 物的稳定性和安全
性。
添加标题
地基承载力与建筑 物安全性的关系: 地基承载力不足可 能导致建筑物沉降、 倾斜甚至倒塌,因 此在进行建筑设计 时,必须充分考虑 地基承载力的要求。
土的基本性质高等土力学课件
Bazant ZP, Oh BH. Microplane model for creep of anisotropic clay. J Eng Mech, ASCE, 1983.
59
蠕变微观机理
9次2×21点在二十面上的非正交对称分布
60
蠕变微观机理
9次2×21点在球面上的正交对称分布
61
蠕变微观机理
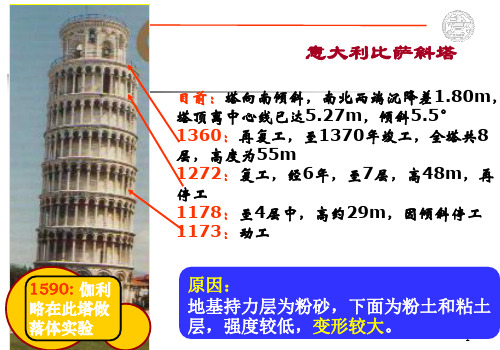
原因: 地基持力层为粉砂,下面为粉土和粘土 层,强度较低,变形较大。
1
2
3
4
1995年阪神地震大阪的街道路面液化
5
1999年台湾大地震中台中县由于液化引 起的楼房倒塌
6
赵洲桥
隋朝石工李春所建,他把石台砌筑于密 实的粗砂 层上,一千三百多年来估计沉 降仅几厘米。
7
提纲
土的构成 土的物理化学性质 土的基本力学性质 土的分类
11次2×33点在多面上的正交对称分布
62
变形
本构模型 固结理论
63
土的分类
64
塑性指数分类指标界限值及土类名称
0 13
7
国家建委TJ7-74规范 砂土
轻亚粘土
水利部土工实验6规范 砂土 砂壤土
10
17
亚粘土 粘土
壤土
粘土
交通部79规范 冶金部冶基规103-77
地质矿产部84规范
砂土 砂土 砂土
ij
f
.
(n)ds
.
ij ij
3
2
bijkm
s
1
.
k2 T
sh1
.
T
k1
f
(n)ds
. km
.
ij
57
蠕变微观机理
高等土力学 pdf

高等土力学
高等土力学是一门深入研究和探讨土力学相关理论的学科,主要包括以下几个方面的内容:
1.土的基本性质:包括土的组成、土的分类和土的物理性质等。
这一部分内容主要涉及土的颗粒级配、孔隙性、含水性、密度、温度和湿度等特性,以及这些性质对土的力学行为的影响。
2.土的力学性质:主要研究土在力作用下的应力-应变关系、强度和稳定性等。
包括土的应力-应变理论、土的强度理论、土的稳定性分析等。
3.土与结构物的相互作用:主要研究土与建筑物、道路和管道等结构物的相互作用,包括土压力、地基承载力和沉降等。
这一部分内容主要关注如何保证结构物的安全和正常使用,同时减少对周围土体的影响。
4.土的渗流:主要研究土中水流的运动规律和影响因素,包括渗透规律、渗透系数、渗透力等。
这一部分内容主要关注如何控制和利用土中的水流,例如在水利工程中的水库建设和运营中。
5.土的动力性质:主要研究土在动力荷载下的力学行为,包括地震、车辆荷载等对土的影响。
这一部分内容主要关注如何评估和预测土在动力荷载下的响应和稳定性。
6.土工试验与数值模拟:主要研究土工试验的原理和方法,以及数值模拟技术在土力学中的应用。
这一部分内容主要涉及对土的性质和行为的实验测定,以及对复杂工程问题的数值模拟和分析。
以上是高等土力学的主要内容,通过学习高等土力学,可以深入了解土的力学行为和工程应用,为解决实际工程问题提供理论依据和技术支持。
高等土力学固结理论课件

目录
• 固结理论概述 • 土的固结特性 • 固结理论的基本方程 • 固结理论的实践应用 • 固结理论的最新研究进展 • 案例分析
01
固结理论概述
固结理论的定义
固结理论是研究土体在压力作用下固 结过程的学科,主要关注土体中孔隙 水压力的变化和消散过程。
固结理论是高等土力学的重要分支, 对于理解土体的力学行为和设计土工 建筑物具有重要意义。
环境工程
土壤改良、土地复垦、污 染土壤修复等领域的土体 固结问题。
02
土的固结特性
土的压缩性
土的压缩性是指土在压力作用下 体积减小的性质。
土的压缩性主要与土的孔隙比、 孔隙分布、孔隙大小等因素有关
。
土的压缩性是土体变形和固结过 程中的重要特性之一,对土体的
稳定性和变形有重要影响。
土的渗透性
土的渗透性是指水在土中流动 的能力,通常用渗透系数来表
示。
渗透系数的大小取决于土的 颗粒大小、形状、排列、孔
隙比等因素。
渗透性是土体中水分和气体流 动的基础,对土体的排水固结 、渗透稳定性等有重要影响。
土的固结过程
土的固结过程是指土体在压力作用下逐渐固 结和稳定的过程。
土的固结过程包括孔隙水排出、孔隙比减小 、土体密度增加等。
固结过程对土体的强度、变形和稳定性有重 要影响,是工程实践中需要考虑的重要因素 之一。
详细描述
在某高速公路建设中,由于地基 土层分布不均,导致高速公路在 通车后出现不均匀沉降,影响了
道路的正常使用。
解决方案
采用高等土力学固结理论对地基 进行加固处理,通过排水、固结 等措施,减小地基沉降,提高地
基稳定性。
工程实例二:某水库大坝的稳定性分析
土力学与基础工程第三章PPT课件

z
P z2
3
1
2[1(r/z)2]5/2
特点
1.应力呈轴对称分布
y
0.5 0.4 0.3
K
0.2 0.1
0
P
o αr
y
x
x
M’
R βz
M
z
0.5 1.0 1.5 2.0 2.5 3.0
r/z
39
z
P z2
23[1(r/1z)2]5/2
2.P作用线上,r=0, a=3/(2π),z=0, σz→∞,z→∞,σz=0
u whw
55
3.4 有效应力原理
有效应力:通过粒间接触面传递的应力称为有 效应力,只有有效应力才能使得土体产生压缩 (或固结)和强度。 把研究平面内所有粒间接触面上接触力的法向 分力之和除以所研究平面的总面积所得的平均 应力来定义有效应力
Ns
A
56
3.4 有效应力原理
57
太沙基有效应力原理
竖直偏心
倾斜偏心
矩 形
基 础 形 状条
形
P L
B
P’ B
P
x y
o
L
B
P’ B
P L
B
P’ B
29
矩形面积中心荷载
P
B
x
L
y
pP A
30
pm mianx P AW MP A16Be
P
P
矩形面积单向偏心荷载
P
B
B
B
e x
e Lx
Ke
Lx
L
y
y
3K y pmin0
p max
pmin0 p max
pmin0 p max
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 土的固结理论3.1概述土的固结-—在荷载作用下,土体中超孔隙水压力生成,在排水条件下,随着时间的流逝,土体中水被排出,超孔隙水压逐步消散,有效应力逐步增大,直至孔隙水压力为零,这一过程称为土的固结。
⎩⎨⎧--提高地基承载力提高强度减少工后沉降产生沉降作用固结Terzaghi (1924)建立了一维固结理论Rendulic (1935)首先将Terzaghi 一维固结理论方程推广到多维情况,得到Terzaghi- Rendulic 扩散方程。
Biot (1940)从连续介质力学基本方程出发得到固结理论,他考虑了孔隙水压力消散与土骨架变形之间的耦合作用。
Barron (1944)给出了砂井地基固结自由应变和等应变条件的解答。
一维固结理论 Terzaghi (1924) 饱和土弹性、小变形 服从Darcy 定律 二维固结理论 Rendulic (1935)三维固结理论 Rendulic (1935)、Biot(1940)砂土地基固结理论 Barron (1944) 自由应变、等应变3.2一维固结理论(单向固结)3.2.1 Terzaghi 一维固结理论1.基本假定(1)土体是饱和土 (2)土体是均质的(3)土颗粒和水是不可压缩的 (4)水的渗流服从Darcy 定律 (5)渗透系数k 是不变的(6)土体压缩系数v a 是不变的 (7)荷载是一次性瞬间施加的 (8)土体固结变形是小变形(9)渗流和变形只发生在一个方向2. 有效应力原理u +='σσ3.固结方程的建立根据上述假设,固结过程中(1)单元体在dt 时间内排水量为dzdxdydt zvdQ ∂∂=a.根据Darcy 定律有w zukki v γ∂∂==式中v —水在土中的渗流速度,m/s i -水力梯度k —渗透系数,m/s u —超孔隙水压力,kPaw γ—水的重度,kN/m 3将v 代入dQ ,得dzdxdydt z u k dQ w 22∂∂=γ(2)单元体在dt 时间内土体压缩量dV 表达式为dxdydzdt e e t dV )1(0+∂∂=式中e —t 时刻土体的孔隙比 0e —土体初始孔隙比b. 孔隙比随有效应力的变化,遵循下面的关系v a e-=∂∂'σc. 根据有效应力原理有u -∂=∂'σ式中v a —竖向压缩系数,1-kPa 'σ—土中有效应力,kPa将de 代入dV ,得 (注意 u -=σσ')dxdydzdt tue a dV v ∂∂+=01d. 根据排水量=压缩量,即dV dQ =,得dxdydzdt zuk dxdydzdt t u e a w v 2201∂∂=∂∂+γ tuz u a e k v w ∂∂=∂∂+⇒220)1(γ tu z u c v ∂∂=∂∂⇒22 热传导方程式中v C —固结系数,m 2/s 。
consolidationws v w v w v kEm k a e k c γγγ==+=)1(0其中v m —体积压缩系数。
1e a m vv +=根据边界条件(t>0,z=0,u=0;z=2H ,u=0)和初始条件(t=0,H z 20≤≤,u=P )可得:∑∞=-=12)ex p(sin 2),(m v T M H Mz Mp t z u式中⋅⋅⋅=-=,2,1,212m m M π v T —时间因子t Hc T vv 2=4. 固结度固结度——在某一荷载作用下经过时间t 土体固结过程完成的程度。
土层中某点的固结度σσσσσu u U -=-==1'土层平均固结度(也称地基固结度)压缩度cctS S U =式中ct S -在某一荷载作用下,经过时间t 所产生的固结变形量ct S , c S -在某一荷载作用下,固结完成时最终沉降量。
或⎰⎰-=H Hdzz dz t z u U 00)(),(1σ 从),(t z u 的表达式中可以看出,只有当∞→t 时,0→u 。
但是,当0.3=v T 时,%99>U ;当0.1=v T 时,%93≈U 。
对工程而言,可以认为固结完成,此时kH m C H t v w v 22γ== 当%30>U 时,固结度的近似表达式)4ex p(8122v T U ππ--=或者采用曾国熙的统一公式)exp(1t U βα--=式中βα,计算参数。
当%60<U 时v T U 128.1≈当%60>U 时)933.00581.0(101+--=v T U5.变载固结度计算(1)线性变载将逐渐加荷的过程简化为在加荷起止时间中点一次瞬时加载,然后再用Terzaghi 固结理论进行计算。
当1t t <时,匀速加载;1t t >时,保持恒载pp p U U t t '2⋅= (10t t <<)21t t t UU -= (1t t ≥)式中t U —对荷载p 而言,t 时刻的固结度;'p —t 时刻(1t t <)的荷载;2t U —对瞬时荷载p 而言,加载时间为2t(1t t <)的固结度;21t t U-—对瞬时荷载p 而言,加载时间为21t t -的固结度。
(2)曲线变载高木俊介(1955)建议τττd q U p U tt t ⎰-=)(1& (1t t ≤) τττd q U pU t t t ⎰-=10)(1& (1t t >) 式中)(τ-t U —荷载增量ττd q &瞬时施加固结时间为(τ-t )的固结度。
变速加载过程(3) 求两级加荷各阶段固结度两级等速加载过程当10T t ≤<时,对p ∆而言的固结度()τατττβττττd e t d U q p d q U p U tt t t t t t ⎰⎰⎰-----=∆=∆=000]1[111&& =⎰tt 01-1)(t e -τρατd =⎥⎦⎤⎢⎣⎡--tt e t t 0)()1(1τβρα =⎥⎦⎤⎢⎣⎡---)(1t e t t ββαβα 对1p ∆而言⎥⎦⎤⎢⎣⎡--=-)1(11t t e t T U ββα 对∑∆p 而言[]⎭⎬⎫⎩⎨⎧---∑∆∆=)exp(1111t t T p p U t ββα当T t T 21≤<,对1p ∆的固结度[]ττβαd q t p U Tt 101})(exp 1{11&---∆=⎰[]{})(ex p )ex p(111T t t T U t ----+=βββα对∑∆p 的固结度⎭⎬⎫⎩⎨⎧-+∑∆∆=⎭⎬⎫⎩⎨⎧-+∑∆∆=------][][1)((11)((1111T t t T t t t e e T p q e e T p p U βββββαβα& 当32T t T ≤<时,对∑∆p 的固结度+⎭⎬⎫⎩⎨⎧-+∑∆=---][)(111T t t t e e T p q U βββα&⎭⎬⎫⎩⎨⎧---∑∆--)1()()(222T t e T t p q ββα& 当3T t >时,对∑∆p 的固结度+⎭⎬⎫⎩⎨⎧-+∑∆=---][)(111T t t t e e T p q U βββα&⎭⎬⎫⎩⎨⎧-+-∑∆----)()()()(23232T t T t e e T T p q βββα& 依此类推,n 级荷载时对∑∆p 的固结度⎭⎬⎫⎩⎨⎧---∑∆=---∑][)(111n n T T t n n n nt e e e T T p q U ββββα& 式中t U —t 时刻n 级等速加载修正后的地基平均固结度,n q &—第n 级荷载加载的速率,∑∆p —各级荷载总和,1-n T 、n T —第n 级荷载的起止时间, α、β—计算参数,见表4-17。
3.2.2 次固结1.定义当超孔隙水压力消散后,试样的变形随时间增加而继续增大,这一现象称为次固结,相应的变形称为次固结变形。
2.图解法Casagrande (1936)提出了主次固结的图解法。
3.次固结产生的原因(1)陈宗基(1958)认为:滞流(剪应力引起)、体积蠕变(静水压力引起)、土骨架硬化。
(2)De Jong (1965)认为:细小的孔隙网格中的水力固结。
3.2.3考虑粘弹性的一维固结理论在Terzaghi 固结理论中将土骨架视为弹性体,而实际土体变形具有粘性、弹性和塑性。
为了考虑土体的这些性质,不少学者推导了相应的一维固结理论。
3.2.4 固结系数的测定土的固结系数越大,土体固结越快。
正确测定固结系数对估计固结速率很重要。
vw wv v a e k m k c γγ)1(0+==式中k —渗透系数,m/sv m —体积压缩系数,1-kPaw γ—水的重度,kN/m 3v a —竖向压缩系数,1-kPa 0e —土体初始孔隙比⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧连续加载固结试验法等应力率固结试验法等梯度固结试验法等应变率固结试验法连续加载压缩试验反弯点法三点法时间对数拟合法时间平方根拟合法常规压缩试验的两类方法测定v c1. 时间平方根拟合法根据土的常规压缩试验,某级压力下垂直变形与时间平方根的关系曲线确定v C 的方法。
(1)在一维固结条件下,当6.0<U时,固结度与时间因子的平方根V T 呈直线关系v T U 128.1=其延长线上,当9.0=U 时,798.0=V T 。
(2)根据V T U ~理论关系式VT eU 42281ππ--=当9.0=U 时,920.0=V T 。
在V T U ~理论曲线图上作两条直线:一条通过点(0,0)和点(0.9,0.798),另一条通过点(0,0)和点(0.9,0.920),两条直线斜率比为15.1798.0920.0=。
(3)在读数与时间平方根90~t d 关系曲线图上,该试验曲线的前面部分呈直线关系,将其延长交于纵轴可得t =0时的0d ,从0d 点引另一直线使其斜率等于试验曲线部分斜率的1.15倍。
该直线交试验曲线于A 点,A 点所对应的时间即为土样达到90%固结度所对应的时间平方根90t 。
由于848.090=V T ,则90290848.0t H c v =式中H ――土体中孔隙水最大渗径,m 。
2. 时间对数拟合法根据土的压缩试验,某级压力下垂直变形与时间对数关系曲线确定v C 的方法。
(1)作t d log ~关系曲线,该试验曲线前面部分呈抛物线,中间和后面部分呈直线,两直线交点所对应的时间代表%100=U 时的时间100t ,对应测微表读数为100d 。
