奥赛模拟试题11
生物奥赛试题卷及答案

生物奥赛试题卷及答案一、选择题(每题2分,共20分)1. 细胞膜的主要功能是什么?A. 维持细胞形态B. 保护细胞内部结构C. 控制物质进出D. 以上都是2. 下列哪个不是真核细胞的特征?A. 有核膜包围的细胞核B. 有线粒体C. 有细胞壁D. 有内质网3. 光合作用中,光能首先被什么物质吸收?A. 叶绿素B. 胡萝卜素C. 核黄素D. 脱镁叶绿素4. 以下哪个是细胞周期的阶段?A. 间期B. 有丝分裂期C. 减数分裂期D. 以上都是5. 酶的催化作用主要依赖于什么?A. 温度B. 酶的浓度C. 酶的活性部位D. 底物的浓度二、填空题(每空1分,共10分)6. 细胞分裂的两种类型是________和________。
7. 细胞膜的流动性主要依赖于________的流动性。
8. 真核细胞的细胞核内含有________,是遗传信息的主要载体。
9. 光合作用的光反应发生在________,暗反应发生在________。
10. 酶的催化效率比无机催化剂高约________倍。
三、简答题(每题10分,共20分)11. 简述DNA复制的过程。
12. 描述细胞有丝分裂的各个阶段。
四、论述题(每题15分,共30分)13. 论述基因突变对生物进化的意义。
14. 讨论生态系统中能量流动的特点。
五、实验题(每题10分,共10分)15. 描述如何通过显微镜观察植物细胞的细胞壁和细胞核。
答案一、选择题1. D2. C3. A4. D5. C二、填空题6. 有丝分裂;减数分裂7. 磷脂双层8. DNA9. 类囊体膜;基质10. 10^7三、简答题11. DNA复制是一个半保留的过程,首先解旋酶解开DNA双链,随后DNA聚合酶在模板链上添加互补的核苷酸,形成新的互补链。
12. 有丝分裂分为四个阶段:前期(染色体可见),中期(染色体排列在赤道面上),后期(染色体分离向两极移动),末期(细胞质分裂,形成两个新细胞)。
四、论述题13. 基因突变是生物进化的原材料,它可以产生新的遗传变异,为自然选择提供多样性,从而推动物种适应环境的变化。
初中数学奥赛试题及答案

初中数学奥赛试题及答案一、选择题(每题5分,共20分)1. 下列哪个数是无理数?A. 3.14159B. √2C. 0.33333D. 1/3答案:B2. 若一个三角形的三个内角分别为α、β、γ,且α+β+γ=180°,则下列哪个等式是正确的?A. α=β+γB. β=α+γC. γ=α+βD. α=180°-β-γ答案:D3. 计算下列哪个表达式的值是正数?A. (-3) × (-2)B. (-3) × 2C. (-3) ÷ 2D. 3 ÷ (-2)答案:A4. 一个数列的前四项为1, 2, 3, 4,若每一项是前一项加上一个递增的自然数,那么第五项是多少?A. 6B. 7C. 8D. 9答案:B二、填空题(每题5分,共20分)5. 一个长方体的长、宽、高分别为2cm、3cm、4cm,其体积为_______cm³。
答案:246. 一个圆的半径为5cm,其周长为_______cm。
答案:31.47. 一个数的相反数是-8,那么这个数是______。
答案:88. 若一个二次方程的两个根为x1=2和x2=3,则该方程可以表示为x²-______+______=0。
答案:5,6三、解答题(每题10分,共60分)9. 已知一个等差数列的前三项分别为2,5,8,求该数列的第10项。
答案:2610. 一个直角三角形的两条直角边长分别为3cm和4cm,求斜边的长度。
答案:5cm11. 计算以下表达式的值:(1/2 + 1/3 + 1/4) × 12。
答案:1512. 一个班级有40名学生,其中25名男生和15名女生。
随机抽取一名学生,求抽到男生的概率。
答案:25/40 = 5/813. 一个数列的前四项为2,4,8,16,求该数列的通项公式。
答案:an = 2^(n-1)14. 一个圆的面积为πcm²,求该圆的半径。
高中奥赛选拔试题及答案

高中奥赛选拔试题及答案一、选择题(每题5分,共20分)1. 已知函数f(x)=2x^2-3x+1,求f(2)的值。
A. 3B. 5C. 7D. 92. 一个圆的半径为5,求该圆的面积。
A. 25πB. 50πC. 75πD. 100π3. 已知数列{an}满足a1=1,an+1=2an+1,求a3的值。
A. 3B. 5C. 7D. 94. 一个物体从静止开始做匀加速直线运动,加速度为2m/s^2,求物体在第3秒末的速度。
A. 4m/sB. 6m/sC. 8m/sD. 10m/s二、填空题(每题5分,共20分)5. 已知等差数列{an}的前三项分别为1,4,7,求该数列的通项公式an=______。
6. 一个三角形的三个内角分别为α,β,γ,已知α+β=120°,求γ的度数。
7. 已知复数z=3+4i,求z的共轭复数。
8. 一个物体在水平面上受到一个恒定的力F作用,使其从静止开始做匀加速直线运动,已知加速度a=5m/s^2,求物体在第5秒末的位置。
三、解答题(每题10分,共60分)9. 已知函数f(x)=x^3-3x^2+2,求函数的极值点。
10. 一个圆的直径为10cm,求该圆的周长和面积。
11. 已知数列{an}满足a1=2,an+1=an+2n,求数列的前5项。
12. 一个物体从高度为h的平台上自由落下,忽略空气阻力,求物体落地时的速度。
答案:一、选择题1. B2. B3. C4. B二、填空题5. an=3n-26. γ=60°7. z的共轭复数为3-4i8. 物体在第5秒末的位置为62.5m三、解答题9. 函数f(x)的导数为f'(x)=3x^2-6x。
令f'(x)=0,解得x=0或x=2。
经检验,x=0时f(x)取得极大值,x=2时f(x)取得极小值。
10. 圆的周长为πd=10πcm,面积为πr^2=25πcm^2。
11. a2=2+2×2=6,a3=6+2×3=12,a4=12+2×4=20,a5=20+2×5=30。
2023年小学数学奥林匹克竞赛模拟题及解答第一部分一节

小学数学奥林匹克竞赛模拟题及解答第一部分一节第一部分有趣的数列很少接触数学竞赛题的学生或家长,总觉得竞赛题很怪,不好捉摸,因而经常望而生畏。
其实,竞赛题的“怪”只是表面现象,它不仅很有规律,解题的思想经常非常简朴,并且用的知识基本上是书本上教过的。
例如这一部分的三节,讲的都是与数列有关的问题,用的知识但是就是乘法对加(减)法的分派律、如何用字母表达数等,所以一点也不可怕。
当然,要不久发现竞赛题中隐含的规律,并纯熟运用学过的知识去解决问题,确非易事。
但是请你记住:任何复杂的问题都是由简朴的东西变化而来的。
如何从简朴的知识去解决复杂的问题,这就是这一部分要介绍的重要思想。
这就好比编织毛衣,虽然基本的针法极其简朴,但是心灵手巧的妈妈们却可以织出千变万化、绚丽多彩的新装!愿你也学会用简朴的知识织出美丽动人的图案!一从三角形谈起长方形(涉及正方形)、平形四边形、三角形及梯形是几个基本的几何图形,从面积公式来看,长方形这种图形最为重要,我们认为它最重要,一是由于长方形的面积公式最简朴,二是由于从长方形面积公式很容易导出平行四边形乃至三角形及梯形的面积公式。
先让我们回忆一下推导给定△ABC面积公式的过程。
一方面画一个与△ABC完全同样的△A1B1C1,如图1.1中的(1)所示,再把△A1B1C1如图1.1(2)那样上下颠倒放置,最后移动△A1B1C1使C1点与A点重合,A1点与C点重合,这样就得到一个平行四边形ABCB1,由平行四边形面积等于底BC之长乘以高AD(见图1.1(3)),再被2除,即得△ABC的面积公式。
(1)作一个与ABC完全同样的三角形A1B1C1(2)把三角形A1B1C1如图这样颠倒过来(3)将两个三角形连结成一个平行四边形图 1.1现在来把上面这个问题,作一点形式上的改变,仍取△ABC,把它的每一边平均提成9等分,按照1.2图把这些分点连结起来,这样就把它提成了若干个形状完全相同的小三角形。
历年高中化学奥赛竞赛试题及答案精编版
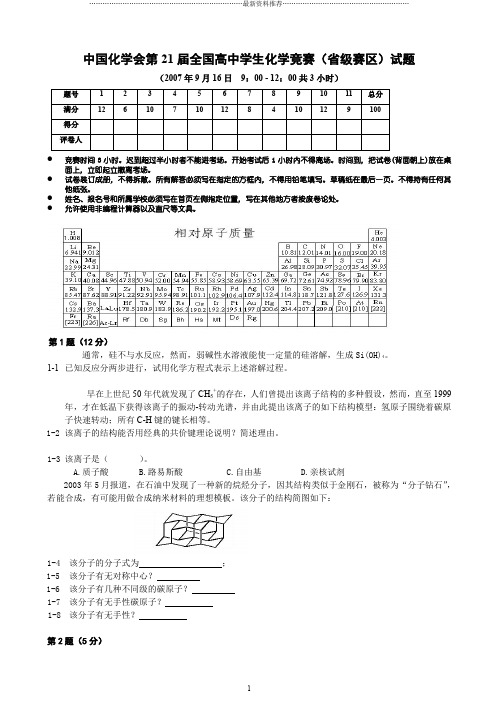
中国化学会第21届全国高中学生化学竞赛(省级赛区)试题(2007年9月16日9:00 - 12:00共3小时)题号 1 2 3 4 5 6 7 8 9 10 11 总分满分12 6 10 7 10 12 8 4 10 12 9 100得分评卷人●竞赛时间3小时。
迟到超过半小时者不能进考场。
开始考试后1小时内不得离场。
时间到,把试卷(背面朝上)放在桌面上,立即起立撤离考场。
●试卷装订成册,不得拆散。
所有解答必须写在指定的方框内,不得用铅笔填写。
草稿纸在最后一页。
不得持有任何其他纸张。
●姓名、报名号和所属学校必须写在首页左侧指定位置,写在其他地方者按废卷论处。
●允许使用非编程计算器以及直尺等文具。
第1题(12分)通常,硅不与水反应,然而,弱碱性水溶液能使一定量的硅溶解,生成Si(OH)4。
1-1已知反应分两步进行,试用化学方程式表示上述溶解过程。
早在上世纪50年代就发现了CH5+的存在,人们曾提出该离子结构的多种假设,然而,直至1999年,才在低温下获得该离子的振动-转动光谱,并由此提出该离子的如下结构模型:氢原子围绕着碳原子快速转动;所有C-H键的键长相等。
1-2该离子的结构能否用经典的共价键理论说明?简述理由。
1-3该离子是()。
A.质子酸B.路易斯酸C.自由基D.亲核试剂2003年5月报道,在石油中发现了一种新的烷烃分子,因其结构类似于金刚石,被称为“分子钻石”,若能合成,有可能用做合成纳米材料的理想模板。
该分子的结构简图如下:1-4该分子的分子式为;1-5该分子有无对称中心?1-6该分子有几种不同级的碳原子?1-7该分子有无手性碳原子?1-8该分子有无手性?第2题(5分)羟胺和用同位素标记氮原子(N﹡)的亚硝酸在不同介质中发生反应,方程式如下:NH2OH+HN﹡O2→A+H2ONH2OH+HN﹡O2→B+H2OA、B脱水都能形成N2O,由A得到N﹡NO和NN﹡O,而由B只得到NN﹡O。
请分别写出A和B的路易斯结构式。
高中数学奥赛试题

高中数学奥赛试题一、选择题1. 设集合A={1, 2, 3, 4, 5},集合B={3, 4, 5, 6, 7},则A与B 的交集的补集为:A. {1, 2}B. {6, 7}C. {1, 2, 6, 7}D. {1, 2, 3, 4, 5, 6, 7}2. 若一个等差数列的前三项分别为a-2, a, a+2,那么其第10项为:A. 3a-6B. 3aC. 3a+6D. 3a+123. 在直角坐标系中,点A(2,3)关于直线y=x的对称点坐标为:A. (3, 2)B. (1, 4)C. (4, 1)D. (3, 1)4. 已知函数f(x) = x^3 - 3x^2 + 2x + 1,求f(x)的最小值:A. -2B. -1C. 0D. 15. 若一个圆的周长为12π,那么这个圆的面积为:A. 3πB. 4πC. 6πD. 9π二、填空题6. 一个等比数列的前三项分别是2, 6, 18,那么其第5项为_______。
7. 在平面直角坐标系中,圆的方程为(x-3)^2 + (y-4)^2 = 49,求该圆的圆心坐标和半径_______。
8. 设函数g(x) = |2x - 3| + |x + 1|,求g(x)的最小值_______。
9. 一个直角三角形的两条直角边长分别为3和4,求该直角三角形的外接圆半径_______。
10. 已知一个等差数列的前n项和为S_n = 3n^2 - 2n,求该等差数列的公差_______。
三、解答题11. (本题满分10分)设数列{an}满足a1 = 2,且对于所有正整数n,有an+1 = an + 3n。
求证:数列{an}的通项公式为an = 3n - 1。
12. (本题满分15分)在直角坐标系中,给定三个点A(1,2),B(4,5)和C(7,8)。
求:(i)线段AB的中点M的坐标;(ii)线段BC的斜率k_BC;(iii)点A到直线BC的距离d_AB。
13. (本题满分20分)已知函数h(x) = x^4 - 4x^3 + 6x^2 - 4x + 1,求:(i)函数h(x)的所有驻点;(ii)函数h(x)在区间[0, 3]上的最大值和最小值。
奥林匹克竞赛模拟试卷11至20

奥林匹克竞赛模拟试卷(十一)一、择题:1、某校学生100人参加数学竞赛,其中至少有女生9人,又知参赛者中任何10人中至少有1名男生,则参赛男生人数为( )(A )89 (B )91 (C )82 (D )632、方程组⎩⎨⎧=+=+2363yz xz yz xy 的正整数解的组数是( )(A )1 (B )2 (C )3 (D )4 3、在△ABC 中,AB=AC=7,BC=4,点M 在AB 上,且BM=31AB ,过M 做EF ⊥AB ,交BC 于E ,交CA 延长线于F ,则EF 的长为( )(A )55 (B )3335 (C )54 (D )56 4、如果方程0)2)(1(2=+--m x x x 的三个根可以做为一个三角形的三边长,那么实数m 的范围是( )(A )10≤<m (B )43≥m (C )143≤<m (D )1≥m 5、一个四位数具有这样的性质:用它的后两位数去除这个四位数得到一个完全平方数(如果它的十位数字是0,就只用个位数字去除),且这个完全平方数正好是前两位数加1的平方,则具有上述性质的四位数共有( )(A )1个 (B )2个 (C )3个 (D )4个6、已知5910102+-=x x y ,且||x y ≤,则x 的取值范围是( )(A )9≤x (B )6-≥x (C )10951≤≤x 或10353≤≤-x (D )92≤≤x 或36-≤≤-x二、填空题1、设二次函数22++--=m mx x y 的图象顶点为A ,与x 轴两个交点为B 、C ,则ABC 的面积的最小值是_________._2、如图,在 Rt △ABC 内有一矩形,D 在AB 边上,G 在AC 边上,EF 在斜边BC 上,已知AB=3,BC=4,矩形DEFG 的面积等于35,则BE 的长等于__________。
3、 设自然数n 使得n 222118++为完全平方数,则n=__________。
我爱奥赛网全国高中化学竞赛模拟试题

我爱奥赛网2011年全国高中化学竞赛模拟试题1.008Zr Nb Mo Tc Ru Rh Pd Ag CdIn Sn Sb Te I Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Ac-Lr HLi BeB C N O F Na MgAl Si P Cl S K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Rb Cs Fr Sr BaRaY La Lu -6.9419.01222.9924.3139.1040.0885.4787.62132.9137.3[223][226]44.9647.8850.9452.0054.9455.8558.9363.5558.6965.3910.8126.9869.7212.0128.0972.61114.8204.4118.7207.2112.4200.6107.9197.0106.4195.1102.9192.2101.1190.298.91186.295.94183.992.91180.991.22178.588.9114.0116.0019.0030.9774.92121.8209.032.0778.96127.6[210][210][210]126.979.9035.454.00320.1839.9583.80131.3[222]HeNe Ar KrXe Rn相对原子质量RfDb Sg Bh Hs Mt第一题(本题共6分)、熔融碳酸盐燃料电池(MCFC)是极有开发前景的发电技术,欧美国家先后建立了100kW-2MW 的MCFC 发电系统,燃料多样化可以为H 2 ,CO ,CH 4 等。
1-1、熔融碳酸盐燃料电池的导电离子为_______1-2、氢气为燃气时的电极反响,阴极为CO 2 与空气的混合气,写出电极反响 阳极________________________________,阴极________________________________ 1-3、MCFC 可运用NiO 作为多孔阴极,但简洁发生短路现象,试分析其缘由? 第二题(本题共10分)、据报道,近来已制得了化合物A (白色晶体),它是用NaNO 3和Na 2O 在银皿中于573K 条件下反响7天后制得的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模拟试卷.11 姓名得分
一、填空题:
2.下面三个数的平均数是170,则圆圈内的数字分别是:
○;○9;○26.
于3,至少要选______个数.
4.图中△AOB的面积为15cm2,线段OB的长度为OD
的3倍,则梯形ABCD的面积为______.
5.有一桶高级饮料,小华一人可饮14天,若和小芳
同饮则可用10天,若小芳独自一人饮,可用______天.6.在1至301的所有奇数中,数字3共出现_______次.
7.某工厂计划生产26500个零件,前5天平均每天生产2180个零件,由于技术革新每天比原来多生产420个零件,完成这批零件一共需要_______天.
8.铁路与公路平行.公路上有一个人在行走,速度是每小时4千米,一列火车追上并超过这个人用了6秒.公路上还有一辆汽车与火车同向行驶,速度是每小时67千米,火车追上并超过这辆汽车用了48秒,则火车速度为______,长度为______.
9.A、B、C、D4个数,每次去掉一个数,将其余3个数求平均数,这样计算了4次,得到下面4个数:23,26,30,33,A、B、C、D4个数的平均数是______.
10.一个圆的周长为1.26米,两只蚂蚁从一条直径的两端同时出发沿圆周相向爬行.这两只蚂蚁每秒分别爬行5.5厘米和3.5厘米.它们每爬行1秒,3秒,5秒,………(连续奇数),就调头爬行.那么,它们相遇时,已爬行的时间是______秒.
二、解答题:
1.小红见到一位白发苍苍的老爷爷,她问老爷爷有多大年岁?老爷爷说:把我的年龄加上10用4除,减去15后用10乘,结果正好是100岁.请问这位老爷爷有多大年龄?
数最小是几?
3.下图中8个顶点处标注数字a,b,c,d,e,f,g,h
,其
f+g+h)的值.
4.底边长为6厘米,高为9厘米的等腰三角形20个,迭放如下图:
每两个等腰三角形有等距离的间隔,底边迭
合在一起的长度是44厘米.回答下列问题:
(1)两个三角形的间隔距离;
(2)三个三角形重迭(两次)部分的面积之
和;
(3)只有两个三角形重迭(一次)部分的面积之和;
(4)迭到一起的总面积.。
