高二数学选修2-1试题及答案
高中数学人教a版高二选修2-1-章末综合测评1有答案

高中数学人教a版高二选修2-1-章末综合测评1有答案(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.命题“若某2<1,则-1<某<1”的逆否命题是()A.若某2≥1,则某≥1,或某≤-1B.若-1<某<1,则某2<1C.若某>1,或某<-1,则某2>1D.若某≥1或某≤-1,则某2≥1【解析】命题“若p,则q”的逆否命题为“若綈q,则綈p”.【答案】D2.命题“所有能被2整除的整数都是偶数”的否定是()A.所有不能被2整除的整数都是偶数B.所有能被2整除的整数都不是偶数C.存在一个不能被2整除的整数是偶数D.存在一个能被2整除的整数不是偶数【解析】把全称量词改为存在量词并把结论否定.【答案】D3.命题p:某+y≠3,命题q:某≠1或y≠2,则命题p是q的()A.充分不必要条件C.充要条件B.必要不充分条件D.既不充分也不必要条件【解析】命题“若p,则q”的逆否命题为:“若某=1且y=2,则某+y=3”,是真命题,故原命题为真,反之不成立.【答案】A4.设点P(某,y),则“某=2且y=-1”是“点P在直线l:某+y-1=0上”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件第-1-页共8页【解析】当某=2且y=-1时,满足方程某+y-1=0,即点P(2,-1)在直线l上.点P′(0,1)在直线l上,但不满足某=2且y=-1,∴“某=2且y=-1”是“点P(某,y)在直线l上”的充分而不必要条件.【答案】A5.“关于某的不等式f(某)>0有解”等价于()A.某0∈R,使得f(某0)>0成立B.某0∈R,使得f(某0)≤0成立C.某∈R,使得f(某)>0成立D.某∈R,f(某)≤0成立【解析】“关于某的不等式f(某)>0有解”等价于“存在实数某0,使得f(某0)>0成立”.故选A.【答案】A6.设四边形ABCD的两条对角线为AC,BD,则“四边形ABCD为菱形”是“AC⊥BD”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【解析】若四边形ABCD为菱形,则AC⊥BD,反之,若AC⊥BD,则四边形ABCD不一定是菱形,故选A.【答案】A7.命题p:函数y=lg(某2+2某-c)的定义域为R;命题q:函数y=lg(某2+2某-c)的值域为R.记命题p为真命题时c的取值集合为A,命题q为真命题时c的取值集合为B,则A∩B=()A.C.{c|c≥-1}B.{c|c【解析】命题p为真命题,即某2+2某-c>0恒成立,则有Δ=4+4c<0,解得c第-2-页共8页【答案】A8.对某∈R,k某2-k某-1<0是真命题,则k的取值范围是()A.-4≤k≤0C.-4<k≤0B.-4≤k<0D.-4<k<0【解析】由题意知k某2-k某-1<0对任意某∈R恒成立,当k=0时,-1<0恒k<0,成立;当k≠0时,有即-4<k<0,所以-4<k≤0.2Δ=k+4k<0,【答案】C9.已知命题p:若(某-1)(某-2)≠0,则某≠1且某≠2;命题q:存在实数某0,使2某0<0.下列选项中为真命题的是()A.綈pC.綈q∧pB.綈p∨qD.q【解析】很明显命题p为真命题,所以綈p为假命题;由于函数y=2某,某∈R的值域是(0,+∞),所以q是假命题,所以綈q是真命题.所以綈p∨q为假命题,綈q∧p为真命题,故选C.【答案】C10.设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件a1>0,a1<0,【解析】等比数列{an}为递增数列的充要条件为或故“q>1”是q>10“”“{an}为递增数列”的既不充分也不必要条件.【答案】D11.已知命题p:某>0,总有(某+1)e某>1,则綈p为()A.某0≤0,使得(某0+1)e某0≤1B.某0>0,使得(某0+1)e某0≤1C.某>0,总有(某+1)e某≤1第-3-页共8页D.某≤0,使得(某+1)e某≤1【解析】因为全称命题某∈M,p(某)的否定为某0∈M,綈p(某),故綈p:某0>0,使得(某0+1)e某0≤1.【答案】B12.已知p:点P在直线y=2某-3上;q:点P在直线y=-3某+2上,则使p∧q为真命题的点P的坐标是()A.(0,-3)C.(1,-1)B.(1,2)D.(-1,1)【解析】因为p∧q为真命题,所以p,q均为真命题.所以点P为直线y=2某y=2某-3,某=1,-3与直线y=-3某+2的交点.解方程组得即点P的坐标为(1,y=-3某+2,y=-1,-1).【答案】C二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)13.命题p:若a,b∈R,则ab=0是a=0的充分条件,命题q:函数y=某-3的定义域是[3,+∞),则“p∨q”“p∧q”“綈p”中是真命题的为________.【解析】p为假命题,q为真命题,故p∨q为真命题,綈p为真命题.【答案】p∨q与綈p14.“末位数字是1或3的整数不能被8整除”的否定形式是________________,否命题是________________.【解析】命题的否定仅否定结论,所以该命题的否定形式是:末位数字是1或3的整数能被8整除;而否命题要同时否定原命题的条件和结论,所以否命题是:末位数字不是1且不是3的整数能被8整除.【答案】末位数字是1或3的整数能被8整除末位数字不是1且不是3的整数能被8整除15.已知f(某)=某2+2某-m,如果f(1)>0是假命题,f(2)>0是真命题,则实数m的取值范围是______.f(1)=3-m≤0,【解析】依题意,∴3≤m<8.f(2)=8-m>0,第-4-页共8页【答案】[3,8)16.给出以下判断:①命题“负数的平方是正数”不是全称命题;3②命题“某∈N,某3>某2”的否定是“某0∈N,使某0>某2;0”③“b=0”是“函数f(某)=a某2+b某+c为偶函数”的充要条件;④“正四棱锥的底面是正方形”的逆命题为真命题.其中正确命题的序号是________.【解析】①②④是假命题,③是真命题.【答案】③三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)写出下列命题的否定,并判断其真假,同时说明理由.(1)q:所有的矩形都是正方形;(2)r:某0∈R,某20+2某0+2≤0;(3):至少有一个实数某0,使某30+3=0.【解】(1)綈q:至少存在一个矩形不是正方形,真命题.这是由于原命题是假命题.(2)綈r:某∈R,某2+2某+2>0,真命题.这是由于某∈R,某2+2某+2=(某+1)2+1≥1>0恒成立.(3)綈:某∈R,某+3≠0,假命题.这是由于当某=-3时,某3+3=0.18.(本小题满分12分)指出下列命题中,p是q的什么条件?(1)p:{某|某>-2或某<3};q:{某|某2-某-6<0};(2)p:a与b都是奇数;q:a+b是偶数;(3)p:03【解】(1)因为{某|某2-某-6<0}={某|-2-2或某<3}/{某|-2-2或某<3}.所以p是q的必要不充分条件.第-5-页共8页33(2)因为a,b都是奇数a+b为偶数,而a+b为偶数/a,b都是奇数,所以p是q的充分不必要条件.(3)m某2-2某+3=01Δ>0,4-12m>0,mm>0m>0m>03所以p是q的充要条件.19.(本小题满分12分)已知命题p:不等式2某-某2q:m2-2m-3≥0,如果“綈p”与“p∧q”同时为假命题,求实数m的取值范围.【解】2某-某2=-(某-1)2+1≤1,所以p为真时,m>1.由m2-2m-3≥0得m≤-1或m≥3,所以q为真时,m≤-1或m≥3.因为“綈p”与“p∧q”同时为假命题,所以p为真命题,q为假命题,所以得m>1,-1即120.(本小题满分12分)已知两个命题p:in某+co某>m,q:某2+m某+1>0,如果对任意某∈R,有p∨q为真,p∧q为假,求实数m的取值范围.【解】当命题p是真命题时,π由于某∈R,则in某+co某=2in某+≥-2,4所以有m<-2.当命题q是真命题时,由于某∈R,某2+m某+1>0,则Δ=m2-4<0,解得-2<m<2.由于p∨q为真,p∧q为假,所以p与q一真一假.考虑到函数f(某)=某2+m某+1的图象为开口向上的抛物线,对任意的某∈R,某2+m某第-6-页共8页+1≤0不可能恒成立.所以只能是p为假,q为真,m≥-2,此时有-2<m<2,解得-2≤m<2,所以实数m的取值范围是[-2,2).21.(本小题满分12分)已知命题p:对数loga(-2t2+7t-5)(a>0,且a≠1)有意义;命题q:实数t满足不等式t2-(a+3)t+a+2<0.(1)若命题p为真,求实数t的取值范围;(2)若p是q的充分不必要条件,求实数a的取值范围.5【解】(1)因为命题p为真,则对数的真数-2t2+7t-5>0,解得125所以实数t的取值范围是1,2.(2)因为p是q解集的真子集.5的充分不必要条件,所以t1的法一因为方程t2-(a+3)t+a+2=0的两根为1和a+2,51所以只需a+2>,解得a>.22即实数a的取值范围为2,+∞.法二令f(t)=t2-(a+3)t+a+2,因为f(1)=0,15所以只需f2<0,解得a>.2即实数a的取值范围为2,+∞.22.(本小题满分12分)设a,b,c为△ABC的三边,求证:方程某2+2a某+b2=0与某2+2c某-b2=0有公共根的充要条件是∠A=90°.【证明】充分性:∵∠A=90°,∴a2=b2+c2.于是方程某2+2a某+b2=0可化为某2+2a某+a2-c2=0,∴某2+2a某+(a+c)(a-c)=0.第-7-页共8页∴[某+(a+c)][某+(a-c)]=0.∴该方程有两根某1=-(a+c),某2=-(a-c),同样另一方程某2+2c某-b2=0也可化为某2+2c某-(a2-c2)=0,即[某+(c+a)][某+(c-a)]=0,∴该方程有两根某3=-(a+c),某4=-(c-a).可以发现,某1=某3,∴方程有公共根.必要性:设某是方程的公共根,某2+2a某+b2=0,①则22某+2c某-b=0,②由①+②,得某=-(a+c),某=0(舍去).代入①并整理,可得a2=b2+c2.∴∠A=90°.∴结论成立.第-8-页共8页。
高二数学选修2-1空间向量试卷及答案
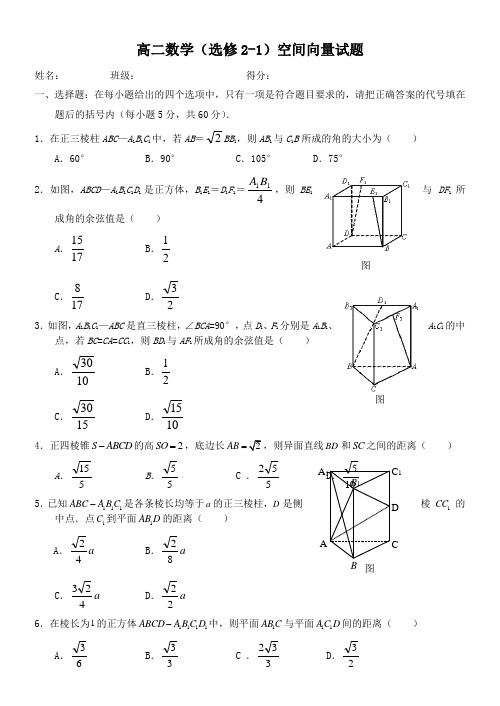
AA 1DCB B 1C 1图高二数学(选修2-1)空间向量试题姓名:_________班级:________ 得分:________一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共60分). 1.在正三棱柱ABC —A 1B 1C 1中,若AB =2BB 1,则AB 1与C 1B 所成的角的大小为( )A .60°B .90°C .105°D .75°2.如图,ABCD —A 1B 1C 1D 1是正方体,B 1E 1=D 1F 1=411B A ,则BE 1与DF 1所成角的余弦值是( )A .1715 B .21 C .178 D .23 3.如图,A 1B 1C 1—ABC 是直三棱柱,∠BCA =90°,点D 1、F 1分别是A 1B 1、A 1C 1的中点,若BC =CA =CC 1,则BD 1与AF 1所成角的余弦值是( )A .1030 B .21 C .1530 D .1015 4.正四棱锥S ABCD -的高2SO =,底边长2AB =,则异面直线BD 和SC 之间的距离( )A .515 B .55 C .552 D .105 5.已知111ABC A B C -是各条棱长均等于a 的正三棱柱,D 是侧棱1CC 的中点.点1C 到平面1AB D 的距离( )A .a 42 B .a 82 C .a 423 D .a 22 6.在棱长为1的正方体1111ABCD A B C D -中,则平面1AB C 与平面11A C D 间的距离( )A .63 B .33 C .332 D .23 图图7.在三棱锥P -ABC 中,AB ⊥BC ,AB =BC =21PA ,点O 、D 分别是AC 、PC 的中点,OP ⊥底面ABC ,则直线OD 与平面PBC 所成角的正弦值( )A .621B .338 C60210 D .302108.在直三棱柱111C B A ABC -中,底面是等腰直角三角形,90=∠ACB ,侧棱21=AA ,D ,E分别是1CC 与B A 1的中点,点E 在平面AB D 上的射影是ABD ∆的重心G .则B A 1与平面AB D 所成角的余弦值( )A .32 B .37C .23 D .73 9.正三棱柱111C B A ABC -的底面边长为3,侧棱3231=AA ,D 是C B 延长线上一点,且BC BD =,则二面角B AD B --1的大小( )A .3π B .6πC .65πD .32π10.正四棱柱1111D C B A ABCD -中,底面边长为22,侧棱长为4,E ,F 分别为棱AB ,CD 的中点,G BD EF =⋂.则三棱锥11EFD B -的体积V ( )A .66 B .3316 C .316D .1611.有以下命题:①如果向量b a ,与任何向量不能构成空间向量的一组基底,那么b a ,的关系是不共线; ②,,,O A B C 为空间四点,且向量OC OB OA ,,不构成空间的一个基底,则点,,,O A B C 一定共面;③已知向量c b a ,,是空间的一个基底,则向量c b a b a ,,-+也是空间的一个基底。
高二数学上:选修2-1答案

高二数学上:选修2-1答案答案:选修2-1 §1.1.1 命题 §1.1.2 四种命题1.B2.B3.B4.B5.略6.若 $a^2>9$,则 $a>3$。
假。
7.若 $AB \neq B$,则 $AB \neq A$,真;8.3;9.原命题是真命题,则它的逆否命题是真命题。
10.略。
11.原命题真;逆命题:“已知 $\alpha,\beta \in \{x|x\neqk\pi+\pi,k\in Z\}$,若 $\tan\alpha=\tan\beta$,则 $\alpha=\beta$”假;否命题:“已知 $\alpha,\beta \in \{x|x\neq k\pi+\pi,k\in Z\}$,若 $\alpha\neq\beta$,则 $\tan\alpha\neq\tan\beta$”假;逆否命题:“已知 $\alpha,\beta \in \{x|x\neq k\pi+\pi,k\in Z\}$,若$\tan\alpha\neq\tan\beta$,则 $\alpha\neq\beta$”真。
改写:选修2-1 §1.1.1 命题 §1.1.2 四种命题1.B2.B3.B4.B5.略6.若 $a^2>9$,则 $a>3$。
这是错误的。
7.若 $AB \neq B$,则 $AB \neq A$,这是正确的;8.3;9.原命题是真命题,则它的逆否命题也是真命题。
10.略。
11.原命题是真命题;逆命题:“已知 $\alpha,\beta \in\{x|x\neq k\pi+\pi,k\in Z\}$,若 $\tan\alpha=\tan\beta$,则$\alpha=\beta$”是错误的;否命题:“已知 $\alpha,\beta \in\{x|x\neq k\pi+\pi,k\in Z\}$,若 $\alpha\neq\beta$,则$\tan\alpha\neq\tan\beta$”是错误的;逆否命题:“已知$\alpha,\beta \in \{x|x\neq k\pi+\pi,k\in Z\}$,若$\tan\alpha\neq\tan\beta$,则 $\alpha\neq\beta$”是正确的。
高二数学选修2-1第三章 空间向量与立体几何练习题及答案

第三章 空间向量与立体几何空间向量的数乘运算 测试题姓名:_________班级:________ 得分:_______ 1. 下列命题中不正确的命题个数是( )①若A 、B 、C 、D 是空间任意四点,则有AB +BC + CD +DA =0;②对空间任意点O 与不共线的三点A 、B 、C ,若OP =x OA +y OB +z OC (其中x 、y 、z ∈R ),则P 、A 、B 、C 四点共面;③若a 、b 共线,则a 与b 所在直线平行。
A .1B .2C .3D .42.设OABC 是四面体,G 1是△ABC 的重心,G 是OG 1上一点,且OG =3GG 1,若OG =x OA +y OB +z OC ,则(x ,y ,z )为( )A .(41,41,41) B .(43,43,43) C .(31,31,31) D .(32,32,32) 3.在平行六面体ABCD -EFGH 中,AG xAC y AF z AH =++,________.x y z ++=则4.已知四边形ABCD 中,AB =a -2c ,CD =5a +6b -8c ,对角线AC 、BD 的中点分别为E 、F ,则EF =_____________.5.已知矩形ABCD ,P 为平面ABCD 外一点,且P A ⊥平面ABCD ,M 、N 分别为PC 、PD 上的点,且M 分PC 成定比2,N 分PD 成定比1,求满足MN xAB y AD z AP =++的实数x 、y 、z 的值.§3.1.3空间向量的数量积运算1.已知正四棱柱1111ABCD A B C D -中,1AA =2AB ,E 为1AA 重点,则异面直线BE 与1CD 所形成角的余弦值为( ) A .1010 B . 15 C .31010 D . 352.如图,设A ,B ,C ,D 是空间不共面的四点,且满足0AB AC ⋅=,0AC AD ⋅=,0AB AD ⋅=,则△BCD 的形状是( )A .钝角三角形B .锐角三角形C .直角三角形D .不确定的_ C _ D _ A _ P_ N _ B_ M3.已知ABCD -A 1B 1C 1D 1 为正方体,则下列命题中错误的命题为__________.;221111111①(A A+A D +A B )=3(A B )()0;C ⋅-=1111②A A B A A 60;︒11向量与向量的夹角为AD A B ③ ⋅⋅11111立方体ABCD-A B C D 的体积为|AB AA AD |;④4.如图,已知:平行六面体ABCD -A 1B 1C 1D 1的底面ABCD 是菱形,且∠C 1CB =∠C 1CD =∠BCD =60° (1)证明:C 1C ⊥BD ; (2)当1CDCC 的值为多少时,能使A 1C ⊥平面C 1BD ?请给出证明. §3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示1.已知向量(2,2,3)OA =-,(,1,4)OB x y z =-,且平行四边形OACB 的对角线的中点坐标为M 31(0,,)22-,则(,,)x y z =( ) A .(2,4,1)--- B .(2,4,1)-- C .(2,4,1)-- D .(2,4,1)--2.已知(2,2,4)a =-,(1,1,2)b =-,(6,6,12)c =--,则向量、、a b c ( ) A .可构成直角三角形 B .可构成锐角三角形 C .可构成钝角三角形 D .不能构成三角形3.若两点的坐标是A (3cosα,3sinα,1),B (2cosθ,2sinθ,1),则|AB |的取值范围是( )A .[0,5]B .[1,5]C .(1,5)D .[1,25] 4.设点C (2a +1,a +1,2)在点P (2,0,0)、A (1,-3,2)、B (8,-1,4)确定的平面上,则a 的值为 . 5.如图,正三棱柱ABC -A 1B 1C 1的底边长为a ,侧棱长为2a .建立适当的坐标系,⑴写出A ,B ,A 1,B 1的坐标;⑵求AC 1与侧面ABB 1A 1所成的角.3.2立体几何中的向量方法1.到一定点(1,0,1)的距离小于或等于2的点的集合为( ) A .222{(,,)|(1)(1)4}x y z x y z -++-≤ B .222{(,,)|(1)(1)4}x y z x y z -++-= C .222{(,,)|(1)(1)2}x y z x y z -++-≤ D .222{(,,)|(1)(1)2}x y z x y z -++-=C 1 B 1 A 1B A2. 正方体ABCD —A 1B 1C 1D 1中,直线BC 1与平面A 1BD 所成角的余弦值为( ) A .42 B .32 C .33 D .23 3. 已知斜三棱柱111ABC A B C -,90BCA ∠=,2AC BC ==,1A 在底面ABC 上的射影恰为AC 的中点D ,又知11BA AC ⊥.(1)求证:1AC ⊥平面1A BC ; (2)求1C 到平面1A AB 的距离; (3)求二面角1A A B C --余弦值的大小.B 4. 如图,在直三棱柱111ABC A B C -中, AB =1,13AC AA ==,∠ABC =60°. (1)证明:1AB A C ⊥;(2)求二面角A —1A C —B 的大小.5. 如右图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是底面边长的2倍,P 为侧棱S D 上的点. (1)求证:AC ⊥SD ;(2)若SD ⊥平面P AC ,求二面角P-AC-D 的大小 (3)在(2)的条件下,侧棱S C 上是否存在一点E , 使得BE ∥平面P AC .若存在,求S E :EC 的值; 若不存在,试说明理由.参考答案第三章 空间向量与立体几何3.1空间向量及其运算§3.1.1空间向量及其加减运算§3.1.2空间向量的数乘运算1.A2.A3.324.3a +3b -5c5.如图所示,取PC 的中点E ,连结NE ,则MN EN EM =-.∵1122EN CD BA ===12AB -,CBA C 1B 1 A1 D 1C 1B 1A 1DABC_ C_ D_ A_S_ F_ B_ P_ N_ EEN PM PE =-=211326PC PC PC -=,连结AC ,则PC AC AP AB AD AP =-=+- ∴11()26MN AB AB AD AP =--+-=211366AB AD AP --+,∴211,,366x y z =-=-=.§3.1.3空间向量的数量积运算1.C2.B3. ③④4.(1)设1,,CB a CD b CC c === ,则||||a b =,BD CD CB b a =-=- ,所以1()||||cos 60||||cos 600CC b a c b c a c b c a c ⋅=-⋅=⋅-⋅=︒-︒=BD ,11BD CC BD CC ∴⊥⊥即 ;(2)1,2,CD x CD CC ==1设则 2CC =x, 111,BD AA C C BD A C ⊥∴⊥ 面 ,11:0x AC CD ∴⋅= 只须求满足, 设1,,A A a AD b DC c ===,11,A C a b c C D a c =++=-,2211242()()6A C C D a b c a c a a b b c c xx ∴⋅=++⋅-=+⋅-⋅-=+-, 令24260x x+-=,则2320x x --=,解得1x =,或23x =-(舍去),111,.A C C BD ∴=⊥1CD时能使平面CC §3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示1.A2.D3.B4.165. (1)建系如图,则A (0,0,0) B (0,a ,0)A 1(0,0,2a ),C 1(-23a ,a 2,2a) (2)解法一:在所建的坐标系中,取A 1B 1的中点M , 于是M (0,a 2,2a),连结AM ,MC 1 则有1(,0,0)2MC =-(0,,0)AB a=,1)AA =, ∴10MC AB ⋅=,110MC AA ⋅=,所以,MC 1⊥平面ABB 1A 1.因此,AC 1与AM 所成的角就是AC 1与侧面ABB 1A 1所成的角.1(,)2a AC =-,(0,)2aAM =,A∴2194a AC AM ⋅=,而|13||3,||2AC a AM a ==,由cos<1,AC AM >=1132||||AC AM AC AM ⋅=,∴ <1,AC AM >=30°.∴AC 1与侧面ABB 1A 1所成的角为30°.3.2立体几何中的向量方法1.A2.C3.(1)如右图,取AB 的中点E ,则//DE BC ,因为BC AC ⊥, 所以DE AC ⊥,又1A D ⊥平面ABC , 以1,,DE DC DA 为,,x y z 轴建立空间坐标系, 则()0,1,0A -,()0,1,0C ,()2,1,0B ,()10,0,A t ,()10,2,C t ,()10,3,AC t =,()12,1,BA t =--,()2,0,0CB =,由10AC CB ⋅=,知1A C CB ⊥, 又11BA AC ⊥,从而1AC ⊥平面1A BC .(2)由1AC ⋅2130BA t =-+=,得3t = 设平面1A AB 的法向量为(),,n x y z =,(13AA =,()2,2,0AB =,所以130220n AA y z n AB x y ⎧⋅=+=⎪⎨⋅=+=⎪⎩,设1z =,则()3,3,1n =-, 所以点1C 到平面1A AB 的距离1AC n d n⋅==221. (3)再设平面1A BC 的法向量为(),,m x y z =,(10,3CA =-,()2,0,0CB =, 所以13020m CA y z m CB x ⎧⋅=-+=⎪⎨⋅==⎪⎩,设1z =,则()0,3,1m =, 故cos ,m n m n m n⋅<>==⋅77-,根据法向量的方向, 可知二面角1A A B C --7. 4.(1)三棱柱111ABC A B C -为直三棱柱,11AB AA AC AA ∴⊥⊥,,Rt ABC ∆,1,3,60AB AC ABC ==∠=︒,由正弦定理030ACB ∠=.090BAC ∴∠=AB AC ⊥即 .如右图,建立空间直角坐标系,则 1(0,0,0),(1,0,0)(0,3,0),(0,0,3)A B C A1(1,0,0),(0,3,3)AB AC ∴==, 110030(3)0AB AC ⋅=⨯+⨯+⨯-=, 1AB A C ∴⊥.(2) 如图可取(1,0,0)m AB ==为平面1AA C 的法向量, 设平面1A BC 的法向量为(,,)n l m n =, 则10,0,130BC n AC n BC ⋅=⋅==-又(,,), 303,330l m l m n m m n ⎧-+=⎪∴∴==⎨-=⎪⎩. 不妨取1,(3,1,1)m n ==则,22222231101015cos ,5(3)11100m n m n m n ⋅⨯+⨯+⨯<>===⋅++⋅++.1A AC BD ∴--15二面角的大小为arccos 5. 5. (1)连结BD ,设AC 交于BD 于O ,由题意知SO ABCD ⊥平面.以O 为坐标原点,OB OC OS ,,分别为x 轴、y 轴、z 轴正方向,建立坐标系O xyz -如右图.设底面边长为a ,则高62SO a =.于是 62(0,0,),(,0,0)22S a D a -,2(0,,0)2C a ,2(0,,0)2OC a =,26(,0,)2SD a =-,0OC SD ⋅= ,故OC SD ⊥.从而 AC SD ⊥. _ C_ A_S_ F_ BO(2)由题设知,平面PAC 的一个法向量(,0,)22DS a a =,平面DAC 的一个法向量002OS =(,,),设所求二面角为θ,则cos 2OS DS OS DSθ⋅==,得所求二面角的大小为30°. (3)在棱SC 上存在一点E 使//BE PAC 平面.由(2)知DS 是平面PAC 的一个法向量,且,0,),(0,,)2222DS a a CS a a ==-(.设,CE tCS = 则(,(1),)222BE BC CE BC tCS a t at =+=+=--,而 103BE DC t ⋅=⇔=.即当:2:1SE EC =时,BE DS ⊥.而BE 不在平面PAC 内,故//BE PAC 平面.(完)。
高二数学(人教B版)选修2-1全册同步练习:2-5直线与圆锥曲线

2.5直线与圆锥曲线一、选择题1.若不论k 为何值,直线y =k (x -2)+b 与曲线x 2-y 2=1总有公共点,则b 的取值范围是( )A .(-3,3)B .[-3,3]C .(-2,2)D .[-2,2][答案] B[解析] 由题意可知,直线所过的定点(2,b )应在双曲线上或内部,即y 2≤x 2-1,∴b 2≤3,∴-3≤b ≤ 3.2.过抛物线y 2=4x 的焦点F 作倾斜角为π3的弦AB ,则|AB |的值为( ) A.837 B.163 C.83 D.1637 [答案] B[解析] 抛物线y 2=4x 的焦点F 为(1,0),过F 且倾斜角为π3的直线方程为y =3(x -1),联立得方程组⎩⎨⎧y =3(x -1)y 2=4x得关于x 的一元二次方程3x 2-10x +3=0.①设交于A (x 1,y 1)B (x 2,y 2)两点.则x 1x 2是①的两根.有x 1+x 2=103.|AB |=|AF |+|BF |=x 1+x 2+p =103+2=163.故选B.3.已知过抛物线y 2=6x 焦点的弦长为12,则此弦所在直线的倾斜角是( ) A.π6或5π6 B.π4或3π4 C.π3或2π3 D.π2[答案] B[解析] 由焦点弦长公式|AB |=2p sin 2θ得 6sin 2θ=12,∴sin θ=22. ∴θ=π4或34π.故选B. 4.(2009·山东烟台4月)已知抛物线y 2=4x 上一点P (x 0,y 0),若y 0∈[1,2],则|PF |的范围是( )A.⎣⎡⎦⎤14,1B.⎣⎡⎦⎤54,2C .[1,2]D .[2,3][答案] B[解析] ∵y 0∈[1,2],∴x 0∈⎣⎡⎦⎤14,1,由定义|PF |=1+x 0∈⎣⎡⎦⎤54,2.故选B.5.直线y =x +m 与椭圆x 24+y 2=1有两个不同的交点,则m 的范围是() A .-5<m <5 B .m <-5,或m > 5C .m < 5D .-5<m < 5[答案] D[解析] 将y =x +m 代入x 24+y 2=1,有5x 2+8mx +4m 2-4=0,Δ=64m 2-80(m 2-1)>0,得m 2<5,∴-5<m < 5.6.直线y =x +1被椭圆x 24+y 22=1所截得的弦的中点坐标是( )A .(23,43)B .(43,73)C .(-23,13D .(-43,-13)[答案] C[解析] 设直线与椭圆交点为A (x 1,y 1),B (x 2,y 2).则⎩⎨⎧ x 214+y 212=1x 224+y 222=1,两式相减得14(x 1-x 2)(x 1+x 2)+12(y 1-y 2)(y 1+y 2)=0y 1-y 2x 1-x 2=-14(x 1+x 2)12(y 1+y 2)=k∴-x 02y 01,又y 0=x 0+1∴x 0=-23,y 0=13. 7.以双曲线y 2-x 23=1的一个焦点为圆心,离心率为半径的圆的方程是( ) A .(x -2)2+y 2=4B .x 2+(y -2)2=2C .(x -2)2+y 2=2D .x 2+(y -2)2=4[答案] D[解析] 双曲线焦点在y 轴上,离心率e =2,∴圆心在y 轴上,半径R =2.故选D.8.(2009·浙江)过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右顶点A 作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B ,C .若AB →=12BC →,则双曲线的离心率是( ) A.2 B.3 C.5 D.10 [答案] C[解析] 由已知,直线方程为x +y -a =0,两渐近线为x a ±y b=0. 由⎩⎪⎨⎪⎧ x +y -a =0bx -ay =0得x B =a 2a +b . 由⎩⎪⎨⎪⎧x +y -a =0bx +ay =0得x C =a 2a -b . ∵AB →=12BC →,∴2(x B -x A )=x C -x B , ∴3x B =2x A +x C ,∴3a 2a +b =a 2a -b+2a ,解得b =2a , ∴c 2=a 2+b 2a 2=5,∴e = 5. 故选C.9.已知a >b >0,e 1与e 2分别为圆锥曲线x 2a 2+y 2b 2=1和x 2a 2-y 2b 2=1的离心率,则lg e 1+lg e 2的值( )A .一定是正值B .一定是零C .一定是负值D .符号不确定[答案] C[解析] ∵e 1=a 2-b 2a ,e 2=a 2+b 2a, ∴e 1e 2=a 4-b 4a 2=1-⎝⎛⎭⎫b 2a 22<1. ∴lg e 1+lg e 2=lg(e 1·e 2)<0.故选C.10.若椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率为32,则双曲线x 2a 2-y 2b 21的离心率为( ) A.54B.52C.32D.54[答案] B[解析] 椭圆离心率e =32,即c a =32⇒a 2-b 2a 2=34,∴b 2a 2=14,则1+b 2a 2=54. ∴双曲线的离心率为e ′=52.故选B. 二、填空题 11.若抛物线y 2=2px 的焦点与双曲线x 23-y 2=1的右焦点重合,则p 的值等于______. [答案] 4[解析] 由已知F ⎝⎛⎭⎫p 2,0与F 2(2,0)重合, ∴p 2=2,∴p =4. 12.点M (5,3)到抛物线x 2=ay (a >0)的准线的距离为6,那么抛物线的方程是______.[答案] x 2=12y[解析] ∵抛物线x 2=ay (a >0)的准线方程为y =-a 4,∴a 4+3=6,∴a =12, ∴抛物线方程为x 2=12y .13.双曲线x 2-y 2=9被直线x -2y +1=0截得的弦长为________.[答案] 4335 [解析] ⎩⎪⎨⎪⎧x 2-y 2=9x -2y +1=0,3y 2-4y -8=0 y 1·y 2=-83,y 1+y 2=43. l =1+1k 2·(y 1+y 2)2-4y 1·y 2=5·169+323=4335. 14.(2008·全国Ⅰ)已知抛物线y =ax 2-1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为________.[答案] 2[解析] 把抛物线方程改写为x 2=1a(y +1)得顶点(0,-1),又原点为焦点, ∴1a=4, ∴抛物线x 2=4(y +1)与x 轴交于两点(2,0),(-2,0).∴所求面积为12×4×1=2. 三、解答题15.直线l :y =2x +1与抛物线y 2=12x 交于A (x 1,y 1),B (x 2,y 2)两点,求线段AB 的长.[解析] 由⎩⎪⎨⎪⎧y =2x +1,y 2=12x ,得4x 2-8x +1=0, 由韦达定理,得x 1+x 2=2,x 1x 2=14. ∴|AB |=1+k 2|x 1-x 2|=(1+k 2)[(x 1+x 2)2-4x 1x 2] =(1+22)(22-4×14)=15. 16.过椭圆x 22+y 2=1的一个焦点F 作直线l 交椭圆于A ,B 两点,椭圆的中心为O ,当△AOB 的面积最大时,求直线l 的方程.[解析] 过椭圆焦点F (1,0)的直线l 垂直于x 轴时,可知此时△AOB 的面积等于22. 当l 不垂直x 轴时,可设直线l 的方程为y =k (x -1).因为|OF |是定值1,所以△AOB 的面积可以用12×1×|y 1-y 2|(其中y 1,y 2是A ,B 的纵坐标)来计算. 将y =kx -k 代入x 22+y 2=1,消去x ,得(1+2k 2)y 2+2ky -k 2=0. 由根与系数的关系可得(y 1-y 2)2=8k 4+8k 2(2k 2+1)2=2-2(2k 2-1)2<2. 可以看出|y 1-y 2|<2,此时△AOB 的面积小于22,所以直线l 的方程为x =1或x =-1. 17.(2010·湖北文,20)已知一条曲线C 在y 轴右边,C 上每一点到点F (1,0)的距离减去它到y 轴距离的差都是1.(1)求曲线C 的方程;(2)是否存在正数m ,对于过点M (m,0)且与曲线C 有两个交点A ,B 的任一直线,都有FA →·FB →<0?若存在,求出m 的取值范围;若不存在,请说明理由.[分析] 本小题主要考查直线与抛物线的位置关系,抛物线的性质等基础知识,同时考查推理运算的能力.[解析] (1)设P (x ,y )是曲线C 上任意一点,那么点P (x ,y )满足:(x -1)2+y 2-x =1(x >0)化简得y 2=4x (x >0)(2)设过点M (m,0)(m >0)的直线l 与曲线C 的交点为A (x 1,y 1),B (x 2,y 2).设l 的方程为x =ty +m ,由⎩⎪⎨⎪⎧x =ty +m y 2=4x 得y 2-4ty -4m =0,此时Δ=16(t 2+m )>0.于是⎩⎪⎨⎪⎧y 1+y 2=4t y 1·y 2=-4m ① 又FA →=(x 1-1,y 1),FB →=(x 2-1,y 2)FA →·FB →<0⇔(x 1-1)(x 2-1)+y 1y 2=x 1·x 2-(x 1+x 2)+1+y 1y 2<0②又x =y 24,于是不等式②等价于y 214·y 224+y 1y 2-(y 214+y 224)+1<0⇔(y 1y 2)26+y 1y 2-14[(y 1+y 2)2-2y 1y 2]+1<0③由①式,不等式③等价于m 2-6m +1<4t 2④对任意实数t,4t 2的最小值为0,所以不等式④对于一切t 成立等价于m 2-6m +1<0, 即3-22<m <3+2 2由此可知,存在正数m ,对于过点M (m,0)且与曲线C 有两个交点A ,B 的任意一直线,都有FA →·FB →<0,且m 的取值范围是(3-22,3+22).18.已知中心在原点的双曲线C 的右焦点为(2,0),右顶点为(3,0),(O 为原点)(1)求双曲线C 的方程.(2)若直线l 1:y =kx +2与双曲线恒有两个不同的交点A 和B ,且OA →·OB →>2,求k 的取值范围.[解析] (1)设双曲线方程为x 2a 2-y 2b 2=1(a >0,b >0). 由已知得a =3,c =2,再由a 2+b 2=22,得b 2=1.所以双曲线C 的方程为x 23-y 2=1. (2)将y =kx +2代入x 23-y 2=1得 (1-3k 2)x 2-62kx -9=0.由直线l 与双曲线交于不同的两点得⎩⎨⎧1-3k 2≠0Δ=(-62k )2+36(1-3k 2)=36(1-k 2)>0,即k 2≠13且k 2<1.① 设A (x A ,y A )、B (x B ,y B ),则x A +x B =62k 1-3k 2,x A x B =-91-3k 2, 由OA →·OB →>2得x A x B +y A y B >2,而x A x B +y A y B =x A x B +(kx A +2)(kx B +2)=(k 2+1)x A x B +2k (x A +x B )+2 =(k 2+1)·-91-3k 2+2k ·62k 1-3k 2+2=3k 2+73k 2-1. 于是3k 2+73k 2-1>2,即-3k 2+93k 2-1>0. 解此不等式得13<k 2<3.② 由①②得13<k 2<1. 故k 的取值范围为(-1,-33)∪(33,1).。
高二数学(人教B版)选修2-1全册同步练习:2-4-3抛物线习题课

2.4.3抛物线习题课一、选择题1.P (x 0,y 0)是抛物线y 2=2px (p ≠0)上任一点,则P 到焦点的距离是( ) A .|x 0-p2|B .|x 0+p2|C .|x 0-p |D .|x 0+p |[答案] B[解析] 利用P 到焦点的距离等于到准线的距离,当p >0时,p 到准线的距离为d =x 0+p 2;当p <0时,p 到准线的距离为d =-p 2-x 0=|p2+x 0|. 2.已知抛物线的准线方程为x =-7,则抛物线的标准方程为( ) A .x 2=-28y B .y 2=28x C .y 2=-28x D .x 2=28y [答案] B[解析] 由题意,知抛物线的标准方程为:y 2=2px (p >0),又准线方程为x =-7,∴p =14.3.抛物线y 2=-4px (p >0)的焦点为F ,准线为l ,则p 表示( ) A .F 到l 的距离B .F 到y 轴的距离C .F 点的横坐标D .F 到l 的距离的14[答案] B[解析] 设y 2=-2p ′x (p ′>0),p ′表示焦点到准线的距离,又2p ′=4p ,p =p ′2,故P 表示焦点到y 轴的距离.4.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,如果x 1+x 2=8,那么|AB |等于( )A .10B .8C .6D .4[答案] A[解析] 设F 为抛物线y 2=4x 的焦点,则由抛物线的定义知|AF |=x 1+p 2=x 1+1,|BF |=x 2+p2=x 2+1,∴|AB |=|AF |+|BF |=x 1+x 2+2=10.5.已知抛物线y 2=2px (p >0)的焦点弦AB 的两端点分别为A (x 1,y 1),B (x 2,y 2),则一定有y 1y2x 1x 2等于( ) A .4 B .-4 C .p 2D .-p 2[答案] B[解析] 设过焦点的直线方程为x +ay -p 20(a ∈R ),则代入抛物线方程有y 2+2apy -p 2=0,故由根与系数的关系知y 1y 2=-p 2.又由y 21=2px 1,①y 22=2px 2,② ①②相乘得y 21y 22=4p 2x 1x 2,∴x 1x 2=p 24,∴y 1y 2x 1x 2=-4. 6.直线y =kx -2交抛物线y 2=8x 于A 、B 两点,若AB 中点的横坐标为2,则k =( ) A .2或-2 B .-1 C .2D .3[答案] C[解析] 由⎩⎪⎨⎪⎧y 2=8xy =kx -2得k 2x 2-4(k +2)x +4=0,则4(k +2)k 2=4,即k =2. 7.(2010·山东文,9)已知抛物线y 2=2px (p >0),过焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( )A .x =1B .x =-1C .x =2D .x =-2[答案] B[解析] 本题考查了抛物线的方程及中点弦问题,属圆锥曲线部分题型,可设A (x 1,y 1),B (x 2,y 2),则中点(x 1+x 22,y 1+y 22),∴y 1+y 22=2,⎩⎪⎨⎪⎧y 21=2px 1 ①y 22=2px 2 ②①-②得y 21-y 22=2p (x 1-x 2)⇒y 1-y 2x 1-x 2=2p y 1+y 2=p y 1+y 22,∴k AB =1=p 2⇒p =2,∴y 2=4x ,∴准线方程式为:x =-1,故选B.8.设O 为坐标原点,F 为抛物线y 2=4x 的焦点,A 为抛物线上一点,若OA →·AF →=-4,则点A 的坐标为( )A .(2,±22)B .(1,±2)C .(1,2)D .(2,22)[答案] B[解析] 依题意F (1,0)设A 点坐标为(x ,y ),则OA →=(x ,y ),AF →=(1-x ,-y ), OA →·AF →=x (1-x )+y (-y )=x -x 2-y 2, x -x 2-4x ,=-x 2-3x =-4.即x 2+3x -4=0解之得x =1或x =-4 又∵x ≥0,∴x =1,y 2=4,y =±2. ∴A (1,±2).9.一动圆的圆心在抛物线y 2=8x 上,且动圆恒与直线x +2=0相切,则动圆必过定点( )A .(4,0)B .(2,0)C .(0,2)D .(0,-2)[答案] B[解析] 由抛物线定义知,抛物线上的点到焦点的距离等于它到准线的距离,又动圆圆心在抛物线上且恒与x +2=0相切.∴动圆过定点F (2,0),故选B.10.(2008·宁夏、海南)已知点P 在抛物线y 2=4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为( )A.⎝⎛⎭⎫14,-1B.⎝⎛⎭⎫14,1C .(1,2)D .(1,-2)[答案] A[解析] 依题意,抛物线的焦点F (1,0),准线为l x =-1.过Q 点作直线l 的垂线交抛物线于P 点,交准线l 于M 点,则|QP |+|PF |=|QP |+|PM |=|QM |=3为所求的最小值,此时P ⎝⎛⎭⎫14,-1.故选A. 二、填空题11.P 点是抛物线y 2=4x 上任一点,到直线x =-1的距离为d ,A (3,4),|PA |+d 的最小值为________.[答案] 2 5[解析] 设抛物线焦点为F (1,0)则d =|PF |,∴|AP |+d =|AP |+|PF |≥|AF |=(3-1)2+(4-0)2=2 5.12.过点P (-1,2)且与曲线y =3x 2-4x +2在点M (1,1)处的切线平行的直线方程是________.[答案] 2x -y +4=0[解析] 设y =3x 2-4x +2在M (1,1)处切线方程为y -1=k (x -1),联立得⎩⎪⎨⎪⎧y =3x 2-4x +2,y -1=k (x -1),∴3x 2-(k +4)x +(k +1)=0. ∵Δ=0,∴k =2.∴过P (-1,2)与切线平行的直线为2x -y +4=0.13.已知点P 在抛物线y 2=2x 上运动,点Q 与点P 关于(1,1)对称,则点Q 的轨迹方程是________.[答案] y 2-4y +2x =0[解析] 设P (x 0,y 0),Q (x ,y )由已知得⎩⎪⎨⎪⎧x 0+x =2,y 0+y =2∴x 0=2-x ,y 0=2-y ,又P (x 0,y 0)在y 2=2x 上, ∴(2-y )2=2(2-x ) 即y 2-4y +2x =0.14.(2010·全国Ⅱ理,15)已知抛物线C :y 2=2px (p >0)的准线为l ,过M (1,0)且斜率为3的直线与l 相交于点A ,与C 的一个交点为B .若AM →=MB →,则p =______.[答案] 2[解析] 如图,设B (x 0,y 0),则MK =12BH ,则x 0+p 2=2⎝⎛⎭⎫1+p 2有x 0=p2+2.可得y 0=p 2+4p ,又直线AB 方程为y =3(x -1),代入有p 2+4p =3⎝⎛⎭⎫p 2+2-1,解得p =2.三、解答题15.已知抛物线y 2=4x ,直线l 过定点P (-2,1),斜率为k ,k 为何值时,直线l 与抛物线满足下列条件:①只有一个公共点; ②有两个公共点; ③没有公共点.[解析] 由题意得直线l 的方程为y -1=k (x +2),由⎩⎪⎨⎪⎧y -1=k (x +2),y 2=4x ,消去x 得ky 2-4y +4(2k +1)=0①, 当k =0时,由方程①得y =1,把y =1代入y 2=4x ,得x =14,此时,直线l 与抛物线只有一个公共点(14,1).当k ≠0时,方程①的判别式为Δ=-16(2k 2+k -1).①当Δ=0,即2k 2+k -1=0,解得k =-1或k =12,此时方程①只有一解,方程组只有一个解,直线l 与抛物线只有一个公共点.②当Δ>0,即2k 2+k -1<0,解得-1<k <12,所以-1<k <12且k ≠0时,直线l 与抛物线有两个公共点.③当Δ<0,即2k 2+k -1>0,解得k >12或k <-1,此时,直线l 与抛物线没有公共点.综上所述可知当k =0或k =-1或k =12时,直线l 与抛物线只有一个公共点;当-1<k <12且k ≠0时,直线l 与抛物线有两个公共点;当k <-1或k >12时,直线l 与抛物线没有公共点.16.已知抛物线y 2=-x 与直线y =k (x +1)相交于A ,B 两点. (1)求证OA ⊥OB ;(2)当△AOB 的面积等于10时, 求k 的值.[解析] (1)证明:如图所示,由方程组⎩⎪⎨⎪⎧y 2=-xy =k (x +1)消去x 得ky 2+y -k =0,设A (x 1,y 1),B (x 2,y 2).由根与系数的关系知y 1y 2=-1.因为A ,B 在抛物线y 2=-x 上,所以y 21=-x 1,y 22=-x 2,y 21y 22=x 1x 2,因为k OA ·k OB =y 1x 1·y 2x 2=y 1y 2x 1x 2=1y 1y 2=-1,所以OA ⊥OB .(2)解:设直线AB 与x 轴交于点N ,显然k ≠0,所以点N 的坐标为(-1,0),因为S △OAB=S △OAN +S △OBN=12|ON ||y 1|+12|ON ||y 2|=12|ON ||y 1-y 2|,所以S △OAB =12·1·(y 1+y 2)2-4y 1y 2=12(1k)2+4,因为S △OAB =10,所以10=121k 2+4,解得k =±16. 17.设抛物线y 2=8x 的焦点是F ,有倾斜角为45°的弦AB ,|AB |=85,求△FAB 的面积.[解析] 设AB 方程为y =x +b , 由⎩⎪⎨⎪⎧y =x +b ,y 2=8x .消去y 得:x 2+(2b -8)x +b 2=0.设A (x 1,y 1),B (x 2,y 2),则 x 1+x 2=8-2b ,x 1·x 2=b 2. ∴|AB |=1+k 2·|x 1-x 2| =2×(x 1+x 2)2-4x 1·x 2 =2[(8-2b )2-4b 2]=85, 解得:b =-3.∴直线方程为y =x -3.即:x -y -3=0, ∴焦点F (2,0)到x -y -3=0的距离为 d =12=22.∴S △FAB =12×85×22=210. 18.已知抛物线y 2=x 上存在两点关于直线l :y =k (x -1)+1对称,求实数k 的取值范围.[解析] 设抛物线上的点A (y 21,y 1),B (y 22,y 2)关于直线l 对称.则⎩⎨⎧k ·y 1-y2y 21-y 22=-1y 1+y 22=k (y 21+y222-1)+1得⎩⎪⎨⎪⎧y 1+y 2=-k y 1y 2=k 22+1k -12,∴y 1、y 2是方程t 2+kt +k 22+1k -12=0的两个不同根.∴Δ=k 2-4(k 22+1k -12)>0得-2<k <0.。
高二数学选修2-1测试试题及答案

(选修2-1)模块测试试题(本试题满分150分;用时100分钟)一、选择题:(本大题共12小题;每小题5分;共60分.在每小题给出的四个选项中;只有一项是符合题目要求的.)1.命题“若a b >;则88a b ->-”的逆否命题是 ( )a b <;则88a b -<-88a b ->-;则a b > a ≤b ;则88a b -≤-88a b -≤-;则a ≤b2.如果方程x 2+k y 2=2表示焦点在y 轴上的椭圆;那么实数k 的取值范围是( ) A .(0; +∞)B .(0; 2)C .(0; 1)D . (1; +∞)3.P:12≥-x ;Q:0232≥+-x x ;则“非P ”是“非Q ”的( )A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件4.双曲线221169x y -=的左、右焦点分别为F 1;F 2;在左支上过点F 1的弦AB 的长为5; 那么△ABF 2的周长是( )A 、24B 、25C 、26D 、 285.若焦点在x 轴上的椭圆1222=+m y x 的离心率为21;则m=( ) A.3 B.23 C.38 D.32 6.在同一坐标系中;方程)0(0122222>>=+=+b a by ax by a x 与的曲线大致是( )7.椭圆221259x y +=的两个焦点分别为F 1、F 2;P 为椭圆上的一点;已知PF 1⊥PF 2;则∆PF 1F 2的面积为( )A.9B.12 8.正方体1111ABCD A B C D -的棱长为1;E 是11A B 的中点;则E 到平面11ABC D 的距离是( ) A.32B.22C.12D.339.若向量a 与b 的夹角为60°;4=b ;(2)(3)72a b a b +-=-;则a =( ) A.2 B.4C.6D.1210.方程22111x y k k表示双曲线;则k 的取值范围是( )A .11<<-kB .0>kC .0≥kD .1>k 或1-<k11.方程12222=+kb y ka x (a >b >0;k >0且k ≠1);与方程12222=+by a x (a >b >0)表示的椭圆( )(A )有等长的短轴、长轴 (B )有共同的焦点(C )有公共的准线 (D )有相同的离心率 12.如图1;梯形ABCD 中;AB CD ∥;且AB ⊥平面α;224AB BC CD ===;点P 为α内一动点;且APB DPC ∠=∠;则P 点的轨迹为( ) A.直线 B.圆 C.椭圆 D.双曲线二、填空题:(本大题共5小题;每小题6分;共30分.将正确答案填在答题卷上对应题号的横线上.)13.设甲、乙、丙是三个命题;如果甲是乙的必要条件;丙是乙的充分条件;但不是乙的必要条件;那么丙是甲的 (①.充分而不必要条件;②.必要而不充分条件 ;③.充要条件) 14.在棱长为a 的正方体1111ABCD A B C D -中;向量1BA 与向量AC 所成的角为 . 15.已知向量)0,3,2(-=a ;)3,0,(k b =;若b a ,成1200的角;则k= .16.抛物线的的方程为22x y =;则抛物线的焦点坐标为____________17.以下三个关于圆锥曲线的命题中:①设A 、B 为两个定点;K 为非零常数;若|PA |-|PB |=K ;则动点P 的轨迹是双曲线。
高二数学选修2-1综合测试题(带答案)

高二数学选修2-1测试题(120分钟150分)班级姓名成绩一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知命题“如果-1≤a≤1,那么关于x的不等式(a2-4)x2+(a+2)x-1≥0的解集为 ”,它的逆命题、否命题、逆否命题及原命题中是假命题的共有( )A.0个B.1个C.2个D.4个【变式训练】命题“若C=90°,则△ABC是直角三角形”与它的逆命题、否命题、逆否命题这4个命题中,真命题的个数是( )A.0B.1C.2D.32.设m,n是平面α内的两条不同直线,l1,l2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是( )A.m∥β且l1∥αB.m∥l1且n∥l2C.m ∥β且n ∥βD.m∥β且n∥l2【变式训练】有下述说法:①a>b>0是a2>b2的充要条件;②a>b>0是<的充要条件;③a>b>0是a3>b3的充要条件.其中正确的说法有( )A.0个B.1个C.2个D.3个3. “1<m<3”是“方程+=1表示椭圆”的( ) A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知抛物线y2=2px(p>0)与双曲线-=1(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( )A. B.+1 C.+1 D.【变式训练】若双曲线C:x 2-=1(b>0)的顶点到渐近线的距离为,则双曲线的离心率e=( )A.2B.C.3D.5.已知命题p:∀x∈R,x ≥2,那么下列结论正确的是( )A.命题p:∀x∈R,x≤2B.命题p:∃x0∈R,x0<2C.命题p:∀x∈R,x≤-2D.命题p:∃x0∈R,x0<-26.已知矩形ABCD中,AB=1,BC=,将矩形ABCD沿对角线AC折起,使平面ABC与平面ACD垂直,则B与D之间的距离为( )A.1B.C.D.7.过抛物线y2=4x焦点的直线交抛物线于A,B两点,若=10,则AB的中点到y轴的距离等于( )A.1B.2C.3D.48.在四边形ABCD中,“∃λ∈R ,使得=λ,=λ”是“四边形ABCD为平行四边形”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件9.已知在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点,则直线AE与平面A1ED1所成角的大小为( )A.60°B.90°C.45°D.以上都不正确10.设F1,F2是双曲线x2-4y2=4a(a>0)的两个焦点,点P在双曲线上,且满足:·=0,||·||=2,则a的值为( )A.2B.C.1D.11.点P是棱长为1的正方体ABCD-A1B1C1D1的底面A1B1C1D1上一点,则·的取值范围是( )A. B.C.[-1,0]D.12.已知正六边形ABCDEF的边长是2,一条抛物线恰好经过该六边形的四个顶点,则抛物线的焦点到准线的距离是( )A. B. C. D.2二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.抛物线焦点在y轴上,且被y=x+1截得的弦长为5,则抛物线的标准方程为.14.在△ABC中,若∠ACB=90°,∠BAC=60°,AB=8,PC⊥平面ABC,PC=4,M是AB上一点,则PM的最小值为.15.在四棱锥P-ABCD中,ABCD为平行四边形,AC与BD交于O,G为BD上一点,BG=2GD,=a,=b,=c,试用基底{a,b,c}表示向量= .16.曲线C是平面内到直线l1:x=-1和直线l2:y=1的距离之积等于常数k2的点的轨迹.给出下列四个结论:①曲线C过点(-1,1);②曲线C关于点(-1,1)对称;③若点P在曲线C上,点A,B分别在直线l1,l2上,则+不小于2k.④设P0为曲线C上任意一点,则点P0关于直线x=-1、点(-1,1)及直线y=1对称的点分别为P1,P2,P3,则四边形P0P1P2P3的面积为定值4k2.其中,所有正确结论的序号是.三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤) 17.(10分)设p:关于x的不等式a x>1(a>0且a ≠1)的解集为{x|x<0},q:函数y=l g(ax2-x+a)的定义域为R.如果p和q有且仅有一个正确,求a的取值范围. 18.(12分)如图,正方体ABCD-A1B1C1D1中,M,N分别为AB,B1C的中点.(1)用向量法证明平面A1BD∥平面B1CD1.(2)用向量法证明MN⊥平面A1BD.19.(12分)已知抛物线C:y2=2px(p>0)过点A(1,-2).(1)求抛物线C的方程,并求其准线方程.(2)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于?若存在,求直线l的方程;若不存在,说明理由.20.(12分)设F1,F2为椭圆+=1的两个焦点,P是椭圆上一点,已知P,F1,F2是一个直角三角形的三个顶点,且|PF1|>|PF2|.(1)求|PF1|的长度.(2)求的值. 21.(12分)如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.(1)求直线BE和平面ABB1A1所成角的正弦值.(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.22.(12分)如图,四棱柱ABCD -A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.(1)证明B1C1⊥CE.(2)求二面角B1-CE-C1的正弦值.(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为,求线段AM的长.高二数学选修2-1测试题答案一、选择题1、【解析】选C.当-1≤a≤1时,Δ=(a+2)2+4(a2-4)=5--12≤5--12<0,所以原命题为真,逆否命题亦为真.反之,如a=-2时,所给不等式的解集即为空集,但a∉[-1,1],所以逆命题为假,故否命题亦为假.【变式训练】【解析】选C.原命题是真命题.其逆命题为“若△ABC是直角三角形,则C=90°”,这是一个假命题,因为当△ABC为直角三角形时,也可能A或B为直角.这样,否命题是假命题,逆否命题是真命题.因此真命题的个数是2.2.【解析】选B.对于选项A,α,β也可能相交,此时,l1,m都平行于交线,是必要不充分条件;对于选项B,由于l1与l2是相交直线,而且由l1∥m可得l1∥α,同理可得l2∥α,故可得α∥β,充分性成立,而由α∥β不一定能得到l1∥m,它们也可以异面,故必要性不成立,故选项B符合题意;对于选项C,由于m,n不一定相交,故是必要不充分条件;对于选项D,由n∥l2可转化为n∥β,同选项C,故不符合题意,【变式训练】【解析】选 A.a>b>0⇒a2>b2,a2>b2⇒|a|>|b|⇒a>b>0,故①错.a>b>0⇒<,但<⇒a>b>0,故②错.a>b>0⇒a3>b3,但a3>b 3⇒a>b>0故③错故选A.3. 【解析】选 B.当方程+=1表示椭圆时,必有所以1<m<3;但当1<m<3时,该方程不一定表示椭圆,如当m=2时,方程变为x 2+y2=1,它表示一个圆.4【解析】选B.如图,由双曲线-=1,且AF⊥x轴得-=1得|y|=,由抛物线y2=2px的定义得AF=p,即=2c.得b2=2ac,所以=,e2-1=2e,所以e=+1.【拓展延伸】求离心率的方法(1)定义法:由椭圆(双曲线)的标准方程可知,不论椭圆(双曲线)的焦点在x轴上还是在y轴上都有关系式a2-b2=c2(a2+b2=c2)以及e=.已知其中的任意两个参数,可以求其他的参数.这是基本且常用的方法.(2)方程法:建立参数a与c之间的齐次关系式,从而求出其离心率.这是求离心率的十分重要的思路及方法.(3)几何法:求与过焦点的三角形有关的离心率问题,根据平面几何性质以及椭圆(双曲线)的定义、几何性质,建立参数之间的关系,通过画出图形,观察线段之间的关系,使问题更形象、直观.【变式训练】【解析】选B.由双曲线方程知a=1,所以c=,所以一条渐近线的方程为y=bx,即bx-y=0.所以=,解得b=1,所以c=,所以e==.5.【解析】选B.全称命题的否定是特称命题,所以命题p:∃x0∈R,x0<2.6. 【解析】选B.过B,D分别向AC作垂线,垂足分别为M,N.则可求得AM=,BM=,CN=,DN=,MN=1.由于=++,所以||2=(++)2=||2+||2+||2+ 2(·+ ·+·)=+12++2(0+0+0)=,所以||=.7.【解析】选D.抛物线y2=4x的焦点(1,0),准线为l:x=-1,设AB的中点为E,过A,E,B分别作准线的垂线,垂足分别为C,F,D,EF交纵轴于点H,如图所示,则由EF为直角梯形的中位线知,|EF|===5,所以EH=EF-1=5-1=4,即AB的中点到y 轴的距离等于4.8. 【解析】选C.若=λ,=λ,则∥,∥,即AB∥DC,AD∥BC,所以四边形ABCD为平行四边形.反之,若四边形ABCD为平行四边形,则有AB∥DC,AD∥BC且AB=DC,AD=BC ,即=,=,此时λ=1,所以∃λ∈R ,使得=λ,=λ成立.所以“∃λ∈R ,使得=λ,=λ”是“四边形ABCD为平行四边形”的充分必要条件.9. 【解析】选B.以点D为原点,直线DA,DC,DD 1分别为x轴,y轴,z轴,建立空间直角坐标系,如图.由题意知,A1(1,0,2),E(1,1,1),D1(0,0,2),A(1,0,0),所以=(0,1,-1),=(1,1,-1),=(0,-1,-1).设平面A1ED1的一个法向量为n=(x,y,z).则⇒令z=1,得y=1,x=0.所以n=(0,1,1),cos<n ,>===-1.所以<n ,>=180°.所以直线AE与平面A1ED1所成的角的大小为90°.10. 【解析】选C.双曲线方程化为-=1(a>0),因为·=0,所以PF1⊥PF2.所以||2+||2=4c2=20a. ①由双曲线定义||-||=±4,②又已知||·||=2,③由①②③得20a-2×2=16a,所以a=1.11. 【解析】选D.如图所示建立空间直角坐标系,则A(1,0,1),C1(0,1,0).设P(x,y,0)其中0≤x≤1,0≤y≤1.则=(1-x,-y,1) =(-x,1-y,0)所以·=(1-x,-y,1)·(-x,1-y,0)=+-,因为+的几何意义是平面区域到点的距离的平方,所以当x=y=时,+有最小值0,当x=y=0或x=y=1或x=1,y=0或x=0,y=1时,+有最大值,所以-≤+-≤0,即·的取值范围是.12. 【解析】选B.设抛物线方程为y2=2px(p>0),根据对称性可知,正六边形ABCDEF的顶点A,B,C,F在抛物线y2=2px上,设A(x1,1),F(x2,2),则即x2=4x1,又AF==2,即(x1-x2)2=(x1-4x1)2=3,所以=,x1=,即p===.二、填空题13.【解析】设抛物线方程为x2=my,联立抛物线方程与直线方程y=x+1并消元,得:2x2-mx-2m=0,所以x1+x2=,x1x2=-m,所以5=,把x1+x2=,x1x2=-m代入解得m=4或m=-20.所以抛物线的标准方程为x2=4y或x2=-20y. 答案:x2=4y或x2=-20y 14.【解析】由条件知PC,AC,BC 两两垂直,设=a ,=b ,=c,则a·b=b·c=c·a=0,因为∠BAC=60°,AB=8,所以|a |=||=8cos60°=4,|b |=||=8sin60°=4,|c |=||=4.设=x=x(b -a),其中x∈[0,1],则=++=-c+a+x(b-a)=(1-x)a+x b-c,||2=(1-x)2|a|2+x2|b|2+|c|2+2(1-x)x a·b-2x b·c-2(1-x)a·c=16(1-x) 2+48x2+16=32(2x2-x+1)=64+28,所以当x=时,||2取最小值28,所以||min =2. 答案:215. 【解析】因为BG=2GD ,所以=.又=+=-+-=a+c-2b,所以=+=b +(a+c-2b)=a -b +c.答案:a -b +c16.【解析】设动点为(x,y),则由条件可知·=k2,①,将(-1,1)代入得0=k2,因为k>0,所以不成立,故方程不过点(-1,1),①错误.②,把方程中的x用-2-x代换,y用2-y代换,方程不变,故此曲线关于点(-1,1)对称,②正确.③,由题意知点P在曲线C上,点A,B分别在直线l1,l2上,则≥,≥,所以+≥2=2k,故③正确.④,由题意知点P0在曲线C上,根据对称性,则四边形P0P1P2P3的面积为2·2=4·=4k2,所以④正确.综上所述,正确结论的序号是②③④.答案:②③④三、解答题17.【解析】当p真时,0<a<1,当q 真时,即a>,所以p假时,a>1,q假时,a ≤.又p和q有且仅有一个正确,当p真q假时,0<a ≤;当p假q真时,a>1. 综上a 的取值范围为∪(1,+∞). 18.【证明】(1)在正方体ABCD-A1B1C1D1中,=-,=-,又因为=,=,所以=,所以BD∥B1D1.又B1D1⊂平面B1CD1,BD⊄平面B1CD1,所以BD∥平面B1CD1,同理可证A1B∥平面B1CD1.又BD∩A1B=B,所以平面A1BD∥平面B1CD1.(2)=++=++(+)=++(-+)=++.设=a ,=b ,=c,则=(a+b+c).又=-=b-a,所以·=(a+b+c)·(b-a)=(b2-a2+c·b-c·a).又因为⊥,⊥,所以c·b=0,c·a=0.又|b|=|a|,所以b2=a2.所以b2-a2=0.所以·=0.所以MN⊥BD.同理可证,MN⊥A1B.又A1B∩BD=B,所以MN⊥平面A1BD.19.【解析】(1)将A(1,-2)代入y2=2px,得(-2)2=2p·1,所以p=2.故所求抛物线C的方程为y2=4x,其准线方程为x=-1.(2)假设存在符合题意的直线l,其方程为y=-2x+t.由得y2+2y-2t=0.因为直线l与抛物线C有公共点,所以Δ=4+8t≥0,解得t≥-.由直线OA与l的距离d=,可得=,解得t=±1.因为-1∉,1∈,所以符合题意的直线l存在,其方程为2x+y-1=0.20.【解析】(1)若∠PF2F1是直角,则|PF1|2=|PF2|2+|F1F2|2,即|PF1|2=(12-|PF1|)2+80,得|PF1|=,若∠F1PF2是直角,则|PF1|2+(12-|PF1|)2=80,即2|PF1|2-24|PF1|+64=0,得|PF1|=8.(2)若∠PF2F1是直角,则|PF1|2=|PF2|2+|F1F2|2,即|PF1|2=(12-|PF1|)2+80,得|PF1|=,|PF2|=,所以=.若∠F1PF2是直角,则|PF1|2+(12-|PF1|)2=80,即2|PF1|2-24|PF1|+64=0,得|PF1|=8,|PF2|=4,所以=2,综上,=2或.21.【解析】设正方体的棱长为1.如图所示,以,,为单位正交基底建立空间直角坐标系Axyz.(1)依题意,得B(1,0,0),E,A(0,0,0),D(0,1,0),所以=,=(0,1,0).在正方体ABCD-A1B1C1D1中,因为AD⊥平面ABB1A1,所以是平面ABB1A1的一个法向量.设直线BE和平面ABB1A1所成的角为θ,则sinθ===.故直线BE和平面ABB1A1所成的角的正弦值为.(2)在棱C1D1上存在点F,使B1F∥平面A1BE.证明如下:依题意,得A1(0,0,1),=(-1,0,1),=.设n=(x,y,z)是平面A1BE的一个法向量,则由n ·=0,n ·=0,得所以x=z,y=z.取z=2,得n=(2,1,2).因为F是棱C1D1上的点,则F(t,1,1)(0≤t≤1). 又B1(1,0,1),所以=(t-1,1,0).而B1F⊄平面A1BE,于是B1F∥平面A1BE ⇒·n=0⇔(t-1,1,0)·(2,1,2)=0⇔2(t-1)+1=0⇔t=⇔F为棱C1D1的中点.这说明在棱C1D1上存在点F(C1D1的中点),使B1F∥平面A1BE.22.【解题指南】方法一:(1)建立空间直角坐标系,写出,的坐标,利用数量积证明.(2)求出平面B1CE与平面CEC1的法向量,由法向量的夹角余弦值求二面角的正弦值.(3)用直线AM的方向向量与平面ADD1A1的法向量表示直线AM与平面ADD1A1所成角的正弦,确定向量的坐标,由向量的模求线段AM的长.方法二:(1)要证明线线垂直,先证明线面垂直,关键是找出与线B1C1垂直的平面CC1E,然后进行证明.(2)要求二面角B1-CE-C1的正弦值,关键是构造出二面角B1-CE-C1的平面角,然后在三角形中求解.(3)首先构造三角形,设AM=x,在直角三角形AHM,C1D1E中用x表示出AH,EH的长度,最后在三角形AEH中利用余弦定理求解.【解析】如图,以点A为坐标原点建立空间直角坐标系,依题意得A(0,0,0),B(0,0,2),C(1,0,1),B1(0,2,2),C1(1,2,1),E(0,1,0).(1)易得=(1,0,-1),=(-1,1,-1),于是·=0,所以B1C1⊥CE.(2)=(1,-2,-1),设平面B1CE的法向量m=(x,y,z),则即消去x,得y+2z=0,不妨设z=1,可得一个法向量为m=(-3,-2,1).由(1)知B1C1⊥CE,又CC1⊥B1C1,可得B1C1⊥平面CEC1,故=(1,0,-1)为平面CEC1的一个法向量.于是cos<m ,>===-,从而sin<m ,>=.所以二面角B1-CE-C1的正弦值为.(3)=(0,1,0),=(1,1,1),设=λ=(λ,λ,λ),0≤λ≤1,有=+=(λ,λ+1,λ).可取=(0,0,2)为平面ADD1A1的一个法向量.设θ为直线AM与平面ADD1A1所成的角,则sinθ====.于是=,解得λ=,所以AM=.【一题多解】(1)因为侧棱CC1⊥底面A1B1C1D1,B1C1⊂平面A1B1C1D1,所以CC1⊥B1C1,经计算可得B1E=,B1C1=,EC1=,从而B1E2=B 1+E,所以在△B1EC1中,B1C1⊥C1E,又CC1,C1E⊂平面CC1E,CC1∩C1E=C1,所以B1C1⊥平面CC1E,又CE⊂平面CC1E,故B1C1⊥CE.(2)过B1作B1G⊥CE于点G,连接C1G,由(1)知,B1C1⊥CE,B1C1,B1G⊂平面B1C1G,B1C1∩B1G=B1,故CE⊥平面B1C1G,又C1G⊂平面B1C1G ,得CE⊥C1G,所以∠B1GC1为二面角B1-CE-C1的平面角.在△CC1E中,由CE=C1E=,CC1=2,可得C1G=.在Rt△B1C1G中,B1G=,所以sin∠B1GC1=,即二面角B1-CE-C1的正弦值为.(3)连接D1E,过点M作MH⊥ED1于点H,可得MH⊥平面ADD1A1,连接AH,AM,则∠MAH为直线AM与平面ADD1A1所成的角.设AM=x,从而在Rt△AHM中,有MH=x,AH=x,在Rt△C1D1E中,C1D1=1,ED1=,得EH=MH=x,在△AEH中,∠AEH=135°,AE=1,由AH2=AE2+EH2-2AE·EHcos135°,得x2=1+x2+x,整理得5x2-2x-6=0,解得x=.所以线段AM的长为.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学(选修2-1)试题
一、选择题(本大题共12小题,每小题6分,共72分) 1、a 3>8是a >2的( )
A .充分非必要条件
B .必要非充分条件
C .充要条件
D .既非充分也非必要条件 2、全称命题“所有被5整除的整数都是奇数”的否定是( ) A .所有被5整除的整数都不是奇数; B .所有奇数都不能被5整除
C .存在一个被5整除的整数不是奇数;
D .存在一个奇数,不能被5整除
3、抛物线281
x y -=的准线方程是( )
A . 321=x
B . 2=y
C . 32
1
=y D . 2-=y
4、有下列命题:①20ax bx c ++=是一元二次方程(0a ≠);②空集是任何集合的真子集;③若a ∈R ,则20a ≥;④若,a b ∈R 且0ab >,则0a >且0b >.其中真命题的个数有( )
A .1
B . 2
C . 3
D . 4
5、椭圆
116
2522=+y x 的离心率为( ) A .35 B . 34 C .45 D . 925
6、以坐标轴为对称轴,以原点为顶点且过圆096222=++-+y x y x 的圆心的抛物线的方程是( )
A .23x y =或23x y -=
B .23x y =
C .x y 92-=或23x y =
D .23x y -=或x y 92=
7、已知a =(2,-3,1),b =(4,-6,x ),若a ⊥b ,则x 等于( )
A .-26
B .-10
C .2
D .10 8、如图,空间四边形ABCD 中,M 、G 分别是BC 、CD 的中点,
则BD BC AB 2
1
21++等于( )
A .AD
B .GA
C .AG
D .MG
9、已知A 、B 、C 三点不共线,对平面ABC 外的任一点O ,下列条件中能确定点M 与点A 、B 、C 一定共面的是( )
A .OM OA O
B O
C =++ B . 2OM OA OB OC =-- C .11
23OM OA OB OC =+
+ D .111
333
OM OA OB OC =++
10、设3=a ,6=b , 若a •b =9,则,<>a b 等于( )
A .90°
B .60°
C .120°
D .45°
11、已知向量a =(1,1,-2),b =12,1,x ⎛
⎫ ⎪⎝
⎭,若a ·b ≥0,则实数x 的取值
范围为( )
A .2
(0,)3 B .2(0,]3
C .(,0)-∞∪2[,)3+∞
D .(,0]-∞∪2[,)3
+∞
12、设R x x ∈21,,常数0>a ,定义运算“﹡”:22122121)()(x x x x x x --+=*,若0≥x ,则动点),(a x x P *的轨迹是( )
A .圆
B .椭圆的一部分
C .双曲线的一部分
D .抛物线的一部分 二、填空题(本大题共5小题,每小题5分,共25分)
13、命题“若2430x x -+=,则x =1或x =3”的逆否命题
为 .
14、给出下列四个命题:①x ∃∈R ,是方程3x -5=0的根;②,||0x x ∀∈>R ; ③2,1x x ∃∈=R ;④2,330x x x ∀∈-+=R 都不是方程的根.
其中假命题...
的序号有 . 15、若方程
11
22
2=-+-k y k x 表示的图形是双曲线,则k 的取值范围为 .
16、抛物线24y x =的准线方程是 .
17、由向量(102)=,,a ,(121)=-,,b 确定的平面的一个法向量是
()x y =,,2n ,则x = ,y = .
三、解答题(本大题共5小题,共53分.解答应写出文字说明、演算步骤或推证过程)
18、(本小题满分8分)
双曲线的离心率等于2,且与椭圆22
1259
x y +=有相同的焦点,求此双曲线方程.
19、(本小题满分10分)
已知命题:P “若,0≥ac 则二次方程02=++c bx ax 没有实根”. (1)写出命题P 的否命题;
(2)判断命题P 的否命题的真假, 并证明你的结论.
20、(本小题满分11分)
已知0≠ab ,求证1=+b a 的充要条件是02233=--++b a ab b a
21、(本小题满分12分)
如图,在正方体ABCD -A 1B 1C 1D 1中,E 、F 分别是BB 1、CD 的中点. (Ⅰ)证明:AD ⊥D 1F ; (Ⅱ)求AE 与D 1F 所成的角; (Ⅲ)证明:面AED ⊥面A 1FD 1.
22、(本小题满分12分)
设椭圆122
22=b y a x +(a >b >0)的左焦点为F 1(-2,0),左准线 L 1 :c
a x 2-=与
x 轴交于点N (-3,0),过点N 且倾斜角为300的直线L 交椭圆于A 、B 两点。
(1)求直线L 和椭圆的方程;
(2)求证:点F 1(-2,0)在以线段AB 为直径的圆上。
参考答案
13、若x ≠1且x ≠3,则2
430x x -+≠ 14、② 15、{}21|><k k k 或
16、1x =- 17、-4,-3 三、解答题
18、解:设双曲线方程为22
221x y a b
-=(a >0,b >0),
∵ 椭圆22
1259
x y +=的焦点坐标为(-4,0)和(4,0),即c =4, 又双曲线的离心率等于2,即
2c
a
=,∴ a =2.∴ 222b c a =-=12. 故所求双曲线方程为
22
1412
x y -=. 19、解:(1)命题P 的否命题为:“若,0<ac 则二次方程02=++c bx ax 有实根”. (2)命题P 的否命题是真命题. 证明如下:
,04,0,02>-=∆⇒>-∴<ac b ac ac
∴二次方程02=++c bx ax 有实根. ∴该命题是真命题.
20、证明:必要性:
()()()0
....111,1,12
233
2
2
3
3
==----+-+=--++∴-==+a a a a a a
b a ab b a a b b a 即
充分性:=--++2233b a ab b a 0
即()()()()()01,0,.
1,0432,
0,0,0.
010223322
2
2222222=--++=+≠=+≠+⎪⎭⎫ ⎝
⎛-=+-≠≠≠=-++-=+--+-+b a ab b a b a ab b a b b a b ab a b a ab b a b ab a b ab a b ab a b a 的充要条件是当综上可知只有且即又
21、解:以点D 为原点,DA 、DC 、DD 1所在的直线分别为x 、y 、z 轴,建立如图的空间直角坐标系,设正方体的棱长为2,则D (0,0,0),A (2,0,0),
D 1(0,0,2),
E (2,2,1),
F (0,1,0). ∴AD =(-2,0,0),1D F =(0,1,-2), AE =(0,2,1)
. (Ⅰ)∵AD ·1D F =0,∴ AD ⊥D 1F .
(Ⅱ)∵AE ·1D F =0,∴AE 与D 1F 所成的角为90°. (Ⅲ)由(Ⅰ)知AD ⊥D 1F ,由(Ⅱ)知AE ⊥D 1F , 又AD ∩AE =A ,所以D 1F ⊥面AED .
又因为D 1F ⊂面A 1FD 1,所以面AED ⊥面A 1FD 1.
22、解:(1)由题意知,c =2及32
=c
a 得 a =6
∴2262
2
=-=b ∴椭圆方程为12
62
2=+y x
直线L 的方程为:y -0=tan300(x +3)即y =
3
3
(x +3) (2)由方程组⎪⎩
⎪⎨⎧+==+)3(33
6
322x y y x 得 03622=++x x 设A (x 1,y 1),B (x 2,y 2),则 x 1+x 2=-3 x 1x 2=
2
3
∵)
2)(2()
3)(3(31
222121221111++++=+⋅+=⋅x x x x x y x y k k B
F A F ]
[14
)(239)(321212121-=++++++=
x x x x x x x x
∴011190=∠⊥B AF B F A F 则
∴点F (-2,0)在以线段AB 为直径的圆上。
