10.1-统计调查---全面调查导学案
七年级下册数学教案《统计调查——全面调查》

七年级下册数学教案《统计调查——全面调查》学情分析学生在小学阶段,已经初步认识统计表、统计图,会绘制条形统计图。
知识层面的内容对初中学生来说比较容易,难点在培养用统计知识解决实际问题的意识,形成统计思想和统计观念。
而统计观念的核心是收集数据、分析数据,要能有意识地从统计的角度思考相关知识。
教学目的1、认识条形图与扇形图。
2、理解相关概念。
3、理解比较条形图与扇形图的优缺点,学会从图表中提取信息。
教学重点理解相关概念。
教学难点归纳条形图与扇形图的特点。
教学方法讲授法、讨论法、演示法、练习法、举例子教学法教学过程一、创设情境从报纸、杂志、电视、互联网等媒体上,我们经常可以看到很多统计数据和统计图表。
例如,从2012年到2021年,我国国内生产总值(GDP)从54万亿元增长到114万亿元,2021年我国义务教育的巩固率达95.4%,某电视节目的收视率为9%,某地年人均生活用水量为36m3等。
这些数据可以帮助人们了解周围世界的现状和变化规律,从而为人们制定决策提供依据。
这些数据和统计表是怎么得到的呢?这节课我们就来学习统计调查。
二、分析解答自学教材136面。
1、收集与整理数据(1)如果要了解全班同学对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,该怎么做?①调查的对象是什么?②怎样达到调查目的?为了解决问题,需要做问卷调查,请设计一份调查问卷。
采用调查问卷,可以收集到全班每位同学最喜爱的节目的编号,我们把它们称为数据。
杂乱无章的数据不利于我们发现其中的规律。
为了清晰地发现数据中的规律,需要对数据进行整理。
此例中,用划记法记录数据,例如画“正”字,“正”字的每一划(笔画)代表一名同学。
2、描述数据的方法为了更直观地看出表中的信息,可以用条形图和扇形图来描述数据。
条形图:通过柱图高度,反映各个部分数量的大小。
扇形图:通过扇形大小,反映各个部分占总体的百分比。
3、思考:条形图和扇形图的优缺点(1)条形图优点:能清楚地反应各个项目的具体数目,便于相互比较。
2022年初中数学《全面调查》导学案(推荐)
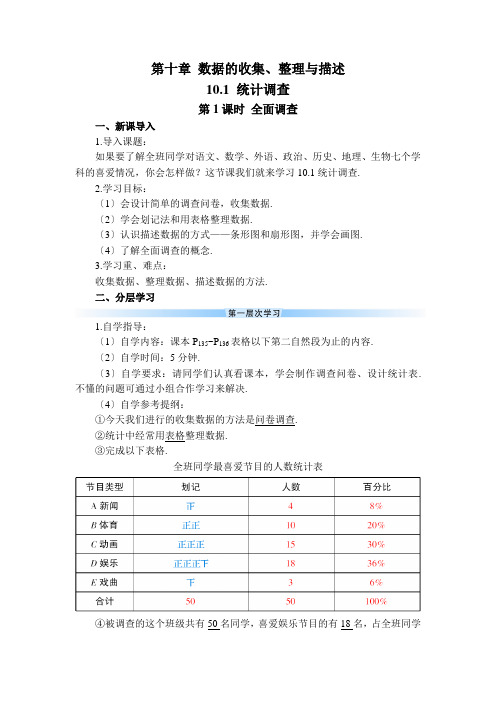
第十章数据的收集、整理与描述10.1 统计调查第1课时全面调查一、新课导入1.导入课题:如果要了解全班同学对语文、数学、外语、政治、历史、地理、生物七个学科的喜爱情况,你会怎样做?这节课我们就来学习10.1统计调查.2.学习目标:〔1〕会设计简单的调查问卷,收集数据.〔2〕学会划记法和用表格整理数据.〔3〕认识描述数据的方式——条形图和扇形图,并学会画图.〔4〕了解全面调查的概念.3.学习重、难点:收集数据、整理数据、描述数据的方法.二、分层学习1.自学指导:〔1〕自学内容:课本P135~P136表格以下第二自然段为止的内容.〔2〕自学时间:5分钟.〔3〕自学要求:请同学们认真看课本,学会制作调查问卷、设计统计表.不懂的问题可通过小组合作学习来解决.〔4〕自学参考提纲:①今天我们进行的收集数据的方法是问卷调查.②统计中经常用表格整理数据.③完成以下表格.全班同学最喜爱节目的人数统计表④被调查的这个班级共有50名同学,喜爱娱乐节目的有18名,占全班同学2.自学:同学们可结合自学指导进行自学.3.助学:〔1〕师助生:①明了学情:教师深入课堂了解自学进度和自学中存在的问题:①能否根据要求设计简单的调查问卷;②用表格划记的方法整理数据是否细致准确.②差异指导:对学习有困难或方法不当的学生进行引导.〔2〕生助生:小组内学生之间相互协作交流,订正和研讨.4.强化:〔1〕收集数据、整理数据的方法.〔2〕练习:小明为了解同学们的课余生活,设计了如下调查问题:你平时最喜欢的一项课余活动是〔〕你认为此问题的答案选项设计合理吗?为什么?如果不合理,请修改.1.自学指导:〔1〕自学内容:课本P136剩下局部至P137“练习〞之前的内容.〔2〕自学时间:5分钟.〔3〕自学要求:认真阅读课文,学会绘制条形图和扇形图来描述数据.〔4〕自学参考提纲:①描述数据还可以用条形图和扇形图.②因为组成扇形图的各扇形圆心角的和是360°,所以只需根据各类节目所占的百分比就可以算出对应扇形圆心角的度数.圆心角越大,扇形在圆中占的比例就大.新闻:360°×°,体育:360°×20%=72°,动画:360°×30%=108°,娱乐:360°×°,戏曲:360°×°.根据算得的圆心角的度数在图中画出相应节目的扇③条形图通过柱图高度来反映各个局部数量的大小,扇形图通过扇形的大小来反映各个局部占总体的百分比.④全面调查是指考察全体对象.2.自学:同学们可结合自学指导进行自学.3.助学:〔1〕师助生:①明了学情:教师深入课堂了解自学进度和自学中存在的问题〔会不会计算扇形的圆心角;会不会绘制条形图和扇形图;能否理解条形图和扇形图统计数据的侧重点〕.②差异指导:对学习有困难和方法不当的学生进行引导.〔2〕生助生:小组内学生之间相互交流,提供帮助.4.强化:〔1〕统计调查的一般步骤.〔2〕描述数据的方法和各种方法反映数据的特点.〔3〕练习:经调查,某班学生上学所用的交通工具中,自行车占60%,公交车占30%,其他占10%,请画出扇形描述以上统计数据.三、评价1.学生的自我评价:各小组长汇报本组的学习收获和困惑.2.教师对学生的评价:〔1〕表现性评价:对学生的学习态度、方法和收效进行点评.〔2〕纸笔评价:课堂评价检测.3.教师的自我评价〔教学反思〕:统计与现实生活的联系是非常紧密的,通过选择学生感兴趣的典型例题对教学课堂概念进行拓展.在教学过程中,充分表达学生是学习的主体,通过让学生亲自动手收集和整理数据,让学生体会到数学活动充满了乐趣,使学生更好地体会统计思想,建立统计概念,培养学生的动手实践能力.(时间:12分钟总分值:100分)一、根底稳固〔70分〕1.〔10分〕用折线统计图,反映某天6时~12时气温变化情况;用条形统计图,反映某班40名同学所穿鞋的码数;用扇形统计图,反映某市五个区的占地面积占全市总面积的比例大小.2.〔10分〕统计中经常用表格整理数据;还可以用条形统计图、扇形统计图来描述数据.3.〔10分〕在扇形统计图中,其中一个扇形的圆心角为72°,那么这个扇形所表示的量占总量的百分比是20%.4.〔20分〕如图1,所提供的信息正确的选项是〔B 〕5.〔20分〕我国体育健儿在七届奥运会上获得奖牌的情况如图2所示.〔1〕七届奥运会上,我国体育健儿共获得多少枚奖牌?解:32+28+54+50+59+63+100=386〔枚〕答:最近七届奥运会上,我国体育健儿共获得386枚奖牌.〔2〕用条形图表示折线图中的信息.解:二、综合运用〔20分〕6.如图的两个统计图,女生人数多的学校是〔D 〕C.甲、乙两校女生人数一样多7.以下列图是根据某班学生上学的三种方式(乘车、步行、骑车)的人数绘制的条形统计图和扇形统计图.如下列图:〔1〕求该班有多少名学生;解:25÷50%=50〔人〕.〔2〕补上人数分布条形统计图的空缺局部.三、拓展延伸〔10分〕8.某学校七年级某班学生都参加兴趣小组,人数统计图如以下列图.〔1〕该班共有多少人参加?解:6+14+12+18+10=60〔人〕.〔2〕哪个小组人最多?哪个小组人最少?解:绘画小组人最多,小提琴小组人最少.〔3〕哪个小组占总人数的百分比最多?解:绘画小组.〔4〕请按画出的扇形图表示各小组人数占总人数的百分比(比例).解:如下列图.5.3.1 平行线的性质一、新课导入1.导入课题:利用同位角、内错角、同旁内角之间的关系可以判定两条直线平行.你还记得这些判定方法分别是如何表达的吗?反过来,如果两条直线平行,那么同位角、内错角、同旁内角又各有什么关系呢?这就是本节课我们所要研究的内容.〔板书课题〕2.学习目标:〔1〕能表达平行线的三条性质.〔2〕能运用平行线的三条性质进行简单的推理和计算.3.学习重、难点:重点:对平行线性质的理解及它们与平行线的判定之间的关系.难点:性质2和性质3的推理过程的逻辑表述.二、分层学习1.自学指导:〔1〕自学内容:课本P18的内容.〔2〕自学时间:8分钟.〔3〕自学要求:正确画图、测量、验证、归纳.〔4〕探究提纲:①画图:画两条平行线a∥b,再画一条截线c与直线a、b相交〔如图1所示〕.②测量:测量这些角的度数,把结果填入表内.③分析:∠1~∠8中,哪些是同位角?它们的度数之间有什么关系?答案:同位角有:∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8,相等.④猜想:两条平行线被第三条直线截得的同位角有什么关系?⑤验证:如果改变截线的位置,你的猜想还成立吗?⑥归纳:a.你能用文字语言表述你发现的结论吗?b.你还能用符号语言表述该结论吗?2.自学:学生按探究提纲进行研讨式学习.3.助学:〔1〕师助生:①明了学情:了解学生围绕探究提纲进行学习的情况及存在的困惑.②差异指导:对个别学生在学法和认知有偏差时进行点拨引导.〔2〕生助生:小组内学生之间相互交流,展示成果,查找并纠正不正确的认识或结论.4.强化:〔1〕平行线的性质1及其几何表述.〔2〕经历平行线的性质1的探究过程,体会研究几何图形的一般方法.1.自学指导:〔1〕自学内容:课本P19的内容.〔2〕自学时间:8分钟.〔3〕自学要求:阅读教材,重要的局部做好圈点,疑点处做好记号.〔4〕自学参考提纲:①与平行线的判定类似,你能由性质1推出两条平行线被第三条直线截得的内错角之间的关系吗?a.结合图2,你能写出推理过程吗?b.类比性质1,你能用文字语言表述上面的结论吗?答案:两直线平行,内错角相等.c.你还能用几何语言表述该结论吗?②a.类似地,可以推出平行线关于同旁内角的性质3:两直线平行,同旁内角互补,如图2,用几何语言表述为:∵a∥b,∴∠2+∠4=180°.b.试写出用性质1推出性质3的推理过程.c.试写出用性质2推出性质3的推理过程.③如图3,平行线AB、CD被直线AE所截.∠1=110°,可以知道∠2是多少度吗?为什么?答案:∠2=110°.两直线平行,内错角相等.∠1=110°,可以知道∠3是多少度吗?为什么?答案:∠3=110°.两直线平行,同位角相等.∠1=110°,可以知道∠4是多少度吗?为什么?答案:∠4=70°.两直线平行,同旁内角互补.④如图4,AB∥CD,AE∥CF,∠A=39°,∠C是多少度?为什么?答案:∠C=39°.∵AB∥CD,∴∠C=∠FGB,又∵AE∥CF,∴∠A=∠FGB,∴∠A=∠C=39°.2.自学:同学们可参照自学参考提纲进行自学.3.助学:〔1〕师助生:①明了学情:教师深入课堂巡视了解学生的自学情况,尤其是性质2和性质3的推理过程,看学生能否写出来.②差异指导:对局部感到困难的学生进行点拨引导.〔2〕生助生:小组内相互交流、研讨、订正.4.强化:〔1〕平行线的性质1、2、3及其几何表述.〔2〕判定与性质的区别:从角的关系得到两直线平行,就是判定;从直线平行得到角相等或互补,就是性质.〔3〕练习:课本P20“练习〞第1题和第2题.三、评价1.学生学习的自我评价:各小组组长对本组的学习成果和困惑进行总结交流.2.教师对学生的评价:〔1〕表现性评价:对学生在学习中的态度、方法、成效及缺乏进行点评.〔2〕纸笔评价:课堂评价检测.3.教师的自我评价〔教学反思〕:这节课比较成功的地方是:①对教学的方式进行了一定的尝试,注重学生的分析能力,启发学生用不同方法解决问题.②尽量锻炼学生使用标准性的几何语言.缺乏的是师生之间的互动配合和默契程度有待加强.(时间:12分钟总分值:100分)一、根底稳固〔60分〕1.〔10分〕如图,由AB∥CD可以得到〔C〕A.∠1=∠2B.∠2=∠3C.∠1=∠4D.∠3=∠4第1题图第2题图2.〔10分〕如图,如果AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=〔C〕A.180°B.270°C.360°D.540°3.〔10分〕如图,一条公路两次转弯后,和原来的方向相同,那么如果第一次拐的角是76°,那么第二次拐的角是76度,根据是两直线平行,内错角相等.4.〔10分〕如图,要在公路的两侧铺设平行管道,如果公路一侧铺设的管道与纵向联通管道的角度为120°,那么,为了使管道对接,另一侧应以60°角度铺设纵向联通管道,根据是两直线平行,同旁内角互补.第3题图第4题图第5题图5.〔20分〕如图,a∥b,c、d是截线,假设∠1=80°,∠5=70°,求∠2、∠3、∠4各是多少度?为什么?解:∵a∥b,∴∠2=∠1=80°〔两直线平行,内错角相等〕,∠3=180°-∠5=110°(两直线平行,同旁内角互补).∵∠4=∠3(两直线平行,同位角相等),∴∠4=110°.二、综合运用〔20分〕6.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1=45°,∠2=122°,求图中其他角的度数.解:由题意得:∠3=∠1=45°,∠1+∠7=180°,∴∠7=180°-∠1=135°.∴∠8=∠7=135°.又∠4=∠2=122°,∠2+∠5=180°,∴∠5=180°-∠2=58°.∴∠6=∠5=58°.三、拓展延伸〔20分〕7.如图,直线DE经过点A,DE∥BC,∠B=44°,∠C=57°.〔1〕∠DAB等于多少度?为什么?〔2〕∠EAC等于多少度?为什么?〔3〕∠BAC等于多少度?〔4〕由〔1〕、〔2〕、〔3〕的结果,你能说明为什么三角形的内角和是180°吗?解:〔1〕∵DE∥BC,∴∠DAB=∠B=44°〔两直线平行,内错角相等〕.〔2〕∵DE∥BC,∴∠EAC=∠C=57°(两直线平行,内错角相等).〔3〕∵∠DAB+∠BAC+∠EAC=180°,∴∠BAC=180°-∠DAB-∠EAC=180°-44°-57°=79°.。
人教版数学七年级下册10.1统计调查全面调查(教案)

2.调查问卷设计的指导。在实践活动环节,部分学生在设计问卷时遇到了困难,问题设置不够合理,选项设计也存在问题。为此,我计划在下一节课中增加一个专门的环节,详细讲解问卷设计的方法和技巧,以便学生能够更好地完成调查任务。
3.重点难点解析:在讲授过程中,我会特别强调全面调查的概念和适用范围,以及调查问卷设计这两个重点。对于难点部分,我会通过举例和比较来帮助大家理解如何设计合理的问卷和实施调查。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与全面调查相关的实际问题,如设计一份关于校园环保意识的全面调查问卷。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解全面调查的基本概念。全面调查是对调查对象进行逐个、全部的调查方式。它是获取准确、全面数据的重要手段,适用于总体数量较小、调查内容简单的情况。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了如何通过全面调查了解全班同学的阅读喜好,以及全面调查如何帮助我们更好地开展课外阅读活动。
3.学生小组讨论的引导。在小组讨论过程中,我发现部分学生参与度不高,可能是因为他们对于讨论主题不感兴趣或者不知道如何发表自己的观点。为了提高学生的参与度,我将在今后的教学中尝试以下方法:一是提前为学生提供讨论话题,让他们有足够的时间进行思考;二是引导学生从不同角度看待问题,激发他们的思维火花。
4.教学内容的拓展。在本次教学中,我注意到学生对全面调查在实际生活中的应用非常感兴趣。因此,我计划在后续的教学中,适当增加一些拓展内容,如全面调查在其他领域的应用、全面调查与抽样调查的优缺点对比等,帮助学生更全面地了解这一知识点。
10.1全面调查导学案

10.1统计调查——全面调查导学案(第一课时)【数学自然课堂:目标导学激发学力】【学习目标】1、掌握全面调查的概念.2、掌握全面调查的一般步骤和适用范围,知道条形统计图和扇形统计图的特征和制作.3、从条形统计图和扇形统计图中获取信息进行相关的计算和说明(解决生活问题).【学习重、难点】重点:掌握全面调查的概念.难点:能用统计图描述数据.【学习过程】【一、自主学习(自由思考)】1、如果要了解全班同学对新闻,体育,动画,娱乐,戏曲五类电视节目的喜爱情况,需要做 .2、统计调查的步骤(1)数据.为此要设计 .如果要想了解男、女生喜爱节目的差异,问卷中还应该包含 .用字母代替节目类型的优点是 .(2)数据.为了更清楚了解数据所蕴含的规律,需要对数据进行整理.统计中常用划记的方法来数据.(3)数据.为了更直观地看出表中的信息,还可以用图和图来描述数据.(利用图可以很直观地看出喜欢各类电视节目的人数,利用图可以很清楚地看出喜欢各类电视节目的人数占总人数的百分比.)(4)得出结论.3、全面调查:是指考察的调查.【数学自然课堂:自然、民主、自由】【二、合作探究、交流、展示、点评】过程:问题:如果想要了解全班同学对赵丽颖、鹿晗、Tfboy的喜爱情况,我们来做一个调查.(一)收集数据. 就上面的问题我们可以设计如下调查问卷:(二)整理数据. 全班同学最喜爱明星的人数统计述数据1、条形图:2、扇形图:(四)得出结论:【数学自然课堂:训练主线、自然发展】【三、当堂检测】1、下列调查适合全面调查的是()A.调查2009年6月份市场上某品牌饮料的质量B.了解中央电视台直播北京奥运会开幕式的全国收视率情况C.环保部门调查5月份黄河某段水域的水质量情况D.了解全班同学本周末参加社区活动的时间2、下列调查方式中.不合适的是()A.了解2008年5月18日晚中央电视台“爱的奉献”抗震救灾文艺晚会的收视率,采用抽查的方式B.了解某渔场中青鱼的平均重量,采用抽查的方式C.了解某型号联想电脑的使用寿命,采用普查的方式D.了解一批汽车的刹车性能,采用普查的方式3、政府为了更好的加强城市建设,就社会热点问题广泛征求市民意见,方式是发调查表,要求每位被调查人员只写一个你最关心的有关城市建设的问题.经统计整理,发现对环境保护问题提出的最多,共700个,同时制作了相应的条形统计图,请回答下列问题:(1)共收回调查表多少张?(2)提道路交通问题的有多少人?(3)请你把这个条形统计图用扇形统计图表示出来.【四、课后延伸】。
10.1统计调查第1课时全面调查课件人教版数学七年级下册

利用调查问卷,可以收集到全班每位同学最喜爱的节目的编号(字母), 我们把它们称为数据.例如,某同学经调查,得到如下50个数据: CCADBCADCD CEABDDBCCC DBDCDDDCDC EBBDDCCEBD ABDDCBCBDD
从这些数据中,你能看出全班同学喜爱各类节目的情况吗?
杂乱无章的数据不利于我们发现其中的规律.为了更清楚地了解数据所
A 弧
O 圆心角
B
扇形
圆心角越大,扇形在圆 中占的百分比就越大.
归纳总结
制作扇形统计图的步骤: (1)计算各部分在总体中所占的百分比; (2)计算各部分相应的扇形圆心角的度数;
扇形的圆心角度数=360°×该部分占总体的百分比. (3)取适当的半径画圆,用量角器画出各圆心角所对的扇形; (4)将各部分代表的名称和相应的百分比标注在对应的扇形中.
蕴含的规律,需要对数据进行整理.统计中经常用表格整理数据,对前
面数据的整理如下.
全班同学最喜爱节目的人数统计表
节目类型 划记
人数 百分比
A 新闻
4
8%
B 体育
10
20%
C 动画
15
30%
D 娱乐
18
36%
E 戏曲
3
6%
合计
50
50
100%
上表中,用划记法记录数据时,“正”字的每一划(笔画)代表一名同学, 例如,编号为A的节目对应的人数是4,记为“ ”.
上表可以清楚地反映全班同学喜爱各类节目的情况.例如,最喜爱新闻 节目的同学有4名,占全班同学的8%;最喜爱体育节目的同学有10名, 占全班同学的20%;等等.
除整理成表,还可以如何 表达整理后的数据?
为了更直观地看出表中的信息,还可以用条形统计图和扇形统计图来 描述数据.
新课标人教版七年级数学下册《10.1 统计调查(第一课时 全面调查) 》导学案

新课标人教版七年级数学下册《10.1 统计调查(第一课时全面调查)》导学案
新课标人教版七年级数学下册《10.1 统计调查(第一课时全面调查)》导学案
二、全面调查:考查全体对象的调查就叫做全面调查(也叫做普查)
三、小结
今天主要学习了统计调查中如何收集、整理、描述和分析数据,这些过程就是我们统计中的基本过程,特别是要会制作条形统计图或扇形统计图来对数据进行直观形象的描述。
(条形统计图能够显示每组中的具体数据,易于比较数据之间的差别;扇形统计图反映了各部分在总体中所占的百分比的大小,易于显示每组数据相对于总数的大小,折线统计图不但可以表示出数量的多少,而且还能够清楚的表示出数量增减变化的情况。
)
四、随堂作业
1、在进行数据描述时,要显示每组中的具体数据,应采用图;要显示部分在总体中所占的百分比,应采用图;要显示数据的变化趋势,应采用图;
2、在扇形统计图中,其中一个扇形的圆心角是216°,则这年扇形所表示的部分占总体的百分数是.
3.已知全班有40位学生,他们有的步行,有的骑车,还有的乘车来上学,根据以下已知信息完成统计表:
上学方式步行骑车乘车。
10.1.1全面调查导学案2022-2023学年人教版数学七年级下册

10.1.1全面调查导学案2022-2023学年人教版数学七年级下册本文以“10.1.1全面调查导学案”为题,为学习2022-2023学年人教版数学七年级下册的同学们提供一些指导和建议。
在本文中,我们将重点讨论如何完成10.1.1这一课的全面调查导学案。
10.1.1课程内容简介在数学七年级下册第十章第一节中,我们将学习全面调查这一知识点。
全面调查是指通过分析数据、调查现象等方式,获取相关的信息和知识,并对这些信息和知识进行整理和分析,形成科学的结论和推论,从而更好地理解和应用相关的知识。
具体的内容包括:1.了解全面调查的基本概念和方法;2.掌握通过总体抽样和随机抽样的方法进行调查;3.学习如何设计调查问卷、如何采访受访者等基本技巧;4.学会如何对调查数据进行分析和统计,并作出相关的结论和推论。
掌握这些知识和技能对于理解和应用数学知识非常重要,也是数学学习的基础。
10.1.1调查思路与方法在学习《全面调查》这一知识点之前,我们需要了解以下几个问题:1.调查的目的是什么;2.调查的对象是谁;3.调查的范围和内容是什么;4.调查的方法和手段是哪些。
只有了解了这些问题,我们才能有针对性地进行调查,并从调查中获得有效的信息和知识。
在进行全面调查之前,我们首先需要设定调查的目的和目标,确定应该采用哪种调查方法和手段,形成调查计划和调查问卷,并进行调查。
一般来说,调查方法可以分为总体抽样和随机抽样两种。
在选择调查方法时,我们应根据实际情况采取不同的方法。
总体抽样是指对于整个调查范围进行抽样,并根据抽样的样本进行分析和推论。
这种方法适用于调查范围比较小,样本比较少的情况。
随机抽样是指对于样本中的每一个元素都有相同的概率被选择,从而对整个调查范围进行分析和推论。
这种方法适用于调查范围比较大,样本比较多的情况。
在进行调查的过程中,我们应该搜集和整理相关的数据、资料和信息,并进行分析和统计。
通过对数据的分析和统计,我们可以得到一些有用的信息和结论,从而更好地理解和应用相关的知识。
101统计调查二导学案及答案

101统计调查二导学案及答案篇一:10.1.1统计调查导学案10.1.1 统计调查导学案班别:姓名:50名同学调查结果如下:E B B C E B D C D BA D C C C D C D C B C E C D C B C B D A D D C D D C D D D C A B D C B D D D B C学生最喜爱的熊猫名字人数统计表条形统计图的绘制:扇形统计图的绘制:统计调查的基本步骤:学以致用1、如图是七年级(2)班“最喜欢的球类运动”的扇形统计图。
A表示乒乓球,B表示篮球,C表示排球,D表示足球,E 表示其他,则(1)E占总人数的百分比是:(2)扇形B所对的圆心角度数为:(3)若喜欢排球人数是12人,那么该班的总人数是多少人?喜欢足球的人数又是多少人?2、如图是某晚报“百姓热线”一周内接听热线电话的统计图,其中有关环境保护问题的电话最多,共有70个,请回答下列问题:(1)本周“百姓热线”共接到热线电话___________个;(2)有关道路交通的电话有_________个;(3)本周内哪个类型的热线电话数最少?(4)从图中,你还能获得哪些信息?3、小明对本班同学上学的交通方式进行了一次调查,他根据采集的数据,绘制了下面的统计图①和图②.请你根据图中提供的信息,解答下列问题:(1)计算本班骑自行车上学的人数,补全图①的统计图;(2)在图②中,求出“乘公共汽车”部分所对应的圆心角的度数,补全图②的统计图(要求写出各部分所占的百分比);(3)观察图①和图②,你能得出哪些结论?(只要求写出一条).篇二:10.1统计调查2导学案凤州初级中学七年级数学导学案(2)【课题】统计调查2 【课型】新授课【学习目标】1、了解总体、个体、样本及样本容的概念以及抽样调查的意义 2、明确在什么情况下采用抽样调查或全面调查 3、进一步熟悉对数据的收集、整理、描述和分析。
【学习重点】对概念的理解及对数据收集整理【学习难点】总体概念的理解和随机抽样的合理性【自主学习】(以下的题目,你能独立完成吗?相信自己,你一定能够做得到。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.1 统计调查----全面调查
【学习目标】
了解全面调查的意义,初步学会简单的数据的收集、整理以及会用条形统计图、扇形统计图直观地描述数据。
【重点、难点】
重点:对数据的收集、整理及描述。
难点:绘制扇形统计图和条形统计图。
【学习过程】
预习课本第151页到153页内容
(一)基本概念:
(1)用收集数据,用整理数据,用和描述数据。
(2)调查方法:全面调查、抽样调查和简单随机抽样调查。
(3)叫做全面调查。
(二))自我制作统计图
1. 条形图的一般步骤
(1)根据图纸的大小,画出两条互相垂直的射线;
(2)在水平射线上,适当分配条形的位置,确定条形的宽度和间隔;
(3)在与水平射线垂直的射线上,根据数据大小的情况,确定单位长度表示多少;
(4)按照数据的大小,画出长短不同的直条,并注明数量。
2.扇形图的一般步骤
(1)先算出各部分数量占的百分之几;
(2)再算出表示各部分数量的扇形的度数;
(3)取适当的半径画一个圆,并按上面算出的度数,在圈里画出各个扇形;
(4)每个扇形中标明所表示的各部分数量名称和所占的,并用不同的颜色或条纹把各个扇形区别开。
(5)圆心角越大,扇形在圆中所占的比例就越大。
活动一:收集数据
1、设计调查问卷:
3、收集数据
第一组: 第二组: 第三组: 第四组: 第五组: 第六组:
活动二:整理数据 百分比= ×100% 把收集的调查数据进行整理,填写下列表格:
1
2、扇形统计图:
对应扇形圆心角的计算方法是: ,各类圆心角分别为: A 类: ; B 类: C 类: ; D 类: ;
活动四:分析数据
; 。
活动五:总结
根据统计调查的结果你想对我们班的同学说点什么呢?
三、课堂总结
1、全面调查的定义:
2、全面调查的基本过程:
→→→→3、条形统计图与扇形统计图的画法以及特点:
四、检测(完成课本P137练习)。
