连续型Hopfield神经网络
合集下载
第8章 神经网络-Hopfield网络
8.2.2 状态轨迹为极限环
如果在某些参数的情况下，状态N(t)的轨迹是一 个圆，或一个环，状态N(t)沿着环重复旋转，永不停 止，此时的输出A(t)也出现周期变化，即出现振荡， 如图8.4中C的轨迹即是极限环出现的情形。
对于DHNN，轨迹变化可能在两种状态下来回跳 动，其极限环为2。如果在r种状态下循环变化，称 其极限环为r。
对于CHNN，因为f(·)是连续的，因而，其轨迹 也是连续的，如图中B、C所示。
对于不同的连接权值wij和输入Pj(i, j=1, 2, … r)， 反馈网络状态轨迹可能出现以下几种情况。
8.2.1 状态轨迹为稳定点
状态轨迹从系统在t0时状态的初值N(t0)开始，经 过一定的时间t(t＞0)后，到达N(t0+t)。如果 N(t0+t+Δt)=N(t0+t)，Δt＞0，则状态N(t0+t)称为网络 的稳定点，或平衡点。
在人工神经网络中，由于输入、输出激活函数是 一个有界函数，虽然状态N(t)是发散的，但其输出A(t) 还是稳定的，而A（t）的稳定反过来又限制了状态的 发散。
一般非线性人工神经网络中发散现象是不会发生 的，除非神经元的输入输出激活函数是线性的。
目前的人工神经网络是利用第一种情况即稳定的专 门轨迹来解决某些问题的。
如果ai=f(ni)中的f(·)为一个连续单调上升的有界 函数，这类网络被称为连续型反馈网络。图8.3中所示 为一个具有饱和线性激活函数，它满足连续单调上升
的有界函数的条件，常作为连续型的激活函数。
图8.2 DHNN中的激活函数 图8.3 CHNN中的激活函数
8.2 状态轨迹
设状态矢量N=[n1, n2, …，nr]，网络的输出矢量 为A＝[a1，a2…，as]T ，
连续Hopfield网络的结构和工作方式
连续Hopfield网络的 网络的 连续 结构和工作方式
1
离散的Hopfield网络
对于每个神经元, 对于每个神经元 有
n si = ∑ wij x j − θ i j =1 xi = f ( si )
1 s ≥0 f (s) = −1 s <0
1
2
将离散的Hopfield神经网络模型扩展到连续时间的动力 学模型，输入和输出都取连续值，其网络的基本结构不变。
根据图示电路有
n V −u dui ui j i + + Ii = ∑ Ci Rij dt Ri j =1 Vi = f (ui )
令
n 1 1 1 = +∑ Ri' Ri j =1 Rij
整理得
通过求解此微分方 程，得到神经元的 输出或状态
n Vj dui ui Ii =− ' +∑ − Ri Ci j =1 Rij Ci Ci dt Vi = f (ui )
对于连续Hopfield 网络 每个神经元的工作方式是 网络, 对于连续
n s i = ∑ w ij x j − θ i j =1 1 dy i yi + si = − τ dt xi = f ( yi )
同样假定
w = wji ij
23
• 连续和离散 连续和离散Hopfield网络的区别 网络的区别 离散Hopfield网络
1 xi = f ( yi ) = 1 + e − µyi
45
Hopfield利用模拟电路设计的连续Hopfield网络的电路模型
6
n s i = ∑ w ij x j − θ i j =1 1 dy i yi + si = − τ dt xi =
1
离散的Hopfield网络
对于每个神经元, 对于每个神经元 有
n si = ∑ wij x j − θ i j =1 xi = f ( si )
1 s ≥0 f (s) = −1 s <0
1
2
将离散的Hopfield神经网络模型扩展到连续时间的动力 学模型，输入和输出都取连续值，其网络的基本结构不变。
根据图示电路有
n V −u dui ui j i + + Ii = ∑ Ci Rij dt Ri j =1 Vi = f (ui )
令
n 1 1 1 = +∑ Ri' Ri j =1 Rij
整理得
通过求解此微分方 程，得到神经元的 输出或状态
n Vj dui ui Ii =− ' +∑ − Ri Ci j =1 Rij Ci Ci dt Vi = f (ui )
对于连续Hopfield 网络 每个神经元的工作方式是 网络, 对于连续
n s i = ∑ w ij x j − θ i j =1 1 dy i yi + si = − τ dt xi = f ( yi )
同样假定
w = wji ij
23
• 连续和离散 连续和离散Hopfield网络的区别 网络的区别 离散Hopfield网络
1 xi = f ( yi ) = 1 + e − µyi
45
Hopfield利用模拟电路设计的连续Hopfield网络的电路模型
6
n s i = ∑ w ij x j − θ i j =1 1 dy i yi + si = − τ dt xi =
第5章 Hopfield神经网络与联想记忆
第5章Hopfield神经网络与联想记忆前面介绍了前向网络及其学习算法，对于所介绍的前向网络，从学习的观点来看，它是一个强有力的学习系统，系统结构简单、易于编程；从系统的观点来看，它是一个静态非线性映射，通过简单非线性处理单元的复合映射可获得复杂系统的非线性处理能力；从计算的观点来看，它并不是一强有力系统，缺乏丰富的动力学行为。
反馈神经网络是一个反馈动力学系统，具有更强的计算能力。
1982年美国物理学家J. Hopfield提出的单层全互连含有对称突触连接的反馈网络是最典型的反馈网络模型。
Hopfield 用能量函数的思想形成了一种新的计算方法，阐明了神经网络与动力学的关系，并用非线性动力学的方法来研究这种神经网络的特性，建立了神经网络稳定性判据，并指出信息存储在网络中神经元之间的连接上，形成了所谓的Hopfield网络，称之为离散Hopfield网络。
而且Hopfield还将该反馈网络同统计物理中的Ising模型相类比，把磁旋的向上和向下方向看成神经元的激活和抑制两种状态，把磁旋的的相互作用看成神经元的突触权值。
这种类推为大量的物理学理论和许多的物理学家进入神经网络领域铺平了道路。
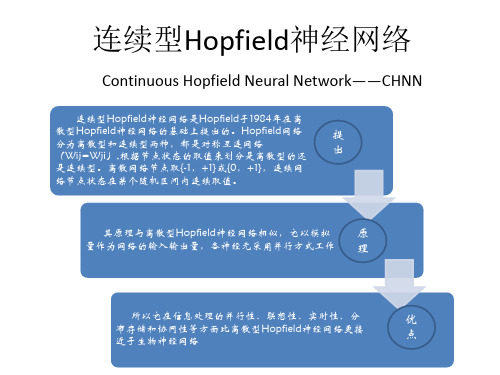
1984年，Hopfield设计与研制了Hopfield网络模型的电路，指出神经元可以用运算放大器来实现，所有神经元的连接可用电子线路来模拟，称之为连续Hopfield网络。
用该电路Hopfield成功的解决了旅行商（TSP）计算难题（优化问题）。
Hopfield网络是神经网络发展历史上的一个重要的里程碑。
把神经网络看作一种非线性的动力学系统，并特别注意其稳定性研究的学科，被称为神经动力学（Neurodynamics）。
Hopfield神经网络可看作一种非线性的动力学系统，所以为了方便介绍Hopfield神经网络，本章首先简单介绍神经动力学。
前面介绍的单层前向网络和多层前向网络，其思路均是先介绍网络模型再介绍相应的学习算法。
霍普菲尔德(Hopfield)神经网络概述
Hopfield网络的应用
组合优化 (TSP问题) 组合优化问题，就是在给定约束条件下， 求出使目标函数极小（或极大）的变量组 合问题。 将Hopfield网络应用于求解组合优化问题， 就是把目标函数转化为网络的能量函数， 把问题的变量对应于网络的状态。这样当 网络的能量函数收敛于极小值时，问题的 最优解也随之求出。
Hopfield网络的特点
单层反馈式网络
x1 o1 W x2 o2 … … xn
on
Hopfield网络的特点
灌输式学习方式 灌输式学习中网络权值不是通过训练逐渐 形成的，而是通过某种设计方法得到的。 权值一旦设计好就一次灌输给网络，不再 变动， 这种学习是死记硬背式的，而不是训练式 的。
Hopfield网络的特点
各神经元的状态在运行中不断更新
x1 o1 W x2 o2 … … xn
on
Hopfield网络的特点
首次引入能量函数
考虑了输入与输出的延迟因素
Hopfield网络的分类
根据激活函数的不同，可以分为： 离散型 Hopfield神经网络（DHNN） 1 netj ≥ 0 f(netj ) = sgn(netj ) = − 1 netj < 0 连续型 Hopfield神经网络（CHNN）
霍普菲尔德（Hopfield Hopfield） Hopfield 神经网络概述
旅行商问题(TSP)
旅行商问题（Traveling Saleman Problem， TSP）又译为旅行推销员问题、货郎担问题， 简称为TSP问题，是最基Байду номын сангаас的路线问题。
是指一名推销员要拜访多个地点时，如何 找到在拜访每个地 TSP问题点一次后再回 到起点的最短路径。
人工神经网络-连续型Hopfield神经网络
两点说明：
1）能量函数为反馈网络的重要概念。 根据能量函数可以方便的判断系统的稳定 性； 2）Hopfield选择的能量函数，只是保 证系统稳定和渐进稳定的充分条件，而不 是必要条件，其能量函数也不是唯一的。
* CHNN的几点结论
1）具有良好的收敛性； 2）具有有限个平衡点； 3）如果平衡点是稳定的，那么它也一定是渐进稳 定的； 4）渐进稳定平衡点为其能量函数的局部极小点； 5）能将任意一组希望存储的正交化矢量综合为网 络的渐进平衡点； 6）网络的存储信息表现为神经元之间互连的分布 式动态存储； 7）网络以大规模、非线性、连续时间并行方式处 理信息，其计算时间就是网络趋于平衡点的时间。
E 1 WijVj I i Ui Vi Ri j
由连续Hopfield运行方程可得
dVi d E dU i dU i C i C i C i f 1 i V dt dV Vi dt dVi i
将上式代入原式可得：
dV i dE C i dt dt j 1 f i V
WijViVj
i 1 j 1
n
n
ViIi
i 1
n
R i i
1
n
1
Vi
0
f 1 dV V
求取 其中：
dE
dt
dE dt
i
E dV i Vi dt
E 1 Vi 2
1 WijVj 2 j
W jiVj j
Ii
1
Ri
Ui
• 由于Wij=Wji 则有：
提 出
其原理与离散型Hopfield神经网络相似，它以模拟 量作为网络的输入输出量，各神经元采用并行方式工作
hopfield网络求解TSP问题
Hopfield神经网络求解TSP问题1.什么是TSP问题旅行商问题，即TSP问题（Traveling Salesman Problem），也是最优化问题。
一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。
路径的选择目标是要求得的路径路程为所有路径之中的最小值。
用数学语言描述TSP如下 :设有限个城市集合 : C = { C1 , C 2 , … , Cn }，每两个城市间的距离为 d（Ci，Cj）∈Z, 其中 Ci，Cj∈C（ 1<=i , j <=n), 即求 minL=∑d（Ci，Cj）的值的问题。
有效路径的方案数目为Rn=（（n-1）！/2）,例如:R4=3,R5=12,R6=120,R10=181440可见路径总数，随n增大而急剧增长,当城市数目增加到一定的程度,计算量增加到无法进行的地步，所以要选择一种合理快速的算法，而不能对所有情况使用人工列举的方法。
2.Hopfield神经网络介绍人工神经网络（Artificial Neural Networks，简写为ANNs）也简称为神经网络（NNs）或称作连接模型（Connection Model），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。
这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的.最基础的为BP、Hopfield网络等。
Hopfield网络是一种互连型网络的一种，它引入类似于Lyapunov 函数的能量函数概念，把神经网络的拓扑结构(用连接权矩阵表示)与所求问题(用目标函数描述)相对应，并将其转换为神经网动力学系统的演化问题。
3.神经元的数学模型人的大脑是由大量神经细胞或神经元组成的。
每个神经元可以看作为一个小的处理单元，这些神经元按照某种方式相互连接起来，构成大脑内部的生理神经元网络系统，他们中各个神经元之间连接的强弱不是固定不变的，而是按照外部的信号激励程度做自适应的变化，而每个神经元又随着接收到的多个激励信号的综合大小呈现兴奋或抑制状态。
hopfield网络
newhop()函数是设计Hopfield网络的一种方法。 给出一系列平衡期望值矩阵T， newhop()函数的 输出为反馈网络的权值和阈值，之前需要保证网 络对应期望值向量具有稳定的平衡点，但是通常 会存在一些伪平衡点，本设计方法是使伪平衡点 数量越少越好。 例：设计一个在三维空间中有两个稳定平衡点的
Hopfield最早提出的网络是二值神经网 络，输出只取1和0，所以也称离散 Hopfield神经网络。输出的离散值1和0分 别表示神经元处于激活和抑制状态。
1、网络结构
DNHH是一种单层的、其输入/输出为二值的反 馈网络。如图：由三个神经元组成的离散 hopfield神经网络。
第0层
第1层
x1
x2
网络，期望值向量T＝[－1 －1 1；1 －1 1]’
构建一个Hopfield网络。 net=newhop(T); Ai=T; [Y,Pf,Af]=sim(net,2,[],Ai); Y
可见网络设计确实能够做到设计点稳 定，下面输入不同于设计点的其他初始值 再来验证: Ai={[-0.9;-0.8;0.7]}; [Y,Pf,Af]=sim(net,{1 5},{},Ai); Y{1}
Hopfield网络
1.1 离散hopfield网络（DHNN） 1.2 连续hopfield网络（CHNN） 1.3 Hopfield网络的设计
Hopfield神经网络模型是一种循环神经 网络，从输出到输入有反馈连接。分为离 散型和连续型。
稳定的 反馈网络：
不稳定的
1.1离散hopfield网络（DHNN）
Coben和Grossberg在1983年给出了关于hopfield网络 稳定的充分条件：如果hopfield网络的权系数矩阵W是一 个对称矩阵，并且对角线元素为0，则这个网络是稳定的。
Hopfield最早提出的网络是二值神经网 络，输出只取1和0，所以也称离散 Hopfield神经网络。输出的离散值1和0分 别表示神经元处于激活和抑制状态。
1、网络结构
DNHH是一种单层的、其输入/输出为二值的反 馈网络。如图：由三个神经元组成的离散 hopfield神经网络。
第0层
第1层
x1
x2
网络，期望值向量T＝[－1 －1 1；1 －1 1]’
构建一个Hopfield网络。 net=newhop(T); Ai=T; [Y,Pf,Af]=sim(net,2,[],Ai); Y
可见网络设计确实能够做到设计点稳 定，下面输入不同于设计点的其他初始值 再来验证: Ai={[-0.9;-0.8;0.7]}; [Y,Pf,Af]=sim(net,{1 5},{},Ai); Y{1}
Hopfield网络
1.1 离散hopfield网络（DHNN） 1.2 连续hopfield网络（CHNN） 1.3 Hopfield网络的设计
Hopfield神经网络模型是一种循环神经 网络，从输出到输入有反馈连接。分为离 散型和连续型。
稳定的 反馈网络：
不稳定的
1.1离散hopfield网络（DHNN）
Coben和Grossberg在1983年给出了关于hopfield网络 稳定的充分条件：如果hopfield网络的权系数矩阵W是一 个对称矩阵，并且对角线元素为0，则这个网络是稳定的。
连续型Hopfield神经网络
油料资源输送，是指利用信息技术在战前和作战过程中 精确预测作战部队的油料需求，精确“可视”全部油料 资源，灵活调遣保障资源，采取多种运输手段，主动地 在需要的时间和地点为作战部队保障油料。随着现代运 输手段的发展，如何安全、快速、准确地输送油料，是 油料部门急需解决的问题。由于作战区域广泛，战争中 前方和后方的界线变得十分模糊，作战部队经常处于不 断移动的状态，因此就存在许多油库供应多个作战部队 油料的情况，存在一个或多个油料供应点到多个油料需 求点的油料输送问题。
精选课件
22
3.连续型Hopfield网络结构及特点
连续型Hopfield网 络结构如右图所示， 它是单层反馈非线 性网络，每一个节 点的输出均反馈至 节点的输入。
精选课件
23
Hopfield网络用模拟 电路实现的神经元节 点如右图。图中电阻 Rio和电容Ci并联，模 拟生物神经元的延时 特性，电阻 Rij(j=1,2,…,n)模拟 突触特征，偏置电流 Ii相当于阈值，运算 放大器模拟神经元的 非线性饱和特性。
将上式代入原式可得：
dE
dt j
CiddV it2 f 1Vi
由于Ci>0, f(U)单调递增，故f -1 (U)也单调递 增，可得：
dE 0 dt
当且仅当， dV i 0 时， dE 0
dt
dt
结论：网络是渐进稳定的，随着时间的推移，网 络的状态向E减小的方向运动，其稳定平衡状态 就是E的极小点。
1) 递归网络 此类网络中，多个神经元互连组织成一个互连神经网络。 有些神经网络输出被反馈至同层或前层神经元。因此， 信号能从正向和反向流通。Hopfield 网络、Elmman 网 络和Jordan 网络是递归网络中具有代表性的例子。递 归网络又叫反馈网络。
精选课件
22
3.连续型Hopfield网络结构及特点
连续型Hopfield网 络结构如右图所示， 它是单层反馈非线 性网络，每一个节 点的输出均反馈至 节点的输入。
精选课件
23
Hopfield网络用模拟 电路实现的神经元节 点如右图。图中电阻 Rio和电容Ci并联，模 拟生物神经元的延时 特性，电阻 Rij(j=1,2,…,n)模拟 突触特征，偏置电流 Ii相当于阈值，运算 放大器模拟神经元的 非线性饱和特性。
将上式代入原式可得：
dE
dt j
CiddV it2 f 1Vi
由于Ci>0, f(U)单调递增，故f -1 (U)也单调递 增，可得：
dE 0 dt
当且仅当， dV i 0 时， dE 0
dt
dt
结论：网络是渐进稳定的，随着时间的推移，网 络的状态向E减小的方向运动，其稳定平衡状态 就是E的极小点。
1) 递归网络 此类网络中，多个神经元互连组织成一个互连神经网络。 有些神经网络输出被反馈至同层或前层神经元。因此， 信号能从正向和反向流通。Hopfield 网络、Elmman 网 络和Jordan 网络是递归网络中具有代表性的例子。递 归网络又叫反馈网络。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Hopfield网络的运行规则
Hopfield网络运行规则主要有以下几步：
① 从网络中随机选出一个神经元i；
② 求出神经元i的所有输入的加权总和；
③ 计算神经元i在第t+1时刻的输出值，即 Ui（t+1）；
④ Ui以外的其他所有输出值保持不变，
Uj（t+1）=Uj（t）
j=1,2,3，…n
ji
⑤ 返回到第一步，直至网络进入稳定状态。
连续型Hopfield神经网络
报告人：彭佳伟 导 师：齐乐华 教授
Outline
人工神经网络简介 Hopfield神经网络概述 连续型Hopfield神经网络结构及特点 简单应用
1 人工神经网络简介
人工神经网络（Artificial Neural Networks，简写为ANN）也简 称为神经网络(NN)或称作连接模型，是对人脑或自然神经网络若干 基本特性的抽象和模拟。人工神经网络是以对大脑的生理研究成果 为基础的，其目的在于模拟大脑的某些机理与机制， 实现某个方 面的功能。
对称型Sigmoid函数
f x 1
1 ex
f
x
1 1
e e
x x
连续型Hopfield神经网络稳定性分析
能量函数的定义（有备注）
1 n
E 2 i1
n
n
n1
WijViV j
j 1
Vi Ii
i1
i1
Ri
Vi f 1 V
0
dV
求取 dE
dt
其中：
dE E dVi
dt i Vi dt
Hopfield网络是一种具有反馈性质的网络，而反馈网络 的一个主要特点就是它应具有稳定状态。当网络结构满 足上面所指出的两个条件时，按上述工作运行规则反复 更新状态，当达到一定程度后，各输出不再变化，网络 达到稳定状态，即Ui（t+1）=Ui（t）=sgn（Hi）。在实 际应用中必须运行许多次才能达到稳定状态。网络运行 达到稳定状态的速度，以及网络的稳定程度主要取决于 网络的“能量函数”。
E 1
Vi 2
j
WijV j
1 2
j
W jiV j
Ii
1 Ri U i
由于Wij=Wji 则有：
E
Vi
jቤተ መጻሕፍቲ ባይዱ
WijV j
Ii
1 Ri
Ui
由连续Hopfield运行方程可得
E Vi
Ci
dU i dt
Ci
dU i dVi
Ci
dVi dt
d dVi
f 1Vi
将上式代入原式可得：
dE
Wij
j 1
Ci
dU i dt
Ui Ri
n
WijVi I i
j 1
Vi f Ui
一般设 U x,V y, RiCi , I / C
则有
dxi
dt
1
xi
1 Ci
Wij y j i
j
yi f xi
式中f(x)为S形激励 函数。一般有以下两 种形式：
非对称型Sigmoid函 数
3.连续型Hopfield网络结构及特点
连续型Hopfield网 络结构如右图所示， 它是单层反馈非线 性网络，每一个节 点的输出均反馈至 节点的输入。
Hopfield网络用模拟 电路实现的神经元节 点如右图。图中电阻 Rio和电容Ci并联，模 拟生物神经元的延时 特性，电阻 Rij(j=1,2,…,n)模拟 突触特征，偏置电流 Ii相当于阈值，运算 放大器模拟神经元的 非线性饱和特性。
n
s wi xi i 1
y s
2.Hopfield神经网络概述
Hopfield网络是J.J.Hopfield在20世纪80年代 提出来的。他指出，如果神经网络的突触联系 是有效对称的，那么系统必将演化到一个固定 的有序状态。于是他引入能量函数的概念，表 明如果突触联系是对称的，则网络的动态演化 过程将达到能量最小的稳定状态。利用这一特 性，Hopfield网络可完成一些诸如最优化和联 想记忆的功能。
人工神经网络的结构分类
人工神经网络的结构基本上分为两类，即递归 网络和前馈网络。
1) 递归网络 此类网络中，多个神经元互连组织成一个互连神经网络。 有些神经网络输出被反馈至同层或前层神经元。因此， 信号能从正向和反向流通。Hopfield 网络、Elmman 网 络和Jordan 网络是递归网络中具有代表性的例子。递 归网络又叫反馈网络。
4.1.基于连续型Hopfield网络的油料资源输送优化
设计一套最佳的巡回路线，在所有可能的路径 方案中选出一个最符合条件的油料输送路径， 是提高战时油料保障军事经济效益的重要途径。 在人工神经网络理论中，连续型Hopfield神经 网络可以实现对油料输送路径的最优化搜索， 能很好地解决油料资源输送优化计算问题，为 提高战时油料资源保障质量效益奠定基础。
在Hopfield网络中，各连接权的值主要是设计出来的， 而不是通过网络运行而学到的，网络的学习过程只能对 它进行微小的调整，所以连接权的值在网络运行过程中 是基本固定的，网络的运行只是通过按一定的规则计算 与更新网络的状态，以求达到网络的一种稳定状态，如 果将这种稳定状态设计在网络能量函数极小值的点上， 那么，就可以用这种网络来记忆一些需要记忆的模式或 得到某些问题的最优解。
人工神经网络的主要学习算法
2) 无导师学习 无导师学习算法不需要知道期望输出，在训练过程中， 只要神经网络提供输入模式，神经网络就能够自动地适 应连接权，以便按相似的特征把输入模式分组聚集。
3) 强化学习 强化学习是有导师学习的特例，它不需要给出目标输出， 强化学习算法采用一个“评论员”来评价与给定输入项 相对应的神经网络输出的优度（质量因数）。强化学习 算法的一个例子是遗传算法（GA）。
连续神经网络模型在简化生物神经元性质的同 时，重点突出了以下特点：
a. 神经元作为一个输入输出变换，其传输特性 具有sigmoid特性。
b. 神经元之间大量的兴奋性、抑制性连接，主 要通过反馈来实现。
c. 既代表产生动作电位的神经元又代表按渐进 方式工作的神经元。 因此，连续神经网络模型准确地保留了生物神 经网络的动态和非线形特征。
油料资源输送，是指利用信息技术在战前和作战过程中 精确预测作战部队的油料需求，精确“可视”全部油料 资源，灵活调遣保障资源，采取多种运输手段，主动地 在需要的时间和地点为作战部队保障油料。随着现代运 输手段的发展，如何安全、快速、准确地输送油料，是 油料部门急需解决的问题。由于作战区域广泛，战争中 前方和后方的界线变得十分模糊，作战部队经常处于不 断移动的状态，因此就存在许多油库供应多个作战部队 油料的情况，存在一个或多个油料供应点到多个油料需 求点的油料输送问题。
（1）分析问题：网络输出与问题的解相对应。 （2）构造网络能量函数：构造合适的网络能量函
数，使其最小值对应问题最佳解。 （3）设计网络结构：将能量函数与标准式相比较，
定出权矩阵与偏置电流。 （4）由网络结构建立网络的电子线路并运行，稳
态优化解。
4.1.基于连续型Hopfield网络的油料资源输送优化
4.连续型Hopfield神经网络应用
Hopfield神经网络的提出就是与其实际应用密切相关的， 其主要功能有联想记忆（离散Hopfield）和优化计算功 能（连续Hopfield）。Hopfield网络除了在模式识别方 面有重要应用以外，对于解决组合优化问题，它也有许 多用途。组合优化问题，就是在给定的约束条件下，求 出使目标函数极小（或极大）的变量组合问题。将 Hopfield网络应用于求解组合优化问题，就是把目标函 数转化为网络的能量函数，把问题的变量对应于网络的 状态。
4.2.利用Hopfield神经网络进行图的同构识别
图的同构问题一直受到数学界与工程技术界, 特别是大 系统建模技术人员的关注和兴趣。所谓图的同构，是指 两个图有相同数量的节点和边，并且节点和边分别存在 着一一对应，且保持关联关系。相应节点自由度相同。
图的同构问题具有很好的应用背景, 特别是应用于系统 建模：如果建模者能够证明需建的模型与已有的某模型 同构, 则勿需再建, 这将大大节省人力物力。传统的方 法检验图的同构间题是非常困难的, 特别是当图的顶点 数较大时, 几乎是不可能的。因此, 人们只能设法寻找 其它途径以求得对此问题有所帮助。
人工神经元模型
常用的人工神经元模 型主要是基于模拟生 物神经元信息传递特 性，即输入、输出关 系。如果将生物神经 元输入、输出脉冲的 密度用模拟电压来表 示，可用右图的模型 来模拟。
人工神经元模型
xi(i=1,2,···,n)为加于输入端（突触）上的输 入信号；wi(i=1,2,···,n)为相应的突触连接权 系数，它是模拟突触传递强度的一个比例系数： Σ表示突触后信号的空间累加；θ表示神经元 的阈值，σ表示神经元的响应函数。该模型的 数学表达式为：
dt
j
Ci
dVi dt
2
f 1Vi
由于Ci>0, f(U)单调递增，故f -1 (U)也单调递 增，可得：
dE 0 dt
当且仅当， dVi 0 时， dE 0
dt
dt
结论：网络是渐进稳定的，随着时间的推移，网 络的状态向E减小的方向运动，其稳定平衡状态 就是E的极小点。
连续型Hopfield神经网络特点
Hopfield网络的运行规则
按以上运行规则，在满足以下两个条件时，Hopfield 学习算法总是收敛的。
a. 网络的连接权矩阵无自连接并且具有对称性： Wii=0 i=1,2，…，n Wij=Wji i，j=1,2，…，n
b. 网络中各神经元以非同步或串行方式，根据运行规则 改变其状态；当某个神经元改变状态时，其他所有神 经元保持原状态不变。