力学第三四章习题课
材料力学课件第3-4章

L M x( x) d x
0 GIP (x)
28
3.5 圆轴扭转时的变形与刚度条件
二. 刚度条件
对等直轴:
d
dx
Mx GIP
单位长度的扭转角
等直圆轴扭转
max
M x max GIP
180
[ ](o /m)
对阶梯轴: 需分段校核。
max
M x max GIP
180
[ ](ο /m)
2. 给出功率, 转速
(kw)
Me = 9549
P n
(N. m)
(r/min)
5
3.2 外力偶矩的计算 扭矩和扭矩图 二.横截面上的内力
截面法求内力: 截,取,代,平
Mx 称为截面上的扭矩
Mx 0 Mx Me 0 即 Mx Me
按右手螺旋法:
指离截面为正,
M x 指向截面为负。
6
3.2 外力偶矩的计算 扭矩和扭矩图
10
3.3 薄壁圆筒的扭转 纯剪切
一. 薄壁筒扭转实验
nm
t
实验观察 分析变形
x
r
nm l
mn没变 x = 0
x = 0
Me
nm
γ
Me
φ
x
r没变 = 0
= 0
nm
Me
nm
Mx
x
n m Mx
11
3.3 薄壁圆筒的扭转 纯剪切
Me Mx
nm
Mx
n m Mx
由于轴为薄壁,所以认
为 沿t 均布.即 =C
max
M x max Wp
31.5 103 m
M x max d 3
16
理论力学习题答案

理论力学习题答案(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 两点受力的构件都是二力杆。
( × ) 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 力的平行四边形法则只适用于刚体。
( × ) 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 只要物体平衡,都能应用加减平衡力系公理。
( × ) 凡是平衡力系,它的作用效果都等于零。
( × ) 合力总是比分力大。
( × ) 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × )若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ )当软绳受两个等值反向的压力时,可以平衡。
( × )静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ )静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )凡是两端用铰链连接的直杆都是二力杆。
( × )如图所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。
对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
第1、2、3、4章练习题

第一章练习题1、物质能以液态形式存在的最高温度为(A)沸腾温度Tb (B)玻义耳温度TB (C)临界温度Tc2、当压缩因子Z<1时,表示该实际气体(A)易压缩(B)不易压缩(C)无法确定3、下列何种条件下真实气体可以液化()(A)Tr>1,Pr>1 (B)Tr>1,Pr<1 (C)Tr=1,Pr<1 (D)Tr<1,Pr=14、对理想气体,压缩因子Z=1。
能否说当气体的Z=1 时,该气体必定是理想气体。
答案:(不能,因为在实际气体的等温线与理想气体的等温线交点处,Z=1)5、当温度足够低时,任何实际气体的Z~P 曲线与理想气体的Z~P 曲线均交于两点。
试解释这种现象。
答案:(这是因为当温度足够低时,气体的玻义耳温度高于体系温度,Z~p 曲线出现极小值。
)6、从范德华方程出发并结合玻义耳温度定义,证明(1)在足够高的温度,实际气体的压缩因子Z>1 。
(2)在低温,低压下,Z<1 。
答案:(当T<=TB,Z>1)(3)当a=0 ,Z 随压力p 的增加而线性增加。
答案:(当a=0,Z=1+bp/RT,恒温时,p 增加,Z 增大。
)7、下列说法何者正确?(1)临界压力是气体可被液化的最低压力。
(2)气体被液化的必要条件是气体温度小于波义耳温度(3)在临界点,饱和液体与饱和蒸气的密度相同。
(4)气体的临界状态与气体的性质无关。
答案:(3)8、气体A、B、C 都服从范德华方程,其范德华常数a和b的大小顺序为a(A)=a(B)>a(C);b(C)>b(B)>b(A)。
问三种气体临界温度的大小顺序。
答案:(T c(A)>T c(B)>T c(C))9、某气体的状态方程为,式中b为常数,n为物质的量。
若该气体经一等温过程,压力自p1变至p2,则下列状态函数的变化,何者为零?(ΔU)第二章练习题1、指出下列说法的错误。
(1)因Qp =ΔH,Qv=ΔU,所以Qp 和Qv 都是状态函数。
《工程力学》课后习题与答案全集

由 ,作出速度平行四边形,如图示:
即:
7.图示平行连杆机构中, mm, 。曲柄 以匀角速度 2rad/s绕 轴转动,通过连杆AB上的套筒C带动杆CD沿垂直于 的导轨运动。试示当 时杆CD的速度和加速度。
解:取CD杆上的点C为动点,AB杆为动系。对动点作速度分析和加速度分析,如图(a)、(b)所示。图中:
解:设该力系主矢为 ,其在两坐标轴上的投影分别为 、 。由合力投影定理有:
=-1.5kN
kN
kN
;
由合力矩定理可求出主矩:
合力大小为: kN,方向
位置: m cm,位于O点的右侧。
2.火箭沿与水平面成 角的方向作匀速直线运动,如图所示。火箭的推力 kN与运动方向成 角。如火箭重 kN,求空气动力 和它与飞行方向的交角 。
(d)由于不计杆重,杆AB在A、C两处受绳索作用的拉力 和 ,在B点受到支座反力 。 和 相交于O点,
根据三力平衡汇交定理,
可以判断 必沿通过
B、O两点的连线。
见图(d).
第二章力系的简化与平衡
思考题:1.√;2.×;3.×;4.×;5.√;6.×;7.×;8.×;9.√.
1.平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm,求此力系向O点简化的结果,并确定其合力位置。
则
(mm/s)
故 =100(mm/s)
又有: ,因
故:
即:
第四章刚体的平面运动
思考题
1.×;2.√; 3.√;4.√;5.×.
习题四
1.图示自行车的车速 m/s,此瞬时后轮角速度 rad/s,车轮接触点A打滑,试求点A的速度。
《理论力学》第四章-力系平衡试题及答案
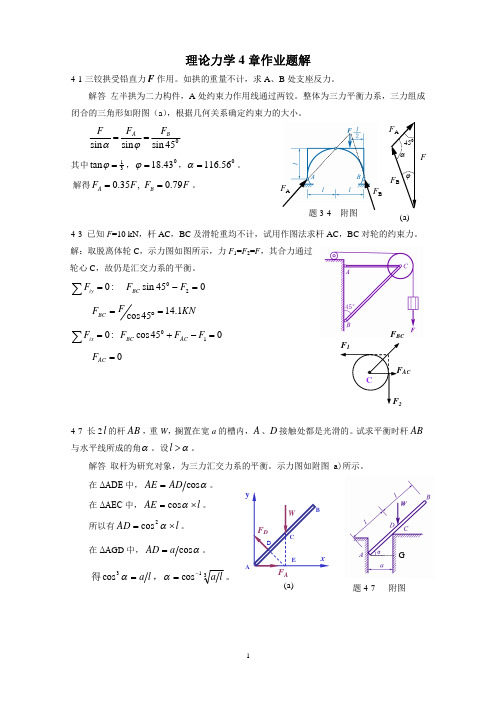
理论力学4章作业题解4-1三铰拱受铅直力F 作用。
如拱的重量不计,求A 、B 处支座反力。
解答 左半拱为二力构件,A 处约束力作用线通过两铰。
整体为三力平衡力系,三力组成闭合的三角形如附图(a ),根据几何关系确定约束力的大小。
45sin sin sin B A F F F ==j a其中31tan =j ,043.18=j ,056.116=a 。
解得F F F F B A 79.0 ,35.0==。
4-3 已知F =10 kN ,杆AC ,BC 及滑轮重均不计,试用作图法求杆AC ,BC 对轮的约束力。
解:取脱离体轮C ,示力图如图所示,力F 1=F 2=F ,其合力通过轮心C ,故仍是汇交力系的平衡。
:0=åiyF 045sin 20=-F F BCKN FF BC 1.1445cos =°=045cos :010=-+=åF F F FAC BC ix0=AC F4-7 长2l 的杆AB ,重W ,搁置在宽a 的槽内,A 、D 接触处都是光滑的。
试求平衡时杆AB 与水平线所成的角a 。
设a >l 。
解答 取杆为研究对象,为三力汇交力系的平衡。
示力图如附图(a)所示。
在ΔADE 中,a cos AD AE =。
在ΔAEC 中,l AE ´=a cos 。
所以有l AD ´=a 2cos 。
在ΔA GD 中,a cos a AD =。
得a =a 3cos ,31cosl a -=a 。
F BCAC题3-4 附图F BF AF BF AFa45j(a)A (a)题4-7 附图G4-9 AB ,AC ,AD 三连杆支撑一重物,如图所示。
已知W=10kN ,AB =4m ,AC =3 m ,且ABEC 在同一水平面内,试求三连杆所受的力。
解:取铰A 研究,示力图如图示,为汇交力系的平衡。
0=åix F : 05430sin =´°+AD AB F F 0=åiy F : 05330sin =´°+AD AC F F 0=åiZF: 030cos =-°W F AD联立求解KNF KNF KN F AD AC AB 5.115.36.4=-=-=4-8 图示结构上作用一水平力F 。
周光炯版流体力学-第三、四章部分习题
(1)
(2)
(3) (4)
(5)
(6)
������ 2
2 −1+√1+8������������1
2
= 0.5439m
(b)沿液面应用能量定理, ������1 + 连续性方程 ������2 = 联立(7) 、 (8)得 ������1 ������1 ������2
解: (a)应用动量定理于截面 1 和 2,有 ������1 ������1 − ������2 ������2 = ������������ (������2 − ������1 ) 流体压强按静压规律分布, 1 1 ������1 = ������������������1 ,������2 = ������������������2 2 2 设垂直于直面的渠道宽为 1,则 ������1 = ������1 ,������2 = ������2 结合连续性方程 ������1 ������1 = ������2 ������2 联立(1) 、 (2) 、 (3) 、 (4)得 1 ������ 2 2 2) 2 1 ������������(������1 − ������2 = ������������1 ( − ������1 ) 2 ������2 经整理后,可变为 ������2 2 ������2 2 ( ) + − 2������������1 =0 ������1 ������1
������1
联立(1) 、 (2) 、 (3) 、 (4) 、 (5) ,可得流量的最终关系式为 1⁄2 ������������ 2������������ ( ������ − 1) ������������ = ������2 [ ] 1 − (������2⁄������1 )4
完整版材料力学性能课后习题答案整理

材料力学性能课后习题答案第一章单向静拉伸力学性能1、解释下列名词。
1弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
2.滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
3.循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
4.包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
5.解理刻面:这种大致以晶粒大小为单位的解理面称为解理刻面。
6.塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
脆性:指金属材料受力时没有发生塑性变形而直接断裂的能力韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成一个高度为b的台阶。
8.河流花样:解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。
是解理台阶的一种标志。
9.解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
10.穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
11.韧脆转变:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变2、说明下列力学性能指标的意义。
答:E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 P15 3、 金属的弹性模量主要取决于什么因素?为什么说它是一个对组织不敏感的力学性能指标?答:主要决定于原子本性和晶格类型。
合金化、热处理、冷塑性变形等能够改变金属材料的组织形态和晶粒大小,但是不改变金属原子的本性和晶格类型。
流体力学答案(3,4)

第三、四章 习题及答案3-8已知流速场u x =xy 2, 313yuy=-, u z =xy, 试求:(1)点(1,2,3)的加速度;(2)是几维流动;(3)是恒定流还是非恒定流;(4)是均匀流还是非均匀流? 解:(1)411633x x x x x xyzu u u u a u u u xy txyz∂∂∂∂=+++==∂∂∂∂2533321331323331216 3 . 06m /sy y z x y a y u y a yu xu xy xy xy a =-===+=-====(2)二元流动 (3)恒定流 (4)非均匀流41xy33-11已知平面流动速度分布为xy 2222cx uu x ycy x y=-=++,, 其中c 为常数。
求流线方程并画出若干条流线。
解:2222-x d x =yd yxyd x d y d x d y c y c x u u xyxy=⇒-=⇒++积分得流线方程:x 2+y 2=c方向由流场中的u x 、u y 确定——逆时针3-17下列两个流动,哪个有旋?哪个无旋?哪个有角变形?哪个无角变形?(1)u x =-ay,u y =ax,u z =0 (2)z2222,,0,a c xycy cxu u u x y x y =-==++式中的、为常数。
z 2222,,0,a c x y cy cx u u u x yx y=-==++式中的、为常数。
解:(1)110 ()()22y xx y z u u a a ax y ωωω∂∂===-=+=∂∂有旋流动xy 11()()0 22y x xy zx u u a a x y εεε∂∂=+=-==∂∂ 无角变形(2)222222222222222222211()2()2()22()()12()2()0 0 2()y x z x y u u x y c cx x y c cy x y x y x y c x y c x y x y ωωω∂⎡⎤∂+-+-=-=+⎢⎥∂∂++⎣⎦⎡⎤+-+====⎢⎥+⎣⎦无旋流动2222xy22222112()()()022()()y x u u c x y c x y x y x y x y ε∂⎡⎤∂---=+==-≠⎢⎥∂∂++⎣⎦ 有角变形4—7变直径管段AB ,d A =0.2m,d B =0.4m ,高差△h=1.5m ,测得p A =30kPa ,p B =40kPa ,B 点处断面平均流速v B =1.5m/s ,试判断水在管中的流动方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.4:如图,试求一个半径为 a的半圆形均匀平板的质心
如图,建立直角坐标系 由对称性知 xc=0 设平板的面密度为 σ 总质量 M = σ π a 2
2
y (0,a)
面元的质量:σdxdy 则
o
(a,0)
x
y
c
=
∫∫
y σ dxdy M
=
4a 3π
即平板的质心为( 0,4a/3π)
4.11:如图,一子弹水平地穿过两个前后并排、静止放置在光滑水 平面上的木块,木块的质量分别为 m1、m2,设子弹穿过木块所用的 时间分别为 Δt1、Δt2。 求:子弹穿过两木块后两木块的运动速度。 (设木块对子弹的阻力为恒力 F)
3、此时,槽对质点的作用力 F与质点所受到 的科里奥利力是一对作用力与反作用力,即
F = 2mωv = 2mω
ω y +v
2
2
2
0
3.12:一圆柱形刚性杆 Ox上套有一质量为 m的小环,杆的一 端固定,整个杆绕着通过固定端 O的竖直轴以恒定的角速度 旋转,旋转时杆与竖直轴的夹角 α保持不变。设小环与杆之 间的摩擦系数为 µ,已知当小环相对于杆运动到图示位置 x 时,其相对于杆的速度为, 试列出此时小环沿杆的运动方程(不要求解此方程)
3.11:一圆盘绕其竖直的对称轴以恒定的角速度ω 旋转。在圆盘上沿径向开有一光滑小槽,槽内一质 量为m的质点以v0的初速从圆心开始沿半径向外运 动。 试求: 1、质点到达图示位置(即 y=y0)时的速度v; 2、质点到达该处所需要的时间 t 3、质点在该处所受到的槽壁对它的侧向作用力 F
z ω
o
m
••
m x = F sin α − mg cos α − f
综上4式可得小环沿杆的运动方程为:
m x = mω2 x sin2α − mg cosα − µ (F cosα + mg sinα )2 + (2mωx sinα )2
= mω2 x sin2α − mg cosα − µ (mω2 x sinα cosα + mgsinα ) + (2mωv sinα )2
解: 动量定理: F∆t = ∆mv 取Δt1时刻m1速度为v1,时刻m2速度为v2。 则有 F •∆ = + 由上两式得:
m1
m2
(m1 m2)v1 F • (∆t + ∆t ) = m v + m v
t1
1 2 1 1 2
1
2
v v
F ∆ = m 1+
=
2
t m F ∆ t m + m
1 1 1
则绳对钉子的压力为
4 wbc b − c ]= F = mg[1 − a a
N
2 2
2
出现的问题
1、绳重w,即w=Mg。w≠M 2、将绳子的质心加速度与 b、c段的加速度混淆: 设绳子一端下降距离为 x
dv 2 x w = wg dt a
质心加速度 不是合外力 w-F=dm/dt 3、对细钉的说明 :忽略半径的影响
C A θ d 2θ B
1、由于AC与AB的夹角极小,所以 2 θρ = d BC = θ d 得:
BC
=
ω
d 2 v
2、子弹在圆盘上的运动轨迹是一个圆弧 3、科里奥利力充当向心力:
F向 = F 科
mν = -2 m ϖ × ν = ρ
→ →
2
即可解得圆弧的曲率半径是
ρ=ν/2ω
出现的问题
1、混淆了惯性系与非惯性系。 将直线AC看成子弹的实际运动轨迹 ,以惯性系中规律 分析非惯性系中的运动 X 2、因v>>wd,所以t=d/v。以这种做法得到的弧长刚好是实际 弧长的一半;曲率半径是实际值的两倍。
时,
a
max
ρA v = 4M
2
r
4.23:一雨滴的初始质量为 m0,在重力作用下从静止开始下落。假设 此雨滴从云中得到质量,其质量的增长率正比于它的瞬间质量和瞬间 速率的乘积,即dm/dt=kmv,其中k为常数。若忽略空气阻力, 试证明雨滴的速率最终成为恒量,并给出最终速率的表达式。
解:方法一 d ( mv 由变质量动量定理知, dt 即 得 积分得
v = ag 2
b a
T - wb = wb ab g wc wc − T = ac g
由于|ab|=|ac|,消去ab,ac得
bc T = 2W a2
F = 2T = 4W bc a2
方法二 对绳取微元 dm 系统受到合外力的冲量 Fdt=dp
dp = vd
= v ( vdt =
m
2
1
− vd
m
y
0
2
2
2
2 0
2
x
0
v = v +v = v +2ω y
总
2
2
2
2
2
y
x
0
0
2、由式
dy dt
=
v = v +ω y
y
0
2
2
2
2
0
得 积分得
2 + 2 2 y ω v0
2 2⎞ ⎛ ⎟ y y0 1 1 ⎜ω y0 ω 0 t =∫ dy= ln⎜ + 1+ 2 ⎟ 0 2 2 2 ω ⎜ v0 v0 ⎟ + y ω v0 ⎝ ⎠
z x N m x v F离 F科 α f摩 mg z x
α o
解: 所受到的科里奥利力为:F 科 = 2 m ω × v = 2 mω v sin α 所受到的惯性离心力为: F = m ω 所受到的摩擦力为: 所受到的合力为:
2
• x sin α
2 f = (F cosα + mgsinα )2 + F科 µ
y
x
解:1、在转动惯性系中, 小球受到惯性离心力: 方向+y,所以在y方向上,
•
F = mω2 y
••
y = ω
2
y
令
v
y =
y
则
dv •• dvdy dv 2 =y= = v =ω y dt dydt dy
积分得在y方向上 垂直于y方向上 所以在y=y0时, 质点的速率为:
v = v +ω y v = (ω y )
dm dt
dm dt
由于最终速度为恒定值, 即 dv
dt
综上可直接得出
= 0
g k
v =
THANKS!!
m dv dt
)
=
F
合
+ v
dm dt
=
=
mg
dm dt
dt
=
kmv
⎫ ⎪ ⎬ ⎪ ⎭
dv g − k
v
2
v (t ) =
g • k
e e
2 2
gk t gk t
−1 +1
当t → +∞时,v(t) →
g k
解:方法二 d ( mv ) 由变质量动量定理知, dt = F 合 即
m dv dt
+ v ⎫ = mg ⎪ ⎬ ⎪ = kmv ⎭
力学第三四章习题课
3.6;3.11;3.12 4.4;4.11;4.15;4.22;4.23
3.6:如图所示,一个圆盘直径为 d,绕通过圆心的 垂直轴以角速度ω匀速旋转,今有一人站在圆盘上 的点A射出一颗子弹,已知子弹出膛速度为 v,v>> ωd。现在希望子弹击中 A点的对径点B(AB是圆盘 直径),则应瞄准点 C,问: 1、BC的弧长是多少 2、这颗子弹在圆盘上的轨迹是什么 3、求出相应的曲率半径
4.22:一质量为M的宇宙飞船,在星际空间飞行。它用面积为 A的洞捕集静 止的氢(每单位体积的质量为ρ),再将其排出,排气的方向与飞船的飞行 方向相反,排气的速率相对于飞船为 vr,问:飞船的速率 v等于多少时,它 的加速度最大?(用 M、ρ、A、vr表示)
解:捕到氢气的质量 dm=ρAvdt。 取飞船飞行的方向为正方向 整个过程动量守恒 dm(v-vr)+M(v+dv)=Mv ρAvdt(v-vr)=M(v-v1)=-Mdv Mdv/dt=- ρAv(v-vr) =- ρ A [ ( v − v r ) − v
2
m m ) − v ( − vdt ) a a
2m v dt a
得到合外力
dp 2m v F= = dt a
2
绳子的质心为
r
c
=
b
2
+ c 2a
2
系统机械能守恒
1 m 2
m
因合外力
v
2
2
= mg ( r c −
r
0
)
v
=
(b − c )
2a
2
mg
2
F = mg −
F
N
=
(b − c ) a
2
mg2Biblioteka 2r24
]
可见,当且仅当 v=vr/2时,飞船有最大加 速度 a = ρ A 4v M
2
r
max
方法二: 对排出的氢气有
F∆t = ρAv∆t (v − vr ) F = ρAv (v − vr )
F a = − M
当 v =
对飞船有
ρ Av ( v − = − M
r
v
r
)
v
2 飞船有最大加速度
,
2
+
2
F ∆
t
2
2
m
4.15:一个长为a,重为w的均匀细绳挂在一个光滑细钉上自由 下滑。当两边的绳长相等时,细绳处于平衡状态。在小扰动下, 从钉上滑落。求: 1、当绳刚脱离细钉时,细绳的速度 2、当绳长一边为b,另一边为 c时,它对钉子的压力。 c
