高中数学立体几何证明题汇总
高中数学必修二立体几何常考证明题汇总
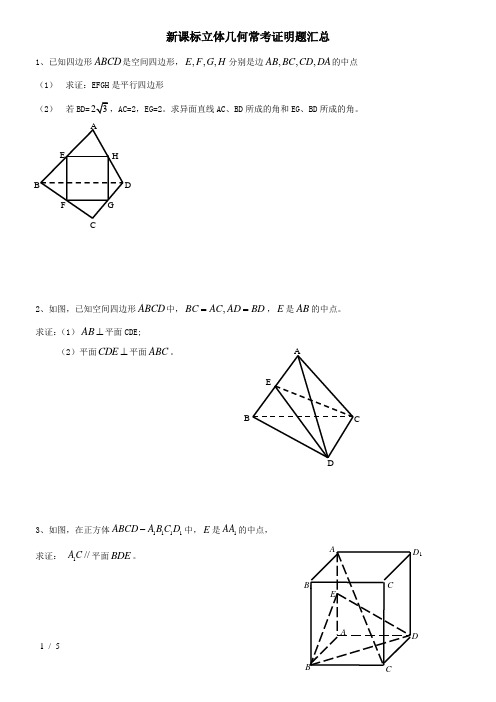
新课标立体几何常考证明题汇总1、已知四边形ABCD 是空间四边形，,,,E F G H 分别是边,,,AB BC CD DA 的中点的中点 （1） 求证：求证：EFGH EFGH 是平行四边形是平行四边形（2） 若BD=23，AC=2AC=2，，EG=2EG=2。
求异面直线。
求异面直线AC AC、、BD 所成的角和EG EG、、BD 所成的角。
所成的角。
证明：在ABD D 中，∵,E H 分别是,AB AD 的中点∴1//,2EH BD EH BD =同理，1//,2FG BD FG BD =∴//,EH FG EH FG =∴四边形EFGH 是平行四边形。
是平行四边形。
(2) 90(2) 90°° 30 30 °°考点：证平行（利用三角形中位线），异面直线所成的角2、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
的中点。
求证：（1）^AB 平面CDE;（2）平面CDE ^平面ABC 。
证明：（1）BC AC CE AB AE BE =üÞ^ý=þ同理，AD BD DE AB AE BE =üÞ^ý=þ又∵CE DE E Ç= ∴∴AB ^平面CDE（2）由（）由（11）有AB ^平面CDE又∵AB Í平面ABC ， ∴平面∴平面CDE ^平面ABC 考点：线面垂直，面面垂直的判定A H G F E D C B A E D B C 3、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点，的中点， 求证：求证： 1//AC 平面BDE 。
证明：连接AC 交BD 于O ，连接EO ， ∵E 为1AA 的中点，O 为AC 的中点的中点 ∴EO 为三角形1A AC 的中位线的中位线 ∴1//EO AC 又EO 在平面BDE 内，1AC 在平面BDE 外∴1//AC 平面BDE 。
新课标立体几何常考证明题汇总
新课标立体几何常考证明题汇总1、已知四边形ABCD 是空间四边形，,,,E F G H 分别是边,,,AB BC CD DA 的中点 （1） 求证：EFGH 是平行四边形（2） 若BD=AC=2，EG=2。
求异面直线AC 、BD 所成的角和EG 、BD 所成的角。
2、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
求证：（1）⊥AB 平面CDE;（2）平面CDE ⊥平面ABC 。
3、如图，在正方体1111ABCD A BC D -中，E 是1AA 的中点， 求证： 1//AC 平面BDE 。
AED 1CB 1DAAHGFEDCB AEDBC4、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证：AD ⊥面SBC ．5、已知正方体1111ABCD A BC D -，O 是底ABCD 对角线的交点. 求证：(１) C 1O ∥面11AB D ；(2)1AC ⊥面11AB D ．7、正方体ABCD —A 1B 1C 1D 1中．(1)求证：平面A 1BD ∥平面B 1D 1C ； (2)若E 、F 分别是AA 1，CC 1的中点，求证：平面EB 1D 1∥平面FBD ． 证明：8、四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，且22EF AC =， 90BDC ∠=，求证：BD ⊥平面ACDSDCBAD 1ODB AC 1B 1A 1CA1NMPCBA9、如图P 是ABC ∆所在平面外一点，,PA PB CB =⊥平面PAB ，M 是PC 的中点，N 是AB 上的点，3AN NB =（1）求证：MN AB ⊥；（2）当90APB ∠=，24AB BC ==时，求MN 的长。
10、如图，在正方体1111ABCD A BC D -中，E 、F 、G 分别是AB 、AD 、11C D 的中点.求证：平面1D EF ∥平面BDG .11、如图，在正方体1111ABCD A BC D -中，E 是1AA 的中点. （1）求证：1//AC 平面BDE ； （2）求证：平面1A AC ⊥平面BDE .12、已知ABCD 是矩形，PA ⊥平面ABCD ，2AB =，4PA AD ==，E 为BC 的中点．（1）求证：DE ⊥平面PAE ；（2）求直线DP 与平面PAE 所成的角．13、如图，在四棱锥P ABCD -中，底面ABCD 是060DAB ∠=且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ．（1）若G 为AD 的中点，求证：BG ⊥平面PAD ； （2）求证：AD PB ⊥；（3）求二面角A BC P --的大小．14、如图1,在正方体1111ABCD A BC D -中，M 为1CC 的中点，AC 交BD 于点O ，求证：1AO ⊥平面MBD ．考点：线面垂直的判定，运用勾股定理寻求线线垂直 15、如图２，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ，作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ．求证：AH ⊥平面BCD ．16、证明：在正方体ABCD －A 1B 1C 1D 1中，A 1C ⊥平面BC 1D17、如图，过S 引三条长度相等但不共面的线段SA 、SB 、SC ，且∠ASB=∠ASC=60°，∠BSC=90°，求证：平面ABC ⊥平面BSC ．18．（本小题满分12分）如图所示，在直三棱柱ABC-A1B1C1中，AC ⊥BC ． (1) 求证：平面AB1C1⊥平面AC1；(2) 若AB1⊥A1C ，求线段AC 与AA1长度之比；(3) 若D 是棱CC1的中点，问在棱AB 上是否存在一点E ，使DE ∥平面AB1C1？若存在，试确定点E 的位置；若不存在，请说明理由．AC111。
高中数学立体几何证明题汇总
高中数学立体几何证明题汇总立体几何常考证明题1.已知四边形ABCD是空间四边形，E,F,G,H分别是边AB,BC,CD,DA的中点。
1）证明EFGH是平行四边形。
2）已知BD=23，AC=2，EG=2，求异面直线AC、BD所成的角和EG、BD所成的角。
2.如图，已知空间四边形ABCD中，BC=AC,AD=BD，E 是AB的中点。
1）证明AB垂直于平面CDE。
2）证明平面CDE垂直于平面ABC。
3.如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点。
证明A1C平行于平面BDE。
4.已知三角形ABC中∠ACB=90，SA垂直于面ABC，AD垂直于SC。
证明AD垂直于面SBC。
5.已知正方体ABCD-A1B1C1D1，O是底面ABCD对角线的交点。
1）证明C1O平行于面AB1D1.2）证明AC1垂直于面AB1D1.6.正方体ABCD-A1B1C1D1中。
1）证明AC垂直于平面B1D1D。
2）证明BD1垂直于平面ACB1.7.正方体ABCD-A1B1C1D1中。
1）证明平面A1BD平行于平面B1DC。
2）已知E、F分别是AA1、CC1的中点，证明平面EB1D1平行于平面FBD。
8.四面体ABCD中，AC=BD，E、F分别为AD、BC的中点，且EF=AC/2，∠XXX。
证明BD垂直于平面ACD。
9.如图P是△ABC所在平面外一点，PA=PB，CB垂直于平面PAB，M是PC的中点，N是AB上的点，AN=3NB。
1）证明XXX垂直于AB。
2）当∠APB=90，AB=2BC=4时，求MN的长度。
10.如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是AB、AD、C1D1的中点。
证明平面D1EF平行于平面BDG。
11.如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点。
1）证明A1C平行于平面BDE。
2）证明平面A1AC垂直于平面BDE。
12、已知矩形ABCD，PA垂直于平面ABCD，AB=2，PA=AD=4，E为BC的中点。
高一数学常考立体几何证明题及答案
高一数学常考立体几何证明题1、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
求证：（1）⊥AB 平面CDE; （2）平面CDE ⊥平面ABC 。
2、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点，求证： 1//AC 平面BDE 。
3、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥, 求证：AD⊥面SBC ．4、已知正方体1111ABCD A BC D -，O 是底ABCD 对角线的交点.求证：(１) C1O ∥面11AB D ；(2)1AC ⊥面11AB D ．5、正方体''''ABCD A B C D -中，求证：''AC B D DB ⊥平面；6、正方体ABCD —A1B1C1D1中．(1)求证：平面A1BD ∥平面B1D1C ；(2)若E 、F 分别是AA1，CC1的中点，求证：平面EB1D1∥平面FBD ．AE D BCAE D 1CB 1DCBASDCBAD 1ODB AC 1B 1A 1CA 1 AB 1BC 1CD 1DG EF7、四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，且22EF AC =，90BDC ∠=，求证：BD ⊥平面ACD8、如图，在正方体1111ABCD A B C D -中，E 、F 、G 分别是AB 、AD 、11C D 的中点.求证：平面1D EF ∥平面BDG .9、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点.（1）求证：1//AC 平面BDE ；（2）求证：平面1A AC ⊥平面BDE .10、已知ABCD 是矩形，PA ⊥平面ABCD ，2AB =，4PA AD ==，E 为BC 的中点．求证：DE ⊥平面PAE ；（2）求直线DP 与平面PAE 所成的角．11、如图，在四棱锥P ABCD -中，底面ABCD 是060DAB ∠=且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ． （1）若G 为AD 的中点，求证：BG ⊥平面PAD ； （2）求证：AD PB ⊥．12、如图1,在正方体1111ABCD A B C D -中，M 为1CC 的中点，AC 交BD于点O ，求证：1AO ⊥平面MBD ．13、如图２，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ， 作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ． 求证：AH ⊥平面BCD ．14．(12分)求证平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形．已知：如图，三棱锥S —ABC ，SC ∥截面EFGH ，AB ∥截面EFGH. 求证：截面EFGH 是平行四边形．15．(12分)已知正方体ABCD —A1B1C1D1的棱长为a ，M 、N 分别为A1B 和AC 上的点，A1M ＝AN ＝23a ，如图． (1)求证：MN ∥面BB1C1C ；16．(12分)(2009·浙江高考)如图，DC ⊥平面ABC ，EB ∥DC ，AC ＝BC ＝EB ＝2DC ＝2，∠ACB ＝120°，P ，Q 分别为AE ，AB 的中点． (1)证明：PQ ∥平面ACD ；17．(12分)如图，在四面体ABCD 中，CB ＝CD ，AD ⊥BD ，点E 、F 分别是AB 、BD 的中点． 求证：(1)直线EF ∥面ACD. （2）平面EFC ⊥平面BCD .N MPCBA20、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点，求证：1//AC 平面BDE 。
(完整版)高一数学常考立体几何证明的题目及答案
1、如图，已知空间四边形ABCD中，BC AC, AD BD , E是AB的中点。
求证：(1) AB 平面CDE; (2)平面CDE 平面ABC。
2、如图，在正方体ABCD A i B1C1D i中，E是AA的中点,求证：AC//平面BDE。
3、已知ABC 中ACB 90o,SA 面ABC, AD SC,求证：AD 面SBC.4、已知正方体ABCD AB1G D1,。
是底ABCD对角线的交点求证：(1 ) CQ // 面AB1D1 ; (2) AC 面AB1D1 .5、正方体ABCD A'B'C'D'中，求证：(1)AC 平面B'D'DB ；(2)BD '平面ACB'.6、正方体ABCD — A1B1C1D1 中.⑴求证：平面A1BD//平面B1D1C;⑵若E、F分别是AA1, CC1的中点，求证：平面EB1D1//平面FBD .7、四面体ABCD 中，AC BD, E,F 分别为AD, BC 的中点，「且EF8、 如图，在正方体 ABCD A 1B 1C 1D 〔中，E 、F 、G 分别是AB BDG .9、 如图，在正方体 ABCD A 1B i C i D i 中，E 是AA 的中点.(1) 求证：A 1C// 平面 BDE ; (2) 求证：平面AAC 平面BDE .ii 、如图，在四棱锥 P ABCD 中，底面 ABCD 是 DAB 60°且边长为a 的菱 侧面PAD 是等边三角形，且平面 PAD 垂直于底面 ABCD . (1) 若G 为AD 的中点，求证:BG 平面PAD; (2) 求证：AD PB .i2、如图i,在正方体 ABCD AB i C i D i 中，M 为CC i 的中点，AC 交BD 于点O,求证：AO 平面MBD .i3、如图 2 ,在三棱锥 A — BCD 中，BC= AC, AD= BD, 作BEX CD, E 为垂足，作AH± BE 于H . 求证：AH±平面BCD10、已知ABCD 是矩形，PA 平面ABCD , AB 2 , PA(1) 求证：DE 平面PAE;(2) 求直线DP 与平面PAE 所成的角.AD 4 , E 为BC 的中点.求证:BD 平面ACD— AC , BDC 90°,2AD 、C i D i 的中点.求证：平面D i EF //平面14. （12分）求证平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形. 已知：如图，三棱锥S- ABC, SC//截面EFGH , AB//截面EFGH .求证：截面EFGH是平行四边形.15 . （12分）已知正方体ABCD — A i B i C i D i的棱长为a, M、N分别为A i B和AC上的点，A i M = AN = ^a,如图.3⑴求证：MN II面BB i C i C;⑵求MN的长.16 . （12 分）（2009 浙江高考）如图，DCL平面ABC, EB// DC, AC = BC= EB= 2DC= 2, Z ACB = 120 °, P, Q 分别为AE, AB的中点.⑴证明：PQ//平面ACD;⑵求AD与平面ABE所成角的正弦值.17 . （12分）如图，在四面体ABCD中，CB= CD , AD ± BD ,点E、F分别是AB、BD的中点.求证：（1）直线EF//面ACD.精彩文档1、如图，已知空间四边形 ABCD 中，BC AC, AD BD , E 是AB 的中点。
高中立体几何证明题
高中立体几何证明题一、线面平行的证明题1已知正方体ABCD - A_{1}B_{1}C_{1}D_{1}，E，F分别是AB，BC的中点，求证：EF∥平面A_{1}C_{1}D。
解析1. 连接AC。
- 在 ABC中，因为E，F分别是AB，BC的中点，所以EF∥ AC。
2. 正方体ABCD - A_{1}B_{1}C_{1}D_{1}中：- AC∥ A_{1}C_{1}。
- 由EF∥ AC和AC∥ A_{1}C_{1}可得EF∥ A_{1}C_{1}。
- 又A_{1}C_{1}⊂平面A_{1}C_{1}D，EFnot⊂平面A_{1}C_{1}D。
- 根据线面平行的判定定理，所以EF∥平面A_{1}C_{1}D。
题2在三棱柱ABC - A_{1}B_{1}C_{1}中，D是AB的中点，求证：AC_{1}∥平面CDB_{1}。
解析1. 连接BC_{1}，交B_{1}C于点E。
- 在三棱柱ABC - A_{1}B_{1}C_{1}中，E为BC_{1}的中点。
2. 因为D是AB的中点：- 所以在 ABC_{1}中，DE∥ AC_{1}。
- 又DE⊂平面CDB_{1}，AC_{1}not⊂平面CDB_{1}。
- 根据线面平行的判定定理，可得AC_{1}∥平面CDB_{1}。
二、线面垂直的证明题3在四棱锥P - ABCD中，底面ABCD是正方形，PA = PB = PC = PD，求证：PA⊥平面ABCD。
解析1. 连接AC，BD交于点O，连接PO。
- 因为底面ABCD是正方形，所以O为AC，BD中点。
- 又PA = PC，PB = PD，根据等腰三角形三线合一的性质：- 可得PO⊥ AC，PO⊥ BD。
- 而AC∩ BD = O，AC⊂平面ABCD，BD⊂平面ABCD。
- 根据直线与平面垂直的判定定理，所以PO⊥平面ABCD。
- 又PA = PB = PC = PD，AO = BO = CO = DO，所以 PAO≅ PBO≅ PCO ≅ PDO。
高一数学常考立体几何证明题
1、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
求证：⊥AB 平面CDE;2、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点， 求证： 1//A C 平面BDE 。
3、已知ABC ∆中90ACB ∠=o,SA ⊥面ABC ,AD SC ⊥, 求证：AD ⊥面SBC ．4、已知正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点.求证：(１) C 1O ∥面11AB D ； (2)1AC ⊥面11AB D ．AEDBCAED 1CB 1DCBASDCB AD 1ODBAC 1B 1A 1C5、正方体''''ABCD A B C D -中，求证： （1）''AC B D DB ⊥平面； （2）''BD ACB ⊥平面.6、正方体ABCD —A 1B 1C 1D 1中． (1)求证：平面A 1BD ∥平面B 1D 1C ；(2)若E 、F 分别是AA 1，CC 1的中点，求证：平面EB 1D 1∥平面FBD ．A 1B 11CD 1DGEF7、如图，在正方体1111ABCD A B C D -中，E 、F 、G 分别是AB 、AD 、11C D 的中点. 求证：平面1D EF ∥平面BDG .8、如图，在四棱锥P ABCD -中，底面ABCD 是060DAB ∠=且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ．（1）若G 为AD 的中点，求证：BG ⊥平面PAD ； （2）求证：AD PB ⊥．9、如图1,在正方体1111ABCD A B C D -中，M 为1CC 的中点，AC 交BD于点O ，求证：1AO ⊥平面MBD ．10．(12分)(2009·浙江高考)如图，DC ⊥平面ABC ，EB ∥DC ，AC ＝BC ＝EB ＝2DC ＝2，∠ACB ＝120°，P ，Q 分别为AE ，AB 的中点．(1)证明：PQ ∥平面ACD ；(2)求AD 与平面ABE 所成角的正弦值．1、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
(完整版)必修二立体几何11道经典证明题
1. 如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点(Ｉ)证明：平面BDC 1⊥平面BDC（Ⅱ）平面BDC 1分此棱柱为两部分，求这两部分体积的比.2. 如图5所示，在四棱锥P ABCD -中，AB ⊥平面PAD ，//AB CD ，PD AD =，E 是PB 的中点，F 是CD 上的点且12DF AB =，PH 为△PAD 中AD 边上的高.（1）证明：PH ⊥平面ABCD ；（2）若1PH =，2AD =，1FC =，求三棱锥E BCF -的体积；（3）证明：EF ⊥平面PAB .3. 如图，在直三棱柱111ABC A B C -中，1111A B AC =，D E ，分别是棱1BC CC ，上的点（点D 不同于点C ），且AD DE F⊥，为11B C 的中点．求证：（1）平面ADE ⊥平面11BCC B ； （2）直线1//A F 平面ADE ．B 1C BADC 1A 14. 如图，四棱锥P —ABCD 中，ABCD 为矩形，△PAD 为等腰直角三角形，∠APD=90°，面PAD ⊥面ABCD ，且AB=1，AD=2，E 、F 分别为PC 和BD 的中点．（1）证明：EF ∥面PAD ； （2）证明：面PDC ⊥面PAD ； （3）求四棱锥P —ABCD 的体积．5. 在如图所示的几何体中，四边形ABCD 是正方形， MA ⊥平面ABCD ，//PD MA ，E 、G 、F 分别为MB 、PB 、PC 的中点，且2AD PD MA ==.（I ）求证：平面EFG ⊥平面PDC ；（II ）求三棱锥P MAB -与四棱锥P ABCD -的体积 之比.ABDPMFGE6. 如图，正方形ABCD 和四边形ACEF 所在的平面互相垂直。
EF//AC ，AB=2,CE=EF=1 （Ⅰ）求证：AF//平面BDE ； （Ⅱ）求证：CF ⊥平面BDF;7.如图，在多面体ABCDEF 中，四边形ABCD 是正方形，AB=2EF=2，EF ∥AB,EF ⊥FB,∠BFC=90°，BF=FC,H 为BC 的中点，(Ⅰ)求证：FH ∥平面EDB;（Ⅱ）求证：AC ⊥平面EDB; （Ⅲ）求四面体B —DEF 的体积；8. 如图，在直三棱柱111ABC A B C -中，E 、F 分别是1A B 、1A C 的中点，点D 在11B C 上，11A D B C⊥。
(完整版)高中数学必修二立体几何常考证明题汇总,推荐文档
新课标立体几何常考证明题汇总1、已知四边形是空间四边形，分别是边的中点ABCD ,,,E F G H ,,,AB BC CD DA 1 求证：EFGH 是平行四边形 2 若BD=，AC=2，EG=2。
求异面直线AC 、BD 所成的角和EG 、BD所成的角。
证明：在中，∵分别是的中点∴ABD ∆,E H ,AB AD 1//,2EH BD EH BD =同理，∴∴四边形是平行四边形。
1//,2FG BD FG BD =//,EH FG EH FG =EFGH (2) 90° 30 °考点：证平行（利用三角形中位线），异面直线所成的角2、如图，已知空间四边形中，，是的中点。
ABCD ,BC AC AD BD ==E AB 求证：（1）平面CDE;⊥AB （2）平面平面。
CDE ⊥ABC 证明：（1）BC AC CE ABAE BE =⎫⇒⊥⎬=⎭同理，AD BD DE ABAE BE =⎫⇒⊥⎬=⎭又∵∴平面CE DE E ⋂=AB ⊥CDE（2）由（1）有平面AB ⊥CDE 又∵平面，∴平面平面AB ⊆ABC CDE ⊥ABC考点：线面垂直，面面垂直的判定D CB3、如图，在正方体中，是的中点，1111ABCD A B C D -E 1AA 求证： 平面。
1//A C BDE 证明：连接交于，连接，AC BD O EO∵为的中点，为的中点E 1AA O AC ∴为三角形的中位线 ∴EO 1A AC 1//EO A C 又在平面内，在平面外EO BDE 1A C BDE ∴平面。
1//A C BDE 考点：线面平行的判定4、已知中,面,,求证：面．ABC ∆90ACB ∠=SA ⊥ABC AD SC ⊥AD ⊥SBC 证明：°90ACB ∠=∵BC AC ∴⊥ 又面SA ⊥ABC SA BC ∴⊥ 面BC ∴⊥SACBC AD ∴⊥又面 ,SC AD SC BC C ⊥⋂=AD ∴⊥SBC 考点：线面垂直的判定5、已知正方体，是底对角线的交点.1111ABCD A B C D -O ABCD 求证：(１) C 1O ∥面；(2)面． 11AB D 1AC ⊥11AB D 证明：（1）连结，设，连结11A C 11111A C B D O ⋂=1AO∵ 是正方体 是平行四边形1111ABCD A B C D -11A ACC ∴∴A 1C 1∥AC 且11A C AC =又分别是的中点，∴O 1C 1∥AO 且1,O O 11,A C AC 11O C AO=是平行四边形11AOC O ∴面，面 ∴C 1O ∥面111,C O AO AO ∴⊂∥11AB D 1C O ⊄11AB D 11AB D （2）面1CC ⊥ 1111A B C D 11!CC B D ∴⊥又， 1111A C B D ⊥∵1111B D AC C ∴⊥面111AC B D ⊥即同理可证， 又11A C AD ⊥1111D B AD D ⋂=面∴1A C ⊥11AB D 考点：线面平行的判定（利用平行四边形），线面垂直的判定1SDCB AD 1ODB AC 1B 1A 1CMP6、正方体中，求证：（1）；（2）.''''ABCD A B C D -''AC B D DB ⊥平面''BD ACB ⊥平面考点：线面垂直的判定7、正方体ABCD —A 1B 1C 1D 1中．(1)求证：平面A 1BD ∥平面B 1D 1C ； (2)若E 、F 分别是AA 1，CC 1的中点，求证：平面EB 1D 1∥平面FBD ．证明：(1)由B 1B ∥DD 1，得四边形BB 1D 1D 是平行四边形，∴B 1D 1∥BD ，又BD ⊄平面B 1D 1C ，B 1D 1平面B 1D 1C ，⊂∴BD ∥平面B 1D 1C ．同理A 1D ∥平面B 1D 1C ．而A 1D ∩BD ＝D ，∴平面A 1BD ∥平面B 1CD ．(2)由BD ∥B 1D 1，得BD ∥平面EB 1D 1．取BB 1中点G ，∴AE ∥B 1G ．从而得B 1E ∥AG ，同理GF ∥AD ．∴AG ∥DF ．∴B 1E ∥DF ．∴DF ∥平面EB 1D 1．∴平面EB 1D 1∥平面FBD ．考点：线面平行的判定（利用平行四边形）8、四面体中，分别为的中点，且，ABCD ,,AC BD EF =,AD BC EF AC =，求证：平面90BDC ∠= BD ⊥ACD 证明：取的中点，连结，∵分别为的中点，∴CD G ,EG FG ,E F ,AD BC EG12//AC =，又∴，∴在中，12//FG BD =,AC BD =12FG AC =EFG ∆222212EG FG AC EF +==∴，∴，又，即，EG FG ⊥BD AC ⊥90BDC ∠=BD CD ⊥AC CD C ⋂=∴平面BD ⊥ACD 考点：线面垂直的判定,三角形中位线，构造直角三角形9、如图是所在平面外一点，平面，是的中点，是P ABC ∆,PA PB CB =⊥PAB M PC N 上的AB 点，3AN NB =（1）求证：；（2）当，时，求的长。
高一数学常考立体几何证明题及答案
高一数学常考立体几何证明题1、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
求证：（1）⊥AB 平面CDE; （2）平面CDE ⊥平面ABC 。
2、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点，求证： 1//A C 平面BDE 。
3、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥, 求证：AD ⊥面SBC ．4、已知正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点.求证：(１) C1O ∥面11AB D ；(2)1AC ⊥面11AB D ．5、正方体''''ABCD A B C D -中，求证：''AC B D DB ⊥平面；6、正方体ABCD —A1B1C1D1中．(1)求证：平面A1BD ∥平面B1D1C ；(2)若E 、F 分别是AA1，CC1的中点，求证：平面EB1D1∥平面FBD ．7、四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，且22EF AC =，90BDC ∠=，AE D BCAE D 1CB 1DCBASDCB AD 1ODBAC 1B 1A 1C A A B 1BC 1CD 1DG EF求证：BD ⊥平面ACD8、如图，在正方体1111ABCD A B C D -中，E 、F 、G 分别是AB 、AD 、11C D 的中点.求证：平面1D EF∥平面BDG .9、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点.（1）求证：1//A C 平面BDE ；（2）求证：平面1A AC ⊥平面BDE .10、已知ABCD 是矩形，PA ⊥平面ABCD ，2AB =，4PA AD ==，E 为BC 的中点．求证：DE ⊥平面PAE ；（2）求直线DP 与平面PAE 所成的角．11、如图，在四棱锥P ABCD -中，底面ABCD 是060DAB ∠=且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ． （1）若G 为AD 的中点，求证：BG ⊥平面PAD ； （2）求证：AD PB ⊥．12、如图1,在正方体1111ABCD A B C D -中，M 为1CC 的中点，AC 交BD于点O ，求证：1AO ⊥平面MBD ．13、如图２，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ， 作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ． 求证：AH ⊥平面BCD ．14．(12分)求证平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形．已知：如图，三棱锥S —ABC ，SC ∥截面EFGH ，AB ∥截面EFGH. 求证：截面EFGH 是平行四边形．15．(12分)已知正方体ABCD —A1B1C1D1的棱长为a ，M 、N 分别为A1B 和AC 上的点，A1M ＝AN ＝23a ，如图． (1)求证：MN ∥面BB1C1C ；16．(12分)(2009·浙江高考)如图，DC ⊥平面ABC ，EB ∥DC ，AC ＝BC ＝EB ＝2DC ＝2，∠ACB ＝120°，P ，Q 分别为AE ，AB 的中点． (1)证明：PQ ∥平面ACD ；17．(12分)如图，在四面体ABCD 中，CB ＝CD ，AD ⊥BD ，点E 、F 分别是AB 、BD 的中点． 求证：(1)直线EF ∥面ACD. （2）平面EFC ⊥平面BCD .20、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点，求证： 1//A C 平面BDE 。
高一数学必修2立体几何证明题汇总.
2、如图，在正方体1111ABCD A B C D 中，E 是1AA 的中点，求证： 1//AC 平面BDE 。
A E D 1 CB 1 DC B A8、如图，在正方体1111ABCD A B C D 中，E 、F 、G 分别是AB 、AD 、11C D 的中点.求证：平面1D EF ∥平面BDG .15．(12分)已知正方体ABCD —A 1B 1C 1D 1的棱长为a ，M 、N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝23a ，如图．(1)求证：MN ∥面BB 1C 1C ；(2)求MN 的长．16．(12分)(2009·浙江高考)如图，DC ⊥平面ABC ，EB ∥DC ，AC ＝BC ＝EB ＝2DC ＝2，∠ACB ＝120°，P ，Q 分别为AE ，AB 的中点．(1)证明：PQ ∥平面ACD ；(2)求AD 与平面ABE 所成角的正弦值．生物练习1．由细胞膜的成分推知，构成细胞膜所必须的化学元素是（）A．C、H、O、N B．C、H、O、N、PC．C、H、O、S、P D．C、H、O、Mg、Fe2．在制备细胞膜的实验中常用新鲜成熟的哺乳动物的红细胞作材料是因为（）A．哺乳动物红细胞在水中容易胀破B．哺乳动物红细胞容易收集C．哺乳动物红细胞内没有核膜、线粒体膜等细胞器膜D．哺乳动物红细胞的细胞膜在分离时容易沉淀在下面3．任何系统都有边界，边界对系统的稳定至关重要。
细胞作为一个基本的生命系统，它的边界是（）A．细胞壁B．细胞膜C．细胞核D．细胞膜表面的蛋白质4．科学上鉴别死细胞和活细胞，常用“染色排除法”，例如，用台盼蓝染色，死的动物细胞会被染成蓝色，而活的动物细胞不着色，从而判断细胞是否死亡。
所利用的是细胞膜的哪种功能（）A．保护细胞内部结构的功能B．进行细胞间的信息交流C．控制物质进出功能D．免疫功能5．经研究发现，动物的唾液腺细胞内高尔基体含量较多。
高中数学立体几何常考证明题汇总精选资料
立体几何常考证明题汇总考点1：证平行（利用三角形中位线），异面直线所成的角已知四边形ABCD 是空间四边形，,,,E F G H 分别是边,,,AB BC CD DA 的中点 （1） 求证：EFGH 是平行四边形（2） 若BD=AC=2，EG=2。
求异面直线AC 、BD 所成的角和EG 、BD 所成的角。
考点2：线面垂直，面面垂直的判定如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
求证：（1）⊥AB 平面CDE;（2）平面CDE ⊥平面ABC 。
考点3：线面平行的判定如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点， 求证： 1//A C 平面BDE 考点4：线面垂直的判定已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证：AD ⊥面SBC ． 考点5：线面平行的判定（利用平行四边形），线面垂直的判定 已知正方体1111-ABCD A B C D ，O 是底ABCD 对角线的交点.求证：(１) C 1O ∥面11AB D ；(2)1AC ⊥面11AB D ． 考点6：线面垂直的判定正方体''''ABCD ABC D -中，求证：（1）''AC B D DB ⊥平面；（2）''BD ACB ⊥平面.考点7：线面平行的判定（利用平行四边形）正方体ABCD —A 1B 1C 1D 1中．(1)求证：平面A 1BD ∥平面B 1D 1C ； (2)若E 、F 分别是AA 1，CC 1的中点，求证：平面EB 1D 1∥平面FBD ． 考点8：线面垂直的判定,三角形中位线，构造直角三角形AE D 1 CB 1DCBAAHGFEDCBAED BCSDCBA D 1ODBAC 1B 1A 1C A 1NMPCBA四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，且EF AC =， 90BDC ∠=，求证：BD ⊥平面ACD考点9：三垂线定理如图P 是ABC ∆所在平面外一点，,PA PB CB =⊥平面PAB ，M 是PC 的中点，N 是AB 上的点，3ANNB =（1）求证：MN AB ⊥；（2）当90APB ∠=，24AB BC ==时，求MN 的长。
高中数学立体几何证明题汇总
立体几何常考证明题1、已知四边形ABCD 是空间四边形，E, F,G, H 分别是边AB,BC,CD , DA 的中点（1）求证：EFGH是平行四边形（2）若BD=2 3 ，AC=2，EG=2。
求异面直线AC、BD所成的角和EG、BD所成的角。
AEHB DF GC2、如图，已知空间四边形ABCD 中，BC AC, AD BD ，E 是AB 的中点。
求证：（1）AB 平面CDE;（2）平面CDE 平面ABC 。
AEB CD3、如图，在正方体A BCD ABC D 中，E 是AA1 的中点，1 1 1 1求证：A1C // 平面BDE 。
A D1B1 CEADBC 14、已知ABC 中ACB 90 , SA 面ABC , AD SC ,求证：AD 面SBC ．SDBAC5、已知正方体ABCD A1B1C1D1，O是底ABCD 对角线的交点. D1C1B1求证：(１) C1O∥面AB1D1 ；(2) A1C 面AB1D1 ．A1DCOA B6、正方体ABCD A'B'C 'D'中，求证：（1）AC 平面B'D 'DB ；（2）BD ' 平面ACB '.27、正方体ABCD —A1B1C1D1 中．(1)求证：平面A1BD∥平面B1D1C；D 1C1 (2)若E、F 分别是AA1，CC1 的中点，求证：平面EB1D1∥平面FBD ．A1B1FEGCDAB8、四面体ABCD 中，AC BD,E, F 分别为AD, BC 的中点，且BDC 90 ，求证：BD 平面ACD2EF AC ，29、如图P 是ABC 所在平面外一点，PA PB, CB 平面PAB ，M 是PC 的中点，N 是AB 上的点，AN 3NBP（1）求证：MN AB ；（2）当APB 90 ，AB 2BC 4 时，求MN 的长。
MCANB310、如图，在正方体ABCD A1B1C1D1 中，E 、F 、G 分别是AB 、AD 、C1D1 的中点. 求证：平面D1EF ∥平面BDG .11、如图，在正方体A BCD ABC D 中，E 是1 1 1 1 AA 的中点.1（1）求证：A1C // 平面BDE ；（2）求证：平面A AC 平面BDE .112、已知ABCD 是矩形，PA 平面ABCD ，AB 2 ，PA AD 4 ，E 为BC 的中点．（1）求证：DE 平面PAE ；（2）求直线DP 与平面PAE 所成的角．413 、如图，在四棱锥P ABCD 中，底面ABCD 是DAB 600 且边长为a的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ．（1）若G 为AD 的中点，求证：BG 平面PAD ；（2）求证：AD PB ；（3）求二面角 A BC P 的大小．14、如图1,在正方体ABCD A1B1C1D1 中，M 为CC1 的中点，AC 交BD 于点O，求证：A1O 平面MBD ．15、如图２，在三棱锥Ａ－BCD中，BC＝AC，AD＝BD，作BE⊥CD，Ｅ为垂足，作AH⊥BE于Ｈ．求证：AH⊥平面BCD．516、证明：在正方体ABCD －A1B1C1D1 中，A 1C⊥平面BC1DD1 C1A 1B 1D CA B17、如图，过S 引三条长度相等但不共面的线段SA、SB、SC，且∠ASB= ∠ASC=60 °，∠BSC=90°，求证：平面ABC ⊥平面BSC．WORD文档6专业资料。
高一数学常考立体几何证明题及答案
11、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
求证：（1）⊥AB 平面CDE; （2）平面CDE ⊥平面ABC 。
2、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点，求证： 1//AC 平面BDE 。
3、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证：AD ⊥面SBC ．4、已知正方体1111ABCD A BC D -，O 是底ABCD 对角线的交点. 求证：(１) C 1O ∥面11AB D ；(2)1AC ⊥面11AB D ．5、正方体''''ABCD A B C D -中，求证： （1）''AC B D DB ⊥平面； （2）''BD ACB ⊥平面.6、正方体ABCD —A 1B 1C 1D 1中． (1)求证：平面A 1BD ∥平面B 1D 1C ；(2)若E 、F 分别是AA 1，CC 1的中点，求证：平面EB 1D 1∥平面FBD ．7、四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，且22EF AC =，90BDC ∠=，求证：BD ⊥平面ACD8、如图，在正方体1111ABCD A B C D -中，E 、F 、G 分别是AB 、AD 、11C D 的中点.求证：平面1D EF ∥平面B D G.9、如图，在正方体AEDBCA 1ED 1C 1B 1DC BA SDCBAD 1C 1B 1A 1A 1A E21111ABCD A B C D -中，E 是1AA 的中点.（1）求证：1//AC 平面BDE ； （2）求证：平面1A AC ⊥平面BDE .10、已知ABCD 是矩形，PA ⊥平面ABCD ，2AB =，4PA AD ==，E 为BC 的中点．（1）求证：DE ⊥平面PAE ；（2）求直线DP 与平面PAE 所成的角．11、如图，在四棱锥P ABCD -中，底面ABCD 是060DAB ∠=且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ．（1）若G 为AD 的中点，求证：BG ⊥平面PAD ； （2）求证：AD PB ⊥．12、如图1,在正方体1111ABCD A B C D -中，M 为1CC 的中点，AC 交BD于点O ，求证：1AO ⊥平面MBD ．13、如图２，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ，作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ．求证：AH ⊥平面BCD ．14．(12分)求证平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形．已知：如图，三棱锥S —ABC ，SC ∥截面EFGH ，AB ∥截面EFGH .求证：截面EFGH 是平行四边形．315．(12分)已知正方体ABCD —A 1B 1C 1D 1的棱长为a ，M 、N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝23a ，如图．(1)求证：MN ∥面BB 1C 1C ； (2)求MN 的长．16．(12分)(2009·浙江高考)如图，DC ⊥平面ABC ，EB ∥DC ，AC ＝BC ＝EB＝2DC ＝2，∠ACB ＝120°，P ，Q 分别为AE ，AB 的中点．(1)证明：PQ ∥平面ACD ；(2)求AD 与平面ABE 所成角的正弦值．17．(12分)如图，在四面体ABCD 中，CB ＝CD ，AD ⊥BD ，点E 、F 分别是AB 、BD 的中点．求证：(1)直线EF ∥面ACD . （2）平面EFC ⊥平面BCD4.1、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
高一数学常考立体几何证明题及答案
1、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
求证：（1）⊥AB 平面CDE; （2）平面CDE ⊥平面ABC 。
2、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点，求证： 1//A C 平面BDE 。
3、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥, 求证：AD ⊥面SBC ．4、已知正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点.求证：(１) C1O ∥面11AB D ；(2)1AC ⊥面11AB D ．5、正方体''''ABCD A B C D -中，求证：''AC B D DB ⊥平面；6、正方体ABCD —A1B1C1D1中． (1)求证：平面A1BD ∥平面B1D1C ；(2)若E 、F 分别是AA1，CC1的中点，求证：平面EB1D1∥平面FBD ．7、四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，且22EF AC=，90BDC ∠=，求证：BD ⊥平面ACD8、如图，在正方体中，、、分别是、、的中点.求证：平面∥平面.9、如图，在正方体中，是的中点.AEDBCAED 1CB 1DCBASDCB AD 1ODBAC 1B 1A 1CA AB 1C 1C D 1D G EFA H G F E D CB （1）求证：平面； （2）求证：平面平面.10、已知是矩形，平面，，，为的中点． 求证：平面；（2）求直线与平面所成的角．11、如图，在四棱锥中，底面是且边长为的菱形，侧面是等边三角形，且平面垂直于底面．（1）若为的中点，求证：平面； （2）求证：．12、如图1,在正方体中，为 的中点，AC 交BD 于点O ，求证：平面MBD ．13、如图２，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ，作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ． 求证：AH ⊥平面BCD ．14．(12分)求证平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形．已知：如图，三棱锥S —ABC ，SC ∥截面EFGH ，AB ∥截面EFGH. 求证：截面EFGH 是平行四边形．15．(12分)已知正方体ABCD —A1B1C1D1的棱长为a ，M 、N 分别为A1B 和AC 上的点，A1M ＝AN ＝23a ，如图． (1)求证：MN ∥面BB1C1C ；16．(12分)(2009·浙江高考)如图，DC ⊥平面ABC ，EB ∥DC ，AC ＝BC ＝EB ＝2DC ＝2，∠ACB ＝120°，P ，Q 分别为AE ，AB 的中点．(1)证明：PQ ∥平面ACD ；17．(12分)如图，在四面体ABCD 中，CB ＝CD ，AD ⊥BD ，点E 、F 分别是AB 、BD 的中点． 求证：(1)直线EF ∥面ACD.（2）平面EFC ⊥平面BCD .18、已知四边形是空间四边形，分别是边的中点求证：EFGH 是平行四边形20、如图，在正方体中，是的中点，D 1OD BA C 1B 1A 1CNMPCBA求证： 平面。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高中数学立体几何常考证明题汇总
1、已知四边形ABCD 是空间四边形，,,,E F G H 分别是边,,,AB BC CD DA 的中点 （1） 求证：EFGH 是平行四边形
（2） 若
BD=AC=2，EG=2。
求异面直线AC 、BD 所成的角和EG 、BD 所成的角。
考点：证平行（利用三角形中位线），异面直线所成的角
2、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
求证：（1）⊥AB 平面CDE;
（2）平面CDE ⊥平面ABC 。
考点：线面垂直，面面垂直的判定
3、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点， 求证： 1//A C 平面BDE 。
考点：线面平行的判定
4、已知ABC ∆中90ACB ∠=o
,SA ⊥面ABC ,AD SC ⊥,求证：AD ⊥面SBC ．
考点：线面垂直的判定
5、已知正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点.
求证：(１) C 1O ∥面11AB D ；(2)1
AC ⊥面11AB D ． 考点：线面平行的判定（利用平行四边形），线面垂直的判定
A E
D
C
B
D C
B A
A
H
G
F
E
D
C
B A E D
B
C
S
D
C
B
A
D 1
O
D
B
A
C 1
B 1
A 1
C
N
M
P
C
B
A
6、正方体''''ABCD A B C D -中，
求证：（1）''AC B D DB ⊥平面；（2）''BD ACB ⊥平面. 考点：线面垂直的判定
7、正方体ABCD —A 1B 1C 1D 1中．(1)求证：平面A 1BD ∥平面B 1D 1C ； (2)若E 、F 分别是AA 1，CC 1的中点，求证：平面EB 1D 1∥平面
FBD ．
考点：线面平行的判定（利用平行四边形）
8、四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，
且2
2
EF AC =
， 90BDC ∠=o ，求证：BD ⊥平面ACD
考点：线面垂直的判定,三角形中位线，构造直角三角形
9、如图P 是ABC ∆所在平面外一点，,PA PB CB =⊥平面PAB ，M
是PC 的中点，N 是AB 上的点，3AN NB =
（1）求证：MN AB ⊥；（2）当90APB ∠=o
，24AB BC ==时，
求MN 的长。
考点：三垂线定理
10、如图，在正方体1111ABCD A B C D -中，E 、F 、G 分别是AB 、
AD 、11C D 的中点.求证：平面1D EF ∥平面BDG .
考点：线面平行的判定（利用三角形中位线）
11、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点. （1）求证：1//A C 平面BDE ； （2）求证：平面1A AC ⊥平面BDE .
考点：线面平行的判定（利用三角形中位线），面面垂直的判定 12、已知ABCD 是矩形，PA ⊥平面ABCD ，2AB =，4PA AD ==，E 为BC 的中点．
（1）求证：DE ⊥平面PAE ；（2）求直线DP 与平面PAE 所成的角． 考点：线面垂直的判定,构造直角三角形
A 1
A
B 1
C 1
D 1
D G E
F
13、如图，在四棱锥P ABCD -中，底面ABCD 是0
60DAB ∠=且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ．
（1）若G 为AD 的中点，求证：BG ⊥平面PAD ； （2）求证：AD PB ⊥；
（3）求二面角A BC P --的大小．
考点：线面垂直的判定,构造直角三角形,面面垂直的性质定理，二面角的求法（定义法）
14、如图1,在正方体1111ABCD A B C D -中，M 为1CC 的中点，
AC 交BD 于点O ，求证：1A O ⊥平面MBD ．
考点：线面垂直的判定，运用勾股定理寻求线线垂直
15、如图２，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ，
作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ．求证：AH ⊥平面BCD ．
考点：线面垂直的判定
16、证明：在正方体ABCD －A 1B 1C 1D 1中，A 1C ⊥平面BC 1D
D 1 C 1
A 1
B 1
D C
A B
考点：线面垂直的判定，三垂线定理
17、如图，过S 引三条长度相等但不共面的线段SA 、SB 、SC ，且∠ASB=∠ASC=60°，∠BSC=90°，求证：平面ABC ⊥平面BSC ． ，
考点：面面垂直的判定（证二面角是直二面角）。