四年级奥数风筝模型和梯形蝴蝶定理(C级)
蝴蝶定理巧解小学竞赛中的图形问题

蝴蝶定理巧解小学竞赛中的图形问题特级教师吴乃华梯形的两条对角线,把梯形分割为“上”、“下”、“左”、“右”四个部分,这四个三角形的面积以及相应边长的比例关系,都是由梯形上、下底的长短或者比例关系所决定的。
由于这四个部分形状有点像蝴蝶,揭示梯形上、下底与“上”、“下”、“左”、“右”四个部分的关系,以及这四个部分相互之间规律的理论,就叫做“梯形蝴蝶定理”。
它的奇妙之处在于,运用这种理论解答图形问题,轻松便捷,化难为易。
下面以几道小学竞赛题的解答,就定理的部分内容作浅显的解读,敬请校正。
一、紧盯翅膀求答案梯形的左右两个三角形,就像蝴蝶的一对翅膀,它们的面积是相等的,这是因为它们分属于同底同高的两个三角形,并且共有一个“上”(或者“下”)三角形。
简记为:“左=右”。
在有关梯形的图形里,关注这一部分的情况,有时能得到答案,有时为解答提供思路。
例1、如图的梯形ABCD中,三角形ABP的面积为20平方厘米,三角形CDQ的面积为35平方厘米,求四边形MPNQ的面积。
解:连接MN,这样把梯形ABCD分成ABNM和MNCD两个小梯形。
由“左=右”知道:S△MNQ=S△CDQ=35;S△MNP=S△ABP=20。
所以,四边形MPNQ的面积是:20+35=55(平方厘米)。
例2、如图所示, 四边形ABCD与四边形CPMN都是平行四边形, 若三角形DFP 与三角形AEF 的面积分别是22 和36, 则三角形BNE 的面积是多少?(第十六届华罗庚金杯赛少年数学邀请赛小学组决赛试题)解:连接AM。
把四边形CPMN以外的部分,分成了AMND和ABGM两个梯形。
由“左=右”知道:S△AFM=22;S△AEM=36-22=14。
所以,三角形BNE 的面积是14。
二、上底下底藏玄机梯形上、下底的长度,决定了对角线交叉所成的角度。
上、下底的比,决定了对角线上、下段的比,也决定了这些线段所围成的三角形面积的比。
所以相应边长的比,等于边长所在的三角形面积的比,反之,三角形面积的比,等于三角形相应边长的比。
梯形蝴蝶定理模型 -回复

梯形蝴蝶定理模型-回复【梯形蝴蝶定理模型】是一种用于解决不确定性问题的数学模型。
它通过将问题分解为多个子问题,并利用逐步逼近的方法来求解,从而得到问题的近似解。
本文将详细介绍梯形蝴蝶定理模型,并逐步回答中括号内所设的主题。
第一步:梯形蝴蝶定理模型的基本原理梯形蝴蝶定理模型最初由数学家冯康发展而来,其基本思想是将待解决的问题划分为一系列子问题,并通过逐步逼近的方式求解这些子问题。
在梯形蝴蝶定理模型中,问题被视为一个巨大的蝴蝶,而子问题则被视为蝴蝶的一个个翅膀。
通过解决这些翅膀,最终得到整体问题的解。
第二步:梯形蝴蝶定理模型的应用领域梯形蝴蝶定理模型可以广泛应用于各种领域,特别是在处理不确定性问题时具有较强的优势。
例如,在金融领域,梯形蝴蝶定理模型可以用于分析股票价格的涨跌趋势,帮助投资者做出更明智的决策。
在供应链管理中,该模型可以用于优化物流调度,提高效率和利润。
在环境保护领域,该模型可以用于评估气候变化对生态系统的影响,并制定相应的保护策略。
第三步:梯形蝴蝶定理模型的基本步骤梯形蝴蝶定理模型的求解过程包括以下几个基本步骤:1. 定义问题:明确待解决的问题,并将其转化为数学建模问题。
2. 划分子问题:将大问题划分为小的子问题,每个子问题对应于解决整体问题的一个局部性质。
3. 设计逐步逼近方案:为每个子问题设计相应的逐步逼近方案,例如使用迭代、递推或优化算法等。
4. 求解子问题:根据逐步逼近方案,依次求解每个子问题,得到一个个局部解。
5. 合并解:根据问题的性质和要求,将局部解进行合并,得到整体问题的近似解。
6. 评估解的准确性:对整体问题的近似解进行评估,判断其是否满足问题的要求。
7. 迭代改进:根据评估结果,对逐步逼近方案进行迭代改进,直到得到满意的解。
第四步:梯形蝴蝶定理模型的优缺点梯形蝴蝶定理模型具有一些显著的优点和一些限制。
其优点包括:1. 灵活性:梯形蝴蝶定理模型可以根据问题的特点和要求进行调整和改进,适用于不同类型的问题。
四年级下册数学竞赛试题-几何.风筝模型和梯形蝴蝶定理C级.学生版-全国通用

6风筝模型和梯形蝴蝶定理例题精讲【例11【巩固1【例21C、、/如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;(2) AG:GC在^ABC中-B D=2:1,DC如图,平行四边形是2、4、4 和6.=?AE=I:3,求OB=?EC OEABCD的对角线交于0点,△ CEF、△ OEF、△ ODF、△ BOE的面积依次求:⑴求△ OCF的面积;⑵求△ GCE的面积.D【巩固】如右上图,已知 BO=2DO C0=5AO 阴影部分的面积和是 11平方厘米,求四边形 ABCD 的面积。
那么三角形DBE 的面积是O如图,边长为1的正方形ABCD 中,BE =2EC , CF =FD ,求三角形AEG 的面积.如图,长方形ABCD 中,BE: EC =2:3,DF :FC =1:2,三角形DFG 的面积为2平方厘米,求 长方形ABCD 的面积.如图,在 MBC 中,已知M 、N 分别在边AC 、BC 上,BM 与AN 相交于0 ,若AAOM 、虫ABO和人BON 的面积分别是3、2、1,则人MNC 的面积是如图4,在三角形 ABC 中,已知三角形 ADE 三角形DCE 三角形BCD 的面积分别是 89、28、26,-J f -I ”【例3】【巩固】【例4】 【巩固】CB【例5】已知ABCD是平行四边形,B C:CE=3:2,三角形ODE的面积为6平方厘米。
贝9阴影部分的面积是平方厘米。
AB E【巩固】在梯形ABCD中,上底长5厘米,下底长10厘米,S郎OC=20平方厘米,则梯形ABCD的面积是平方厘米。
【例6】如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG的面积是11,三角形BCH 的面积是23,求四边形EGFH的面积.【巩固】如图,长方形中,若三角形1的面积与三角形3的面积比为4比5,四边形2的面积为36,则三角形1的面积为在下图的正方形 ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1如图所示,BD 、CF 将长方形ABCD 分成4块,心DEF 的面积是4平方厘米,ACED 的面积是6 平方厘米.问:四边形 ABEF 的面积是多少平方厘米?如图, MBC 是等腰直角三角形,DEFG 是正方形,线段 AB 与CD 相交于K 点.已知正方形DEFG 的面积48, AK : KB =1:3,则虫BKD 的面积是多少?如图所示,ABCD 是梯形,AADE 面积是1.8,心ABF 的面积是9,也BCF 的面积是27 .那么阴影 MEC 面积是多少?【例7】 平方厘米,那么正方形 ABCD 面积是平方厘米.【巩固】【例8】【巩固】方厘米,则四边形 PMON 勺面积是平方厘米。
风筝模型和梯形蝴蝶定理

风筝模型和梯形蝴蝶定理知识框架板块一 风筝模型:(又叫任意四边形模型)S 4S 3S 2S 1O DC BA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO baS 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)例题精讲【例 1】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?76EDC BA76【巩固】 如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?OCDBA【例 2】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;⑵:AG GC ?CB【巩固】 在△ABC 中DC BD =2:1, EC AE =1:3,求OEOB=?【例 3】 如图相邻两个格点间的距离是1,则图中阴影三角形的面积为 .BA【巩固】 如图,每个小方格的边长都是1,求三角形ABC 的面积.A B【例 4】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGF EDC BA【巩固】 如右上图,已知BO=2DO ,CO=5AO ,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
四年级奥数风筝模型和梯形蝴蝶定理

风筝模型和梯形蝴蝶定理知识框架板块一 风筝模型:(又叫任意四边形模型)S 4S 3S 2S 1O DC BA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO baS 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)例题精讲【例 1】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;⑵:AG GC =?B【巩固】在△ABC中DCBD=2:1,ECAE=1:3,求OEOB=?【例 2】如图,平行四边形ABCD的对角线交于O点,CEF△、OEF△、ODF△、BOE△的面积依次是2、4、4和6.求:⑴求OCF△的面积;⑵求GCE△的面积.OGFEDCBA【巩固】如右上图,已知BO=2DO,CO=5AO,阴影部分的面积和是11平方厘米,求四边形ABCD的面积。
【例 3】如图,边长为1的正方形ABCD中,2BE EC=,CF FD=,求三角形AEG的面积.AB CDEFG 【巩固】如图,长方形ABCD中,:2:3BE EC=,:1:2DF FC=,三角形DFG的面积为2平方厘米,求长方形ABCD的面积.AB CDEFG【例 4】 如图,在ABC ∆中,已知M 、N 分别在边AC 、BC 上,BM 与AN 相交于O ,若AOM ∆、ABO∆和BON ∆的面积分别是3、2、1,则MNC ∆的面积是 .OM NCBA【巩固】 如图4,在三角形ABC 中,已知三角形ADE 、三角形DCE 、三角形BCD 的面积分别是89、28、26,那么三角形DBE 的面积是 。
四年级奥数.几何.风筝模型和梯形蝴蝶定理(C级).学生版

板块一 风筝模型:(又叫任意四边形模型)S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO baS 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)知识框架风筝模型和梯形蝴蝶定理【例 1】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;⑵:AG GC ?321GDCBA【巩固】 在△ABC 中DC BD =2:1, EC AE =1:3,求OEOB=?例题精讲【例 2】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGF EDC BA【巩固】 如右上图,已知BO=2DO ,CO=5AO ,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
【例 3】 如图,边长为1的正方形ABCD 中,2BE EC =,CF FD =,求三角形AEG 的面积.ABCDEF G。
奥数专题:蝴蝶定理和风筝定理
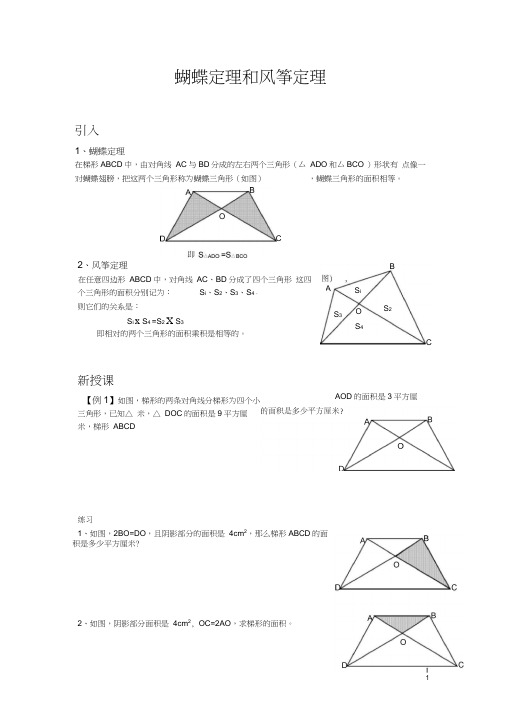
蝴蝶定理和风筝定理引入1、蝴蝶定理在梯形ABCD 中,由对角线 AC 与BD 分成的左右两个三角形(厶 ADO 和厶BCO )形状有 点像一对蝴蝶翅膀,把这两个三角形称为蝴蝶三角形(如图),蝴蝶三角形的面积相等。
2、风筝定理在任意四边形 ABCD 中,对角线 AC 、BD 分成了四个三角形 这四个三角形的面积分别记为: S i 、S 2、S 3、S 4。
则它们的关系是:S i x S 4 =S 2 X S 3即相对的两个三角形的面积乘积是相等的。
新授课【例1】如图,梯形的两条对角线分梯形为四个小三角形,已知△ 米,△ DOC 的面积是9平方厘米,梯形 ABCD练习1、如图,2BO=DO ,且阴影部分的面积是 4cm 2,那么梯形ABCD 的面积是多少平方厘米?2、如图,阴影部分面积是 4cm 2, OC=2AO ,求梯形的面积。
CBAS i S 2O S 3S 4CAOD 的面积是3平方厘【例2】如图,BD , CF 将长方形ABCD 分成四块,红色三角形的面积是4平方厘米,黄色三角形的面积是 8平方厘米,那么绿色四边形的面积是多少平方厘米?练习1如图,BD ,CF 将长方形ABCD 分成4块,红色三角形面积是 面积是6平方厘米,则绿色四边形的面积是多少平方厘米?2、如图,平行四边形 ABCD 的面积是36平方厘米,对角线 AC 、BD 交于0点,E 为CD 上一点,已知四边形 EFOG 的面积是3平方厘米,则阴影部分的面积为多少平方厘米?【例3】如图,四边形ABCD 是边长为18厘米的正方形,已知CE 的长是ED 的2倍。
求:(1)三角形CEF 的面积,(2)DF 的长度练习 正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍。
三角形DEF 的面积是多少平 方厘米? CF 长多少厘米?4平方厘米,黄色三角形DDFC【例4】正方形ABCD 和正方形CEFG ,且正方形 ABCD 边长为10厘米,则图中三角形BDF 面积为多少平方厘米?2、三个正方形 ABCD 、BEFG 、FHKP 如图排列,正方形 BEFG 的边长是3厘米,求三角形 DEK 的面积。
奥数专题:蝴蝶定理和风筝定理

蝴蝶定理和风筝定理引入1、蝴蝶定理在梯形 ABCD 中,由对角线 AC 与 BD 分成的左右两个三角形(△ ADO 和△ BCO )形状有 点像一对蝴蝶翅膀,把这两个三角形称为蝴蝶三角形(如图) , 蝴蝶三角形的面积相等。
2、风筝定理在任意四边形 ABCD 中,对角线 AC 、 BD 分成了四个三角形 这四个三角形的面积分别记为: S 1 、S 2 、S 3 、 S 4。
则它们的关系是:S 1× S 4 =S 2× S 3 即相对的两个三角形的面积乘积是相等的。
新授课【例 1】如图,梯形的两条对角线分梯形为四个小三角形,已知△ 米,△ DOC 的面积是 9 平方厘米,梯形 ABCD练习1、如图, 2BO=DO ,且阴影部分的面积是 4cm 2,那么梯形 ABCD 的面积是多少平方厘米?2、如图,阴影部分面积是 4cm 2,OC=2AO ,求梯形的面积。
CBAS 1 S 2O S 3 S 4CAOD 的面积是 3 平方厘例 2】如图, BD ,CF 将长方形 ABCD 分成四块,红色三角形的面积是 4平方厘米,黄色三角形的面积是 8 平方厘米,那么绿色四边形的面积是多少平方厘米?练习1、如图, BD ,CF 将长方形 ABCD 分成 4块,红色三角形面积是 面积是 6 平方厘米,则绿色四边形的面积是多少平方厘米?2、如图,平行四边形 ABCD 的面积是 36平方厘米,对角线 AC 、BD 交于 O 点,E 为 CD 上一点,已知四边形 EFOG 的面积是 3 平方厘米,则阴影部分的面积为多少平方厘米?例 3】如图, 四边形 ABCD 是边长为 18 厘米的正方形, 已知 CE 的长是 ED 的 2 倍。
求: 1)三角形 CEF 的面积,( 2)DF 的长度练习 正方形 ABCD 的边长是 12 厘米,已知 DE 是 EC 长度的 2 倍。
三角形 DEF 的面积是多少平 方厘米? CF 长多少厘米?4 平方厘米,黄色三角形DDFC【例 4】正方形 ABCD 和正方形 CEFG ,且正方形 ABCD 边长为 10 厘米,则图中三角形BDF 面积为多少平方厘米?2、三个正方形 ABCD 、BEFG 、FHKP 如图排列,正方形 BEFG 的边长是 3 厘米,求三角形 DEK 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
板块一风筝模型:(又叫任意四边形模型)
①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++
风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.
板块二梯形模型的应用
梯形中比例关系(“梯形蝴蝶定理”):
①2213::S S a b =
②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2
a b +.
梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)
S 4
S 3
S 2
S 1O D
C
B
A A B
C
D
O b
a
S 3
S 2
S 1S 4
知识框架
风筝模型和梯形蝴蝶定理
【例 1】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的
面积;⑵:AG GC ?
【巩固】 在△ABC 中
DC BD =2:1, EC AE =1:3,求OE
OB
=?
【例 2】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次
是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.
【巩固】 如右上图,已知BO=2DO ,CO=5AO ,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
321G
D
C
B
A O
G
F E
D
C B
A
例题精讲
【例 3】 如图,边长为1的正方形ABCD 中,2BE EC =,CF FD =,求三角形AEG 的面积.
【巩固】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长
方形ABCD 的面积.
【例 4】 如图,在ABC ∆中,已知M 、N 分别在边AC 、BC 上,BM 与AN 相交于O ,若AOM ∆、ABO
∆和BON ∆的面积分别是3、2、1,则MNC ∆的面积是.
【巩固】 如图4,在三角形ABC 中,已知三角形ADE 、三角形DCE 、三角形BCD 的面积分别是89、28、26,
那么三角形DBE 的面积是。
A
B
C
D
E
F G
A
B
C
D
E
F G
O
M N
C
B
A
E
D
C B
A
【例 5】 已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE 的面积为6平方厘米。
则阴影部分的面
积是平方厘米。
【巩固】 在梯形ABCD 中,上底长5厘米,下底长10厘米,20=∆BOC S 平方厘米,则梯形ABCD 的面积是 平方厘米。
【例 6】 如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG 的面积是11,三角形BCH
的面积是23,求四边形EGFH 的面积.
【巩固】 如图,长方形中,若三角形1的面积与三角形3的面积比为4比5,四边形2的面积为36,则三
角形1的面积为________.
O
E D
C
B
A
H
G F
E
D
C
B A
3
21
【例 7】 在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1
平方厘米,那么正方形ABCD 面积是平方厘米.
【巩固】 如图所示,BD 、CF 将长方形ABCD 分成4块,DEF ∆的面积是4平方厘米,CED ∆的面积是6
平方厘米.问:四边形ABEF 的面积是多少平方厘米?
【例 8】 如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形DEFG
的面积48,:1:3AK KB =,则BKD ∆的面积是多少?
【巩固】 如图所示,ABCD 是梯形,ADE ∆面积是1.8,ABF ∆的面积是9,BCF ∆的面积是27.那么阴影
AEC ∆面积是多少?
A B
C
D
E
F 6
4A
B
C
D
E
F
K
G
F E D
C
B
A F
E D
C
B
A
【例 9】 如图,正六边形面积为6,那么阴影部分面积为多少?
【巩固】 如图,在一个边长为6的正方形中,放入一个边长为2的正方形,保持与原正方形的边平行,现
在分别连接大正方形的一个顶点与小正方形的两个顶点,形成了图中的阴影图形,那么阴影部分的面积为.
【例 10】 如图所示,长方形ABCD 内的阴影部分的面积之和为70,AB=8,AD=15四边形EFGO 的面积为
______.
【巩固】 如图5所示,矩形ABCD 的面积是24平方厘米,、三角形ADM 与三角形BCN 的面积之和是7.8平方
厘米,则四边形PMON 的面积是平方厘米。
15
8
O
G
F
E
D
C
B
A
【随练1】 如左下图,E 是长方形ABCD 边AB 的中点,已知三角形EBF 的面积是1平方厘米,求长方形ABCD
的面积。
【随练2】 正方形ABCD 的边长为6,E 是BC 的中点(如图)。
四边形OECD 的面积为。
【随练3】 如图,在长方形ABCD 中,6AB =厘米,2AD =厘米,AE EF FB ==,求阴影部分的面积.
O
E
D
C B
A
B
C
A
D
E
F
O
课堂检测
【作业1】 (2003北京市第十九届小学生“迎春杯”数学竞赛)四边形ABCD 的对角线AC 与BD 交于点O
(如图)所示。
如果三角形ABD 的面积等于三角形BCD 的面积的1
3
,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
【作业2】 如图面积为12平方厘米的正方形ABCD 中,,E F 是DC 边上的三等分点,求阴影部分的面积.
【作业3】 如图所示,BD 、CF 将长方形ABCD 分成4块,D EF ∆的面积是4平方厘米,CED ∆的面积是6
平方厘米.问:四边形ABEF 的面积是多少平方厘米?
D
A
O
C
B
6
4A
B
C
D
E
F
家庭作业
【作业4】 如图所示,长方形ABCD 内的阴影部分的面积之和为70,四边形EFGO 的面积为10,长方形的
面积是.
【作业5】 如图,已知D 是BC 中点,E 是CD 的中点,F 是AC 的中点.三角形ABC 由①~⑥这6部分组
成,其中②比⑤多6平方厘米.那么三角形ABC 的面积是多少平方厘米?
【作业6】 如图,正方形ABCD 中,2BE EC =,CF FD =,三角形AEG 的面积是1,求正方形ABCD 的面积.
15
8
O
G
F
E
D
C
B
A
⑥
⑤
④
③
②①
B
F
E
D C
A
A
B
C
D
E
F G。
