直曲表
RTK-南方工程之星道路放样步骤

第六章道路设计和放样道路设计以及放样也是我们比较常用的功能,本章主要介绍道路设计的步骤和道路放样。
§6.1 道路设计“道路设计”功能是道路图形设计的简单工具,标准道路一般是由直线、圆曲线和综合曲线组合而成,修建公路之前,首先设计单位需要设计出公路的《直曲表》,就是该条公路的参数数据,然后勘测方会根据该《直曲表》进行勘察放样工作,勘察放样前就需要使用道路设计,将设计方提供的《直曲表》在软件中输入生成道路设计文件,使用该道路设计文件进行勘测放样作业。
道路设计菜单包括两种道路设计模式:元素模式和交点模式。
图6-1 道路设计§6.1.1 道路基本要素以及特殊类型说明在介绍设计的两种方法之前,我们先对道路的一些基础的东西做一下介绍,《直曲表》中的主要项目:坐标和桩号:起始点和各交点的里程和坐标计算方位角:直线的方位角曲线间直线长:直线长度转角:Z表示左偏,Y表示右偏;元素法设计中,转角左偏时,半径需要输入负值。
半径:圆曲的半径曲线长度:一般包含第一缓曲长、圆曲长和第二缓曲长。
曲线总长:第一缓曲长+圆曲长+第二缓曲长(某些直曲表中,只有第一、第二缓曲长和曲线总长,那么圆曲长就要通过计算的到了)断链:因局部改线、分段测量或量距中发生错误等等均会造成里程桩号与实际距离不相符,这种在里程中间不连续(桩号不相连接)的情况叫“断链”长链:桩号重叠的称长链短链:桩号间断的称短链。
对于断链的处理,一定要使用分段处理,生成两个道路设计文件。
卵形曲线:是指在两半径不等的同向圆曲线间插入一段缓和曲线。
即圆缓圆的情况;也就是说:卵形曲线本身是缓和曲线的一段,只是在插入的时候去掉了靠近半径无穷大方向的一段,而非是一条完整的缓和曲线。
我们简单的理解,出现圆缓圆的情况,即是卵形曲线,必须使用元素法设计。
一般高速公路的匝道都是卵形曲线。
回头曲线:曲线总转向角大于或接近180°的曲线称为回头曲线,也称套线。
回头曲线也必须使用元素法设计,回头曲线在山区的公路建设中比较常见。
EXCEL中关于角度的输入、输出及转换计算技巧
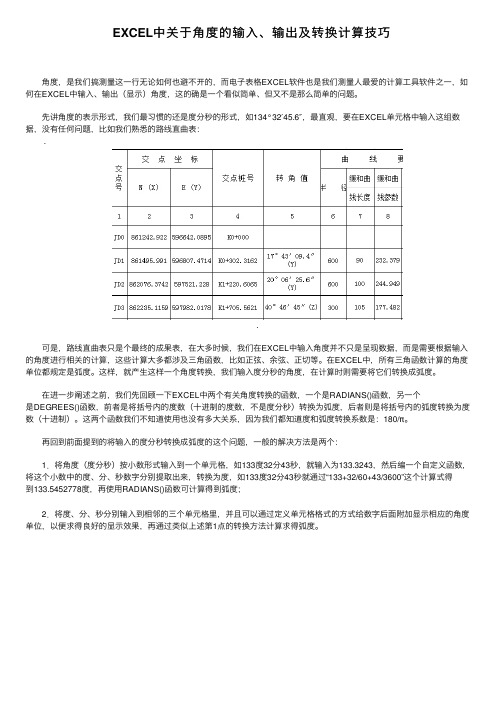
EXCEL中关于⾓度的输⼊、输出及转换计算技巧⾓度,是我们搞测量这⼀⾏⽆论如何也避不开的,⽽电⼦表格EXCEL软件也是我们测量⼈最爱的计算⼯具软件之⼀,如何在EXCEL中输⼊、输出(显⽰)⾓度,这的确是⼀个看似简单、但⼜不是那么简单的问题。
先讲⾓度的表⽰形式,我们最习惯的还是度分秒的形式,如134°32′45.6″,最直观,要在EXCEL单元格中输⼊这组数据,没有任何问题,⽐如我们熟悉的路线直曲表:..可是,路线直曲表只是个最终的成果表,在⼤多时候,我们在EXCEL中输⼊⾓度并不只是呈现数据,⽽是需要根据输⼊的⾓度进⾏相关的计算,这些计算⼤多都涉及三⾓函数,⽐如正弦、余弦、正切等。
在EXCEL中,所有三⾓函数计算的⾓度单位都规定是弧度。
这样,就产⽣这样⼀个⾓度转换,我们输⼊度分秒的⾓度,在计算时则需要将它们转换成弧度。
在进⼀步阐述之前,我们先回顾⼀下EXCEL中两个有关⾓度转换的函数,⼀个是RADIANS()函数,另⼀个是DEGREES()函数,前者是将括号内的度数(⼗进制的度数,不是度分秒)转换为弧度,后者则是将括号内的弧度转换为度数(⼗进制)。
这两个函数我们不知道使⽤也没有多⼤关系,因为我们都知道度和弧度转换系数是:180/π。
再回到前⾯提到的将输⼊的度分秒转换成弧度的这个问题,⼀般的解决⽅法是两个:1.将⾓度(度分秒)按⼩数形式输⼊到⼀个单元格,如133度32分43秒,就输⼊为133.3243,然后编⼀个⾃定义函数,将这个⼩数中的度、分、秒数字分别提取出来,转换为度,如133度32分43秒就通过“133+32/60+43/3600”这个计算式得到133.5452778度,再使⽤RADIANS()函数可计算得到弧度;2.将度、分、秒分别输⼊到相邻的三个单元格⾥,并且可以通过定义单元格格式的⽅式给数字后⾯附加显⽰相应的⾓度单位,以便求得良好的显⽰效果,再通过类似上述第1点的转换⽅法计算求得弧度。
线元法输入示例直曲表

558.267 724.934
X 35.366
Y
500 166.667
407.415
方
0
0.000
275.711
桩
X 2768793.828 X 2768263.814 X 2768097.682
Y 522824.873
Y 522660.050
Y 522647.003
方 207°56′12.3″ 方 186°36′45.0″ 方 183°25′45.8″
X 30.016
Y
2754173.681 518435.478
X 2754049.467 Y 518324.388
X 2753791.040 Y 517994.006
X 2753713.131 Y 517846.696
500 166.667
381.038
方 220°44′48.9″ 方 223°55′48.1″ 方 240°00′15.8″ 方 243°11′15.0″
X 2758056.892 Y 520939.708
X 2757891.709 Y 520917.693
874.311 186°31′49.8″
0
500 166.667 500 166.667
469.551 404.760
方 215°23′40.1″ 方 212°12′41.0″ 方 189°42′48.9″ 方 186°31′49.8″ 桩 K12+932.543 桩 K13+099.210 桩 K13+565.520 桩 K13+732.187
Y 522613.282
Y 522530.410
Y
方 183°25′45.8″ 方 193°55′52.6″ 方
公路断链的计算方法

断链的处理一、先把断链搞清楚断链其实在道路路线中经常会遇到,甚至可以说没有遇到断链反而不正常,那么什么是断链,什么是长链,什么又是短链,可能还有很多现场测量人员还不十分熟悉。
1.断链的产生先来看看断链是怎么产生的。
断链,指的是因局部改线或分段测量等原因造成的桩号不连续的现象。
分段测量,这个很好理解,我曾经就遇到过,1999年在湖南沅陵,进行一条县道的改建勘测,总长45公里左右,分两支队伍同时测量,我所在的队伍测后面那一段,当时勘测起点就按老道路的桩号假定了一个起点桩号,很显然,这个假定的桩号肯定不会与前面那段道路测量的终点桩号正好一样(不然可以去买彩票了),这样就产生了断链,此处桩号不连续。
局部改线,怎么会发生局部改线呢,其实,这种情况大多会发生在勘测设计文件在评审后的修改上,专家在评审设计文件,会提出很多意见(体现专家的作用),有些意见就会说:某某路段半径要改大(或改小)一点,以便占用更少的农田;某某路段要向这个方向偏移一些,以减少填方数量;这段路线走这里不行,从村外绕过去。
得,专家的意见,若拿不出充足的理由来反驳,就乖乖地照做吧。
于是集合队伍,又开拔到现场,重新计算路线,打桩,测量,数据出来了,当调整的路段重新回到原设计的路线上时,桩号不连续了,设断链吧。
还有时候,当现场勘测人员现场拿不定注意,在某某路段选取了两个路线方案,测量对自己推荐一条路线方案,连续推算桩号过去,另一条作为比较线,推算桩号与正线汇合时,汇合点的桩号不连续,后来专家一评审,觉得比较线要好,就用它了(设计院怎么就这么背),得,断链又产生了。
还有一种情况,都不好意思讲,有一次我碰到了,就是,测量过的路线,回过头来突然发现某个交点的要素计算错误,导致桩号也算错了,有错就改啊,断链于是又产生了。
总而言之,言而总之,一条路线,不产生断链,基本可以说是不正常滴。
有人说了,既然断链是桩号不连续,那为什么不把断链后面的桩号重新推算,使它连续呢?不就解决了吗?这个问题的提出者,显然没有搞过路线勘测,先拖出去打……。
线路中长、短链

线路中的长、短链1先把断链搞清楚断链其实在道路路线中经常会遇到,甚至可以说没有遇到断链反而不正常,那么什么是断链,什么是长链,什么又是短链,可能还有很多现场测量人员还不十分熟悉。
1.1断链的产生先来看看断链是怎么产生的。
断链,指的是因局部改线或分段测量等原因造成的桩号不连续的现象。
分段测量,这个很好理解,我曾经就遇到过,1999年在湖南沅陵,进行一条县道的改建勘测,总长45公里左右,分两支队伍同时测量,我所在的队伍测后面那一段,当时勘测起点就按老道路的桩号假定了一个起点桩号,很显然,这个假定的桩号肯定不会与前面那段道路测量的终点桩号正好一样(不然可以去买彩票了),这样就产生了断链,此处桩号不连续。
局部改线,怎么会发生局部改线呢,其实,这种情况大多会发生在勘测设计文件在评审后的修改上,专家在评审设计文件,会提出很多意见(体现专家的作用),有些意见就会说:某某路段半径要改大(或改小)一点,以便占用更少的农田;某某路段要向这个方向偏移一些,以减少填方数量;这段路线走这里不行,从村外绕过去。
得,专家的意见,若拿不出充足的理由来反驳,就乖乖地照做吧。
于是集合队伍,又开拔到现场,重新计算路线,打桩,测量,数据出来了,当调整的路段重新回到原设计的路线上时,桩号不连续了,设断链吧。
还有时候,当现场勘测人员现场拿不定注意,在某某路段选取了两个路线方案,测量对自己推荐一条路线方案,连续推算桩号过去,另一条作为比较线,推算桩号与正线汇合时,汇合点的桩号不连续,后来专家一评审,觉得比较线要好,就用它了(设计院怎么就这么背),得,断链又产生了。
还有一种情况,都不好意思讲,有一次我碰到了,就是,测量过的路线,回过头来突然发现某个交点的要素计算错误,导致桩号也算错了,有错就改啊,断链于是又产生了。
总而言之,言而总之,一条路线,不产生断链,基本可以说是不正常滴。
有人说了,既然断链是桩号不连续,那为什么不把断链后面的桩号重新推算,使它连续呢?不就解决了吗?这个问题的提出者,显然没有搞过路线勘测,先拖出去打……。
如何将直曲表元素转换为线元法所需要的元素(起点坐标,方位角)?

如何将直曲表元素转换为线元法所需要的元素(起点坐标,方位角)?直线上的切线方位角不变缓和曲线的转角=Ls/2/R(弧度)圆曲线的转角=Lc/R(弧度)所以,已知起点切线方位角为A(弧度)的情况下ZH点的切线方位角=AHY点的切线方位角=A+Ls/2/RYH点的切线方位角=A+Ls/2/R+Lc/RHZ点的切线方位角=A+Ls/R+Lc/R,同时应与本交点到下一交点的坐标方位角相等。
上式中,Ls为缓和曲线长,Lc为圆曲线长,R为圆曲线半径,曲线左偏时加负号。
各主点的坐标相信你如果懂积木法算桩坐标的话应该都可以计算得出,同时记得将HZ点的坐标计算值和交点法算得的坐标相较以检验分两步计算:1、计算曲线要素P=S²÷(24R);Q=S÷2-S³÷(240R²);T=(P+R)tan|0.5B|+Q;L=πRB÷180+SZH(C)=A-T;HY(D)=C+S;YH(H)=C+L-S;HZ(G)=C+L式中:F----方位角;A----交点桩号;B-----路线偏角(左偏为负,右偏为正),R----半径;S---缓和曲线长T----切线长;L-----曲线长2、计算方位角:ZH=F;HY=F+S÷2R;HZ=F+B;YH=HZ-S÷2R;(当F<0时S÷2R为负,大于0时为正)P=(E-D)/(G-F):K=H-F:S=PK:T=22.5K/π:Q=C+(4S+8D)T式中:ED为起终点的曲率,GF为起终点的桩号,H为待求点的桩号,C为起点的切线方位角,Q为所求桩号的切线方位角。
曲率右转为正,左转为负,直线为0我再补充如下:先计算曲率变化率P=(E-D)/(G-F),曲率是半径的倒数,知道了曲率变化率,那么可以根据待求点到曲线起点的距离算出待求点的曲率(D+PK),设D+PK=1/ R2 ,然后按下式计算待求点切线方位角:Q=C+(D+1/R2)K*90/π.本公式可以计算直线\圆曲线\缓和曲线(包括不完整的),不知我这样回答可否帮助你方位角左转的时候是加还是减顺时针走的时候左加右减,逆时针反之,看你的走向了曲线上任一点切线方位角计算通用公式:P=1/R1+(1/R2-1/R1)*ABS(DKP-DKA)/ABS(DKB-DKA)....式中P为所切点曲率;1/R1为起点曲率、1/R2为终点曲率、DKP为计算点桩号、DKA为起点桩号、DKB 为终点桩号。
道路设计手册

四. 各元素输入时的规定: 1.第一个元素必须是点,且除了第一个元素外,后面的元素均不能为点。 2.第二个元素必须是直线,长度可以为零,但必须输入方位角。
缓曲 ,35.0000
缓曲 ,40.2700
圆曲 ,63.1310
,119.9100
缓曲 ,55.3470
缓曲 ,60.9120
圆曲 ,22.8120
,-124.5530 [因为是左转,所以圆曲半径输入负值]
缓曲 ,35.0000 [下一交点下无第一缓曲,曲线间直线长为零,一般都是卵形曲线]
圆曲 ,56.8230
新建的贺广段道路文件 ts_gghg1.ip,按直曲 表输入交点。注意:不 要忘记输入起点里程; 间隔表示计算时每隔多 少距离计算一个逐桩坐 标。
rod中增加一条零直线中增加一条零直线经典卵形曲线直曲表前缓或后缓长度为零经典卵形曲线直曲表前缓或后缓长度为零曲线间直线曲线间直线直曲表示例二直曲表示例二昆明市轿子山昆明市轿子山1414元素元素东坐标东坐标长度长度北坐标北坐标方位角方位角半径半径510252141028682160450510252141028682160450直线直线3217203593743611111321720359374361111142000042000023709012000002370901200000因为是左转因为是左转所以圆曲半径输入负值所以圆曲半径输入负值3500003500004027004027006313101199100631310119910055347055347060912060912022812012455302281201245530因为是左转因为是左转所以圆曲半径输入负值所以圆曲半径输入负值下一交点下无第一缓曲下一交点下无第一缓曲曲线间直线长为零曲线间直线长为零一般都是卵形曲线一般都是卵形曲线56823033256105682303325610因为是左转因为是左转所以圆曲半径输入负值所以圆曲半径输入负值450000450000直线直线2435710333446194444424357103334461944444505060938100292609381002924040交点法交点法交点组成交点组成交点法相对于元素法而言无论是理解上还是输入时都相对交点法相对于元素法而言无论是理解上还是输入时都相对简单
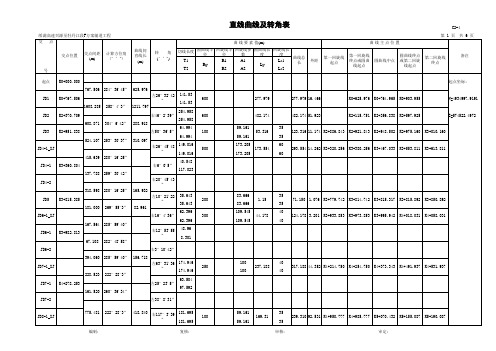
直曲表
C2-4 第 3 页 共 6 页
曲 线 要 素 值(m) 曲线间 直线长 (m) 转 角 (°’") 切线长度圆曲线半径 回旋线半径 回旋线参数 圆曲线长度 回旋线长度 T1 T2 Ry 65 200 R1 R2 A1 A2 47.697 83.666 83.666 20 102.47 102.47 335.4 115.827 115.827 100 59.161 59.161 15 59.161 59.161 50 35.355 35.355 20 20 20 13.898 7.026 36.039 35 35 25 25 20 20 53.898 11.464 K8+670.638 57.026 3.226 K8+603.949 21.502 6.447 23.968 35 35 40 40 35 35 36.039 26.535 91.502 4.659 K7+650.360 86.447 1.005 K7+316.494 Ly 8.699 30.435 Ls1 Ls2 35 35 35 23.968 4.219
交点间距 (m)
计算方位角 (°’")
Ry
R1 R2
A1 A2 59.161 59.161
Ly
Ls1 Ls2 35 35
圆曲线中点
第二回旋线 终点
100
169.31
239.310 92.531 K4+950.777
K4+985.777
K5+070.432
K5+155.087
K5+190.087
42.079 -53.938
288.918
