A星算法求解八数码问题
A星算法求解八数码技术报告

A*算法求解八数码问题●open 表、closed 表数据结构的选择:1)把s放入open表,记f=h,令closed为空表。
2)重复下列过程,直到找到目标节点为止。
若open表为空表,则宣告失败。
3)选取open表中未设置过的具有最小f值的节点为最佳节点bestnode,并把它放入closed表。
4)若bestnode为一目标节点,则成功求得一解。
5)若bestnode不是目标节点,则扩展之,产生后继节点succssor。
6)对每个succssor进行下列过称:a)对每个succssor返回bestnode的指针。
b)计算g(suc)=g(bes)+k(bes,suc)。
c)如果succssore open,称此节点为old,并填到bestnode的后继节点表中。
d)比较新旧路劲代价。
如果g(suc)<g(old),则重新确定old的父辈节点为bestnode,记下较小代价g(old),并修真f(old)值。
e)若至old节点的代价较低或一样,则停止扩展节点。
f)若succssore不再closed表中,则看其是否在closed表中。
g)若succssore在closed表中,则转向(c)。
h)若succssore既不在open表中,又不在closed表中,则把它放入open表中,并添入bestnode后裔表中,然后转向(7)。
i)计算f值j)Go loop●节点的数据结构:static int target[9]={1,2,3,8,0,4,7,6,5}; 全局静态变量,表示目标状态class eight_num{private:int num[9]; 定义八数码的初始状态int not_in_position_num; 定义不在正确位置八数码的个数int deapth; 定义了搜索的深度int eva_function; 评价函数的值,每次选取最小的进行扩展public:eight_num* parent; 指向节点的父节点eight_num* leaf_next; 指向open表的下一个节点eight_num* leaf_pre; 指向open 表的前一个节点初始状态的构造函数eight_num(int init_num[9]);eight_num(int num1,int num2,int num3,int num4,int num5,int num6,int num7,int num8,int num9){}eight_num(void){ }计算启发函数g(n)的值void eight_num::cul_para(void){}显示当前节点的状态void eight_num::show(){}复制当前节点状态到一个另数组中void eight_num::get_numbers_to(int other_num[9]){}设置当前节点状态(欲设置的状态记录的other数组中)void eight_num::set_num(int other_num[9]){}eight_num& eight_num::operator=(eight_num& another_8num){} eight_num& eight_num::operator=(int other_num[9]){}int eight_num::operator==(eight_num& another_8num){}int eight_num::operator==(int other_num[9]){}空格向上移int move_up(int num[9]){}空格向下移int move_down(int num[9]){}空格向左移int move_left(int num[9]){}空格向右移int move_right(int num[9]){}判断可否解出int icansolve(int num[9],int target[9]){}判断有无重复int existed(int num[9],eight_num *where){}寻找估价函数最小的叶子节点eight_num* find_OK_leaf(eight_num* start){}}A*算法求解框图:●分析估价函数对搜索算法的影响:估价函数就是评价函数,它用来评价子结点的好坏,因为准确评价是不可能的,所以称为估值。
A星算法求八数码问题实验报告

A星算法求八数码问题实验报告人工智能实验报告实验名称:八数码问题姓名:xx学号:2012210xxxx计算机学院2014年1月14日一.实验目的掌握A*的思想,启发式搜索,来求解在代价最小的情况下将九宫格从一个状态转为另状态的路径。
二.实验内容给定九宫格的初始状态,要求在有限步的操作内,使其转化为目标状态,且所得到的解是代价最小解(2 8 31 6 47 0 52 8 31 6 47 0 5三、A*算法思想:1、思想:A*算法是一种静态路网中求解最短路最有效的直接搜索方法。
估价值与实际值越接近,估价函数取得就越好2、原理:估价函数公式表示为: f(n)=g(n)+h(n),其中 f(n) 是从初始点经由节点n到目标点的估价函数,g(n) 是在状态空间中从初始节点到n节点的实际代价,h(n) 是从n到目标节点最佳路径的估计代价。
保证找到最短路径(最优解的)条件,关键在于估价函数h(n)的选取:估价值h(n)<= n到目标节点的距离实际值,这种情况下,搜索的点数多,搜索范围大,效率低。
但能得到最优解。
并且如果h(n)=d(n),即距离估计h(n)等于最短距离,那么搜索将严格沿着最短路径进行此时的搜索效率是最高的。
如果估价值>实际值,搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
四、算法流程:Heuristic_Search(启发式搜索)While是从未拓展表中删N为目是,输出路径否,生成n的所有子状态Case:此子状Case:此子状Case:此子状计算该子状记录比已有记录比已有返回五、关键技术:1、使用了CreateChild()函数,求得了任意未拓展九宫格的扩展结点,便于拓展子空间,搜索所有情况。
关键代码:bool CreateChild(NOExtend ns[],NOExtend ne){int i,j,k=0;for(i=0;i<3;i++){for(j=0;j<3;j++){if(ne.cur_sudoku.num[i][j]==0){ //寻找九宫格空缺所在的坐标if(i-1>=0){ //将空格向上移动CopySudoku(ns[k].cur_sudoku,ne.cur_sudo ku);//先把未改变的九宫格复制给九宫格数组的某一元素ns[k].cur_sudoku.num[i][j]=ne.cur_sudoku.num[i-1][j];//然后仅改变此二维九宫格的两项值即可ns[k].cur_sudoku.num[i-1][j]=0;ns[k].dx=1;k++;}if(j+1<=2){ //将空格向右移动CopySudoku(ns[k].cur_sudoku,ne.cur_sudo ku);ns[k].cur_sudoku.num[i][j]=ns[k].cur_su doku.num[i][j+1];ns[k].cur_sudoku.num[i][j+1]=0;ns[k].dx=1;k++;}if(i+1<=2){ //将空格向下移动CopySudoku(ns[k].cur_sudoku,ne.cur_sudo ku);ns[k].cur_sudoku.num[i][j]=ns[k].cur_su doku.num[i+1][j];ns[k].cur_sudoku.num[i+1][j]=0;ns[k].dx=1;k++;}if(j-1>=0){ //将空格向左移动CopySudoku(ns[k].cur_sudoku,ne.cur_sudo ku);ns[k].cur_sudoku.num[i][j]=ns[k].cur_su doku.num[i][j-1];ns[k].cur_sudoku.num[i][j-1]=0;ns[k].dx=1;k++;}return 1;}}}return 0;2、用启发式搜索函数寻找求解路径,运用了A*算法的思想,能够更快的求解出最优解。
a星算法求解八数码问题python

a星算法求解八数码问题python一、介绍八数码问题是一种经典的智力游戏,也是人工智能领域中的经典问题之一。
在这个问题中,有一个3×3的棋盘,上面摆着1至8这8个数字和一个空格,初始状态和目标状态都已知。
要求通过移动数字,将初始状态变换成目标状态。
其中空格可以和相邻的数字交换位置。
为了解决这个问题,我们可以使用A*算法。
本文将详细介绍如何用Python实现A*算法来求解八数码问题。
二、A*算法简介A*算法是一种启发式搜索算法,常用于寻找最短路径或最优解等问题。
它基于Dijkstra算法,并加入了启发式函数来加速搜索过程。
在A*算法中,每个节点都有两个估价值:g值和h值。
g值表示从起点到该节点的实际代价,h值表示从该节点到目标节点的估计代价。
启发式函数f(n) = g(n) + h(n) 表示从起点到目标节点的估计总代价。
A*算法采用优先队列来保存待扩展的节点,并按照f(n)值从小到大排序。
每次取出队头元素进行扩展,并将扩展出来的新节点按照f(n)值插入队列中。
当扩展出目标节点时,算法结束。
三、八数码问题的状态表示在八数码问题中,每个状态都可以表示为一个3×3的矩阵。
我们可以用一个一维数组来表示这个矩阵,其中0表示空格。
例如,初始状态可以表示为[2, 8, 3, 1, 6, 4, 7, 0, 5],目标状态可以表示为[1, 2, 3, 8, 0, 4, 7, 6, 5]。
四、A*算法求解八数码问题的步骤1.将初始状态加入优先队列中,并设置g值和h值为0。
2.从队头取出一个节点进行扩展。
如果该节点是目标节点,则搜索结束;否则,将扩展出来的新节点加入优先队列中。
3.对于每个新节点,计算g值和h值,并更新f(n)值。
如果该节点已经在优先队列中,则更新其估价值;否则,将其加入优先队列中。
4.重复第2步至第3步直到搜索结束。
五、Python实现以下是用Python实现A*算法求解八数码问题的代码:```import heapqimport copy# 目标状态goal_state = [1,2,3,8,0,4,7,6,5]# 启发式函数:曼哈顿距离def h(state):distance = 0for i in range(9):if state[i] == 0:continuerow = i // 3col = i % 3goal_row = (state[i]-1) // 3goal_col = (state[i]-1) % 3distance += abs(row - goal_row) + abs(col - goal_col)return distance# A*算法def A_star(start_state):# 初始化优先队列和已访问集合queue = []visited = set()# 将初始状态加入优先队列中,并设置g值和h值为0heapq.heappush(queue, (h(start_state), start_state, 0))while queue:# 取出队头元素进行扩展f, state, g = heapq.heappop(queue)# 如果该节点是目标节点,则搜索结束;否则,将扩展出来的新节点加入优先队列中。
基于启发式搜索算法A星解决八数码问题

int statue[size][size]; //记录当前节点的状态 struct Node * Tparent; //用来构成搜索树,该树由搜索图的反向指针构成 struct Node * opennext; //用来构成 open 表,该指针指向该节点在 open 表中的下一个 节点 struct Node * closenext; //用来构成 open 表,该指针指向该节点在 close 表中的下一个 节点 struct Node * brothernext; //构成兄弟链表,该指针指向该节点在兄弟链表中的下一个节 点 int f; //记录当前节点的 f 函数值 int g; //记录当前节点的 g 函数的值 int h; //记录当前节点的 h 函数的值 };
5
get_bestroute (bestNode); return; }
2.2.7 生成 bestNode 所指节点的后继节点
定义一个后继节点链表,表头为 head_b,将 bestNode 所指节点的不是前驱节点的后继 节点,链接到后继及诶单链表中。getchild 函数可以实现这个功能。
//产生 bestNode 的一切后继节点。。 head head_b; //定义 bestNode 的后继节点表 head_b.next=NULL; getchild (&head_b,bestNode); //产生 bestNode 的子节点,将不是 bestNode 的父节点的
while (head_b.next!=NULL) { Node *tmp=getbrother (&head_b); //从后继节点表中取出一个节点记为 tmp,并从
A星八数码求解资料讲解

friend bool operator <(const P &a,const P &b){//按f(n)=g(n)+h(n)大小排序
return a.d+a.w>b.d+b.w; //最大堆
}
}p;
const int N=3;//棋盘大小
const string t="123405678";//目标状态
估价函数的形式可定义如下式所示:
f(n)=g(n)+h(n)其中n是被评价的当前节点。f(n)、g(n)和h(n)分别表示是对f*(n)、g*(n)和h*(n)3个函数值的估计值。
利用估价函数f(n)=g(n)+h(n)来排列open表节点顺序的图搜索算法称为算法A。在A算法中,如果对所有的x,
h(x)<=h*(x)成立,则称好h(x)为h*(x)的下界,它表示某种偏于保守的估计。采用h*(x)的下界h(x)为启发函数的A算法,称为A*算法。
而第二成节点只有654个,比第一种少了很多:
原因分析:
通过实验结果也说明了估计函数对启发式搜索算法的重要影响,因为第二种估价函数p(n)是节点与目标节点相比所需移动次数的总和,与第一种估价函数w(n)(只考虑错误位数)相比,p(n)不仅考虑了错位信息,还考虑了错位的距离,比w(n)更完美,所以它的执行效率更高。
}
}
}
if(flag%2!=0)
return -1;//搜索失败
}
6源程序(采用上述中更高效的第二种估价函数)。
//************************************
//*八数码问题
八数码问题C语言A星算法详细实验报告含代码【范本模板】

一、实验内容和要求八数码问题:在3×3的方格棋盘上,摆放着1到8这八个数码,有1个方格是空的,其初始状态如图1所示,要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。
例如:图1 八数码问题示意图请任选一种盲目搜索算法(广度优先搜索或深度优先搜索)或任选一种启发式搜索方法(全局择优搜索,加权状态图搜索,A 算法或A*算法)编程求解八数码问题(初始状态任选)。
选择一个初始状态,画出搜索树,填写相应的OPEN 表和CLOSED表,给出解路径,对实验结果进行分析总结,得出结论。
二、实验目的1. 熟悉人工智能系统中的问题求解过程;2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用;3. 熟悉对八数码问题的建模、求解及编程语言的应用。
三、实验算法A*算法是一种常用的启发式搜索算法.在A*算法中,一个结点位置的好坏用估价函数来对它进行评估.A*算法的估价函数可表示为:f'(n)= g’(n)+ h’(n)这里,f'(n)是估价函数,g'(n)是起点到终点的最短路径值(也称为最小耗费或最小代价),h’(n)是n到目标的最短路经的启发值。
由于这个f’(n)其实是无法预先知道的,所以实际上使用的是下面的估价函数:f(n) = g(n) + h(n)其中g(n)是从初始结点到节点n的实际代价,h(n)是从结点n到目标结点的最佳路径的估计代价。
在这里主要是h(n)体现了搜索的启发信息,因为g(n)是已知的。
用f(n)作为f’(n)的近似,也就是用g(n)代替g'(n),h(n)代替h'(n)。
这样必须满足两个条件:(1)g(n)〉=g’(n)(大多数情况下都是满足的,可以不用考虑),且f必须保持单调递增。
(2)h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n).第二点特别的重要。
可以证明应用这样的估价函数是可以找到最短路径的。
基于A星算法的8数码问题求解方案设计(1)

基于A星算法的8数码问题求解⽅案设计(1)⼀、问题描述8数码问题⼜称9宫问题,与游戏“华容道”类似。
意在给定的33棋格的8个格⼦内分别放⼀个符号,符号之间互不相同,余下的⼀格为空格。
并且通常把8个符号在棋格上的排列顺序称作8数码的状态。
开始时,规则给定⼀个初始状态和⼀个⽬标状态,并要求被试者对棋格内的符号经过若⼲次移动由初始状态达到⽬标状态,这个过程中只有空格附近的符号可以朝空格的⽅向移动,且每次只能移动⼀个符号。
为⽅便编程和表⽰,本⽂中8个格⼦内的符号分别取1—8的8个数字表⽰,空格⽤0表⽰。
并给定8数码的初始状态和⽬标状态分别如图1、2所⽰。
图1 初始状态图2 ⽬标状态则要求以图1为初始状态,通过交换0和0的上、下、左、右四个⽅位的数字(每次只能和其中⼀个交换),达到图2所⽰⽬标状态。
⼆、实验⽬的熟悉和掌握启发式搜索的定义、估价函数和算法过程,并利⽤A*算法求解N数码难题,理解求解流程和搜索顺序。
三、实验任务1)实现类似于如图所⽰N数码难题演⽰程序。
2)⽤你所熟悉的程序语⾔实现,可以B/S实现,也可以C/S实现四、算法设计根据任务要求,本⽂采⽤A*搜索算法。
但要在计算机上通过编程解决该问题,还应当解决该问题在计算机上表⽰的⽅式,并设计合适的启发函数,以提⾼搜索效率。
①状态的表⽰在A*算法中,需要⽤到open表和closed表,特别是在open表中,待扩展节点间有很严格的扩展顺序。
因此在表⽰当前状态的变量中,必须要有能指向下⼀个扩展节点的指针,以完成对open表中元素的索引。
从这⼀点上看,open表中的元素相互间即构成了⼀个线性表,因此初步选定使⽤结构体表⽰问题的状态。
如图3所⽰,表⽰问题的结构体包括表⽰当前节点状态的DATA和指向open 表中下⼀个待扩展节点的指针NEXT。
图3 结构体现在进⼀步考虑DATA中包括的内容:如图1、2所⽰,8数码问题的提出是以⼀个33数表表⽰的,因此本⽂中采⽤⼀个33的⼆维数组s[3][3]表⽰当前状态的具体信息。
A-star-算法-八数码问题-C++-报告+代码+详细注释1
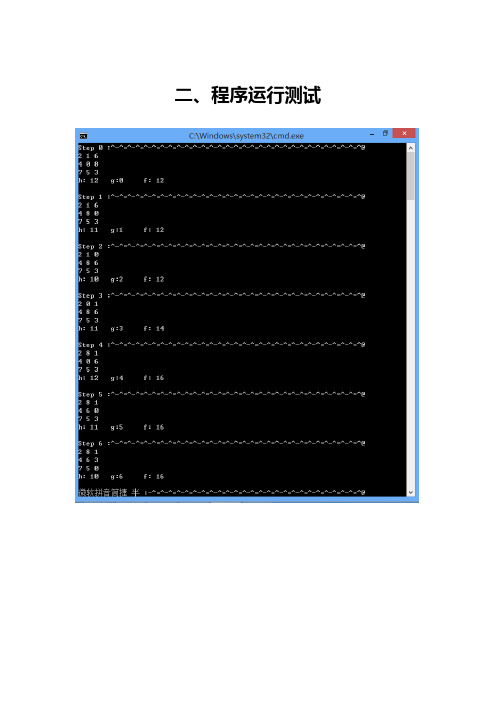
二、程序运行测试A*算法求解八数码问题一、详细设计说明1.评价函数以当前状态下各将牌到目标位置的距离之和作为节点的评价标准。
距离的定义为: “某将牌行下标与目标位置行下标之差的绝对值 + 列下标与目标位置列下标之差的绝对值”。
距离越小, 该节点的效果越好。
某个状态所有将牌到目标位置的距离之和用“h值”表示。
2.主要函数2.1countH(state & st);countH函数功能是计算st状态的h值。
2.2计算过程中将会用到rightPos数组, 数组里记录的是目标状态下, 0~9每个将牌在九宫格里的位置(位置 = 行下标 * 3 + 列下标)。
2.3f(state * p);f()=h()+level2.4look_up_dup(vector<state*> & vec, state * p);2.5在open表或close表中, 是否存在指定状态p, 当找到与p完全相等的节点时, 退出函数。
2.6search(state & start);在open表不为空时, 按f值由小到大对open表中元素进行排序。
调用findZero()函数找到0值元素的位置。
空格可以向上下左右四个方向移动, 前提是移动后不能越过九宫格的边界线。
确定某方向可走后, 空格移动一步, 生成状态p’。
2.7此时, 检查open表中是否已有p’, 若有, 更新p’数据;检查close表中是否已有p’, 若有, 将p’从close表中删除, 添加到open表中。
2.8重复的执行这个过程, 直到某状态的h值为零。
2.9dump_solution(state * q);在终端输出解路径。
// A*算法八数码问题#include"stdafx.h"#include<iostream>#include<vector>#include<time.h>#include<algorithm>using namespace std;const int GRID = 3; //Grid表示表格的行数(列数), 这是3*3的九宫格int rightPos[9] = { 4, 0, 1, 2, 5, 8, 7, 6, 3 };//目标状态时, 若p[i][j]=OMG,那么3*i+j = rightPos[OMG]struct state{int panel[GRID][GRID];int level; //记录深度int h;state * parent;state(int level) :level(level){}bool operator == (state & q){//判断两个状态是否完全相等(对应位置元素相等), 完全相等返回true,否则返回falsefor (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){if (panel[i][j] != q.panel[i][j])return false;}}return true;}state & operator = (state & p){ //以状态p为当前状态赋值, 对应位置元素相同for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){panel[i][j] = p.panel[i][j];}}return *this;}};void dump_panel(state * p){ //将八数码按3*3矩阵形式输出for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++)cout << p->panel[i][j] << " ";cout << endl;}}int countH(state & st){ //给定状态st, 计算它的h值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A*算法求解八数码问题1、八数码问题描述所谓八数码问题起源于一种游戏:在一个3×3的方阵中放入八个数码1、2、3、4、5、6、7、8,其中一个单元格是空的。
将任意摆放的数码盘(城初始状态)逐步摆成某个指定的数码盘的排列(目标状态),如图1所示图1 八数码问题的某个初始状态和目标状态对于以上问题,我们可以把数码的移动等效城空格的移动。
如图1的初始排列,数码7右移等于空格左移。
那么对于每一个排列,可能的一次数码移动最多只有4中,即空格左移、空格右移、空格上移、空格下移。
最少有两种(当空格位于方阵的4个角时)。
所以,问题就转换成如何从初始状态开始,使空格经过最小的移动次数最后排列成目标状态。
2、八数码问题的求解算法2.1 盲目搜索宽度优先搜索算法、深度优先搜索算法2.2 启发式搜索启发式搜索算法的基本思想是:定义一个评价函数f,对当前的搜索状态进行评估,找出一个最有希望的节点来扩展。
先定义下面几个函数的含义:f*(n)=g*(n)+h*(n) (1)式中g*(n)表示从初始节点s到当前节点n的最短路径的耗散值;h*(n)表示从当前节点n到目标节点g的最短路径的耗散值,f*(n)表示从初始节点s经过n到目标节点g 的最短路径的耗散值。
评价函数的形式可定义如(2)式所示:f(n)=g(n)+h(n) (2)其中n是被评价的当前节点。
f(n)、g(n)和h(n)分别表示是对f*(n)、g*(n)和h*(n)3个函数值的估计值。
利用评价函数f(n)=g(n)+h(n)来排列OPEN表节点顺序的图搜索算法称为算法A。
在A算法中,如果对所有的x,h(x)<=h*(x) (3)成立,则称好h(x)为h*(x)的下界,它表示某种偏于保守的估计。
采用h*(x)的下界h(x)为启发函数的A算法,称为A*算法。
针对八数码问题启发函数设计如下:f(n)=d(n)+p(n) (4)其中A*算法中的g(n)根据具体情况设计为d(n),意为n节点的深度,而h(n)设计为图2 A*算法流程图p(n),意为放错的数码与正确的位置距离之和。
由于实际情况中,一个将牌的移动都是单步进行的,没有交换拍等这样的操作。
所以要把所有的不在位的将牌,移动到各自的目标位置上,至少要移动从他们各自的位置到目标位置的距离和这么多次,所以最有路径的耗散值不会比该值小,因此该启发函数h(n)满足A*算法的条件。
3、A*算法流程图,如图24、A*算法总结4.1,把起始状态添加到开启列表。
4.2,重复如下工作:a) 寻找开启列表中f值最低的节点,我们称它为BESTNOEb) 把它切换到关闭列表中。
c) 对相邻的4个节点中的每一个*如果它不在开启列表,也不在关闭列表,把它添加到开启列表中。
把BESTNODE 作为这一节点的父节点。
记录这一节点的f和g值*如果它已在开启或关闭列表中,用g值为参考检查新的路径是否更好。
更低的g值意味着更好的路径。
如果这样,就把这一节点的父节点改为BESTNODE,并且重新计算这一节点的f和g值,如果保持开启列表的f值排序,改变之后需要重新对开启列表排序。
d) 停止把目标节点添加到关闭列表,这时候路径被找到,或者没有找到路径,开启列表已经空了,这时候路径不存在。
4.3,保存路径。
从目标节点开始,沿着每一节点的父节点移动直到回到起始节点。
这就是求得的路径。
5、数据结构采用结构体来保存八数码的状态、f和g的值以及该节点的父节点;struct Node{int s[3][3];//保存八数码状态,0代表空格int f,g;//启发函数中的f和g值struct Node * next;struct Node *previous;//保存其父节点};6、实验结果,如图3所示图3 A*算法求解八数码问题实验结果7、源代码//-----------------------------------------------------------------------------//代码:利用A*算法求解八数码问题。
//八数码问题的启发函数设计为:f(n)=d(n)+p(n),其中A*算法中的g(n)根据具体情况设计为d(n),意为n节点的深度,而h(n)设计为p(n),意为放错的数码与正确的位置距离之和。
//后继结点的获取:数码的移动等效为空格的移动。
首先判断空格上下左右的可移动性,其次移动空格获取后继结点。
//-----------------------------------------------------------------------------#include<stdio.h>#include<stdlib.h>#include<math.h>//八数码状态对应的节点结构体struct Node{int s[3][3];//保存八数码状态,0代表空格int f,g;//启发函数中的f和g值struct Node * next;struct Node *previous;//保存其父节点};int open_N=0; //记录Open列表中节点数目//八数码初始状态int inital_s[3][3]={2,8,3,1,6,4,7,0,5};//八数码目标状态int final_s[3][3]={1,2,3,8,0,4,7,6,5};//------------------------------------------------------------------------//添加节点函数入口,方法:通过插入排序向指定表添加//------------------------------------------------------------------------void Add_Node( struct Node *head, struct Node *p){struct Node *q;if(head->next)//考虑链表为空{ q = head->next;if(p->f < head->next->f){//考虑插入的节点值比链表的第一个节点值小p->next = head->next;head->next = p;}else {while(q->next)//考虑插入节点x,形如a<= x <=b{if((q->f < p->f ||q->f == p->f) && (q->next->f > p->f || q->next->f == p->f)){p->next = q->next;q->next = p;break;}q = q->next;}if(q->next == NULL) //考虑插入的节点值比链表最后一个元素的值更大q->next = p;}}else head->next = p;}//------------------------------------------------------------------------//删除节点函数入口//------------------------------------------------------------------------void del_Node(struct Node * head, struct Node *p ){struct Node *q;q = head;while(q->next){if(q->next == p){q->next = p->next;p->next = NULL;if(q->next == NULL) return;// free(p);}q = q->next;}}//------------------------------------------------------------------------//判断两个数组是否相等函数入口//------------------------------------------------------------------------int equal(int s1[3][3], int s2[3][3]){int i,j,flag=0;for(i=0; i< 3 ; i++)for(j=0; j< 3 ;j++)if(s1[i][j] != s2[i][j]){flag = 1; break;}if(!flag)return 1;else return 0;}//------------------------------------------------------------------------//判断后继节点是否存在于Open或Closed表中函数入口//------------------------------------------------------------------------int exit_Node(struct Node * head,int s[3][3], struct Node *Old_Node) {struct Node *q=head->next;int flag = 0;while(q)if(equal(q->s,s)) {flag=1;Old_Node->next = q;return 1;}else q = q->next;if(!flag) return 0;}//------------------------------------------------------------------------//计算p(n)的函数入口//其中p(n)为放错位的数码与其正确的位置之间距离之和//具体方法:放错位的数码与其正确的位置对应下标差的绝对值之和//------------------------------------------------------------------------int wrong_sum(int s[3][3]){int i,j,fi,fj,sum=0;for(i=0 ; i<3; i++)for(j=0; j<3; j++){for(fi=0; fi<3; fi++)for(fj=0; fj<3; fj++)if((final_s[fi][fj] == s[i][j])){sum += fabs(i - fi) + fabs(j - fj);break;}}return sum;}//------------------------------------------------------------------------//获取后继结点函数入口//检查空格每种移动的合法性,如果合法则移动空格得到后继结点//------------------------------------------------------------------------int get_successor(struct Node * BESTNODE, int direction, struct Node *Successor)//扩展BESTNODE,产生其后继结点SUCCESSOR{int i,j,i_0,j_0,temp;for(i=0; i<3; i++)for(j=0; j<3; j++)Successor->s[i][j] = BESTNODE->s[i][j];//获取空格所在位置for(i=0; i<3; i++)for(j=0; j<3; j++)if(BESTNODE->s[i][j] == 0){i_0 = i; j_0 = j;break;} switch(direction){case 0: if((i_0-1)>-1 ){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0-1][j_0];Successor->s[i_0-1][j_0] = temp;return 1;}else return 0;case 1: if((j_0-1)>-1){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0][j_0-1];Successor->s[i_0][j_0-1] = temp;return 1;}else return 0;case 2: if( (j_0+1)<3){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0][j_0+1];Successor->s[i_0][j_0+1] = temp;return 1;}else return 0;case 3: if((i_0+1)<3 ){temp = Successor->s[i_0][j_0];Successor->s[i_0][j_0] = Successor->s[i_0+1][j_0];Successor->s[i_0+1][j_0] = temp;return 1;}else return 0;}}//------------------------------------------------------------------------//从OPen表获取最佳节点函数入口//------------------------------------------------------------------------struct Node * get_BESTNODE(struct Node *Open){return Open->next;}//------------------------------------------------------------------------//输出最佳路径函数入口//------------------------------------------------------------------------void print_Path(struct Node * head){struct Node *q, *q1,*p;int i,j,count=1;p = (struct Node *)malloc(sizeof(struct Node));//通过头插法变更节点输出次序p->previous = NULL;q = head;while(q){q1 = q->previous;q->previous = p->previous;p->previous = q;q = q1;}q = p->previous;while(q){if(q == p->previous)printf("八数码的初始状态:\n");else if(q->previous == NULL)printf("八数码的目标状态:\n");else printf("八数码的中间态%d\n",count++);for(i=0; i<3; i++)for(j=0; j<3; j++){printf("%4d",q->s[i][j]);if(j == 2)printf("\n");}printf("f=%d, g=%d\n\n",q->f,q->g);q = q->previous;}}//------------------------------------------------------------------------//A*子算法入口:处理后继结点//------------------------------------------------------------------------void sub_A_algorithm(struct Node * Open, struct Node * BESTNODE, struct Node * Closed,struct Node *Successor){struct Node * Old_Node = (struct Node *)malloc(sizeof(struct Node)); Successor->previous = BESTNODE;//建立从successor返回BESTNODE的指针Successor->g = BESTNODE->g + 1;//计算后继结点的g值//检查后继结点是否已存在于Open和Closed表中,如果存在:该节点记为old_Node,比较后继结点的g值和表中old_Node节点//g值,前者小代表新的路径比老路径更好,将Old_Node的父节点改为BESTNODE,并修改其f,g值,后者小则什么也不做。
