图论习题
图论习题答案

习题一1. 一个工厂为一结点;若两个工厂之间有业务联系,则此两点之间用边相联;这样就得到一个无向图。
若每点的度数为3,则总度数为27,与图的总度数总是偶数的性质矛盾。
若仅有四个点的度数为偶数,则其余五个点度数均为奇数,从而总度数为奇数,仍与图的总度数总是偶数的性质矛盾。
2. 若存在孤立点,则m 不超过K n-1的边数, 故 m <= (n-1)(n-2)/2, 与题设矛盾。
3.4. 用向量(a 1,a 2,a 3)表示三个量杯中水的量, 其中a i 为第i 杯中水的量, i = 1,2,3.以满足a 1+a 2+a 3 = 8 (a 1,a 2,a 3为非负整数)的所有向量作为各结点, 如果(a 1,a 2,a 3)中某杯的水倒满另一杯得到 ( a ’1, a ’2, a ’3 ) , 则由结点到结点画一条有向边。
这样可得一个有向图。
本题即为在此图中找一条由( 8, 0, 0 )到( 4, 4, 0 )的一条有向路,以下即是这样的一条:5. 可以。
7. 同构。
同构的双射如下:8. 记e 1= (v 1,v 2), e 2= ( v 1,v 4), e 3= (v 3,v 1), e 4= (v 2,v 5), e 5= (v 6,v 3), e 6= (v 6,v 4), e 7= (v 5,v 3), e 8= (v 3,v 4), e 9 = (v 6,v 1), 则邻接矩阵为: 关联矩阵为:∑∑∑∑∑∑∑==+====-=++=-==---=--=ni i n i i n i n i n i ni i i n i i n i i i i a a n n a a a n n n a n a v v 1111121212/)1()1(2)1(])1[(。
, 所以 因为 ,+ 的负度数,则为结点的正度数,为结点记-----22 222 i i C a a ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---------100110000001001000010100010011010100000001001100000111, 001101000100000000001001010000001010⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡( 8, 0, 0 ) ( 5, 3, 0 ) ( 5, 0, 3 ) ( 2, 3, 3 ) ( 2, 5, 1 )(7, 0, 1 ) ( 7, 1, 0 ) ( 4, 4, 0 )( 4, 1, 3 )边列表为:A= (1,1,3,2,6,6,5,3,6), B= (2,4,1,5,3,4,3,4,1). 正向表为:A= (1,3,4,6,6,7,10), B= (2,4,5,1,4,3,3,4,1).习题二1. 用数学归纳法。
离散数学图论部分经典试题及答案
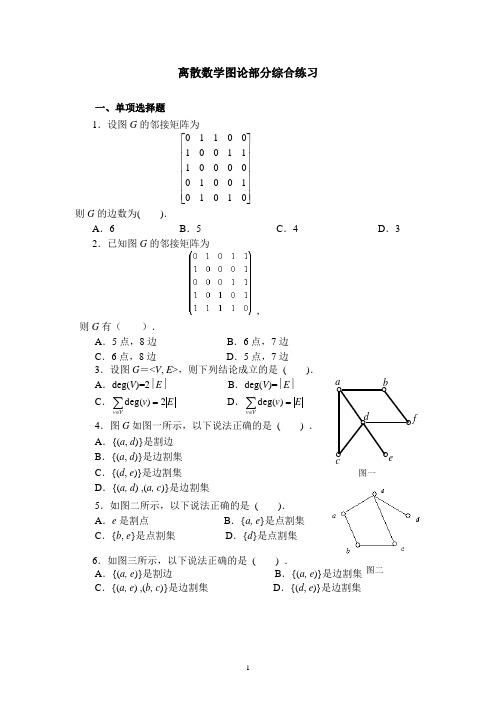
离散数学图论部分综合练习一、单项选择题1.设图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010*******11100100110则G 的边数为( ).A .6B .5C .4D .32.已知图G 的邻接矩阵为, 则G 有( ).A .5点,8边B .6点,7边C .6点,8边D .5点,7边3.设图G =<V , E >,则下列结论成立的是 ( ).A .deg(V )=2∣E ∣B .deg(V )=∣E ∣C .E v Vv 2)deg(=∑∈ D .E v Vv =∑∈)deg(4.图G 如图一所示,以下说法正确的是 ( ) . A .{(a , d )}是割边 B .{(a , d )}是边割集 C .{(d , e )}是边割集 D .{(a, d ) ,(a, c )}是边割集5.如图二所示,以下说法正确的是 ( ). A .e 是割点 B .{a, e }是点割集 C .{b , e }是点割集 D .{d }是点割集6.如图三所示,以下说法正确的是 ( ) .A .{(a, e )}是割边B .{(a, e )}是边割集C .{(a, e ) ,(b, c )}是边割集D .{(d , e )}是边割集οο ο ο οca b edο f图一图二图三7.设有向图(a )、(b )、(c )与(d )如图四所示,则下列结论成立的是 ( ).图四A .(a )是强连通的B .(b )是强连通的C .(c )是强连通的D .(d )是强连通的 应该填写:D8.设完全图K n 有n 个结点(n ≥2),m 条边,当( )时,K n 中存在欧拉回路.A .m 为奇数B .n 为偶数C .n 为奇数D .m 为偶数 9.设G 是连通平面图,有v 个结点,e 条边,r 个面,则r = ( ).A .e -v +2B .v +e -2C .e -v -2D .e +v +2 10.无向图G 存在欧拉通路,当且仅当( ). A .G 中所有结点的度数全为偶数 B .G 中至多有两个奇数度结点 C .G 连通且所有结点的度数全为偶数 D .G 连通且至多有两个奇数度结点11.设G 是有n 个结点,m 条边的连通图,必须删去G 的( )条边,才能确定G 的一棵生成树.A .1m n -+B .m n -C .1m n ++D .1n m -+ 12.无向简单图G 是棵树,当且仅当( ).A .G 连通且边数比结点数少1B .G 连通且结点数比边数少1C .G 的边数比结点数少1D .G 中没有回路.二、填空题1.已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G 的边数是 . 2.设给定图G (如图四所示),则图G 的点割ο οο οc a b f集是 .3.若图G=<V , E>中具有一条汉密尔顿回路, 则对于结点集V 的每个非空子集S ,在G 中删除S 中的所有结点得到的连通分支数为W ,则S 中结点 数|S|与W 满足的关系式为 .4.无向图G 存在欧拉回路,当且仅当G 连通 且 .5.设有向图D 为欧拉图,则图D 中每个结点的入度 . 应该填写:等于出度6.设完全图K n 有n 个结点(n 2),m 条边,当 时,K n 中存在欧拉回路.7.设G 是连通平面图,v , e , r 分别表示G 的结点数,边数和面数,则v ,e 和r 满足的关系式 .8.设连通平面图G 的结点数为5,边数为6,则面数为 . 9.结点数v 与边数e 满足 关系的无向连通图就是树.10.设图G 是有6个结点的连通图,结点的总度数为18,则可从G 中删去 条边后使之变成树.11.已知一棵无向树T 中有8个结点,4度,3度,2度的分支点各一个,T 的树叶数为 .12.设G =<V , E >是有6个结点,8条边的连通图,则从G 中删去 条边,可以确定图G 的一棵生成树.13.给定一个序列集合{000,001,01,10,0},若去掉其中的元素 ,则该序列集合构成前缀码.三、判断说明题1.如图六所示的图G 存在一条欧拉回路.2.给定两个图G 1,G 2(如图七所示):(1)试判断它们是否为欧拉图、汉密尔顿图?并说明理由. (2)若是欧拉图,请写出一条欧拉回路.v 123图六图七3.判别图G (如图八所示)是不是平面图, 并说明理由.4.设G 是一个有6个结点14条边的连 通图,则G 为平面图.四、计算题1.设图G =<V ,E >,其中V ={a 1, a 2, a 3, a 4, a 5},E ={<a 1, a 2>,<a 2, a 4>,<a 3, a 1>,<a 4, a 5>,<a 5, a 2>}(1)试给出G 的图形表示; (2)求G 的邻接矩阵;(3)判断图G 是强连通图、单侧连通图还是弱连通图?2.设图G =<V ,E >,V ={ v 1,v 2,v 3,v 4,v 5},E ={ (v 1, v 2),(v 1, v 3),(v 2, v 3),(v 2, v 4),(v 3, v 4),(v 3, v 5),(v 4, v 5) },试(1)画出G 的图形表示; (2)写出其邻接矩阵;(2)求出每个结点的度数; (4)画出图G 的补图的图形. 3.设G =<V ,E >,V ={ v 1,v 2,v 3,v 4,v 5},E ={ (v 1,v 3),(v 2,v 3),(v 2,v 4),(v 3,v 4),(v 3,v 5),(v 4,v 5) },试(1)给出G 的图形表示; (2)写出其邻接矩阵; (3)求出每个结点的度数; (4)画出其补图的图形. 4.图G =<V , E >,其中V ={ a , b , c , d , e },E ={ (a , b ), (a , c ), (a , e ), (b , d ), (b , e ), (c , e ), (c , d ), (d , e ) },对应边的权值依次为2、1、2、3、6、1、4及5,试(1)画出G 的图形; (2)写出G 的邻接矩阵;(3)求出G 权最小的生成树及其权值.5.用Dijkstra 算法求右图中A 点到其它各点的最短路径。
图论习题

习题八8.1 设V={u,v,w,x,y}, 画出图G: (V ,E).(1) E={(u,v),(u,x),(v,w),(v,y),(x,y)} (2) E={(u,v),(v,w),(w,x),(w,y),(x,y)} 再求每个结点的次数。
8.2 设G 是具有4个结点的完全图:(1) 写出G 的所有子图; (2) 写出G 的所有生成子图。
8.3 画出一个多重图,使它们的邻接矩阵为1300301101220120⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭. 8.4 对于图1,试求(1) 从a 到h 的所有基本通路; (2) 从a 到h 的所有简单通路; (3) 从a 到h 的距离。
he d图18.5 图2中哪个有欧拉通路、有欧拉回路、有汉密尔顿通路、有汉密尔顿回路?b ce图28.6 图G 1,G 2的邻接矩阵分别为A 1,A 2,试求:(1) 23231122,,,A A A A ;(2) 在G 1内列出每两个结点间的距离; (3) 列出G 1,G 2中的所有基本回路。
10011000001100101010001001A ⎛⎫ ⎪⎪ ⎪= ⎪ ⎪⎪⎝⎭,20001100000001100010001010100100100001000000100000A ⎛⎫⎪⎪ ⎪ ⎪= ⎪ ⎪⎪⎪ ⎪⎝⎭8.7 设有向图D 如下,试求:(1) 每个结点的入次与出次; (2) 它的邻接矩阵M D ; (3) D 是强连通、弱连通还是单向连通? (4) 求从a 到c 长度小于或等于3的通路数。
8.8 D 是具有结点v 1、v 2、v 3、v 4的有向图,它的邻接矩阵表示如下:0111011011011000⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭(1) 画出这个图; (2) D 是强连通还是单向连通?(3) 求从v 1到v 1长度是3的回路,从v 1到v 2、v 1到v 3、v 1到v 4长度是3的通路数。
习题九9.4 设有代数表示式如下:42(35)(2)x y a b c -+,试画出这个表示式的树. 第四篇1. 在图G=(V,E)中,结点次数与边数的关系是下面4个中的哪一个? (1) deg()2||i v E = (2) deg()||i v E = (3)deg()2||v Vv E ∈=∑ (4) deg()||v Vv E ∈=∑2. 设G 是n 个结点的无向完全图,则图G 的边数是多少?设D 是n 个结点的有向完全图,则图D 的边数又是多少?3. 仅有一个结点是图称为什么图?4. 设G=(V ,E)为无向简单图,|V|=n ,∆(G)为G 中结点的最大次数,请指出下面4个中哪个不等式是正确的。
图论复习题

图论复习题(二)图论复习题一、选择题1.设图G =<V , E >,v ∈V ,则下列结论成立的是 ( C ) . A .deg(v )=2∣E ∣ B . deg(v )=∣E ∣ C .E v Vv 2)deg(=∑∈ [PPT 23] D .Ev Vv =∑∈)deg(定理1 图G=(V ,E )中,所有点的次之和为边数的两倍 2.设无向图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010010000011100100110则G 的边数为( B ).A .6B .5C .4D .33、 设完全图K n 有n 个结点(n ≥2),m 条边,当( C )时,K n 中存在欧拉回路.A .m 为奇数B .n 为偶数C .n 为奇数D .m 为偶数解释:K n 每个结点的度都为n -1,所以若存在欧拉回路则n -1必为偶数。
n 必为奇数。
4.欧拉回路是( B )A. 路径B. 简单回路[PPT 40]C. 既是基本回路也是简单回路D.既非基本回路也非简单回路5.哈密尔顿回路是( C )A. 路径B. 简单回路C. 既是基本回路也是简单回路D.既非基本回路也非简单回路[PPT 40]:哈密尔顿回路要求走遍所有的点,即是基本回路的点不重复,也可以是简单回路的边不重复。
6.设G 是简单有向图,可达矩阵P(G)刻划下列关系中的是( C ) A 、点与边 B 、边与点 C 、点与点 D 、边与边7.下列哪一种图不一定是树(C )。
A.无简单回路的连通图B. 有n 个顶点n-1条边的连通图C. 每对顶点间都有通路的图D. 连通但删去一条边便不连通的图8.在有n 个结点的连通图中,其边数(B )A.最多有n-1条B.至少有n-1条C.最多有n 条D.至少有n 条9.下列图为树的是(C )。
A 、>><><><=<},,,,,{},,,,{1d c b a a a d c b a GB 、>><><><=<},,,,,{},,,,{2d c d b b a d c b a GC 、>><><><=<},,,,,{},,,,{3a c d a b a d c b a GD 、>><><><=<},,,,,{},,,,{4d d c a b a d c b a G 10、下面的图7-22是(C )。
图论习题及答案

作业解答练习题2 利用matlab编程FFD算法完成下题:设有6种物品,它们的体积分别为:60、45、35、20、20和20单位体积,箱子的容积为100个单位体积。
解答一:function [num,s] = BinPackingFFD(w,capacity)%一维装箱问题的FFD(降序首次适应)算法求解:先将物体按长度从大到小排序,%然后按FF算法对物体装箱%输入参数w为物品体积,capacity为箱子容量%输出参数num为所用箱子个数,s为元胞数组,表示装箱方案,s{i}为第i个箱子所装—%物品体积数组%例w = [60,45,35,20,20,20]; capacity = 100;% num=3,s={[1,3],[2,4,5],6};w = sort(w,'descend');n = length(w);s = cell(1,n);bin = capacity * ones(1,n);num = 1;for i = 1:n;for j = 1:num + 1if w(i) < bin(j)bin(j) = bin(j) - w(i);s{j} = [s{j},i];if j == num + 1num = num + 1;endbreak;endend`ends = s(1:num);解答二:clear;clc;V=100;v=[60 45 35 20 20 20];n=length(v);v=fliplr(sort(v));·box_count=1;x=zeros(n,n);V_Left=100;for i=1:nif v(i)>=max(V_Left)box_count=box_count+1;x(i,box_count)=1;V_Left=[V_Left V-v(i)];elsej=1;。
while(v(i)>V_Left(j))j=j+1;endx(i,j)=1;V_Left(j)=V_Left(j)-v(i);endtemp=find(x(i,:)==1);fprintf('第%d个物品放在第%d个容器\n',i,temp) end(output:第1个物品放在第1个容器第2个物品放在第2个容器第3个物品放在第1个容器第4个物品放在第2个容器第5个物品放在第2个容器第6个物品放在第3个容器解答三:function box_count=FFD(x)《%降序首次适应算法v=100;x=fliplr(sort(x));%v=input('请输入箱子的容积:');n=length(x);I=ones(n);E=zeros(1,n);box=v*I;box_count=0;for i=1:n《j=1;while(j<=box_count)if x(i)>box(j)j=j+1;continue;elsebox(j)=box(j)-x(i);E(i)=j;break;end&endif j>box_countbox_count=box_count+1;box(box_count)=box(box_count)-x(i);E(i)=j;endenddisp(E);在命令窗口输入:;>> x=[60,45,35,20,20,20];>> FFD(x)1 2 1 2 2 3ans =3练习题5 “超市大赢家”提供了50种商品作为奖品供中奖顾客选择,车的容量为1000dm3, 奖品i占用的空间为w i dm3,价值为v i元, 具体的数据如下:v i= { 220, 208, 198, 192, 180, 180, 165, 162, 160, 158,155, 130, 125, 122, 120, 118, 115, 110, 105, 101, 100, 100, 98,96, 95, 90, 88, 82, 80, 77, 75, 73, 72, 70, 69, 66, 65, 63, 60, 58,56, 50, 30, 20, 15, 10, 8, 5, 3, 1}w i = {80, 82, 85, 70, 72, 70, 66, 50, 55, 25, 50, 55, 40, 48,50, 32, 22, 60, 30, 32, 40, 38, 35, 32, 25, 28, 30, 22, 50, 30, 45,30, 60, 50, 20, 65, 20, 25, 30, 10, 20, 25, 15, 10, 10, 10, 4, 4, 2,1}。
图论习题

课前练习一、填空题1、图G 是简单图当且仅当 。
2、简单图G 是二部图当且仅当 。
3、若简单图G 满足(G)δ≥3,则G 中存在长度至少为 的圈。
4、连通图G 具有欧拉通路,而无欧拉回路的充要条件为 。
5、一颗树有两个2度分支点,一个3度分支点,三个4度分支点,则该树有 片树叶。
6、设T 为高为k 的二叉树,则T 最多有 个顶点。
7、设图G 是具有6条边、4个顶点的平面图,则图G 的面数为 。
8、一个图为非平面图当且仅当 。
9、S V ⊂,S 是图G 的极大独立集,则()V G S -是图G 的 。
10、带权为1,3,5,7,8,11,13的最优二叉树T 的权W(T)= 。
二、解答题1、求下图G 1的色多项式,并指出其色数、点连通度和边连通度。
图G 12、(1)证明自补图的阶数n 4k =或者n 4k 1=+,k 为某个自然数。
(2)找出所有4阶的自补图。
3、(1)证明:设G 是有v 个顶点ε条边,且G 是自对偶平面图,则2v 2ε=-。
(2)已知一颗无向树T 有三个3度结点,一个二度结点,其余都是1度结点。
①T 有几个1度结点?②试画出两棵满足上述度数要求的非同构的无向树。
4、通过布尔变量的运算,求下图3的全部极小支配集。
V 16 图3图G 25、用破圈法求下图G 3中的一颗最小生成树,写出具体过程,并计算生成树的权。
图G 36、设简单图,, |V|=n, |E|=m,G V E =<> 若有212n m C -≥+,则G 是哈密尔顿图。
7、证明:5K 不是平面图.8、证明:若,(,1)m n K m n ≥是哈密顿图,则必有.m n = 9、若,m n K 是树,求,m n 应满足的条件.132411253e 6e 1e 2e 3e 4e 5e 7e 8e 9。
图论习题参考答案

二、应用题题0:(1996年全国数学联赛)有n(n≥6)个人聚会,已知每个人至少认识其中的[n/2]个人,而对任意的[n/2]个人,或者其中有两个人相互认识,或者余下的n-[n/2]个人中有两个人相互认识。
证明这n个人中必有3个人互相认识。
注:[n/2]表示不超过n/2的最大整数。
证明将n个人用n个顶点表示,如其中的两个人互相认识,就在相应的两个顶点之间连一条边,得图G。
由条件可知,G是具有n个顶点的简单图,并且有(1)对每个顶点x,)(xN G≥[n/2];(2)对V的任一个子集S,只要S=[n/2],S中有两个顶点相邻或V-S中有两个顶点相邻。
需要证明G中有三个顶点两两相邻。
反证,若G中不存在三个两两相邻的顶点。
在G中取两个相邻的顶点x1和y1,记N G(x1)={y1,y2,……,y t}和N G(y1)={x1,x2,……,x k},则N G(x1)和N G(y1)不相交,并且N G(x1)(N G(y1))中没有相邻的顶点对。
情况一;n=2r:此时[n/2]=r,由(1)和上述假设,t=k=r且N G(y1)=V-N G(x1),但N G(x1)中没有相邻的顶点对,由(2),N G(y1)中有相邻的顶点对,矛盾。
情况二;n=2r+1: 此时[n /2]=r ,由于N G (x 1)和N G (y 1)不相交,t ≥r,k ≥r,所以r+1≥t,r+1≥k 。
若t=r+1,则k=r ,即N G (y 1)=r ,N G (x 1)=V-N G (y 1),由(2),N G (x 1)或N G (y 1)中有相邻的顶点对,矛盾。
故k ≠r+1,同理t ≠r+1。
所以t=r,k=r 。
记w ∈V- N G (x 1) ∪N G (y 1),由(2),w 分别与N G (x 1)和N G (y 1)中一个顶点相邻,设wx i0∈E, wy j0∈E 。
若x i0y j0∈E ,则w ,x i0, y j0两两相邻,矛盾。
图论测试题及答案

图论测试题及答案一、选择题1. 在图论中,如果一个图的每个顶点的度数都是偶数,那么这个图一定存在欧拉路径吗?A. 是的B. 不一定C. 没有欧拉路径D. 无法确定答案:B2. 图论中的哈密顿路径是指什么?A. 经过图中所有顶点的路径B. 经过图中所有顶点的回路C. 经过图中某些顶点的路径D. 经过图中某些顶点的回路答案:A3. 如果一个图是完全图,那么它的边数是多少?A. 顶点数的一半B. 顶点数的平方C. 顶点数的两倍D. 顶点数减一答案:B二、填空题4. 在无向图中,如果存在一条路径,使得每个顶点只被经过一次,并且起点和终点相同,这样的路径被称为________。
答案:欧拉回路5. 图论中的二分图是指图中的顶点可以被分成两个不相交的集合,使得同一个集合内的顶点之间没有边,而不同集合之间的顶点之间有边,这种图也被称为________。
答案:二部图三、简答题6. 请简述图论中的最短路径问题,并给出解决该问题的一种算法。
答案:最短路径问题是在图中找到两个顶点之间的最短路径的问题。
解决该问题的一种算法是迪杰斯特拉算法(Dijkstra's algorithm),该算法通过维护一个顶点集合来记录已经找到最短路径的顶点,并迭代更新距离,直到找到从起点到所有顶点的最短路径。
7. 描述图论中的图着色问题,并说明其在实际生活中的应用。
答案:图着色问题是将图的顶点着色,使得任何两个相邻的顶点颜色不同。
在实际生活中,图着色问题可以应用于时间表的安排、频率分配、电路设计等领域,其中每个顶点代表一个任务或频道,而颜色则代表不同的时间段或频率。
结束语:以上是图论测试题及答案,希望能够帮助大家更好地理解和掌握图论的基本概念和算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考研习题与经典习题 2004-5
一、握手定理的应用 二、平面图、欧拉公式的应用 三、图的基本概念与应用 四、欧拉图和哈密顿图 五、图的着色
一、握手定理的应用
1. 已知具有n个度数都为3的结点的简单 图G有e条边, (1)若e=3n-6,证明G在同构意义下唯 一,并求e,n。 (2)若n=6,证明G在同构意义下不唯 一。
1,关于平面图的不等式的证明 欧拉公式及其推论的运用 2,非平面图的判定 应用库拉托斯基定理
1. 设G是n个结点的连通简单平面图,若 n3,则G中必有一个结点度数不超过5。
提示:涉及度数,握手定理;连通平面 图,欧拉公式;简单平面图,若n3,欧 拉公式的推论 (西南交大1999考研)
3)解:3个结点或者6个结点的完全图的 边数分别为3和15,是奇数;所以不存在 3个结点或者6个结点的自补图。
连通性
证明连通的两种方法: 直接证明/反证法. 证明连通的直接证明方法:任取图中两点, 寻找这两点间必定存在路。 证明连通的反证法: 首先假设图不连通, 则它具有多个连通分支,然后根据题目条 件推出矛盾。推矛盾的过程,通常是将具 有多个连通分支的图的边数放到最大的过 程(放缩法),即使每个连通分支都是完 全图,然后推出边仍然不满足条件。
/*华中科技大学2000考研
9. 能否画一个简单无向连通图,使各结点的 度数与下面给出的序列一致?如可能,则画出 符合条件的图,所画图是二分图?如不能,则 说明原因。 (1)1,2,3,2,1,1 (2)1,1,2,3,2,2 (3)1,2,3,4,5,5 (4)2,2,2,3,3,4 (西南交大1995考研)
提示:反证
分析: (1) e属于每一棵生成树, 要证G删去e后 必不连通,否则矛盾。 (2)
证明:(1) : e属于每一棵生成树, 若{e}不是G的 割集,G-e连通,则G-e中必存在生成树T, 因为T也是G的生成树,但T不包含e,导 致矛盾。 :设{e}不是G的割集,若有G的生成树 T,则T+e包含回路。则删去e后连通, 则与{e}是G的割集的假设矛盾。
/*中国科学院自动化所1998考研
证明方法: 1)反证法(简捷) 2)数学归纳法:对顶点数进行数学归纳
反证法: 证明:假设G不是连通的,则G至少存在 两个连通分支。设G有两个连通分支C1和 C2,则G的最大可能的边数m=x(x1)/2+(n-x)(n-x-1)/2,其中1xn-1;所 2 以m的最大 Cn 1 所以导致矛盾,则G是连通的。
解:由握手定理,e=(3n/2);由已知, e=2n-2;所以n=6,e=9。 在同构意义下G不是唯一的。
4. 设树T有17条边,12片树叶,4个4度 内结点,1个3度内结点,求T的树根的度 数。
(提示:握手定理。北大1997考研)
解:结点数为17+1=18 由握手定理,12*1+4*4+1*3+1*l=34, l=3.
2
向量组的秩 如果向量组1, 2, …., s中存在r个 线性无关的向量,且其中任一个向量可 由这r个线性无关的向量线性表示,则数r 称为向量组的秩,记作{1, 2, …., s }=r。
9. 若图G=(V, E)是连通图,且eE,证 明: (1)e属于每一棵生成树的充要条件是{e} 为G的割集; (2)e不属于G的任何一棵生成树的充要条 件是e为G中的环。
4. 设G=(V, E)是连通简单图,但不是完全图, 则存在3个结点u、v和w, 使(u, v), (v, w)E, 但(u, w)E。
/*中国科学院计算所1993考研
证明方法: 1)反证法 2)数学归纳法
5. 设G为非平凡有向图,V为G的结点集合,若 对V的任一非空子集S,G中起始结点在S中, 终止结点在V-S中的有向边至少有k条,则称G 是k边连通的。 证明:非平凡有向图是强连通的充要条件为它一个图如果同构于它的补图, 则该图 称为自补图. 1)试给出一个5个结点的自补图; 2)证明: 一个图是自补图, 其对应的完全 图的边数必是偶数; 3)是否有3个结点或者6个结点的自补图.
2)证明:如果一个图是自补图,设该图 的边数为e,则该图的自补图的边数也为 e,所以对应的完全图的边数是2e,为偶 数。
10 设图G有n个结点,r个连通分支,则 图G的路径矩阵的秩为n-r。
证明:设图G的r个连通分支为G1, G2, …,
Gr。得分块路径矩阵如下:
0 P(G1 ) 0 P ( G ) 2 P(G ) ...... ...... 0 0
0 ...... 0 ...... 0 ...... P(Gr ) ......
(2)证明:(反证法) 假设G中至多有5个结点的度数小于 等于5。因为(G)=4,则 d(v)54+6(n-5)。因为d(v)=2e,则 e3n-5。由(1),e3n-6。
5. 设G是由n个结点,e条边,(2)个连通 分支的平面图,G的每个面至少由k(k3)条 边围成,则
k ( n 1) e k 2
证明:设G的面数为f,各面的度数之和 为T,T=2e。因为G的每个面至少由k条 边围成,所以k*fT=2e。由欧拉公式的 推广,f=+1+e-n, k*( +1+e-n)2e. 所以命题成立。
三、图的基本概念与应用
1. 补图 2. 连通性
/*中国科学院计算所1999考研
证明: /*必要性证明*/ 因为设G为强连通的,假设从S到V-S没有 有向边,则S中的任一顶点u到V-S中的任 一顶点v均没有有向道路,从而与G为强 连通的相矛盾。所以从S到V-S至少有一 条有向边,即G为一边连通的。
/*充分性证明*/ 设G为一边连通的,对任意的u, vV, 则 {u}到V(G-u)至少有一条边,设为(u, u1), 而{u, u1}到V-{u, u1}至少有一条有向边 (u, u2)或(u1, u2)。无论哪种情况都有从u 到u2的有向道路,因为G中结点数有限, 所以通过如上递归地求解,一定有从u到 v的有向道路。所以G为强连通的。
(西安交通大学1997考研)
3. 证明小于30条边的简单平面图G中, 至少有一个度数小于等于4的结点。
证明:不妨设G是连通图。 因为e3n-6,假设所有顶点度数大 于等于5;由握手定理,dev(vi)=2e; 所以2e5n,则有n2e/5。 代入e3n-6,则e6e/5-6, 从而 e30。所以矛盾。
1. n个结点的简单图G,n>2且n奇数,G 和G补图中度数为奇数的结点个数是否相 等?请证明或给出反例。
(西南交大2001考研)
解:一定相等。 因为n>2且n奇数,则对于奇数个结点的 完全图,每个结点的度数必为偶数。若G 中度数为奇数的结点个数是m,则G的补 图中m个结点的度数为(偶数-奇数)=奇 数。 G中度数为偶数的结点,在G的补图 中这些结点的度数仍为(偶数-偶数)=偶 数。 所以命题成立。
(1) V1={a, c, e}, V2={b, d, f}. (2) 不可能画出图。(顶点度数之和为偶数) (3) 不可能画出图和二分图。由于有两个结点 的度数为5,则该两个结点的度数必与其余5个 结点有边相连(因为是简单图),所以其余4 个结点度数至少为2,但有一个结点的度数为1。 (4) (1, 6, 4, 5, 6, 1),回路长度为奇数,所以 不是二分图。
6. 设简单平面图G中顶点数n=7,边数e=15, 证明G是连通的。
提示:反证
7.简单图G由图H和两个孤立点组成,图 H不含孤立点,Ğ为平面图,证明H为连 通图。
(中国科学院软件所1994考研)
8. 若G为简单图, 且m Cn21, 则G是连通的. 其中m和n分别为该图的边数和顶点数. 给出一个有n个结点而不连通的简单图, 2 其边数恰好为 Cn 1 .
5. 设无向树T有3个3度,2个2度结点, 其余结点都是树叶,问T有几片树叶?
握手定理
6. 证明:在任何两个或两个以上人的组 内,存在两个人在组内有相同个数的朋 友。
/*等价于:至少有两个顶点的简单图有两个相
同度数的顶点 /*中国科学院自动化所1998考研
二、平面图、欧拉公式的应用
补图
1. 证明无向图G是不连通的,则它的补图是连 通的。
提示:分而治之(西南交大1999考研) 证明连通的两种方法:直接证明,反证法
证明:设G=(V, E), 根据连通分支将V划分为{V1, V2, ……, Vn},并设Vi={u1, u2, …, ur},Vj={v1, v2, …, vs},ij,1i,jn,Ek表示完全图的边集。 任取V中两个结点,分两种情况讨论: (1)设uiVi, vjVj. (ui, vj)E, 则(ui, vj) Ek –E. 所以ui, vj是连通的。即在不同连通分支中的两个 结点在补图中是连通的。 (2)设ui, ujVi, vjVj. 由(1),(ui, vj) Ek –E, (uj, vj) Ek –E. 所以ui, uj通过vj连通。即在相同 连通分支中的两个结点在补图中是连通的。 所以,命题成立。
4. 证明在简单平面图G中, f 和n分别表 示该图的面数和结点数, (1) 如果n3,则f 2n-4。 (2) G中结点最小的度(G)=4,则G中至 少有6个结点的度数小于等于5。
