指数函数典型例题详细解析
4.2 指数函数(精讲)(原卷版附答案).docx
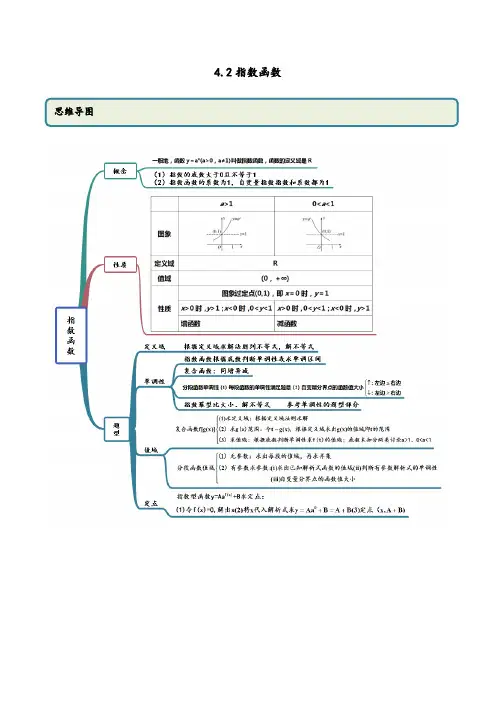
4.2指数函数考点一 指数函数的判断【例1-1】（2019·河北桥西.邢台一中高一月考）下列函数中指数函数的个数是（ ）①23x y =⋅ ②13x y += ③3xy = ④()21xy a =-（a 为常数,12a >,1a ≠） ⑤3y x = ⑥4xy =- ⑦()4xy =-A ．1B ．2C ．3D ．4【例1-2】（2019·河南中原.郑州一中高一开学考试）函数f (x )=(a 2﹣3a +3)a x 是指数函数,则a 的值为（ ） A ．1 B ．3 C ．2 D ．1或3【一隅三反】1．（2019·山东高三学业考试）函数()2xy a a =-是指数函数,则（ ）A ．1a =或3a =B ．1a =C ．3a =D ．0a >且1a ≠2．（2019·呼和浩特开来中学高一期中）若函数1()(3)2xf x a a =-⋅是指数函数,则1()2f 的值为( )A ．2B ．-2C ．-D ．3．（2019·辽宁葫芦岛.高一月考）下列函数不是指数函数的是（ ） A ．12x y +=B ．3x y -=C ．4x y =D ．32x y =考点二 定义域和值域【例2-1】（2020·全国高一课时练习）求下列函数的定义域和值域：（1）142x y -=；（2）23y ⎛= ⎪⎝⎭（3）22312x x y --⎛⎫=⎪⎝⎭.【例2-2】（2018·湖南开福.长沙一中高一月考）若函数y =的值域为[0,+∞）,则实数a 的取值范围是_____．【一隅三反】1．（2020·全国高一课时练习）求下列函数的定义域和值域； （1）12x y +=；（2）y =（3）y =2．（2020·全国高一课时练习）求下列函数的定义域与值域.（1）y =（2）1(0,1x x a y a a -=>+且1)a ≠（3）110.3;x y -=（4）y =3．（2020·河北新华.石家庄二中高二期末）若函数()1,121,14xxx f x a x ⎧⎛⎫<⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪+≥ ⎪⎪⎝⎭⎩的值域为(),+∞a ,则a 的取值范围为（ ）A ．1,4⎡⎫+∞⎪⎢⎣⎭B ．11,42⎡⎤⎢⎥⎣⎦C ．1,12⎡⎤⎢⎥⎣⎦D ．1,14⎛⎤⎥⎝⎦4．（2020·云南五华.昆明一中高三其他（理））设函数y =A ,函数12x y -=的值域为B ,则AB =( )A ．()0,1B ．(]0,1C ．()1,1-D ．[]1,1-5．（2019·湖南高一期中）若函数2411()3ax x f x -+⎛⎫= ⎪⎝⎭有最大值3,则实数a 的值为（ ）A ．2-B ．1-C ．1D ．2考点三 指数函数性质【例3】（1）（2020·贵溪市实验中学高二期末（文））若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( )A ．9,34⎛⎫⎪⎝⎭B ．9,34⎡⎫⎪⎢⎣⎭C ．()1,3D ．()2,3（2）（2019·湖南岳阳楼.岳阳一中高一期中）已知函数1()2xf x ⎛⎫= ⎪⎝⎭,则不等式()24(3)f a f a ->的解集为( ) A ．(4,1)-B ．(1,4)-C ．(1,4)D ．(0,4)（3）（2019·湖北襄阳）如果1111222b a⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭,那么（ ）A ．a b a a a b <<B ．a a b a b a <<C ．b a a a a b <<D ．b a a a b a <<【一隅三反】1．（2019·浙江南湖.嘉兴一中高一月考）函数2213x xy -+⎛⎫= ⎪⎝⎭为增函数的区间是（ ）A ．[)1,-+∞B ．(],1-∞-C ．[)1,+∞D ．(],1-∞2．（2019·浙江柯城.衢州二中高三一模）已知定义在R 上的函数()||32x m f x -+=+m 为实数）为偶函数,记()0.2log 3a f =,()5log b f e =,()c f m π=+,则( )A ．c b a <<B ．c a b <<C ．a c b <<D ．a b c <<3．（2020·浙江高一课时练习）设0.914y =,0.4828y =, 1.5312y -⎛⎫= ⎪⎝⎭,则（ ）A ．312y y y >>B ．213y y y >>C ．123y y y >>D ．132y y y >>1.指数函数性质记忆口诀指数增减要看清,抓住底数不放松； 反正底数大于0,不等于1已表明； 底数若是大于1,图象从下往上增； 底数0到1之间,图象从上往下减； 无论函数增和减,图象都过(0,1)点． 2.比较幂值大小的三种类型及处理方法4．（2020·永安市第三中学高二月考）若关于x 的方程()94340xxa ++⋅+=有解,则实数a 的取值范围是（ ）A ．(,8][0,)-∞-+∞B ．(),4-∞-C ．[8,4)--D ．(,8]-∞-5（2020·上海高一课时练习）已知函数2221()2x x f x ++⎛⎫= ⎪⎝⎭,则该函数的单调递增区间是__________.6．（2020·上海普陀.曹杨二中高一期末）函数12x y =-的单调递增区间为________7．（2020·全国高一课时练习）比较下列各题中的两个值的大小． （1）0.10.8-,0.21.25；（2）1ππ-⎛⎫ ⎪⎝⎭,1；（3）30.2-,()0.23-.考点四 定点【例4】（2020·浙江高一课时练习）函数()-1=4+x f x a （0a >,且1a ≠）的图象过定点P ,则P 点的坐标为（ ） A ．(1,5) B ．(1,4) C ．(0,5)D ．(0,4)【一隅三反】1．（2019·涡阳县第九中学高二期末）函数()10,1xy a a a =+>≠的图象必经过点（ ）A ．(0,1)B ．(1,1)C ．()0,2D ．(2,2)2．（2019·贵州省织金县第二中学高一期中）函数21()x f x a-=(0a >且1)a ≠过定点（ ） A ．(1,1) B ．1(,0)2C ．(1,0)D ．1(,1)23．（2020·宁夏贺兰县景博中学高一月考）函数y=a x ﹣1+2（a ＞0且a≠1）图象一定过点（ ）A ．（1,1）B ．（1,3）C ．（2,0）D ．（4,0）考点五 图像【例5-1】（2020·广东顺德一中高一期中）函数1(0,1)xy a a a a=->≠的图像可能是（ ）． A ． B ．C ．D ．【例5-2】（2020·浙江高一课时练习）若函数(01,1)xy a a a m =>-≠+的图像在第一、三、四象限内,则（ ） A ．1a >B ．1a >,且0m <C ．01a <<,且0m >D ．01a <<【一隅三反】1．（2019·浙江高一期中）函数y x a =+与xy a =,其中0a >,且1a ≠,它们的大致图象在同一直角坐标系中有可能是 ( )A ．B ．C ．D ．2．（2020·全国高一课时练习）在如图所示的图象中,二次函数2y ax bx c =++与函数xb y a ⎛⎫= ⎪⎝⎭的图象可能是（ ）A ．B ．C ．D ．3．（2020·上海高一课时练习）若函数2xy m =+的图像不经过第二象限,则m 的取值范围是( )A ．m 1≥B ．1m <C ．1m >-D ．1m ≤-4．（2020·内蒙古集宁一中高二期末（理））若直线2y a =与函数|1|(0,1)x y a a a =->≠的图象有两个大众点,则a的取值范围是___________4.2指数函数考点一 指数函数的判断【例1-1】（2019·河北桥西.邢台一中高一月考）下列函数中指数函数的个数是（ ）①23x y =⋅ ②13x y += ③3xy = ④()21xy a =-（a 为常数,12a >,1a ≠） ⑤3y x = ⑥4xy =- ⑦()4xy =-A ．1B ．2C ．3D ．4【参考答案】B【解析】对①：指数式的系数为2,不是1,故不是指数函数；对②：其指数为1x +,不是x ,故不是指数函数； 对③④：满足指数函数的定义,故都是指数函数； 对⑤：是幂函数,不是指数函数；对⑥：指数式的系数为-1,不是1,故不是指数函数；对⑦：指数的底数为-4,不满足底数大于零且不为1的要求,故不是； 综上,是指数函数的只有③④,故选：B.【例1-2】（2019·河南中原.郑州一中高一开学考试）函数f (x )=(a 2﹣3a +3)a x 是指数函数,则a 的值为（ ） A ．1B ．3C ．2D ．1或3【参考答案】C【解析】因为函数f (x )=(a 2﹣3a +3)a x 是指数函数,故可得2331a a -+=解得1a =或2a =, 当1a =时,不是指数函数,舍去.故选：C.【一隅三反】1．（2019·山东高三学业考试）函数()2xy a a =-是指数函数,则（ ）A ．1a =或3a =B ．1a =C ．3a =D ．0a >且1a ≠【参考答案】C【解析】因为函数()2xy a a =-是指数函数所以21a -=,0a >且1a ≠,解得3a =.故选：C.2．（2019·呼和浩特开来中学高一期中）若函数1()(3)2xf x a a =-⋅是指数函数,则1()2f 的值为( )A ．2B ．-2C．-D．【参考答案】D【解析】∵函数f （x ）＝（12a ﹣3）•a x 是指数函数,∴12a ﹣3＝1,a ＞0,a ≠1,解得a ＝8, ∴f （x ）＝8x ,∴f （12）==,故选：D ． 3．（2019·辽宁葫芦岛.高一月考）下列函数不是指数函数的是（ ） A ．12x y += B ．3x y -= C ．4x y = D ．32x y =【参考答案】A【解析】指数函数是形如xy a =（0a >且1a ≠）的函数. 对于A ：1222x x y +==⨯,系数不是1,所以不是指数函数；对于B ：133xx y -⎛⎫== ⎪⎝⎭,符合指数函数的定义,所以是指数函数；对于C ：4xy =,符合指数函数的定义,所以是指数函数；对于D ：382x xy ==,符合指数函数的定义,所以是指数函数.故选：A.考点二 定义域和值域【例2-1】（2020·全国高一课时练习）求下列函数的定义域和值域： （1）142x y -=；（2）23y ⎛= ⎪⎝⎭（3）22312x x y --⎛⎫=⎪⎝⎭.【参考答案】（1）定义域{|4}x x ≠,值域为{|0y y >且1}y ≠； （2）定义域{|0}x x =,值域{|1}y y =；（3）定义域R ,值域(]0,16【解析】（1）要使函数式有意义,则40x -≠,解得4x ≠.所以函数142x y -=的定义域为{|4}x x ≠.因为104x ≠-,所以1421x -≠,即函数142x y -=的值域为{|01}y y y >≠，且. （2）要使函数式有意义,则||0x -,解得0x =,所以函数23y ⎛= ⎪⎝⎭{|0}x x =.因为0x =,所以022133⎛⎛⎫== ⎪ ⎪⎝⎭⎝⎭,即函数23y ⎛= ⎪⎝⎭{|1}y y =.（3）函数的定义域为R .因为2223(1)44x x x --=--≥-,所以2234111622x x ---⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭. 又223102x x --⎛⎫>⎪⎝⎭,所以函数22312x x y --⎛⎫= ⎪⎝⎭的值域为(]0,16.【例2-2】（2018·湖南开福.长沙一中高一月考）若函数y =的值域为[0,+∞）,则实数a 的取值范围是_____． 【参考答案】（﹣∞,﹣2]【解析】设()421x x g x a =+⋅+,若函数y =的值域为[0,)+∞,则等价于[0,)+∞是()g x 值域的子集,2()421(2)21x x x x g x a a =+⋅+=+⋅+,设2x t =,则0t >,则2()1y h t t at ==++,(0)10h =>,∴当对称轴02at =-,即0a 时,不满足条件． 当02at =->,即0a <时,则判别式△240a =-,即022a a a <⎧⎨-⎩或,则2a -, 即实数a 的取值范围是(-∞,2]-.故参考答案为：(-∞,2]-【一隅三反】1．（2020·全国高一课时练习）求下列函数的定义域和值域； （1）12x y +=；（2）y =（3）y =【参考答案】（1）定义域为R ,值域为(0,)+∞；（2）(,0]-∞,[0,1)；（3）[0,)+∞,[1,)+∞.【解析】（1）12x y +=的定义域为R ,值域为(0,)+∞.（2）由120x -≥知0x ,故y =(,0]-∞；由0121x -<知0121x -<,故y =[0,1).（3）y =[0,)+∞0x 知1x,故y =[1,)+∞.2．（2020·全国高一课时练习）求下列函数的定义域与值域.（1）y =（2）1(0,1x x a y a a -=>+且1)a ≠（3）110.3;x y -=（4）y =【参考答案】（1）定义域为[0,)+∞；值域为[0,1)；（2）定义域为R ；值域为(－1,1)；（3）定义域为{1}xx ≠∣；值域为{0y y >∣且1}y ≠；（4）定义域为15xx ⎧⎫≥⎨⎬⎩⎭∣；值域为{1}yy ≥∣. 【解析】（1）1102x⎛⎫-≥ ⎪⎝⎭,解得：0x ≥, ∴原函数的定义域为[0,)+∞,令11(0)2xt x ⎛⎫=-≥ ⎪⎝⎭,则01,01t ≤<∴≤∴原函数的值域为[0,1) （2）原函数的定义域为R.设x a t =,则(0,)t ∈+∞,11221111t t y t t t -+-===-+++, 0,11t t >∴+>,1201,2011t t -∴<<∴-<<++,21111t ∴-<-<+,即原函数的值域为(1,1)-. （3）由10x -≠得1x ≠,所以函数定义域为{|1}x x ≠,由101x ≠-得1y ≠, 所以函数值域为{|0y y >且1}y ≠.(4)由510x -≥得15x ≥,所以函数定义域为15x x ⎧⎫≥⎨⎬⎩⎭∣,0≥得1y ≥,所以函数值域为{1}yy ≥∣. 3．（2020·河北新华.石家庄二中高二期末）若函数()1,121,14xxx f x a x ⎧⎛⎫<⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪+≥⎪⎪⎝⎭⎩的值域为(),+∞a ,则a 的取值范围为（ ）A ．1,4⎡⎫+∞⎪⎢⎣⎭B ．11,42⎡⎤⎢⎥⎣⎦C ．1,12⎡⎤⎢⎥⎣⎦D ．1,14⎛⎤ ⎥⎝⎦【参考答案】B【解析】当1x <时,()1,212xf x ⎛⎫∈+∞⎛ ⎪⎝⎫= ⎪⎭⎭⎝ 当1≥x 时,()114,4xf x a a a ⎛⎤∈+⎛⎫=+ ⎪⎝⎭ ⎥⎝⎦ 函数()f x 的值域为(),+∞a 114212a a ⎧+≥⎪⎪∴⎨⎪≤⎪⎩,即11,42a ⎡⎤∈⎢⎥⎣⎦故选：B 4．（2020·云南五华.昆明一中高三其他（理））设函数y =A ,函数12x y -=的值域为B ,则AB =( )A ．()0,1B ．(]0,1C ．()1,1-D ．[]1,1-【参考答案】A【解析】函数定义域满足：210x ->,即11x -<<,所以{}11A x x =-<<,函数12x y -=的值域{}0B y y =>,所以()0,1AB =,故选：A.5．（2019·湖南高一期中）若函数2411()3ax x f x -+⎛⎫= ⎪⎝⎭有最大值3,则实数a 的值为（ ）A ．2-B ．1-C ．1D ．2【参考答案】D【解析】由于函数2411()3ax x f x -+⎛⎫= ⎪⎝⎭有最大值3,所以0a >,且当422x a a-=-=时,()f x 取得最大值为2224411412113333a a a aaf a ⎛⎫⋅-⋅+-+ ⎪-⎝⎭⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故4411,2,2a a a-===.故选：D 考点三 指数函数性质【例3】（1）（2020·贵溪市实验中学高二期末（文））若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( )A ．9,34⎛⎫⎪⎝⎭B ．9,34⎡⎫⎪⎢⎣⎭C ．()1,3D ．()2,3（2）（2019·湖南岳阳楼.岳阳一中高一期中）已知函数1()2xf x ⎛⎫= ⎪⎝⎭,则不等式()24(3)f a f a ->的解集为( ) A ．(4,1)-B ．(1,4)-C ．(1,4)D ．(0,4)（3）（2019·湖北襄阳）如果1111222b a⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭,那么（ ）A ．a b a a a b <<B ．a a b a b a <<C ．b a a a a b <<D ．b a a a b a <<【参考答案】（1）B （2）B(3)C【解析】（1）函数6(3)3,7(),7x a x x f x a x ---⎧=⎨>⎩单调递增,()301373a a a a⎧->⎪∴>⎨⎪-⨯-≤⎩解得934a ≤<所以实数a 的取值范围是9,34⎡⎫⎪⎢⎣⎭．故选：B ．（2）可知函数()f x 为减函数,由2(4)(3)f a f a ->,可得243a a-<,整理得2340a a --<,解得14a -<<,所以不等式的解集为(1,4)-．故选B.(3) 根据函数()1()2x f x =在R 是减函数,且1111222ba⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭,所以10b a >>>,所以a a b a b a <<,故选C.【一隅三反】1．（2019·浙江南湖.嘉兴一中高一月考）函数2213x xy -+⎛⎫= ⎪⎝⎭为增函数的区间是（ ）A ．[)1,-+∞B ．(],1-∞-C ．[)1,+∞D ．(],1-∞【参考答案】C【解析】∵13uy ⎛⎫= ⎪⎝⎭是减函数,222(1)1u x x x =-+=--+在(,1]-∞上递增,在[1,)+∞上递减,∴函数2213x xy -+⎛⎫= ⎪⎝⎭的增区间是[1,)+∞．故选：C ．2．（2019·浙江柯城.衢州二中高三一模）已知定义在R 上的函数()||32x m f x -+=+m 为实数）为偶函数,记()0.2log 3a f =,()5log b f e =,()c f m π=+,则( )11.指数函数性质记忆口诀指数增减要看清,抓住底数不放松； 反正底数大于0,不等于1已表明； 底数若是大于1,图象从下往上增； 底数0到1之间,图象从上往下减； 无论函数增和减,图象都过(0,1)点． 2.比较幂值大小的三种类型及处理方法A ．c b a <<B ．c a b <<C ．a c b <<D ．a b c <<【参考答案】B【解析】()f x 为偶函数,()()f x f x ∴-=,||||3232x m x m --+-+∴+=+,||||x m x m ∴-+=+；0m ∴=；||()32x f x -∴=+；()f x ∴在[0,)+∞上单调递减,并且0.25(|log 3|)(log 3)a f f ==,5(log )b f e =,()()c f m f ππ=+=550log log 3e π<<<c a b ∴<<．故选：B ．3．（2020·浙江高一课时练习）设0.914y =,0.4828y =, 1.5312y -⎛⎫= ⎪⎝⎭,则（ ）A ．312y y y >>B ．213y y y >>C ．123y y y >>D ．132y y y >>【参考答案】D【解析】 1.50.920.9 1.80.4830.481.44 1.35121422,22282,y y y -⨯⨯⎛⎫======⎝== ⎪⎭,因为函数2xy =在定义域上为单调递增函数,所以132y y y >>．故选：D ．4．（2020·永安市第三中学高二月考）若关于x 的方程()94340xxa ++⋅+=有解,则实数a 的取值范围是（ ）A ．(,8][0,)-∞-+∞B ．(),4-∞-C ．[8,4)--D ．(,8]-∞-【参考答案】D【解析】由9(4)340x xa ++⋅+=,得443(4)0,(4)3433xxx x a a +++=∴-+=+≥（当且仅当32x =时等号成立）,解得8a ≤-故选D5（2020·上海高一课时练习）已知函数2221()2x x f x ++⎛⎫= ⎪⎝⎭,则该函数的单调递增区间是__________.【参考答案】(,1]-∞-【解析】由题得函数的定义域为R . 设2122,()2uu x x v =++=,函数222,u x x =++在∞(-,-1]单调递减,在[1,)-+∞单调递增,函数1()2uv =在其定义域内单调递减,所以2221()2x x f x ++⎛⎫= ⎪⎝⎭在∞(-,-1]单调递增,在[1,)-+∞单调递减.故参考答案为：(,1]-∞-.6．（2020·上海普陀.曹杨二中高一期末）函数12x y =-的单调递增区间为________【参考答案】(,0]-∞【解析】函数12,010221,1x xxy x x ⎧->⎪=⎨⎛⎫-≤⎪ ⎪⎝⎭=⎩-, 根据指数函数单调性可得,函数在(,0]-∞单调递增,在0,单调递减,所以函数12xy =-的单调递增区间为(,0]-∞.故参考答案为：(,0]-∞ 7．（2020·全国高一课时练习）比较下列各题中的两个值的大小． （1）0.10.8-,0.21.25；（2）1ππ-⎛⎫ ⎪⎝⎭,1；（3）30.2-,()0.23-.【参考答案】（1）0.10.20.81.25-<（2）11ππ-⎛⎫> ⎪⎝⎭（3）()0.230.23->-【解析】（1）因为0.10.10.1450.854--⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭, 0.20.251.254⎛⎫= ⎪⎝⎭, 又指数函数54xy ⎛⎫= ⎪⎝⎭为增函数,且0.10.2<,所以0.10.25544⎛⎫⎛⎫< ⎪⎪⎝⎭⎝⎭,即0.10.20.8 1.25-<. （2）1ππ-⎛⎫ ⎪⎝⎭01πππ=>=,（3）30.2-00.21>=,()()10.25330-=-=<,所以()0.230.23->-.考点四 定点【例4】（2020·浙江高一课时练习）函数()-1=4+x f x a （0a >,且1a ≠）的图象过定点P ,则P 点的坐标为（ ） A ．(1,5) B ．(1,4) C ．(0,5)D ．(0,4)【参考答案】A【解析】因为xy a =的图象恒过(0,1)点,则1x y a-=的图象恒过(1,1)点,所以()-1=4+x f x a恒过定点()1,5P .故选A .【一隅三反】1．（2019·涡阳县第九中学高二期末）函数()10,1xy a a a =+>≠的图象必经过点（ ）A ．(0,1)B ．(1,1)C ．()0,2D ．(2,2)【参考答案】C【解析】函数x y a =的图象过点(0,1),而函数1x y a =+的图象是把函数x y a =的图象向上平移1个单位,∴函数1x y a =+的图象必经过的点(0,2)．故选：C ．2．（2019·贵州省织金县第二中学高一期中）函数21()x f x a-=(0a >且1)a ≠过定点（ ） A ．(1,1) B ．1(,0)2C ．(1,0)D ．1(,1)2【参考答案】D【解析】令12102x x -=⇒=,所以函数21()x f x a -=(0a >且1)a ≠过定点1(,1)2． 3．（2020·宁夏贺兰县景博中学高一月考）函数y=a x ﹣1+2（a ＞0且a≠1）图象一定过点（ ）A ．（1,1）B ．（1,3）C ．（2,0）D ．（4,0）【参考答案】B 由x ﹣1=0,解得x=1,此时y=1+2=3,即函数的图象过定点（1,3）,故选B考点五 图像【例5-1】（2020·广东顺德一中高一期中）函数1(0,1)xy a a a a=->≠的图像可能是（ ）． A ． B ．C ．D ．【参考答案】D 【解析】∵0a >,∴10a>,∴函数x y a =需向下平移1a 个单位,不过（0,1）点,所以排除A,当1a >时,∴101a <<,所以排除B,当01a <<时,∴11a>,所以排除C,故选D. 【例5-2】（2020·浙江高一课时练习）若函数(01,1)xy a a a m =>-≠+的图像在第一、三、四象限内,则（ ） A ．1a >B ．1a >,且0m <C ．01a <<,且0m >D ．01a <<【参考答案】B【解析】因为函数xy a =的图像在第一、二象限内,所以欲使其图像在第三、四象限内,必须将xy a =向下移动,因为当01a <<时,图像向下移动,只能经过第一、二、四象限或第二、三、四象限, 所以只有当1a >时,图像向下移动才可能经过第一、三、四象限,故1a >,因为图像向下移动小于一个单位时,图像经过第一、二、三象限,而向下移动一个单位时,图像恰好经过原点和第一、三象限,所以欲使图像经过第一、三、四象限,则必须向下平移超过一个单位, 故11m -<-,0m <,故选：B.【一隅三反】1．（2019·浙江高一期中）函数y x a =+与xy a =,其中0a >,且1a ≠,它们的大致图象在同一直角坐标系中有可能是 ( )A ．B ．C ．D ．【参考答案】D【解析】因为函数y x a =+单调递增,所以排除AC 选项；当1a >时,y x a =+与y 轴交点纵坐标大于1,函数xy a =单调递增,B 选项错误；当01a <<时,y x a =+与y 轴交点纵坐标大于0小于1,函数xy a =单调递减；D 选项正确.故选：D2．（2020·全国高一课时练习）在如图所示的图象中,二次函数2y ax bx c =++与函数xb y a ⎛⎫= ⎪⎝⎭的图象可能是（ ）A ．B ．C ．D ．【参考答案】A【解析】根据选项中二次函数图象,可知0c ,根据选项中指数函数的图象,可知01b a <<,所以1022b a-<-<, 所以二次函数2y ax bx c =++的对称轴在y 轴左侧,且1,022b x a ⎛⎫=-∈- ⎪⎝⎭, 所以可排除B 、C 、D,只有A 符合题意.故选：A.3．（2020·上海高一课时练习）若函数2xy m =+的图像不经过第二象限,则m 的取值范围是( )A ．m 1≥B ．1m <C ．1m >-D ．1m ≤-【参考答案】D【解析】指数函数2x y =过点0,1,则函数2xy m =+过点()0,1m +,若图像不经过第二象限,则10m +≤,即1m ≤-,故选：D4．（2020·内蒙古集宁一中高二期末（理））若直线2y a =与函数|1|(0,1)x y a a a =->≠的图象有两个大众点,则a 的取值范围是___________【参考答案】102⎛⎫ ⎪⎝⎭，【解析】当01,1a a <<>时,做出|1|xy a =-图象,如下图所示,直线2y a =与函数|1|(0,1)x y a a a =->≠的图象有两个大众点时,1021,02a a <<<<. 故参考答案为:102⎛⎫ ⎪⎝⎭，知识改变命运。
高一数学指数函数试题答案及解析
高一数学指数函数试题答案及解析1.（本小题12分）不用计算器求下列各式的值⑴⑵【答案】(1)(2)【解析】（1）……6分（2）……12分【考点】本小题主要考查指数和对数的运算，考查学生的运算求解能力.点评：指数和对数的运算性质的灵活应用是解决此类问题的关键，另外也经常用到. 2.要使方程x＋px＋q = 0的两根a、b满足lg(a＋b) = lga＋lgb，试确定p和q应满足的关系．【答案】p＋q = 0且q＞0【解析】由已知得，又lg(a＋b) = lga＋lgb，即a＋b = ab，再注意到a＞0，b＞0，可得－p = q＞0，所以p和q满足的关系式为p＋q = 0且q＞0．3.计算：＝【答案】【解析】原式4.当时，不等式恒成立，则实数的取值范围是（）A．B．C．D．【答案】A【解析】，当时，，则，解得，故选A。
点睛：利用分离参数法得到，因为对任意的，不等式恒成立，则只需，解得，最后求得的取值范围。
函数恒成立问题，分离参数法是最常用的方法，属于含参函数题型的通法之一。
5.已知：，则__________．【答案】2【解析】由题意得.6.设，，，则的大小关系是（）A．B．C．D．【答案】A【解析】∵在x＞0时是增函数∴a＞c又∵在x＞0时是减函数，所以c＞b故答案选A。
7.已知，，，则，，的大小关系是（）A．B．C．D．【答案】C【解析】因为，，，所以，故选C.8.化简计算下列各式：（1）；（2）．【答案】（1）；（2）．【解析】（1）根据指数幂的运算法则即可求出；（2）根据对数的运算法则及特殊值的对数即可求解.试题解析：（1）原式．（2）原式．9.函数y＝a x(－2≤x≤3)的最大值为2，则a＝________．【答案】或【解析】当0<a<1时，y＝a x在[－2，3]上是减函数，＝a－2＝2，得a＝；所以ymax当a>1时，y＝a x在[－2，3]上是增函数，＝a3＝2，解得a＝.综上知a＝或.所以ymax10.要得到函数y＝21－2x的图像，只需将指数函数y＝的图像()A．向左平移1个单位B．向右平移1个单位C．向左平移个单位D．向右平移个单位【答案】D【解析】，所以可以由图象右移个单位，故选D。
高中数学《指数函数图像与性质》精选练习(含详细解析)
高中数学《指数函数图像与性质》精选练习（含详细解析）一、选择题1.函数y=的定义域为( )A.RB.(-∞,+∞)C.(-∞,0)D.{x|x≠0,x∈R}2.定义运算:a·b=则函数f(x)=1·2x的图象大致为( )3.若函数y=(1-a)x是实数集R上的减函数,则实数a的取值范围是( )A.(-1,0)B.(0,1)C.(-2,0)D.(0,2)4.下列函数中,值域为的函数是( )A.y=B.y=C.y=D.y=5.若函数f=a x-1(a>0且a≠1)的定义域和值域都是[0,2],则实数a等于( )A.1B.C.1或D.26函数f(x)=a x-b的图象如图所示,其中a,b均为常数,则下列结论正确的是( )A.a>1,b>0B.a>1,b<0C.0<a<1,b>0D.0<a<1,b<02.已知实数a,b满足等式2a=3b,下列五个关系式:①0<b<a;②a<b<0;③0<a<b;④b<a<0;⑤a=b.其中可能成立的关系式有( )A.①②③B.①②⑤C.①③⑤D.③④⑤二、填空题7.若函数f(x)=(a2-2a+2)(a+1)x是指数函数,则a= .8.函数y=2a x-2+1(a>0,且a≠1)的图象过定点.9.当x>0时,函数f(x)=的值总是大于1,则a的取值范围是. 【补偿训练】当x<0时,函数y=(2a-1)x的值总小于1,则a的取值范围是.【解析】由题意,2a-1>1,所以a>1.答案:a>110已知函数f(x)=a x+b(a>0,且a≠1),经过点(-1,5),(0,4),则f(-2)的值为.11.函数y=(a>0,且a≠1)的定义域是(-∞,0],则实数a的取值范围为.三、解答题(每小题10分,共20分)12.求下列函数的定义域和值域:(1)y=-1.(2)y=.13已知函数f(x)=a x-1(x≥0)的图象经过点,其中a>0且a≠1.(1)求a的值.(2)求函数y=f(x≥0)的值域.14.若y=(a-3)(a-2)x是指数函数,求函数f(x)=的定义域与值域..15.已知函数f(x)=-1.(1)作出f(x)的简图.(2)若关于x的方程f(x)=3m有两个解,求m取值范围.(2).参考答案与解析1【解析】选D.因为2x-1≠0,所以x≠0.2【解析】选A.f(x)=3【解析】选B.由于函数y=(1-a)x是实数集R上的减函数,则有0<1-a<1,解得0<a<1.4【解析】选D.y=中y>0且y≠1,y=中y可以为0,y=中y>1.5【解析】选B.由题意知或解得a=.6【解析】选D.f(x)=a x-b的图象是由y=a x的图象平移得到的,由图象可知f(x)在R上是递减函数,所以0<a<1,由y=a x过点(0,1)得知y=a x的图象向左平移|b|个单位得f(x)的图象,所以b<0.7【解析】由指数函数的定义得解得a=1.答案:1【解析】令x-2=0,解得x=2,则y=3,所以过定点(2,3).答案:(2,3)【解题指南】指数函数只有底数大于1时,才会有x>0时,函数值总大于1.9【解析】由题意知,a2-1>1,即a2>2,解得a>或a<-.答案:a>或a<-10【解析】由已知得解得所以f(x)=+3,所以f(-2)=+3=4+3=7.答案:711【解析】由题意,当x≤0时,a x≥1,所以0<a<1.答案:0<a<1【误区警示】本题由x≤0时,a x≥1,易得出a>1的错误答案.12【解析】(1)要使y=-1有意义,需x≠0,则>0且≠1,故-1>-1且-1≠0,故函数y=-1的定义域为,函数的值域为(-1,0)∪(0,+∞).(2)函数y=的定义域为实数集R,由于2x2≥0,则2x2-2≥-2,故0<≤9,所以函数y=的值域为(0,9].13【解析】(1)函数图象经过点,所以a2-1=,则a=.(2)由(1)知函数为f(x)=(x≥0),由x≥0,得x-1≥-1.于是0<≤=2,所以函数的值域为(0,2].14【解析】因为y=(a-3)(a-2)x是指数函数,所以解得a=4,所以f(x)=,由x+2≠0,得x≠-2,所以f(x)的定义域是∪,令t=,所以t≠0,即f(x)≠1,所以f(x)的值域是∪15【解析】(1)f(x)=如图所示.作出直线y=3m,当-1<3m<0时,即-<m<0时,函数y=f(x)与y=3m有两个交点,即关于x的方程f(x)=3m有两个解。
指数函数的性质及常考题型(含解析)
【变式 1-2】下列函数：① = 3 ；② = 6 ；③ = 6 ⋅ 2 ；④ = 8 + 1；⑤ = −6 .
其中一定为指数函数的有（
A．0 个
）
B．1 个
C．2 个
D．3 个
【解题思路】根据指数函数的定义判断即可；
【解答过程】解：形如 =
( > 0且 ≠ 1)为指数函数，其解析式需满足①底数为大于
数
函
数
︶
如图是指数函数（1）y＝ax，
（2）y＝bx，
（3）y＝cx，(4)y＝dx 的图象，底数 a，b，c，
d 与 1 之间的大小关系为 c>d>1>a>b．
由此我们可得到以下规律：在 y 轴右(左)侧图象越高(低)，其底数越大．
3．比较指数幂的大小的方法
比较指数幂的大小的方法（分三种情况）
：
（1）底数相同，指数不同：利用指数函数的单调性来判断；
培
优
篇
高
【变式 5-2】已知函数() = ⋅ 的图像经过点(1,2)，(2,4)．
中
（1）求()的解析式；
数
（2）解不等式( + 3) > (4)．
学
︵
指
数
函
数
︶
【变式 5-3】已知函数() = + (0 < < 1)的图象经过点(0, −1)．
（1）求实数 b；
B．0 < < 1,0 < < 1
指
C．0 < < 1, > 1
D． > 1,0 < < 1
数
函
【变式 6-2】如图中，①②③④中不属于函数 = 3 ， = 2 ， =
4.2 指数函数(精练)(解析版) -人教版高中数学精讲精练(必修一)
x
2
1 ，故值域为 y
|
0
y
1
.
8．（2021·黑龙江·绥化市第一中学高一期中）已知函数 f x 4x a 2x 3 ， a R ．
(1)当 a 4 ，且 x 0, 2 时，求函数 f x 的值域；
(2)若函数 f x 在0, 2 的最小值为1，求实数 a 的值；
【答案】(1)1,3 (2) a 2 2
③
y
2
x
是指数函数；
④ y xx 的底数是 x 不是常数，不是指数函数；
⑤
y
3
1 x
的指数不是自变量
x
，不是指数函数；
1
⑥ y x3 是幂函数．
故答案为：③
9．（2021·全国·高一专题练习）函数 y a2 5a 5 ax 是指数函数，则 a 的值为________．
【答案】 4
f
x
ax2 2x ,
a
1 x
x 1
3a,
x
1 的最小值为
2，则实数
a 的取值范围是______.
【答案】1,
【解析】由题意，函数
f
x
ax2 2x ,
a 1 x
x 1
3a, x
1 的最小值为
2
，
因为函数 f x 在[1, ) 上为增函数，可得 x 1时，函数 f x 有最小值为 2 ，
则当 x (,1) 时，函数 f x 2 ， min
）
A． c a b
B． c b a
【答案】A
1
2
【解析】
b
1 4
3
1 2
3
，
C． b c a
指数函数习题(经典含答案及详细解析)
指数函数习题一、选择题1．概念运算⎩⎨⎧>≤=⊗ba b b a a b a ，那么函数x x f 21)(⊗=的图象大致为( )2．函数f (x )＝x 2－bx ＋c 知足f (1＋x )＝f (1－x )且f (0)＝3，那么f (b x )与f (c x )的大小关系是( )A ．f (b x )≤f (c x )B ．f (b x )≥f (c x )C ．f (b x )>f (c x )D ．大小关系随x 的不同而不同3．函数y ＝|2x －1|在区间(k －1，k ＋1)内不单调，那么k 的取值范围是( )A ．(－1，＋∞)B ．(－∞，1)C ．(－1,1)D ．(0,2)4．设函数f (x )＝ln[(x －1)(2－x )]的概念域是A ，函数g (x )＝lg(a x －2x －1)的概念域是B ，假设A ⊆B ，那么正数a 的取值范围( )A ．a >3B ．a ≥3C ．a > 5D ．a ≥ 55．已知函数⎩⎨⎧>≤--=-77)3)(3()(6x a x x a x f x ，假设数列{a n }知足a n ＝f (n )(n ∈N *)，且{a n }是递增数列，那么实数a 的取值范围是( )A ．[94，3) B ．(94，3) C ．(2,3)D ．(1,3) 6．已知a >0且a ≠1，f (x )＝x 2－a x ，当x ∈(－1,1)时，均有f (x )<12，那么实数a 的取值范围是( ) A ．(0，12]∪[2，＋∞) B ．[14，1)∪(1,4] C ．[12，1)∪(1,2] D ．(0，14)∪[4，＋∞) 二、填空题7．函数y ＝a x (a >0，且a ≠1)在[1,2]上的最大值比最小值大a 2，那么a 的值是________． 8．假设曲线|y |＝2x ＋1与直线y ＝b 没有公共点，那么b 的取值范围是________．9．(2020·滨州模拟)概念：区间[x 1，x 2](x 1<x 2)的长度为x 2－x 1.已知函数y ＝2|x |的概念域为[a ，b ]，值域为[1,2]，那么区间[a ，b ]的长度的最大值与最小值的差为________．三、解答题10．求函数y ＝2342x x ---+的概念域、值域和单调区间．11．(2020·银川模拟)假设函数y ＝a 2x ＋2a x －1(a >0且a ≠1)在x ∈[－1,1]上的最大值为14，求a 的值．12．已知函数f (x )＝3x ，f (a ＋2)＝18，g (x )＝λ·3ax －4x 的概念域为[0,1]．(1)求a 的值；(2)假设函数g (x )在区间[0,1]上是单调递减函数，求实数λ的取值范围．指数函数答案1.解析：由a ⊗b ＝⎩⎪⎨⎪⎧ a a ≤b b a >b 得f (x )＝1⊗2x ＝⎩⎪⎨⎪⎧ 2x x ≤0，1 x >0.答案：A2. 解析：∵f (1＋x )＝f (1－x )，∴f (x )的对称轴为直线x ＝1，由此得b ＝2.又f (0)＝3，∴c ＝3.∴f (x )在(－∞，1)上递减，在(1，＋∞)上递增．若x ≥0，那么3x ≥2x ≥1，∴f (3x )≥f (2x )．若x <0，那么3x <2x <1，∴f (3x )>f (2x )．∴f (3x )≥f (2x )．答案：A3.解析：由于函数y ＝|2x －1|在(－∞，0)内单调递减，在(0，＋∞)内单调递增，而函数在区间(k －1，k ＋1)内不单调，因此有k －1<0<k ＋1，解得－1<k <1.答案：C4. 解析：由题意得：A ＝(1,2)，a x －2x >1且a >2，由A ⊆B 知a x －2x >1在(1,2)上恒成立，即a x －2x －1>0在(1,2)上恒成立，令u (x )＝a x －2x －1，那么u ′(x )＝a x ln a －2x ln2>0，因此函数u (x )在(1,2)上单调递增，那么u (x )>u (1)＝a －3，即a ≥3.答案：B5. 解析：数列{a n }知足a n ＝f (n )(n ∈N *)，那么函数f (n )为增函数，注意a 8－6>(3－a )×7－3，因此⎩⎪⎨⎪⎧ a >13－a >0a 8－6>3－a ×7－3，解得2<a <3.答案：C6. 解析：f (x )<12⇔x 2－a x <12⇔x 2－12<a x ，考查函数y ＝a x 与y ＝x 2－12的图象，当a >1时，必有a －1≥12，即1<a ≤2， 当0<a <1时，必有a ≥12，即12≤a <1， 综上，12≤a <1或1<a ≤2. 答案：C7. 解析：当a >1时，y ＝a x 在[1,2]上单调递增，故a 2－a ＝a 2，得a ＝32.当0<a <1时，y ＝a x 在[1,2]上单调递减，故a －a 2＝a 2，得a ＝12.故a ＝12或32. 答案：12或328. 解析：别离作出两个函数的图象，通过图象的交点个数来判定参数的取值范围．曲线|y |＝2x ＋1与直线y ＝b 的图象如下图，由图象可得：若是|y |＝2x ＋1与直线y ＝b 没有公共点，那么b 应知足的条件是b ∈[－1,1]． 答案：[－1,1]9. 解析：如图知足条件的区间[a ，b ]，当a ＝－1，b ＝0或a ＝0，b ＝1时区间长度最小，最小值为1，当a ＝－1，b ＝1时区间长度最大，最大值为2，故其差为1. 答案：110. 解：要使函数成心义，那么只需－x 2－3x ＋4≥0，即x 2＋3x －4≤0，解得－4≤x ≤1.∴函数的概念域为{x |－4≤x ≤1}．令t ＝－x 2－3x ＋4，那么t ＝－x 2－3x ＋4＝－(x ＋32)2＋254， ∴当－4≤x ≤1时，t max ＝254，现在x ＝－32，t min ＝0，现在x ＝－4或x ＝1. ∴0≤t ≤254.∴0≤－x 2－3x ＋4≤52. ∴函数y ＝2341()2x x --+[28，1]．由t ＝－x 2－3x ＋4＝－(x ＋32)2＋254(－4≤x ≤1)可知， 当－4≤x ≤－32时，t 是增函数， 当－32≤x ≤1时，t 是减函数． 依照复合函数的单调性知：y ＝1()2在[－4，－32]上是减函数，在[－32，1]上是增函数． ∴函数的单调增区间是[－32，1]，单调减区间是[－4，－32]． 11. 解：令a x ＝t ，∴t >0，那么y ＝t 2＋2t －1＝(t ＋1)2－2，其对称轴为t ＝－1.该二次函数在[－1，＋∞)上是增函数．①若a >1，∵x ∈[－1,1]，∴t ＝a x ∈[1a，a ]，故当t ＝a ，即x ＝1时，y max ＝a 2＋2a －1＝14，解得a ＝3(a ＝－5舍去)．②假设0<a <1，∵x ∈[－1,1]，∴t ＝a x ∈[a ，1a ]，故当t ＝1a，即x ＝－1时， y max ＝(1a＋1)2－2＝14. ∴a ＝13或－15(舍去)． 综上可得a ＝3或13. 12. 解：法一：(1)由已知得3a ＋2＝18⇒3a ＝2⇒a ＝log 32.(2)现在g (x )＝λ·2x －4x ，设0≤x 1<x 2≤1，因为g (x )在区间[0,1]上是单调减函数，因此g (x 1)－g (x 2)＝(2x 1－2x 2)(λ－2x 2－2x 1)>0恒成立，即λ<2x 2＋2x 1恒成立．由于2x 2＋2x 1>20＋20＝2，因此实数λ的取值范围是λ≤2.法二：(1)同法一．(2)现在g (x )＝λ·2x －4x ，因为g (x )在区间[0,1]上是单调减函数，因此有g ′(x )＝λln2·2x －ln4·4x ＝ln2[－2·(2x )2＋λ·2x ]≤0成立．设2x ＝u ∈[1,2]，上式成立等价于－2u 2＋λu ≤0恒成立．因为u ∈[1,2]，只需λ≤2u 恒成立，因此实数λ的取值范围是λ≤2.。
高一数学典型例题分析 指数函数 试题
卜人入州八九几市潮王学校指数函数·例题解析【例1】求以下函数的定义域与值域：解(1)定义域为x∈R且x≠2．值域y＞0且y≠1．(2)由2x+2－1≥0，得定义域{x|x≥－2}，值域为y≥0．(3)由3－3x-1≥0，得定义域是{x|x≤2}，∵0≤3－3x－1＜3，【例2】指数函数y＝a x，y＝b x，y＝c x，y＝d x的图像如图2．6－2所示，那么a、b、c、d、1之间的大小关系是[] A．a＜b＜1＜c＜dB．a＜b＜1＜d＜cC．b＜a＜1＜d＜cD．c＜d＜1＜a＜b解选(c)，在x轴上任取一点(x，0)，那么得b＜a＜1＜d＜c．【例3】比较大小：(3)解(3)借助数打桥，利用指数函数的单调性，＞，作函数y1＝x，y2＝x的图像如图2．6－3，取x＝，得＞∴＞．说明如何比较两个幂的大小：假设不同底先化为同底的幂，再利用指数函数的单调性进展比较，如例2中的(1)．假设是两个不同底且指数也不同的幂比较大小时，有两个技巧，其一借助1作桥梁，如例2中的(2)．其二构造一个新的幂作桥梁，这个新的幂具有与同底与同指数的特点，即为(或者)，如例2中的(3)．【例5】作出以下函数的图像：(3)y＝2|x-1| (4)y＝|1－3x|解(2)y＝2x－2的图像(如图2．6－5)是把函数y＝2x的图像向下平移2个单位得到的．解(3)利用翻折变换，先作y＝2|x|的图像，再把y＝2|x|的图像向右平移1个单位，就得y ＝2|x-1|的图像(如图2．6－6)．解(4)作函数y＝3x的图像关于x轴的对称图像得y＝－3x的图像，再把y＝－3x的图像向上平移1个单位，保存其在x轴及x轴上方局部不变，把x轴下方的图像以x轴为对称轴翻折到x轴上方而得到．(如图2．6－7)当x＝0时，函数y有最大值为1．(1)判断f(x)的奇偶性；(2)求f(x)的值域；(3)证明f(x)在区间(－∞，＋∞)上是增函数．解(1)定义域是R．∴函数f(x)为奇函数．即f(x)的值域为(－1，1)．(3)设任意取两个值x1、x2∈(－∞，＋∞)且x1＜x2．f(x1)－f(x2)。
指数函数习题（经典含答案及详细解析）
2．函数f (x )＝x 2－bx ＋c 满足f (1＋x )＝f (1－x )且A ．f (b x )≤f (c x) B ．f (b x )≥f (c x) lg(a x －2x－5 ≥5 [9，(9，1，，1[1，[1，，1)上的最大值比最小值大，则234x x ---+11．(2011·银川模拟)若函数y ＝a 2x ＋2a x－1(a >0且a ≠1)在x ∈[－1,1]上的最大值为14，求a 的值．的值．12．已知函数f (x )＝3x ，f (a ＋2)＝18，g (x )＝λ·3ax －4x的定义域为[0,1]． (1)求a 的值；的值；(2)若函数g (x )在区间[0,1]上是单调递减函数，求实数λ的取值范围．的取值范围．指数函数答案指数函数答案1.1.解析：由解析：由a ⊗b ＝îïíïìa a ≤bba >b得f (x )＝1⊗2x＝îïíïì2xx，1x答案：答案：A A 2. 2. 解析：∵解析：∵f (1(1＋＋x )＝f (1(1－－x )，∴f (x )的对称轴为直线x ＝1，由此得b ＝2. 又f (0)(0)＝＝3，∴c ＝3.3.∴∴f (x )在(－∞，－∞，1)1)1)上递减，在上递减，在上递减，在(1(1(1，＋∞)上递增．，＋∞)上递增．，＋∞)上递增．若x ≥0，则3x ≥2x ≥1，∴f (3x )≥f (2x)．若x <0<0，则，则3x<2x<1<1，∴，∴f (3x)>f (2x)． ∴f (3x )≥f (2x )． 答案：答案：A A3.3.解析：由于函数解析：由于函数y ＝|2x－1|1|在在(－∞，－∞，0)0)0)内单调递减，在内单调递减，在内单调递减，在(0(0(0，＋∞)内单调递增，而函数在，＋∞)内单调递增，而函数在区间区间((k －1，k ＋1)1)内不单调，所以有内不单调，所以有k －1<0<k ＋1，解得－，解得－1<1<k <1. 答案：答案：C C4. 4. 解析：由题意得：解析：由题意得：A ＝(1,2)(1,2)，，a x －2x >1且a >2>2，由，由A ⊆B 知a x －2x>1在(1,2)(1,2)上恒成立，即上恒成立，即a x －2x －1>0在(1,2)(1,2)上恒成立，令上恒成立，令u (x )＝a x －2x －1，则u ′(x )＝a x ln a －2x ln2>0ln2>0，所以函数，所以函数u (x )在(1,2)(1,2)上单调递增，则上单调递增，则u (x )>u (1)(1)＝＝a －3，即a ≥3.≥3. 答案：答案：B B5. 5. 解析：数列解析：数列解析：数列{{a n }满足a n ＝f (n )(n ∈N *)，则函数f (n )为增函数，为增函数，注意a 8－6>(3>(3－－a )×7－)×7－33，所以îïíïìa >13－a >0a8－6－a －3，解得2<a <3.答案：答案：C C6. 6. 解析：解析：f (x )<12⇔x 2－a x <12⇔x 2－12<a x ，考查函数y ＝a x 与y ＝x 2－12的图象，的图象，当a >1时，必有a －1≥12，即1<a ≤2，≤2，当0<a <1时，必有a ≥12，即12≤a <1<1，，综上，12≤a <1或1<a ≤2.≤2.答案：答案：C C7. 7. 解析：当解析：当a >1时，y ＝a x 在[1,2][1,2]上单调递增，故上单调递增，故a 2－a ＝a 2，得a ＝32.当0<a <1时，y ＝ax 在[1,2][1,2]上单调递减，故上单调递减，故a －a 2＝a 2，得a ＝12.故a ＝12或32.答案：12或328. 8. 解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．曲线曲线||y |＝2x＋1与直线y ＝b 的图象如图所示，由图象可得：如果的图象如图所示，由图象可得：如果||y |＝2x＋1与直线y ＝b 没有公共点，则b 应满足的条件是b ∈[－1,1]1,1]．． 答案：答案：[[－1,1]9. 9. 解析：如图满足条件的区间解析：如图满足条件的区间解析：如图满足条件的区间[[a ，b ]，当a ＝－＝－11，b ＝0或a ＝0，b ＝1时区间长度最小，最小值为1，当a ＝－＝－11，b ＝1时区间长度最大，最大值为2，故其差为1. 答案：答案：1 110. 10. 解：要使函数有意义，则只需－解：要使函数有意义，则只需－x 2－3x ＋4≥0，即x 2＋3x －4≤0，解得－4≤x ≤1.≤1. ∴函数的定义域为∴函数的定义域为{{x |－4≤x ≤1}．≤1}． 令t ＝－x 2－3x ＋4，则t ＝－x 2－3x ＋4＝－＝－((x ＋32)2＋254，∴当－4≤x ≤1时，t max ＝254，此时x ＝－32，t min ＝0，此时x ＝－＝－44或x ＝1.∴0≤t ≤254.∴0≤－x 2－3x ＋4≤52.∴函数y ＝2341()2x x ---+的值域为的值域为[[28，1]1]．．＋)＋(≤－时，≤234()2x x ---+在，－32]－32，－32，，－32][1a，，1a ]＝1a，即(1a＋＝13或－15(或13.。
指数函数典型例题详细解析
指数函数典型例题详细解析指数函数·例题解析第一课时例1：求下列函数的定义域与值域：1) $y=\frac{3}{2-x}$解：定义域为$x\in R$且$x\neq 2$，值域为$y>0$且$y\neq1$。
2) $y=2x+2-1$解：由$2^{\frac{x+2}{2}-1}\geq 0$，得定义域为$x\geq -2$，值域为$|y|\geq 0$。
3) $y=3-3x-1$解：由$3-3^{\frac{x-1}{2}}\geq 0$，得定义域为$x\leq 2$，由$3-3^{\frac{x-1}{2}}<3$，得值域为$y<3$。
1.指数函数$y=a^x$（$a>0$且$a\neq 1$）的定义域是$R$，值域是$(0,+\infty)$。
2.求定义域的几个原则：①含根式（被开方数不为负）②含分式，分母不为$0$③形如$a^0$，($a\neq 0$)3.求函数的值域：①利用函数$y=a^x$单调性②函数的有界性($x^2\geq 0;a^x>0$)③换元法。
例如：$y=4x+\frac{6}{2x-8}$($1\leq x\leq 2$)，先换元，再利用二次函数图象与性质（注意新元的范围）。
例2：指数函数$y=a^x$，$y=b^x$，$y=c^x$，$y=d^x$的图像如图2.6-2所示，则$a$、$b$、$c$、$d$、$1$之间的大小关系是？解：选$(c)$，在$x$轴上任取一点$(x,0)$，则得$b<a<1<d<c$。
例3：比较大小：1)$2$、$3^2$、$5^4$、$8^8$、$9^{16}$的大小关系是：$2<3^2<5^4<8^8<9^{16}$。
2)$\frac{0.6}{4}-\frac{5}{13}-2$，$2$的大小关系是：$\frac{0.6}{4}-\frac{5}{13}-2<2$。
指数函数及其性质(含解析、答案)
A 基础练习2.1.2指数函数（1时） 1．下列函数是指数函数的是( ) A ．y ＝－2xB ．y ＝2x ＋1 C ．y ＝2－x D ．y ＝1x【解析】 y ＝2－x＝⎝⎛⎭⎫12x，符合指数函数的定义，故选C.【答案】 C 2．函数y ＝(a －2)x 在R 上为增函数，则a 的取值范围是( )A ．a>0且a ≠1B ．a>3C ．a<3D ．2<a<3【解析】 由指数函数单调性知，底数大于1时为增函数，∴a －2>1，∴a>3，故选B. 【答案】 B 3．已知a ＝5－12，函数f(x)＝a x ，若实数m 、n 满足f(m)>f(n)，则m 、n 的大小关系为________．【解析】 ∵a ＝5－12∈(0,1)， 故a m >a n ⇒m<n. 【答案】 m<n4．已知指数函数f(x)的图象过点(2,4)，求f(－3)的值．【解析】 设指数函数f(x)＝a x (a>0且a ≠1)，由题意得a 2＝4，∴a ＝2，∴f(x)＝2x ， ∴f(－3)＝2－3＝18.B 综合应用一、选择题(每小题5分，共20分) 1．函数y ＝a x －2＋1(a>0，a ≠1)的图象必经过点( )A ．(0,1)B ．(1,1)C ．(2,0)D ．(2,2)【解析】 由于函数y ＝a x 经过定点(0,1)，所以函数y ＝a x－2经过定点(2,1)，于是函数y ＝a x －2＋1经过定点(2,2)．【答案】 D2．f(x)＝⎝⎛⎭⎫12|x|，x ∈R ，那么f(x)是( ) A ．奇函数且在(0，＋∞)上是增函数 B ．偶函数且在(0，＋∞)上是增函数 C ．奇函数且在(0，＋∞)上是减函数 D ．偶函数且在(0，＋∞)上是减函数 【解析】因为函数f(x)= |x|= 图象如右图． 由图象可知答案显然是D. 【答案】 D3．下列四个函数中，值域为(0，＋∞)的函数是( )A ．y ＝21x B ．y ＝2x －1C ．y ＝2x ＋1D ．y ＝⎝⎛⎭⎫122－x【解析】 在A 中，∵1x ≠0，∴21x≠1，即y ＝21x的值域为(0,1)∪(1，＋∞)．在B 中，2x －1≥0，∴y ＝2x －1的值域为[0，＋∞)． 在C中，∵2x >0，∴2x ＋1>1.∴y ＝2x ＋1的值域为(1，＋∞)． 在D 中，∵2－x ∈R ，∴y ＝⎝⎛⎭⎫122－x>0. ∴y ＝⎝⎛⎭⎫122－x 的值域为(0，＋∞)．故选D.【答案】 D 4．方程4x －1＝116的解为( ) A ．2 B ．－2 C ．－1 D ．1 【解析】 ∵4x －1＝116＝4－2，∴x －1＝－2，∴x ＝－1.故选C. 【答案】 C二、填空题(每小题5分，共10分) 5．函数y ＝a x －1的定义域是(－∞，0]，则实数a 的取值范围为________．【解析】 由a x －1≥0，得a x ≥1＝a 0，因为x ∈(－∞，0]，由指数函数的性质知0<a<1.【答案】 (0,1)6．函数f(x)＝⎝⎛⎭⎫13x－1，x ∈[－1,2]的值域为________．【解析】 函数y ＝⎝⎛⎭⎫13x 在区间[－1,2]上是减函数，所以⎝⎛⎭⎫132≤⎝⎛⎭⎫13x ≤⎝⎛⎭⎫13－1，即19≤⎝⎛⎭⎫13x ≤3， 于是19－1≤f(x)≤3－1，即－89≤f(x)≤2.【答案】 [－89，2]三、解答题(每小题10分，共20分) 7．已知函数f(x)＝a x －2(x ≥0)的图象经过点⎝⎛⎭⎫4，19，其中a>0且a ≠1. (1)求a 的值；(2)求函数y ＝f(x)(x ≥0)的值域． 【解析】 (1)函数图象过点⎝⎛⎭⎫4，19， 所以a 4－2＝19＝⎝⎛⎭⎫132，∴a ＝13，(2)f(x)＝⎝⎛⎭⎫13x －2(x ≥0)， 由x ≥0，得x －2≥－2， ∴0<⎝⎛⎭⎫13x －2≤⎝⎛⎭⎫13－2＝9，∴函数y ＝f(x)(x ≥0)的值域为(0,9]． 8．画出下列函数的图象，并说明它们是由函数f(x)＝2x 的图象经过怎样的变换得到的．(1)y ＝2x －1；(2)y ＝2x ＋1；(3)y ＝2|x|； (4)y ＝－2x .【解析】 如图所示．y=2x-1的图象是由y=2x 的图象向右平移1个单位得到；y=2x+1的图象是由y=2x 的图象向上平移1个单位得到；y=2|x|的图象是由y=2x 的y 轴右边的图象和其关于y 轴对称的图象组成的；y=-2x 的图象与y=2x 的图象关于x 轴对称．9．(10分)函数f(x)＝a x (a>0，且a ≠1)在区间[1,2]上的最大值比最小值大a2，求a的值．【解析】 (1)若a>1，则f(x)在[1,2]上递增，∴a 2－a ＝a 2，即a ＝32或a ＝0(舍去)．(2)若0<a<1，则f(x)在[1,2]上递减， ∴a －a 2＝a 2，即a ＝12或a ＝0(舍去)，综上所述，所求a 的值为12或32.2.1.2指数函数（2时） A 基础练习1．已知集合M ＝{－1,1}，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪12<2x ＋1<4，x ∈Z ，则M ∩N 等于( ) A ．{－1,1} B ．{－1} C ．{0} D ．{－1,0} 【解析】 因为N ＝{x|2－1<2x ＋1<22，x ∈Z }，又函数y ＝2x 在R 上为增函数， ∴N ＝{x|－1<x ＋1<2，x ∈Z } ＝{x|－2<x<1，x ∈Z }＝{－1,0}． ∴M ∩N ＝{－1,1}∩{－1,0}＝{－1}．故选B.【答案】 B2．设14<⎝⎛⎭⎫14b <⎝⎛⎭⎫14a<1，那么( )A ．a a <a b <b aB ．a a <b a <a bC ．a b <a a <b aD ．a b <b a <a a【解析】 由已知及函数y ＝⎝⎛⎭⎫14x是R 上的减函数， 得0<a<b<1.由y ＝a x (0<a<1)的单调性及a<b ，得a b <a a .由0<a<b<1知0<a b <1.∵⎝⎛⎭⎫a b a <⎝⎛⎭⎫a b 0＝1.∴a a <b a.故选C. 也可采用特殊值法，如取a ＝13，b ＝12.【答案】 C3．已知函数f(x)＝a －12x ＋1，若f(x)为奇函数，则a ＝________.【解析】 解法1：∵f(x)的定义域为R ，又∵f(x)为奇函数，∴f(0)＝0，即a －120＋1＝0.∴a ＝12.解法2：∵f(x)为奇函数，∴f(－x)＝－f(x)，即a －12－x ＋1＝12x ＋1－a ，解得a ＝12.【答案】 124．函数y ＝2－x 2＋ax －1在区间(－∞，3)内递增，求a 的取值范围．【解析】 对u ＝－x 2＋ax －1＝－⎝⎛⎭⎫x －a 22＋a 24－1，增区间为⎝⎛⎦⎤－∞，a 2，∴y 的增区间为⎝⎛⎦⎤－∞，a2，由题意知3≤a2，∴a ≥6. ∴a 的取值范围是a ≥6. B 综合应用一、选择题(每小题5分，共20分) 1．设y 1＝40.9，y 2＝80.48，y 3＝(12)－1.5，则( )A ．y 3>y 1>y 2B ．y 2>y 1>y 3C ．y 1>y 2>y 3D ．y 1>y 3>y 2 【解析】 y 1＝40.9＝21.8，y 2＝80.48＝21.44，y 3＝(12)－1.5＝21.5，∵y ＝2x 在定义域内为增函数， 且1.8>1.5>1.44， ∴y 1>y 3>y 2. 【答案】 D2．若⎝⎛⎭⎫142a ＋1<⎝⎛⎭⎫143－2a，则实数a 的取值范围是( )A.⎝⎛⎭⎫12，＋∞B.()1，＋∞ C ．(－∞，1) D.⎝⎛⎭⎫－∞，12 【解析】 函数y ＝⎝⎛⎭⎫14x在R 上为减函数，∴2a ＋1>3－2a ，∴a>12.故选A.【答案】 A3．设函数f(x)定义在实数集上，它的图象关于直线x ＝1对称，且当x ≥1时，f(x)＝3x －1，则有( )A ．f(13)<f(32)<f(23)B ．f(23)<f(32)<f(13)C ．f(23)<f(13)<f(32)D ．f(32)<f(23)<f(13)【解析】 因为f(x)的图象关于直线x ＝1对称，所以f(13)＝f(53)，f(23)＝f(43)，因为函数f(x)＝3x －1在[1，＋∞)上是增函数，所以f(53)>f(32)>f(43)，即f(23)<f(32)<f(13)．故选B.【答案】 B4．如果函数f(x)＝(1－2a)x 在实数集R 上是减函数，那么实数a 的取值范围是( )A ．(0，12)B ．(12，＋∞)C ．(－∞，12)D ．(－12，12)【解析】 根据指数函数的概念及性质求解．由已知得，实数a 应满足⎩⎪⎨⎪⎧1－2a>01－2a<1，解得⎩⎪⎨⎪⎧a<12a>0，即a ∈(0，12)．故选A.【答案】 A二、填空题(每小题5分，共10分) 5．设a>0，f(x)＝e x a ＋ae x (e>1)，是R 上的偶函数，则a ＝________.【解析】 依题意，对一切x ∈R ，都有f(x)＝f(－x)，∴e x a ＋a e x ＝1ae x ＋ae x ， ∴(a －1a )(e x －1e x )＝0.∴a －1a ＝0，即a 2＝1.又a>0，∴a ＝1. 【答案】 16．下列空格中填“>、<或＝”． (1)1.52.5________1.53.2，(2)0.5－1.2________0.5－1.5.【解析】 (1)考察指数函数y ＝1.5x . 因为1.5>1，所以y ＝1.5x 在R 上是单调增函数．又因为2.5<3.2，所以1.52.5<1.53.2. (2)考察指数函数y ＝0.5x .因为0<0.5<1，所以y ＝0.5x 在R 上是单调减函数．又因为－1.2>－1.5，所以0.5－1.2<0.5－1.5.【答案】 <，<三、解答题(每小题10分，共20分) 7．根据下列条件确定实数x 的取值范围：a<⎝⎛⎭⎫1a 1－2x(a>0且a ≠1)．【解析】 原不等式可以化为a 2x －1>a 12，因为函数y ＝a x (a>0且a ≠1)当底数a 大于1时在R 上是增函数；当底数a 大于0小于1时在R 上是减函数，所以当a>1时，由2x －1>12，解得x>34；当0<a<1时，由2x －1<12，解得x<34.综上可知：当a>1时，x>34；当0<a<1时，x<34.8．已知a>0且a ≠1，讨论f(x)＝a －x 2＋3x ＋2的单调性．【解析】 设u ＝－x 2＋3x ＋2＝－⎝⎛⎭⎫x －322＋174， 则当x ≥32时，u 是减函数，当x ≤32时，u 是增函数．又当a>1时，y ＝a u 是增函数，当0<a<1时，y ＝a u 是减函数，所以当a>1时，原函数f(x)＝a －x 2＋3x ＋2在⎣⎡⎭⎫32，＋∞上是减函数，在⎝⎛⎦⎤－∞，32上是增函数．当0<a<1时，原函数f(x)＝a －x 2＋3x ＋2在⎣⎡⎭⎫32，＋∞上是增函数，在⎝⎛⎦⎤－∞，32上是减函数．9．(10分)已知函数f(x)＝3x ＋3－x . (1)判断函数的奇偶性；(2)求函数的单调增区间，并证明．【解析】 (1)f(－x)＝3－x ＋3－(－x)＝3－x＋3x ＝f(x)且x ∈R ，∴函数f(x)＝3x ＋3－x是偶函数．(2)由(1)知，函数的单调区间为(－∞，0]及[0，＋∞)，且[0，＋∞)是单调增区间．现证明如下：设0≤x 1<x 2，则f(x 1)－f(x 2)＝3x 1＋3－x 1－3x 2－2－x 2＝3x 1－3x 2＋13x 1－13x 2＝3x 1－3x 2＋3x 2－3x 13x 13x 2＝(3x 2－3x 1)·1－3x 1＋x 23x 1＋x 2.∵0≤x 1<x 2，∴3x 2>3x 1，3x 1＋x 2>1， ∴f(x 1)－f(x 2)<0，即f(x 1)<f(x 2)， ∴函数在[0，＋∞)上单调递增， 即函数的单调增区间为[0，＋∞)．。
指数函数经典例题(问题详解)
指数函数1．指数函数の定义：函数)1(≠>=aaay x且叫做指数函数，其中x是自变量，函数定义域是R 2.指数函数の图象和性质：在同一坐标系中分别作出函数y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101の图象.我们观察y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101图象特征，就可以得到)1(≠>=aaay x且の图象和性质。
a>1 0<a<1图象00性质(1)定义域：R（2）值域：（0，+∞）（3）过点（0，1），即x=0时，y=1（4）在 R上是增函数（4）在R上是减函数指数函数是高中数学中の一个基本初等函数，有关指数函数の图象与性质の题目类型较多，同时也是学习后续数学内容の基础和高考考查の重点，本文对此部分题目类型作了初步总结，与大家共同探讨．1．比较大小例1 已知函数2()f x x bx c=-+满足(1)(1)f x f x+=-，且(0)3f=，则()xf b与()x f c の大小关系是_____．分析：先求b c ，の值再比较大小，要注意x x b c ，の取值是否在同一单调区间内．解：∵(1)(1)f x f x +=-， ∴函数()f x の对称轴是1x =． 故2b =，又(0)3f =，∴3c =．∴函数()f x 在(]1-，∞上递减，在[)1+，∞上递增． 若0x ≥，则321x x ≥≥，∴(3)(2)x x f f ≥； 若0x <，则321x x <<，∴(3)(2)x x f f >． 综上可得(3)(2)x x f f ≥，即()()x x f c f b ≥．评注：①比较大小の常用方法有：作差法、作商法、利用函数の单调性或中间量等．②对于含有参数の大小比较问题，有时需要对参数进行讨论． 2．求解有关指数不等式例2 已知2321(25)(25)x x a a a a -++>++，则x の取值范围是___________． 分析：利用指数函数の单调性求解，注意底数の取值范围． 解：∵2225(1)441a a a ++=++>≥，∴函数2(25)x y a a =++在()-+，∞∞上是增函数，∴31x x >-，解得14x >．∴x の取值范围是14⎛⎫+ ⎪⎝⎭，∞． 评注：利用指数函数の单调性解不等式，需将不等式两边都凑成底数相同の指数式，并判断底数与1の大小，对于含有参数の要注意对参数进行讨论． 3．求定义域及值域问题例3 求函数y =の定义域和值域． 解：由题意可得2160x --≥，即261x -≤，∴20x -≤，故2x ≤． ∴函数()f x の定义域是(]2-，∞．令26x t -=，则y =，又∵2x ≤，∴20x -≤． ∴2061x -<≤，即01t <≤． ∴011t -<≤，即01y <≤．∴函数の值域是[)01，． 评注：利用指数函数の单调性求值域时，要注意定义域对它の影响．4．最值问题例4 函数221(01)x x y a a a a =+->≠且在区间[11]-，上有最大值14，则a の值是_______．分析：令x t a =可将问题转化成二次函数の最值问题，需注意换元后t の取值范围．解：令x t a =，则0t >，函数221x x y a a =+-可化为2(1)2y t =+-，其对称轴为1t =-．∴当1a >时，∵[]11x ∈-，，∴1x a a a ≤≤，即1t a a≤≤． ∴当t a =时，2max (1)214y a =+-=． 解得3a =或5a =-（舍去）；当01a <<时，∵[]11x ∈-，，∴1x a a a ≤≤，即1a t a≤≤，∴ 1t a =时，2max 11214y a ⎛⎫=+-= ⎪⎝⎭， 解得13a =或15a =-（舍去），∴a の值是3或13．评注：利用指数函数の单调性求最值时注意一些方法の运用，比如：换元法，整体代入等． 5．解指数方程例5 解方程223380x x +--=．解：原方程可化为29(3)80390x x ⨯-⨯-=，令3(0)x t t =>，上述方程可化为298090t t --=，解得9t =或19t =-（舍去），∴39x =，∴2x =，经检验原方程の解是2x =．评注：解指数方程通常是通过换元转化成二次方程求解，要注意验根． 6．图象变换及应用问题例6 为了得到函数935x y =⨯+の图象，可以把函数3x y =の图象（ ）． A ．向左平移9个单位长度，再向上平移5个单位长度 B ．向右平移9个单位长度，再向下平移5个单位长度 C ．向左平移2个单位长度，再向上平移5个单位长度D ．向右平移2个单位长度，再向下平移5个单位长度分析：注意先将函数935x y =⨯+转化为235x t +=+，再利用图象の平移规律进行判断．解：∵293535x x y +=⨯+=+，∴把函数3x y =の图象向左平移2个单位长度，再向上平移5个单位长度，可得到函数935x y =⨯+の图象，故选（C ）． 评注：用函数图象解决问题是中学数学の重要方法，利用其直观性实现数形结合解题，所以要熟悉基本函数の图象，并掌握图象の变化规律，比如：平移、伸缩、对称等． 习题1、比较下列各组数の大小： （1）若 ，比较 与 ； （2）若 ，比较 与 ； （3）若 ，比较与；（4）若 ，且，比较a 与b ； （5）若 ，且，比较a 与b ．解：（1）由 ，故 ，此时函数为减函数．由，故 ．（2）由 ，故．又 ，故 ．从而 ． （3）由 ，因，故．又，故．从而．（4）应有．因若，则．又，故 ，这样 ．又因，故 ．从而 ，这与已知 矛盾． （5）应有．因若，则．又，故，这样有．又因 ，且 ，故 ．从而 ，这与已知矛盾．小结：比较通常借助相应函数の单调性、奇偶性、图象来求解．2，曲线 分别是指数函数,和の图象,则 与1の大小关系是 ( ).(分析:首先可以根据指数函数单调性,确定,在 轴右侧令,对应の函数值由小到大依次为 ,故应选 .小结:这种类型题目是比较典型の数形结合の题目,第(1)题是由数到形の转化,第(2)题则是由图到数の翻译,它の主要目の是提高学生识图,用图の意识. 求最值3，求下列函数の定义域与值域.(1)y ＝231-x ; (2)y ＝4x +2x+1+1.解：(1)∵x-3≠0，∴y ＝231-x の定义域为｛x ｜x ∈R 且x ≠3｝.又∵31-x ≠0，∴231-x ≠1，∴y ＝231-x の值域为｛y ｜y>0且y ≠1｝.(2)y ＝4x +2x+1+1の定义域为R.∵2x >0,∴y ＝4x +2x+1+1＝(2x )2+2·2x +1＝(2x +1)2>1.∴y ＝4x +2x+1+1の值域为｛y ｜y>1｝.4，已知-1≤x ≤2,求函数f(x)=3+2·3x+1-9x の最大值和最小值解：设t=3x ,因为-1≤x ≤2，所以931≤≤t ，且f(x)=g(t)=-(t-3)2+12,故当t=3即x=1时，f(x)取最大值12，当t=9即x=2时f(x)取最小值-24。
高中数学指数函数的性质及相关题目解析
高中数学指数函数的性质及相关题目解析一、指数函数的定义与性质指数函数是高中数学中重要的一类函数，它的定义形式为$f(x)=a^x$，其中$a$为常数且$a>0$且$a\neq 1$。
指数函数具有以下几个性质：1. 定义域和值域：指数函数的定义域为全体实数，值域为正实数集$(0,+\infty)$。
2. 增减性：当$a>1$时，指数函数是递增函数；当$0<a<1$时，指数函数是递减函数。
3. 对称性：指数函数关于$y$轴对称。
4. 连续性：指数函数在其定义域上连续。
5. 无界性：当$a>1$时，指数函数在$x\to-\infty$时趋于0；当$0<a<1$时，指数函数在$x\to+\infty$时趋于0。
二、指数函数的常见题型及解析1. 指数函数的图像与性质题目：已知函数$f(x)=2^x$，求函数$f(x)$的图像及其性质。
解析：我们可以通过计算$f(x)$在不同$x$值上的函数值，绘制出函数$f(x)$的图像。
例如，当$x=-2$时，$f(x)=2^{-2}=\frac{1}{4}$；当$x=-1$时，$f(x)=2^{-1}=\frac{1}{2}$；当$x=0$时，$f(x)=2^0=1$；当$x=1$时，$f(x)=2^1=2$；当$x=2$时，$f(x)=2^2=4$。
根据这些函数值，我们可以绘制出函数$f(x)$的图像。
同时，根据指数函数的性质，我们可以得出以下结论：函数$f(x)=2^x$是递增函数，对称于$y$轴，定义域为全体实数，值域为正实数集$(0,+\infty)$。
此外，由于$a>1$，所以函数$f(x)$在$x\to-\infty$时趋于0。
2. 指数函数的性质应用题题目：已知指数函数$f(x)=2^x$，若$f(a)=8$，求实数$a$的值。
解析：根据题目中已知条件$f(a)=8$，我们可以得到方程$2^a=8$。
由指数函数的性质可知，$2^3=8$，因此$a=3$。
专题4.2 指数函数(解析版)
专题4.2指数函数1、指数函数的概念：一般地，函数xy a 叫做指数函数，其中x是自变量，函数的定义域为R．注意：指数函数的底数的取值范围，底数不能是负数、零和1．即a>0且a≠12、指数函数的图象和性质0<a<1a>1定义域R,值域（0，+∞）(2)在R上是增函数注意：指数增长模型：y=N(1+p)x指数型函数：y=ka x3考点：（1）a b=N,当b>0时，a,N在1的同侧；当b<0时，a,N在1的异侧。
（2）指数函数的单调性由底数决定的，底数不明确的时候要进行讨论。
掌握利用单调性比较幂的大小，同底找对应的指数函数，底数不同指数也不同插进1(=a0)进行传递或者利用（1）的知识。
（3）求指数型函数的定义域可将底数去掉只看指数的式子，值域求法用单调性。
（4）分辨不同底的指数函数图象利用a 1=a ，用x=1去截图象得到对应的底数。
一、单选题1．若函数()21xy m m m =--⋅是指数函数，则m 等于（）A ．1-或2B ．1-C ．2D ．12【答案】C【解析】由题意可得21101m m m m ⎧--=⎪>⎨⎪≠⎩，解得2m =.故选：C.2．函数11x y a -=+，（0a >且1a ≠）的图象必经过一个定点，则这个定点的坐标是（）A ．()0,1B ．()1,2C ．()2,3D ．()3,4【答案】B【解析】解：令10x -=，解得1x =，所以当1x =时，10112x y a a -=+=+=，所以函数11x y a -=+过定点()1,2.故选：B3．若函数()22x xf x a x -=+⋅-为R 上的奇函数，则实数a 的值为（）A ．1-B ．2-C ．1D ．2【答案】A【解析】函数()22x xf x a x -=+⋅-为R 上的奇函数,故()010f a =+=，得1a =-，当1a =-时，()22x xf x x --=-满足()()f x f x -=-，即此时()22x xf x x --=-为奇函数，故1a =-，故选：A4．已知()f x 是定义在R 上的奇函数，且(4)()f x f x +=，当(0,2)x ∈时，()2x f x =，则()2021f -=（）A ．2B ．－2C ．0D【答案】B【解析】由题意，()f x 的周期为4，又()f x 是定义在R 上的奇函数，所以(2021)(2021)(45051)(1)2f f f f -=-=-⨯+=-=-．故选：B ．5．已知f (x )=22,5(3),5x x x f x x ⎧-≥⎨+<⎩，则f (4)+f (-4)=（）A ．63B ．83C ．86D ．91【答案】C【解析】依题意，当x <5时，f (x )=f (x +3)，于是得f (-4)=f (-1)=f (2)=f (5)，f (4)=f (7)，当x ≥5时，f (x )=2x -x 2，则f (5)=25-52=7，f (7)=27-72=79，所以f (4)+f (-4)=86.故选：C6．函数()()32sin 1x xe x xf x e -=+的图象大致为（）A ．BC．D【答案】A【解析】由题意，得()()332sin sin 1x x x xe x x x xf x e e e---==++，所以()()3sin x x f x x e e x f x --+==-+-，所以()f x 是奇函数，其图象关于原点对称，所以排除B ，D ．又因为33ππππ6666ππ1πsin π662606f e ee e--⎛⎫⎛⎫-- ⎪ ⎪⎛⎫⎝⎭⎝⎭==> ⎪⎝⎭++，()()32π2πsin 2π2π2π0f e e--=<+，所以排除C ．故选：A7．若221333111,,252a b c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则a ､b ､c 的大小关系是（）A ．b a c <<B ．b c a <<C ．c a b<<D ．c b a<<【答案】A【解析】因为23y x =在(0,)+∞上单调递增，且1125>，所以22331125⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，即a b >，因为12xy ⎛⎫= ⎪⎝⎭在R 上单调递减，且2133>，所以21331122⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，即c a >，所以c a b >>，即b a c <<故选：A 8．设函数()f x 对任意的x ∈R ，都有()()f x f x -=，()()2f x f x -=-，且当[]1,0x ∈-时，()2x f x =，则()2022f =（）A ．1-B ．1C ．12D ．12-【答案】A【解析】由()()2f x f x -=-得()()()222+-=-+=f x f x f x ，所以()()()42-+=+=-f x f x f x ，即()()4f x f x +=，所以()f x 的周期为4，()()()2022505422=⨯+=f f f ，由()()2f x f x -=-得()()022221-=-==f f ，所以()21f =-.故选：A.9．()f x 是定义域为R 的函数，且2()f x x -为奇函数，()2x f x +为偶函数，则(2)f 的值是（）A ．178B ．174C ．478D ．474【答案】A【解析】由题意，222()((()))f x x x f x f x x =--=----，即2()()2f x f x x -+=，(22))(x x f x f x -=++-，即()22()x x f x f x --=--，所以22(2)22x x f x x -=+-，可得2112)2(x x f x x ----=+，故2212122217(2)8f ----==+.故选：A.10．若2||()2x f x x =+，则下列关系式一定成立的是（）A ．()(3)()f f f e π>->B ．(3)()()f f f e π->>C ．()(3)()f e f f π>->D ．()()(3)f e f f π>>-【答案】A【解析】由2||()2x f x x =+可知：()()f x f x -=，()f x ∴为偶函数，又2222,0()22,0x xxx x f x x x x -⎧+≥=+=⎨+<⎩,知()f x 在(,0]-∞上单调递减，在[0,)+∞上单调递增，故()(3)(3)(e)f f f f π>=->，故选：A.11．已知函数()f x 是定义在R 上的偶函数，当0x ≥时，()21xf x x =+-，则不等式()12f x -<的解集为（）A ．()0,2B ．(),2-∞C ．()2,+∞D ．()(),02,-∞+∞【答案】A【解析】当0x ≥时，()21xf x x =+-，则()f x 在[)0,∞+上单调递增，又函数()f x 是R 上的偶函数，且(1)2f =，因此，()()()121111f x f x f x -⇔-⇔-<，解得02x <<，所以不等式()12f x -<的解集为()0,2.故选：A12．已知函数()22,12,1xx ax a x f x x ⎧-+-≤=⎨>⎩在R 上单调递增，则实数a 的取值范围是（）A ．(],1-∞B ．[]1,3C ．[)3,+∞D ．(][),13,-∞⋃+∞【答案】B【解析】∵()22,12,1x x ax a x f x x ⎧-+-≤=⎨>⎩在R 上单调递增，∴21122a a a ≥⎧⎨-+-≤⎩，解得13a ≤≤.故选：B.13．函数1()(2f x =）A ．1,2⎛⎤-∞ ⎥⎝⎦B ．12⎤⎥⎝⎦C ．12⎡⎢⎣⎦D ．1,2⎡⎫+∞⎪⎢⎣⎭【答案】C【解析】依题意，210x x -++≥，解得：1122x ≤≤，即()f x 定义域为11[,]22，令u =，则函数u =在11[]22上单调递增，在11[,]22上单调递减，而函数1()2u y =在R 上单调递减，因此，()f x 在151[]22上单调递减，在11[,]22上单调递增，所以函数1()(2f x =1[2.故选：C14．已知函数()1424x x f x +=-+，[]1,1x ∈-，则函数()y f x =的值域为（）．A ．[)3,+∞B ．[]3,4C ．133,4⎡⎤⎢⎥⎣⎦D ．13,44⎡⎤⎢⎥⎣⎦【答案】B 依题意，函数()2)(2224x xf x =-⨯+，[]1,1x ∈-，令2x t =，则2x t =在[]1,1x ∈-上单调递增，即122t ≤≤，于是有2224(1)3y t t t =-+=-+，当1t =时，min 3y =，此时0x =，min ()3f x =，当2t =时，max 4y =，此时1x =，max ()4f x =，所以函数()y f x =的值域为[]3,4.故选：B15．函数2()f x x x =-，+1()42x x g x m =-+，若对1[1,2]x ∀∈，都存在2[1,1]x ∈-，使()()12f x g x >成立，则m 的取值范围是（）A ．0m <B ．1m <C ．2m <D ．3m <【答案】B【解析】若对1[1,2]x ∀∈，都存在2[1,1]x ∈-，使()()12f x g x >成立，则需()()min min >f x g x ，又2()f x x x =-，[1,2]x ∈，所以()()2min 1110f x f =-==，令2x t =，因为[1,1]x ∈-，所以1[,2]2t ∈，所以()2()211g x t t m g m =-+≥=-，所以0>1m -，解得1m <，则m 的取值范围是1m <，故选：B.【点睛】结论点睛：本题考查不等式的恒成立与有解问题，可按如下规则转化：一般地，已知函数()[],,y f x x a b =∈，()[],,y g x x c d =∈（1）若[]1,x a b ∀∈，[]2,x c d ∀∈，总有()()12f x g x <成立，故()()2max min f x g x <；（2）若[]1,x a b ∀∈，[]2,x c d ∃∈，有()()12f x g x <成立，故()()2max max f x g x <；（3）若[]1,x a b ∃∈，[]2,x c d ∃∈，有()()12f x g x <成立，故()()2min min f x g x <；（4）若[]1,x a b ∀∈，[]2,x c d ∃∈，有()()12f x g x =，则()f x 的值域是()g x 值域的子集．二、多选题16．已知函数()33x xf x -=-，则（）A ．()f x 的值域为RB ．()f x 是R 上的增函数C ．()f x 是R 上的奇函数D ．()f x 有最大值【答案】ABC【解析】()()30,x g x ∞=∈+，而()()3,0xh x ∞-=-∈-，所以()33x x f x -=-值域为R ，A 正确，D 错误；因为()3x g x =是递增函数，而()3x h x -=-是递增函数，所以()33x xf x -=-是递增函数，B正确；因为定义域为R ，且()()33x xf x f x --=-=-，所以()f x 是R 上的奇函数，C 正确；故选：ABC17．已知函数13()13xxf x -=+，则下列结论正确的有（）A ．()f x 的图象关于坐标原点对称B ．()f x 的图象关于y 轴对称C ．()f x 的最大值为1D ．()f x 在定义域上单调递减【答案】AD【解析】因为1331()()1331x x x x f x f x -----===-++，所以()f x 为奇函数，图象关于坐标原点对称，故A 正确；因为131(1)132f -==-+，1113(1)1213f --==+，(1)(1)f f ≠-，所以()f x 不是偶函数，图象不关于y 轴对称，故不B 正确；因为3122()13131x x xf x +-=-=-+++，又30x >，所以311x +>，所以20231x <<+，所以()(1,1)f x ∈-，故C 不正确；因为3122()13131x x xf x +-=-=-+++，且3x y =为增函数，所以()f x 在定义域(,)-∞+∞上单调递减，故D 正确.故选：AD18．下列结论中，正确的是（）A ．函数12x y -=是指数函数B ．函数2213x xy -+⎛⎫= ⎪⎝⎭的单调增区间是()1,+∞C ．若(0,1)m n a a a a >>≠则m n>D ．函数2()3(0,1)x f x a a a -=->≠的图像必过定点(2,2)-【答案】BD【解析】由指数函数定义得函数12x y -=不是指数函数，A 错；函数2213x xy -+⎛⎫= ⎪⎝⎭中，222(1)1u x x x =-+=--+，在(,1)-∞上递增，在(1,)+∞上递减，因此函数2213x xy -+⎛⎫= ⎪⎝⎭的单调增区间是()1,+∞，B 正确；01a <<时，由m n a a >得m n <，C 错；函数2()3(0,1)x f x a a a -=->≠中，由20x -=得2x =，(2)2f =-，即函数()f x 图象过点(2,2)-，D 正确．故选：BD ．19．已知函数21()21x xf x -=+，则下列结论正确的是（）A ．函数()f x 的定义域为RB ．函数()f x 的值域为(1,1)-C ．函数()f x 的图象关于y 轴对称D ．函数()f x 在R 上为增函数【答案】ABD【解析】A ：因为20x >，所以函数()f x 的定义域为R ，因此本选项结论正确；B ：212()12121x x xf x -==-++，由12220211012011212121x xx x x >⇒+>⇒<<⇒-<-<⇒-<-<+++，所以函数()f x 的值域为(1,1)-，因此本选项结论正确；C ：因为2112()()2112x xxxf x f x -----===-++，所以函数()f x 是奇函数，其图象关于原点对称，不关于y 轴对称，因此本选项说法不正确；D ：因为函数21x y =+是增函数，因为211x y =+>，所以函数221x y =+是减函数，因此函数2()121x f x =-+是增函数，所以本选项结论正确，故选：ABD20．已知()f x ，()g x 都是定义在R 上的函数，其中()f x 是奇函数，()g x 为偶函数，且()()2x f x g x +=，则下列说法正确的是（）A ．()()f g x 为偶函数B ．()00g =C ．()()22f xg x -为定值D ．()()2,02,0x xx f x g x x -⎧≥+=⎨<⎩【答案】ACD【解析】()()2xf xg x +=令x 为x -得()()2x f x g x --+-=即()()2xf xg x --+=解得()222x x g x -+=，()222x xf x --=对于A.()()()()f g g x x f -=，故()()f g x 为偶函数对于B.()01g =，故B 错C.()()22222222122x x x x f x g x --⎛⎫⎛⎫+--= ⎪ ⎪⎝⎝⎭-=⎭，故C 对D.当0x ≥时，()222x x f x --=，()()2222222x x x xxf xg x ---++=+当0x <时，()222x x f x --=，()()2222222x x x xxf xg x ----++=()()2,02,0x xx f x g x x -⎧≥+=⎨<⎩故D 对故选：ACD三、填空题21．已知函数()312xf x x ⎛⎫=- ⎪⎝⎭，若()()211f a f a +>-，则实数a 的取值范围是___.【答案】(),2-∞-【解析】：12xy ⎛⎫= ⎪⎝⎭和3y x =-在R 上都是单调递减，()312xf x x ⎛⎫∴=- ⎪⎝⎭在R 上单调递减，∴由()()211f a f a +>-，可得211a a +<-，解得2a <-，即(),2a ∈-∞-．故答案为：(),2-∞-22．已知函数()()12xf xg x =+-为定义在R 上的奇函数，则()()()012g g g ++=____.【答案】72或3.5【解析】因为()f x 是定义在R 上的奇函数，所以()()f x f x =--，特别地，当0x =时，得到()00f =．由()()12xf xg x =+-取0x =，所以()()011f g =-，所以()11g =．再分别令1x =-和1x =，得()()1102f g --=-，()()122f g =-，两式相加得()()()()1110222f f g g --+=-+-，且()()110f f -+=，则()()02g g +52=，所以()()()012g g g ++=57122+=．故答案为：72.23．已知()f x 是定义在R 上的奇函数，且()()4f x f x +=，当()0,2x ∈时，()2xf x =，则()9f -=___________.【答案】2-【解析】：因为()()4f x f x +=，所以函数()f x 是以4为周期的周期函数，又因()f x 是定义在R 上的奇函数，所以()()()9912f f f -=-=-=-.故答案为：2-.24．设不等式()44210x x xm -++≥对于任意的[]0,1x ∈恒成立，则实数m 的取值范围是_______．【答案】1,3⎛⎤-∞ ⎥⎝⎦【解析】：由()44210x x x m -++≥，得()4214x x xm ++≤，即4111421124x x x x xm ≤=++++，[]0,1x ∈，11,122x ⎡⎤∴∈⎢⎥⎣⎦，则221111371,3222244x x x ⎛⎫⎛⎫⎡⎤++=++∈ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，114,1137124x x ⎡⎤∴∈⎢⎥⎣⎦++，则13m ≤，即1,3m ⎛⎤∈-∞ ⎥⎝⎦．故答案为：1,3⎛⎤-∞ ⎥⎝⎦四、解答题25．已知定义在()1,1-上的奇函数()f x ．在()1,0x ∈-时，()22x xf x -=+．(1)试求()f x 的表达式；(2)若对于()0,1x ∈上的每一个值，不等式()241x xt f x <⋅⋅-恒成立，求实数t 的取值范围．【答案】(1)()()()221,000220,1x x x x x f x x x --⎧+∈-⎪==⎨⎪--∈⎩(2)0t ≥【解析】(1)：()f x 是定义在()1,1-上的奇函数，()00f ∴=，因为在()1,0x ∈-时，()22x xf x -=+，设()0,1x ∈，则()1,0x -∈-，则()()()22x xf x f x -=--=-+，故()()()221,000220,1x x x x x f x x x --⎧+∈-⎪==⎨⎪--∈⎩.(2)：由题意，()241x x t f x <⋅⋅-可化为()22241x x x xt --<⋅⋅--化简可得4141x x t -+>+，令()41214141x x xg x -+==-+++，()0,1x ∈，因为41x y =+在定义域()0,1上单调递增，2y x=在()2,5上单调递减，所以()g x 在()0,1上单调递减，()()0201041g x g ∴<=-+=+，故0t ≥．26．已知函数()()()313x xf x m m R -=--∈是定义域为R 的奇函数.(1)若集合(){}|0A x f x =≥，|0x m B x x m -⎧⎫=<⎨⎬+⎩⎭，求A B ；(2)设()()22332x xg x af x -=+-，且()g x 在[)1,+∞上的最小值为-7，求实数a 的值.【答案】(1){}|02A B x x =≤<(2)3a =【解析】(1)解：因为()f x 是定义域为R 的奇函数，所以()00f =，可得2m =，当2m =时，()33x x f x -=-，所以()33x xf x --=-，()()f x f x -=-，所以()33x x f x -=-为奇函数，所以2m =；由()0f x ≥，得1303xx -≥，即23103x x -≥，因为30x >，所以2310x -≥，所以0x ≥，即{}|0A x x =≥；由0x mx m-<+，且2m =，得()()220x x -+<，即22x -<<，所以{}|22B x x =-<<，所以{}|02A B x x =≤<；(2)因为()()2233233x x x xg x a --=+--，()()2332332x x x x a --=---+，令33x x t -=-，因为1≥x ，所以83t ≥，所以()()()22282223g x t t at t a a t ϕ⎛⎫==-+=-+-≥ ⎪⎝⎭，当83a >时，()t ϕ在8,3a ⎡⎤⎢⎥⎣⎦上为减函数，在[),a +∞上为增函数，所以()()2min 2t a a ϕϕ==-，即()2min 2g x a =-，所以227a -=-，解得3a =，或3a =-（舍去）；当83a ≤时，()t ϕ在8,3⎡⎫+∞⎪⎢⎣⎭上为增函数，所以()min 88216393at ϕϕ⎛⎫==- ⎪⎝⎭，即()min 821693a g x =-，所以8216793a -=-，解得1458483a =>（舍去），所以3a =.27．已知定义在[]2,2-上的奇函数()f x ，当[]2,0x ∈-时，函数解析式为()()193x x f x a a -=+⋅∈R ．(1)求a 的值，并求出()f x 在[]2,2-上的解析式；(2)若对任意的(]0,2x ∈，总有()22f x t t ≥-，求实数t 的取值范围．【答案】(1)-3，()93,2039,02x x x xx f x x --⎧--≤≤=⎨-<≤⎩；(2)[]0,2.【解析】(1)根据题意，()f x 是定义在[]2,2-上的奇函数，则有()00=f ，当[]2,0x ∈-时()193x x f x a -=+⋅，则()10103f a =+=，解得：3a =-，当[]2,0x ∈-时，()93x xf x =-，设(]0,2x ∈，则[)2,0x -∈-，则()93x xf x ---=-，又()f x 为奇函数，所以()()39x xf x f x --=--=-，综上，()93,2039,02x x x xx f x x --⎧--≤≤=⎨-<≤⎩，(2)由（1），(]0,2x ∈时，()2113933xxx x f x --⎛⎫=-=- ⎪⎝⎭，设13x m =，则119m ≤<，则原函数可化为：()221124m m m m ϕ⎛⎫=-=--+ ⎪⎝⎭，由18981ϕ⎛⎫= ⎪⎝⎭，()10ϕ=知：()0f x >在(]0,2上恒成立，要使()22f x t t ≥-在(]0,2x ∈上恒成立，只需220t t -≤，解得：02t ≤≤，所以t 的取值范围为[]0,2．28．已知函数()1221xx f x -=+.(1)求()()22f f -+的值；(2)求函数()f x 的值域；(3)若()()24221x a g x f x a ⎡⎤=-+⎣⎦+，且对任意的1x 、2x ∈R ，都有()()123g x g x -<，求实数a 的取值范围.【答案】(1)0；(2)()1,1-；(3)11a ≤.【解析】(1)：()()22221112121433422012121415514f f -------+==+=-=++++.(2)解：()()212212121x x x f x -++==-++.20x >，则211x +>，则20221x<<+，所以，211121x-<-<+，∴函数()f x 的值域为()1,1-.(3)解：()()()()()2224222122121x x a g x f x a f x a f x af x ⎛⎫⎡⎤⎡⎤⎡⎤=-+=--=- ⎪⎣⎦⎣⎦⎣⎦++⎝⎭，令()t f x =，则()()22g x h t t at ==-，()1,1t ∈-，函数()h t 的对称轴为直线t a =.①当1a ≥时，函数()h t 在()1,1-上单调递减，()()()()12113g x g x h h ∴-<--≤，()()12123a a ∴+--≤，解得34a ≤，此时a 的取值不存在；②当1a ≤-时，函数()h t 在()1,1-上单调递增，()()()()12113g x g x h h ∴-<--≤，()()12123a a ∴--+≤，解得34a ≥-，此时a 的取值不存在；③当11a -<<时，函数()h t 在()1,a -上单调递减，在(),1a 上单调递增，()()()()121g x g x h h a ∴-<--，且()()()()121g x g x h h a -<-，所以，()()()()2211231123h h a a a h h a a a ⎧--=++≤⎪⎨-=-+≤⎪⎩，解得11a ≤≤，此时11a -≤.综上，实数a 的取值范围为11a ≤≤.29．设函数()()2x xf x a k a -=-+（0a >且1a ≠）是定义域为R 的奇函数．(1)求实数k 的值；(2)若()312f =，()()222x xg x a a mf x -=+-，且当[)1,x ∞∈+时，()0g x ≥恒成立，求实数m的取值范围．【答案】(1)1-(2)1712m ≤【解析】(1)函数()()2x xf x a k a -=-+（0a >且1a ≠）是定义域为R 的奇函数,则()()()0002120f a k a k =-+=-+=，所以1k =-，又1k =-时，()x xf x a a -=-，对任意的R x ∈，都有()()()x x x x f x a a a a f x ---=-=--=-成立，满足题意，所以1k =-；(2)由（1）知，()x xf x a a -=-，且()312f =，所以，()1312f a a =-=，所以，2a =或12a =-（舍），()()()()22222222222222x x x x x xx x g x m m ----=+--=---+令()221x xt x -=-≥，则32t ≥，由当[)1,x ∞∈+时，()0g x ≥恒成立，得2220t mt -+≥在32t ≥时恒成立，则22m t t ≤+在时32t ≥恒成立，又2y t t =+在3,2⎡⎫+∞⎪⎢⎣⎭上单调递增，所以，1726m ≤，所以，1712m ≤.。
指数函数典型例题详细解析
指数函数·例题解析第一课时【例1】（基础题）求下列函数的定义域与值域：(1)y 3(2)y (3)y 12x＝＝＝-+---213321x x解 (1)定义域为{x|x ∈R 且x ≠2}．值域{y|y ＞0且y ≠1}． (2)由2x+2－1≥0，得定义域{x|x ≥－2}，值域为{|y|y ≥0}． (3)由3－3x-1≥0，得定义域是{x|x ≤2}，∵0≤3－3x －1＜3，∴值域是≤＜．0y 31.指数函数Y=ax （a>0且a ≠1）的定义域是R ，值域是（0，+∞）2. 求定义域的几个原则：①含根式（被开方数不为负）②含分式，分母不为０③形如a0,(a ≠ 0)3. 求函数的值域:①利用函数Y=ax 单调性②函数的有界性(x2≥0;ax>0)③换元法.如:y=4x+6×2x-8(1≤x ≤2) 先换元,再利用二次函数图象与性质(注意新元的范围)【例2】（基础题）指数函数y ＝a x ，y ＝b x ，y ＝c x ，y ＝d x 的图像如图2．6－2所示，则a 、b 、c 、d 、1之间的大小关系是[ ]A ．a ＜b ＜1＜c ＜dB ．a ＜b ＜1＜d ＜cC ． b ＜a ＜1＜d ＜cD ．c ＜d ＜1＜a ＜b解 选(c)，在x 轴上任取一点(x ，0)，则得b ＜a ＜1＜d ＜c ．【例3】（基础题）比较大小：(1)2(2)0.6、、、、的大小关系是：．248163235894512--()(3)4.54.1________3.73.6解(1)y 221()x ∵，，，，，函数＝，＞，该函数在－∞，＋∞上是增函数，又＜＜＜＜，∴＜＜＜＜．222242821621338254912284162123135258389493859=====解 (2)0.6110.6∵＞，＞，∴＞．----451245123232()() 解 (3)借助数4.53.6打桥，利用指数函数的单调性，4.54.1＞4.53.6，作函数y 1＝4.5x ，y 2＝3.7x 的图像如图2．6－3，取x ＝3.6，得4.53.6＞3.73.6∴ 4.54.1＞3.73.6．说明 如何比较两个幂的大小：若不同底先化为同底的幂，再利用指数函数的单调性进行比较，如例2中的(1)．若是两个不同底且指数也不同的幂比较大小时，有两个技巧，其一借助1作桥梁，如例2中的(2)．其二构造一个新的幂作桥梁，这个新的幂具有与4.54.1同底与3.73.6同指数的特点，即为4.53.6(或3.74.1)，如例2中的(3)．例题4（中档题）【例4】解比较大小与＞且≠，＞．当＜＜，∵＞，＞，a a a aan n n n n n nn n nn n -+-+-=-11111111(a 0a 1n 1)0a 1n 10()()∴＜，∴＜当＞时，∵＞，＞，∴＞，＞aa a n n aa a n n n n n n n n n n n n 1111111111()()()--+--+-1a 1n 101【例5】（中档题）作出下列函数的图像：图像变换法(1)y (2)y 22x ＝＝－，()121x +(3)y ＝2|x-1|(4)y ＝|1－3x |解 (1)y (264)(0)(11)y 1＝的图像如图．－，过点，及－，．是把函数＝的图像向左平移个单位得到的．()()1212121x x+解 (2)y ＝2x －2的图像(如图2．6－5)是把函数y ＝2x 的图像向下平移2个单位得到的．解(3)利用翻折变换，先作y＝2|x|的图像，再把y＝2|x|的图像向右平移1个单位，就得y＝2|x-1|的图像(如图2．6－6)．解(4)作函数y＝3x的图像关于x轴的对称图像得y＝－3x的图像，再把y＝－3x的图像向上平移1个单位，保留其在x轴及x轴上方部分不变，把x轴下方的图像以x轴为对称轴翻折到x轴上方而得到．(如图2．6－7)例6（中档题）：用函数单调性定义证明：当a ＞1时，y = a x是增函数.【解析】设x 1，x 2∈R 且x 1＜x 2，并令x 2 = x 1 + h (h ＞0，h ∈R)，很独特的方式 则有)1(11112-=-=-+h x x h x x x a a a a a a ， ∵a ＞1，h ＞0，∴1,01>>h x a a ， ∴012>-x x a a ，即故y = a x (a ＞1)为R 上的增函数，同理可证0＜a ＜1时，y = a x 21x x a a <是R 上的减函数.【例6】解求函数＝的单调区间及值域．令＝－＋，则＝是关于的减函数，而＝－－＋y u x 5x 6y u u x 5xx 25x 622()()3434u＋在∈∞，上是减函数，在∈，∞上是增函数．∴函数＝的单调增区间是∞，，单调减区间是，∞．－＋6x x y x 25x 6(][)()(][)-+-+5252345252又∵＝－＋＝≥，函数＝，在∈，∞上是减函数，所以函数＝的值域是，．－＋u x 5x 6y u y 2x 25x 6()()[)()(]x u ----+5214143414340108324例题7 中档题）指数函数与二次函数的复合函数(由内到外分析） 二次函数为内层函数，指数函数为外层函数变式1 求函数y=（21）xx 22-的单调区间，并证明之.解法一（在解答题）：在R 上任取x 1、x 2，且x 1＜x 2，则12y y =12122222)21()21(x x x x --=（21）（x 2－x 1）（x 2+x 1－2） 【（21）为底数，红色部分为指数】 ，∵x 1＜x 2，∴x 2－x 1＞0.当x 1、x 2∈（－∞，1］时，x 1+x 2－2＜0.这时（x 2－x 1）（x 2+x 1－2）＜0，则12y y ＞1.∴y 2＞y 1，函数在（－∞，1］上单调递增.当x 1、x 2∈［1，+∞）时，x 1+x 2－2＞0，这时（x 2－x 1）（x 2+x 1－2）＞0，即12y y ＜1.（此处点评：上述证明过程中，在对商式正负判断时，利用了指数函数的值域及单调性）∴y 2＜y 1，函数在［1，+∞上单调递减.综上，函数y 在（－∞，1］上单调递增，在［1，+∞）上单调递减.合作探究：在填空、选择题中用上述方法就比较麻烦，因此我们可以考虑用复合函数的单调性来解题.解法二、在填空、选择题中（用复合函数的单调性）：设：x x u 22-=则：uy ⎪⎭⎫⎝⎛=21对任意的211x x <<，有21u u <，又∵uy ⎪⎭⎫⎝⎛=21是减函数∴21y y < ∴xx y 2221-⎪⎭⎫ ⎝⎛=在),1[+∞是减函数对任意的121≤<x x ，有21u u >又∵uy ⎪⎭⎫⎝⎛=21是减函数∴21y y < ∴xx y 2221-⎪⎭⎫ ⎝⎛=在),1[+∞是增函数在该问题中先确定内层函数（x x u 22-=）和外层函数（uy ⎪⎭⎫⎝⎛=21）的单调情况，再根据内外层函数的单调性确定复合函数的单调性.变式2 已知0>a 且1≠a ，讨论232)(++-=x x ax f 的单调性.【分析】这是一道与指数函数有关的复合函数讨论单调性题，指数417)23(2322+--=++-x x x ，当x ≥23时是减函数，x ≤23时是增函数， 而)(x f 的单调性又与10<<a 和1>a 两种范围有关，应分类讨论. 【解析】设232u x x =-++2317()24x =--+，则当x ≥23时，u 是减函数， 当x ≤23时，u 是增函数， 又当1>a 时，u a y =是增函数， 当10<<a 时，u a y =是减函数，所以当1>a 时，原函数232)(++-=x x a x f 在),23[+∞上是减函数，在]23,(-∞上是增函数.当10<<a 时，原函数232)(++-=x x a x f 在),23[+∞上是增函数，在]23,(-∞上是减函数.【小结】一般情况下，两个函数都是增函数或都是减函数，则其复合函数是增函数； ；如果两个函数中一增一减，则其复合函数是减函数，但一定注意考虑复合函数的定义域.第二课时例题8：（疑难题）指数函数与二次函数的复合函数换元法 先换元,再利用二次函数图象与性质(注意新元u 的范围)【例7】解求函数＝＋≥的单调区间及它的最大值．＝，令＝，∵≥，∴＜≤，又∵＝是∈，＋∞上的减函数，函数＝y 1(x 0) y u x 00u 1u x 0)y ()()[()]()[()]()()[()141212121121234121212222x x x x x x x u --+=-+-+-3401212121212121412在∈，上为减函数，在，上是增函数．但由＜≤得≥，由≤≤，得≤≤，∴函数＝＋单调增区间是，＋∞，单调减区间，u 1)0x 110x 1y 11)[01](][()()()()[x x x x当x ＝0时，函数y 有最大值为1．内层指数函数u=(1/2)x 为减，当u 在（0，1/2】时，此时外层二次f （u)为减函数，即x 在【1，正无穷大），，则复合函数为增（画草图分析法）点评：（1）指数函数的有界性（值域）：x2≥0; ax>0（2）上述证明过程中，在两次求x 的范围时，逆向利用了指数函数的值域及逆向利用了指数函数的单调性，是关键及疑难点。
指数函数典型例题讲解
指数函数典型例题讲解27的3次方根3273=， 27-的3次方根3273-=-， 32的5次方根2325=， 32-的5次方根2325-=-． 例1．求下列各式的值：（1）()338- （2）()210- （3）()443π- 例2．已知,0<<b a *∈>N n n ,1， 化简：()()n n n n b a b a ++-． 解：当n 是奇数时，原式a b a b a 2)()(=++-=当n 是偶数时，原式a b a a b b a b a 2)()(||||-=--+-=++-=所以，()()n n n n b a b a ++-22a n a n ⎧=⎨-⎩为奇数为偶数．例3．计算：407407-++解：407407-++52)25()25(22=-++=例4．求值：54925-+． 解：54925-+425254549252）（-+=-+= 452622525+=-+=2154152+=+=）（ 例5． 用分数指数幂的形式表示下列各式()a o >：2a 3a .解：2a 11522222a a aa +⋅==；3a =211333a a a ⋅=；=1113322224a a a a ⎛⎫⎛⎫⋅== ⎪ ⎪⎝⎭⎝⎭．例6．计算下列各式的值（式中字母都是正数）．（1）211511336622263a b a b a b ⎛⎫⎛⎫⎛⎫-÷- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭； （2）83184m n -⎛⎫ ⎪⎝⎭；解（1）211511336622263a b a b a b ⎛⎫⎛⎫⎛⎫-÷- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭=()()211115326236263a b+-+-⨯-÷-⎡⎤⎣⎦=044ab a =；（2） 83184m n -⎛⎫ ⎪⎝⎭=883184m n -⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭=2233m m n n -=．例7．计算下列各式：（1）（2)20a >．解：（1）231324555⎛⎫-÷ ⎪⎝⎭=213134245555÷-÷=5512455-= （22=5262132a a a a==．综合应用例1．化简：11555x x x -+++.解：11555x x x -+++=15(1525)x -++=1315x -⨯=3155x⨯. 例2．化简：)()(41412121y x y x -÷-.解：11112244()()x y x y -÷-111111444444()()()x y x y x y =+-÷- 1144x y =+． 评述：此题注重了分子、分母指数间的联系，即21241)(x x =，由此联想到平方差公式的特点，进而使问题得到解决。
职高求指数函数的定义域的例题及解析
职高求指数函数的定义域的例题及解析
【要点梳理】
1.函数的定义域是自变量x的取值集合，函数的值域是因变量y的取值集合，
2.已知函数解析式，求定义域，其主要依据是使函数的解析式有意义，主要形式有：
(1)分式函数，分母不为0；(2)偶次根式函数，被开方数非负数；(3)一次函数、二次函数的这定义域为R:(4)x”中的底数不等于0：(5)指数函数=“的定义域为R:(6)对数函数y=l吧：x的定义域为{x>0；(7)y=nxJ=csx 的定义装约为，
⑧，-的定义装的因+竖e,o= 的定义域均为{x≠知，kE习
3.求抽象函数的定义域：
(1)由y=fx)的定义域为D,求y=f几g(的定义，须解f(x)eD:
(2)由y=f几g(x]的定义域D,求v=fx)的定，.只须解g(x)在D上的值域就是函数y=fx)的定义域
(3)由y=f几gx的定义域D,术y=力的定义域
4.实际问题中的函数的定义域，除了使解析式本身有意义，还要使实际问题有意【例题精析】
考点一函数的定义域
函数的定义域及其求法是近几年高考考查的重点内容之一，这里主要帮助考生灵话掌握求定义域的各种方法，并会应用用函数的定义域解决有关问题。
指数函数典型例题
指数函数典型例题典型例题比较大小例1、比较下列各组数的大小:(1)和 ; (2)和 ;(3)和 ; (4)和 , .分析:当两个幂形数底数相同时,要比较这两个数的大小可根据它们的特征构造相应的指数函数,借助函数的单调性来比较大小.解: (1)在上是减函数,又 ,故< .(2) = ,由的单调性可得, >即> .(3)由 >1而 <1,可知 > .(4)当时, < ,当时, > .小结:此题中第(3)小题的两个数不能看成某个指数函数的两个函数值,此时可以借助一些特殊数如0或1来搭桥间接比较两个数的大小,而(2)小题则可以通过指数运算化为底数相同的两个幂,可构造指数函数来比较大小.根据条件比较字母的大小例1、比较下列各组数的大小：（1）若，比较与；（2）若，比较与；（3）若，比较与；（4）若，且，比较a与b；（5）若，且，比较a与b．分析：设均为正数，则，即比较两个正数的大小，可比较它们的商与1的大小．掌握指数函数的图象规律，还要掌握底的变化对图象形状的影响．这主要有两方面：其一是对；对．用语言叙述即在y轴右侧，底越大其图象越远离x轴；在y轴左侧，底越大，其图象越接近x轴．这部分内容即本题（2），（3）所说的内容．其二是当底均大于1时，底越大，其图象越接近y轴；当底均小于1时，底越小，其图象越接近y轴．一个便于记忆的方法是：若以离1远者为底，则其图象接近y轴．当然这是指底数均大于1或均小于1．这部分内容即本题（4）与（5）．解：（1）由，故，此时函数为减函数．由，故．（2）由，故．又，故．从而．（3）由，因，故．又，故．从而．（4）应有．因若，则．又，故，这样．又因，故．从而，这与已知矛盾．（5）应有．因若，则．又，故，这样有．又因，且，故．从而，这与已知矛盾．小结：比较通常借助相应函数的单调性、奇偶性、图象来求解．根据图象比较底数大小例1、(1)指数函数①②满足不等式 ,则它们的图象是 ( ).分析:此题应首先根据底数的范围判断图象的升降性,再根据两个底数的大小比较判断对应的曲线.解:由可知①②应为两条递减的曲线,故只可能是或 ,进而再判断①②与和的对应关系,此时判断的方法很多,不妨选特殊点法,令 ,①②对应的函数值分别为和 ,由可知应选 .(2)曲线分别是指数函数 ,和的图象,则与1的大小关系是 ( ).(分析:首先可以根据指数函数单调性,确定 ,在轴右侧令 ,对应的函数值由小到大依次为 ,故应选 .小结:这种类型题目是比较典型的数形结合的题目,第(1)题是由数到形的转化,第(2)题则是由图到数的翻译,它的主要目的是提高学生识图,用图的意识.化简例1、已知 ,试把用含的式子表示出来,并化简.分析:此题涉及指数式的变换和分类讨论的使用.解: 由可知 ,= ,当时,若 ,则 ,此时 ,若 ,则 ,此时 .当时, .当时, 若 ,则 ,此时 ,若 ,则 ,此时 .小结:此题中涉及对根式的化简,绝对值的概念及指数函数单调性的使用,特别是对和的讨论要分清楚.利用换元法求最值例1、设，求函数的最大值和最小值．分析：注意到，设，则原来的函数成为，利用闭区间上二次函数的值域的求法，可求得函数的最值．解：设，由知，，函数成为，，对称轴，故函数最小值为，因端点较距对称轴远，故函数的最大值为．小结：换元法是一种常用的数学方法，在涉及指数形式的换元时，经常用到诸如，等．二次函数在有界区间上求最值时，可以借助于图形求解．选题角度：比较大小、根据条件比较字母的大小、根据图象比较底数大小、利用换元法求最值求函数单调区间及值域、求函数的定义域、人口增长、讨论字母求单调区间、指数函数图象的变换。
专题11指数函数(解析版)
专题11指数函数【学习目标】1.掌握指数函数的概念，了解对底数的限制条件的合理性，明确指数函数的定义域；2.掌握指数函数图象：(1)能在基本性质的指导下，用列表描点法画出指数函数的图象，能从数形两方面认识指数函数的性质；(2)掌握底数对指数函数图象的影响； (3)从图象上体会指数增长与直线上升的区别．3.学会利用指数函数单调性来比较大小，包括较为复杂的含字母讨论的类型；4.通过对指数函数的概念、图象、性质的学习，培养观察、分析归纳的能力，进一步体会数形结合的思想方法；5.通过对指数函数的研究，要认识到数学的应用价值，更善于从现实生活中发现问题，解决问题．【考点梳理】考点一、指数函数的概念：函数y=a x(a>0且a ≠1)叫做指数函数，其中x 是自变量，a 为常数，函数定义域为R. 【微点拨】：（1）形式上的严格性：只有形如y=a x(a>0且a ≠1)的函数才是指数函数．像23xy =⋅，12xy =，31x y =+等函数都不是指数函数．（2）为什么规定底数a 大于零且不等于1：①如果0a =，则000x x ⎧>⎪⎨≤⎪⎩xx时，a 恒等于，时,a 无意义.②如果0a <，则对于一些函数，比如(4)xy =-，当11,,24x x ==⋅⋅⋅时，在实数范围内函数值不存在．③如果1a =，则11xy ==是个常量，就没研究的必要了．考点二、指数函数的图象及性质：y=a x0<a<1时图象a>1时图象性质①定义域R ，值域 （0，+∞）②a 0=1, 即x=0时，y=1，图象都经过(0，1)点③a x=a ，即x=1时，y 等于底数a④在定义域上是单调减函数④在定义域上是单调增函数⑤x<0时，a x >1 x>0时，0<a x <1⑤x<0时，0<a x<1 x>0时，a x>1⑥ 既不是奇函数，也不是偶函数【微点拨】：（1）当底数大小不定时，必须分“1a >”和“01a <<”两种情形讨论． （2）当01a <<时，,0x y →+∞→；当1a >时,0x y →-∞→． 当1a >时，a 的值越大，图象越靠近y 轴，递增速度越快． 当01a <<时，a 的值越小，图象越靠近y 轴，递减的速度越快．（3）指数函数xy a =与1xy a ⎛⎫= ⎪⎝⎭的图象关于y 轴对称．考点三、指数函数底数变化与图像分布规律 （1）①x y a = ②x y b = ③x y c = ④x y d =则：0＜b ＜a ＜1＜d ＜c又即：x ∈(0,+∞)时，x x x x b a d c <<< （底大幂大） x ∈(－∞,0)时，x x x x b a d c >>> （2）特殊函数112,3,(),()23x x x x y y y y ====的图像：考点四、指数式大小比较方法(1)单调性法：化为同底数指数式，利用指数函数的单调性进行比较. (2)中间量法 (3)分类讨论法 (4)比较法比较法有作差比较与作商比较两种，其原理分别为：①若0A B A B ->⇔>；0A B A B -<⇔<；0A B A B -=⇔=； ②当两个式子均为正值的情况下，可用作商法，判断1A B >，或1AB<即可． 【典型例题】类型一、函数的定义域、值域 例1．求下列函数的定义域、值域.(1)313x xy =+；(2)y=4x -2x+1；(3)21139x --；(4)211xx y a -+=(a 为大于1的常数)【答案】（1）R ，(0，1)；（2）R [+∞,43)；（3）1,2⎡⎫-+∞⎪⎢⎣⎭[)0,+∞；（4）(-∞，-1)∪[1，+∞)[1，a)∪(a ，+∞)【解析】(1)函数的定义域为R (∵对一切x ∈R ，3x≠-1).∵ (13)1111313x x xy +-==-++，又∵ 3x >0， 1+3x>1， ∴ 10113x <<+， ∴ 11013x-<-<+， ∴ 101113x<-<+， ∴值域为(0，1).(2)定义域为R ，43)212(12)2(22+-=+-=xxx y ，∵ 2x >0， ∴ 212=x 即 x=-1时，y 取最小值43，同时y 可以取一切大于43的实数，∴ 值域为[+∞,43).(3)要使函数有意义可得到不等式211309x --≥，即21233x --≥，又函数3x y =是增函数，所以212x -≥-，即12x ≥-，即1,2⎡⎫-+∞⎪⎢⎣⎭，值域是[)0,+∞. (4)∵011112≥+-=-+x x x x ∴ 定义域为(-∞，-1)∪[1，+∞)， 又∵111011≠+-≥+-x x x x 且，∴ a ay a y x xx x≠=≥=-+-+1121121且， ∴值域为[1，a)∪(a ，+∞).【总结】求值域时有时要用到函数单调性；第(4)小题中112111≠+-=+-x x x 不能遗漏.【变式1】求下列函数的定义域：(1)2-12x y = (2)y =(3)y =0,1)y a a =>≠【答案】（1）R ；（2）(]-3∞，；（3）[)0,+∞；（4）a>1时，(]-0∞，；0<a<1时，[)0+∞， 【解析】(1)R(2)要使原式有意义，需满足3-x ≥0，即3x ≤，即(]-3∞，．(3) 为使得原函数有意义，需满足2x-1≥0，即2x≥1，故x ≥0，即[)0,+∞(4) 为使得原函数有意义，需满足10xa -≥，即1xa ≤，所以a>1时，(]-0∞，；0<a<1时，[)0+∞，.【总结】本题中解不等式的依据主要是指数函数的单调性，根据所给的同底指数幂的大小关系，结合单调性来判断指数的大小关系.类型二、指数函数的单调性及其应用 例2．讨论函数221()3x xf x -⎛⎫= ⎪⎝⎭的单调性，并求其值域．【点拨】对于x ∈R ，22103x x-⎛⎫> ⎪⎝⎭恒成立，因此可以通过作商讨论函数()f x 的单调区间．此函数是由指数函数及二次函数复合而成的函数，因此可以逐层讨论它的单调性，综合得到结果．【答案】函数()f x 在区间（－∞，1）上是增函数，在区间[1，+∞）上是减函数 （0，3]【解析】解法一：∵函数()f x 的定义域为（－∞，+∞），设x 1、x 2∈（－∞，+∞）且有x 1＜x 2，∴222221()3x x f x -⎛⎫= ⎪⎝⎭，211211()3x x f x -⎛⎫= ⎪⎝⎭，222222121212121122()()(2)2211()113()3313x x x x x x x x x x x x f x f x -----+--⎛⎫ ⎪⎛⎫⎛⎫⎝⎭=== ⎪ ⎪⎝⎭⎝⎭⎛⎫ ⎪⎝⎭． （1）当x 1＜x 2＜1时，x 1+x 2＜2，即有x 1+x 2－2＜0．又∵x 2－x 1＞0，∴(x 2―x 1)(x 2+x 1―2)＜0，则知2121()(2)113x x x x -+-⎛⎫> ⎪⎝⎭．又对于x ∈R ，()0f x >恒成立，∴21()()f x f x >． ∴函数()f x 在（－∞，1）上单调递增．（2）当1≤x 1＜x 2时，x 1+x 2＞2，即有x 1+x 2－2＞0． 又∵x 2－x 1＞0，∴(x 2―x 1)(x 2+x 1―2)＞0，则知2121()(2)1013x x x x -+-⎛⎫<< ⎪⎝⎭．∴21()()f x f x <．∴函数()f x 在[1，+∞）上单调递减．综上，函数()f x 在区间（－∞，1）上是增函数，在区间[1，+∞）上是减函数．∵x 2―2x=(x ―1)2―1≥－1，1013<<，221110333x x--⎛⎫⎛⎫<≤= ⎪⎪⎝⎭⎝⎭． ∴函数()f x 的值域为（0，3]．解法二：∵函数()f x 的定义域为R ，令u=x 2－2x ，则1()3uf u ⎛⎫= ⎪⎝⎭．∵u=x 2―2x=(x ―1)2―1，在（―∞，1]上是减函数，1()3uf u ⎛⎫= ⎪⎝⎭在其定义域内是减函数，∴函数()f x 在（－∞，1]内为增函数．又1()3uf u ⎛⎫= ⎪⎝⎭在其定义域内为减函数，而u=x 2―2x=(x ―1)2―1在[1，+∞）上是增函数，∴函数()f x 在[1，+∞）上是减函数．值域的求法同解法一．【总结】由本例可知，研究()f x y a=型的复合函数的单调性用复合法，比用定义法要简便些，一般地有：即当a ＞1时，()f x y a =的单调性与()y f x =的单调性相同；当0＜a＜1时，()f x y a=的单调与()y f x =的单调性相反．【变式1】求函数2323xx y -+-=的单调区间及值域.【答案】3(,]2x ∈-∞上单增，在3[,)2x ∈+∞上单减. 14(0,3]【解析】[1]复合函数——分解为：u=-x 2+3x-2， y=3u；[2]利用复合函数单调性判断方法求单调区间； [3]求值域. 设u=-x 2+3x-2， y=3u，其中y=3u为R 上的单调增函数，u=-x 2+3x-2在3(,]2x ∈-∞上单增，u=-x 2+3x-2在3[,)2x ∈+∞上单减，则2323x x y -+-=在3(,]2x ∈-∞上单增，在3[,)2x ∈+∞上单减.又u=-x 2+3x-22311()244x =--+≤， 2323x x y -+-=的值域为14(0,3].【变式2】求函数2-2()(01)xxf x a a a =>≠其中，且的单调区间.【解析】当a>1时，外层函数y=a u在()-∞+∞，上为增函数，内函数u=x 2-2x 在区间(1)-∞，上为减函数，在区间[)1+∞，上为增函数，故函数2-2()(-1)xxf x a =∞在区间，上为减函数，在区间[)1+∞，上为增函数；当0<a<1时，外层函数y=a u 在()-∞+∞，上为减函数，内函数u=x 2-2x 在区间(1)-∞，上为减函数，在区间[)1+∞，上为增函数，故函数2-2()x xf x a =在区间(1)-∞，上为增函数，在区间[)1,+∞上为减函数.例3．讨论函数111242x x y -⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭的单调性．【答案】在（－∞，0]上递减，在[0，+∞）上递增【解析】注意21142xx⎡⎤⎛⎫⎛⎫=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦．因而原函数是指数函数12x t ⎛⎫= ⎪⎝⎭与二次函数y=t 2－2t+2的复合函数．令12x t ⎛⎫= ⎪⎝⎭，则y=t 2―2t+2．由12xt ⎛⎫= ⎪⎝⎭在R 上递减，又y=t 2―2t+2在（―∞，1]上递减，在[1，+∞）上递增，而当112x t ⎛⎫=≤ ⎪⎝⎭，则x ≥0；当112xt ⎛⎫=≥ ⎪⎝⎭，则x ≤0．∴函数111242x x y -⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭在（－∞，0]上递减，在[0，+∞）上递增．【总结】研究()xy f a =型的复合函数的单调性，一般用复合法，即设xt a =，再由内函数xt a =与外函数()y f t =的单调性来确定()xy f a =的单调性．【变式1】 求函数1)21()41(+-=xxy (x ∈[-3，2])的单调区间，并求出它的值域. 【答案】单调增区间是[1，2]，单调减区间是[-3，1] [43，57] 【解析】令xu )21(=， 则43)21(122+-=+-=u u u y ，∵ x ∈[-3，2]， ∴ 8)21(41≤=≤x u ， ∴5743≤≤y ， ∴ 值域为[43，57]，再求单调区间.(1)2141≤≤u 即21)21(41≤≤x 即x ∈[1，2]时，x u )21(=是单调减函数，43)21(2+-=u y 是单调减函数，故43]21)21[(2+-=x y 是单调增函数.(2)821≤≤u 即8)21(21≤≤x 即x ∈[-3，1]时，x u )21(=是单调减函数，43)21(2+-=u y 是单调增函数，故43]21)21[(2+-=x y 是单调减函数，∴ 函数的单调增区间是[1，2]，单调减区间是[-3，1].【总结】形如y=Aa 2x+Ba x+C(a>0，且a ≠1)的函数若令a x=u ，便有y=Au 2+Bu+C ，但应注意u>0【变式2】（2015年福建高考）若函数1()2x f x -=(a ∈R )满足(1)(1)f x f x +=-，且()f x 在[m ，+∞)单调递增，则实数m 的最小值等于_______．【答案】1【解析】由(1)(1)f x f x +=-得函数()f x 关于x =1对称，故a =1，则1()2x f x -=，由复合函数单调性得()f x 在[1，+∞)递增，故m ≥1，所以实数m 的最小值等于1．例4．(1)1.8a与1.8a+1； (2)24-231(),3,()331(3)22.5，(2.5)0， 2.51()2(4)0,1)a a >≠ 【点拨】利用指数函数的性质去比较大小．【答案】（1）1.8a<1.8a+1（2）2-24311()<()<333 （3） 2.50 2.51()<(2.5)<22（4）当a>1时，<0<a<1时，>【解析】(1)因为底数1.8>1，所以函数y=1.8x为单调增函数， 又因为a<a+1，所以1.8a<1.8a+1.(2)因为44133-⎛⎫= ⎪⎝⎭，又13x y ⎛⎫= ⎪⎝⎭是减函数，所以-42-23111()<()<333⎛⎫ ⎪⎝⎭，即2-24311()<()<333． (3)因为 2.521>， 2.5112⎛⎫< ⎪⎝⎭，所以 2.50 2.51()<(2.5)<22(4)当a>1时，<0<a<1时，>．【总结】(1)注意利用单调性解题的规范书写；(2)不是同底的尽量化为同底数幂进行比较(因为同底才能用单调性)；(3)不能化为同底的，借助一个中间量来比较大小(常用的中间量是“0”和“1”). 【变式1】比较大小： 122，133，166；【答案】（1）133>122>166【解析】（1）解：122=31136662(2)8== 12112366633(3)9=== 作出8,9,6xxxy y y ===的图象知 986xxxy y y =>=>= 所以133>122>166【变式2】 比较1.5-0.2， 1.30.7， 132()3的大小.【答案】7.02.0313.15.1)32(<<- 【解析】先比较31512.02.0)32()32()23(5.1与==--的大小.由于底数32∈(0，1)， ∴ x y )32(=在R 上是减函数，∵ 05131>>， ∴ 1)32()32()32(005131=<<<，再考虑指数函数y=1.3x， 由于1.3>1， 所以y=1.3x在R 上为增函数1.30.7>1.30=1，∴ 7.02.0313.15.1)32(<<-. 【总结】在进行数的大小比较时，若底数相同，则可根据指数函数的性质得出结果，若底数不相同，则首先考虑能否化成同底数，然后根据指数函数的性质得出结果；不能化成同底数的，要考虑引进第三个数(如0，1等)分别与之比较，从而得出结果.总之比较时要尽量转化成底的形式，根据指数函数单调性进行判断.【变式3】如果215x x aa +-≤（0a >，且1a ≠），求x 的取值范围．【答案】当01a <<时，6x ≥-；当1a >时，6x ≤- 【解析】（1）当01a <<时，由于215x x aa +-≤，215x x ∴+≥-，解得6x ≥-．（2）当1a >时，由于215x x aa +-≤，215x x ∴+≤-，解得6x ≤-．综上所述，x 的取值范围是：当01a <<时，6x ≥-；当1a >时，6x ≤-． 类型三、判断函数的奇偶性例5．判断下列函数的奇偶性：)()21121()(x x f xϕ+-= (()x ϕ为奇函数) 【答案】偶函数【解析】f(x)定义域关于原点对称(∵()x ϕ定义域关于原点对称，且f(x)的定义域是()x ϕ定义域除掉0这个元素)，令21121)(+-=xx g ，则211222121221121)(+--=+-=+-=--xx x x xx g )()21121(21121121121)12(x g x x x x -=+--=+---=+----=∴ g(x)为奇函数， 又 ∵()x ϕ为奇函数，∴ f(x)为偶函数.【总结】求()()()f x g x x ϕ=⋅的奇偶性，可以先判断()g x 与()x ϕ的奇偶性，然后在根据奇·奇=偶，偶·偶=偶，奇·偶=奇，得出()f x 的奇偶性．【变式1】判断函数的奇偶性：()221xx xf x =+-. 【答案】偶函数【解析】定义域{x|x ∈R 且x ≠0}，又112121()()()()222211221x x xx x f x x x x --=-+=-+=---- 21111111()(1)()()222212121x xx x x x x f x -+=-=+-=+=---， ∴ f(-x)=f(x)，则f(x)偶函数.类型四：指数函数的图象问题例6．如图的曲线C 1、C 2、C 3、C 4是指数函数xy a =的图象，而12,,3,22a π⎧⎫⎪⎪∈⎨⎬⎪⎪⎩⎭，则图象C 1、C 2、C 3、C 4对应的函数的底数依次是________、________、________、________．【答案】22 12π 3 【解析】由底数变化引起指数函数图象的变化规律可知，C 2的底数＜C 1的底数＜C 4的底数＜C 3的底数．【总结】利用底数与指数函数图象之间的关系可以快速地解答像本题这样的有关问题，同时还可以解决有关不同底的幂的大小比较的问题，因此我们必须熟练掌握这一性质，这一性质可简单地记作：在y 轴的右边“底大图高”，在y 轴的左边“底大图低”．【变式1】 设()|31|xf x =-，c ＜b ＜a 且()()()f c f a f b >>，则下列关系式中一定成立的是（ ）A ．33a b <B ．33c b >C ．332c a +>D ．332c a+< 【答案】D【解析】f （x ）=|3x-1|=31130xxx x ⎧-≥⎪⎨-<⎪⎩ 0 故可作出f （x ）=|3x-1|的图象如图所示，由图可知，要使c ＜b ＜a 且f （c ）＞f （a ）＞f （b ）成立，则有c ＜0且a ＞0，故必有1331c a->-，所以3c+3a＜2． 故选D ．例7．若直线2y a =与函数|1|1xy a =-+（0,a >且1a ≠）的图象有两个公共点，则a 的取值范围是．【点拨】画出2y a =与|1|1xy a =-+的图象，利用数形结合的方法去解题． 【答案】112a << 【解析】当1a >时，通过平移变换和翻折可得如图所示的图象，则由图可知122a <<，即112a <<与1a >矛盾．当01a <<时，同样通过平移和翻折可得如图所示的图象，则由图可知122a <<，即112a <<，即为所求．【总结】（1）解答此题时，要注意底数的不确定性，因此作图时要注意讨论；（2）根据条件确定直线2y a =与函数的图象位置关系，然后由位置关系建立不等式，进而求得结果，其处理的过程体现了数形结合的思想．【变式1】如图是指数函数①xy a =，②xy b =，③xy c =，④xy d =的图象，则a ，b ，c ，d 与1的大小关系为（ ）A ．a ＜b ＜1＜c ＜dB ．b ＜a ＜1＜d ＜cC ．1＜a ＜b ＜c ＜dD ．a ＜b ＜1＜d ＜c 【答案】B例8．（2016 山西忻州期末）已知函数||1()()2x f x =． （1）作出函数f （x ）的图象； （2）指出该函数的单调递增区间； （3）求函数f （x ）的值域．【答案】（1）略；（2）（－∞，0）；（3）（0，1] 【解析】（1）图象如图所示：（2）由图象可知，函数的单调递增区间为（－∞，0）， （3）由图象可知，函数的值域为（0，1]． 类型五：指数函数的应用例9．假设A 型进口汽车关税率在2010年是2005年的25％，2005年A 型进口汽车每辆价格为64万元（其中含32万元关税款），（1）已知与A 型车性能相近的B 型国产车，2005年每辆价格为46万元，若A 型车价格只受关税降低的影响，为了保证2010年B 型车的价格不高于A 型车价格的90％，B 型车价格要逐年降低，问平均每年至少要降多少万元？（2）某人在2005年将33万元存入银行，假设银行扣除利息税后的年利率为1.8％（五年内不变），且每年按复利计算（例如第一年的利息计入第二年本金），那么五年到期时，这笔钱连本带息是否一定能够买一辆按（1）所述降价后的B 型汽车？【答案】2 能买【解析】（1）∵2010年的关税率为2005年的关税率的14，故所减少的关税款为32×34=24（万元）．∴2010年A 型车价格为64－24=40（万元）．∵5年后B 型车价格不高于A 型车价格的90％，∴有B 型车价格≤40×90％=36（万元）．∵2005年B 型车价格为46万元，故5年中至少要降10万元，∴平均每年至少要降2万元．（2）根据题意，2005年存入的33万元，5年到期时连本带息可得33×(1+1.8％)5（万元）．通过计算器算得33×(1+1.8％)5≈36.08（万元）．∴到期时，这笔钱连本带息一定能够买一辆按（1）所述降价后的B 型汽车．【总结】本题是涉及指数函数的应用题，与指数函数相关的应用题较多，如放射性物质的衰变、人口的增长问题、国民生产总值的增长问题、成本的增长或降低等问题．它的基本模型是：设原有产值为N ，平均增长率为P ，则对于经过x 年后的总产值y 可以用y=N(1+P)x表示．本例（2）在计算五年到期连本带息的和时，用到了公式()(1)nf n a r =+（其中a为开始存入时的本金，r 为每期的利率，n 为期数），该公式可用特例归纳法得到：第l 期到期时本利和为a+ar=a(1+r)；第2期到期时本利和为a(1+r)+a(1+r)r=a(1+r)2；第3期到期时本利和为a(1+r)2+a(1+r)2r=a(1+r)3；…；第n 期到期时本利和为a(1+r)n ―1+a(1+r)n ―1r=a(1+r)n．【变式1】 某乡镇现在人均粮食占有量为360千克，如果该乡镇人口平均每年增长1.2%，粮食总产量平均每年增长4%．设x 年后年人均粮食占有量为y 千克，求出函数y 关于x 的解析式．【答案】360(14%)(1 1.2%)xxM y M +=+【解析】设该乡镇人口数量为M ，则该乡镇现在一年的粮食总产量为360M 千克，经过x 年后，该乡镇粮食总产量为 360M(1+4%)x，人口数量为M(1+1.2%)x，则经过x 年后，人均占有粮食360(14%)(1 1.2%)xxM y M +=+千克． 即所求函数解析式为 1.04360(*)1.012xy x ⎛⎫=∈ ⎪⎝⎭N ．类型六：指数函数性质的综合例10．设12()2x x af x b+-+=+（a ，b 为实常数）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
指数函数典型例题详细解析指数函数·例题解析第一课时【例1】（基础题）求下列函数的定义域与值域：(1)y 3(2)y (3)y 12x＝＝＝-+---213321x x解 (1)定义域为{x|x ∈R 且x ≠2}．值域{y|y ＞0且y ≠1}．(2)由2x+2－1≥0，得定义域{x|x ≥－2}，值域为{|y|y ≥0}．(3)由3－3x-1≥0，得定义域是{x|x ≤2}，∵0≤3－3x －1＜3，∴值域是≤＜．0y 31.指数函数Y=ax （a>0且a ≠1）的定义域是R ，值域是（0，+∞）2. 求定义域的几个原则：①含根式（被开方数不为负）②含分式，分母不为０③形如a0,(a ≠ 0)3. 求函数的值域:①利用函数Y=ax单调性②函数的有界性(x2≥0;ax>0)③换元法.如:y=4x+6×2x-8(1≤x≤2) 先换元,再利用二次函数图象与性质(注意新元的范围)【例2】（基础题）指数函数y＝a x，y＝b x，y ＝c x，y＝d x的图像如图2．6－2所示，则a、b、c、d、1之间的大小关系是[ ] A．a＜b＜1＜c＜dB．a＜b＜1＜d＜cC．b＜a＜1＜d＜cD．c＜d＜1＜a＜b解 选(c)，在x 轴上任取一点(x ，0)，则得b ＜a ＜1＜d ＜c ．【例3】（基础题）比较大小：(1)2(2)0.6、、、、的大小关系是：．248163235894512--()(3)4.54.1________3.73.6解(1)y 221()x ∵，，，，，函数＝，＞，该函数在－∞，＋∞上是增函数，又＜＜＜＜，∴＜＜＜＜．222242821621338254912284162123135258389493859=====解 (2)0.6110.6∵＞，＞，∴＞．----451245123232()()解 (3)借助数4.53.6打桥，利用指数函数的单调性，4.54.1＞4.53.6，作函数y 1＝4.5x ，y 2＝3.7x 的图像如图2．6－3，取x ＝3.6，得4.53.6＞3.73.6 ∴ 4.54.1＞3.73.6．说明 如何比较两个幂的大小：若不同底先化为同底的幂，再利用指数函数的单调性进行比较，如例2中的(1)．若是两个不同底且指数也不同的幂比较大小时，有两个技巧，其一借助1作桥梁，如例2中的(2)．其二构造一个新的幂作桥梁，这个新的幂具有与4.54.1同底与3.73.6同指数的特点，即为4.53.6(或3.74.1)，如例2中的(3)．【例4】解比较大小与＞且≠，＞．当＜＜，∵＞，＞，a a a aan n n n n n nn n nn n -+-+-=-11111111(a 0a 1n 1)0a 1n 10()()∴＜，∴＜当＞时，∵＞，＞，∴＞，＞aa a n n aa a n n n n n n n n n n n n 1111111111()()()--+--+-1a 1n 101【例5】（中档题）作出下列函数的图像：图像变换法例题4（中档题）(1)y (2)y 22x ＝＝－，()121x +(3)y ＝2|x-1|(4)y ＝|1－3x |解 (1)y (264)(0)(11)y 1＝的图像如图．－，过点，及－，．是把函数＝的图像向左平移个单位得到的．()()1212121x x +解 (2)y ＝2x －2的图像(如图2．6－5)是把函数y ＝2x 的图像向下平移2个单位得到的．解 (3)利用翻折变换，先作y ＝2|x|的图像，再把y ＝2|x|的图像向右平移1个单位，就得y ＝2|x-1|的图像(如图2．6－6)． 解 (4)作函数y ＝3x 的图像关于x 轴的对称图像得y ＝－3x 的图像，再把y ＝－3x 的图像向上平移1个单位，保留其在x 轴及x 轴上方部分不变，把x 轴下方的图像以x 轴为对称轴翻折到x 轴上方而得到．(如图2．6－7)例6（中档题） ： 用函数单调性定义证明：当a ＞1时，y = a x 是增函数.【解析】设x 1，x 2∈R 且x 1＜x 2，并令x 2 =x 1 + h (h ＞0，h ∈R)，很独特的方式则有)1(11112-=-=-+hx x hx x x a a a a a a ， ∵a ＞1，h ＞0，∴1,01>>hx a a ，∴012>-x x a a ，即故y = a x (a ＞1)为R 上的增函数，同理可证0＜a ＜1时，y = a x 21x x a a <是R 上的减函数.【例6】解求函数＝的单调区间及值域．令＝－＋，则＝是关于的减函数，而＝－－＋y u x 5x 6y u u x 5xx 25x 622()()3434u＋在∈∞，上是减函数，在∈，∞上是增函数．∴函数＝的单调增区间是∞，，单调减区间是，∞．－＋6x x y x 25x 6(][)()(][)-+-+5252345252又∵＝－＋＝≥，函数＝，在∈，∞上是减函数，所以函数＝的值域是，．－＋u x 5x 6y u y 2x 25x 6()()[)()(]x u ----+5214143414340108324例题7 中档题） 指数函数与二次函数的复合函数(由内到外分析） 二次函数为内层函数，指数函数为外层函数变式1 求函数y=（21）xx 22-的单调区间，并证明之.解法一（在解答题）：在R 上任取x 1、x 2，且x 1＜x 2，则12yy =12122222)21()21(x x x x --=（21）（x 2－x 1）（x 2+x 1－2） 【（21）为底数，红色部分为指数】 ，∵x 1＜x 2，∴x 2－x 1＞0.当x 1、x 2∈（－∞，1］时，x 1+x 2－2＜0.这时（x 2－x 1）（x 2+x 1－2）＜0，则12yy ＞1. ∴y 2＞y 1，函数在（－∞，1］上单调递增. 当x 1、x 2∈［1，+∞）时，x 1+x 2－2＞0，这时（x 2－x 1）（x 2+x 1－2）＞0，即12yy ＜1. （此处点评：上述证明过程中，在对商式正负判断时，利用了指数函数的值域及单调性）∴y 2＜y 1，函数在［1，+∞上单调递减. 综上，函数y 在（－∞，1］上单调递增，在［1，+∞）上单调递减.合作探究：在填空、选择题中用上述方法就比较麻烦，因此我们可以考虑用复合函数的单调性来解题.解法二、在填空、选择题中（用复合函数的单调性）：设：x x u 22-=则：uy ⎪⎭⎫ ⎝⎛=21对任意的211x x <<，有21u u<，又∵uy ⎪⎭⎫ ⎝⎛=21是减函数∴21y y< ∴xx y 2221-⎪⎭⎫⎝⎛=在),1[+∞是减函数对任意的121≤<x x，有21u u>又∵uy ⎪⎭⎫ ⎝⎛=21是减函数∴21y y< ∴xx y 2221-⎪⎭⎫⎝⎛=在),1[+∞是增函数在该问题中先确定内层函数（x x u 22-=）和外层函数（uy ⎪⎭⎫ ⎝⎛=21）的单调情况，再根据内外层函数的单调性确定复合函数的单调性.变式2 已知0>a 且1≠a ，讨论232)(++-=x x a x f 的单调性. 【分析】这是一道与指数函数有关的复合函数讨论单调性题，指数417)23(2322+--=++-x x x，当x ≥23时是减函数，x ≤23时是增函数， 而)(x f 的单调性又与10<<a 和1>a 两种范围有关，应分类讨论.【解析】设232u x x =-++2317()24x =--+，则当x ≥23时，u 是减函数， 当x ≤23时，u是增函数，又当1>a 时，u a y =是增函数， 当10<<a 时，ua y =是减函数，所以当1>a 时，原函数232)(++-=x x ax f 在),23[+∞上是减函数，在]23,(-∞上是增函数. 当10<<a 时，原函数232)(++-=x x ax f 在),23[+∞上是增函数，在]23,(-∞上是减函数. 【小结】一般情况下，两个函数都是增函数或都是减函数，则其复合函数是增函数； ；如果两个函数中一增一减，则其复合函数是减函数，但一定注意考虑复合函数的定义域.第二课时例题8：（疑难题）指数函数与二次函数的复合函数换元法 先换元,再利用二次函数图象与性质(注意新元u 的范围)【例7】解求函数＝＋≥的单调区间及它的最大值．＝，令＝，∵≥，∴＜≤，又∵＝是∈，＋∞上的减函数，函数＝y 1(x 0) y u x 00u 1u x 0)y ()()[()]()[()]()()[()141212121121234121212222x x x x x x x u --+=-+-+-3401212121212121412在∈，上为减函数，在，上是增函数．但由＜≤得≥，由≤≤，得≤≤，∴函数＝＋单调增区间是，＋∞，单调减区间，u 1)0x 110x 1y 11)[01](][()()()()[x x x x当x ＝0时，函数y 有最大值为1．内层指数函数u=(1/2)x 为减，当u 在（0，1/2】时，此时外层二次f （u)为减函数，即x 在【1，正无穷大），，则复合函数为增（画草图分析法）点评：（1）指数函数的有界性（值域）：x2≥0; ax>0（2）上述证明过程中，在两次求x 的范围时，逆向利用了指数函数的值域及逆向利用了指数函数的单调性，是关键及疑难点。
变式： 求（3）1241++=+x xy 的值域.解1421x x y +=++ R x ∈ y 22(2)221(21),x xx=+⋅+=+ 且1,02>∴>y x.故1241++=+x xy 的值域为}1|{>y y . 【小结】求与指数函数有关的函数的值域时，要注意到充分考虑并利用指数函数本身的要求，并利用好指数函数的单调性.例题9 （中档题）分式型指数函数【例8】已知＝＞f(x)(a 1)a a x x -+11(1)判断f(x)的奇偶性； (2)求f(x)的值域；(3)证明f(x)在区间(－∞，＋∞)上是增函数．解 (1)定义域是R ．f(x)f(x)－＝＝－，a a a a x x x x ---+=--+1111 ∴函数f(x)为奇函数．(2)y y 1a 1y 1x 函数＝，∵≠，∴有＝＞－＜＜，a a y y y y x x -+---=+-⇒1111110反函数法，用指数即f(x)的值域为(－1，1)．(3)设任意取两个值x 1、x 2∈(－∞，＋∞)且x 1＜x 2． f(x 1)－f(x 2)＝＝，∵＞，＜，＜，＋＋＞，∴＜，故在上为增函数．a a a a a a a a a a a a x l x l x x x l x x l xx x x x -+-+--++112121*********()()()a 1x x (1)(1)0f(x )f(x )f(x)R 1212变式1 设a 是实数，)(122)(R x a x f x ∈+-=试证明对于任意a,)(x f 为增函数；证明：设21,x x ∈R,且 21x x <则12()()f x f x -1222()()2121x x a a =---++1221122(22)22212(21)(21)x x x x x x-=-=+++由于指数函数y=x2在R 上是增函数,且21x x <,所以 2122x x <即2122x x -<0， 又由 x2 >0得 12x +1>0, 22x +1>0所以)()(21x f x f -<0即)()(21x f x f <因为此结论与a 取值无关，所以对于 a 取任意实数，)(x f 为增函数例题10（中档题）抽象函数第三课时复合函数作业课本：课本P 习题。