高一复习考试指数函数经典例题
指数函数例题集锦(学生版)

2、指数函数例题集锦一、指数和指数的运算 例1、化简求值(1)1213112364162(8)27---⎡⎤+-⨯-⎣⎦ 3122726141-⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛- (2)(2)211511336622(2)(6)(3)a b a b a b ⋅-÷- 2433221---÷⎪⎪⎭⎫ ⎝⎛⋅a b b a例2、已知11223a a -+=,求下列各式的值:122(1);(2)a a a a--++(3)2323-+aa拓展提升:1)已知1122112212,9,,x y x y xy x y x y-+==<+且求的值。
2).若a >1,b <0,且a b +a -b =22,则a b -a-b的值等于________.例3、化简计算(1)324+ (2)34-7347++ (3)40-7407++ (4))0(-3>a ax (5)a1-拓展练习:1、===+24310,310,210yx y x 则2、==x x则若,9323、解方程273291-=⋅--x x二、指数函数的概念例1、下列函数是指数函数的是( )例2、1)函数y=(a 2-3a+3)a x是指数函数,求a 的值 2)若有y=(a-4)x 是指数函数,求a 的范围.3)若函数y=(2a+1)x 是一个减函数,求a 的范围例3、函数 y = a x -2 +3 的图象是否恒过定点?若是,求出定点坐标,若不是,说明理由拓展练习::函数)10(33≠>+=-a a a y x 且的图象恒过定点____________。
xy D )(.31=13.+=x y C x y B 3.-=x y A )3(.-=例4、在下列图象中,二次函数y =ax 2+bx +c 与函数y =(ab )x的图象可能是( ) 例5、比较下面各组数的大小 (1)10.332,2; (2)()()10.330.3,0.3; (3)()20.32,0.3 (4)227.0,8.0(5) 1.50.90.4812314,8,2y y y -⎛⎫=== ⎪⎝⎭拓展练习:1)设01a <<,则下列不等式正确的是( ) A .32(1)(1)a a ->+ B .1(1)1aa +-> C . 1(1)1a a -+>D .1132(1)(1)a a ->+2)设10<<<b a ,则下列不等式正确的是( )a b a a b a b a a b D b a C b b B b a A <<<<....例5、解不等式(基础训练P40,例题2和变式训练)04211233)1,0()2(22112613132>-⋅-⋅≠>≥≥⎪⎭⎫ ⎝⎛++--x x x x x x a a a a)(且)(三、指数函数图像的特点例1、若函数(1)(0,1)xy a b a a =-+>≠的图像经过第一、三、四象限,则一定有( )A .01>>b a 且B .010<<<b a 且C .010><<b a 且D .11>>b a 且拓展练习:函数21xy k =+-的图像不经过第四象限的条件是例2下图是①y=a x ②y=b x ③y=c x ④y=d x 的图像,则 a,b,c,d 与1的大小关系是 ( ) A.a<b<1<c<d B.b<a<1<d<c C.1<a<b<c<d D.a<b<1<d<c例3、作出函数||1-2)312)2,2)1x x x y y y =+==1 1Oxy ①③④②x x x x y y y y 2)6|,12|2)52)42|||2|-=-===++ 的图像小结: 拓展训练:1、方程2|x|+x=2的实根的个数为_______2、直线a y 3=与函数)10(1≠>-=a a a y x且的图像有两个公共点,则a 的取值范围是________例4、设f(x)定义域为R ,对任意x 都有f(x)=f(2-x),且当x ≥1时,f(x)=2x -1,则有() A .f(13)<f(32)<f(23) B .f(23)<f(32)<f(13) C .f(23)<f(13)<f(32) D .f(32)<f(23)<f(13)四、指数函数的定义域值域例1、求下列函数的定义域和值域(1)121x y =- (2)222)31(-=x y (3)xy 121)(= (4) 2221++-⎪⎭⎫⎝⎛=x x y (5) 1121+-⎪⎭⎫⎝⎛=x x y (6)xxy 212+=小结:拓展训练:1、设集合2{|3,},{|1,}xS y y x R T y y x x R ==∈==-∈,则ST 是A 、∅B 、TC 、SD 、有限集 2、函数22811(31)3x x y x --+⎛⎫=- ⎪⎝⎭≤≤的值域是4.已知函数f (x )的定义域是(0,1),那么f (2x)的定义域是( ) A .(0,1) B .(21,1) C .(-∞,0) D .(0,+∞)五、指数函数的单调性和奇偶性 例1、 求下列函数的单调区间(1)241()()2x x f x -= (2)211()3x x f x +-=22141)(31+⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=-x x x f )( (4))10(,)(232≠>=++-a a a x f x x且小结:拓展练习: 1、已知函数332+-=x xa y 在[0,2]上有最小值8,求正数a 的值2、若指数函数xa y =在[-1,1]上的最大值与最小值的差是1,则底数a 等于 ( )A .251+ B .251+- C .251± D .215± 例2、函数y =3x-(13)x 在区间[-1,1]上的最大值为拓展练习:已知).1(1)(R x a aa x f x x∈>-= (1)判断并证明)(x f 的奇偶性与单调性(2)若0)()32(22>--++-x x m f x x f 对任意的]1,0[∈x 均成立,求实数m 的取值范围例3、已知[]3,2x ∈-,求11()142xx f x =-+的最小值与最大值。
指数函数的性质及常考题型(含解析)

【变式 1-2】下列函数:① = 3 ;② = 6 ;③ = 6 ⋅ 2 ;④ = 8 + 1;⑤ = −6 .
其中一定为指数函数的有(
A.0 个
)
B.1 个
C.2 个
D.3 个
【解题思路】根据指数函数的定义判断即可;
【解答过程】解:形如 =
( > 0且 ≠ 1)为指数函数,其解析式需满足①底数为大于
数
函
数
︶
如图是指数函数(1)y=ax,
(2)y=bx,
(3)y=cx,(4)y=dx 的图象,底数 a,b,c,
d 与 1 之间的大小关系为 c>d>1>a>b.
由此我们可得到以下规律:在 y 轴右(左)侧图象越高(低),其底数越大.
3.比较指数幂的大小的方法
比较指数幂的大小的方法(分三种情况)
:
(1)底数相同,指数不同:利用指数函数的单调性来判断;
培
优
篇
高
【变式 5-2】已知函数() = ⋅ 的图像经过点(1,2),(2,4).
中
(1)求()的解析式;
数
(2)解不等式( + 3) > (4).
学
︵
指
数
函
数
︶
【变式 5-3】已知函数() = + (0 < < 1)的图象经过点(0, −1).
(1)求实数 b;
B.0 < < 1,0 < < 1
指
C.0 < < 1, > 1
D. > 1,0 < < 1
数
函
【变式 6-2】如图中,①②③④中不属于函数 = 3 , = 2 , =
4.2 指数函数(精练)(解析版) -人教版高中数学精讲精练(必修一)

x
2
1 ,故值域为 y
|
0
y
1
.
8.(2021·黑龙江·绥化市第一中学高一期中)已知函数 f x 4x a 2x 3 , a R .
(1)当 a 4 ,且 x 0, 2 时,求函数 f x 的值域;
(2)若函数 f x 在0, 2 的最小值为1,求实数 a 的值;
【答案】(1)1,3 (2) a 2 2
③
y
2
x
是指数函数;
④ y xx 的底数是 x 不是常数,不是指数函数;
⑤
y
3
1 x
的指数不是自变量
x
,不是指数函数;
1
⑥ y x3 是幂函数.
故答案为:③
9.(2021·全国·高一专题练习)函数 y a2 5a 5 ax 是指数函数,则 a 的值为________.
【答案】 4
f
x
ax2 2x ,
a
1 x
x 1
3a,
x
1 的最小值为
2,则实数
a 的取值范围是______.
【答案】1,
【解析】由题意,函数
f
x
ax2 2x ,
a 1 x
x 1
3a, x
1 的最小值为
2
,
因为函数 f x 在[1, ) 上为增函数,可得 x 1时,函数 f x 有最小值为 2 ,
则当 x (,1) 时,函数 f x 2 , min
)
A. c a b
B. c b a
【答案】A
1
2
【解析】
b
1 4
3
1 2
3
,
C. b c a
指数函数习题(经典含答案及详细解析)

指数函数习题一、选择题1.概念运算⎩⎨⎧>≤=⊗ba b b a a b a ,那么函数x x f 21)(⊗=的图象大致为( )2.函数f (x )=x 2-bx +c 知足f (1+x )=f (1-x )且f (0)=3,那么f (b x )与f (c x )的大小关系是( )A .f (b x )≤f (c x )B .f (b x )≥f (c x )C .f (b x )>f (c x )D .大小关系随x 的不同而不同3.函数y =|2x -1|在区间(k -1,k +1)内不单调,那么k 的取值范围是( )A .(-1,+∞)B .(-∞,1)C .(-1,1)D .(0,2)4.设函数f (x )=ln[(x -1)(2-x )]的概念域是A ,函数g (x )=lg(a x -2x -1)的概念域是B ,假设A ⊆B ,那么正数a 的取值范围( )A .a >3B .a ≥3C .a > 5D .a ≥ 55.已知函数⎩⎨⎧>≤--=-77)3)(3()(6x a x x a x f x ,假设数列{a n }知足a n =f (n )(n ∈N *),且{a n }是递增数列,那么实数a 的取值范围是( )A .[94,3) B .(94,3) C .(2,3)D .(1,3) 6.已知a >0且a ≠1,f (x )=x 2-a x ,当x ∈(-1,1)时,均有f (x )<12,那么实数a 的取值范围是( ) A .(0,12]∪[2,+∞) B .[14,1)∪(1,4] C .[12,1)∪(1,2] D .(0,14)∪[4,+∞) 二、填空题7.函数y =a x (a >0,且a ≠1)在[1,2]上的最大值比最小值大a 2,那么a 的值是________. 8.假设曲线|y |=2x +1与直线y =b 没有公共点,那么b 的取值范围是________.9.(2020·滨州模拟)概念:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的概念域为[a ,b ],值域为[1,2],那么区间[a ,b ]的长度的最大值与最小值的差为________.三、解答题10.求函数y =2342x x ---+的概念域、值域和单调区间.11.(2020·银川模拟)假设函数y =a 2x +2a x -1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x 的概念域为[0,1].(1)求a 的值;(2)假设函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.指数函数答案1.解析:由a ⊗b =⎩⎪⎨⎪⎧ a a ≤b b a >b 得f (x )=1⊗2x =⎩⎪⎨⎪⎧ 2x x ≤0,1 x >0.答案:A2. 解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2.又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增.若x ≥0,那么3x ≥2x ≥1,∴f (3x )≥f (2x ).若x <0,那么3x <2x <1,∴f (3x )>f (2x ).∴f (3x )≥f (2x ).答案:A3.解析:由于函数y =|2x -1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k -1,k +1)内不单调,因此有k -1<0<k +1,解得-1<k <1.答案:C4. 解析:由题意得:A =(1,2),a x -2x >1且a >2,由A ⊆B 知a x -2x >1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,那么u ′(x )=a x ln a -2x ln2>0,因此函数u (x )在(1,2)上单调递增,那么u (x )>u (1)=a -3,即a ≥3.答案:B5. 解析:数列{a n }知足a n =f (n )(n ∈N *),那么函数f (n )为增函数,注意a 8-6>(3-a )×7-3,因此⎩⎪⎨⎪⎧ a >13-a >0a 8-6>3-a ×7-3,解得2<a <3.答案:C6. 解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,当a >1时,必有a -1≥12,即1<a ≤2, 当0<a <1时,必有a ≥12,即12≤a <1, 综上,12≤a <1或1<a ≤2. 答案:C7. 解析:当a >1时,y =a x 在[1,2]上单调递增,故a 2-a =a 2,得a =32.当0<a <1时,y =a x 在[1,2]上单调递减,故a -a 2=a 2,得a =12.故a =12或32. 答案:12或328. 解析:别离作出两个函数的图象,通过图象的交点个数来判定参数的取值范围.曲线|y |=2x +1与直线y =b 的图象如下图,由图象可得:若是|y |=2x +1与直线y =b 没有公共点,那么b 应知足的条件是b ∈[-1,1]. 答案:[-1,1]9. 解析:如图知足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110. 解:要使函数成心义,那么只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1.∴函数的概念域为{x |-4≤x ≤1}.令t =-x 2-3x +4,那么t =-x 2-3x +4=-(x +32)2+254, ∴当-4≤x ≤1时,t max =254,现在x =-32,t min =0,现在x =-4或x =1. ∴0≤t ≤254.∴0≤-x 2-3x +4≤52. ∴函数y =2341()2x x --+[28,1].由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知, 当-4≤x ≤-32时,t 是增函数, 当-32≤x ≤1时,t 是减函数. 依照复合函数的单调性知:y =1()2在[-4,-32]上是减函数,在[-32,1]上是增函数. ∴函数的单调增区间是[-32,1],单调减区间是[-4,-32]. 11. 解:令a x =t ,∴t >0,那么y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x ∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去).②假设0<a <1,∵x ∈[-1,1],∴t =a x ∈[a ,1a ],故当t =1a,即x =-1时, y max =(1a+1)2-2=14. ∴a =13或-15(舍去). 综上可得a =3或13. 12. 解:法一:(1)由已知得3a +2=18⇒3a =2⇒a =log 32.(2)现在g (x )=λ·2x -4x ,设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,因此g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立.由于2x 2+2x 1>20+20=2,因此实数λ的取值范围是λ≤2.法二:(1)同法一.(2)现在g (x )=λ·2x -4x ,因为g (x )在区间[0,1]上是单调减函数,因此有g ′(x )=λln2·2x -ln4·4x =ln2[-2·(2x )2+λ·2x ]≤0成立.设2x =u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立.因为u ∈[1,2],只需λ≤2u 恒成立,因此实数λ的取值范围是λ≤2.。
高一数学指数运算及指数函数试题(有答案)

高一数学指数运算及指数函数试题一.选择题x x=22.若非零实数a、b、c满足,则的值等于(B)∴设=3.已知,则a等于()解:因为4.若a>1,b>1,p=,则a p等于()p=b.6.若lgx﹣lgy=2a,则=(C)lg lg=lg﹣lg=lg﹣lglg(=7.已知函数,若实数a,b满足f(a)+f(b﹣2)=0,则a+b=x+8.=()×+1=9.设,则=()解:∵∴(()10.,则实数a的取值区间应为(C)=log11.若lgx﹣lgy=a,则=(A)解:12.设,则()13.已知a,b,c均为正数,且都不等于1,若实数x,y,z满足,满足=log14.化简a2•••的结果是(C)••x y xy2x x2x x2解可得,18.若关于x的方程=3﹣2a有解,则a的范围是(A)≤a<≥<a<≤≤,二.填空题19.,则m=10.+=log20.已知x+y=12,xy=9,且x<y,则=.=x+y+2=12+6=18,故答案为:21.化简:=(或或)..故答案为:(或或22.=1.23.函数在区间[﹣1,2]上的值域是[,8].=;=[,[24.函数的值域为(0,8].25.函数(﹣3≤x≤1)的值域是[3﹣9,39],单调递增区间是(﹣2,+∞)..y=三.解答题26.计算:(1);(2).)27.(1)若,求的值;(2)化简(a>0,b>0).=3=..28.已知函数f (x )=4x﹣2x+1+3. (1)当f (x )=11时,求x 的值;(2)当x ∈[﹣2,1]时,求f (x )的最大值和最小值.29.已知函数||22)(x x x f -=. (1)若2)(=x f ,求x 的值;(2)若0)()2(2≥+t mf t f t 对于]2,1[∈t 恒成立,求实数m 的取值范围。
(1)当0<x 时,0)(=x f ;当0≥x 时,x x x f 212)(-=. 由条件可知 2212=-x x ,即 012222=-⋅-x x , 解得 212±=x . 02>x ,()21log 2+=∴x . (2)当]2,1[∈t 时,021*******≥⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-t t t t t m , 即 ()()121242--≥-t t m . 0122>-t , ∴ ()122+-≥t m . ()]5,17[21],2,1[2--∈+-∴∈t t ,故m 的取值范围是),5[∞+-.30.如果函数)1,0(122≠>-+=a a a ay x x 在区间[—1,1]上的最大值是14,求a 的值。
高中数学第四章指数函数与对数函数典型例题(带答案)

高中数学第四章指数函数与对数函数典型例题单选题1、已知a=lg2,10b=3,则log56=()A.a+b1+a B.a+b1−aC.a−b1+aD.a−b1−a答案:B分析:指数式化为对数式求b,再利用换底公式及对数运算性质变形. ∵a=lg2,0b=3,∴b=lg3,∴log56=lg6lg5=lg2×3lg102=lg2+lg31−lg2=a+b1−a.故选:B.2、函数f(x)=|x|⋅22−|x|在区间[−2,2]上的图象可能是()A.B.C.D.答案:C分析:首先判断函数的奇偶性,再根据特殊值判断即可;解:∵f(−x)=|x|⋅22−|x|=f(x),∴f(x)是偶函数,函数图象关于y轴对称,排除A,B选项;∵f(1)=2=f(2),∴f(x)在[0,2]上不单调,排除D选项.故选:C3、式子√m⋅√m 43√m 56m >0)的计算结果为( )A .1B .m 120C .m 512D .m 答案:D分析:由指数运算法则直接计算可得结果.√m⋅√m 43√m 56=m 12⋅m 43m 56=m 12+43−56=m .故选:D.4、若f(x)={(6−a)x −a,x <1log a x +3,x ≥1是定义在R 上的增函数,实数a 的取值范围是( )A .[1,5]B .[32,5) C .(32,5)D .(1,5) 答案:B分析:由题意得{6−a >1a >1log a 1+3≥(6−a)−a ,解不等式组可求得答案因为f(x)={(6−a)x −a,x <1log a x +3,x ≥1是定义在R 上的增函数,所以{6−a >1a >1log a 1+3≥(6−a)−a ,解得32≤a <5,故选:B5、函数f (x )=√3−x +log 13(x +1)的定义域是( )A .[−1,3)B .(−1,3)C .(−1,3]D .[−1,3] 答案:C分析:由题可得{3−x ≥0x +1>0,即得.由题意得{3−x ≥0x +1>0,解得−1<x ≤3, 即函数的定义域是(−1,3].故选:C.6、下列函数中是增函数的为( )A .f (x )=−xB .f (x )=(23)xC .f (x )=x 2D .f (x )=√x 3答案:D分析:根据基本初等函数的性质逐项判断后可得正确的选项. 对于A ,f (x )=−x 为R 上的减函数,不合题意,舍. 对于B ,f (x )=(23)x为R 上的减函数,不合题意,舍.对于C ,f (x )=x 2在(−∞,0)为减函数,不合题意,舍. 对于D ,f (x )=√x 3为R 上的增函数,符合题意, 故选:D.7、下列计算中结果正确的是( ) A .log 102+log 105=1B .log 46log 43=log 42=12C .(log 515)3=3log 515=−3D .13log 28=√log 283=√33答案:A分析:直接根据对数的运算性质及换底公式计算可得;解:对于A :log 102+log 105=log 10(2×5)=log 1010=1,故A 正确; 对于B :log 46log 43=log 36,故B 错误;对于C :(log 515)3=(log 55−1)3=(−log 55)3=−1,故C 错误; 对于D :13log 28=13log 223=13×3log 22=1,故D 错误; 故选:A8、荀子《劝学》中说:“不积跬步,无以至千里;不积小流,无以成江海.”所以说学习是日积月累的过程,每天进步一点点,前进不止一小点.我们可以把(1+1%)365看作是每天的“进步”率都是1%,一年后是1.01365≈37.7834;而把(1−1%)365看作是每天“退步”率都是1%,一年后是0.99365≈0.0255.若“进步”的值是“退步”的值的100倍,大约经过(参考数据:lg101≈2.0043,lg99≈1.9956) ( )天.A .200天B .210天C .220天D .230天 答案:D分析:根据题意可列出方程100×0.99x =1.01x ,求解即可.设经过x 天“进步”的值是“退步”的值的100倍,则100×0.99x=1.01x,即(1.010.99)x =100,∴x =log 1.010.99100=lg lg 1.010.99=lg lg 10199=2lg−lg≈22.0043−1.9956=20.0087≈230.故选:D . 多选题9、已知函数f(x)=1−2x 1+2x,则下面几个结论正确的有( )A .f(x)的图象关于原点对称B .f(x)的图象关于y 轴对称C .f(x)的值域为(−1,1)D .∀x 1,x 2∈R ,且x 1≠x 2,f (x 1)−f (x 2)x 1−x 2<0恒成立答案:ACD分析:利用奇函数的定义和性质可判断AB 的正误,利用参数分离和指数函数的性质可判断CD 的正误. 对于A ,f(x)=1−2x1+2x ,则f(−x)=1−2−x1+2−x =2x −11+2x =−f(x), 则f(x)为奇函数,故图象关于原点对称,故A 正确.对于B ,计算f(1)=−13,f(−1)=13≠f(1),故f(x)的图象不关于y 轴对称,故B 错误. 对于C ,f(x)=1−2x1+2x =−1+21+2x ,1+2x =t,t ∈(1,+∞),故y =f(x)=−1+2t ,易知:−1+2t ∈(−1,1),故f(x)的值域为(−1,1),故C 正确. 对于D ,f(x)=1−2x1+2x =−1+21+2x ,因为y =1+2x 在R 上为增函数,y =−1+21+t 为(1,+∞)上的减函数, 由复合函数的单调性的判断法则可得f (x )在R 上单调递减,故∀x 1,x 2∈R ,且x 1≠x 2,f(x 1)−f(x 2)x 1−x 2<0恒成立,故D 正确.故选:ACD.小提示:方法点睛:复合函数的单调性的研究,往往需要将其转化为简单函数的复合,通过内外函数的单调性结合“同增异减”的原则来判断.10、设函数f (x )=ax 2+bx +c (a,b,c ∈R,a >0),则下列说法正确的是( ) A .若f (x )=x 有实根,则方程f(f (x ))=x 有实根 B .若f (x )=x 无实根,则方程f(f (x ))=x 无实根 C .若f (−b 2a)<0,则函数y =f (x )与y =f(f (x ))都恰有2个零点D .若f (f (−b 2a))<0,则函数y =f (x )与y =f(f (x ))都恰有2零点答案:ABD分析:直接利用代入法可判断A 选项的正误;推导出f (x )−x >0对任意的x ∈R 恒成立,结合该不等式可判断B 选项的正误;取f (x )=x 2−x ,结合方程思想可判断C 选项的正误;利用二次函数的基本性质可判断D 选项的正误.对于A 选项,设f (x )=x 有实根x =x 0,则f(f (x 0))=f (x 0)=x 0,A 选项正确; 对于B 选项,因为a >0,若方程f (x )=x 无实根,则f (x )−x >0对任意的x ∈R 恒成立, 故f(f (x ))>f (x )>x ,从而方程f(f (x ))=x 无实根,B 选项正确;对于C 选项,取f (x )=x 2−x ,则f (12)=−14<0,函数y =f (x )有两个零点, 则f(f (x ))=[f (x )]2−f (x )=0,可得f (x )=0或f (x )=1,即x 2−x =0或x 2−x =1. 解方程x 2−x =0可得x =0或1,解方程x 2−x −1=0,解得x =1±√52. 此时,函数y =f(f (x ))有4个零点,C 选项错误;对于D 选项,因为f (f (−b2a ))<0,设t =f (−b2a ),则t =f (x )min , 因为f (t )<0且a >0,所以,函数f (x )必有两个零点,设为x 1、x 2且x 1<x 2, 则x 1<t <x 2,所以,方程f (x )=x 1无解,方程f (x )=x 2有两解,因此,若f(f(−b))<0,则函数y=f(x)与y=f(f(x))都恰有2零点,D选项正确.2a故选:ABD.小提示:思路点睛:对于复合函数y=f[g(x)]的零点个数问题,求解思路如下:(1)确定内层函数u=g(x)和外层函数y=f(u);(2)确定外层函数y=f(u)的零点u=u i(i=1,2,3,⋯,n);(3)确定直线u=u i(i=1,2,3,⋯,n)与内层函数u=g(x)图象的交点个数分别为a1、a2、a3、⋯、a n,则函数y=f[g(x)]的零点个数为a1+a2+a3+⋯+a n.11、(多选题)某市出租车收费标准如下:起步价为8元,起步里程为3km(不超过3km按起步价付费);超过3km 但不超过8km时,超过部分按每千米2.15元收费;超过8km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.下列结论正确的是()A.出租车行驶4km,乘客需付费9.6元B.出租车行驶10km,乘客需付费25.45元C.某人乘出租车行驶5km两次的费用超过他乘出租车行驶10km一次的费用D.某人乘坐一次出租车付费22.6元,则此次出租车行驶了9km答案:BCD分析:根据题意分别计算各个选项的情况,即可得答案.对于A选项:出租车行驶4km,乘客需付费8+1×2.15+1=11.15元,故A错误;对于B选项:出租车行驶10 km,乘客需付费8+2.15×5+2.85×(10-8)+1=25.45元,故B正确;对于C选项:乘出租车行驶5km,乘客需付费8+2×2.15+1=13.30元,乘坐两次需付费26.6元,26.6>25.45,故C正确;对于D选项:设出租车行驶x km时,付费y元,由8+5×2.15+1=19.75<22.6,知x>8,因此由y=8+2.15×5+2.85(x-8)+1=22.6,解得x=9,故D正确.故选:BCD.小提示:本题考查函数模型的应用,解题要点为认真审题,根据题意逐一分析选项即可,属基础题.12、若log2m=log4n,则()A.n=2m B.log9n=log3mC.lnn=2lnm D.log2m=log8(mn)答案:BCD分析:利用对数运算化简已知条件,然后对选项进行分析,从而确定正确选项.依题意log2m=log4n,所以m>0,n>0,log2m=log22n=12log2n=log2n12,所以m=n 12,m2=n,A选项错误.log9n=log32m2=22log3m=log3m,B选项正确.lnn=lnm2=2lnm,C选项正确.log8(mn)=log23m3=33log2m=log2m,D选项正确.故选:BCD13、在平面直角坐标系中,我们把横纵坐标相等的点称之为“完美点”,下列函数的图象中存在完美点的是()A.y=﹣2x B.y=x﹣6C.y=3xD.y=x2﹣3x+4答案:ACD分析:横纵坐标相等的函数即y=x,与y=x有交点即存在完美点,依次计算即可.横纵坐标相等的函数即y=x,与y=x有交点即存在完美点,对于A,{y=xy=−2x,解得{x=0y=0,即存在完美点(0,0),对于B,{y=xy=x−6,无解,即不存在完美点,对于C,{y=xy=3x,解得{x=√3y=√3或{x=−√3y=−√3,即存在完美点(√3,√3),(−√3,−√3)对于D,{y=xy=x2−3x+4,x2−3x+4=x,即x2−4x+4=0,解得x=2,即存在完美点(2,2).故选:ACD.填空题14、化简(√a−1)2+√(1−a)2+√(1−a)33=________.答案:a-1分析:根据根式的性质即可求解.由(√a−1)2知a-1≥0,a≥1.故原式=a-1+|1-a|+1-a=a-1.所以答案是:a-115、对数型函数f(x)的值域为[0,+∞),且在(0,+∞)上单调递增,则满足题意的一个函数解析式为______.答案:f(x)=|log2(x+1)|(答案不唯一,满足f(x)=|log a(x+b)|,a>1,b≥1即可)分析:根据题意可利用对数函数的性质和图像的翻折进行构造函数.∵函数f(x)的值域为[0,+∞),且在(0,+∞)上单调递增,∴满足题意的一个函数是f(x)=|log2(x+1)|.所以答案是:f(x)=|log2(x+1)|(答案不唯一)16、函数y=log a(x+1)-2(a>0且a≠1)的图象恒过点________.答案:(0,-2)分析:由对数函数的图象所过定点求解.解:依题意,x+1=1,即x=0时,y=log a(0+1)-2=0-2=-2,故图象恒过定点(0,-2).所以答案是:(0,-2)解答题17、(1)计算0.027−13−(−16)−2+810.75+(19)0−3−1;(2)若x 12+x−12=√6,求x 2+x −2的值.答案:(1)-5;(2)14.分析:(1)由题意利用分数指数幂的运算法则,计算求得结果. (2)由题意两次利用完全平方公式,计算求得结果. (1)0.027−13−(−16)−2+810.75+(19)0−3−1=0.3﹣1﹣36+33+1−13=103−36+27+1−13=−5.(2)若x 12+x −12=√6,∴x +1x +2=6,x +1x =4,∴x 2+x ﹣2+2=16,∴x 2+x ﹣2=14.18、已知函数f (x )=2x −12x +1.(1)判断并证明f (x )在其定义域上的单调性;(2)若f (k ⋅3x )+f (3x −9x +2)<0对任意x ≥1恒成立,求实数k 的取值范围. 答案:(1)f (x )在R 上单调递增;证明见解析 (2)(−∞,43)分析:(1)设x 2>x 1,可整理得到f (x 2)−f (x 1)=2(2x 2−2x 1)(2x 2+1)(2x 1+1)>0,由此可得结论;(2)利用奇偶性定义可证得f (x )为奇函数,结合单调性可将恒成立的不等式化为k <g (x )=3x −23x −1,由g (x )单调性可求得g (x )≥43,由此可得k 的取值范围.(1)f (x )在R 上单调递增,证明如下: 设x 2>x 1,∴f (x 2)−f (x 1)=2x 2−12x 2+1−2x 1−12x 1+1=(2x 2−1)(2x 1+1)−(2x 2+1)(2x 1−1)(2x 2+1)(2x 1+1)=2(2x 2−2x 1)(2x 2+1)(2x 1+1);∵x 2>x 1,∴2x 2−2x 1>0,又2x 2+1>0,2x 1+1>0,∴f (x 2)−f (x 1)>0, ∴f (x )在R 上单调递增. (2)∵f (−x )=2−x −12−x +1=1−2x1+2x =−f (x ),∴f (x )为R 上的奇函数,由f(k⋅3x)+f(3x−9x+2)<0得:f(k⋅3x)<−f(3x−9x+2)=f(9x−3x−2),由(1)知:f(x)在R上单调递增,∴k⋅3x<9x−3x−2在[1,+∞)上恒成立;当x≥1时,3x≥3,∴k<3x−23x−1在[1,+∞)上恒成立;令g(x)=3x−23x−1,∵y=3x在[1,+∞)上单调递增,y=23x在[1,+∞)上单调递减,∴g(x)在[1,+∞)上单调递增,∴g(x)≥g(1)=3−23−1=43,∴k<43,即实数k的取值范围为(−∞,43).。
高一数学指数函数试题答案及解析

高一数学指数函数试题答案及解析1.函数的单调递减区间【答案】【解析】因为,根据复合函数的单调性可知该函数的单调递减区间为.【考点】本小题主要考查复合函数的单调区间的求法.点评:考查复合函数的单调性时,要注意“同增异减”,还要注意函数的定义域.2.设a,b,c∈R,且3= 4= 6,则( ).A.=+B.=+C.=+D.=+【答案】B【解析】设3= 4= 6= k,则a = log k,b= log k,c = log k,从而= log 6 = log3+log 4 =+,故=+,所以选(B).3.设指数函数,则下列等式中不正确的是()A.f(x+y)=f(x)·f(y)B.C.D.【答案】D【解析】根据指数幂的运算律知:A,B,C正确;。
故选D4.若函数是定义在R上的奇函数,则函数的图象关于()A.轴对称B.轴对称C.原点对称D.以上均不对【答案】B【解析】因为函数是定义在R上的奇函数,所以则所以是偶函数。
故选B5.三个数,,之间的大小关系为()A.B.C.D.【答案】B【解析】因为,,,所以,故应选.【考点】1、指数与指数函数;2、对数与对数函数;6.定义运算为:,例如:,则的取值范围是__________.【答案】【解析】由题意可得,,∵时,,综上可得,的取值范围是,故答案为.7.已知,则三者的大小关系是A.B.C.D.【答案】A【解析】由函数的图象与性质可知:;由函数的图象与性质可知:;∴故选:A8.若,则等于A.B.C.D.【答案】A【解析】因为,故选A.9.已知函数(,且).(1)若函数在上的最大值为2,求的值;(2)若,求使得成立的的取值范围.【答案】(1)或;(2).【解析】(1)分类讨论和两种情况,结合函数的单调性可得:或;(2)结合函数的解析式,利用指数函数的单调性可得,求解对数不等式可得的取值范围是.试题解析:(1)当时,在上单调递增,因此,,即;当时,在上单调递减,因此,,即.综上,或.(2)不等式即.又,则,即,所以.10.已知,,,则,,的大小关系是()A.B.C.D.【答案】C【解析】因为,,,所以,故选C.11.若3<a<4,化简的结果是()A.7-2a B.2a-7C.1D.-1【答案】C【解析】∵,∴,。
指数函数经典例题(答案)
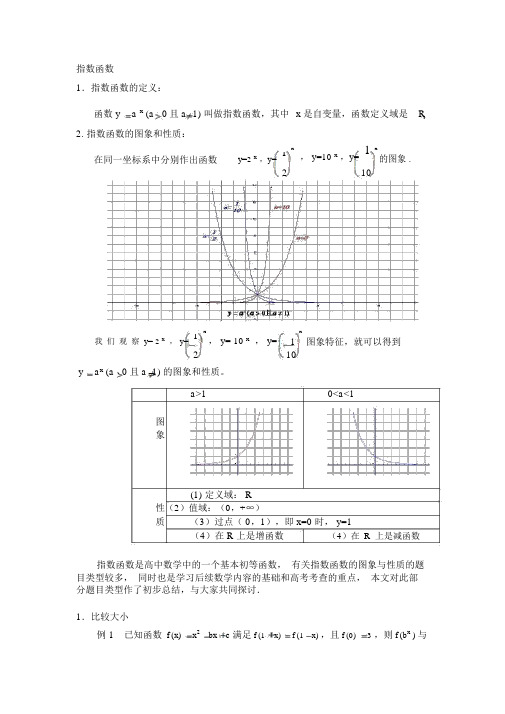
指数函数1.指数函数的定义:函数 y a x (a 0且a 1) 叫做指数函数,其中 x 是自变量,函数定义域是 R2. 指数函数的图象和性质:x , y=10 x ,y=1x在同一坐标系中分别作出函数y=2 x,y=1的图象 .2 10x x我 们 观 察 y= 2 x , y=1, y= 10 x , y=1 图象特征,就可以得到 210y a x (a 0且a 1) 的图象和性质。
a>10<a<1图象11(1) 定义域: R性(2)值域:(0,+∞) 质 (3)过点( 0,1),即 x=0 时, y=1(4)在 R 上是增函数 (4)在 R 上是减函数指数函数是高中数学中的一个基本初等函数, 有关指数函数的图象与性质的题目类型较多, 同时也是学习后续数学内容的基础和高考考查的重点, 本文对此部分题目类型作了初步总结,与大家共同探讨. 1.比较大小例 1 已知函数 f (x)x 2 bx c 满足 f (1 x) f (1 x) ,且 f (0) 3 ,则 f (b x ) 与f ( c x ) 的大小关系是_____.分析:先求 b, c 的值再比较大小,要注意b x, c x的取值是否在同一单调区间内.解:∵ f (1 x) f (1 x) ,∴函数 f ( x) 的对称轴是x 1 .故 b 2,又 f (0) 3 ,∴c 3 .∴函数 f ( x) 在∞,1 上递减,在1,∞上递增.若 x ≥ 0 ,则 3x≥ 2x≥ 1 ,∴f(3x)≥f(2x);若 x 0 ,则3x 2 x 1 ,∴f (3x) f (2x ) .综上可得 f (3x )≥ f (2x ) ,即 f (c x ) ≥ f (b x ) .评注:①比较大小的常用方法有:作差法、作商法、利用函数的单调性或中间量等.②对于含有参数的大小比较问题,有时需要对参数进行讨论.2.求解有关指数不等式例 2 已知(a22a5)3 x(a22a 5)1 x,则x的取值范围是___________.分析:利用指数函数的单调性求解,注意底数的取值范围.解:∵ a22a 5 ( a 1)24≥4 1,∴函数 y(a22a5)x在(∞,∞)上是增函数,∴ 3x 1x ,解得x 1.∴ x 的取值范围是1,∞.44评注:利用指数函数的单调性解不等式,需将不等式两边都凑成底数相同的指数式,并判断底数与 1 的大小,对于含有参数的要注意对参数进行讨论.3.求定义域及值域问题例 3求函数 y 1 6x 2的定义域和值域.解:由题意可得 16x2≥ 0 ,即 6x 2≤ 1 ,∴ x 2 ≤ 0 ,故 x ≤ 2.∴函数 f (x) 的定义域是∞,2 .令 t6x 2,则 y1t ,又∵ x≤ 2 ,∴ x 2 ≤ 0 .∴ 0 6x 2≤ 1 ,即 0 t ≤ 1 .∴ 0 ≤ 1 t 1,即 0 ≤ y 1 .∴函数的值域是01,.评注:利用指数函数的单调性求值域时,要注意定义域对它的影响.4.最值问题例 4函数y a2x2a x1(a 0且a 1)在区间[ 11],上有最大值14,则 a 的值是 _______.分析:令 t a x可将问题转化成二次函数的最值问题,需注意换元后t 的取值范围.解:令t a x,则t0 ,函数y a2 x2a x 1 可化为y(t1)2 2 ,其对称轴为t1.∴当 a 1 时,∵x11,,∴1≤ a x≤ a ,即1≤ t ≤ a .a a∴当 t a 时,y max(a1)2214.解得 a 3 或 a 5 (舍去);当 0 a 1 时,∵x11,,∴ a ≤ a x≤1,即 a ≤ t ≤1,a a1时, y max12∴ t1214 ,a a解得 a 1或 a1(舍去),∴ a 的值是 3 或1.353评注:利用指数函数的单调性求最值时注意一些方法的运用,比如:换元法,整体代入等.5.解指数方程例 5 解方程3x 232x80 .解:原方程可化为9 (3x )280 3x9 0 ,令 t3x (t0),上述方程可化为9t 280t 9 0 ,解得t9或 t1(舍去),∴ 3x9,∴ x 2 ,经检验原方程的9解是 x 2 .评注:解指数方程通常是通过换元转化成二次方程求解,要注意验根.6.图象变换及应用问题例 6 为了得到函数y 9 3x 5 的图象,可以把函数y3x的图象().A.向左平移 9 个单位长度,再向上平移 5 个单位长度B.向右平移 9 个单位长度,再向下平移 5 个单位长度C.向左平移 2 个单位长度,再向上平移 5 个单位长度D.向右平移 2 个单位长度,再向下平移 5 个单位长度分析:注意先将函数 y9 3x 5 转化为t3x 2 5 ,再利用图象的平移规律进行判断.解:∵ y 9 3x 5 3x 2 5 ,∴把函数y 3 x的图象向左平移2个单位长度,再向上平移 5 个单位长度,可得到函数y 93x 5 的图象,故选(C).评注:用函数图象解决问题是中学数学的重要方法,利用其直观性实现数形结合解题,所以要熟悉基本函数的图象,并掌握图象的变化规律,比如:平移、伸缩、对称等.习题1、比较下列各组数的大小:(1)若,比较与;(2)若,比较与;(3)若,比较与;()若,且,比较 a 与 b;4 a 与 b.()若,且,比较5解:(1)由,故,此时函数为减函数.由,故.( 2)由,故.又,故.从而.而(3)由.,因,故.又,故.从(4)应有.又因.因若,故,则.从而.又,故,这与已知,这样矛盾.(5)应有.又因.因若,且,则,故.又.从而,故,这样有,这与已知矛盾.小结:比较通常借助相应函数的单调性、奇偶性、图象来求解.2,曲线则分别是指数函数与 1 的大小关系是 ( ).,和的图象 ,(分析 : 首先可以根据指数函数单调性 , 确定, 在轴右侧令, 对应的函数值由小到大依次为 ,故应选 .小结 : 这种类型题目是比较典型的数形结合的题目 , 第(1) 题是由数到形的转化 , 第(2) 题则是由图到数的翻译 , 它的主要目的是提高学生识图 , 用图的意识 . 求最值3,求下列函数的定义域与值域 .1(1)y =2 x 3 ; (2)y=4x +2x+1+1.11解:(1) ∵ x-3 ≠0,∴ y =2 x 3 的定义域为{ x | x ∈R 且 x ≠3}. 又∵ ≠x 310,∴ 2 x 3 ≠1,1∴y =2 x 3 的值域为{ y |y>0 且 y ≠1}.(2)y = 4x +2x+1+1 的定义域为 R. ∵ 2x >0, ∴ y = 4x +2x+1+1= (2 x ) 2+2· 2x +1=x2(2 +1) >1.∴ y =4x +2x+1 +1 的值域为{ y | y>1}.4,已知-1≤x ≤2, 求函数 f(x)=3+2 ·3x+1-9 x 的最大值和最小值解:设 t=3 x, 因为 -1 ≤ x ≤ 2,所以1t 9 ,且 f(x)=g(t)=-(t-3)2+12, 故当 t=33即 x=1 时, f(x) 取最大值 12,当 t=9 即 x=2 时 f(x) 取最小值 -24 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数函数指数函数是高中数学中的一个基本初等函数,有关指数函数的图象与性质的题目类型较多,同时也是学习后续数学内容的基础和高考考查的重点,本文对此部分题目类型作了初步总结,与大家共同探讨. 1.比较大小例1 已知函数2()f x x bx c =-+满足(1)(1)f x f x +=-,且(0)3f =,则()x f b 与()xf c 的大小关系是_____. 分析:先求b c ,的值再比较大小,要注意xxb c ,的取值是否在同一单调区间内. 解:∵(1)(1)f x f x +=-, ∴函数()f x 的对称轴是1x =. 故2b =,又(0)3f =,∴3c =.∴函数()f x 在(]1-,∞上递减,在[)1+,∞上递增. 若0x ≥,则321xx ≥≥,∴(3)(2)x x f f ≥;若0x <,则321x x<<,∴(3)(2)x xf f >. 综上可得(3)(2)xxf f ≥,即()()xxf c f b ≥.评注:①比较大小的常用方法有:作差法、作商法、利用函数的单调性或中间量等.②对于含有参数的大小比较问题,有时需要对参数进行讨论.2.求解有关指数不等式 例2 已知2321(25)(25)xx a a a a -++>++,则x 的取值范围是___________.分析:利用指数函数的单调性求解,注意底数的取值范围. 解:∵2225(1)441a a a ++=++>≥,∴函数2(25)xy a a =++在()-+,∞∞上是增函数, ∴31x x >-,解得14x >.∴x 的取值范围是14⎛⎫+ ⎪⎝⎭,∞. 评注:利用指数函数的单调性解不等式,需将不等式两边都凑成底数相同的指数式,并判断底数与1的大小,对于含有参数的要注意对参数进行讨论.3.求定义域及值域问题 例3 求函数216x y -=-的定义域和值域.解:由题意可得2160x --≥,即261x -≤,∴20x -≤,故2x ≤. ∴函数()f x 的定义域是(]2-,∞. 令26x t -=,则1y t =-,又∵2x ≤,∴20x -≤. ∴2061x -<≤,即01t <≤.∴011t -<≤,即01y <≤.∴函数的值域是[)01,. 评注:利用指数函数的单调性求值域时,要注意定义域对它的影响.4.最值问题 例4 函数221(01)xx y aa a a =+->≠且在区间[11]-,上有最大值14,则a 的值是_______.分析:令xt a =可将问题转化成二次函数的最值问题,需注意换元后t 的取值范围. 解:令xt a =,则0t >,函数221xx y aa =+-可化为2(1)2y t =+-,其对称轴为1t =-.∴当1a >时,∵[]11x ∈-,,∴1x a a a ≤≤,即1t a a≤≤. ∴当t a =时,2max (1)214y a =+-=. 解得3a =或5a =-(舍去);当01a <<时,∵[]11x ∈-,,∴1x a a a ≤≤,即1a t a≤≤, ∴ 1t a =时,2max 11214y a ⎛⎫=+-= ⎪⎝⎭,解得13a =或15a =-(舍去),∴a 的值是3或13.评注:利用指数函数的单调性求最值时注意一些方法的运用,比如:换元法,整体代入等. 5.解指数方程 例5 解方程223380x x +--=.解:原方程可化为29(3)80390x x⨯-⨯-=,令3(0)xt t =>,上述方程可化为298090t t --=,解得9t =或19t =-(舍去),∴39x=,∴2x =,经检验原方程的解是2x =.评注:解指数方程通常是通过换元转化成二次方程求解,要注意验根. 6.图象变换及应用问题例6 为了得到函数935x y =⨯+的图象,可以把函数3xy =的图象( ). A .向左平移9个单位长度,再向上平移5个单位长度 B .向右平移9个单位长度,再向下平移5个单位长度 C .向左平移2个单位长度,再向上平移5个单位长度 D .向右平移2个单位长度,再向下平移5个单位长度 分析:注意先将函数935xy =⨯+转化为235x t +=+,再利用图象的平移规律进行判断.解:∵293535xx y +=⨯+=+,∴把函数3x y =的图象向左平移2个单位长度,再向上平移5个单位长度,可得到函数935xy =⨯+的图象,故选(C ).评注:用函数图象解决问题是中学数学的重要方法,利用其直观性实现数形结合解题,所以要熟悉基本函数的图象,并掌握图象的变化规律,比如:平移、伸缩、对称等.习题1、比较下列各组数的大小:(1)若,比较与;(2)若,比较与;(3)若,比较与;(4)若,且,比较a 与b;(5)若,且,比较a 与b.解:(1)由,故,此时函数为减函数.由,故.(2)由,故.又,故.从而.(3)由,因,故.又,故.从而.(4)应有.因若,则.又,故,这样.又因,故.从而,这与已知矛盾.(5)应有.因若,则.又,故,这样有.又因,且,故.从而,这与已知矛盾.小结:比较通常借助相应函数的单调性、奇偶性、图象来求解.2曲线分别是指数函数,和的图象,则与1的大小关系是 ( ).(分析:首先可以根据指数函数单调性,确定 ,在轴右侧令 ,对应的函数值由小到大依次为 ,故应选.小结:这种类型题目是比较典型的数形结合的题目,第(1)题是由数到形的转化,第(2)题则是由图到数的翻译,它的主要目的是提高学生识图,用图的意识. 求最值3 求下列函数的定义域与值域.(1)y =231-x ; (2)y =4x +2x+1+1.解:(1)∵x-3≠0,∴y =231-x 的定义域为{x |x ∈R 且x ≠3}.又∵31-x ≠0,∴231-x ≠1,∴y =231-x 的值域为{y |y>0且y ≠1}.(2)y =4x+2x+1+1的定义域为R.∵2x>0,∴y =4x+2x+1+1=(2x )2+2·2x+1=(2x+1)2>1. ∴y =4x+2x+1+1的值域为{y |y>1}.4 已知-1≤x ≤2,求函数f(x)=3+2·3x+1-9x的最大值和最小值 解:设t=3x,因为-1≤x ≤2,所以931≤≤t ,且f(x)=g(t)=-(t-3)2+12,故当t=3即x=1时,f(x)取最大值12,当t=9即x=2时f(x)取最小值-24。
5、设,求函数的最大值和最小值.分析:注意到,设,则原来的函数成为,利用闭区间上二次函数的值域的求法,可求得函数的最值.解:设,由知,,函数成为,,对称轴,故函数最小值为,因端点较距对称轴 远,故函数的最大值为 .6(9分)已知函数)1(122>-+=a a a y x x 在区间[-1,1]上的最大值是14,求a 的值..解:)1(122>-+=a a a y x x , 换元为)1(122a t at t y <<-+=,对称轴为1-=t .当1>a ,a t =,即x =1时取最大值,略解得 a =3 (a = -5舍去)7.已知函数(且)(1)求的最小值;(2)若,求的取值范围..解:(1),当即时,有最小值为(2) ,解得当 时, ;当时, .8(10分)(1)已知m x f x+-=132)(是奇函数,求常数m 的值; (2)画出函数|13|-=x y 的图象,并利用图象回答:k 为何值时,方程|3X-1|=k 无解?有一解?有两解?解: (1)常数m =1(2)当k <0时,直线y =k 与函数|13|-=x y 的图象无交点,即方程无解;当k =0或k ≥1时, 直线y =k 与函数|13|-=xy 的图象有唯一的交点,所以方程有一解;当0<k <1时, 直线y =k 与函数|13|-=x y 的图象有两个不同交点,所以方程有两解。
9.若函数 是奇函数,求 的值..解: 为奇函数, ,即 ,则 ,10. 已知9x -10.3x +9≤0,求函数y=(41)x-1-4·(21)x +2的最大值和最小值 解:由已知得(3x )2-10·3x +9≤0 得(3x -9)(3x -1)≤0 ∴1≤3x ≤9 故0≤x ≤2 而y=(41)x-1-4·(21)x +2= 4·(21)2x -4·(21)x +2令t=(21)x (141≤≤t ) 则y=f (t )=4t 2-4t+2=4(t-21)2+1当t=21即x=1时,y min =1当t=1即x=0时,y max =211.已知 ,求函数 的值域.解:由得,即,解之得,于是,即,故所求函数的值域为12. (9分)求函数2222++-=x x y 的定义域,值域和单调区间定义域为R 值域(0,8〕。
(3)在(-∞, 1〕上是增函数在〔1,+∞)上是减函数。
13 求函数y =23231+-⎪⎭⎫⎝⎛x x 的单调区间.分析 这是复合函数求单调区间的问题可设y =u ⎪⎭⎫ ⎝⎛31,u =x 2-3x+2,其中y =u⎪⎭⎫⎝⎛31为减函数∴u =x 2-3x+2的减区间就是原函数的增区间(即减减→增)u =x 2-3x+2的增区间就是原函数的减区间(即减、增→减)解:设y =u⎪⎭⎫⎝⎛31,u =x 2-3x+2,y 关于u 递减,当x ∈(-∞,23)时,u 为减函数,∴y 关于x 为增函数;当x ∈[23,+∞)时,u 为增函数,y 关于x 为减函数. 14 已知函数f(x)=11+-x x a a (a>0且a ≠1). (1)求f(x)的定义域和值域;(2)讨论f(x)的奇偶性;(3)讨论f(x)的单调性.解:(1)易得f(x)的定义域为{x |x ∈R }.设y =11+-x x a a ,解得a x =-11-+y y ①∵a x>0当且仅当-11-+y y >0时,方程①有解.解-11-+y y >0得-1<y<1. ∴f(x)的值域为{y |-1<y <1}.(2)∵f(-x)=11+---x x a a =x xa a +-11=-f(x)且定义域为R ,∴f(x)是奇函数.(3)f(x)=12)1(+-+x x a a =1-12+x a . 1°当a>1时,∵a x +1为增函数,且a x+1>0. ∴12+x a 为减函数,从而f(x)=1-12+x a =11+-x x a a 为增函数.2°当0<a<1时,类似地可得f(x)=11+-x x a a 为减函数. 15、已知函数f (x )=a -122+x (a ∈R ), (1) 求证:对任何a ∈R ,f (x )为增函数.(2) 若f (x )为奇函数时,求a 的值。
