【最新】河南中考面对面届中考数学总复习 单元限时练1pdf
合集下载
数学知识点【河南中考面对面】届中考数学总复习 6.3 与圆有关的计算课堂过关检测(pdf)【含解析】

.已知圆锥的母线长是 1 2c m , 它的侧面展开图的圆 6 2 0 ʎ , 则它的底面圆的直径为㊀㊀㊀㊀c m . 心角是 1 考点二 .如图, 在R t C B中, 9 0 ʎ , C A= C B= 4 , 分别 △A ∠C= 7 1 以A 、 B 、 C为圆心, 以 A C为半径画弧, 三条弧与 2 边A B所围成的阴影部分的面积是 ㊀㊀㊀. ( 结果 考点三 保留 π ) ㊀㊀㊀㊀ 第 7题图 第 8题图 8 .如图, A B是⊙O的直径, A C是 ⊙O的切线, A为切 点, A B= 8 , 连接 B C交⊙O于点 D , 若 ∠C= 5 0 ʎ , 则 考点一 l ㊀㊀㊀㊀. A D= .如图, A B是 ⊙O直径, 弦A C= 9 , B C= 3 0 ʎ , 则图中阴影部 ∠A 2 分的面积是㊀㊀㊀㊀. 考点三 第 9题图
1 .( 新人教 九 上 P 圆的半径是 1 1 5习 题 第 1题 改 编) 9c m , 则6 0 ʎ 的圆心角所对的弧长是 ( ㊀㊀) A . 2 m ㊀㊀B . 3 m ㊀㊀C . 4 m ㊀㊀D . 5 m πc πc πc πc 考点一 2 .一个扇形的弧长是 2 0 m , 半径是 2 4c m , 则扇形 πc ㊀㊀) 的面积是 ( 2 2 A . 2 4 0c m B . 4 8 0c m 2 2 考点二 C . 2 4 0 m D . 4 8 0 m πc πc 3 .若圆锥的轴截图为等边三角形, 则称此圆锥为正 圆锥, 则正圆锥的侧面展开图的圆心角是 ( ㊀㊀) A . 9 0 ʎ B . 1 2 0 ʎ C . 1 5 0 ʎ D . 1 8 0 ʎ 考点三 4 .如 图, 在 R t B C中, B C= △A ∠A ʎ , A B=B C=2 , 以 A为 顶 点, 9 0 A B为半径画弧, 交A C于 D点, 则阴影部分面积为 ( ㊀㊀) A . 4- B . 2- π π 第 4题图 π π 考点三 C . 2- D . 2- 4 2 5 .已知圆柱的底面半径为 2c m , 若圆柱的侧面积是 2 考点二 2 0 m , 则该圆柱的高为㊀㊀【 解析】 圆的周长 = 2 9= 1 8 m , 6 0 ʎ 的圆心角所对的弧长是 πˑ πc 6 0 ˑ 1 8 3 m . π= πc 3 6 0 1 2 2 0 .C ㊀【 解析】 ˑ 2 4= 2 4 0 ( c m ) . πˑ π 2 2 3 .D ㊀【 解析】 设正圆锥的底面半径是 r , 则母线长是 2 r , 底面周长是 2 r ·π n = 2 2 r , 然后设正圆锥的侧面展开图的圆心角是 n ʎ , 则 r , π π 1 8 0 解得: n = 1 8 0 . 4 .D ㊀【 解析】 在R t B C中, ȵ ∠A B C= 9 0 ʎ , A B=B C= 2 , ʑ ∠A= △A 2 4 5 1 2 4 πˑ π 2ˑ 2- = 2- . 5 ʎ , ʑ阴影部分的面积 = ˑ 2 3 6 0 2 . 5c m ㊀【 解析】 圆柱的侧面积 = 2 r ˑ h , 2 0 2 2 h , h = 5c m . π π= πˑ 5 . 8 ㊀【 解析】 设圆锥的底面半径为 r . 圆锥的侧面展开图扇形的半径 6 1 2 0 1 2 πˑ 为1 = 2 , ȵ 它的侧面展开图的圆心角是 1 2 0 ʎ , ʑ 弧长 = 1 8 0 , 即圆锥底面的周长是 8 , ʑ8 2 r , 解得 r = 4c m , ʑ底面圆的 π π π= π 8 m . 直径为 8c 2 2 1 9 0 2 4 5 2 ˑ 2 πˑ πˑ 7 . 8- 2 ㊀【 解析】 4ˑ 4ˑ - - = 8- 2 . π π 2 3 6 0 3 6 0 1 6 . π ㊀【 解析】 ȵA B是 ⊙O的直径, A C切 ⊙O于点 A , ʑB A C , ⊥A 8 9 又ȵ∠C= 5 0 ʎ , ʑ ∠A B C= 4 0 ʎ , ʑ ∠A O D= 2 B C=8 0 ʎ . ʑl = ∠A A D n 0 ·2 R 8 1 6 π = ·2 ·4= π . π 3 6 0 3 6 0 9 4 π . - 3 ㊀【 解析】 如解图, 连接 O C . ȵO B= O C , 9 3 槡 ʑ∠O B C= C B= 3 0 ʎ , ʑ∠B O C= 1 8 0 ʎ - 3 0 ʎ - ∠O 3 ʎ = 1 2 0 ʎ . 又ȵA B 是 直 径, ʑ ∠A C B =9 0 ʎ , 0 ʑ在 R t B C 中, A C= 2 , B C= 3 0 ʎ , 则A B= △A ∠A 2 2 2 A C=4 , B C= 槡 A B - A C =2槡 3 . ȵO C是 第9 题解图 1 A B C 斜边上的中 线, ʑ S = S △ O C B C= △B △A 2 1 1 1 ˑ ˑ 2ˑ 2 A C · B C = 3= 3 , ʑS S S 槡 槡 阴影 = 扇形O B C- O C= △B 2 2 4 2 1 4 2 0 2 πˑ - 3 = π- 3 . 槡 3 6 0 3 槡
数学知识点【河南中考面对面】届中考数学总复习 单元限时练4(pdf)【含解析】
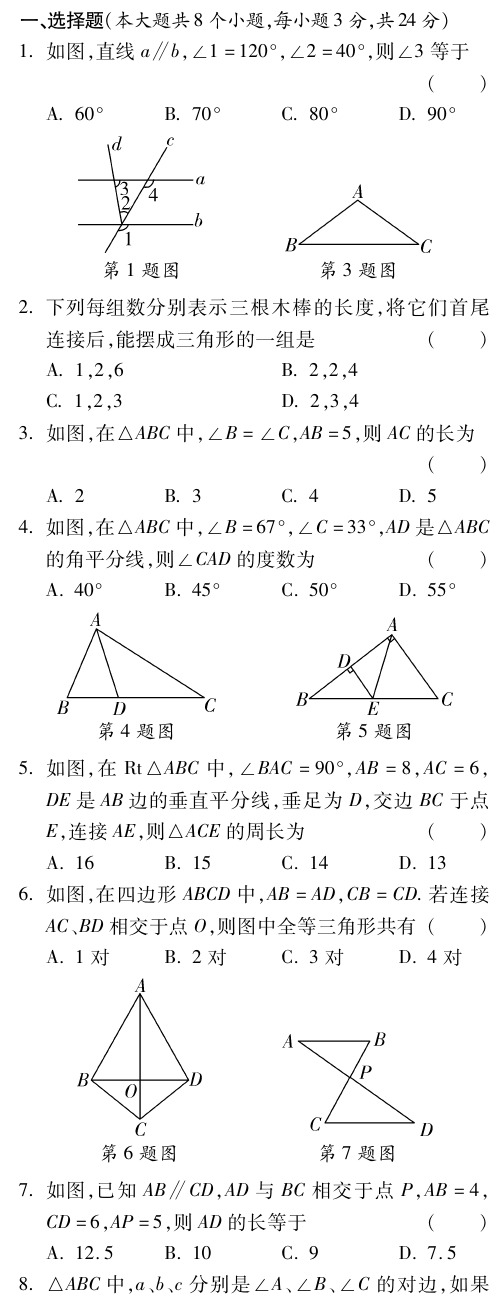
1 .如图, 直线 a , 1 2 0 ʎ , 4 0 ʎ , 则 ∠3等于 ∥b ∠1= ∠2= ( ㊀㊀) A . 6 0 ʎ ㊀㊀㊀B . 7 0 ʎ ㊀㊀㊀C . 8 0 ʎ ㊀㊀㊀D . 9 0 ʎ ㊀㊀㊀㊀ 第 1题图 第 3题图 2 .下列每组数分别表示三根木棒的长度, 将它们首尾 ㊀㊀) 连接后, 能摆成三角形的一组是 ( A . 1 , 2 , 6 B . 2 , 2 , 4 C . 1 , 2 , 3 D . 2 , 3 , 4 3 .如图, 在△A B C中, , A B= 5 , 则A C的长为 ∠B= ∠C ㊀㊀) ( A . 2 B . 3 C . 4 D . 5 4 .如图, 在△A B C中, 6 7 ʎ , 3 3 ʎ , A D是 △A B C ∠ B= ∠C= 的角平分线, 则∠C A D的度数为 ( ㊀㊀) A . 4 0 ʎ B . 4 5 ʎ C . 5 0 ʎ D . 5 5 ʎ ㊀㊀㊀㊀ 第 4题图 第 5题图 5 .如图, 在R t B C中, A C=9 0 ʎ , A B=8 , A C=6 , △A ∠B D E是 A B边的垂直平分线, 垂足为 D , 交边 B C于点 E , 连接 A E , 则△A C E的周长为 ( ㊀㊀) A . 1 6 B . 1 5 C . 1 4 D . 1 3 .如图, 在四边形 A B C D中, A B=A D , C B=C D . 若连接 6 A C 、 B D相交于点 O , 则图中全等三角形共有 ( ㊀㊀) A . 1对 B . 2对 C . 3对 D . 4对 ㊀㊀㊀㊀ 第 6题图 第 7题图 7 .如图, 已知 A B D , A D与 B C相交于点 P , A B= 4 , ∥C C D= 6 , A P= 5 , 则A D的长等于 ( ㊀㊀) A . 1 2 . 5 B . 1 0 C . 9 D . 7 . 5 8 .△ A B C中, a 、 b 、 c 分别是 ∠A 、 、 如果 ∠B ∠ C的对边,
【最新】河南中考面对面届中考数学总复习 51 平行四边形备考试题演练pdf

∠B 角线, 9 .( ’ 1 4临沂) 如图, 在 A B C D中, B C=1 0 , s i n B= 9 , A C= B C , 则A B C D的面积是㊀㊀㊀㊀. 1 0 ㊀㊀ 第 9题图 第1 0题图 1 0 .( ’ 1 4洛阳模拟) 如图, 在 △A B C中, A B=A C= 5 , , E , F分别是 A C , B C , B A延长线上的点, 四边 点D D E F为平行四边形, D E= 2 , 则A D= ㊀㊀㊀㊀. 形A 1 1 .( ’ 1 4毕节) 将四根木条钉成的长方形木框变形 为平行四边形 A B C D的形状, 并使其面积为长方 形面积的一半( 木条宽度忽略不计) , 则这个平行 四边形的一个最小内角为㊀㊀㊀㊀度. 第1 1题图 1 2 .( ’ 1 4长春) 如图, 在 A B C D中, 点 O是对角线 A C 、 B D的交点, 点 E是边 C D的中点, 点 F在 B C 1 的延长线上, 且C F= B C . 求证: 四边形 O C F E 2 是平行四边形. 第1 2题图
1 3 .( ’ 1 4郴州) 如图, 已知四边形 A B C D是平行四边 形, 点E 、 B 、 D 、 F在同一直线上, 且B E= D F . 求证: A E= C F . 第1 3题图 1 4 .( ’ 1 4广元) 如图, 点A 、 F 、 C 、 D在同一直线上, 点B 和点 E分别在直线 A D的两侧, 且A B= D E , ∠A= , A F= D C . ∠D ( 1 ) 请写出图中两对全等的三角形; 2 ) 求证: 四边形 B C E F是平行四边形. ( 第1 4题图
1 3 .( ’ 1 4郴州) 如图, 已知四边形 A B C D是平行四边 形, 点E 、 B 、 D 、 F在同一直线上, 且B E= D F . 求证: A E= C F . 第1 3题图 1 4 .( ’ 1 4广元) 如图, 点A 、 F 、 C 、 D在同一直线上, 点B 和点 E分别在直线 A D的两侧, 且A B= D E , ∠A= , A F= D C . ∠D ( 1 ) 请写出图中两对全等的三角形; 2 ) 求证: 四边形 B C E F是平行四边形. ( 第1 4题图
数学知识点【河南中考面对面】届中考数学总复习 3.2 一次函数及其(含三年中考,pdf)【含解析】

1 .( ’ 1 2河南 7题 3分) 如图, 函数 y = 2 x 和y = a x + 4 的图象相交于点 A ( m , 3 ) , 则不 等式 2 x < a x + 4的解集为 ( ㊀㊀) 3 A .x < ㊀㊀㊀㊀㊀㊀B .x < 3 2 第 1题图 3 C .x D .x > > 3 2 2 .( ’ 1 2河南 1 9题 9分) 甲、 乙两人同时从相距 9 0千 甲乘汽车, 乙骑摩托车, 甲到 米的 A地前往 B地, 达 B地停留半小时后返回 A地, 如图是他们离 A 地的距离 y ( 千米) 与时间 x ( 时) 之间的函数关系式 . ( 1 ) 求甲从 B地返回 A地的过程中, y 与x 之间的 函数关系式, 并写出自变量 x 的取值范围; ( 2 ) 若乙出发后 2小时和甲相遇, 求乙从 A地到 B 地用了多长时间? 第 2题图
.( ’ 1 3河南 2 1题 1 0分) 某文具商店销售功能相同 3 、 B两种品牌的计算器, 购买 2个 A品牌和 3 的A 个 B品牌的计算器共需 1 5 6元; 购买 3个 A品牌 2 2元. 和 1个 B品牌的计算器共需 1 ( 1 ) 求这两种品牌计算器的单价; ( 2 ) 学校开学前夕, 该商店对这两种计算器开展了 促销活动, 具体办法如下: A 品牌计算器按原价的 八折销售, B品牌计算器 5个以上超出部分按原价 的七折销售. 设购买 x 个 A品牌的计算器需要 y 1 元, 购买 x 个 B品牌的计算器需要 y 分别求出 2 元, y 、 y 的函数关系式; 1 2 关于 x ( 3 ) 小明准备联系一部分同学集体购买同一品牌 的计算器, 若购买计算器的数量超过 5个, 购买哪 种品牌的计算器更合算?请说明理由.
.( ’ 1 3河南 2 1题 1 0分) 某文具商店销售功能相同 3 、 B两种品牌的计算器, 购买 2个 A品牌和 3 的A 个 B品牌的计算器共需 1 5 6元; 购买 3个 A品牌 2 2元. 和 1个 B品牌的计算器共需 1 ( 1 ) 求这两种品牌计算器的单价; ( 2 ) 学校开学前夕, 该商店对这两种计算器开展了 促销活动, 具体办法如下: A 品牌计算器按原价的 八折销售, B品牌计算器 5个以上超出部分按原价 的七折销售. 设购买 x 个 A品牌的计算器需要 y 1 元, 购买 x 个 B品牌的计算器需要 y 分别求出 2 元, y 、 y 的函数关系式; 1 2 关于 x ( 3 ) 小明准备联系一部分同学集体购买同一品牌 的计算器, 若购买计算器的数量超过 5个, 购买哪 种品牌的计算器更合算?请说明理由.
数学知识点【河南中考面对面】届中考数学总复习 1.1 实数(含三年中考,pdf)【含解析】

1 .( ’ 1 3河南 1题 3分)- 2的相反数是
.( ’ 1 2河南 3题 3分) 一种花瓣的花粉颗粒直径约 4 . 0 0 0 0 0 6 5米, 0 . 0 0 0 0 0 6 5用科学记数法表示为 为0 ㊀㊀) ( - 5 - 6 . 6 . 5ˑ 1 0 B . 6 . 5ˑ 1 0 A - 7 - 6 C . 6 . 5ˑ 1 0 D . 6 5ˑ 1 0 3 5 .( ’ 1 4 河南 9 题3 分) 计算: 2 7 -| - 2 | = ㊀㊀㊀㊀. 槡 .( ’ 1 3河南 9题 3分) 计算: | - 3 | - 4= ㊀㊀㊀㊀. 6 槡 0 2 .( ’ 1 2河南 9题 3分) 计算: (- 2 ) +(- 3 ) = 槡 7 ㊀㊀㊀㊀.
1 .A ㊀【 解析】 根据相反数的概念: 如果两个数只有符号不同, 那么称 其中一个数为另一个数的相反数, 可以得出, 求一个数的相反数, 只 要改变该数的符号即可. 即 a的相反数是 -a ( 特别地, 0的相反数 ) , 所以有 - 2的相反数是 2 . 是0 2 .D ㊀【 解析】 根据正数大于 0和一切负数, 0大于一切负数, 故排除 1 A 、 B两项, 两个负数比较大小, 绝对值大的数值反而小, ȵ| - | < 3 1 | - 3 | , ʑ- 3<- , 故最小的数是 - 3 . 3 3 .B ㊀【 解析】 本题考查大数的科学记数法. 先将计数单位“ 亿” 化为 8 8 3 8 1 0 , 即3 8 7 5 . 5亿 = 3 8 7 5 . 5ˑ 1 0 = 3 . 8 7 5 5ˑ 1 0 ˑ 1 0 = 3 . 8 7 5 5ˑ 1 1 1 0. 故可确定 n = 1 1 . - 6 4 .B ㊀【 解析】 0 . 0 0 0 0 0 6 5. 1 ㊀【 解析】 ȵ槡 2 7= 3 , | - 2 | = 2 , ʑ原式 = 3- 2= 1 . 6 . 1 ㊀【 解析】 本题考查实数的运算, 涉及绝对值与根式运算 . 由| - 3 | =
数学知识点【河南中考面对面】届中考数学总复习 4.2 三角形及其性质课堂过关检测(pdf)【含解析】

若B D= C D , D E , D E= 2 , 则A B的长度是 ∠B= ∠C ( ㊀㊀) 考点三 A . 4 B . 5 C . 6 D . 7 ㊀㊀㊀ 第 3题图 第 4题图 .( 新人教八上 P 习题第 1题改编) 如图, C B= ∠A 4 1 4
9 . 2 3 ㊀【 解析】 ȵ∠A= 3 0 ʎ , 9 0 ʎ , ʑ∠A C B= 1 8 0 ʎ - 3 0 ʎ - 9 0 ʎ = ∠B= 槡 6 0 ʎ , ȵD E垂 直 平 分 斜 边 A C , ʑA D =C D , C D =3 0 ʎ , ∠A=∠A ʑ∠D C B= 6 0 ʎ - 3 0 ʎ = 3 0 ʎ , ȵB D= 1 , ʑC D= 2= A D , ʑA B= 1+ 2= , 在R t C D中, 由勾股定理得: C B= 3 , 在R t B C中, 由勾股定 3 △B △A 槡
1 .在 △A B C中, 2 0 ʎ , 6 0 ʎ , 则 △A B C的形 ∠A= ∠B= 状是 ( ㊀㊀) A .等边三角形㊀㊀㊀㊀㊀B .锐角三角形 C .直角三角形 D .钝角三角形 考点一 2 .已知三角形两边的长分别是 4和 1 0 , 则此三角形 第三边的长可能是 ( ㊀㊀) A . 5 ㊀㊀㊀B . 6 ㊀㊀㊀C . 1 1 ㊀㊀㊀D . 1 6 考点二 3 .如图, 在△A B C中, D 、 E两点分别在 B C 、 A C边上.
, 若 ∠B=3 0 ʎ , 0 ʎ , 则 ∠B A C= ∠E=2 长线于点 E ㊀㊀㊀㊀. 考点二 ㊀㊀㊀ 第 7题图 第 8题图 .如 图, B C中, A B=A C , 若 ∠B=5 0 ʎ , 则 ∠A= △A 8 考点四 ㊀㊀㊀㊀. 9 .如图, 在R t B C中, 3 0 ʎ , D E垂直平分斜边 △A ∠A= C , 交A B于 D , E为垂足, 连接 C D , 若B D= 1 , 则 A 考点四 C的长是㊀㊀㊀㊀. A ㊀㊀㊀ 第 9题图 第1 0题图 1 0 .如图, 在△A B C中, A B= A C , A D C , 垂足为点 D , E ⊥B 是A C的中点. 若D E= 5 , 则A B的长为㊀㊀㊀㊀. 考点四
数学知识点【河南中考面对面】届中考数学总复习 题型一 函数图象与性质(pdf)【含解析】

y 轴交于点 A , 过点 A与 x 轴平行的直线交抛物线 12 y = x 于点 B 、 C , 则B C的长为㊀㊀㊀㊀. 4 12 3 .已知当 x a , x b , x c 时, 二次函数 y = x + 1= 2= 3= 1 2 m x 对应的函数值分别为 y , y , y , 若正整数 a , b , 1 2 3 c 恰好是一个三角形的三边长, 且当 a< b < c 时, , 则实数 m的取值范围是 都有 y 1 <y 2 <y 3 ㊀㊀㊀㊀. 1 4 .( ’ 1 4天津) 已知二次函数 y 2 = a x+ b x + c ( a ) 的图象 ≠0 如图所示, 且关于 x的一元 2 二次方程 a x + b x + c - m= 0 没 有 实 数 根, 有 下 列 结 论: 2 4 a c > 0 ; b c < 0 ;③ ①b - ②a 第1 4题图 m> 2 . 其中, 正确结论的个数是㊀㊀㊀㊀. 5 .已知二次函数的图象经过原点及点(- 2 ,- 2 ) , 1 且图象与 x 轴的另一个交点到原点的距离为 4 , 那么该二次函数的解析式为㊀㊀㊀㊀㊀㊀㊀.
b k 的值是㊀㊀㊀㊀. k 1 0 .如图, 双曲线 y = 经过 R t O C斜边上的点 A , △B x A O 2 且满足 = , 与B C交 于 点 D , S =2 1 , 求 O D △B A B 3 k = ㊀㊀㊀㊀. ㊀㊀㊀ 第1 0题图 第1 2题图 6 1 1 .如果一个正比例函数的图象与反比例函数 y = x 的图象交于 A ( x , y ) 、 B ( x , y ) 两点, 那么( x - 1 1 2 2 2 x ) ( y y ) 的值为㊀㊀㊀㊀. 1 2- 1 2 1 2 .如图, 在平面直角坐标系中, 抛物线 y = a x + 4与 9 .一次函数 y = k x + b , 当1 , 3 则 ≤x ≤4 ≤y ≤6时,
数学知识点【河南中考面对面】届中考数学总复习 题型四 类型三 实际应用型问题(pdf)【含解析】

2 ) 该企业计划 2 0 1 4年将上述两种垃圾处理总量 ( 减少到 2 4 0吨, 且建筑垃圾处理量不超过餐厨垃 圾处理量的 3倍, 则2 0 1 4年该企业最少需要支付 这两种垃圾处理费共多少元? 2 .( ’ 1 4赤峰 1 0分) 某养殖专业户计划购买甲、 乙两 种牲畜, 已知乙种牲畜的单价是甲种牲畜单价的 2 倍多 2 0 0元, 买 3头甲种牲畜和 1头乙种牲畜共需 7 0 0元. 5 ( 1 ) 甲、 乙两种牲畜的单价各是多少元? ( 2 ) 若购买以上两种牲畜 5 0头, 共需资金 9 . 4万 元, 求甲、 乙两种牲畜各购买多少头? 3 ) 相关资料表明: 甲、 乙两种牲畜的成活率分别 ( 为9 5 %和 9 9 %, 若使这 5 0头牲畜的成活率不低于 9 7 %且购买的总费用最低, 应如何购买?
原题信息 整理后的信息 2 0 1 3年, 餐厨垃圾处理费 设 2 0 1 3年, 餐厨垃圾 x 一 2 5元 / 吨, 建 筑 垃 圾 处 理 吨, 建筑 垃圾 y 吨, 则处 费1 6元 / 吨 理费( 2 5 x + 1 6 y ) 元 2 0 1 3年 共 支 付 餐 厨 和 建 2 5 x + 1 6 y = 5 2 0 0 二 筑垃圾处理费 5 2 0 0元 若该企 业 2 0 1 4年 处 理 的 2 0 1 4年, 餐厨垃圾 x 吨, 三 这两 种 垃 圾 数 量 与 2 0 1 3 建筑垃圾 y 吨 年相比没有变化 2 0 1 4年收费标准上调 为: 餐厨垃圾处理费 1 0 0元 / 2 0 1 4年, 垃圾处理费 四 吨, 建 筑 垃 圾 处 理 ( 1 0 0x + 3 0y ) 元 费3 0元 / 吨 2 0 1 4年 要 多 支 付 垃 圾 处 1 0 0 x + 3 0 y = 5 2 0 0+ 8 8 0 0 五 理费 8 8 0 0元 解: 设2 0 1 3年该企业处理的餐厨垃圾为 x 吨, 建筑垃圾为 y 吨, 根 据题意, 得 2 5 x + 1 6 y = 5 2 0 0 , 3分) ( 1 0 0 x + 3 0 y = 5 2 0 0+ 8 8 0 0 . x = 8 0 , 解得 y = 2 0 0 . 即2 0 1 3年该企业处理的餐厨垃圾为 8 0吨, 建筑垃圾为 2 0 0吨. 5分) ( ( 2 ) 【 信息梳理】 设2 0 1 4年该企业处理的餐厨垃圾为 x 吨, 建筑垃 吨, 需要支付的这两种垃圾处理费是 z 元. 圾为 y 原题信息 整理后的信息 该企业 计 划 2 0 1 4年 将 上 述 两 一 x + y = 2 4 0 种垃圾处理量减少到 2 4 0吨 建筑垃圾处理量不超过餐厨垃 二 y x ≤3 圾处理量的 3倍 2 0 1 4年该企业最少需要支付这 三 z = 1 0 0x + 3 0 y 两种垃圾处理费共多少元 解: 设2 0 1 4年该企业处理的餐厨垃圾为 x 吨, 建筑垃圾为 y 吨, 需 要支付的这两种垃圾处理费是 z 元. 根据题意得 x + y = 2 4 0 , 且y x , 解得 x 0 , ≤3 ≥6 z = 1 0 0x + 3 0y = 1 0 0x + 3 0 ( 2 4 0- x )= 7 0x + 7 2 0 0 . ( 7分) ȵ7 0> 0 , ʑz 的值随 x 的增大而增大, 所以当 x = 6 0时, z 最小, 7 0ˑ 6 0+ 7 2 0 0= 1 1 4 0 0元. 最小值 = 即2 0 1 4年该企业最少需要支付这两种垃圾处理费共 1 1 4 0 0元. 1 0分) ( 2 .解: ( 1 ) 设甲种牲畜的单价是 x 元, 依题意得: 3 x + 2 x + 2 0 0= 5 7 0 0 , ( 2分) ㊀㊀㊀㊀ 解得: x = 1 1 0 0 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 选择题( 本大题共 1 2 个小题, 每小题 2 分, 共2 4 分)
.下列各式计算正确的是 ( ㊀㊀) 2 1 1 - 2 A . 1 8-槡 3 2=- 2 B .(- 3 ) =- 槡 槡 9 0 2 .a = 1 D .槡 (- 2 ) =- 2 C 填空题( 本大题共 9 个小题, 每小题 3 分, 共2 7 分) 二、 1 3 . 9的平方根是 ㊀㊀㊀㊀ . x - 4 1 4 .当 x = ㊀㊀㊀㊀ 时, 分式 的值为 0 . x + 2 3 槡 1 5 .计算: 2 7- = ㊀㊀㊀㊀ . 槡 2 6 .比 较 大 小: 7㊀ ㊀ ㊀ ㊀ 槡 5 0 . ( 填 “<” 、 “=” 或 1 “> ” ) 1 3 7 .分解因式: x - 4 x = ㊀㊀㊀㊀ . 8 .若 | b - 1 | +| a - 4 | = 0 , 则a - 4 b = ㊀㊀㊀㊀ . 1 1 9 .按照下图所示的操作步骤, 若输入 x 的值为 2 , 则输 出的值为 ㊀㊀㊀㊀ . 第1 9题图 3 0 2 0 .计算: (- 2 )+ ( 3- 1 )= ㊀㊀㊀㊀ . 槡 2 1 . 某校艺术班同学每人都会弹钢琴或古筝, 其中会弹 钢琴的人数比会弹古筝的人数多 1 0人, 两种都会 设会弹古筝的有 m人, 则该班同学共有 的有 7人, ㊀㊀㊀㊀ 人( 用含有 m的代数式表示) . 解答题 ( 共 8题, 满分 4 9分) 三、 2 0 1 5 - 1 0 2 2 .( 4分) 计算: (- 1 ) - 2 + s i n 3 0 ʎ + ( 3 . 1 4 ) . π- 1 -1 0 2 3 .( 4分) 计算: 8- 2 s i n 4 5 ʎ + ( 2- ) - ( ) . π 槡 3
1 1 . - 的相反数是 ( ㊀㊀) 3 1 1 A . 3 ㊀㊀㊀B .- 3 ㊀㊀㊀C . - ㊀㊀㊀D . 3 3 1 2 .实数 π , , 0 , - 1中, 是无理数的是 ( ㊀㊀) 5 1 A .π ㊀㊀㊀B . ㊀㊀㊀C . 0 ㊀㊀㊀D .- 1 5 3 .计算( 4- 5 )+ (- 2 ) 的结果是 ( ㊀㊀) A .- 1 B . 0 C .- 3 D .- 2 4 .如图, 数轴的单位长度为 1 , 如果点 A 、 B表示的数的 绝对值相等, 那么点 A表示的数是 ( ㊀㊀) 第 4题图 A .- 4 B .- 2 C . 0 D . 4 5 . 2 0 1 4年两会期间, 多名辽宁全国政协委员建议加快 渤海海峡跨海通道进程, 据悉该工程总投资约 3 0 6 0 亿元, 3 0 6 0亿用科学记数法可表示为 ( ㊀㊀) 1 0 1 1 A . 3 0 . 6ˑ 1 0 B . 3 . 0 6ˑ 1 0 1 2 1 0 C . 0 . 3 0 6ˑ 1 0 D . 3 . 0 6ˑ 1 0 3 2 6 .计算( 2 xy ) 的结果是 ( ㊀㊀) 6 2 6 2 5 2 5 2 A . 4 x y B . 8 x y C . 4 x y D . 8 x y 7 .下列各运算中, 正确的是 ( ㊀㊀) 2 3 2 6 A . 3 a + 2 a = 5 a B .(- 3 a )= 9 a 6 2 3 2 2 C .a ː a= a D .( a + 2 )= a+ 4 8 .下列因式分解正确的是 ( ㊀㊀) 2 A .x - x y + x = x ( x - y ) 3 2 2 2 B .a - 2 a b + a b = a ( a - b ) 2 2 C .x - 2 x + 4= ( x - 1 )+ 3 2 D .a x - 9= a ( x + 3 ) ( x - 3 ) 9 .估计槡 6+ 1的值在 ( ㊀㊀) A . 2到 3之间 B . 3到 4之间 C . 4到 5之间 D . 5到 6之间 1 0 .已知实数 m 、 n在数轴上的对应点的位置如图所示, ㊀㊀) 则下列判断正确的是 ( A .m> 0 B .n < 0 第1 0题图 C .m n < 0 D .m- n > 0 2 1 1 .若 m- n =- 1 , 则( m- n ) - 2 m+ 2 n 的值是 ( ㊀㊀) A . 3 B .各式计算正确的是 ( ㊀㊀) 2 1 1 - 2 A . 1 8-槡 3 2=- 2 B .(- 3 ) =- 槡 槡 9 0 2 .a = 1 D .槡 (- 2 ) =- 2 C 填空题( 本大题共 9 个小题, 每小题 3 分, 共2 7 分) 二、 1 3 . 9的平方根是 ㊀㊀㊀㊀ . x - 4 1 4 .当 x = ㊀㊀㊀㊀ 时, 分式 的值为 0 . x + 2 3 槡 1 5 .计算: 2 7- = ㊀㊀㊀㊀ . 槡 2 6 .比 较 大 小: 7㊀ ㊀ ㊀ ㊀ 槡 5 0 . ( 填 “<” 、 “=” 或 1 “> ” ) 1 3 7 .分解因式: x - 4 x = ㊀㊀㊀㊀ . 8 .若 | b - 1 | +| a - 4 | = 0 , 则a - 4 b = ㊀㊀㊀㊀ . 1 1 9 .按照下图所示的操作步骤, 若输入 x 的值为 2 , 则输 出的值为 ㊀㊀㊀㊀ . 第1 9题图 3 0 2 0 .计算: (- 2 )+ ( 3- 1 )= ㊀㊀㊀㊀ . 槡 2 1 . 某校艺术班同学每人都会弹钢琴或古筝, 其中会弹 钢琴的人数比会弹古筝的人数多 1 0人, 两种都会 设会弹古筝的有 m人, 则该班同学共有 的有 7人, ㊀㊀㊀㊀ 人( 用含有 m的代数式表示) . 解答题 ( 共 8题, 满分 4 9分) 三、 2 0 1 5 - 1 0 2 2 .( 4分) 计算: (- 1 ) - 2 + s i n 3 0 ʎ + ( 3 . 1 4 ) . π- 1 -1 0 2 3 .( 4分) 计算: 8- 2 s i n 4 5 ʎ + ( 2- ) - ( ) . π 槡 3
