静电场习题课
合集下载
第一章(5)习题课

∴
E
0,
( r R)
E的方向垂直轴线沿径向, > 0则背离轴线;
R ˆ, ( r R ) r 0r
< 0则指向轴线。
11、无限大的均匀带电平面,电荷面密度为,P点与 平面的垂直距离为d,若取平面的电势为零,则P点的 电势 V p d / 2 0 ,若在P点由静止释放一个电子(其 质量为m,电量绝对值为e)则电子到达平面的速率为:
3、一均匀静电场,场强 E (400i 600 j )V m 1 , 则点a(3、2)和点b(1、0)之间的电势差为 Vab 2000V
解 : E 400i 600 j
b b a a
dl dxi dyj
Vab E dl (400i 600 j ) (dxi dyj )
侧 面 EdS E 侧 面 dS 2πrhE
(1) r < R时,
qi 0 ,
qi 由高斯定理 Φ ε0
即 2πrhE 0, 得 E 0 (2) r > R时, q i 2πRhσ ,
qi 由高斯定理 Φ ε0
σR 即 2πrhE 2πRhσ / ε0 , 得 E ε0 r
2
10.( 第一章习题二 .9) 无限长均匀带电圆柱面,电荷 面密度为,半径为R,求圆柱面内外的场强分布。
解:作一半径为r,高为h的同轴圆柱面
R r
E
为高斯面, 根据对称性分析,圆柱面 侧面上任一点的场强大小相等, 方向
h E
S
ˆ r
沿矢径方向。 Φ S E dS 上底 E dS 下底 E dS 侧面 E dS
14静电场习题课

0
X
由于左右半圆环电荷分布的对称性,合场强的y分量抵消 由于左右半圆环电荷分布的对称性,合场强的y
λ dl + )=- dEx=dEcos( π φ 2cos φ 4ππR 0 λR 0 2 =- d 2cosφ φ 4ππR 0
λ0 2π 2 Ex=- ∫ cos φd φ 4πε R 0 0 λ0 2π 1-cos 2φ =- dφ ∫ 0 4πε R 2 0 λ0 =- 4ε0 R
2
d
•
⇒ E = 0 试指出其错误。 试指出其错误。
答:所选球面上场强的大小不处处相等,不能用: 所选球面上场强的大小不处处相等,不能用:
E • dS = E • 4πr ∫∫
S
2
〔例5〕已知空间电场强度分布为 〕 求(1)通过图示立方体的电通量, )通过图示立方体的电通量, (2)该立方体内的总电荷是多少? )该立方体内的总电荷是多少? 解:(1) :( )
q ∴U 0= =U球 4πε r 0
〔例14〕正电荷均匀分布在半径为R的球形体积内,电荷体 〕正电荷均匀分布在半径为R的球形体积内, 密度为ρ,求球内a点与球外b点的电势差时, ρ,求球内 密度为ρ,求球内a点与球外b点的电势差时,得出结果
R O
σ
x
X
σ -σ x E= i + 〔1- i〕 2 2 2ε 2ε R +x 0 0 σ x = i 2 2 2ε R +x 0
U= E •d l ∫Ecos π = -E(-dx) = dl ∫ ∫
0 x 0 x 0 x
σ 0 x 注意符号变换! 注意符号变换! dx = ∫ 2 x 2 2ε R +x 0 -1 σ 01 2 2 = ∫(R +x ) 2d(R 2+x2) x 2ε 2 0 σ 1 (R +x )2 0 σ = 〔 • 〕 = 〔R- R 2+x2〕 x 1 2ε 2 2ε 0 0 2
X
由于左右半圆环电荷分布的对称性,合场强的y分量抵消 由于左右半圆环电荷分布的对称性,合场强的y
λ dl + )=- dEx=dEcos( π φ 2cos φ 4ππR 0 λR 0 2 =- d 2cosφ φ 4ππR 0
λ0 2π 2 Ex=- ∫ cos φd φ 4πε R 0 0 λ0 2π 1-cos 2φ =- dφ ∫ 0 4πε R 2 0 λ0 =- 4ε0 R
2
d
•
⇒ E = 0 试指出其错误。 试指出其错误。
答:所选球面上场强的大小不处处相等,不能用: 所选球面上场强的大小不处处相等,不能用:
E • dS = E • 4πr ∫∫
S
2
〔例5〕已知空间电场强度分布为 〕 求(1)通过图示立方体的电通量, )通过图示立方体的电通量, (2)该立方体内的总电荷是多少? )该立方体内的总电荷是多少? 解:(1) :( )
q ∴U 0= =U球 4πε r 0
〔例14〕正电荷均匀分布在半径为R的球形体积内,电荷体 〕正电荷均匀分布在半径为R的球形体积内, 密度为ρ,求球内a点与球外b点的电势差时, ρ,求球内 密度为ρ,求球内a点与球外b点的电势差时,得出结果
R O
σ
x
X
σ -σ x E= i + 〔1- i〕 2 2 2ε 2ε R +x 0 0 σ x = i 2 2 2ε R +x 0
U= E •d l ∫Ecos π = -E(-dx) = dl ∫ ∫
0 x 0 x 0 x
σ 0 x 注意符号变换! 注意符号变换! dx = ∫ 2 x 2 2ε R +x 0 -1 σ 01 2 2 = ∫(R +x ) 2d(R 2+x2) x 2ε 2 0 σ 1 (R +x )2 0 σ = 〔 • 〕 = 〔R- R 2+x2〕 x 1 2ε 2 2ε 0 0 2
05静电场——习题课
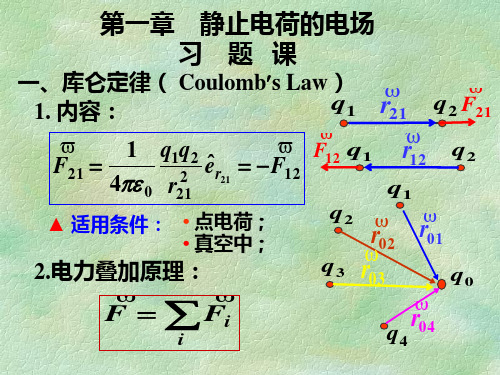
1.14(1)点电荷 位于边长为 的正立方体的中心, ( )点电荷q位于边长为 的正立方体的中心, 位于边长为a 通过此立方体的每一面的电通量各是多少? 通过此立方体的每一面的电通量各是多少? (2)若电荷移至正方体的一个顶点上,那么通过每 )若电荷移至正方体的一个顶点上, 个面的电通量又各是多少? 个面的电通量又各是多少? q 解: 1)由于立方体的 6 个侧面对于其 ( ) ● 中心对称, 则由Gauss定理知,通过各 定理知, 中心对称, 则由 定理知 个面的电通量都相等。 个面的电通量都相等。且等于整个闭合 q ● 高斯面电能量的六分之一, 高斯面电能量的六分之一,所以每个面 通过的电通量应为 q / (6ε0)。 。 填空题1039 (本题 分)在边长为 的正 本题3分 在边长为a的正 填空题 a 方形平面的中垂线上,距中心o点 方形平面的中垂线上,距中心 点a/2 处 q 有一电量q的正电荷,则通过该平面的电 有一电量 的正电荷, 的正电荷 ● a a/2 场强度通量为 q / (6ε0) 。 为边长作一个正六面体。 解:以a 为边长作一个正六面体。
ε0
E = 0 (r < a ) r > a , q int = 2π al σ , E 在筒外, 在筒外, δa (r ≥ a ) E = ε 0r o E-r 曲线如图。 曲线如图。
E∝1 r
a
r
1.18 两个无限长同轴圆筒半径分别为R1和R2,单位长 两个无限长同轴圆筒半径分别为 度带电量分别为+λ和 。求内筒内、 度带电量分别为 和-λ。求内筒内、两筒间及外筒外的 电场分布。 电场分布。 根据电场分布的轴对称性, 解:根据电场分布的轴对称性,可以选与圆筒同轴的圆 柱面(上下封顶 作高斯面。再根据高斯定律即可得出: 上下封顶)作高斯面 柱面 上下封顶 作高斯面。再根据高斯定律即可得出: 在筒内, 在筒内,r < R1 : E = 0 在筒间, 在筒间, R1 < r < R2 :
静电习题课

5、给出电场强度的方向
xdq dE 2 2 3/ 2 4 0 ( r x )
哈尔滨工程大学理学院
静电场习题课
y
dl R r O x R x R x
y
r
O dE
r R sin ,
x R cos ,
dl Rd
E
/2
0
2R 3 sin cos d 3 4 0 40 R
哈尔滨工程大学理学院
静电场习题课 2. 一锥顶角为θ的圆台,上下底面半径分别为R1和R2 , 在它的侧面上均匀带电,电荷面密度σ,求:顶角O的 电势。(以无穷远处电势为零点)
R1
R2
哈尔滨工程大学理学院
静电场习题课 1、判断带电体类型(均匀的连续面分布) 2、选坐标 3、找微元
dq ds
4 r q U 4 r
i 1 0
i
连续分布的带电体 场无对称性
U
dq 4 r
0
场有对称性
哈尔滨工程大学理学院
U P E dl
P
静电场习题课
F
定理
D ds q
0
qq ˆ r 4 r 1
1 2 2
i
有源场
s
静 电 学
方向沿x正方向
电荷元在球面电荷电场中具有电势能: dW = (qdx) / (40 x) 整个线电荷在电场中具有电势能:
q W 4 0
哈尔滨工程大学理学院
r0 l r0
r0 l dx q ln x 4 0 r0
静电场习题课 8.一电容器由两个很长的同轴薄圆筒组成,内、外圆筒半 径分别为R1 = 2 cm,R2 = 5 cm,其间充满相对介电常量 为r 的各向同性、均匀电介质.电容器接在电压U = 32 V 的电源上,(如图所示),试求距离轴线R = 3.5 cm处的A点 的电场强度和A点与外筒间的电势差.
xdq dE 2 2 3/ 2 4 0 ( r x )
哈尔滨工程大学理学院
静电场习题课
y
dl R r O x R x R x
y
r
O dE
r R sin ,
x R cos ,
dl Rd
E
/2
0
2R 3 sin cos d 3 4 0 40 R
哈尔滨工程大学理学院
静电场习题课 2. 一锥顶角为θ的圆台,上下底面半径分别为R1和R2 , 在它的侧面上均匀带电,电荷面密度σ,求:顶角O的 电势。(以无穷远处电势为零点)
R1
R2
哈尔滨工程大学理学院
静电场习题课 1、判断带电体类型(均匀的连续面分布) 2、选坐标 3、找微元
dq ds
4 r q U 4 r
i 1 0
i
连续分布的带电体 场无对称性
U
dq 4 r
0
场有对称性
哈尔滨工程大学理学院
U P E dl
P
静电场习题课
F
定理
D ds q
0
qq ˆ r 4 r 1
1 2 2
i
有源场
s
静 电 学
方向沿x正方向
电荷元在球面电荷电场中具有电势能: dW = (qdx) / (40 x) 整个线电荷在电场中具有电势能:
q W 4 0
哈尔滨工程大学理学院
r0 l r0
r0 l dx q ln x 4 0 r0
静电场习题课 8.一电容器由两个很长的同轴薄圆筒组成,内、外圆筒半 径分别为R1 = 2 cm,R2 = 5 cm,其间充满相对介电常量 为r 的各向同性、均匀电介质.电容器接在电压U = 32 V 的电源上,(如图所示),试求距离轴线R = 3.5 cm处的A点 的电场强度和A点与外筒间的电势差.
第6章 静电场习题课

E1
1 ∴ ρ = ε 0 (E 2 − E1 h
)
h
∆S
S
=4.43×10-13 C/m3
(1)
E2
(2) 设地面面电荷密度为σ.由于电荷只分布在地表面, 由于电荷只分布在地表面, 所以电力线终止于地面,取高斯面如图 所以电力线终止于地面,取高斯面如图(2) 1 v 1 v ∆ 由高斯定理 ∫∫ E · dS = ∑ qi -E∆S= ε σ ∆S ε0 0 =-8.9 ∴σ =-ε 0 E=- ×10-10 C/m3 =-
1-2 题图
以正电荷为中心作一边长为a/2的立方体形的高斯面 以正电荷为中心作一边长为 的立方体形的高斯面 由高斯定理, 由高斯定理,总通量为 φ =
q
ε0 q 则通过一面的电通量为 φ = 6ε 0
5. 一半径为 的带电球体,其电荷体密度分布为 一半径为R的带电球体 的带电球体, ρ = 0 (r>R) ρ = Ar (r≤R) , A为一常量.试求球体内外的场强分布. 为一常量.试求球体内外的场强分布. 为一常量
S2
ε0
2
⋅d
ρd ⇒ Ex = 2ε 0
φ
1. 带电细线弯成半径为 的半圆形 电荷线密度为 λ = λ0 sin φ 带电细线弯成半径为R的半圆形 的半圆形,电荷线密度为 式中λ 为一常数, 为半径R与 轴所成的夹角 如图所示. 轴所成的夹角, 式中 0为一常数,Φ为半径 与x轴所成的夹角,如图所示. 试求环心O处的电场强度 处的电场强度. 试求环心 处的电场强度. 处取电荷元, 解:在 φ 处取电荷元,其电荷为
v v v r1 − r2 = a
3ε 0
v ρ v ∴E = a 3ε 0
点在空腔中位置无关。 与P点在空腔中位置无关。 点在空腔中位置无关
1 ∴ ρ = ε 0 (E 2 − E1 h
)
h
∆S
S
=4.43×10-13 C/m3
(1)
E2
(2) 设地面面电荷密度为σ.由于电荷只分布在地表面, 由于电荷只分布在地表面, 所以电力线终止于地面,取高斯面如图 所以电力线终止于地面,取高斯面如图(2) 1 v 1 v ∆ 由高斯定理 ∫∫ E · dS = ∑ qi -E∆S= ε σ ∆S ε0 0 =-8.9 ∴σ =-ε 0 E=- ×10-10 C/m3 =-
1-2 题图
以正电荷为中心作一边长为a/2的立方体形的高斯面 以正电荷为中心作一边长为 的立方体形的高斯面 由高斯定理, 由高斯定理,总通量为 φ =
q
ε0 q 则通过一面的电通量为 φ = 6ε 0
5. 一半径为 的带电球体,其电荷体密度分布为 一半径为R的带电球体 的带电球体, ρ = 0 (r>R) ρ = Ar (r≤R) , A为一常量.试求球体内外的场强分布. 为一常量.试求球体内外的场强分布. 为一常量
S2
ε0
2
⋅d
ρd ⇒ Ex = 2ε 0
φ
1. 带电细线弯成半径为 的半圆形 电荷线密度为 λ = λ0 sin φ 带电细线弯成半径为R的半圆形 的半圆形,电荷线密度为 式中λ 为一常数, 为半径R与 轴所成的夹角 如图所示. 轴所成的夹角, 式中 0为一常数,Φ为半径 与x轴所成的夹角,如图所示. 试求环心O处的电场强度 处的电场强度. 试求环心 处的电场强度. 处取电荷元, 解:在 φ 处取电荷元,其电荷为
v v v r1 − r2 = a
3ε 0
v ρ v ∴E = a 3ε 0
点在空腔中位置无关。 与P点在空腔中位置无关。 点在空腔中位置无关
静电场习题课

Q2 Q2 C2 , W2 , W1:W2 2: 1 ; 串:W1 2C1 2C 2 C1
1 1 C1 2 2 1: 2; 并:W1 C1U , W2 C 2U , W1:W2 2 2 C2
12. 若把电子想象为一个相 对介电常数 r 1 的球体, 它的电荷 e 在球体内部均匀分布, 假设电子的静电能 量 m0 c 2 时,求电子的半径R。
②电势
UP
P(零点) 0
P
W PP0 E dl = q0
是从带电体在电场力作用下移动时,电场力对 它做功而引入的描述电场本身性质的又一物理量。
q 1 点电荷 U , 点电荷系 U= 4 0 r 4 0 1 dq 电荷连续分布 U 4 0 r 1 qi i ri
q q 定义:C , C , U U1 U 2 孤立导体球C 4 0 R, 平行板电容器 C
0S
d
,
4 0 R1 R2 2 0 L 球形电容器C , 圆柱形电容器 C R2 R1 ln R2 / R1
⑤电极化强度矢量
P
pe
V
⑥电位移矢量 D o E P, 对各向同性介质 D 0 r E E
q v0
x
O
2 rdr
4 0 r 2 x 2
b
R rdr 2 2 U ( x R x) 2 2 0 2 0 2 0 r x
R 当 x 0, U 0 。 当 x b, U b ( b 2 R 2 b) 2 0 2 0
静电场习题课
一、小结 1.基本概念:①电场强度矢量
F E q0
最新静电场习题课(北邮版08级用[1].)
![最新静电场习题课(北邮版08级用[1].)](https://img.taocdn.com/s3/m/97411f3caeaad1f347933f61.png)
A.导体是个等势体,导体表面是个等势面。
B. 导体内部各点(宏观点)净余电荷为零;电荷只 能分布在表面。
C. 导体表面附近一点的总电场强度方向
D. 与导体表面垂直;场强大小与导体 E. 表面对应点的电荷面密度成正比。
E
0
1 2 3 4
例:设静电平衡后E,va金lu属ati板on各on面ly.所带
ea电•te当荷d w两面it板密hCA带度ospp等之yors量i间ge.h异S的tl2i号关d0e0电s系4f-荷o2r0 时.11 N1 :EA T4 s1p3 ,o.5 s4= e2 C0 P l,it ey n2L3 ttP dr.o3file 5.2.0
23. 接地线的存在意味着: A.导体的电势为零;
B.接地线只提供导体与地交换电荷的通道,并不 保证导体腔外壁上的电荷在任何情况下都为零。
例:如图,两导体板分别带qa和
2 3
qb当一导体接地时,求两板之间
的场强。E 2 qa
S
ea222t564e...d电w有D i孤位t介h C立移A质o0 s导矢ppr 时yE o体量r si的ge= 0的.hD S高tl的电2EiE 斯d 0v引容e0a0s定4sl入uf-o理2art0i.1CoN1n EAoe Tqns pl3yo..5sS D eCPlditS eyn Lqt atPidr.q oq0 fiible 5.2.0
(当电荷分布具有一定的对称性时,用高斯定理很容易求
出场强分布,这种情况下用该式求电势较方便) 外
例: 半径为R,带电量为 q 的均
内
匀带电球面的电场中的电势分布。
R
eateUd外 with4CAoq spp外 yorrsige.hStl2Eid0ve0Uas4l内uf-o=2art0i.1o4N1nqEAoT外nsRpl3yo..5seCPliteynLt tPdr.ofile 5.2.0
静电场习题课

O
原电荷
P点E 1
2 0
R
圆孔
P点
E220(1
x) x2R2
x EE1E22 x2R2
E
PX
三.“无限”带电体零电势点的选取
1.求无限长均匀带电直线的电势分布
场强分布 E
2 0r
由定义
uPEdr r 20rdr
PQ
r
发散
R
选有限远为电势零点( Q )
uPR rEd 2 r0rd r20ln R r
2
二.补偿法求场强
d
1.带电圆弧 已知: R50 cm
Eo
d2cm q3.12109C
求: Eo
o
R
解:圆弧
q 2 R
带电园环
园弧上电荷
空隙
o处的 E1 0
o 点电荷
处的 E24q0 R240 d R2
d Eo E2 40R2
2. 球体内挖一空腔
已知: R r d
求: Eo
Eo
❖证明空腔内为均匀电场
解:
0处
原电荷
E1 0
R Eo r
0
0
d
空腔
0 处
dq 4r3
sE2dsE24d2s0
3
0
E2
4r3
3
40d2
r3 30d2
r3 Eo E2 30d2
O 点场强的计算
0 处
空腔
原电荷
dq 4d3
sE1dsE14d2s0
3
0
0 处
E2 0
E1
4d3
3
4 0d2
d 30
R
0
Eo
dy
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
2
(2)两离子初速度分别为 v、v/,则
L 2v L qE n m
L 2v l′ + qE = v m
L 2m Δt=t-t′ = (v v ) vv qE
L 2m 0 要使 Δt=0,则须 vv qE 2mvv 所以:E= qL
7.如图所示,同一竖直平面内固定着两水平绝缘细杆 AB、CD,长 均为 L,两杆间竖直距离为 h,BD 两端以光滑绝缘的半圆形细杆 相连,半圆形细杆与 AB、CD 在同一竖直面内,且 AB、CD 恰为半 圆形圆弧在 B、D 两处的切线,O 为 AD、BC 连线的交点,在 O 点 固定一电量为 Q 的正点电荷.质量为 m 的小球 P 带正电荷,电量 为 q,穿在细杆上,从 A 以一定初速度出发,沿杆滑动,最后可 到达 C 点.已知小球与两水平杆之间动摩擦因数为μ ,小球所受 库仑力始终小于小球重力.求: (1) P 在水平细杆上滑动时受摩擦力的极大值和极小值; (2) P 从 A 点出发时初速度的最小值.
1 2 -mgh-2mg·2L=0- 2 mv0 ,
得 v0= 2 gh(h 2L) .
8.一个质量为m,带有电荷-q的小物体,可在倾角 为θ 的绝缘斜面上运动,斜面底端有一与斜面垂 直的固定绝缘挡板,斜面顶端距底端的高度为h, 整个斜面置于匀强电场中,场强大小为E,方向水 平向右,如图所示.小物体与斜面的动摩擦因数 为μ ,且小物体与档板碰撞时不损失机械能。求: (1) 为使小物体能从静止开始沿斜面下滑,μ 、q、 E、θ 各量间必须满足的关系。 (2) 小物体自斜面顶端从静止开始沿斜面下滑到 停止运动所通过的总路程。
6.飞行时间质谱仪可通过测量离子飞行时间得到离子的荷质比 q/m,如 图 1。 带正电的离子经电压为 U 的电场加速后进入长度为 L 的真空管 AB, 可测得离子飞越 AB 所用时间 t1。改进以上方法,如图 2,让离子飞越 AB 后进入场强为 E(方向如图)的匀强电场区域 BC,在电场的作用下 离子返回 B 端,此时,测得离子从 A 出发后飞行的总时间 t2, (不计离 子重力) ⑴忽略离子源中离子的初速度, ①用 t1 计算荷质比; ②用 t2 计算荷质比。
(2)根据题意,小物体最终停在底端挡板处,由动能定理有:
mgh qEh cot 解得 S (mg cos qE sin )
9.一质量为 m、电荷量为 q 的小球,从 O 点 以和水平方向成 α 角的初速度 v0 抛出,当达 到最高点 A 时, 恰进入一匀强电场中, 如图, 经过一段时间后,小球从 A 点沿水平直线运 动到与 A 相距为 S 的 A`点后又折返回到 A 点,紧接着沿原来斜上抛运动的轨迹逆方向 运动又落回原抛出点,求 (1)该匀强电场的场强 E 的大小和方向; (即求出图中的 θ 角,并在图中标明 E 的方 向) (2)从 O 点抛出又落回 O 点所需的时间。
φ
U0 o -U0 T/2 T 3T/2 2T t
解:从 t=0 时刻释放电子,如果两板间距离足够大,电子将向 右先匀加速 T/2,接着匀减速 T/2,速度减小到零后,又开始 向右匀加速 T/2,接着匀减速 T/2„„直到打在右极板上。电 子不可能向左运动; 如果两板间距离不够大, 电子也始终向右 运动,直到打到右极板上。从 t=T/4 时刻释放电子,如果两板 间距离足够大,电子将向右先匀加速 T/4,接着匀减速 T/4,速 度减小到零后,改为向左先匀加速 T/4,接着匀减速 T/4。即在 两板间振动; 如果两板间距离不够大, 则电子在第一次向右运 动过程中就有可能打在右极板上。从 t=3T/8 时刻释放电子, 如果两板间距离不够大, 电子将在第一次向右运动过程中就打 在右极板上; 如果第一次向右运动没有打在右极板上, 那就一 定会在第一次向左运动过程中打在左极板上。选 AC
m
F L
M
E
解:(1)当拉力 F0 作用于滑块 m 上,木板能够产生的最 大加速度为: a M
(mg qE)
M
2.0m / s 2
为使滑块与木板共同运动,滑块最大加速度 am≤aM 对于滑块有: F0
(mg qE) ma m
F0 (mg qE) ma m 6.0 N
⑵离子源中相同荷质比离子的 初速度不尽相同,设两个荷质 比都为q/m的离子在A端的速度 分别为v和v/(v≠v/),在改进 后的方法中,它们飞行的总时 间通常不同,存在时间差Δt, 可通过调节电场E使Δt=0。求 此时E的大小。
离 子 源
A
L
B O
离 子 源
A
L
B
C
真空管
真空管
E
U
U
图1
图2
⑴ ①设离子带电量为 q,质量为 m,经电场加速后的速度为 v,则
即为使滑块与木板之间无相对滑动,力 F0 不应超过 6.0N. (2)设滑块相对于水平面的加速度为 a1,木板的加速度为 a2,由运动学关系可知:
1 2 s1 a1t 2
对滑块: F
,
1 s 2 a 2 t 2 , s1 s 2 L 2
2 2
滑动过程中木板的加速度 a2=2.0m/s ,则可得滑块运动的加速度 a1=5.0m/s
A.因电场力分别对球 A 和球 B 做正功,故系统机械能不断增加 B.因两个小球所受电场力等大反向,故系统机械能守恒 C.当弹簧长度达到最大值时,系统机械能最小
D D.当小球所受电场力与弹簧的弹力相等时,系统动能最大
A
-
B +
E
4.已知如图,匀强电场方向水平向右,场强 6 E=1.5× V/m, 10 丝线长 l=40cm, 上端系于 O -4 点,下端系质量为 m=1.0× 10 kg,带电量为 -10 q=+4.9× 10 C 的小球,将小球从最低点 A 由静止释放,求:⑴小球摆到最高点时丝线 与竖直方向的夹角多大?⑵摆动过程中小 球的最大速度是多大?
Oθ θ A
C
E B
解:⑴这是个“歪摆” 。由已知电 场力 Fe=0.75G 摆动到平衡位置时 丝线与竖直方向成 37°角,因此 最大摆角为 74°。 ⑵小球通过平衡位置时速度最 大 。 由 动 能 定 理 : 2 1.25mg0.2l=mvB /2,vB=1.4m/s。
5.如图所示,热电子由阴极飞出时的初速忽略不计,电子发 射 装 置 的 加 速 电 压 为 U0 。 电 容 器 板 长 和 板 间 距 离 均 为 L=10cm ,下 极板 接地 。电容器 右端 到荧 光屏的 距离 也是 L=10cm。在电容器两极板间接一交变电压,上极板的电势随 时间变化的图象如左图。 (每个电子穿过平行板的时间极短, 可以认为电压是不变的)求:①在 t=0.06s 时刻,电子打在荧 光屏上的何处?②荧光屏上有电子打到的区间有多长?③屏 上的亮点如何移动?
C O P A
D
v
B
(1) 小球 O 点正一方所受的支持力最大,易得
f max
4kQq 4kQq (mg 2 ) f min (mg 2 ) , h h
(2) 经 O 点任意作一直线,与 AB、CD 相交得两点 两点处小球所受的弹力之和恒为 2mg,小球从 A 点到 C 点的过程中,运用动能定理得,
(mg qE) ma1 9.0 N
(3)在将小滑块从木板右端拉出的过程中,相同的内能增加了:
Q (mg qE) L 6.0 J
11.如图所示,光滑水平面上放有用绝缘材料制成的“L”型滑 板,其质量为 M,平面部分的上表面光滑且足够长.在距滑板 A 端为 l 的C(可 视为质点) ,在水平的匀强电场作用下,由静止开始运动.已知: M=3m, 电场强度为 E.假设物体 C 在运动及与滑板 A 端相碰过 程中电荷量不变. ⑴求物体 C 第一次与滑板 A 端相碰前瞬间的速度大小. ⑵若物体 C 与滑板 A 端相碰的时间极短,而且碰后弹回的速度 大小是碰前速度大小的 1/5,求滑板被碰后的速度大小.
2.如图所示,两平行金属板竖直放置,左极板接地,中间有小孔。 右极板电势随时间变化的规律如图所示。 电子原来静止在左极板小 孔处。 (不计重力作用)下列说法中正确的是 A.从 t=0 时刻释放电子,电子将始终向右运动,直到打到右极板 上 B.从 t=0 时刻释放电子,电子可能在两板间振动 C.从 t=T/4 时刻释放电子,电子可能在两板间振动,也可能打到 右极板上 D.从 t=3T/8 时刻释放电子,电子必将打到左极板上
本章习题课
1.在点电荷 Q 的电场中,一个 α 粒子( 4 He )通过时的轨迹如图 2 实线所示,a、b 为两个等势面,则下列判 断中正确的是( ). (A)Q 可能为正电荷,也可能为负电荷 (B)运动中.粒子总是克服电场力做功 (C)α 粒子经过两等势面的动能 Eka>Ekb C (D)α 粒子在两等势面上的电势能 Epa>Epb
由以上三式得:
E= m
v04 cos4 4 g 2 s 2 2qs
arctan
2 gs 2 v0 cos2
方向斜向上
(2)小球沿 A A 做匀减速直线运动,于 A 点折返做匀加速运动所需时间
2v0 sin 4s t g v0 cos
10.质量为 m=1.0kg、带电量 q=+2.5×10-4C 的小滑块(可视为质点) 放在质量为 M=2.0kg 的绝缘长木板的左端,木板放在光滑水平面 上,滑块与木板之间的动摩擦因数为μ =0.2,木板长 L=1.5m,开 始时两者都处于静止状态, 所在空间加有一个方向竖直向下强度为 E=4.0×104N/C 的匀强电场,如图所示.取 g=10m/s2,试求: (1)用水平力 F0 拉小滑块,要使小滑块与木板以相同的速度一 起运动,力 F0 应满足什么条件? (2)用水平恒力 F 拉小滑块向木板的右端运动,在 1.0s 末使滑 块从木板右端滑出,力 F 应为多大? (3)按第(2)问的力 F 作用,在小滑块刚刚从木板右端滑出时, 系统的内能增加了多少?(设 m 与 M 之间最大静摩擦力与它们之 间的滑动摩擦力大小相等,滑块在运动中带电量不变)
2
(2)两离子初速度分别为 v、v/,则
L 2v L qE n m
L 2v l′ + qE = v m
L 2m Δt=t-t′ = (v v ) vv qE
L 2m 0 要使 Δt=0,则须 vv qE 2mvv 所以:E= qL
7.如图所示,同一竖直平面内固定着两水平绝缘细杆 AB、CD,长 均为 L,两杆间竖直距离为 h,BD 两端以光滑绝缘的半圆形细杆 相连,半圆形细杆与 AB、CD 在同一竖直面内,且 AB、CD 恰为半 圆形圆弧在 B、D 两处的切线,O 为 AD、BC 连线的交点,在 O 点 固定一电量为 Q 的正点电荷.质量为 m 的小球 P 带正电荷,电量 为 q,穿在细杆上,从 A 以一定初速度出发,沿杆滑动,最后可 到达 C 点.已知小球与两水平杆之间动摩擦因数为μ ,小球所受 库仑力始终小于小球重力.求: (1) P 在水平细杆上滑动时受摩擦力的极大值和极小值; (2) P 从 A 点出发时初速度的最小值.
1 2 -mgh-2mg·2L=0- 2 mv0 ,
得 v0= 2 gh(h 2L) .
8.一个质量为m,带有电荷-q的小物体,可在倾角 为θ 的绝缘斜面上运动,斜面底端有一与斜面垂 直的固定绝缘挡板,斜面顶端距底端的高度为h, 整个斜面置于匀强电场中,场强大小为E,方向水 平向右,如图所示.小物体与斜面的动摩擦因数 为μ ,且小物体与档板碰撞时不损失机械能。求: (1) 为使小物体能从静止开始沿斜面下滑,μ 、q、 E、θ 各量间必须满足的关系。 (2) 小物体自斜面顶端从静止开始沿斜面下滑到 停止运动所通过的总路程。
6.飞行时间质谱仪可通过测量离子飞行时间得到离子的荷质比 q/m,如 图 1。 带正电的离子经电压为 U 的电场加速后进入长度为 L 的真空管 AB, 可测得离子飞越 AB 所用时间 t1。改进以上方法,如图 2,让离子飞越 AB 后进入场强为 E(方向如图)的匀强电场区域 BC,在电场的作用下 离子返回 B 端,此时,测得离子从 A 出发后飞行的总时间 t2, (不计离 子重力) ⑴忽略离子源中离子的初速度, ①用 t1 计算荷质比; ②用 t2 计算荷质比。
(2)根据题意,小物体最终停在底端挡板处,由动能定理有:
mgh qEh cot 解得 S (mg cos qE sin )
9.一质量为 m、电荷量为 q 的小球,从 O 点 以和水平方向成 α 角的初速度 v0 抛出,当达 到最高点 A 时, 恰进入一匀强电场中, 如图, 经过一段时间后,小球从 A 点沿水平直线运 动到与 A 相距为 S 的 A`点后又折返回到 A 点,紧接着沿原来斜上抛运动的轨迹逆方向 运动又落回原抛出点,求 (1)该匀强电场的场强 E 的大小和方向; (即求出图中的 θ 角,并在图中标明 E 的方 向) (2)从 O 点抛出又落回 O 点所需的时间。
φ
U0 o -U0 T/2 T 3T/2 2T t
解:从 t=0 时刻释放电子,如果两板间距离足够大,电子将向 右先匀加速 T/2,接着匀减速 T/2,速度减小到零后,又开始 向右匀加速 T/2,接着匀减速 T/2„„直到打在右极板上。电 子不可能向左运动; 如果两板间距离不够大, 电子也始终向右 运动,直到打到右极板上。从 t=T/4 时刻释放电子,如果两板 间距离足够大,电子将向右先匀加速 T/4,接着匀减速 T/4,速 度减小到零后,改为向左先匀加速 T/4,接着匀减速 T/4。即在 两板间振动; 如果两板间距离不够大, 则电子在第一次向右运 动过程中就有可能打在右极板上。从 t=3T/8 时刻释放电子, 如果两板间距离不够大, 电子将在第一次向右运动过程中就打 在右极板上; 如果第一次向右运动没有打在右极板上, 那就一 定会在第一次向左运动过程中打在左极板上。选 AC
m
F L
M
E
解:(1)当拉力 F0 作用于滑块 m 上,木板能够产生的最 大加速度为: a M
(mg qE)
M
2.0m / s 2
为使滑块与木板共同运动,滑块最大加速度 am≤aM 对于滑块有: F0
(mg qE) ma m
F0 (mg qE) ma m 6.0 N
⑵离子源中相同荷质比离子的 初速度不尽相同,设两个荷质 比都为q/m的离子在A端的速度 分别为v和v/(v≠v/),在改进 后的方法中,它们飞行的总时 间通常不同,存在时间差Δt, 可通过调节电场E使Δt=0。求 此时E的大小。
离 子 源
A
L
B O
离 子 源
A
L
B
C
真空管
真空管
E
U
U
图1
图2
⑴ ①设离子带电量为 q,质量为 m,经电场加速后的速度为 v,则
即为使滑块与木板之间无相对滑动,力 F0 不应超过 6.0N. (2)设滑块相对于水平面的加速度为 a1,木板的加速度为 a2,由运动学关系可知:
1 2 s1 a1t 2
对滑块: F
,
1 s 2 a 2 t 2 , s1 s 2 L 2
2 2
滑动过程中木板的加速度 a2=2.0m/s ,则可得滑块运动的加速度 a1=5.0m/s
A.因电场力分别对球 A 和球 B 做正功,故系统机械能不断增加 B.因两个小球所受电场力等大反向,故系统机械能守恒 C.当弹簧长度达到最大值时,系统机械能最小
D D.当小球所受电场力与弹簧的弹力相等时,系统动能最大
A
-
B +
E
4.已知如图,匀强电场方向水平向右,场强 6 E=1.5× V/m, 10 丝线长 l=40cm, 上端系于 O -4 点,下端系质量为 m=1.0× 10 kg,带电量为 -10 q=+4.9× 10 C 的小球,将小球从最低点 A 由静止释放,求:⑴小球摆到最高点时丝线 与竖直方向的夹角多大?⑵摆动过程中小 球的最大速度是多大?
Oθ θ A
C
E B
解:⑴这是个“歪摆” 。由已知电 场力 Fe=0.75G 摆动到平衡位置时 丝线与竖直方向成 37°角,因此 最大摆角为 74°。 ⑵小球通过平衡位置时速度最 大 。 由 动 能 定 理 : 2 1.25mg0.2l=mvB /2,vB=1.4m/s。
5.如图所示,热电子由阴极飞出时的初速忽略不计,电子发 射 装 置 的 加 速 电 压 为 U0 。 电 容 器 板 长 和 板 间 距 离 均 为 L=10cm ,下 极板 接地 。电容器 右端 到荧 光屏的 距离 也是 L=10cm。在电容器两极板间接一交变电压,上极板的电势随 时间变化的图象如左图。 (每个电子穿过平行板的时间极短, 可以认为电压是不变的)求:①在 t=0.06s 时刻,电子打在荧 光屏上的何处?②荧光屏上有电子打到的区间有多长?③屏 上的亮点如何移动?
C O P A
D
v
B
(1) 小球 O 点正一方所受的支持力最大,易得
f max
4kQq 4kQq (mg 2 ) f min (mg 2 ) , h h
(2) 经 O 点任意作一直线,与 AB、CD 相交得两点 两点处小球所受的弹力之和恒为 2mg,小球从 A 点到 C 点的过程中,运用动能定理得,
(mg qE) ma1 9.0 N
(3)在将小滑块从木板右端拉出的过程中,相同的内能增加了:
Q (mg qE) L 6.0 J
11.如图所示,光滑水平面上放有用绝缘材料制成的“L”型滑 板,其质量为 M,平面部分的上表面光滑且足够长.在距滑板 A 端为 l 的C(可 视为质点) ,在水平的匀强电场作用下,由静止开始运动.已知: M=3m, 电场强度为 E.假设物体 C 在运动及与滑板 A 端相碰过 程中电荷量不变. ⑴求物体 C 第一次与滑板 A 端相碰前瞬间的速度大小. ⑵若物体 C 与滑板 A 端相碰的时间极短,而且碰后弹回的速度 大小是碰前速度大小的 1/5,求滑板被碰后的速度大小.
2.如图所示,两平行金属板竖直放置,左极板接地,中间有小孔。 右极板电势随时间变化的规律如图所示。 电子原来静止在左极板小 孔处。 (不计重力作用)下列说法中正确的是 A.从 t=0 时刻释放电子,电子将始终向右运动,直到打到右极板 上 B.从 t=0 时刻释放电子,电子可能在两板间振动 C.从 t=T/4 时刻释放电子,电子可能在两板间振动,也可能打到 右极板上 D.从 t=3T/8 时刻释放电子,电子必将打到左极板上
本章习题课
1.在点电荷 Q 的电场中,一个 α 粒子( 4 He )通过时的轨迹如图 2 实线所示,a、b 为两个等势面,则下列判 断中正确的是( ). (A)Q 可能为正电荷,也可能为负电荷 (B)运动中.粒子总是克服电场力做功 (C)α 粒子经过两等势面的动能 Eka>Ekb C (D)α 粒子在两等势面上的电势能 Epa>Epb
由以上三式得:
E= m
v04 cos4 4 g 2 s 2 2qs
arctan
2 gs 2 v0 cos2
方向斜向上
(2)小球沿 A A 做匀减速直线运动,于 A 点折返做匀加速运动所需时间
2v0 sin 4s t g v0 cos
10.质量为 m=1.0kg、带电量 q=+2.5×10-4C 的小滑块(可视为质点) 放在质量为 M=2.0kg 的绝缘长木板的左端,木板放在光滑水平面 上,滑块与木板之间的动摩擦因数为μ =0.2,木板长 L=1.5m,开 始时两者都处于静止状态, 所在空间加有一个方向竖直向下强度为 E=4.0×104N/C 的匀强电场,如图所示.取 g=10m/s2,试求: (1)用水平力 F0 拉小滑块,要使小滑块与木板以相同的速度一 起运动,力 F0 应满足什么条件? (2)用水平恒力 F 拉小滑块向木板的右端运动,在 1.0s 末使滑 块从木板右端滑出,力 F 应为多大? (3)按第(2)问的力 F 作用,在小滑块刚刚从木板右端滑出时, 系统的内能增加了多少?(设 m 与 M 之间最大静摩擦力与它们之 间的滑动摩擦力大小相等,滑块在运动中带电量不变)
