山西省长治二中2020学年高一数学上学期期末考试试题
山西省2020-2021学年高一上学期期末考试数学试题 含答案

的单调性,并用定义证明.
(2)设g(x)=3f(x)−3e
,试判断函数
x
(x)=sinx+3sinxcosx.
2
17.(10分)已知函数f
f(x)
(1)求函数
的单调递增区间;
5
x0,
f(x)m
恒成立,求实数m的取值范围.
(2)当
时,
12
(x)=x−ax−a−1
R
18.(10分)已知函数f
(1)若关于x的不等式
.
30=lg10+
M
13
N
−
由已知可得:
,
40=Mlg10+N
−12
30=−13M+N
M=10
即
,解之得
,
40=−12M+N
N=160
所以解析式为:
(2)由已知可得:当40D70
所以
D=10lgI+160.
时,适合人与人交流谈话,
4010lgI+16070,
即:
−12010lgI−90,
9
−12lgI−9
(x)=
综上,f
.
max4−4,0
aa
[0,1],则u[6,9]
.
u=x+2x+6x
(2)令
2
,
g(x)
u[6,9]
,
y=
logu
函数
换元得:
,
3
(x)=log9=2
根据函数的单调性,可得g
.
max
3
1
x,2
x
[0,1],
2
由任意的
山西省长治市第二中学2020学年高一数学上学期期末考试试题

山西省长治市第二中学2020学年高一数学上学期期末考试试题【满分150分,考试时间120分钟】一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合 {}2420,0,1x M x x x N x x Z x ⎧-⎫=-->=≤∈⎨⎬+⎩⎭,则M N ⋂所有子集个数为A .3B .4C .7D .82.如图是某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为 A .85,84 B .84,85 C .86,84 D. 84,84 3.已知{}1,1,2,3α∈-,则使函数y x α=的值域为R ,且为奇函数的所有α的值为 A .1,3B .1,1-C .1,3-D .1,1,3-4.在区间(0,5)内任取一个数,则使23x -有意义的概率为 A .25B .12C .35D .7105.将一个骰子抛掷一次,设事件A 表示向上的一面出现的点数不超过2,事件B 表示向上的一面出现的点数不小于3,事件C 表示向上的一面出现奇数点,则 A .A 与B 是对立事件 B .A 与B 是互斥而非对立事件 C .B 与C 是互斥而非对立事件 D .B 与C 是对立事件 6.采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,3,...,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[]1,450的人做问卷A ,编号落入区间[]451,750的人做问卷B ,其余的人做问卷C .则抽到的人中,做问卷B 的人数为A .7B .9C .10D .157.已知某地A 、B 、C 三个村的人口户数及贫困情况分别如图(1)和图(2)所示,为了解该地三个村的贫困原因,当地政府决定采用分层抽样的方法抽取10%的户数进行调査,则样本容量和抽取C 村贫困户的户数分别是A .100,20B .100,10C .200,20D .200,108.已知小张每次射击命中十环的概率都为40%,现采用随机模拟的方法估计小张三次射击恰有两次命中十环的概率,先由计算器产生0到9之间取整数值的随机数,指定2,4,6,8表示命中十环,0,1,3,5,7,9表示未命中十环,再以每三个随机数为一组,代表三次射击的结果,经随机模拟产生了如下20组随机数:321,421,292,925,274,632,800,478,598,663,531,297,396,021,506,318,230,113,507,965.据此估计,小张三次射击恰有两次命中十环的概率为A .0.25B .0.30C .0.35D .0.409.一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是A .57.2,3.6B .57.2,56.4C .62.8,63.6D .62.8,3.6 10.设{}c b a ,,m in 表示c b a ,,三者中的最小者,若函数{}x x x f x224,,2m in )(2-=,则当[]5,1∈x 时,)(x f 的值域是 A .[]32,1 B .[]14,1C .[]14,2D .[]16,1 11.已知函数()()2log 2a f x x ax =-在[]4,5上为增函数,则a 的取值范围是A .()1,4B . (]1,4C .()1,2D .(]1,212.已知函数()⎪⎩⎪⎨⎧>-≤+=1,1ln 1,222)(x x x x f x ,若32)()()(2+-=x af x f x F 的零点个数为4个时,实数a 的取值范围为 A .⎪⎭⎫ ⎝⎛+∞⋃⎥⎦⎤⎝⎛,3735,362 B .⎪⎪⎭⎫ ⎝⎛37,362 C .⎪⎭⎫⎢⎣⎡2,35 D .()+∞⋃⎥⎦⎤ ⎝⎛,235,362 二、填空题:本大题共4小题,每小题5分,共20分.13.如图,矩形的长为6,宽为3,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆为125颗,则我们可以估计出阴影部分的面积约为________.14.一个样本a ,3,5,7的平均数是b ,且a ,b 是方程2540x x -+=的两根,则这个样本的方差是 .15.一只蚂蚁在边长分别为6,8,10的ABC ∆区域内随机爬行,则其恰在到顶点A 或顶点B 或顶点C 的距离小于1的地方的概率为___________. 16.下列说法:①函数()212log 23y x x =--的单调增区间是(),1-∞;②若函数()y f x =定义域为R 且满足()()11f x f x -=+,则它的图象关于y 轴对称; ③函数()()1xf x x R x=∈+的值域为()1,1-; ④函数23y x =-的图象和直线()y a a R =∈的公共点个数是m ,则m 的值可能是0,2,3,4;⑤若函数()()2251f x x ax a =-+>在[]1,3x ∈上有零点,则实数a 的取值范围是5,3⎡⎤⎣⎦. 其中正确的序号是_________.三、解答题:本大题共70分 17.(本题满分10分)某学校高二年级举办了一次数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行 序号分组组中值频数频率(i ) (分数) (G i ) (人数) (F i ) 1 65 6 ① 2 75 ② 0.40 3 85 ③ 0.24 495④0.24合计 501(1)填出频率分布表中的空格;(2)为鼓励更多的学生了解“数学史”知识,成绩不低于80分的同学能获奖,请估计在参加的800名学生中大概有多少名学生获奖?(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的S 的值.18.(本题满分12分)口袋中有质地、大小完全相同的5个小球,编号分别为1、2、3、4、5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸出一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.(1)求甲赢且编号的和为6的事件发生的概率; (2)这种游戏规则公平吗?试说明理由.19.(本题满分12分)某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:单价x 元 9 9.2 9.4 9.6 9.8 10 销量y 件1009493908578(1)若销量y 与单价x 服从线性相关关系,求该回归方程;(2)在(1)的前提下,若该产品的成本是5元/件,问:产品该如何确定单价,可使工厂获得最大利润。
2020年山西省长治市县第二中学高一数学理期末试卷含解析

2020年山西省长治市县第二中学高一数学理期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 若实数满足,则的最大值为 ( )(A)(B)(C)0 (D)参考答案:B略2. 我国古代数学家刘徽在《九章算术注》中提出割圆术:“割之弥细,所失弥少,割之割,以至于不可割,则与圆合体,而无所失矣”,即通过圆内接正多边形细割圆,并使正多边形的面积无限接近圆的面积,进而来求得较为精确的圆周率.如果用圆的内接正n边形逼近圆,算得圆周率的近似值记为,那么用圆的内接正2n边形逼近圆,算得圆周率的近似值加可表示成()A. B. C. D.参考答案:C【分析】设圆的半径为,由内接正边形的面积无限接近圆的面积可得:,由内接正边形的面积无限接近圆的面积可得:,问题得解.【详解】设圆的半径为,将内接正边形分成个小三角形,由内接正边形的面积无限接近圆的面积可得:,整理得:,此时,即:同理,由内接正边形的面积无限接近圆的面积可得:,整理得:此时所以故选:C【点睛】本题主要考查了圆的面积公式及三角形面积公式的应用,还考查了正弦的二倍角公式,考查计算能力,属于中档题。
3. 若函数图象关于对称,则实数的值为A. B. C. D .参考答案:C略4. 在△ABC中,若内角和边长满足,,则角A =()(A)(B)(C)(D)参考答案:A略5. 下列函数中,既是偶函数又在区间(0,+ ∞)上单调递减的是()()A.B.C.D.参考答案:C6. 设角属于第二象限,且,则角属于()A 第一象限B 第二象限C 第三象限D 第四象限参考答案:C7. 已知角的终边经过点,则A、B、C、D、参考答案:B根据正弦函数的定义得. 故选B.8. 等比数列{an}各项均为正数且,( )A. 15B.10C. 12D.参考答案:A略9. 集合A={1,3},B={1,2,3,4},则A∩B=()A.{1,2} B.{1,4} C.{1} D.{1,3}参考答案:D【考点】交集及其运算.【专题】计算题;集合思想;集合.【分析】由A与B,求出两集合的交集即可.【解答】解:∵A={1,3},B={1,2,3,4},∴A∩B={1,3},故选:D.【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.10. 函数在(-∞,+∞)上是减函数,则()A . B. C. D.参考答案:A二、填空题:本大题共7小题,每小题4分,共28分11. 幂函数f(x)的图象过点,则f(x)的解析式是______________.参考答案:设幂函数的解析式为,由题意可得:,解得:,即f(x)的解析式是.12. 已知随机事件A发生的频率是0.02,事件A出现了10次,那么共进行了________次试验.参考答案:500设共进行了n次试验,则=0.02,解得n=500.13. 已知点在直线上,且点到原点与到直线的距离相等,则点的坐标为_____.参考答案:或14. 在平面直角坐标系中,①若直线y=x+b与圆x2+y2=4相切,即圆x2+y2=4上恰有一个点到直线y=x+b的距离为0,则b的值为;②若将①中的“圆x2+y2=4”改为“曲线x=”,将“恰有一个点”改为“恰有三个点”,将“距离为0”改为“距离为1”,即若曲线x=上恰有三个点到直线y=x+b的距离为1,则b的取值范围是.参考答案:(﹣,﹣2]考点:直线和圆的方程的应用;类比推理.专题:直线与圆.分析:①利用直线和圆相切的关系进行求解.②曲线x=表示圆x2+y2=4的右半部分,由距离公式可得临界直线,数形结合可得.解答:解:①若直线y=x+b与圆x2+y2=4相切,则圆心到直线的距离d=,即|b|=2,即b=,由x=得x2+y2=4(x≥0),则对应的曲线为圆的右半部分,直线y=x+b的斜率为1,(如图),设满足条件的两条临界直线分别为m和l,根据题意,曲线上恰好有三个点到直线y=x+b的距离为1,因此其中两个交点必须在直线m″(过点(0,﹣2))和直线l″之间,设(0,﹣2)到直线m的距离为1,可得=1,解得b=﹣2,或b=2+(舍去),∴直线m的截距为﹣2,设直线l″为圆的切线,则直线l″的方程为x﹣y﹣2=0,由l到l″的距离为1可得=1,解方程可得b=,即直线l的截距为﹣,根据题意可知,直线在m和l之间,∴b的取值范围为:(﹣,﹣2]故答案为:,(﹣,﹣2].点评:本题主要考查直线和圆的综合应用,利用数形结合以及点到直线的距离公式是解决本题的关键.综合性较强,有一定的难度.15. 数列{a n}的通项公式,则该数列的前项之和等于9.参考答案:99【考点】8E:数列的求和.【分析】将数列通项化简,利用叠加法,即可求得结论.【解答】解:∵,∴∴S n=a1+a2+…+a n=+…+=令,则n=99故答案为:9916. 已知,则.参考答案:-117. 求值:= .参考答案:三、解答题:本大题共5小题,共72分。
山西省长治市第二中学校2024届高一上数学期末学业质量监测模拟试题含解析

(3)若关于 x
的方程
f
(x) a
0
在区间
0,
2
内有两个实数根
x1, x2
,记 t
a cos(x1
x2 ) ,求实数 t
的取值范围
.
19.已知函数
f
x
Asin x
A
0,
0, 0
ቤተ መጻሕፍቲ ባይዱ
2
部分图象如图所示.
的
(1)当
x
3
, 4
时,求
f
x 的最值;
(2)设 g x
f
x
2cos
6
2
x
y
sin
x
2
D.
y
sin
4x
2
8.已知在海中一孤岛 D 的周围有两个观察站 A、C ,且观察站 A 在岛 D 的正北 5 海里处,观察站 C 在岛 D 的正西方.
现在海面上有一船 B ,在 A 点测得其在南偏西 60°方向相距 4 海里处,在 C 点测得其在北偏西 30°方向,则两个观
察站 A 与 C 的距离为
4
(3)当
x
1 m
,
1 n
,
(m
0,
n
0)
时,若函数
f
(x)
值域为
2
3m,
2
3n
,求
m,
n
的值.
18.已知函数 f (x) 2 3 sin x cos x 2 cos2 x . (1)求 f ( ) 的值;
12
(2)若函数 f (x) 在区间 m, m 是单调递增函数,求实数 m 的取值范围;
c a b .
故选:C.
2020学年高一上学期数学期末考试试卷
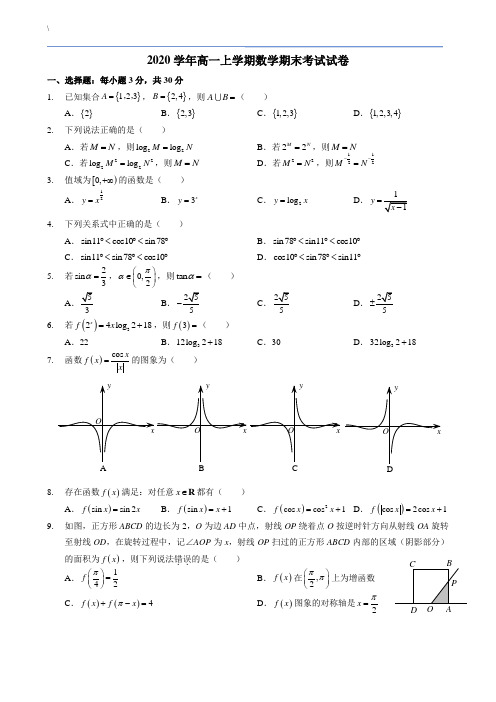
2020学年高一上学期数学期末考试试卷一、选择题:每小题3分,共30分1. 已知集合{}123A =,,,{}2,4B =,则A B =( )A .{}2B .{}2,3C .{}1,2,3D .{}1,2,3,42. 下列说法正确的是( ) A .若M N =,则22log log M N = B .若22M N =,则M N =C .若2222log log M N =,则M N =D .若22M N =,则1122MN --=3. 值域为[)0,+∞的函数是( )A .12y x =B .3x y =C .2log y x =D.y =4. 下列关系式中正确的是( ) A .sin11cos10sin78︒<︒<︒B .sin78sin11cos10︒<︒<︒C .sin11sin78cos10︒<︒<︒D .cos10sin78sin11︒<︒<︒5. 若2sin 3α=,0,2πα⎛⎫∈ ⎪⎝⎭,则tan α=( )AB. CD. 6. 若()324log 218x f x =+,则()3f =( )A .22B .312log 218+C .30D .332log 218+7. 函数()cos xf x x=的图象为( )8. 存在函数()f x 满足:对任意x ∈R 都有( )A .()sin sin 2f x x =B .()sin 1f x x =+C .()2cos cos 1f x x =+D .()cos 2cos 1f x x =+9. 如图,正方形ABCD 的边长为2,O 为边AD 中点,射线OP 绕着点O 按逆时针方向从射线OA 旋转至射线OD ,在旋转过程中,记∠AOP 为x ,射线OP 扫过的正方形ABCD 内部的区域(阴影部分)的面积为()f x ,则下列说法错误..的是( ) A .142f π⎛⎫= ⎪⎝⎭B .()f x 在,2ππ⎛⎫⎪⎝⎭上为增函数C .()()4f x f x π+-=D .()f x 图象的对称轴是2x π=D10. 设()()22212,0lg ,0x a x a x f x x x ⎧+++-≤⎪=⎨->⎪⎩,若函数()y f x =与函数()3y a x =-的图象有且只有3个公共点,则实数a 的取值范围是( )A .()[),10,-∞-+∞B .(]1,0-C .(][),10,-∞-+∞D .[]0,1二、填空题:每小题3分,共18分11.若2log a =2a = .12. 已知4sin 5α=,0,2πα⎛⎫∈ ⎪⎝⎭,则sin 2πα⎛⎫+= ⎪⎝⎭ .13. 已知扇形的圆心角为3π,半径为3,则该扇形的面积是 . 14. 已知0a >,且1a ≠ ,函数()()22,1log 1,1x ax f x x x ⎧+≤⎪=⎨->⎪⎩ ,若()02f f =⎡⎤⎣⎦ ,则a = . 15. 设函数()sin 44f x x π⎛⎫=+ ⎪⎝⎭,90,16x π⎡⎤∈⎢⎥⎣⎦.若关于x 的方程()f x a =恰好有三个根1x ,2x ,()3123x x x x <<,则12323x x x ++= .16. 设关于x 的三个方程210x ax --=,220x x a --=,e 10a x -=的实根分别为1x ,2x ,3x ,4x ,5x ,若13524x x x x x <<<<,则实数a 的取值范围是 .三、解答题:5小题,共52分17. (本题满分10分)已知集合(){}2|220A x x a x a =-++=,{}22,5,512B a a =+-.(1)若3A ∈,求实数a 的值; (2)若{}5BA =,求实数a 的值.18. (本题满分10分)已知函数()()()cos 20f x x ϕπϕ=+-<<的图象经过点1,62π⎛⎫⎪⎝⎭.(1)求ϕ的值以及函数()f x 的单调递增区间;(2)若()35f θ=,求cos 23πθ⎛⎫+ ⎪⎝⎭的值.19. (本题满分10分)已知集合1|,02xA y y x ⎧⎫⎪⎪⎛⎫==≥⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,(){}2|lg B x y ax x ==-.(1)若A B ⊆,求实数a 的取值范围; (2)若A B =∅,求实数a 的取值范围.20. (本题满分10分)已知函数()()21ax f x a x+=∈R .(1)求()f x 的单调递减区间;(2)设0a >,函数()22sin cos 1a x g x x =+,若对于任意123,34x ππ⎡⎤∈⎢⎥⎣⎦,都存在实数2x ,使得()()12g x f x = 成立,求a 的取值范围.21. (本题满分12分)已知函数()()2,f x x ax a b a b =+-+∈R .(1)若2b =,()lg y f x =⎡⎤⎣⎦在71,2x ⎡⎤∈⎢⎥⎣⎦上有意义且不单调,求a 的取值范围;(2)若集合(){}0A x f x =≤,(){}11B x f f x =+≤⎡⎤⎣⎦,且A B =≠∅,求a 的取值范围.。
山西省长治市高一上学期期末数学试卷

山西省长治市高一上学期期末数学试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共16分)1. (1分) (2019高一上·黑龙江月考) 已知,,,则 ________2. (1分)(2020·吉林模拟) 已知数列的前项和且,设,则的值等于________ .3. (1分) (2020高一下·济南月考) 已知,且,则向量的坐标是________.4. (1分)已知集合A={a,b},B={a,b,c,d,e},满足条件A⊆M⊆B的集合M的个数为________.5. (1分) (2017高一上·威海期末) 已知函数则 =________.6. (1分) (2019高一下·上海月考) 已知角是三角形一内角,且,则 ________.7. (2分) (2018高一上·杭州期中) 函数且的图象恒过定点P,则点P坐标为________;若点P在幂函数的图象上,则 ________.8. (1分) (2018高一上·定远月考) 函数,则 ________9. (2分)已知=(sinx,m+cosx),=(cosx,-m+cosx),且f(x)=•,当x[-,]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值________ ,此时x=________10. (1分) (2020高一上·那曲期末) 已知,若,则 ________.11. (1分)已知sin(α+)=,则sin(2α﹣)=________12. (1分)函数f(x)=loga|x|在(0,+∞)上单调递减,则f(﹣2)________ f(a+1)(填“<”,“=”,“>”之一).13. (1分) (2019高一下·柳江期中) 已知正方形ABCD的边长为2,E为的CD中点,则 ________.14. (1分) (2016高一下·石门期末) 给出下列命题:(1)函数y=tanx在定义域内单调递增;(2)若α,β是锐角△ABC的内角,则sinα>cosβ;(3)函数y=cos( x+ )的对称轴x= +kπ,k∈Z;(4)函数y=sin2x的图象向左平移个单位,得到y=sin(2x+ )的图象.其中正确的命题的序号是________.二、解答题 (共6题;共50分)15. (10分) (2016高一上·南京期中) 设全集为R,集合A=(﹣∞,﹣1)∪(3,+∞),记函数f(x)=的定义域为集合B(1)分别求A∩B,A∩∁RB;(2)设集合C={x|a+3<x<4a﹣3},若B∩C=C,求实数a的取值范围.16. (5分)已知向量=(6,2),=(﹣2,k),k为实数.(1)若∥,求k的值;(2)若⊥,求k的值;(3)若与的夹角为钝角,求k的取值范围.17. (10分) (2016高一上·湄潭期中) 定义在R上的奇函数f(x),当x>0时,f(x)=x﹣2(1)求函数f(x)的解析式;(2)求不等式f(x)<2的解集.18. (10分) (2018高一上·上饶月考) 已知幂函数为偶函数.(1)求的解析式;(2)若在上不是单调函数,求实数的取值范围.19. (10分) (2019高二下·长春期末) 在中,角A,B,C的对边分别是,且.(1)求角C的大小;(2)已知等差数列的公差不为零,若,且,,成等比数列,求数列的前项和 .20. (5分) (2019高一上·北碚月考) 设函数 .(Ⅰ)求的最小值,并求使取得最小值的的集合;(Ⅱ)不画图,说明函数的图像可由的图象经过怎样的变化得到.参考答案一、填空题 (共14题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题;共50分)15-1、15-2、16-1、17-1、17-2、18-1、18-2、19-1、19-2、20-1、。
山西省2020学年高一数学上学期期末考试试题

第一学期高一期末考试数学试题【满分150分,考试时间120分钟】一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}13<<-=x x A ,{}1,0,1,2,3---=B ,则=⋂B A ( ) A .{}1,0,1,2-- B .{}0,1,2,3--- C .{}0,1,2-- D .{}1,2,3--- 2.为了解高一年级1200学生的视力情况,采用系统抽样的方法,从中抽取容量为60的样本,则分段间隔为( )A .10B .20C .40D .603.用秦九韶算法计算多项式187654)(2345+++++=x x x x x x f 当4.0=x 的值时,需要做乘法和加法的次数分别是( )A .5,5B .4,5C .4,4D .5,44.如图所示的程序框图中,输出S 的值是( ) A .80 B .100 C .120 D .140 5.一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )A .至多有一次中靶B .两次都中靶C .只有一次中靶D .两次都不中靶 6.已知4log ,2,21.331.3===--c b a ,则,,a b c 的大小关系是( )A .a b c <<B .a c b <<C .b c a <<D .c b a <<7.已知函数)(x f 为奇函数,且0≥x 时,m x x f x ++=2)(,则=-)1(f ( )A .21-B .21C .2-D .2 8.如图,正方形ABCD 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是( ) A .14B .8π C .12 D .4π9.已知某射击运动员每次击中目标的概率都是0.7,现采用随机模拟的方法估计该运动员射击4次,至少击中2次的概率:先由计算器算出0~9之间取整数值的随机数,指定0,1,2表示没有击中目标,3,4,5,6,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:5727 0293 7140 9857 0347 4373 8636 9647 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 6710 4281据此估计,该射击运动员射击4次至少击中2次的概率为( )A .0.8B .0.85C .0.9D .0.9510.设奇函数()f x 在),0(+∞上为单调递减函数,且0)2(=f ,则不等式05)(2)(3≤--xx f x f 的解集为 ( )A .]2,0()0,2[⋃-B .),2[]0,2[+∞⋃-C .),2[]2,(+∞⋃--∞D .]2,0(]2,(⋃--∞ 11.已知函数()()2,log x a f x ag x x -== (0a >且1a ≠),若()()440f g -<,则()(),f x g x 在同一坐标系内的图象大致是( )A .B .C .D .12.已知定义在R 上的函数)(x f 满足)()(x f x f =-,且当0≥x 时,⎪⎩⎪⎨⎧≥-<≤+-=1,2210,1)(2x x x x f x,若对任意的]1,[+∈m m x ,不等式)()1(m x f x f +≤-恒成立,则实数m 的最大值是( ) A .1- B .21- C .31- D .31二、填空题:本大题共4小题,每小题5分,共20分. 13.将十进制数38化为二进制数为 .14.已知函数⎩⎨⎧>≤=0,log 0,3)(3x x x x f x ,若21)(=a f,则实数=a .15.运行如图所示的程序框图,设输出数据构成的集合为A ,从集合A 中任取一个元素a ,则函数ax y =, ),0(+∞∈x 是增函数的概率为 .16.已知函数22log (1),131910,322x x f x x x x ⎧-<≤⎪⎨-+>⎪⎩()=若方程m x f =)(有4个不同的实根1x ,2x ,3x ,4x ,且1234x x x x <<<,则=++))(11(4321x x x x . 三、解答题:本大题共70分17.(本题满分10分)甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如右图所示 (1)写出甲、乙的中位数和众数;(2)计算甲、乙的平均数与方差,并依此说明甲、乙两名技工哪名更为优秀.18.(本题满分12分) 某地区某农产品近几年的产量统计如表:(1)根据表中数据,建立y 关于t 的线性回归方程+=a t b y ; (2)根据线性回归方程预测2019年该地区该农产品的年产量.附:∑==∧---∑=ni ii i ni t ty y t t b 121)())((,t b y a ∧∧-=.参考数据:8.2))((61=--∑=i i iy y t t19.(本题满分12分)某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在[120,130)内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分; (2)用分层抽样的方法,在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段[120,130)内的概率.20.(本题满分12分)已知函数()()()2f x x x a =-+.(1)若()f x 的图象关于直线1x =对称,求a 的值; (2)若()f x 在区间[]0,1上的最小值是2,求a 的值.21.(本题满分12分)已知)(x f 是定义在R 上的奇函数,且当0>x 时,xx f 31)(-=.(1)求函数)(x f 的解析式;(2)当]8,2[∈x 时,不等式0)log 5()(log 222≥-+x a f x f 恒成立,求实数a 的取值范围.22.(12分)已知)(x f 满足)1(log )21()1(log )2()()(244x m x m x f x f +-+--=-+(1)讨论)(x f 的奇偶性;(2)当)(x f 为奇函数时,若方程221)2(ax f x +=-在0>x 时有实根,求实数a 的取值范围.答案1.C2.B3.A4.C5.D6.D7.C8.B9.D 10.A 11.B 12.C 13.)2(10011014. 32log 3或- 15.5316. 9 17. 解:(1)甲的中位数为2020202+=,众数为20;乙的中位数为192019.52+=,众数为23. (2)181920202122206x +++++==甲,()()()()()()2222222182019202020202021202220563S -+-+-+-+-+-==甲, 171819202323206x +++++==乙,()()()()()()22222221720182019202020232023201663S -+-+-+-+-+-==乙, 由于x x =甲乙,且22S S <甲乙,所以甲更为优秀.18.解(1)由题意可知:5.3=t ,7=y ,()5.175.25.15.0)5.0()5.1(5.2)(222222261=+++-+-+-=-∑=i i t t ,16.05.178.2)())((26161==---=∴∑∑==∧i ii i it ty y t tb ,所以44.65.316.07=⨯-=-=∧∧t b y a ∴y 关于t 的线性回归方程为44.616.0+=∧t y .(2)由(1)可得,当年份为2019年时,年份代码8=t ,此时72.744.6816.0=+⨯=∧y ,所以,可预测2019年该地区该农产品的年产量约为7.72万吨.19.解(1)分数在[120,130)内的频率为1-(0.1+0.15+0.15+0.25+0.05)=0.3.03.0=组距频率(直方图略)(2)平均分为:95×0.1+105×0.15+115×0.15+125×0.3+135×0.25+145×0.05=121. (3)由题意,[110,120)分数段的人数为:60×0.15=9人,[120,130)分数段的人数为:60×0.3=18人.∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,抽样比929186=+=k∴需在[110,120)分数段内抽取2992=⨯人,并分别记为m ,n ; 在[120,130)分数段内抽取41892=⨯人并分别记为a ,b ,c ,d ;设“从样本中任取2人,至多有1人在分数段[120,130)内”为事件A , 则基本事件有:(m ,n ),(m ,a ),(m ,b ),(m ,c ),(m ,d ),(n ,a ),(n ,b ), (n ,c ),(n ,d ),(a ,b ),(a ,c ),(a ,d ),(b ,c ),(b ,d ),(c ,d )共15种. 事件A 包含的基本事件有:(m ,n ),(m ,a ),(m ,b ),(m ,c ),(m ,d ),(n ,a ), (n ,b ),(n ,c ),(n ,d )共9种.∴53159)(==A P 20.(1)法一 因为()()()()2222f x x x a x a x a =-+=+--,所以, ()f x 的图象的对称轴为直线22a x -=.由212a-=,解得0a =, 法二 因为函数()f x 的图象关于1x =对称,所以()()02f f =成立,即20a -=,解得0a =.(2)函数()f x 的图象的对称轴为直线22ax -=. ①当2012a-<<,即02a <<时, 因为()f x 在区间20,2a -⎛⎫ ⎪⎝⎭上单调递减,在区间2,12a -⎛⎫⎪⎝⎭上单调递增, 所以()f x 在区间[]0,1上的最小值为22222a a f -+⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭, 令2222a +⎛⎫-= ⎪⎝⎭,此方程无解; ②当21122a a-=-≥,即0a ≤时,因为()f x 在区间[]0,1上单调递减,所以在区间[]0,1上的最小值为()()11f a =-+, 令()12a -+=,解得3a =-. ③当022≤-a,即2≥a 时,因为()f x 在区间[]0,1上单调递增,所以在区间[]0,1上的最小值为a f 20-=)(, 令22=a -,解得1-=a ,不成立. 综上, 3a =-.21(1)⎪⎩⎪⎨⎧≥-<-=-0,310,13)(x x x f xx(2)当0≥x 时,xx f 31)(-=,则)(x f 在),0[+∞上单调递减,又)(x f 为R 上的奇函数,)(x f ∴在R 上单调递减,若0)log 5()(log 222≥-+x a f x f 在]8,2[∈x 上恒成立则)log ()(log )log 5(22222x f x f x a f -=-≥-,x x a 222log log 5-≤-∴在]8,2[∈x 上恒成立设t x =2log ,则]3,1[∈t ,此时关于t 的一元二次不等式052≤+-at t 在]3,1[∈t 时恒成立;设5)(2+-=at t t f ,由⎩⎨⎧≤≤0)3(0)1(f f 得6≥a ,所以a 的取值范围为),6[+∞。
山西省2020学年高一数学上学期期末测评考试试题(II)

山西省2020学年高一数学上学期期末测评考试试题(II )注意事项:1. 答卷前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
2. 全部答案在答题卡上完成,答在本试题上无效。
3. 回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案用0.5mm黑色笔迹签字笔写在答题卡上。
4. 考试结束后,将本试题和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一.. 项是符合题目要求的。
1. 若集合A= {x|x> —1} , B= { —2,—1, 1, 2},则A A B=A.{1 , 2}B.{ —1, 1 , 2}C.{x|x >—1}D.{ —2, —1} U ( —1 ,+^)2. 如图,正方形ABCD的边长为2,以正方形的每个顶点为圆心,1为半径作圆,在正方形内随机取一点,则此点取自阴影部分的概率是1A. —B.1——C.D.—44483.72和168的最大公约数是A.24B.36C.42D.72 4.下列两个变量具有正相关关系的是A.正方形的面积与边长B. 吸烟与健康D.汽车的重量与汽车每消耗1L汽油所行驶的平均路程5. 执行右边的程序,若输入n=3,则输出S=WHIIZ i<=nS=S*<i4-l t=i+ IWFM)C.数学成绩与物理成绩A.9B.16C.25D.3610. 小明将本班的51个同学编号为01, 02 , 03,…,51,并依次将其平分为 17个小组,组号为1 , 2,…,17,现用系统抽样法抽取一个容量为 17的样本,若样本中有一个同学的编号为46,则组号为6的小组中抽到的号码为 A.16 B.17C.18D.1911. 右图是甲、乙两人六次综合测评成绩的茎叶图, 其中一个数字被污损, 已知x €N *且X V 10,则甲的中位数超过乙的中位数的概率为A.4B.6C.8D.106.下面是某实验中学157班第一小组5位同学的立定跳远、跳绳、 800米跑的成绩折线图,则,130,3.88 D.1.98 ,130,3.657.若A ,B 为互斥事件,则 A.P(A) + P(B) V 1 B.P(A)+ P(B) > 1 C.P(A) + P(B) = 1D.P(A)+ P(B) W 121 8.若函数f(x)=ax — 2x+1在区间[—2 丄]上具有单调性,则实数 4a 的取值范围是A.( —s, -2) U [0 , 4]B.[—2, 4] C.(—s,— 2] U (0 , 4] D.[— 2, 0]9.执行如图所示的程序框图,如果输入的 N= 7,则输出的S 是这5位同学立定跳远的中位数,跳绳的平均数,800米跑的众数分别是A.1.98,131,3.88B.1.87 ,130,3.88C.1.98 /榆人人/ J=- I ,>-01甲乙95 E 9i i 112 01 ■1 51 2 1 A.— B.—C.-D 993当 x >0 时,f(x)log 1 x 2,0 x2x 1,x 1,若 f(a)fl 11A. -B.—3 C. —或3 D444小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020学年第一学期高一期末考试数学试题【满分150分,考试时间120分钟】一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}13<<-=x x A ,{}1,0,1,2,3---=B ,则=⋂B A ( ) A .{}1,0,1,2-- B .{}0,1,2,3--- C .{}0,1,2-- D .{}1,2,3--- 2.为了解高一年级1200学生的视力情况,采用系统抽样的方法,从中抽取容量为60的样本,则分段间隔为( )A .10B .20C .40D .603.用秦九韶算法计算多项式187654)(2345+++++=x x x x x x f 当4.0=x 的值时,需要做乘法和加法的次数分别是( )A .5,5B .4,5C .4,4D .5,44.如图所示的程序框图中,输出S 的值是( ) A .80 B .100 C .120 D .140 5.一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )A .至多有一次中靶B .两次都中靶C .只有一次中靶D .两次都不中靶 6.已知4log ,2,21.331.3===--c b a ,则,,a b c 的大小关系是( )A .a b c <<B .a c b <<C .b c a <<D .c b a <<7.已知函数)(x f 为奇函数,且0≥x 时,m x x f x ++=2)(,则=-)1(f ( )A .21-B .21C .2-D .2 8.如图,正方形ABCD 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是( ) A .14B .8π C .12 D .4π9.已知某射击运动员每次击中目标的概率都是0.7,现采用随机模拟的方法估计该运动员射击4次,至少击中2次的概率:先由计算器算出0~9之间取整数值的随机数,指定0,1,2表示没有击中目标,3,4,5,6,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:5727 0293 7140 9857 0347 4373 8636 9647 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 6710 4281据此估计,该射击运动员射击4次至少击中2次的概率为( )A .0.8B .0.85C .0.9D .0.9510.设奇函数()f x 在),0(+∞上为单调递减函数,且0)2(=f ,则不等式05)(2)(3≤--xx f x f 的解集为 ( )A .]2,0()0,2[⋃-B .),2[]0,2[+∞⋃-C .),2[]2,(+∞⋃--∞D .]2,0(]2,(⋃--∞ 11.已知函数()()2,log x a f x ag x x -== (0a >且1a ≠),若()()440f g -<,则()(),f x g x 在同一坐标系内的图象大致是( )A .B .C .D .12.已知定义在R 上的函数)(x f 满足)()(x f x f =-,且当0≥x 时,⎪⎩⎪⎨⎧≥-<≤+-=1,2210,1)(2x x x x f x,若对任意的]1,[+∈m m x ,不等式)()1(m x f x f +≤-恒成立,则实数m 的最大值是( ) A .1- B .21- C .31- D .31二、填空题:本大题共4小题,每小题5分,共20分. 13.将十进制数38化为二进制数为 .14.已知函数⎩⎨⎧>≤=0,log 0,3)(3x x x x f x ,若21)(=a f ,则实数=a .15.运行如图所示的程序框图,设输出数据构成的集合为A ,从集合A 中任取一个元素a ,则函数ax y =, ),0(+∞∈x 是增函数的概率为 .16.已知函数22log (1),131910,322x x f x x x x ⎧-<≤⎪⎨-+>⎪⎩()=若方程m x f =)(有4个不同的实根1x ,2x ,3x ,4x ,且1234x x x x <<<,则=++))(11(4321x x x x . 三、解答题:本大题共70分17.(本题满分10分)甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如右图所示 (1)写出甲、乙的中位数和众数;(2)计算甲、乙的平均数与方差,并依此说明甲、乙两名技工哪名更为优秀.18.(本题满分12分) 某地区某农产品近几年的产量统计如表:年份 2020 2020 2020 2020 2020 2020 年份代码t12 3 4 5 6 年产量y (万吨) 6.66.777.17.27.4(1)根据表中数据,建立y 关于t 的线性回归方程∧∧+=a t b y ; (2)根据线性回归方程预测2020年该地区该农产品的年产量.附:∑==∧---∑=ni ii i ni t ty y t t b 121)())((,t b y a ∧∧-=.参考数据:8.2))((61=--∑=i i iy y t t19.(本题满分12分)某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在[120,130)内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分; (2)用分层抽样的方法,在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段[120,130)内的概率.20.(本题满分12分)已知函数()()()2f x x x a =-+.(1)若()f x 的图象关于直线1x =对称,求a 的值; (2)若()f x 在区间[]0,1上的最小值是2,求a 的值.21.(本题满分12分)已知)(x f 是定义在R 上的奇函数,且当0>x 时,xx f 31)(-=.(1)求函数)(x f 的解析式;(2)当]8,2[∈x 时,不等式0)log 5()(log 222≥-+x a f x f 恒成立,求实数a 的取值范围.22.(12分)已知)(x f 满足)1(log )21()1(log )2()()(244x m x m x f x f +-+--=-+(1)讨论)(x f 的奇偶性;(2)当)(x f 为奇函数时,若方程221)2(ax f x +=-在0>x 时有实根,求实数a 的取值范围.2020学年第一学期高一期末考试数学试题答案1.C2.B3.A4.C5.D6.D7.C8.B9.D 10.A 11.B 12.C 13.)2(10011014. 32log 3或- 15.5316. 9 17. 解:(1)甲的中位数为2020202+=,众数为20;乙的中位数为192019.52+=,众数为23. (2)181920202122206x +++++==甲,()()()()()()2222222182019202020202021202220563S -+-+-+-+-+-==甲, 171819202323206x +++++==乙,()()()()()()22222221720182019202020232023201663S -+-+-+-+-+-==乙, 由于x x =甲乙,且22S S <甲乙,所以甲更为优秀.18.解(1)由题意可知:5.3=t ,7=y ,()5.175.25.15.0)5.0()5.1(5.2)(222222261=+++-+-+-=-∑=i i t t ,16.05.178.2)())((26161==---=∴∑∑==∧i ii i it ty y t tb ,所以44.65.316.07=⨯-=-=∧∧t b y a ∴y 关于t 的线性回归方程为44.616.0+=∧t y .(2)由(1)可得,当年份为2020年时,年份代码8=t ,此时72.744.6816.0=+⨯=∧y ,所以,可预测2020年该地区该农产品的年产量约为7.72万吨.19.解(1)分数在[120,130)内的频率为1-(0.1+0.15+0.15+0.25+0.05)=0.3.03.0=组距频率(直方图略)(2)平均分为:95×0.1+105×0.15+115×0.15+125×0.3+135×0.25+145×0.05=121. (3)由题意,[110,120)分数段的人数为:60×0.15=9人,[120,130)分数段的人数为:60×0.3=18人.∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,抽样比929186=+=k∴需在[110,120)分数段内抽取2992=⨯人,并分别记为m ,n ; 在[120,130)分数段内抽取41892=⨯人并分别记为a ,b ,c ,d ;设“从样本中任取2人,至多有1人在分数段[120,130)内”为事件A , 则基本事件有:(m ,n ),(m ,a ),(m ,b ),(m ,c ),(m ,d ),(n ,a ),(n ,b ), (n ,c ),(n ,d ),(a ,b ),(a ,c ),(a ,d ),(b ,c ),(b ,d ),(c ,d )共15种. 事件A 包含的基本事件有:(m ,n ),(m ,a ),(m ,b ),(m ,c ),(m ,d ),(n ,a ), (n ,b ),(n ,c ),(n ,d )共9种.∴53159)(==A P 20.(1)法一 因为()()()()2222f x x x a x a x a =-+=+--,所以, ()f x 的图象的对称轴为直线22a x -=.由212a-=,解得0a =, 法二 因为函数()f x 的图象关于1x =对称,所以()()02f f =成立,即20a -=,解得0a =.(2)函数()f x 的图象的对称轴为直线22ax -=. ①当2012a-<<,即02a <<时, 因为()f x 在区间20,2a -⎛⎫ ⎪⎝⎭上单调递减,在区间2,12a -⎛⎫⎪⎝⎭上单调递增, 所以()f x 在区间[]0,1上的最小值为22222a a f -+⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭, 令2222a +⎛⎫-= ⎪⎝⎭,此方程无解; ②当21122a a-=-≥,即0a ≤时,因为()f x 在区间[]0,1上单调递减,所以在区间[]0,1上的最小值为()()11f a =-+, 令()12a -+=,解得3a =-. ③当022≤-a,即2≥a 时,因为()f x 在区间[]0,1上单调递增,所以在区间[]0,1上的最小值为a f 20-=)(, 令22=a -,解得1-=a ,不成立. 综上, 3a =-.21(1)⎪⎩⎪⎨⎧≥-<-=-0,310,13)(x x x f xx(2)当0≥x 时,xx f 31)(-=,则)(x f 在),0[+∞上单调递减,又)(x f 为R 上的奇函数,)(x f ∴在R 上单调递减,若0)log 5()(log 222≥-+x a f x f 在]8,2[∈x 上恒成立则)log ()(log )log 5(22222x f x f x a f -=-≥-,x x a 222log log 5-≤-∴在]8,2[∈x 上恒成立设t x =2log ,则]3,1[∈t ,此时关于t 的一元二次不等式052≤+-at t 在]3,1[∈t 时恒成立;设5)(2+-=at t t f ,由⎩⎨⎧≤≤0)3(0)1(f f 得6≥a ,所以a 的取值范围为),6[+∞。
