《管理运筹学》习题3解答
管理运筹学(第3版)章后习题解析(下)

− 0.2 x1 − 0.2 x2 + 0.8 x3 − d 3+ + d3− = 0
+ − 2.5 x1 + 0.5 x2 + 0.3x3 − d 4 + d4 = 20
d1− = 0
− d2 =0
d3+ = 0 x1 , x2 , x3 , di+ , di− ≥ 0, i = 1, 2,3, 4
1.解: 最优解为 A―B2―C1―D1―E 或 A―B3―C1―D1―E 或 A―B3―C2―D2―E。 最优值为 13。 2.解: 最优解是项目 A 为 300 万元,项目 B 为 0 万元、项目 C 为 100 万元。 最优值 z=71+49+70=190 万元。 3.解: , 设每个月的产量是 xi 百台(i=1, 2, 3, 4) 最优解:x1=4,x2=0,x3=4,x4=3。即第一个月生产 4 百台,第二个月生产 0 台,第三 个月生产 4 百台,第四个月生产 3 百台。 最优值 z=252 000 元。 4.解: 最优解为运送第一种产品 5 件。 最优值 z=500 元。 5.解: 最大利润 2 790 万元。最优安排如表 10-1 所示。
表 10-1 年 1 2 3 4 5 度 年初完好设备 125 100 80 64 32 高负荷工作设备数 0 0 0 64 32 低负荷工作设备数 125 100 80 0 0
6.解: 最优解(0,200,300,100)或(200,100,200,100)或者(100,100,300,100)或 (200,200,0,200) 。总利润最大增长额为 134 万。 7.解: 在一区建 3 个分店,在二区建 2 个分店,不在三区建立分店。最大总利润为 32。 8.解: 最优解为第一年继续使用,第二年继续使用,第三年更新,第四年继续使用,第五年继续 使用,总成本=450 000 元。 9.解: 最优采购策略为若第一、二、三周原料价格为 500 元,则立即采购设备,否则在以后的几 周内再采购;若第四周原料价格为 500 元或 550 元,则立即采购设备,否则等第五周再采购;
《管理运筹学》第三版习题答案(韩伯棠教授)

第 2 章 线性规划的图解法11a.可行域为 OABC 。
b.等值线为图中虚线所示。
12c.由图可知,最优解为 B 点,最优解: x 1 = 769 。
7 2、解:15 x 2 =7, 最优目标函数值:a x 210.60.1O1有唯一解x 1 = 0.2函数值为 3.6x 2 = 0.6b 无可行解c 无界解d 无可行解e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解:a 标准形式:b 标准形式:c 标准形式:x 2 = 3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 303x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ≥= −4 x 1 − 6x 3 − 0s 1 − 0s 23x 1 − x 2 − s 1 =6x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x ' − 2 x ''− 0s − 0s'''− 3x 1 + 5x 2 − 5x 2 + s 1 = 70 2 x ' − 5x ' + 5x '' = 50122' ' ''3x 1 + 2 x 2 − 2x 2 − s 2 = 30'' ''4 、解:x 1 , x 2, x 2, s 1 , s 2 ≥ 0标准形式: max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式: min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 203x 1 + 3x 2 − s 2 = 18 4 x 1 + 9x 2 − s 3 = 36 x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解:b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6 x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。
《管理运筹学》第三版习题答案(韩伯棠教授)

0.057(其他
c 不变时, c 在 2 到正无穷的范围内变化,其最优解不变
2 1
e 约束条件 1 的右边值在 300000 到正无穷的范围内变化,对偶价格仍为 0.1 约束条件 2 的右边值在 0 到 1200000 的范围内变化,对偶价格仍为-0.06 600000 300000 f + = 100% 故对偶价格不变 900000 900000 4、解: a x1 = 8 5 x2 = 1 5 x3 = 0 x4 = 1 最优目标函数 18.5
s = 0, s = 0, s = 13
1 2 3
6 、解: b 1 ≤ c1 ≤ 3 c 2 ≤ c2 ≤ 6 d x1 = 6 x2 = 4
e x 1 ∈ [ 4 , 8 ] x 2 = 16 − 2 x 1 f 变化。原斜率从 − 7、解: 模型:
1
2 3
变为− 1
max z = 500x + 400x 2x 1 ≤ 300 3x 2 ≤ 540 2x + 2x ≤ 440
设按 14 种方案下料的原材料的根数分别为 x1,x2,x3,x4,x5,x6,x7,x8,x9, x10, x11,x12,x13,x14,则可列出下面的数学模型: min f = x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14 s.t. 2x1+x2+x3+x4 ≥ 80 x2+3x5+2x6+2x7+x8+x9+x10 ≥ 350 x3+x6+2x8+x9+3x11+x12+x13 ≥ 420 x4+x7+x9+2x10+x12+2x13+3x14 ≥ 10 x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14≥ 0 用 管理运筹学软件我们可以求得此问题的解为: x1=40,x2=0,x3=0,x4=0,x5=116.667,x6=0,x7=0,x8=0, x9 =0,x10=0,x11=140,x12=0,x13=0,x14=3.333 最优值为 300。 2、解:从上午 11 时到下午 10 时分成 11 个班次,设 xi表示第 i 班次安排的临时 工的人数,则可列出下面的数学模型: min f = 16 ( x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11 ) s.t. x1+1 ≥ 9 x1+x2+1 ≥ 9 x1+x2+x3+2 ≥ 9 x1+x2+x3+x4+2 ≥ 3
管理运筹学第三章习题答案

(1)解:, 53351042..715min 212112121≥≥+≥≥++=y y y y y y y t s y y ω(2)解:无限制32132131323213121,0,0 2520474235323..86max y y y y y y y y y y y y y y y t s y y ≤≥=++≤-=+≥+--≤++=ω解:例3原问题6,,1,0603020506070..min 166554433221654321Λ=≥≥+≥+≥+≥+≥+≥++++++=j x x x x x x x x x x x x x t s x x x x x x z j对偶问题:6,,1,0111111..603020506070max 655443322161654321Λ=≥≤+≤+≤+≤+≤+≤++++++=j y y y x y y y y y y y y y t s y y y y y y j ω解:(1)由最优单纯形表可以知道原问题求max ,其初始基变量为54,x x ,最优基的逆阵为⎪⎪⎪⎪⎭⎫ ⎝⎛-=-31610211B 。
由P32式()()()可知b B b 1-=',5,,1,,1Λ='-=='-j P C c P B P j B j j j j σ,其中b 和jP 都是初始数据。
设⎪⎪⎭⎫⎝⎛=21b b b ,5,,1,21Λ=⎪⎪⎭⎫ ⎝⎛=j a a P j j j ,()321,,c c c C =,则⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-⇒='-25253161021211b b b B b ,即⎪⎩⎪⎨⎧=+-=2531612521211b b b ,解得⎩⎨⎧==10521b b ⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛-⇒='-021********10212322211312111a a a a a a P B P j j ,即 ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=+-=-=+-==+-=03161121213161212113161021231313221212211111a a a a a a a a a ,解得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==-====121130231322122111a a a a a a()()()⎪⎪⎪⎪⎭⎫⎝⎛---=---⇒'-=31612102121,0,0,2,4,4132c c c P C c j B j j σ,即 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=+--=+-2314612142121113132c c c c c c ,解得⎪⎩⎪⎨⎧==-=6102132c c c所以原问题为:,, 10352..1026max 32132132321≥≤+-≤++-=x x x x x x x x t s x x x z对偶问题为:, 102263..105min 212121221≥≥+-≥-≥+=y y y y y y y t s y y ω(2)由于对偶问题的最优解为()()()2,4,,5454*=-=-=σσσc c C Y IB IB解:(1)因为3x 的检验数0353≤⨯-c ,所以3c 的可变范围是153≤c 。
《管理运筹学》课后习题答案59页word
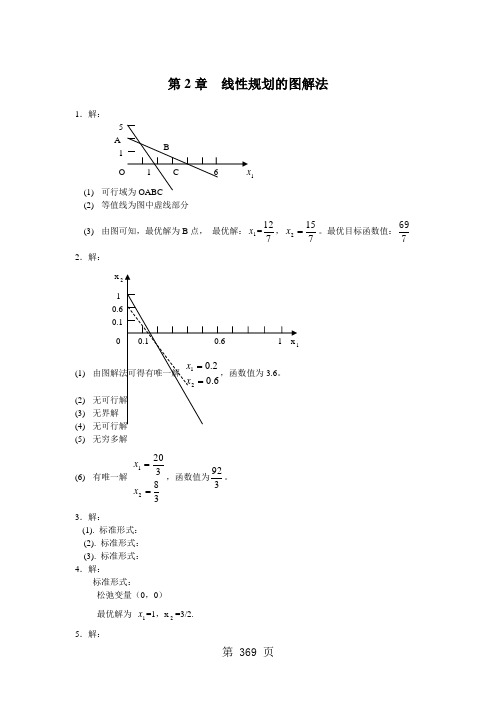
第2章 线性规划的图解法1.解: 5 A 11 (1) (2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 1 0(1) (2) (3) 无界解 (4) (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式: (2). 标准形式:(3). 标准形式: 4.解:标准形式:松弛变量(0,0) 最优解为 1x =1,x 2=3/2. 5.解:标准形式:剩余变量(0.0.13) 最优解为 x 1=1,x 2=5. 6.解:(1) 最优解为 x 1=3,x 2=7. (2) 最优解为 x 1=8,x 2=0. (3) 不变化。
因为当斜率31121-≤-≤-c c ,最优解不变,变化后斜率为1,所以最优解不变. 7.解:模型:(1) 1501=x ,702=x ,即目标函数最优值是103000 (2) 2,4有剩余,分别是330,15,均为松弛变量. (3) 50,0,200,0。
(4) 在[]500,0变化,最优解不变。
在400到正无穷变化,最优解不变. (5) 因为143045021-≤-=-c c ,所以原来的最优产品组合不变. 8.解:(1) 模型:b a x x f 38min +=基金a,b 分别为4000,10000,回报率为60000。
(2) 模型变为:b a x x z 45max +=推导出:180001=x 30002=x ,故基金a 投资90万,基金b 投资30万。
第3章 线性规划问题的计算机求解1.解:(1) 1501=x ,702=x 。
目标函数最优值103000。
(2) 1,3车间的加工工时已使用完;2,4车间的加工工时没用完;没用完的加工工时数为2车间330小时,4车间15小时. (3) 50,0,200,0含义:1车间每增加1工时,总利润增加50元;3车间每增加1工时,总利润增加200元;2车间与4车间每增加一个工时,总利润不增加。
管理运筹学(第四版)第三章习题答案参考word

目标函数值为2×30+5×10+1×10+5×10+3×25+7×5+6×20+10×40=800目标函数值为2×30+5×10+1×10+5×10+3×25+7×5+6×20+10×40=800(2)最小元素法:先从311=c 开始分配先从325=c 开始分配,需迭代4次,具体见QM 的迭代 逼近法(结果同最小元素法——先从313=c 开始分配)vj2 2 0 u i1 2 3 产量 0 1 2 10 7 2 8 × 7 × 2 1 2 3 2 1 0 × 2 2 4 1 3 11 3 8 8 × 3 7 × 3 2 4 4 9 2 1 5 × 5 6 -2 5 0 0 0 4 0 × 2 × 4销量757目标函数值为33。
4.5第一种解法(求最大)A B C 产量 甲 18 16 21 180 乙 16 18 22 250 丙 19 14 19 320 销量 250300200用QM 解得玩 具利 润工人第二种解法(求最小)A B C产量甲526449180乙546248250丙516651320销量250300200用QM解得即甲工人做C玩具180个,乙工人做B玩具250个,丙工人做A玩具250个,做B玩具50个,做C玩具20个。
最大利润为:70×250+80×300+70×200-41390=14110元甲乙丙产量A151822400B212516450最低需求290250270最高需求320250350甲1甲2乙丙1丙2产量A1515182222400B2121251616450C M0M M070需求2903025027080用QM解得玩具费用工人地区运费厂家地区运费厂家即A厂供给甲地区化肥150万吨,供给乙地区化肥250万吨;B厂供给甲地区化肥140万吨,供给丙地区化肥310万吨,总运费为14650万元。
卫生管理运筹学第二版第三章课后答案

卫生管理运筹学第二版第三章课后答案1、31.不属于急性动脉栓塞的早期症状: ()[单选题] *A. 疼痛B. 肢体麻木C.肢体温度低D.患肢紫绀(正确答案)2、73.下列哪类患者的尿液中有烂苹果味: ()[单选题] *A.前列腺炎B.尿道炎C.膀胱炎D.糖尿病酸中毒(正确答案)3、20.乳癌最多见于: C [单选题] *A.25~40 岁,50~54岁(正确答案)B.30~50岁,55~60岁C.45~49岁,60~64岁D.50~54岁4、23.穿隔离衣的正确顺序为()[单选题] *A.扣领扣一穿袖子一系袖带一系腰带B.穿袖子一扣领扣一系袖带一系腰带(正确答案)C.穿袖子一扣领扣一系腰带一系袖带D.穿袖子一系袖带一系腰带一扣领扣5、63、抢救青霉素过敏性休克的首选药物是()[单选题] *A、盐酸异丙嗪B、去甲肾上腺素C、盐酸肾上腺素(正确答案)D、异丙肾上腺素6、50.急性乳腺炎多发于:(? ) [单选题] *A. 青年产妇B. 中年产妇C. 任何哺乳期的妇女D. 产后哺乳期的初产妇(正确答案)7、31.死亡病人最后消失的感知觉是()[单选题] *A.触觉B.听觉(正确答案)C.视觉D.嗅觉8、7.肌肉注射常见并发症有()*A.疼痛(正确答案)B.神经性损伤(正确答案)C.局部或全身感染(正确答案)D.针口渗液(正确答案)9、16、血液病患者最适宜输入()[单选题] *A.新鲜血(正确答案)B.库存血C.血浆D.白蛋白10、17.母婴护理员可以协助产妇用()比例高锰酸钾溶液擦洗会阴。
[单选题] *A.1:1000B.1:4000C.1:5000(正确答案)D.1:1000011、37. 使用无菌容器操作正确的是(A B D )[单选题] *A.检查名称标示、灭菌指示带、灭菌日期、密闭情况(正确答案)B.打开无菌容器盖时,盖的内面向上放置C.用毕立即将容器盖盖好D.无菌容器每周清洁、灭菌一次12、5.产后每月要进行一次乳房自查,()要到医院对乳房进行一次检查,这对乳腺疾病,包括乳腺癌等的早发现、早治疗很有好处。
《管理运筹学》课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么就是线性规划?线性规划的三要素就是什么?答:线性规划(Linear Programming,LP)就是运筹学中最成熟的一个分支,并且就是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,就是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量就是决策问题待定的量值,取值一般为非负;约束条件就是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数就是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域就是空集。
当无界解与没有可行解时,可能就是建模时有错。
3.什么就是线性规划的标准型?松弛变量与剩余变量的管理含义就是什么? 答:线性规划的标准型就是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不就是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6 x22 1 x23 5 x24 0 4 1 4 -1 3 5 1 0 0
x31 2 3
因为min(σ33)=σ33=-1<0,所以初始方案并非最优方案,需进一步调整, x33为进基变量。 法二:用闭回路法求检验数 σ12=5-0+0-1=4;σ13=7-0+0-5=2;σ21=6-3+0-0=3;σ32=4-2+3-0+01=4(注:图中画出了非基变量x33的闭回路);σ33=3-2+3-0+0-5=-1; σ34=0-2+3-0=1 因为min(σ33)=σ33=-1<0,所以初始方案并非最优方案,需进一步调整, x33为进基变量。 第三步:求θ值,调整方案。 过程如下: 以X33作为进基变量。调整量θ=min(10,20,20)=10,按照上图所示 进行调整,选择x14 作为出基变量。 方案调整后为方案二,如下: 用位势法可求出方案二非基变量检验数: 销地 销地一销地二销地三 销地四 Ui
x1 d-3 d+3
0 1 2 3 4 5 6 7 8 9 10 5 4 3 2 1 A
d+2 d-2 d+1 d-1 d+4 d-4 直线x2=2、x12x2=4分别交于C(k-4,2)
B D C
、D(2+k/2,k/4-1) 两点。 当x1≤k-4时,t= ad3-=a(4-x1+2x2)= a(4-k+4x2) ∴当k=9, x2=2, x1=5 时,min t1=3a; 当k-4≤x1≤2+k/2 时,t= ad3-+d4-= a(4-x1+2x2)+(2-x2)= (4-k)a+2+(4a-1)x2 ∴若a≥1/4时k=9, x2=5/4, x1=13/2时,min t2=3/4; 若0<a<1/4时k=9, x2=2, x1=5时,min t2=3a<3/4
产地 产地一 产地二 产地三 Vj x11 3 2 5 5 3 7 1 0 0 1 -1
6 x22 1 x23 5 x24 0 5 0 4 x33 3 4 2 -1 0
x31 2 3
因为所有非基变量检验数σij都大于零,所以方案二就是唯一最优方案。 第四步: 决策结论:产地一向销地一调拨物资10吨,产地二分别向销地二、销地 三调拨物资各10吨,产地二过剩生产的物资为10吨;产地三分别向销地 一、销地三调拨物资10吨、10吨。最小总运费= 10×3+10×1+10×5+10×2+10×3=140(百元)。 2、求下列线性规划问题的对偶问题: 解:根据原模型很容易判断x1是自由变量,而x2≥0。 方法一:按对称形式变换 (1)原模型可变换为如下模型: (2)按对称形式变换关系可写出它的对偶问题,模型如下:
Cj→ CB XB B-1b 0 x1 1 0 0 0 0 x2 0 0 0 1 P1 d10 -1 0 0 1 1 w2/4 w1- w2/4 w2/4 1 w2/4 1 1 -1 0 -1 -1 1 0 0 0 1 0 0 0 -1 0 -2 0 4 1 w2 2 0 -4 -1 P4 d1+ 0 1 0 0 0 d2P2 w1P3 d2+ d30 d3+ w2P3 d40 0 1 0 0 d4+ 0 0 -1 0 - 3 θ
需求量 20 10 20 (件) 要求:(1)请建立该问题的线性规划模型,然后再化为标准问题。 (2)用表上作业法求解:用最小元素法确定初始方案;用位势法验证 初始方案是否最优?如果非最优,请用闭回路法调整,直至求出最优方 案。
解:
(1)设第i个产地(i=1,2,3)到第j个销地(j=1,2,3)的该种商品的数量 为xij吨,则可以建立以下模型: (2)因为总产量60(=10+30+20)大于总需求量50(=20+10+20), 所以本问题不是标准运输问题。增加一个虚拟销地,它的单位运价c14
E D C
d-4 d+4 d-1 d+1 d-2 d+2
B
A 5 4 3 2 1 0 1 2 3 4 5 6 7 9 10 d+3 d-3
x1 x2 令t=5d3-+3d4当x1≤2时,t=5d3=5(4-x1+2x2)=5(10-2x1) ∴min t=30,此时对应 x1=2,x2=2 当2<x1≤5时,t=5d3+3d4-=5(4-x1+2x2)+ 3(2-x2)=-4+17x2 ∴min t=30,此时对应 x1=2,x2=2 当5<x1≤6时,t=3d4=3(2-x2) ∴min t=9/2,此时对 应x1=5,x2=1/2。 综上所述,满意解为 x1=5,x2=1/2。可见,交换目标等级,满意解发生了变化,由 (13/2,5/4)→(5,1/2)。 本小题也可以用单纯形法求解,学生可自行运算,这里略去。 (2)①用图解法。 令a=w1/w2, t= ad3-+d4-(a>0) 由(1)分析知道:满足目标P1、P2 x2 的区域为x1+2x2=k(6≤k≤9),它与
《管理运筹学》习题3及参考答案 1、某公司从三个产地A1,A2, A3将物品运往三个销地B1,B2,B3,产 量平衡表和单位运价表如表1所示。问如何调运,使得总运输费用最 小? 表1 产销平衡表和单位运价表 销地Bj B1 B2 B3 产量 (件) 产地Ai A1 A2 A3 3 6 2 5 1 4 7 5 3 10 30 20
σj=cjzj θj 2 3 0 x1 x2 x5
σj=cj- 7 zj
∵所有非基变量检验数σj<0(j=3,4,6), ∴得到唯一最优解X*= (2,1,0,0,1)T,max z=7 即:A、B、C的产量调整为2吨、1吨、0吨,利润总和下降到7(千 元)。 4、(选做题)已知目标规划问题 用单纯形法求解时,得到如下最优表。分析目标函数分别变为①、②两 种情况时解的变化。可绘制图进行分析或者列单纯形表进行分析。
0 x1 13/2 P4 d + 3 1 3P3 3/4 d4- 5/4 0 x2 P1 P2 P3 P4
1/2 -1/2 -1/2 -1/2 1 -1 0 0 -1/4 1/4 1/4 -1/4 1/4 -1/4 -1/4 0
σj=cj-zj
1
-1
(1) (2) (w1,w2为权重比例且都大于零) 解:①如图1所示:依次满足目标P1、P2和P3的区域是线段CEBD。方程: x1+2x2=6 C(0,3)、E(2,2)、B(5,1/2)、D (6,0)。
2 CB 2 3 0 XB x1 x2 x6 B-1b x1 1 2 -1 1 0 0 0 3 x2 0 1 0 0 1 x3 -1 2 -2 -3 1.5 2 1 1 1 0 0 0 1 1 0 0 1 0 2 -1 0 x4 4 -1 -2 -5 2.5 6 -3 2 -3 0 x5 0 x6
-1 0 1 0 [-1] 1 -1 1 0 0 1 0 -1 1 -1 -1 0
7/2 -1/2 -1/2 1/2 -4 -2
σj=cj- 10 0 zj
∵所有非基变量检验数σj<0(j=2,4,5), ∴得到唯一最优解X*= (2,0,1,0,0)T,max z=10 即:A、B、C的产量调整为2吨、0吨、1吨,利润总和上升到10(千 元)。 (2)x1为基变量,若所有非基变量检验数 即3/4≤c1≤3(千元/吨)时,原最优解不变。但c1由2变为4,,所以最 优产量计划要变化。在原最优表基础上继续迭代,直至求出新的最优产 量方案。计算过程如下: 4 3 1 0 0 θi CB XB B-1b x1 4 3 x1 1 x2 2 1 0 0 1 0 x2 0 1 0 x3 x4 x5
-1 4 -1 - 2 -1 [1] 2 -1 -13 1 3 0 -1 1 3 2
σj=cjzj 4 0 x1 3 x5 2
1 1 [1] 2
σj=cj- 12 0 zj
-1 -3 -12 0
∵所有非基变量检验数σj<0(j=2,3,4), ∴得到唯一最优解X*= (3,0,0,0,2)T,max z=12 即:A、B、C的产量调整为3吨、0吨、0吨,利润总和上升到12(千 元)。 (3)若(吨)时,上述最优基不变。 劳动力约束增加1个单位时总利润的增加量就是劳动力资源的影子价 格,显然总利润增加量=-σ4=-(-5)=5(千元)。或者:∵,∴原问题 最优基不变。总利润增加量。(注:cBB-1就是最优表上松弛变量检验数 的相反数) (4)设生产产品D为x'4单位, ∴新产品D 不值得生产。 (5)新的设备台时约束条件:。代X*=(1,2,0,0,0)T入此条件,可知该条 件不成立。所以原问题最优表对应的产量最优方案需要改进。 由最优表第一行约束条件得到:; 由最优表第二行约束条件得到: 将上述两个表达式带入设备台时约束条件,并添加松弛变量x6,整理得 到:。将其添加到原问题最优表上,用对偶单纯形法继续迭代求解,求 解过程和结果如下:
=c24=c34,需求量为60-50=10。
(3)第一步:用最小元素法确定初始方案(方案不唯一,增补的零元素不能位
于同行或同列)。
方法二:伏格尔法(最接近最优解)
方法三:西北角法(初始解离最优解较远)
第二步:求非基变量检验数,验证初始方案(最小元素法求得的初始方 案)是否为最优方案。 法一:用位势法求检验数。 求解见下表所示: 销地 销地一销地二销地三 销地四 Ui 产地 产地一 产地二 产地三 Vj x11 3 3 4 5 2 7 x14 0 0 0 -1
(3)令,将上一步得到的模型整理为:
方法二:根据原问题和对偶问题的对应关系直接变换 (1)将原模型作如下变换: (2)根据上述问题和对偶问题的对应关系,直接写出其对偶问题, 即:(实际上和方法一得到的结果是一样的)
