第3章 习题解答
第三章习题解答

第三章习题解答一、判断下列说法是否正确,凡对的在括号内打“√”,否则打“×”。
(1)现测得两个共射放大电路空载时的电压放大倍数均为-100,将它们连成两级放大电路,其电压放大倍数应为10000。
( )(2)阻容耦合多级放大电路各级的Q点相互独立,( )它只能放大交流信号。
( )(3)直接耦合多级放大电路各级的Q点相互影响,( )它只能放大直流信号。
( )(4)只有直接耦合放大电路中晶休管的参数才随温度而变化。
( )(5)互补输出级应采用共集或共漏接法。
( )二、现有基本放大电路:A.共射电路B.共集电路C.共基电路D.共源电路E.共漏电路根据要求选择合适电路组成两级放大电路。
(1)要求输入电阻为1kΩ至2kΩ,电压放大倍数大于3000,第一级应采用,第二级应采用。
(2)要求输入电阻大于10MΩ,电压放大倍数大于300,第一级应采用,第二级应采用。
(3)要求输入电阻为100kΩ~200kΩ,电压放大倍数数值大于100,第一级应采用,第二级应采用。
(4)要求电压放大倍数的数值大于10,输入电阻大于10MΩ,输出电阻小于100Ω,第一级应采用,第二级应采用。
(5)设信号源为内阻很大的电压源,要求将输入电流转换成输出电压,且,输出电阻R o<100,第一级应采用,第二级应采用。
三、选择合适答案填入空内。
(1)直接耦合放大电路存在零点漂移的原因是。
A.电阻阻值有误差B.晶体管参数的分散性C.晶体管参数受温度影响D.电源电压不稳定(2)集成放大电路采用直接耦合方式的原因是。
A.便于设计B.放大交流信号C.不易制作大容量电容(3)选用差分放大电路的原因是。
A.克服温漂B. 提高输入电阻C.稳定放入倍数(4)差分放大电路的差模信号是两个输入端信号的,共模信号是两个输入端信号的。
A.差B.和C.平均值(5)用恒流源取代长尾式差分放大电路中的发射极电阻R e,将使电路的。
A.差模放大倍数数值增大B.抑制共模信号能力增强C.差模输入电阻增大(6)互补输出级采用共集形式是为了使。
第三章 信道与信道容量 习题解答

,
,求
,
,
和
;
(2) 求该信道的信道容量及其达到信道容量时的输入概率分布。
解:
(1)先写出
:
根据公式
计算联合概率:
信宿端符号分布概率:
根据公式
计算:
3
求各熵: 信源熵:
比特/消息
信宿熵:
比特/消息
可疑度:
平均互信息量: 噪声熵: (2)二元对称离散信道的信道容量:
比特/消息 比特/消息
比特/秒
信源等概分布时(
解:设下标 1为原状况,下标 2为改变后状况。由
可得:
,
倍
如果功率节省一半则
倍 ,为 了 使 功 率 节 省 一 半 又 不 损 失 信 息 量 I,根 据
,可以: (1) 加大信道带宽 W,用带宽换取信噪比
,
,
7
缺点是对设备要求高。 (2) 加大传输时间 T,用传输时间换取信噪比,同理可得:
缺点是传输速度降低了。
噪声熵:
(5)平均互信息量:
2.有一个生产 A、B、C、D四种消息的信源其出现的概率相等,通过某一通信系统传输时,B和 C无误,A 以 1/4概率传为 A,以 1/4概率误传为 B、C、D,而 D以 1/2概率正确传输,以 1/2概率误传为 C,
(1)试求其可疑度?(2)收到的信号中哪一个最可靠?(3)散布度为多少? 解:(1)
,
将各数据代入: 解得:
如果
则
将各数据代入: 解得:
14.在理想系统中,若信道带宽与消息带宽的比为 10,当接收机输入端功率信噪比分别为 0.1和 10时,试
比较输出端功率信噪比的改善程度,并说明
与
之间是否存在阀值效应。
化工原理答案-第三章习题答案-150

第三章习题解答3-1 某圆柱形固定床填充的催化剂直径为p d ,高为h ,试求等体积的当量直径及球形度。
解:h d d e 2p 346ππ=,32p 23h d d e = ()p 312p p 2322218)24(23d h h d h d d h d P P +=⋅⋅+⨯⎪⎭⎫ ⎝⎛=πππφ3-2 求20mm×20mm×25mm 的长方体颗粒的体积当量直径,表面积当量直径,比表面积当量直径及形状系数。
解:体积当量直径:mm V d ev 7.262520206633=⨯⨯⨯==ππ表面积当量直径:mm Sd es 8.282)252020202020(=⨯⨯+⨯+⨯==ππ比表面积当量直径:mm S V a d ea 1.232)252020202020(252020666=⨯⨯+⨯+⨯⨯⨯⨯=== 形状系数:86.08.287.26222222=====es ev es ev P s d d d d S S ππφ 3-3 由边长皆为2mm 的立方体,直径和高度均为2mm 的圆柱体及直径为3mm 的球体各10kg 组成的均匀颗粒床层,床层直径为0.2m ,高度为 1 m 。
已知颗粒的密度皆为1900kg/m 3,求床层的空隙率和颗粒的平均比表面积。
解: 床层体积:3220314.012.044m h d V b =⨯⨯==ππ颗粒体积:30158.01900310m V P =⨯= 床层空隙率:497.00314.00158.00314.0=-=-=bpb V V V ε 颗粒的平均比表面积:3球柱立a a a a ++=-13000002.0002.0002.06002.0002.0-=⨯⨯⨯⨯=m a 立 1223000002.0)002.0(4002.02)002.0(4-=⨯⨯⋅+⨯⨯=m a πππ柱 1322000003.066003.0003.0-==⨯⨯=m a ππ球 11 2.67676232000300030003---==++=++=mm m a a a a 球柱立 3-4 某形状近似球形的微小固体颗粒,其沉降运动处于斯托克斯定理区,试计算(1)该颗粒在20℃与200℃的常压空气中的沉降速度之比为多少?(2)该颗粒在20℃与50℃的水中的沉降速度之比为多少?[(1)1.44,(2)0.55]解:(1)20℃空气的粘度s Pa ⋅⨯=-51081.1μ,200℃空气的粘度s Pa ⋅⨯=-5'106.2μ,因沉降速度处于斯托克斯定律区,ρρ>>p ,故()()()()44.11081.1106.2181855''''22'=⨯⨯=--=--=--μρρμρρμρρμρρs s s s t t g d gd u u (2)20℃水的粘度s Pa ⋅⨯=-3101μ,50℃水的粘度s Pa ⋅⨯=-3'1055.0μ,因沉降速度处于斯托克斯定律区,并考虑到液体的密度随温度变化很小,故()()()()55.01011055.0181833'''''22'=⨯⨯=≈--=--=--μμμρρμρρμρρμρρs s p p p p t t g d g d u u 无论是气体还是液体,温度的改变主要是通过粘度的变化而影响沉降速度。
第三章习题解答

第3章 力学基本定律与守恒律 习题及答案1.作用在质量为10 kg 的物体上的力为i t F)210(+=N ,式中t 的单位是s ,(1)求4s 后,这物体的动量和速度的变化.(2)为了使这力的冲量为200 N ·s ,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度j 6-m ·s -1的物体,回答这两个问题.解: (1)若物体原来静止,则i t i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向,ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速,则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理, 12v v ∆=∆,12I I=这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理. (2)同上理,两种情况中的作用时间相同,即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ,(s 20='t 舍去)2.一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入,得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 3.如图所示,一质量为m 的球,在质量为M 半径为R 的1/4圆弧形滑槽中从静止滑下。
第3章 习题解答 哈工大习题册
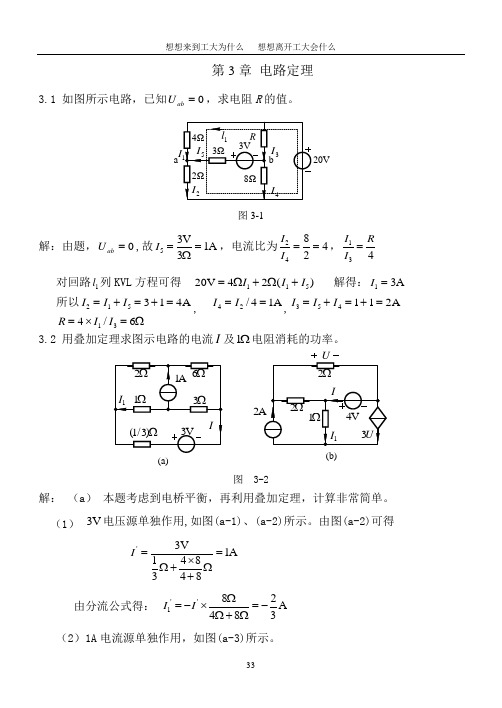
第3章 电路定理3.1 如图所示电路,已知0=ab U ,求电阻R 的值。
a图3-1解:由题,0=ab U ,故53V1A 3I ==Ω,电流比为24842I I ==,134I R I =对回路1l 列KVL 方程可得 11520V 42()I I I =Ω+Ω+ 解得:13AI =所以215314A I I I =+=+=, 42/41A I I ==,354112A I I I =+=+=134/6R I I =⨯=Ω3.2 用叠加定理求图示电路的电流I 及1Ω电阻消耗的功率。
(a)(b)2图 3-2解: (a ) 本题考虑到电桥平衡,再利用叠加定理,计算非常简单。
(1) 3V 电压源单独作用,如图(a-1)、(a-2)所示。
由图(a-2)可得'3V1A 148348I ==⨯Ω+Ω+由分流公式得: ''182A 483I I Ω=-⨯=-Ω+Ω(2)1A 电流源单独作用,如图(a-3)所示。
考虑到电桥平衡,0I ''=,133(1A)A 134I ''=-⨯=-+ (3)叠加:1A I I I '''=+=,11117/12A I I I '''=+=-2111 2.007WP I Ω=⨯=(a-1)(a-2)(a-3)(b )(1)4V 电压源单独作用,如图(b-1)所示。
24V 2V 22U Ω'=⨯=Ω+Ω,136A I U ''=-=-,125A I I I '''=+=- (2)2A 电流源单独作用,如图(b-2)所示。
'2I '(b-1)(b-2)222A 2V 22U Ω⨯Ω''=⨯=Ω+Ω,22/21A I U ''''== 对节点②列KCL 方程得1234A I U ''''=-=-对节点③列KCL 方程得235A I I U ''''''=-=- (3) 叠加 '"1116A 4A=10A I I I =+=---'"5A 5A=10A I I I =+=---2111100W P I Ω=⨯Ω=注释:不能用各独立源单独作用时电阻消耗的功率之和来计算电阻在电路中消耗的功率。
第三章 习题解答-2.0
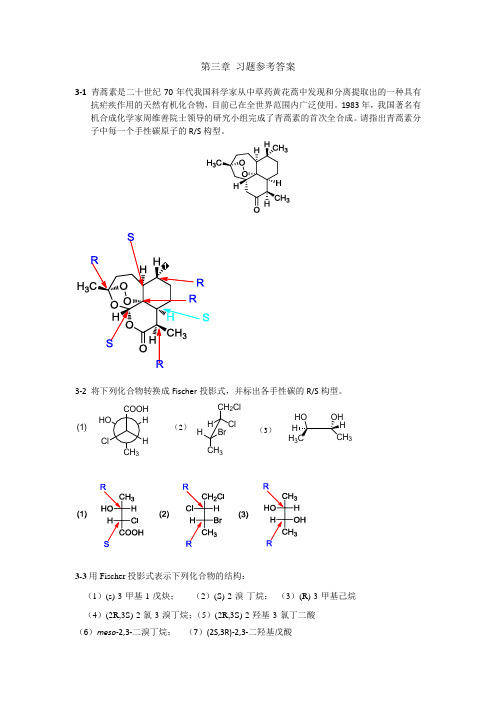
第三章 习题参考答案3-1 青蒿素是二十世纪70年代我国科学家从中草药黄花蒿中发现和分离提取出的一种具有抗疟疾作用的天然有机化合物,目前已在全世界范围内广泛使用。
1983年,我国著名有机合成化学家周维善院士领导的研究小组完成了青蒿素的首次全合成。
请指出青蒿素分子中每一个手性碳原子的R/S 构型。
3-2 将下列化合物转换成Fischer 投影式,并标出各手性碳的R/S 构型。
(2)(3)3BrHCH 3HClCH 2ClH 3H 3(1)3-3用Fischer 投影式表示下列化合物的结构:(1)(s)-3-甲基-1-戊炔; (2)(S)-2-溴-丁烷; (3)(R)-3-甲基己烷 (4)(2R,3S)-2-氯-3-溴丁烷;(5)(2R,3S)-2-羟基-3-氯丁二酸 (6)meso -2,3-二溴丁烷; (7)(2S,3R)-2,3-二羟基戊酸本题答案不唯一。
在画Fisher投影式时,习惯把含碳原子的基团放在竖键上,并把命名时编号最小的碳原子放在上端。
以下是较为符合习惯的Fisher投影式。
3-4下列化合物中哪些有手性?(1)、(3)、(5)、(7)、(9)无手性(2)、(4)、(6、)(8)、(10)有手性3-5长尾粉蚧壳虫信息素A是雌性长尾粉蚧壳虫(一种植物害虫)分泌的性激素,其外消旋体目前已被人工合成,并商业化用于农田害虫的控制和诱杀。
最近,化学家通过全合成途径确定了天然长尾粉蚧壳虫信息素的绝对构型(J. Org. Chem. 2013, 78, 6281−6284)。
通过全合成方法分别得到了A的2种立体异构体,发现其中的(S)-(+)-异构体具有吸引雄性长尾粉蚧壳虫的活性,而它的对映体(R)-( )-A则无此生物活性。
此结果表明雌性长尾粉蚧壳虫分泌的天然长尾粉蚧壳虫信息素为(S)-A。
商业化使用的外消旋体与纯的(S)-对映体生物活性相似,说明(R)-A对(S)-A的生物活性无抑制作用。
写出(R)-A和(S)-A的结构式。
习题答案第3章

t s (2%) 4T
T ,为惯性环节的时间常数。 将已知数据 t s (2%)=15 秒代入上式,求得惯性环节的时间常数 T
则闭环传递函数为
3.75 秒。
WB ( s )
单位反馈系统的开环传递函数为
1 15s 1
WK ( s )
WB ( s) 1 1 WB ( s ) 15s
s0
劳斯表中出现 s 行为全 0 行,且无符号变化,则闭环系统临界稳定,有 2 对对称于原 点的特征根。可通过辅助方程得到。
3
令 F ( s ) 3s 18s 12 0
4 2
解得
3-9 系统如图 P3-4 所示,问 取何值系统方能稳定。
s1, 2 j 0.87 , s 3, 4 j 2.29 10 s ( s 1)
则 令 xc (t ) 0
xc (t ) L1 [ X c ( s )] 1 e t cos(3t )
可得 t m 0.94 s
阶跃响应的最大峰值 根据超调量的定义
x max (t m ) 1.37
%
调节时间 t s (5%)
x max (t m ) xc () 100% 37% x c ( )
0.2 sX c ( s ) 2 X r ( s )
又输入信号为 X r ( s )
1 ,则输出 s
X c ( s ) 10 s2
拉氏反变换后,得单位阶跃响应为
xc (t ) 10t
c (t ) 0.24 x c (t ) (2) 0.04 x
微分方程两侧同时取拉氏变换,得
5 4 3 2
(4) s 4 s 4 s 4 s 7 s 8s 10 0
第三章部分习题解答
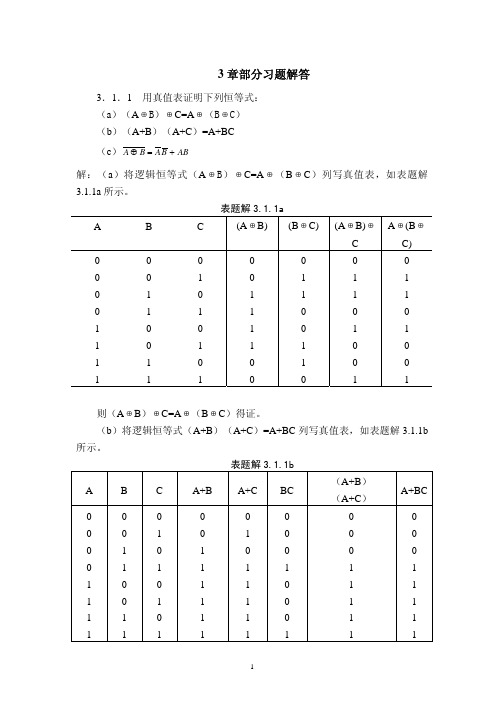
(b) ( A + B)(AB ) = AAB + BAB = AB
(c) ABC(B + C ) = ( A + B + C )(B + C ) = C + B( A + B ) = C + AB
(d) A + ABC + ABC + CB + CB = A(1 + BC + BC) + C(B + B ) = A + C
L3 = A3 ⊕ C
可分别用异或门、三态门设计逻辑电路,如图题解 3.4.4a、b 所示。
图题解 3.4.4
7
3.4.7 某雷达站有 3 部雷达 A、B、C,其中 A 和 B 功率消耗相等,C 的 功率是 A 的两倍。这些雷达由两台发电机 X 和 Y 供电,发电机 X 的最大输出功 率等于雷达 A 的功率消耗,发电机 Y 的最大输出功率是 X 的 3 倍。要求设计一 个逻辑电路,能够根据各雷达的启动和关闭信号,以最节约电能的方式启、停 发电机。
X = ABC + ABC + ABC + ABC = AB ⊕ C + B A ⊕ C
Y =AB+C 由逻辑表达式可设计出最节约电能的发电机启、停方式的逻辑电路,如图 题解 3.4.7b 所示。
表题解 3.4.7
A
B
C
X
Y
0
0
0
0
0
0
0
1
0
1
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 习题解答(部分)[1]求以下序列)(n x 的频谱()j X e ω,其中0a >。
(2)()an e u n - (5)0sin()()an e n u n ω-解:对题中所给的)(n x 先进行z 变换,再求其频谱。
(2)由于111)]([)(----==ze n u e Z z X a an ,所以ωωωj a ez j e e z X e X j --=-==11)()(。
(5)由于aa a ane z e z e z n u n eZ z X 2201010cos 21sin )]()sin([)(-------+-==ωωω,所以ωωj e z j z X e X ==)()(aj a j a j e e e e e e 2200c o s 21s i n ------+-=ωωωωω [2] 设()j X e ω和()j Y e ω分别是()x n 和()y n 的傅里叶变换,试求下面序列的傅里叶变换。
(7)(2)x n (8)(),()20n x n g n n ⎧⎪=⎨⎪⎩=偶,=奇解:(7)2)()2()]2([ωωn jn n jn en x en x n x DTFT -∞∞-∞=-∑∑==为偶数 2)]()1()([21ωn j nn e n x n x -∞-∞=-+=∑)(21)(21)(21)(212222⎪⎭⎫⎝⎛+∞-∞=⎪⎭⎫⎝⎛+-∞-∞=-+=+=∑∑πωωπωωj j n n j n n j e X e X e n x e n x(8))()'()2/()]([2''2ωωωj n n j n jn e X en x en x n g DTFT ===∑∑∞-∞=-∞-为偶数[3]求出下面序列的傅里叶变换(1))5(2)(-δ=n n x (4))3()2()(--+=n u n u n x解:由DFT 定义有:(1)ωωωδ52)5(2)(j n jn j e en e X -∞-∞=-=-=∑(4)ωωωωωωj j j n jn n jn j ee e een u n u e X ---=-∞-∞=---==--+=∑∑1)]3()2([)(3222⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=--=------ωωωωωωωωωωωω21sin 25sin 11222225252525j j j j j j j j j j e e e e e e e e e e [5]已知001,()0,j X e ωωωωωπ⎧≤⎪=⎨<≤⎪⎩,求()j X e ω的傅里叶逆变换()x n 。
解:()0000sin 121)(21)(ωπωωπωπωπωωωππωωn Sa n n d e d e e X n x jn jn j ====⎰⎰-- [9]已知系统的单位脉冲响应()()n h n a u n =,01a <<,输入序列为()()2(2)x n n n δδ=+-(1)求出系统的输出序列()y n ;(2)分别求出)(n x 、()h n 和()y n 的傅里叶变换。
解:(1) 系统的输出序列()y n 等系统的单位冲激响应与输入序列的卷积,即[])2(2)()()()()(-+*=*=n n n u a n x n h n y n δδ)2(2)(2-+=-n u a n u a n n(2)由于 ωωωδδ221)]2(2)([)(j n jn j e e n n e X -∞-∞=-+=-+=∑ωωωωj n j n n nj n n j ae e a en u a e H --∞=-∞-∞=-===∑∑11)()(0所以由卷积定理:)()()()(ωωj j e H e X n h n x ↔*得:ωωωωωj j j j j ae e e X e H e Y ---+=⋅=121)()()(2[14]在变换区间01n N ≤≤-内,计算下列序列的N 点DFT 。
(1)()1x n = (2)0()()x n n n δ=- 00n N <<(3)()()M x n R n = 0M N << (4)0()()j n N x n e R n ω=⋅解:由DFT 的定义得: (1)k NjkN N jN n kn Nj nk N N n eeeW k X πππ22121111)(---=--=--==⋅=∑∑⎩⎨⎧-===1 , ,2 ,1 ,00,N k k N (2)0212010)()()(kn NjN n kn Nj nk NN n een n Wn n k X ππδδ--=--==-=⋅-=∑∑, 1 , ,1 ,0-=N k(3)k NjkM N jM n kn Nj nk N N n M eeeW n R k X πππ2212111)()(---=--=--==⋅=∑∑, 1 , ,1 ,0-=N k(4))2()2(1)2(1000011)(k Nj N k N j N n nk Nj nk NN n nj eeeWek X πωπωπωω---=--=--==⋅=∑∑ )2(0011k Nj N j ee ωω---=,1 , ,1 ,0-=N k[16]长度为10N =的两个有限长序列11,04()0,59n x n n ≤≤⎧=⎨≤≤⎩ , 21,04()1,59n x n n ≤≤⎧=⎨-≤≤⎩作图表示1()x n 、2()x n 和)()(1n x n y =⑩)(2n x 。
解:)()(1n x n y =⑩)())(()()(101029012n R m n x m x n x m ⎥⎦⎤⎢⎣⎡-=∑=的计算值如表3-1所示。
表3-1 )()(1n x n y =⑩)(2n x 的值因此,)(1n x 、)(2n x 和)()(1n x n y =⑩)(2n x 分别如图3-6(a)、(b)、(c)所示。
(a)图3-6 习题1-14图[22]已知[]()()DFT x n X k =,0m N <<,试求(1)2()cos DFT x n mn N π⎡⎤⎛⎫⎪⎢⎥⎝⎭⎣⎦ (2)2()sin DFT x n mn N π⎡⎤⎛⎫ ⎪⎢⎥⎝⎭⎣⎦ 解:(1)2()cos DFT x n mn N π⎡⎤⎛⎫ ⎪⎢⎥⎝⎭⎣⎦kn Nj N n mn N j mn Nj ee e n x πππ2122)(21--=-∑⎥⎦⎤⎢⎣⎡+=∑-=+---⎥⎦⎤⎢⎣⎡+=10)(2)(2)(21N n n m k N j n m k Nj e e n x ππ )]()([21m k X m k X ++-= (2)2()sin DFT x n mn N π⎡⎤⎛⎫ ⎪⎢⎥⎝⎭⎣⎦kn Nj N n mn N j mn Nj ee e n x j πππ21022)(21--=-∑⎥⎦⎤⎢⎣⎡-=∑-=+---⎥⎦⎤⎢⎣⎡-=10)(2)(2)(21N n n m k N j n m k Nj e e n x j ππ )]()([21m k X m k X j+--=[26]已知()x n 和()y n 为实有限长序列,若()()()f n x n jy n =+,[]()()F k DFT f n =,试求以下两种情况的[]()()X k DFT x n =、[]()()Y k DFT y n =及()x n 和()y n 。
(1)11()11N Nk kN Na b F k j aW bW --=+-- (2)()1F k jN =+,N 为整数 解:由DFT 的共轭对称性知道,)()()]([k F k X n x DFT ep ==,)()()]([k F k jY n jy DFT op ==(1) 11()11N Nk kN Na b F k j aW bW --=+-- []kNN ep aW a k N F k F k F k X --=-+==*11)()(21)()( []kN N op bW b k N F k F j k jF k Y --=--=-=*11)()(21)()(10,)(-≤≤=N n a n x n 10 ,)(-≤≤=N n b n y n(2) jN k F +=1)([]1]11[21)()(21)()(=-++=-+==*jN jN k N F k F k F k X ep []N k N F k F jk jF k Y op =--=-=*)()(21)()( 所以 )(1)(1n WNn x N k kn Nδ==∑-=-, )(1)(1n N NWNn y N k kn Nδ==∑-=-。
[27]()x n 是长度8N =点的有限长序列,()y n 是长度20N =点的有限长序列,()R k 为两个序列20点的离散傅里叶变换相乘,求()r n ,并指出()r n 的哪些点与()x n 、()y n 的线性卷积相同。
解:记)()()(n y n x n rl *=,而)()]([)(n x k R IDFT n r ==)(n y 。
)(n r l 长度为27,)(n r 长度为20。
圆周卷积与线性卷积的关系为:)()20()(20n Rm n r n r m l⋅+=∑∞-∞=只有在如上周期延拓序列中无混叠的点上,才满足)()(n r n r l =,所以)()()()(n y n x n r n r l *== , 197≤≤n[28]用微处理器对实序列作谱分析,要求频谱分辨率50F Hz ≤,信号最高频率为1kHz ,试确定以下各参数:(1)最小记录时间min p T ; (2)最大抽样间隔max T ; (3)最少抽样点数min N ; (4)在频带宽度不变的情况下,将频率分辨率提高一倍的N 值。
解:(1)已知频谱分辨率Hz F 50=min p T =s F 02.05011== (2)根据抽样定理,kHz f f h s 22=≥,即ms 5.020001211==≤=h s f f T (3)40502000min ===F f N s (4)若频率分辨率提高一倍,则F 应减少一半,即Hz F 25=,则80252000===F f N s。
