计量经济学部分习题答案解析
计量经济学题库(超完整版)及答案.详解

计量经济学题库(超完整版)及答案.详解计量经济学题库计算与分析题(每⼩题10分)1X:年均汇率(⽇元/美元) Y:汽车出⼝数量(万辆)问题:(1)画出X 与Y 关系的散点图。
(2)计算X 与Y 的相关系数。
其中X 129.3=,Y 554.2=,2X X 4432.1∑(-)=,2Y Y 68113.6∑(-)=,()()X X Y Y ∑--=16195.4 (3)采⽤直线回归⽅程拟和出的模型为 ?81.72 3.65YX =+ t 值 1.2427 7.2797 R 2=0.8688 F=52.99解释参数的经济意义。
2.已知⼀模型的最⼩⼆乘的回归结果如下:i i ?Y =101.4-4.78X 标准差(45.2)(1.53) n=30 R 2=0.31 其中,Y :政府债券价格(百美元),X :利率(%)。
回答以下问题:(1)系数的符号是否正确,并说明理由;(2)为什么左边是iY ⽽不是i Y ;(3)在此模型中是否漏了误差项i u ;(4)该模型参数的经济意义是什么。
3.估计消费函数模型i i i C =Y u αβ++得i i ?C =150.81Y + t 值(13.1)(18.7) n=19 R 2=0.81 其中,C :消费(元) Y :收⼊(元)已知0.025(19) 2.0930t =,0.05(19) 1.729t =,0.025(17) 2.1098t =,0.05(17) 1.7396t =。
问:(1)利⽤t 值检验参数β的显著性(α=0.05);(2)确定参数β的标准差;(3)判断⼀下该模型的拟合情况。
4.已知估计回归模型得i i ?Y =81.7230 3.6541X + 且2X X 4432.1∑(-)=,2Y Y 68113.6∑(-)=,求判定系数和相关系数。
5.有如下表数据(1拟合什么样的模型⽐较合适?(2)根据以上数据,分别拟合了以下两个模型:模型⼀:16.3219.14P U=-+ 模型⼆:8.64 2.87P U =-分别求两个模型的样本决定系数。
计量经济学习题及参考答案解析详细版

计量经济学习题及参考答案解析详细版计量经济学(第四版)习题参考答案潘省初第⼀章绪论试列出计量经济分析的主要步骤。
⼀般说来,计量经济分析按照以下步骤进⾏:(1)陈述理论(或假说)(2)建⽴计量经济模型(3)收集数据(4)估计参数(5)假设检验(6)预测和政策分析计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对⽽⾔不重要因⽽未被引⼊模型的变量,以及纯粹的随机因素。
什么是时间序列和横截⾯数据? 试举例说明⼆者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民⽣产总值、就业、货币供给、财政⾚字或某⼈⼀⽣中每年的收⼊都是时间序列的例⼦。
横截⾯数据是在同⼀时点收集的不同个体(如个⼈、公司、国家等)的数据。
如⼈⼝普查数据、世界各国2000年国民⽣产总值、全班学⽣计量经济学成绩等都是横截⾯数据的例⼦。
估计量和估计值有何区别?估计量是指⼀个公式或⽅法,它告诉⼈们怎样⽤⼿中样本所提供的信息去估计总体参数。
在⼀项应⽤中,依据估计量算出的⼀个具体的数值,称为估计值。
如Y就是⼀个估计量,1nii YY n==∑。
现有⼀样本,共4个数,100,104,96,130,则根据这个样本的数据运⽤均值估计量得出的均值估计值为5.107413096104100=+++。
第⼆章计量经济分析的统计学基础略,参考教材。
请⽤例中的数据求北京男⽣平均⾝⾼的99%置信区间NS S x ==45= ⽤也就是说,根据样本,我们有99%的把握说,北京男⾼中⽣的平均⾝⾼在⾄厘⽶之间。
25个雇员的随机样本的平均周薪为130元,试问此样本是否取⾃⼀个均值为120元、标准差为10元的正态总体?原假设120:0=µH备择假设 120:1≠µH 检验统计量()10/2510/25XX µσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即此样本不是取⾃⼀个均值为120元、标准差为10元的正态总体。
计量经济学习题集及详解答案

第一章绪论一、填空题:1.计量经济学是以揭示经济活动中客观存在的__________为内容的分支学科,挪威经济学家弗里希,将计量经济学定义为__________、__________、__________三者的结合。
2.数理经济模型揭示经济活动中各个因素之间的__________关系,用__________性的数学方程加以描述,计量经济模型揭示经济活动中各因素之间__________的关系,用__________性的数学方程加以描述。
3.经济数学模型是用__________描述经济活动。
4.计量经济学根据研究对象和内容侧重面不同,可以分为__________计量经济学和__________计量经济学。
5.计量经济学模型包括__________和__________两大类。
6.建模过程中理论模型的设计主要包括三部分工作,即__________、____________________、____________________。
7.确定理论模型中所包含的变量,主要指确定__________。
8.可以作为解释变量的几类变量有__________变量、__________变量、__________变量和__________变量。
9.选择模型数学形式的主要依据是__________。
10.研究经济问题时,一般要处理三种类型的数据:__________数据、__________数据和__________数据。
11.样本数据的质量包括四个方面__________、__________、__________、__________。
12.模型参数的估计包括__________、__________和软件的应用等内容。
13.计量经济学模型用于预测前必须通过的检验分别是__________检验、__________检验、__________检验和__________检验。
14.计量经济模型的计量经济检验通常包括随机误差项的__________检验、__________检验、解释变量的__________检验。
计量经济学部分习题答案

第4章 P .1041 (4) 利用回归标准误差公式 (4.19)得残差平方和22(2)(1002)11512961SSR n SER =-=-⨯.=.利用2R 公式 (4.16)得总平方和:22129611304411008SSR TSS R ===.--.样本方差 2Y s =TSS130441991318.n -==. 于是标准差为115.Y s . 2.样本容量 200.n = 回归方程估计为29941394081SER 102Weight Height R =-.+.,=.,=..(a) 将70, 65,and 74Height = 英寸代入上述方程中,得体重预测分别为176.39,156.69, 和 192.15 英镑.(b) 39439415591.Weight Height ∆=.⨯∆=.⨯.=.(c) 已知: 1254and 104536.in cm lb kg =.=. 则用厘米——千克单位表示的回归方程为01ˆˆWeight Height γγ=+. 其中 0ˆ99410453645092;kg γ=-.⨯.=-. 045362541ˆ39407036kg γ..=.⨯=./ cm . 2R 无量纲,仍为 2081R =.. 回归标准误差1020453646267.SER kg =.⨯.=.5.(a) u i 表示除考试时间之外影响成绩的因素,如花在学习上的时间,学习能力等等.有些学生花在学习上的时间多于平均水平而有些少;又有些学生的学习能力强于平均水平而有些低于平均水平,等等. (b) 由于考试时间是随机分配给学生的,所以 u i 与 X i 独立. 又因为 u i 表示距离均值E (u i ) = 0的偏差,故 E (u i |X i ) = E (u i ) = 0. (c) 如果今年这个班是其它班级的典型代表,也就是说,今年这个班的学生可视为是从班级学生总体中随机抽取的,则条件(2) 满足. 因为0 ≤ Y i ≤ 100 且 X i 智能取90 和120两个值,所以条件 (3) 满足.(d) (i) 490.249070.6; 490.2412077.8; 490.2415085.0+⨯=+⨯=+⨯=(ii) 0.2410 2.4.⨯=第5章 P .1325 (a) 在小班中估计测试成绩提高13.9 分. 这近似等于1/5的测试成绩标准差, 提高幅度中等。
计量经济学习题及全部答案

《计量经济学》习题(一)一、判断正误1.在研究经济变量之间的非确定性关系时,回归分析是唯一可用的分析方法。
( ) 2.最小二乘法进行参数估计的基本原理是使残差平方和最小。
( )3.无论回归模型中包括多少个解释变量,总离差平方和的自由度总为(n -1)。
( ) 4.当我们说估计的回归系数在统计上是显着的,意思是说它显着地异于0。
( ) 5.总离差平方和(TSS )可分解为残差平方和(ESS )与回归平方和(RSS )之和,其中残差平方和(ESS )表示总离差平方和中可由样本回归直线解释的部分。
( )6.多元线性回归模型的F 检验和t 检验是一致的。
( )7.当存在严重的多重共线性时,普通最小二乘估计往往会低估参数估计量的方差。
( )8.如果随机误差项的方差随解释变量变化而变化,则线性回归模型存在随机误差项的自相关。
( )9.在存在异方差的情况下,会对回归模型的正确建立和统计推断带来严重后果。
( )10...DW 检验只能检验一阶自相关。
( ) 二、单选题1.样本回归函数(方程)的表达式为( )。
A .i Y =01i i X u ββ++B .(/)i E Y X =01i X ββ+C .i Y =01ˆˆi i X e ββ++D .ˆi Y =01ˆˆiX ββ+2.下图中“{”所指的距离是( )。
A .随机干扰项B .残差C .i Y 的离差D .ˆiY 的离差 3.在总体回归方程(/)E Y X =01X ββ+中,1β表示( )。
A .当X 增加一个单位时,Y 增加1β个单位B .当X 增加一个单位时,Y 平均增加1β个单位C .当Y 增加一个单位时,X 增加1β个单位D .当Y 增加一个单位时,X 平均增加1β个单位 4.可决系数2R 是指( )。
A .剩余平方和占总离差平方和的比重B .总离差平方和占回归平方和的比重C .回归平方和占总离差平方和的比重D .回归平方和占剩余平方和的比重 5.已知含有截距项的三元线性回归模型估计的残差平方和为2i e ∑=800,估计用的样本容量为24,则随机误差项i u 的方差估计量为( )。
计量经济学部分习题答案与解析

第三章 一元线性回归模型P56.3.3 从某公司分布在11个地区的销售点的销售量()Y 和销售价格()X 观测值得出以下结果:519.8X = 217.82Y = 23134543i X =∑ 1296836i i X Y =∑2539512iY=∑(1)、估计截距0β和斜率系数1β及其标准误,并进行t 检验; (2)、销售的总离差平方和中,样本回归直线未解释的比例是多少? (3)、对0β和1β分别建立95%的置信区间。
解:(1)、设01i i Y X ββ=+,根据OLS 估计量有:µ()()()11111122222211112=129683611519.8217.820.32313454311519.8N N NNNi i i ii i iii i i i i NNNN i ii i i i i i N Y X Y X N Y X N X NYY XN X YN X N X XN XN X X β=========---==⎛⎫--- ⎪⎝⎭-⨯⨯==-⨯∑∑∑∑∑∑∑∑∑µµ01217.820.32519.851.48Y X ββ=-=-⨯= 残差平方和:$()µ()µµµ()µµµµ()µµµµ222112222220111111122222222010101011111111=225395121NNi ii i i NNNNN N ii i i i ii i i i i i N N N N N i i i i i i i i i i i u RSS TSS ESS Y YYY Y Y Y Y Y X N N Y X X Y N X X ββββββββββ===============-=---⎛⎫⎛⎫--+=-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫=-++=-++ ⎪⎝⎭=-∑∑∑∑∑∑∑∑∑∑∑∑∑∑()22151.480.32313454320.3251.4811519.8997.20224⨯+⨯+⨯⨯⨯⨯=另解:对$()µ()22211NNi ii i i u RSS TSS ESS Y YYY ====-=---∑∑∑,根据OLS估计µµ01Y X ββ=-知µµ01+Y X ββ=,因此有 µµµµµ()µ()01011=++i i iY Y X X X X βββββ--=-,所以 $()µ()()µ()22222211111=NNNNiiiii i i i i u Y Y YY Y Y X Xβ=====------∑∑∑∑∑标准差: µ10.53σ==µ1β的标准误: µ()µµµ10.026se β===== 设原假设和备择假设分别为:01=0H β: 110H β≠: 将原假设带入t 统计量:µµ()()10.02510.3212.31 2.26290.026t t se ββ===>= 即拒绝原假设,认为销售价格()X 显著地解释了销售量()Y 的总体平均变化。
计量经济学 课后练习题答案解析
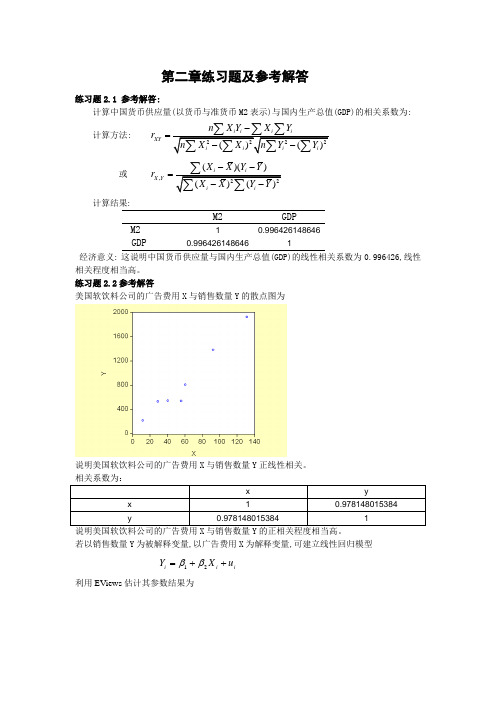
第二章练习题及参考解答练习题2.1 参考解答:计算中国货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相关系数为:计算方法: XY n X Y X Y r -=或,()()X Y X X Y Y r --=计算结果:M2GDPM2 10.996426148646GDP0.9964261486461经济意义: 这说明中国货币供应量与国内生产总值(GDP)的线性相关系数为0.996426,线性相关程度相当高。
练习题2.2参考解答美国软饮料公司的广告费用X 与销售数量Y 的散点图为说明美国软饮料公司的广告费用X 与销售数量Y 正线性相关。
相关系数为:说明美国软饮料公司的广告费用X 与销售数量Y 的正相关程度相当高。
若以销售数量Y 为被解释变量,以广告费用X 为解释变量,可建立线性回归模型 i i i u X Y ++=21ββ 利用EViews 估计其参数结果为经t 检验表明, 广告费用X 对美国软饮料公司的销售数量Y 确有显著影响。
回归结果表明,广告费用X 每增加1百万美元, 平均说来软饮料公司的销售数量将增加14.40359(百万箱)。
练习题2.3参考解答:1、 建立深圳地方预算内财政收入对GDP 的回归模型,建立EViews 文件,利用地方预算内财政收入(Y )和GDP 的数据表,作散点图可看出地方预算内财政收入(Y )和GDP 的关系近似直线关系,可建立线性回归模型: t t t u GDP Y ++=21ββ 利用EViews 估计其参数结果为即 ˆ20.46110.0850t tY GDP =+ (9.8674) (0.0033)t=(2.0736) (26.1038) R 2=0.9771 F=681.4064经检验说明,深圳市的GDP 对地方财政收入确有显著影响。
20.9771R =,说明GDP 解释了地方财政收入变动的近98%,模型拟合程度较好。
模型说明当GDP 每增长1亿元时,平均说来地方财政收入将增长0.0850亿元。
计量经济学习题集与答案解析1教学文案

计量经济学习题集与答案解析1习题讲解(一)一、选择题1、样本回归函数(方程)的表达式为( D )A.i i i X Y μββ++=10B.i i X X Y E 10)(ββ+=C.i i i e X Y ++=10ˆˆββD.ii X Y 10ˆˆˆββ+= 2、反映由模型中解释变量所解释的那部分离差大小的是( B )A.总离差平方和B.回归平方和C.残差平方和D.都不是3、设k 为回归模型中的参数个数(不包括常数项),n 为样本容量,RSS 为残差平方和,ESS 为回归平方和,则对总体回归模型进行显著性检验时构造的F 统计量为( B ) A.TSSESS F = B.)1(--=k n RSS k ESS F C.)1(1---=k n TSS k ESS F D.TSSRSS F = 4、对于某样本回归模型,已求得DW 的值为l ,则模型残差的自相关系数∧ρ近似等于( C )A.-0.5B.0C.0.5D.15、下列哪种方法不能用来检验异方差( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.D-W 检验6、根据一个n =30的样本估计tt t e X Y ++=10ˆˆββ后计算得D.W.=1.2,已知在5%的显著水平下,35.1=L d ,49.1=U d ,则认为原模型( C )。
A.不存在一阶序列相关B.不能判断是否存在一阶序列相关C.存在正的一阶序列相关D.存在负的一阶序列相关7、某商品需求函数模型为i i i X Y μββ++=10,其中Y 为需求量,X 为价格。
为了考虑“地区”(农村、城市)和“季节”(春、夏、秋、冬)两个因素的影响,拟引入虚拟变量,则应引入虚拟变量的个数为( B )A.2B.4C.5D.68、可以用于联立方程计量模型方程间误差传递性检验的统计量是( C )A.均方百分比误差B.F 检验统计量C.均方根误差D.滚动预测检验9、下列属于有限分布滞后模型的是( D )A. t t t t X X Y μβββ++++=-Λ1210B. t t t t t Y Y X Y μββββ++++=--231210C. t t t t Y Y Y μβββ++++=-Λ1210D. t k t k t t t X X X Y μββββ+++++=+--11210Λ10、估计模型Y t =β0+β1X t +β2Y t-1+μt (其中μt 满足线性模型的全部假设)参数的适当方法是( D )A.二阶段最小二乘法B.间接最小二乘法C.广义差分法D.工具变量法11、考察某地区农作物种植面积与农作物产值的关系,建立一元线性回归模型i i i X Y μββ++=10(X 表示农作物种植面积、Y 表示农作物产值),采用30个样本,根据OLS 方法得54.0ˆ1=β,对应标准差045.01ˆ=βS ,那么,1β对应的统计量t 为( )A.12B.0.0243C.2.048D.1.70112、一无线性回归模型 的最小二乘回归结果显示,残差平方和RSS=40.32,样本容量为25,则回归模型的标准差 为( B )A.1.270B.1.324C.1.613D.1.75313、k 表示模型系统中先决变量的个数(含常数项),i k 表示第i 个方程中先决变量的个数(含常数项),i g 表示第i 个方程中内生变量的个数,识别的阶条件为1-<-i i g k k ,表示( B )A.第i 个方程恰好识别B.第i 个方程不可识别C.第i 个方程过度识别D.第i 个方程具有唯一的统计形式14、当随机误差项存在序列相关时,单位根检验采用的是( B )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 一元线性回归模型P56.3.3 从某公司分布在11个地区的销售点的销售量()Y 和销售价格()X 观测值得出以下结果:519.8X = 217.82Y = 23134543i X =∑ 1296836i i X Y =∑2539512i Y =∑(1)、估计截距0β和斜率系数1β及其标准误,并进行t 检验; (2)、销售的总离差平方和中,样本回归直线未解释的比例是多少? (3)、对0β和1β分别建立95%的置信区间。
解:(1)、设01i i Y X ββ=+,根据OLS 估计量有:µ()()()11111122222211112=129683611519.8217.820.32313454311519.8N N NNNi i i ii i iii i i i i NNNN i ii i i i i i N Y X Y X N Y X N X NYY XN X YN X N X XN XN X X β=========---==⎛⎫--- ⎪⎝⎭-⨯⨯==-⨯∑∑∑∑∑∑∑∑∑µµ01217.820.32519.851.48Y X ββ=-=-⨯= 残差平方和:$()µ()µµµ()µµµµ()µµµµ222112222220111111122222222010101011111111=225395121NNi i i i i NNNNN N ii i i i ii i i i i i N N N N N i i i i i i i i i i i u RSS TSS ESS Y YYY Y Y Y Y Y X N N Y X X Y N X X ββββββββββ===============-=---⎛⎫⎛⎫--+=-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫=-++=-++ ⎪⎝⎭=-∑∑∑∑∑∑∑∑∑∑∑∑∑∑()22151.480.32313454320.3251.4811519.8997.20224⨯+⨯+⨯⨯⨯⨯=另解:对$()µ()22211NNi i i i i u RSS TSS ESS Y YYY ====-=---∑∑∑,根据OLS估计µµ01Y X ββ=-知µµ01+Y X ββ=,因此有µµµµµ()µ()01011=++i i iY Y X X X X βββββ--=-,所以 $()µ()()µ()22222211111=NNNNiiiii i i i i u Y Y YY Y Y X Xβ=====------∑∑∑∑∑标准差: µ10.53σ==µ1β的标准误: µ()µµµ10.026se β=====设原假设和备择假设分别为:01=0H β: 110H β≠: 将原假设带入t 统计量:µµ()()10.02510.3212.31 2.26290.026t t se ββ===>= 即拒绝原假设,认为销售价格()X 显著地解释了销售量()Y 的总体平均变化。
(2)、回归直线中未解释部分比列:$()$222222977.202240.05553951211217.82i iiiu u RSSTSSYNYY Y ====-⨯--∑∑∑∑ (3)、µ0β的标准误: µ()s 10.5313.95e βσσσ====⨯=根据置信区间计算式:µµ()µµ()()22,t se t se ααββββ-+得µ0β的95%的置信区间:()51.48 2.26213.95,51.48+2.26213.95-⨯⨯即()19.9383.03,µ1β的95%的置信区间:()0.32 2.2620.026,0.32+2.2620.026-⨯⨯即()0.260.38,3.4 在一个回归中,得到下表,但空缺了两个数据。
(2) 如果显著性水平=0.05α,请用p 值法进行t 检验 解:(1)根据µµ()282.2434==0.9825287.2649t se ββ=µµ()11=20.540260.0369280.7585t se ββ⨯=⨯= (2)从回归估计的结果看,斜率参数µ1=0.7585β,显著性概率=0.0000p ,在显著性水平=0.05α的条件下,p α<,即拒绝原假设,接受备择假设,1β显著不为0,变量X 的变化能显著地解释Y 的总体平均变化。
对截距项µ0=282.2434β,其显著性概率0.33400.05p α=>=,故不能拒绝截距为零的原假设。
(截距一般没有明确的经济含义,但是大多数模型包含截距,以截取没有被X 所解释的Y 的变化,因此,计量经济学一般不对截距进行假设检验)第四章 多元线性回归分析P93.4.2 在分析变量Y 的影响因素时,学生甲建立了如下的多元回归方程:01122t t t t Y X X αααε=+++学生乙也在研究研究同样的经济问题,她只学习了一元线性回归模型。
为了考察在2X 不变时,1X 对Y 的影响,学生乙进行了如下的三步回归分析:0122t t t Y X ββε=++ (a )10122t t t X X γγε=++(b )$$1213t t t ελεε=+(c )其中,$1t ε,$2t ε分别是回归方程()a 、()b 的残差项。
(1) 参数1α和参数1λ有什么样的关系?解释你的理由 (2) 参数2α和参数1β是同一参数吗?解释你的理由 (3) 回归方程()c 为什么没有截距项? 解:(1、2)由方程(b )得到21012t t t X X εγγ=--带入方程(c )得到$()1110123t t t t X X ελγγε=--+带入方程(a )得到()0111112310t t t t Y X X βλβλγελγ=++-+-又01122t t t t Y X X αααε=+++11=αλ∴、21αβ≠(3)假设方程()c 有截距项μ,则$µ$1213+t t t εμλεε=+µ()10tE ε=Q 即 µ$()µ()¶()¶()213123+=+=0t t t t E E E E μλεεμλεε++ 又¶()2=0tE εQ 、¶()3=0tE εµ()=0E μ∴ 即µ=0μ4.3 在基于受约束和无约束回归方程的估计结果检验线性约束时,需要建立F检验统计量。
有读者在相关文献中看到了如下的F 检验统计量:()()()()222,111urr urRR qF F q N K R N K -=-----:(1)说明该F 统计量的形式是如何得到的。
(2)在使用该统计量形式时需要注意什么条件?(3)在分析生产函数时,如果无约束和受约束方程分别为012ln ln ln t t t t Q K K βββε=+++和()()01ln ln t t t t t Q L K L ββε=++那么,本题中所给出的F 统计量计算公式是否还适用?给出你的理由。
解:(1)()()()()()()()()()()()()22222211=1111,111r ur r ur r ur ur ur ur ur ur urr urR R q RSS RSS q RSS RSS TSS q F RSS N K RSS TSS N K R N K RR qF q N K R N K ⎡⎤-----⎣⎦==--------=-----g g :(2)在(1)中默认了ur r TSS TSS =,因此在使用该统计量形式时需注意无约束回归方程和受约束回归方程的被解释变量应该一致。
(3)不适用。
被解释变量分别为ln t Q 、()ln t t Q L4.4为了分析羊肉的需求特征,有研究者建立并估计了如下的模型:012132ln t i t t t Q Y P P ββββε=+++参数估计值:130.329.10.130.085.86.6 1.8 1.50.0000.0000.08350.146t p --=--= 20.700R = 样本容量30T = 其中:Q :羊肉年人均需求量(单位:kg ) Y :当地居民的年人均收入水平(元)1P :羊肉年平均价格(元/kg ) 2P :牛肉年平均价格(元/kg )(1)基于经济理论和对经济现实的观察,你对各解释变量系数符合有怎样的先验预期?简要说明理由(2)基于你对解释变量系数的预期,建立相应的假设并进行检验(3)根据t 检验的p 值,该研究者认为:“在5%显著性水平上,1P 和2P 的影响都不显著;在10%显著性水平上,1P 的影响显著,2P 的影响不显著。
”是否同意这一解释?说明理由(4)系数1β估计值为29.1,解释其经济含义解:(1)10β>,在其他经济变量保持不变的情况下,人均收入水平Y 提高意味着居民变得更富有,对羊肉的人均需求量Q 会增加;20β<,羊肉平均价格1P 提高,相对而言更贵了,人们会选择羊肉的替代品牛肉,所以对羊肉的人均需求量Q 会降低;30β>,牛肉平均价格2P 提高,在1P 不变的情况下,人们会选择牛肉的替代品羊肉,Q 增加。
(2)对1β的检验,假设01:0H β≤,11:0H β>。
构造统计量µµ()µµ()0t se se βββββ--==根据t 检验的p 值判断,0.0000.102pα=<=(此处是单侧检验,故取2p )拒绝原假设,即认为10β>。
同理可检验2β、3β(3)不同意。
在5%显著性水平上,1P 的影响显著,2P 的影响不显著;在10%显著性水平上,1P 和2P 的影响都显著。
(判断方法见(2))(4)在其他变量保持不变的情况下,人均收入水平i Y 每变化一个百分点,人均需求量变化0.291个单位。
期中测试题1. 已知回归模型E N αβμ=++,式中E 为某公司一名新员工的起始薪金(元),N 为所受教育水平(年)。
随机扰动项μ的分布未知,其他所有假设均满足。
(1)从直观经济角度解释α、β的含义。
(2)OLS 估计量µα、µβ是否满足线性性、无偏性及有效性,说明理由 (3)对参数的假设检验是否能够进行,说明理由 解:(1)回归模型的截距为α,即受教育年限0N =时的平均起始薪金,斜率系数为β,即受教育水平每增加1年,起始薪金E 平均增加β个单位。
