数学建模作业、微分方程实验、北京工业大学
北工大工程数学-数学建模实验03
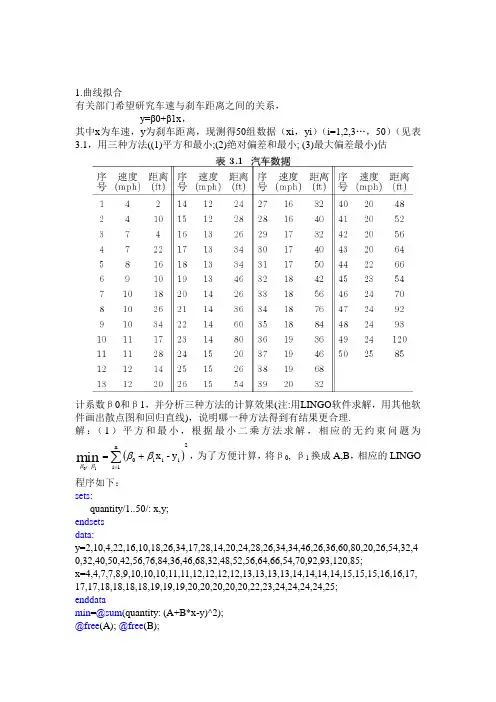
1.曲线拟合有关部门希望研究车速与刹车距离之间的关系， y=β0+β1x ，其中x 为车速，y 为刹车距离，现测得50组数据（xi ，yi ）（i=1,2,3…，50）（见表3.1，用三种方法((1)平方和最小;(2)绝对偏差和最小; (3)最大偏差最小)估计系数β0和β1，并分析三种方法的计算效果(注:用LINGO 软件求解，用其他软件画出散点图和回归直线)，说明哪一种方法得到有结果更合理. 解：（1）平方和最小，根据最小二乘方法求解，相应的无约束问题为()2n1i i i 10y -x min 10∑=+=ββββ，，为了方便计算，将β0, β1换成A,B ，相应的LINGO程序如下： sets :quantity/1..50/: x,y; endsets data :y=2,10,4,22,16,10,18,26,34,17,28,14,20,24,28,26,34,34,46,26,36,60,80,20,26,54,32,40,32,40,50,42,56,76,84,36,46,68,32,48,52,56,64,66,54,70,92,93,120,85;x=4,4,7,7,8,9,10,10,10,11,11,12,12,12,12,13,13,13,13,14,14,14,14,15,15,15,16,16,17,17,17,18,18,18,18,19,19,19,20,20,20,20,20,22,23,24,24,24,24,25; enddatamin =@sum (quantity: (A+B*x-y)^2); @free (A); @free(B);计算结果如图所示用LINGO解得：A= -17.57909,B=3.932409，所以y= -17.57909+3.932409*x. β0= -17.57909,β1=3.932409（2）绝对偏差和最小，根据最小一乘方法求解，相应的无约束问题为∑=+=ni1ii1y-xmin1ββββ，，为了方便计算，将β0, β1换成A,B，相应的LINGO程序如下：sets:quantity/1..50/: x,y;endsetsdata:y=2,10,4,22,16,10,18,26,34,17,28,14,20,24,28,26,34,34,46,26,36,60,80,20,26,54,32,4 0,32,40,50,42,56,76,84,36,46,68,32,48,52,56,64,66,54,70,92,93,120,85;x=4,4,7,7,8,9,10,10,10,11,11,12,12,12,12,13,13,13,13,14,14,14,14,15,15,15,16,16,17, 17,17,18,18,18,18,19,19,19,20,20,20,20,20,22,23,24,24,24,24,25;enddatamin=@sum(quantity: @abs(A+B*x-y));@free(A); @free(B);计算结果如图所示用LINGO 解得：A= -11.6,B=3.4， 所以y= -11.6+3.4*x. β0= -11.6,β1=3.4（3）最大偏差最小，根据最大偏差的最小的方法求解，相应的无约束问题为i i 101y -x max min 10ββββ+=≤≤ni ，，为了方便计算，将β0, β1换成A,B ，相应的LINGO程序如下： sets :quantity/1..50/: x,y; endsets data :y=2,10,4,22,16,10,18,26,34,17,28,14,20,24,28,26,34,34,46,26,36,60,80,20,26,54,32,40,32,40,50,42,56,76,84,36,46,68,32,48,52,56,64,66,54,70,92,93,120,85;x=4,4,7,7,8,9,10,10,10,11,11,12,12,12,12,13,13,13,13,14,14,14,14,15,15,15,16,16,17,17,17,18,18,18,18,19,19,19,20,20,20,20,20,22,23,24,24,24,24,25; enddatamin =@max (quantity: @abs (A+B*x-y)); @free (A); @free (B); 计算结果如图所示用LINGO解得：A= -12,B=4，所以y= -12+4*x. β0= -12,β1=4X轴为速度，Y轴为距离，蓝色点多已知数据点，y1,y2,y3分别为前三种方法求得的数据点，黑色线为通过蓝色数据点得到的线性回归方程y=1.445x+6.121,比较三种方法得到曲线，可以看到与红色曲线吻合度高于其他两种方法，所以第一种方法得到的结果更为合理。
数学建模作业北工大薛毅实验3.docx
第三次作业1.生产计划安排某公司使用三种操作装配三种玩具一玩具火车、玩具卡车和玩具汽车.对于二种操作可冃时间限制分别是每天430分钟、460分钟和420分钟，玩具火车、玩具代车和玩具汽车的单位收入分別是3美元、2美元和5美元•每辆玩具火车在三种操作的装配时间分別是1分钟、3分钟和1分钟•毎辆玩具K车和每辆玩具汽车相应的时间是(2,0,4)和(1,2,0)分钟(零时间表示不使用该项操作).(1)将间题建立成一个线性规划模型，确定最优的生产方案.(2)对于操作1,假定超过它当前每天43()分钟能力的任何附加时间必须依靠每小时50美元的加班获得•每小时成本包括劳动力和机器运行费两个方面. 对于操作1,使用加班在经济I：冇利吗？如果冇利，最多増加多少时间？(3)假定操作2的操作员已同意每天加班工作2小时，其加班费是45美元•小时.还有，操作自身的成本是•小时10美元.这项活动对于每天收入的实际结果是什么？(4)操作3需要加班时间吗？解：(1)设生产玩具火车、玩具卡车和玩具汽车的数量分别为XI, X2, X3,则H 标函数为：max Z=3X 1+2X2+5X3约朿条件：XI +2X2 +X3V 二4303X1 +2X3<=460XI +4X2 <=420Xl>=0； X2>=0； X3>=0输到ling。
里面的结果为；Global optimal solution found.Objective value:1350.000Infeasibilities: 0.000000Total solver iterations: 2Model Class: LPTotal variables: 3Non linear variables: 0Total constraints: 4Nonlinear constraints:Total non zeros:10Non linear non zeros:VariableValue Reduced CostXI0.000000 4.000000X2100.0000 0.000000X3230.00000.000000RowSlack or SurplusDual Price11350.0001.000000 2 0.000000 1.0000003 0.000000 2.000000420.000000.000000所以玩具火车、玩具卡车和玩具汽车的生产数量分别为：0、100. 230； 最大的收入为1350.(2)表明操作1每工作1分钟的利润是2美元，如果是要加50美元每小时的加工费的话，一定 是赚的。
北京工业大学数学建模实验3
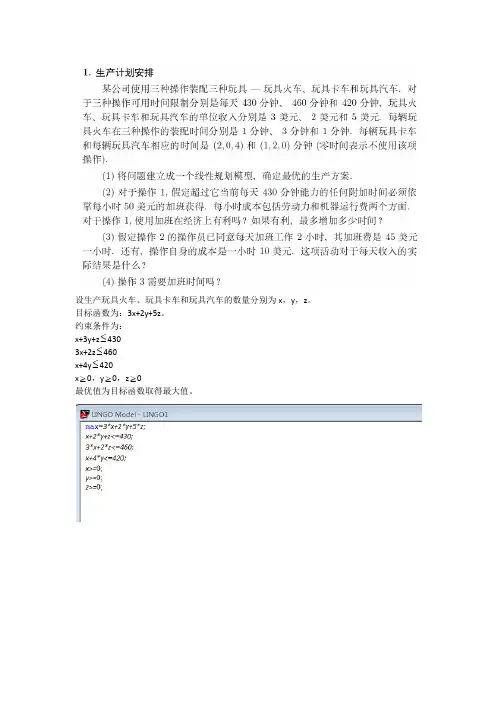
设生产玩具火车、玩具卡车和玩具汽车的数量分别为x，y，z。
目标函数为：3x+2y+5z。
约束条件为：x+3y+z≤4303x+2z≤460x+4y≤420x≥0，y≥0，z≥0最优值为目标函数取得最大值。
（1）最优的生产方案为：玩具火车、玩具卡车和玩具汽车的生产数量分别为：0、100、230；收入为1350美元。
（2）由Dual Price第二行可知，当操作1每增加1分钟收入增加1美元，加班一小时收入60美元，60>50，使用加班在经济上是有利的。
最多加班10分钟，此时操作1工作的每1分钟收入和操作员收入相同。
（3）由运算结果第三行可知，当操作2每加班1分钟时，收入增加2美元。
2*120-（45+10）*2=130美元。
收入130美元。
（4）不需要操作3加班，因为其影子价格为0。
设使用燕麦、玉米和糖渣分别为x、y、z千克。
目标函数为：1.3*x+1.7*y+1.2*z+2.5*(x+y)+0.5*(x+y+z)。
约束条件为：x>=0x<=11900y>=0y<=23500z>=0z<=750x+y+z>=2100013.6*x+4.1*y+5*z>=9.5*210007.1*x+2.4*y+0.3*z>=2*210007*x+3.7*y+25*z<=6*21000最小成本为92667.95+9000*4.2+12000*1.7=150867.95元。
燕麦11896.63千克，玉米8678.905千克，糖渣424.4658千克。
每种原料的的3/7生产颗粒饲料，剩下的4/7生产粉状饲料。
设x i，y i，z i，w i分别为第i年对四个项目的投资。
目标函数为：1.2X3+1.6Z2+1.4W3。
约束条件为：X1+Y1=30X2+Z2=1.2X1X3+W3=1.2X2+1.5y1y1<=20z2<=15w3<=10投资计划：第一年12.5万投资A，17.5万投资B。
数学建模作业 北工大薛毅 实验4
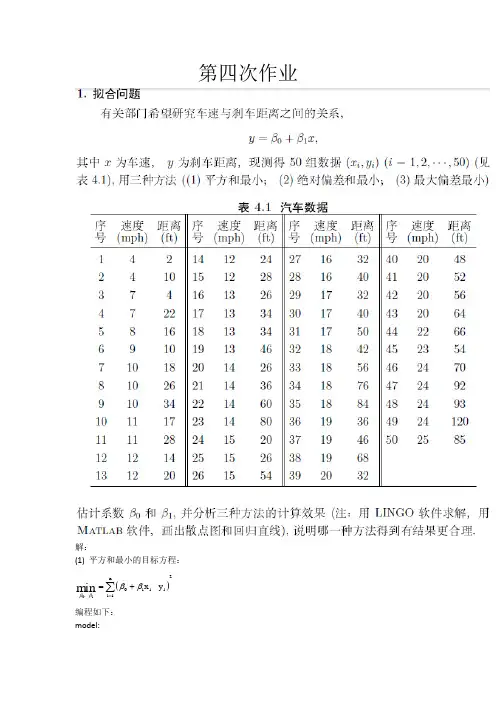
第四次作业解：(1) 平方和最小的目标方程：()2n 1i i i 10y -x min 10∑=+=ββββ，编程如下：model:sets:quantity/1..50/: x,y;endsetsmin=@sum(quantity: (B0+B1*x-y)^2);data:y=2 10 4 22 16 10 18 26 34 17 28 14 20 24 28 26 34 34 46 26 36 60 80 20 26 54 32 40 32 40 50 42 56 76 84 36 46 68 32 48 52 56 64 66 54 70 92 93 120 85;x=4 4 7 7 8 9 10 10 10 11 11 12 12 12 12 13 13 13 13 14 14 14 14 15 15 15 16 16 17 17 17 18 18 18 18 19 19 19 20 20 20 20 20 22 23 24 24 24 24 25;enddata@free(B0); @free(B1);End得到结果如下：Local optimal solution found.Objective value: 11353.52Infeasibilities: 0.000000Extended solver steps: 5Total solver iterations: 18Model Class: NLPTotal variables: 3Nonlinear variables: 2Integer variables: 0Total constraints: 2Nonlinear constraints: 1Total nonzeros: 3Nonlinear nonzeros: 2Variable Value Reduced CostB0 -17.57909 0.000000B1 3.932409 0.000000X( 1) 4.000000 0.000000X( 2) 4.000000 0.000000X( 3) 7.000000 0.000000X( 4) 7.000000 0.000000X( 5) 8.000000 0.000000X( 6) 9.000000 0.000000X( 7) 10.00000 0.000000X( 8) 10.00000 0.000000X( 9) 10.00000 0.000000X( 10) 11.00000 0.000000X( 11) 11.00000 0.000000 X( 12) 12.00000 0.000000 X( 13) 12.00000 0.000000 X( 14) 12.00000 0.000000 X( 15) 12.00000 0.000000 X( 16) 13.00000 0.000000 X( 17) 13.00000 0.000000 X( 18) 13.00000 0.000000 X( 19) 13.00000 0.000000 X( 20) 14.00000 0.000000 X( 21) 14.00000 0.000000 X( 22) 14.00000 0.000000 X( 23) 14.00000 0.000000 X( 24) 15.00000 0.000000 X( 25) 15.00000 0.000000 X( 26) 15.00000 0.000000 X( 27) 16.00000 0.000000 X( 28) 16.00000 0.000000 X( 29) 17.00000 0.000000 X( 30) 17.00000 0.000000 X( 31) 17.00000 0.000000 X( 32) 18.00000 0.000000 X( 33) 18.00000 0.000000 X( 34) 18.00000 0.000000 X( 35) 18.00000 0.000000 X( 36) 19.00000 0.000000 X( 37) 19.00000 0.000000 X( 38) 19.00000 0.000000 X( 39) 20.00000 0.000000 X( 40) 20.00000 0.000000 X( 41) 20.00000 0.000000 X( 42) 20.00000 0.000000 X( 43) 20.00000 0.000000 X( 44) 22.00000 0.000000 X( 45) 23.00000 0.000000 X( 46) 24.00000 0.000000 X( 47) 24.00000 0.000000 X( 48) 24.00000 0.000000 X( 49) 24.00000 0.000000 X( 50) 25.00000 0.000000 Y( 1) 2.000000 0.000000 Y( 2) 10.00000 0.000000 Y( 3) 4.000000 0.000000 Y( 4) 22.00000 0.000000Y( 5) 16.00000 0.000000 Y( 6) 10.00000 0.000000 Y( 7) 18.00000 0.000000 Y( 8) 26.00000 0.000000 Y( 9) 34.00000 0.000000 Y( 10) 17.00000 0.000000 Y( 11) 28.00000 0.000000 Y( 12) 14.00000 0.000000 Y( 13) 20.00000 0.000000 Y( 14) 24.00000 0.000000 Y( 15) 28.00000 0.000000 Y( 16) 26.00000 0.000000 Y( 17) 34.00000 0.000000 Y( 18) 34.00000 0.000000 Y( 19) 46.00000 0.000000 Y( 20) 26.00000 0.000000 Y( 21) 36.00000 0.000000 Y( 22) 60.00000 0.000000 Y( 23) 80.00000 0.000000 Y( 24) 20.00000 0.000000 Y( 25) 26.00000 0.000000 Y( 26) 54.00000 0.000000 Y( 27) 32.00000 0.000000 Y( 28) 40.00000 0.000000 Y( 29) 32.00000 0.000000 Y( 30) 40.00000 0.000000 Y( 31) 50.00000 0.000000 Y( 32) 42.00000 0.000000 Y( 33) 56.00000 0.000000 Y( 34) 76.00000 0.000000 Y( 35) 84.00000 0.000000 Y( 36) 36.00000 0.000000 Y( 37) 46.00000 0.000000 Y( 38) 68.00000 0.000000 Y( 39) 32.00000 0.000000 Y( 40) 48.00000 0.000000 Y( 41) 52.00000 0.000000 Y( 42) 56.00000 0.000000 Y( 43) 64.00000 0.000000 Y( 44) 66.00000 0.000000 Y( 45) 54.00000 0.000000 Y( 46) 70.00000 0.000000 Y( 47) 92.00000 0.000000 Y( 48) 93.00000 0.000000Y( 49) 120.0000 0.000000Y( 50) 85.00000 0.000000Row Slack or Surplus Dual Price1 11353.52 -1.000000 所以得到平方和最小时的β0为-17.57909，β1为3.932409。
北京工业大学数学建模工程数学实验4
设Wxy为从第二年开始算，使用x年到y年的购买设备的总消费W12=100-17.2+1.5-50=34.3W13=100-15.5+1.7+1.5-30=57.7W14=100-14+1.5+1.7+1.8-10=81W15=100-12.2+1.5+1.7+1.8+2.2-5=90W23=100-15.5+1.7-30=56.2W24=100-14+1.7+1.8-10=79.5W25=100-12.2+1.7+1.8+2.2-5=88.5W34=100-14+1.8-10=77.8W35=100-12.2+1.8+2.2-5=86.8W45=100-12.2+2.2-5=85Lingo：sets:nodes/1..5/;arcs(nodes, nodes)|&1 #lt# &2: w, x;endsetsdata:w = 34.3 57.7 81 90 56.2 79.5 88.5 77.8 86.8 85;enddata n = @size(nodes);min = @sum(arcs: w * x);@for(nodes(i)| i #ne# 1 #and# i #ne# n:@sum(arcs(i,j): x(i,j)) = @sum(arcs(j,i): x(j,i)) );@sum(arcs(i,j)| i #eq# 1 : x(i,j)) = 1;运行结果：从程序结果分析可知按着W15花费最少。
即该单位应该在第3年购买新设备第6年年底卖掉设备，最小花费为90万元。
（1）设第一季度、第二季度、第三季度、第四季度生产量分别为a、b、c、d，a1为第一季度后剩余量，b1为第二季度后剩余量，c1为第三季度后剩余量，d1为第四季度后的剩余量。
每季度的生产的除臭剂应该小于等于最大产量，大于等于订货量，第一个季度以为的季度中 实际货物量应该等于上月的剩余量加该月的产量，以此类推，可以得出Lingo:model:min =5*a+5*b+6*c+6*d+ya1+b1+c1+d1;a>=10; a<=14;a1= a-10;b+a1>=14;b<=15;b1=b+a1-14;c+b1>=20;c<=15;c1=c+b1-20;d+ c1>=8;d<=13;d1=d+c1-8;输出结果：Variable Value Reduced CostA 14.00000 0.000000B 15.00000 0.000000C 15.00000 0.000000D 8.000000 0.000000第一个季度应生产14万盒，第二季度应该生产15万盒，第三季度应该生产15万盒，第四季度应该生产8万盒除臭剂。
数学建模作业实验2微分方程实验
数学建模作业(实验2微分方程实验)基本实验1．微分方程稳定性分析绘出下列自治系统相应的轨线，并标出随t 增加的运动方向，确定平衡点，并按稳定的、渐近稳定的、或不稳定的进行分类：,,,+1,(1)(2)(3)(4);2;2;2.dx dx dx dxx x y x dt dt dt dt dy dy dy dy y y x y dt dt dt dt ⎧⎧⎧⎧==-==-⎪⎪⎪⎪⎪⎪⎪⎪⎨⎨⎨⎨⎪⎪⎪⎪===-=-⎪⎪⎪⎪⎩⎩⎩⎩解答解：（1）由平衡点的定义可得，f （x ）=x=0，f （y ）=y=0，因此平衡点为（0,0），微分方程组的系数矩阵为1001A ⎡⎤=⎢⎥⎣⎦，显然其特征值为12=1=1λλ，；由根与系数的关系可得：1212()2010p q λλλλ=-+=-<==>，且24p q >，由平衡点与稳定性的各种情况可知，平衡点（0，0）是不稳定的。
自治系统相应轨线为：（2）由平衡点的定义可得，f （x）=-x=0，f （y ）=2y=0，因此平衡点为（0,0），微分方程组的系数矩阵为-1002A ⎡⎤=⎢⎥⎣⎦，显然其特征值为12=-1=2λλ，；由根与系数的关系可得：121210-(2<0)p q λλλλ=-+=-<==，，平衡点（0，0）是不稳定的。
自治系统相应轨线为：（3）由平衡点的定义可得，f （x ）=y=0，f （y ）=-2x=0，因此平衡点为（0,0），微分方程组的系数矩阵为0120A ⎡⎤=⎢⎥-⎣⎦，显然其特征值为121.4142=4142=-1.i i λλ，；由根与系数的关系可得：12120 1.41420()p q λλλλ=-+===>，，由平衡点与稳定性的各种情况可知，平衡点（0，0）是不稳定的。
自治系统相应轨线为：（4）由平衡点的定义可得，f （x ）=-x=0，f （y ）=-2y=0，因此平衡点为（0,0），微分方程组的系数矩阵为-100-2A ⎡⎤=⎢⎥⎣⎦，显然其特征值为12==-12-λλ，；由根与系数的关系可得：1212()3020p q λλλλ=-+=>==>，且24p q >，由平衡点与稳定性的各种情况可知，平衡点（0，0）是稳定的。
北京工业大学、薛毅、数学模型作业二、作业2、实验二
实验二解：（1）将线性方程组写成矩阵形式dXdt =AX,A=a11a12a21a22=1001若det(A)≠0,则X0=(0,0)T,是唯一平衡点。
p=-(a11+a22)=-2,q=det(A)=1,因为p<0,q>0,所以平衡点不稳定。
（2）将线性方程组写成矩阵形式dXdt =AX,A=a11a12a21a22=−1002若det(A)≠0,则X0=(0,0)T,是唯一平衡点。
p=-(a11+a22)=-1,q=det(A)=-2,因为p<0,q<0,所以平衡点不稳定。
（3）将线性方程组写成矩阵形式dXdt =AX,A=a11a12a21a22=01−20若det(A)≠0,则X0=(0,0)T,是唯一平衡点。
p=-(a11+a22)=0,q=det(A)=2,因为p=0,q>0,所以平衡点不稳定。
（4）将线性方程组写成矩阵形式dXdt =AX,A=a11a12a21a22=−100−2若det(A)≠0,则X0=(0,0)T,是唯一平衡点。
p=-(a11+a22)=3,q=det(A)=2,因为p>0,q>0,p2>4q,所以平衡点稳定。
解:f(N)=R-KN,令f(N)=0,则N=k/Rf`(N)=-K<0,则N=k/R是稳定的。
当N<k/R时f(N)>0,N`(t)>0,N(t)递增；N>k/R时f(N)<0,N`(t)<0,N(t)递减ð2N ðt2=∂f∂N∙ðNðt=-K(R-KN),表明N=k/R为拐点，当N<k/R时N``(t)<0,N>k/R时N``(t)>0从图中可以看出N=k/R是营养平衡值，无论大于或小于这个值，细胞都会向这个点调整，偏离越大调整速率越大，接近平衡值时速率变小。
解：列满足条件的微分方程∂N=r1N−r2N12求平衡点，令f N=r1N−r2N1=0,解得N1=0，N2=r22r12ð2N ðt =∂f∂N∙ðNðt=(r1−12r2N−12)(r1N−r2N12）,解得N=r224r12从图中可以看出N1=0不稳定，N2=r22r12是稳定的解：令f x=r1−xNx−Ex=0得平衡点x1=N1−Er,x2=0f`(x1)=E-r,f`(x2)= r-E.若E<r,则有f`(x1)<0,f`(x2)>0.则x1是稳定的，x2是不稳定的。
北京工业大学数学建模-实验1答案
他妻子驾车至火车站接他回家。一日他提前下班，乘早一班火车于 17:30 抵达 A 市火车站，随 即步行回家，他妻子像往常一样驾车前来，在半路相遇将他接回家。到家时张先生发现比往常 提前了 10 分钟，问张先生步行了多长时间？ 解：假设他的妻子和他在半路相遇后仍载着他开往车站并返回家中，则他并不会比平时早到 10 分钟，早到的这 10 分钟是由于他和妻子没有从半路相遇点到车站之间往返产生的，即从相 遇点到车站车行时间为 5 分钟， 即他和妻子相遇时刻为 18:00 前 5 分钟即 17:55， 他 17:30 到达 车站，则其步行时间为 25 分钟。 （4）一男孩和一女孩分别在距家 2 公里和 1 公里且方向相反的两所学校上学，每天同时放学 后分别以每小时 4 公里和每小时 2 公里的速度步行回家。 一小狗以每小时 6 公里的速度由男孩 处奔向女孩，又从女孩处奔向男孩，如此往返直至回到家中。问小狗奔波了多少路程。如果男 孩和女孩上学时，小狗也往返奔波在他们中间，问当他们到达学校时小狗在何处？ 解：男孩女孩从各自学校回家的时间都是 0.5 小时，所以小狗奔跑的时间也是 0.5 小时，这个 过程中，小狗的奔跑路程为 3km。如果男孩女孩上学时，小狗也往返在他们之间，那小狗出现 的位置可能有两种情况，因为最初的跑动方向可能是男孩方向也可能是女孩方向。
dT (t ) k (T (t ) T0 ) （1） dt
式（1）的通解为： T (t ) T0 Cekt 。 早上 6 点时 t=0， T(0)=26℃， 早上 8 点时 t=2， T(2)=18℃.假设死者死亡时体温正常 T(t0)=37℃， 由通解表达式可知：
T (0) 10 C 26
加分实验
基本投票问题
某部门推出一专项基金目的在于培养优秀人才，根据评比结果来确定资助的额度。许多单 位的优秀者都申请了该基金，于是该基金的委员会聘请了数名专家，按照如下规则讲行评比。
北工大 数学建模 实验5
（1）输入程序：X<-c(1067,919,1196,785,1126,936,918,1156,920,948)t.test(X,al="g")R程序：有结果可知95%的灯泡至少可以使用920.8小时(2)当使用时间至少为1000小时：查阅标准正态分布表可以得出对应的概率为1-Ф（(1000-µ)/δ）=1-Ф（(1000-997.1)/124.797）=1-Ф（0.02324）=1-0.5106=0.4894即由题可以得出使用时间在1000小时以上的概率为48.94%。
解：设原假设为H0:225，对立假设H1:225输入程序：X<-c(220,188,162,230,145,160,238,188,247,113,126,245,164,231,256,183,190,158,2 24,175)t.test(X,mu=225)R程序为结果得出：P-=0.002516<0.05，所以拒绝H0，置信区间为[172.3827,211.9173]，最大值小于225。
因此可以认为油漆作业对人体血小板计数有影响（1） 1、方差相同时设原假设H0:µ1>=µ2，对立假设H1:µ1<µ2X<-c(-0.70,-5.60,2.00,2.80,0.70,3.50,4.00,5.80,7.10,-0.50,2.50,-1.60,1.70,3.00 ,0.40,4.50,4.60,2.50,6.00,-1.40)Y<-c(3.70,6.50,5.00,5.20,0.80,0.20,0.60,3.40,6.60,-1.10,6.00,3.80,2.00,1.60,2.00,2.20,1.20,3.10,1.70,-2.00)t.test(X,Y,var.equal=TRUE)P-值=0.52>0.05，接受原假设H0，所以有差异。
北京工业大学数学建模作业汇总
第一次作业数学建模入门1.冷却定律与破案按照Newton冷却定律，温度为T的物体在温度为To (To<T)的环境中冷却的速度与温差T-To成正比。
你能用该定律确定张某是否是下面案件中的犯罪嫌疑人。
某公安局于晚上7时30分发现一具女尸，当晚8时20分法医测得尸体温度为32.6℃,一小时后，尸体被抬走时又测得尸体温度为31.4℃,，已知室温在几个小时内均为21.1℃,由案情分析得知张某是此案的主要犯罪嫌疑人，但张某矢口否认，并有证人说:“下午张某一直在办公室，下午5时打一个电话后才离开办公室”。
从办公室到案发现场步行需要5分钟，问张某是否能被排除在犯罪嫌疑人之外？解答：首先，牛顿冷却定律为温度为T(t)的物体在温度的环境中冷却的速度与温度差成正比。
所以，得出微分方程 （ ，K为比例常数。
任意时刻t，物体的温度为 ，C为常数根据已知条件，记晚上8时20分为t=0时刻，T（0）=32.6℃，T（1）=31.4℃，=21.1℃：求解函数得，k=-0.11，C=11.5，即假定人的正常体温为37℃，代入公式得t-2.95小时, 即遇害时间为8.33-2.95=5.38≈5时23分。
张某在5时离开办公室，步行需要5分钟到达案发地点，所以张某不能排除作案嫌疑。
2.锻炼想象力、洞察力和判断力的问题（1）某人早8时从山下旅店出发沿一条山路上山，下午5时到达山顶并留宿，次日8时沿同一条路径下山，下午5时回到旅店。
该人必在两天中的同一是可经过路径中的同一地点，为什么？解答：令：A(t)表示此人第一天上山时t时刻离山脚的路程；B(t)表示此人第二天下山时t时刻离山脚的路程。
假设山顶到山下的总路程为S，由已知条件可知：A(8)=0，A(17)= SB(8)= S，B(17)=0令：C(t)= A(t)- B(t)；则C(8)=-S，C(17)= S；由于C(t)为连续函数，由零点定理推出结论：在t=[8,17]中间，至少存在一点 t 使C(t)= A(t)- B(t)=0；即A(t)= B(t),可证明这人必在两天中的同一时刻经过路径中的同一地点。
北京工业大学工程数学-实验1-数学建模入门
解答：
根据题中描述可知，坐乙站发的车的概率为甲站的九倍。可以理解为从乙站发车经过丙站的时刻要比另一个晚9分钟（或者叫做早1分钟）。
某部门推出一专项基金目的在于培养优秀人才，根据评比结果确定资助的额度。许多单位的优秀者都申请了该基金，于是该基金的委员会聘请了数名专家，按照如下规则进行评比。
（1）为了公平性，评委对本单位选手不给分；
（2）每位评委对每位参与申请的人（除本单位选手外）都必须打分，且不打相同的分；
（3）评委打分方法为给参加申请的人排序，根据优劣分别记1分、2分、…以此类推。
（4）评判结束后，求出各选手的平均分，按平均分从低到高排序，依次确定本次评比的名次，即平均分最低者获得资助最高，依次类推。
(1,0,0,0)
(1,0,0,1)
(1,0,1,0)
(1,1,0,0)
(1,0,0,0)
(1,0,1,0)
1
2
3
4
5
6
7
8
(1,1,1,1)
(0,1,0,1)
(1,1,0,1)
(0,0,0,1)
(1,1,0,1)
(0,0,1,0)
(1,0,1,0)
(0,0,0,0)
(1,0,1,0)
(1,0,0,0)
（2）因为增加必要的档案、文书等管理工作，因此，要预付给借贷公司贷款总额10%的佣金。
试分析，小王夫妇是否要请这家借贷公司帮助还款。
北京工业大学数学建模作业3
数学建模作业3 线性规划和整数规划实验：线性规划和整数规划实验：1生产计划安排：某厂生产A ，B ，C 三种产品，其所需劳动力，材料等有关数据如下：三种产品，其所需劳动力，材料等有关数据如下： 产品，消耗定额，资源产品，消耗定额，资源 A B C A B C A B C 可用量（单位）可用量（单位）可用量（单位） 劳动力劳动力 6 3 5 45 6 3 5 45 6 3 5 45 材料材料 3 4 5 30 3 4 5 30 3 4 5 30 产品利润（元产品利润（元//件）件） 3 1 4 3 1 4 3 1 4要求：要求：（a ）确定获利最大的产品生产计划；）确定获利最大的产品生产计划；（b ）产品A 的利润在什么范围内变动时，上述最有计划不变；的利润在什么范围内变动时，上述最有计划不变；（c ）如果劳动力数量不增，材料不足时可从市场购买，每单位0.4元，问该厂要不要购进原材料扩大生产，以购多少为宜原材料扩大生产，以购多少为宜（d ）如果设计一种新产品D ，单件劳动力消耗为8单位，材料消耗为2单位，每件可获利3元，问该种产品是否值得生产？元，问该种产品是否值得生产？解：max 3x1+x2+4x3 !max 3x1+x2+4x3 !利润最大值目标函数利润最大值目标函数利润最大值目标函数 x1,x2,x3 x1,x2,x3分别为ABC 的生产数量的生产数量 st !st !限制条件限制条件限制条件6x1+3x2+5x3<45 !6x1+3x2+5x3<45 !劳动力的限制条件劳动力的限制条件劳动力的限制条件 3x1+4x2+5x3<30 !3x1+4x2+5x3<30 !材料的限制条件材料的限制条件材料的限制条件 end !end !结束限制条件结束限制条件结束限制条件把上面的语句直接复制到lindo 中点solve,solve,可以得到以下结果可以得到以下结果可以得到以下结果 1.生产产品A5件,C 3件可以得到最大利润,27元 2.A 利润在2.4-4.8元之间变动,最优生产计划不变 3.max 3x1+x2+4x3 .max 3x1+x2+4x3 st st6x1+3x2+5x3<45 6x1+3x2+5x3<45 end end可得到生产产品B 9件时利润最大,最大利润为36元,应该购入原材料扩大生产,购入15个单位4.max 3x1+x2+4x3+3x4 .max 3x1+x2+4x3+3x4 st st6x1+3x2+5x3+8x4<45 6x1+3x2+5x3+8x4<45 3x1+4x2+5x3+2x4<30 3x1+4x2+5x3+2x4<30 end end gin x1 gin x1 gin x2 gin x2 gin x3 gin x3 gin x4 gin x4利润没有增加,不值得生产 2工程进度问题：某城市在未来的五年内将启动四个城市住房改造工程每项工程有不同的开始时间，工程周期也不一样.表3.1提供这此项目的基本数据. 工程1和工程4必须在规定的周期内全部完成必要时，其余的二项工程必要时，其余的二项工程 可以在预算的限制内完成部分.然而，每个工程在它的规定时间内必须至少完成25%.每年底，工程完成的部分立刻入住，并目实现一定比例的收入.例如，如果工程1在第一年完成40%，在第三年完成剩下的60%，在五年计划范围内的相应收入是0.4 x 50(第二年)+0.4 x 50(第三年)+ }0.4+0.6) x 50(第四年)+ (0.4+0.6) x 50(第五年)=(4x0.4+2x0.6)x50(单位:万元).试为工程确定最优的时间进度表，使得五年内的总收入达到最大. 解：设某年某工程的完成量为Xij ，i 表示工程的代号（i=1，2，3），j 表示年数（j=1，2，3，4，5）如第一年工程1完成X11，工程3完成X31，到第二年工程已完成X12，工程3完成X32。
北京工业大学数学建模-实验7答案
数学建模作业7&8基本实验解：（1）根据题意使用interval estimate()函数进行区间估计，编写R程序如下：X <- c(1067,919,1196,785,1126,936,918,1156,920,948)interval_estimate(X)运行结果为：mean df a b1 997.1 9 902.9965 1091.203根据运行结果可知，这种灯泡的使用寿命的均值为997.1小时，置信系数为0.95的置信区间为[902.9965,1091.203]，因此这批灯泡中大约95%的灯泡至少使用902.9965小时。
（2）编写R程序如下：pnorm(1000,mean(x),sd(X))运行结果为：[1] 0.5087941根据运行结果可知，这批灯泡能够使用1000小时以上的概率为50.87941%。
解：题中给出了正常男子的血小板计数均值为μ0=225×109/L。
我们可以假设血小板的计数分布服从正态分布。
那么从事油漆作业工人的血小板计数就是均值μ和方差σ2未知的正态分布。
可以根据题中给出的20名男子的血小板计数值，估计出从事油漆作业工人的平均血小板计数值μ1。
然后对比正常男子和从事油漆作业男子的血小板计数值，来判断油漆作业对人体血小板计数是否有影响。
这里可以使用函数t.test()做单个正态总体的单边检验。
假设H0:μ1<μ0，H1:μ1>μ0。
编写R程序如下：X<-c(220,188,162,230,145,160,238,188,247,113,126,245,164, 231,256,183,190,158,224,175)t.test(X, alternative = "greater", mu = 225)运行结果为：One Sample t-testdata: Xt = -3.4783, df = 19, p-value = 0.9987alternative hypothesis: true mean is greater than 22595 percent confidence interval:175.8194 Infsample estimates:mean of x192.15由运行结果可知，p-value=0.9987>0.05，不能拒绝原假设，接收H0，即认为油漆作业工人的血小板计数均值小于正常男子的血小板计数均值。
北工大 数学建模实验2
1、生产计划安排解：（1）设生产4种电缆数量分别为X1，X2，X3，X4最大获利为Max=9.4*X1+10.8*X2+8.75*X3+7.8*X4;···········公式1 限制条件：10.5*X1+9.3*X2+11.6*X3+8.2*X4<=4800;20.4*X1+24.6* X2 +17.7* X3 +26.5* X4 <=9600;3.2* X1 +2.5* X2 +3.6* X3 +5.5* X4 <=4700;5.0*( X1 + X2 + X3 + X4)<=4500;X1 >=100;X2 >=100;X3 >=100;X4 >=100;@gin(X1);@gin(X2);@gin(X3);@gin(X4);所以当SC320为100根，SC325为100根，SC340为139根，SC370为100根时，有最大值4011.158（2）用LINGO基于对偶价格分析得：我推荐增加“焊接”技术的能力，因为用LINGO得出它的对偶价格是0.4943，其它的对偶价格均为0.（3）如果采用最低生产皮昂，那么公式1为MAX=⨯+⨯+⨯+⨯=3675,<4011.16,所以不利9.410010.81008.751007.81002、工程问题解：设某年某工程完成量W XY，X代表工程名称，Y代表年份∴工程1利润50W11+50（W11+W12）+50(W11+W12+W13)+50(W11+W12+W13)工程2利润70W22+70(W22+W23)+70(W22+W23+W24)工程3利润150W31+150(W31+W32)+150(W31+W32+W33)+150(W31+W32+W33+W34)工程4利润20W43+20（W43+W44）MAX=50*W11+50*（W11+W12）+50*(W11+W12+W13)+50(W11+W12+W13)+70*W22+70*(W22+W23)+ 70*(W22+W23+W24)+150*W31+150*(W31+W32)+150*(W31+W32+W33)+150*(W31+W32+W33+W34 )+20*W43+20*（W43+W44）;约束条件5000*W11+15000*W31<=3000;5000*W12+8000*W22+15000*W32<=6000;5000*W13+8000*W23+15000*W33+1200*W43<=7000;8000*W24+15000*W34+1200*W44<=7000;8000*W25+15000*W34<=7000;W11+W12+W13=1;W22+W23+W24+W25>=0.25;W22+W23+W24+W25<=1;W31+W32+W33+W34+W35>=0.25;W31+W32+W33+W34+W35<=1;W43+W44=1;3投资问题解：假设，一年后的收益看做年末收益，并，设X n A, X n B, n=1,2,3,n表示第n年初给项目A,B的投资金额，A计划可每年投资，B计划可以在第一年投资，或，第二年投资∴Max=1. 7X3A+4X2B;X1A+X1B=10;1. 7X1A= X2A+X2B;1. 7X2A+4X1B=X3A;LINgo：Max=1. 7*X3A+4*X2B;X1A+X1B=10;1. 7*X1A= X2A+X2B;1. 7*X2A+4*X1B=X3A;由lingo可得第一年，B计划投资100000美元。
数学建模 作业北工大薛毅 实验2
第二次作业（1）得到平衡点P(0,0)，列出A={1,0}，{0,1}所以特征值为λ1=1，λ2=1，知p=-(λ1+λ2)<0，q=λ1λ2>0，所以P(0，0)是不稳定的（2）得到平衡点P(0, 0)，列出A={-1,0}{0,2}所以其特征值λ1=-1，λ2=2；p=-(λ1+λ2)<0，q=-2<0；所以P(0, 0)是不稳定的（3）平衡点P(0, 0)列出A={0,1}{-2,0}所以特征值λ1= 2i，λ2=- 2i；p=-(λ1+λ2)=0，q=λ1λ2=2；所以平衡点(0, 0)是不稳定的。
（4）得到平衡点P(0, 0)，列出A={-1，0} {0，-2}所以其特征值λ1=-1，λ2=-2；p=-(λ1+λ2) >0，q=λ1λ2>0；易知平衡点(0, 0)是稳定的。
解：KN R dtdN-=(1) 得N=R/K.由（1）得到：)(22KN R K dtNd -∙-=(2) 得N=R/K.方程为kt Ce KRt N -+=)(当t →无穷大，N(t) → R/K.画出N （t ）的图形，如下图所示：解：1212dNr N r N dt =- (1)所以N 1=0, N 2=2221/r r ； 由(1)得：11222121221()()2d N r r N r N r N dt -=-⋅-(2)所以N=2221/4r r画出N （t ）的图形，如下图所示：其中N 1=0是不稳定的；N 2=2221/r r 是稳定的。
解：设F(x)=1-x-Ex dx x r dt N=（）= 0 (1) 得到：0(1)Ex N r=-，10x = 又知E N xr dtx d --=)21(22（2） 带入x 0，x 1 得()'(*)(*)dxF x F x x x dt=⋅- （3） 所以(*)()*F x t x t C e x =⋅+当E<r 时， 01F'(x )<0,F'(x )>0⇒ x 0是稳定平衡点，x 1不是；所以当捕捞适度时,可使渔场产量稳定在0(1)Ex N r=-， 可以持续获得产量 此时考虑最大的产量的条件。
数学建模实习作业
碎纸片的拼接复原摘要图像碎片自动拼接复原是需要借助计算机把大量碎片重新拼接复原成初始图像的完整模型，这一研究在考古、刑侦犯罪、古生物学、医学图像分析、遥感图像处理以及壁画保存复原等方面具有广泛、实际的应用。
本文主要解决碎纸机破碎文档的自动拼接复原问题。
我们利用图像数字化技术，借助Matlab软件将图像转化为矩阵。
通过建立数学模型，运用矩阵论、自定义相似度方法、遗传算法等方法，对数据进行处理，实现对图像碎片自动拼接，从而将所给碎片拼接复原为完整图像。
我们首先把碎片图形进行二值化处理，根据所给纵切黑白碎片边缘的像素关系(相邻两张碎片，一张碎片矩阵右边的像素与另一张碎片左边的像素相同 )，我们采和自定义相似度算法，利用附件求出碎片间的相似度，然后根据所需要满足的条件即相似度最大原则，建立了纵切碎片拼接模型一及其算法，运用Matlab编程实现该模型，并得到碎片复原结果（见附录1）。
关键词：碎片拼接矩阵论图形二值化相似度模型一、问题重述1.1背景：破碎文件的拼接和复原对于司法物证复原、历史文献再现和军事情报获取等方面都有极其重要的作用。
于是碎纸片的拼接复原技术便成为图像处理与模式识别领域中的一个崭新典型的应用。
图像配准是图像拼接复原的基础，而且图像配准算法的计算量一般非常大，因此图像拼接复原技术的发展很大程度上取决于图像配准技术的创新。
本文将通过图像提取技术获取一组碎纸片的形状、颜色、文字等信息，然后利用计算机进行相应的处理从而实现对这些碎纸片的自动拼接复原。
1.2重述：该题研究的是如何对碎纸片进行拼接复原。
传统上，拼接复原工作需由人工完成，准确率较高，但是效率低。
随着计算机技术的发展，当碎纸片数量巨大的时候，人们试图开发碎纸片的自动拼接技术，以提高拼接复原的效率。
对于给定的来自同一页印刷文字文件的碎纸机破碎纸片（仅纵切），建立碎纸片拼接复原模型和算法，并针对附件给出的中文文件的碎片数据进行拼接复原。
如果复原过程需要人工干预，写出干预方式及干预的时间节点。
北京工业大学数学建模-实验4答案
最
大值 约束条件为：
1x11 2x12 3x13 3x21 5x22 6x23 2 x31 4 x32 5x33 10 x11 x12 x13 1
x21 x22 x23 1 x31 x32 x33 1
xij 0或1
采用 LINGO 软件进行计算：
运行结果：
Linearization components added: Constraints: Variables: Integers: 21 18 9
Local optimal solution found. Objective value: Objective bound: Infeasibilities: Extended solver steps: Total solver iterations: Model Class: Total variables: Nonlinear variables: Integer variables: Total constraints: Nonlinear constraints: Total nonzeros: Nonlinear nonzeros: Variable Y1 X1 -0.5000000E-03 Y2 X2 Y3 X3 Row 1 2 3 4 5 6 1.000000 2000.000 0.000000 999.0000 Slack or Surplus 6000000. 0.000000 10000.00 0.000000 0.000000 0.000000 0.000000 0.000000 999000.0 0.000000 Dual Price 1.000000 1000.000 0.000000 499500.0 0.000000 0.000000 75 18 Value 0.000000 999.0000 Reduced Cost 0.000000 24 6 12 27 3 6000000. 6000000. 0.000000 3 120 MINLP
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2微分方程实验1、微分方程稳定性分析绘出下列自治系统相应的轨线，并标出随 t 增加的运动方向，确定平■衡点, 并按稳定的、渐近稳定的、或不稳定的进行分类：解：（1）由 f （x ） =x=0, f （y ） =y=0;可得平衡点为（0,0）,___ 1 0系数矩阵A，求得特征值入1=1,入2=1;0 1p=-（入1+入2）=-2<0 , q=入1入2=1>0;对照稳定性的情况表，可知平■衡点（0, 0） 是不稳定的。
图形如下：（2）如上题可求得平衡点为（0,0 ），特征值入1=-1,入2=2;p=-（入1+入2）=-1<0 , q-入1入2=-2<0;对照稳定性的情况表，可知平■衡点（0, 0） 是不稳定的。
其图形如下:dx⑴dt dtx, y;dxdtdydt dx x, ⑶尸 2y ；晋 dx y， (4) ? 2x;也 dtx+1, 2y.(3) 如上题可求得平■衡点为(0,0 )，特征值入1=0 + 1.4142i,入2=0 -1.4142i; p=-(入1+入2)= 0, q-入1入2=1.4142>0;对照稳定性的情况表，可知平■衡点(0, 0)是不稳定的。
其图形如下：(4) 如上题可求得平衡点为(1,0 )，特征值入1=-1,入2=-2;p=-(入1+入2)= 3>0, q=入1入2=2>0;对照稳定性的情况表，可知平■衡点(1, 0) 是稳定的。
其图形如下：2、种群增长模型一个片子上的一群病菌趋向丁繁殖成一个圆菌落.设病菌的数目为N,单位成员的增长率为r1，则由Malthus生长律有竺r1 N，但是，处丁周界表面的dt那些病菌由丁寒冷而受到损伤，它们死亡的数量与N2成比例，其比例系数为r2, 求N满足的微分方程.不用求解，图示其解族.方程是否有平衡解，如果有，是否为稳定的？解：由题意很容易列出N满足的微分方程：坐r1N r2N； f(N)dt令f(N)=O,可求得方程的两个平■衡点N1=0,N2=「22/r i21 1d2N 1 5 52 (r1 r2N 2) (r1N r2N 2)dt 2进而求得A d2N 令r dt2 2 0可求得N=r2 /4r〔则N=N1 N=N2 N=r22/4r i2可以把第一象限划为三部分，且从下到上三部分中分0,冬dt2.2 2 c dN cdN c dN cdN 0, ；—0, —r 0; —0, ―rdt dt dt dt则可以画出N (t) 的图形，即微分方程的解族，如下图所示:由图形也可以看出，对丁方程的两个平■衡点，其中N1=0是不稳定的；N2=^2 /「；是稳定的o3、有限资源竞争模型1926年Volterra 提出了两个物种为共同的、有限的食物来源而竞争的模型当[b MX h 2X 2)]x dt dX2 电 2(h i X i h 2X 2)]X 2dt假设也 坦，称垣为物种i 对食物不足的敏感度，(1) 证明当x1(t0)>0时，物种2最终要灭亡； (2) 用图形分析方法来说明物种 2最终要灭亡.解：(1)由上述方程组 f (x1) =[b 1〔S' h 2x 2)]x 1=0,f (x2)=电2 (h 1X 1h 2X 2)]X 2=0,可得方程的平■衡点为R (0,0), P 1 (E,0),P 2 (0, M).2 h 2对平衡点P 。
(0,0 ),bi h 1 1X1h2 1X 2h2 2X1。
0系数矩阵Ah1 2X2b2n 2为h1 2X20 b 2则p=- (b1+b2) <0,所以该平■衡点不稳定。
对平■衡点P l J ),i h i系数矩阵1 X)h2 1 X2K 2X2h2 2为b2 h1 2X1 h1 2X2b1h2b2h1b1 2则p= b1b2 b1 21q= bi(b2由题意3您,X1(t0)>01 2,可以得出p>0,q>0,因此该平■衡点是稳定的。
即t 时，(X1(t), X2(t))b i(一二,0)，说明物种2最终要灭亡。
对平衡点P2 (0, E2h2同理可以得到q<0,在该平■衡点不稳定。
因此，在b,X1(t0)>01 2的条件下，物种2最终要灭亡。
(2)对丁线性方程组bib21(^X1 h2X2)2(h l X1 h2X2)在平■面上匹配两条直线l 2,由题意41 垣,X1(t0)>0 ,可将第一象限分为2三个区域。
在最左边区域，X1,X2都大于0;在中间区域，X1, X2都小于0,在最右边区域，X 1,X 2分别是大于0和小于0.，由各区域中X 1,X 2的取值可得到如下图形:x2终要灭亡。
4、蝴蝶效应与混沌解考虑Lorenz模型X i (t) X i(t) X2(t)X3(t)'_ _ 一一一一X2(t) X2(t) X3(t)X3(t) X i(t)X2(t) X2(t) X3(t)其中 b =i0, p =28, 6 =8/3，且初值为,Xi (0) =X2 (0) =0, X3 (0) 一个小常数，假设c =i0-i°,且0V t < i00。
(i)用函数ode45求解，并画出x2~xi,x2~x3,x3~xi的平■面图；(2)适当地调整参数b , P , 6值，和初始值Xi (0), X2 (0) =0,复一的工作，看有什么现象发生。
解：(i)编写Lorenz函数，function xdot=lorenzi(t,x,b,a,c)xdot=[-b*x (i)+x(2) *X(3);-a*x(2)+a*x(3);-x(i)*x(2)+c*x(2) -X(3)];对各参数赋值并用ode45函数求解，可得数值解：Columns i through 90 0.i250 0.2500 0.3750 0.5000 0.5352 0.6057 0.64090 0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 0.00000 0.0000 0.0000 -0.0000 -0.0000 0.0000物种2最=£ , &为〔3(0),重0.57050.00000.0000 -0.0000 -0.00000.0000 0.0000 Columns 10 through 180.6761 0.7114 0.74660.9776 1.01050.0000 0.0000 0.0000 0.0000 0.00000.0000 0.0000 0.0000 0.0000 0.00000.0000 0.0000 0.00000.0000 0.0000 Columns 19 through 271.0434 1.0763 1.1092 1.2797 1.31860.0000 0.0000 0.0000 0.0000 0.00000.0000 0.0000 0.0000 0.0001 0.00010.0000 0.0000 0.00000.0002 0.0002 Columns 28 through 361.3575 1.3964 1.4246 1.5656 1.59380.0000 0.0000 0.00000.0000 0.00000.0002 0.0003 0.0004 0.0021 0.00290.0004 0.0006 0.00080.0045 0.0063Columns 5590 through 559899.575199.5921 99.6090 99.6260 99.6462 99.6664 99.6867 99.7069 99.733816.9457 16.526116.2010 15.9854 15.8978 16.0348 16.4476 17.1933 18.7894-3.3551 -3.7119 -4.1098 -4.5568 -5.1636 -5.8601 -6.6527 -7.5438 -8.8677-5.3476 -5.9274-6.5941-7.3519-8.3766-9.5370-10.8209-12.1944 -14.07250.0000 0.0000 0.0000 -0.00000.78180.8308 0.8797 0.9286 0.0000 0.0000 0.0000 0.0000 0.00000.00000.00000.00000.00000.00000.00000.00001.1421 1.1750 1.2079 1.2409 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000.00000.00010.00011.45281.4810 1.5092 1.5374 0.0000 0.0000 0.0000 0.0000 0.0005 0.0008 0.0011 0.0015 0.0012 0.0016 0.0023 0.0032-10 ------------------------ 1----------------------- 1------------------------- 1 ----------------------- 1 ----------------------- 1 ----------------------- -30 -20 -10 0 10 20 30 (2)令参数b , p , 6值各减1,初始值X1 (0), X2 (0)不变，X3 (0) =10-8分别得到得到x2~x1,x2~x3,x3~x1的平■面图如下：可以看出，参数(T , P , 6值各减1 ,初始值X1 (0) , X2 (0)不变，X3 (0) 数值变为X3 (0) =10一8,参数和初始值很小的改变，就会导致最后图形发生很大的变化。
5、用微分方程考察共振现象设物体沿X轴运动(如图所示)其平衡位置取为原点0,物体的质量为1,在时间t物体的位置为X(t)其所受的恢复为(如弹性力等)与物体所在位置的坐标成正比，即k2X，其中常数k称为恢复系数，运动过程所受的阻力(由丁介质及摩擦等)设与速度成正比，即2h虫，h>0,称为阻尼系数。
dt(1) 根据Newton第二定律，建立相应的微分方程.不妨设初始位置为1, 初始速度为0,取k=2, h=0(当h = 0称为简谐振动的方程)和h=0.1,用Matlab软件得到相应的数值解，并在t-X平面上画出X (t)的图形。
(2) 如果物体还受到附加外力的干扰，且外力是一个依据时间t的函数f(t)(设f (t)=B sinwt)，建立相应的微分方程(该方程称为强迫振动方程).在上述参数不变的情况下，取振幅B=1，分别取w=1, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2,2.4, 2.6, 2.8, 3.0,用Matlab软件得到相应的数值解，并在t-x平面上画出x(t)的图形。