三角函数数值对照表
高中三角函数常用数值表

高中三角函数常用数值表
1. 正弦函数Sin(x) 值表
x(度)0°30°45°60°90°180°270°360°
Sin(x)00.5√2/2√3/210-10
2. 余弦函数Cos(x) 值表
x(度)0°30°45°60°90°180°270°360°
Cos(x)1√3/2√2/20.50-101
3. 正切函数Tan(x) 值表
x(度)0°30°45°60°90°180°270°360°
Tan(x)0√3/31√3不存在0不存在0
4. 余切函数Cot(x) 值表
x(度)0°30°45°60°90°180°270°360°Cot(x)不存在√31√3/30不存在0不存在
在数学上,三角函数是中学数学中的重要内容之一,它们
的数值表可以帮助我们更好地理解三角函数在不同角度下的值。
通过这些数值表,我们可以方便地求解各种三角函数的数值,进而解决相关数学问题。
三角函数常用的角度有0°、30°、45°、60°、90°、180°、270°和360°,这些角度下的三角函数数值表格如上所示。
通
过观察这些数值表,我们可以发现各个三角函数在不同角度下的变化规律,从而更好地掌握三角函数的特性和应用。
特殊三角函数值对照表(特殊角的三角函数值)

特殊三角函数值对照表(特殊角的三角函数值)《特殊角的三角函数值》是人教版数学九年级下册第二十八章的内容,特殊三角函数值一般指在0,30°,45°,60°,90°,180°角下的正余弦值。
这些角度的三角函数值是经常用到的。
并且利用两角和与差的三角函数公式,可以求出一些其他角度的三角函数值。
具体的三角函数值如下表:扩展资料:黄金三角函数介绍:α=18°(π/10) sinα=(√5-1)/4 cosα=√(10+2√5)/4tαnα=√(25-10√5)/5cscα=√5+1 secα=√(50-10√5)/5 cotα=√(5+2√5)α=36°(π/5) sinα=√(10-2√5)/4 cosα=(√5+1)/4tαnα=√(5-2√5)cscα=√(50+10√5)/5 secα=√5-1 cotα=√(25+10√5)/5α=54°(3π/10) sinα=(√5+1)/4 cosα=√(10-2√5)/4 tαnα=√(25+10√5)/5是数学中属于初等函数中的超越函数的一类函数。
它们的本质是任意角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。
另一种定义是在直角三角形中,但并不完全。
扩展资料:三角函数在复数中有重要的应用。
三角函数也是物理学中的常用工具。
它有六种基本函数函数名正弦余弦正切余切正割余割符号 sin cos tan cot sec csc正弦函数sin(A)=a/c余弦函数cos(A)=b/c正切函数tan(A)=a/b余切函数cot(A)=b/a其中a为对边,b为邻边,c为斜边特殊角的值如下表:在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A 的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边。
扩展资料:sinα = tanα × cosα(即sinα / cosα = tanα )cosα = cotα × sinα (即cosα / sinα = cotα)tanα = sinα × secα (即tanα / sinα = secα)sin ( α ± β ) = sinα · cosβ ± cosα · sinβsin ( α + β + γ ) = sinα · cosβ · cosγ +cosα · sinβ · cosγ + cosα · cosβ · sinγ - sinα · sinβ · sinγcos ( α ± β ) = cosα cosβ ∓ sinβ sinαtan ( α ± β ) = ( tanα ± tanβ ) / ( 1 ∓ tanα tanβ )完整初中三角函数值表如下图所示:常见的三角函数有正弦函数、余弦函数和正切函数。
高中三角函数值大全表格

高中三角函数值大全表格
一、正弦函数(Sine Function)
正弦函数是三角函数中最常见的函数之一,它表示一个角
的正弦值,通常用sin来表示。
正弦函数的定义域为实数集合,值域为[-1, 1]之间的实数。
下表列出了正弦函数在常见角度下
的数值:
角度(度)弧度正弦值
000
30π/61/2
45π/4√2/2
60π/3√3/2
90π/21
二、余弦函数(Cosine Function)
余弦函数是正弦函数的互补函数,表示一个角的余弦值,
通常用cos来表示。
余弦函数的定义域为实数集合,值域也为[-1, 1]之间的实数。
下表列出了余弦函数在常见角度下的数值:角度(度)弧度余弦值
001
30π/6√3/2
45π/4√2/2
60π/31/2
90π/20
三、正切函数(Tangent Function)
正切函数表示一个角的正切值,通常用tan来表示。
正切
函数的定义域为除了所有余弦值为0的角度之外的实数,值
域为实数集合。
下表列出了正切函数在常见角度下的数值:
角度(度)弧度正切值
000
30π/6√3/3
45π/41
60π/3√3
90π/2无穷大
通过以上表格可以清晰地了解到常见角度下的三角函数值,为进一步学习三角函数提供了重要参考。
三角函数值对照表
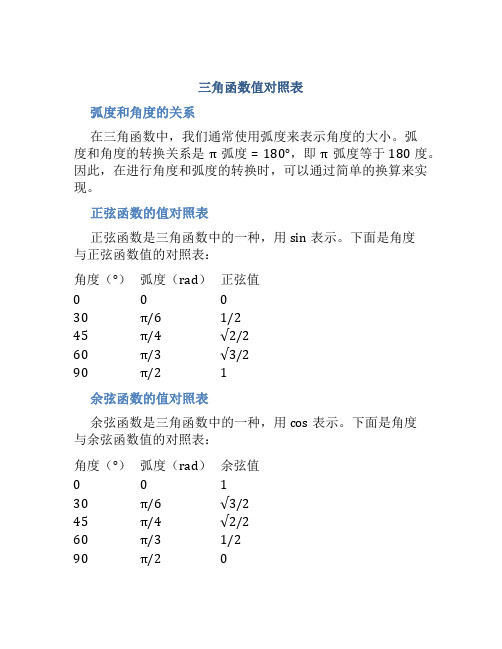
三角函数值对照表
弧度和角度的关系
在三角函数中,我们通常使用弧度来表示角度的大小。
弧
度和角度的转换关系是π 弧度 = 180°,即π 弧度等于180度。
因此,在进行角度和弧度的转换时,可以通过简单的换算来实现。
正弦函数的值对照表
正弦函数是三角函数中的一种,用sin表示。
下面是角度
与正弦函数值的对照表:
角度(°)弧度(rad)正弦值
000
30π/61/2
45π/4√2/2
60π/3√3/2
90π/21
余弦函数的值对照表
余弦函数是三角函数中的一种,用cos表示。
下面是角度
与余弦函数值的对照表:
角度(°)弧度(rad)余弦值
001
30π/6√3/2
45π/4√2/2
60π/31/2
90π/20
正切函数的值对照表
正切函数是三角函数中的一种,用tan表示。
下面是角度与正切函数值的对照表:
角度(°)弧度(rad)正切值
000
30π/6√3/3
45π/41
60π/3√3
90π/2未定义
总结
通过以上对照表可以清晰地显示出不同角度下三角函数的值,对于理解三角函数在不同角度下的表现具有重要意义,也方便我们在数学计算中的应用。
熟练掌握三角函数值的对照表有助于提高数学运算效率,希望对您有所帮助。
三角函数值(附三角函数值表)

三角函数值(附三角函数值表)1)特殊角三角函数值sin0=0sin30=0.5sin45=0.7071 二分之根号2sin60=0.8660 二分之根号3sin90=1cos0=1cos30=0.866025404 二分之根号3cos45=0.707106781 二分之根号2cos60=0.5cos90=0tan0=0tan30=0.577350269 三分之根号3tan45=1tan60=1.732050808 根号3tan90=无cot0=无cot30=1.732050808 根号3cot45=1cot60=0.577350269 三分之根号3cot90=0(2)0°~90°的任意角的三角函数值,查三角函数表。
(见下)(3)锐角三角函数值的变化情况(i)锐角三角函数值都是正值(ii)当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)余切值随着角度的增大(或减小)而减小(或增大)(iii)当角度在0°≤α≤90°间变化时,0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时,tanα>0, cotα>0.“锐角三角函数”属于三角学,是《数学课程标准》中“空间与图形”领域的重要内容。
从《数学课程标准》看,中学数学把三角学内容分成两个部分,第一部分放在义务教育第三学段,第二部分放在高中阶段。
在义务教育第三学段,主要研究锐角三角函数和解直角三角形的内容,本套教科书安排了一章的内容,就是本章“锐角三角函数”。
在高中阶段的三角内容是三角学的主体部分,包括解斜三角形、三角函数、反三角函数和简单的三角方程。
无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
常见三角函数值对照表

常见三角函数值对照表
三角函数的本质是任意角的集合与一组比值的变量之间的映射。
接下来分享常见的三角函数值对照表。
三角函数值对照表
三角函数值口诀
30°,45°,60°这三个角的正弦值和余弦值的共同点是:分母都是2,若把分子都加上根号,则被开方数就相应地变成了1,2,3.正切的特点是将分子全部都带上根号,令分母值为3,则相应的被开方数就是3,9,27。
记忆口诀一
三十,四五,六十度,三角函数记牢固;
分母弦二切是三,分子要把根号添;
一二三来三二一,切值三九二十七;
递增正切和正弦,余弦函数要递减.
记忆口诀二
一二三三二一,戴上根号对半劈。
两边根号三,中间竖旗杆。
分清是增减,试把分母安。
正首余末三,好记又简单。
零度九十度,斜线z形连。
端点均为零,余下竖横填。
判断三角函数值的符号
记忆公式是:奇变偶变,符号看象限。
对于π/2*k±α(k∈Z)的三角函数值,
①当k是偶数时,得到α的同名函数值,即函数名不改变;
②当k是奇数时,得到α相应的余函数值,即
sin→cos;cos→sin;tan→cot,cot→tan.(奇变偶不变),然后在前面加上把α看成锐角时原函数值的符号。
(符号看象限)
示例:
sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。
当α是锐角时,2π-α∈(270°,360°),sin(2π-α)<0,符号为“-”。
所以sin(2π-α)=-sinα。
常用的九个三角函数值表
常用的九个三角函数值表
在数学中,三角函数是描述角的函数,共有六个基础三角函数:正弦、余弦、正切、余切、正割和余割。
这些函数在数学和科学领域中具有广泛的应用。
在本文中,我们将列出常用的九个三角函数值表,包括正弦、余弦、正切、余切、正割、余割、余弦、余切、余割函数的计算结果。
常用的九个三角函数值表
正弦函数值表
角度(°)正弦值
00
301/2
45√2/2
60√3/2
901
余弦函数值表
角度(°)余弦值
01
30√3/2
45√2/2
601/2
900
正切函数值表
角度(°)正切值
00
30√3/3
451
60√3
90无穷大
余切函数值表
角度(°)余切值
0无穷大
30√3
451
60√3/3
900
正割函数值表
角度(°)正割值
0无穷大
302/√3
45√2
602
901
余割函数值表
角度(°)余割值
01
30√3/3
45√2
602/√3
90无穷大
总结
在数学中,三角函数是非常重要的概念,它们在各种科学和工程领域中均有广泛的应用。
通过熟练掌握常用的九个三角
函数的数值表,我们可以更好地理解和解决与角度和三角函数相关的问题。
希望这份三角函数值表可以帮助您更好地理解这一内容。
以上就是我整理的常用的九个三角函数值表,希望对您有所帮助!。
完整的三角函数表值查表0-360
完整的三角函数表值查表0-360
三角函数是初中数学的重要知识点,熟练的掌握常见的初中三角函数值对大家解题有事半功倍的效果,接下来就把常见的特殊三角函数值表分享出来。
0-360度三角函数值
三角函数是基本初等函数之一,是以角度为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
常见的三角函数包括正弦函数、余弦函数和正切函数。
正弦函数:sinα
在直角三角形中,将大小为α(单位为弧度)的角对边长度比斜边长度的比值求出,函数值为上述比的比值,也是csc(α)的倒数。
余弦函数:cos(α)
在直角三角形中,将大小为α(单位为弧度)的角邻边长度比斜边长度的比值求出,函数值为上述比的比值,也是sec(α)的倒数。
正切函数:tan(α)
在直角三角形中,将大小为α(单位为弧度)的角对边长度比邻边长度的比值求出,函数值为上述比的比值,也是cot(α)的倒数。
三角函数的函数关系
(一)倒数关系
①tanαcotα=1
②sinαcscα=1
③cosαsecα=1 (二)商数关系tanα=sinα/cosαcotα=cosα/sinα(三)平方关系
①sin²α+cos²=1
②1+tan²α=sec²α
③1+cot²α=csc²α。
cos函数度数表
三角函数0~360°度数表sin(0°)=0.000000,cos(0°)=1.000000,tan(0°)=0.000000 sin(1°)=0.017452,cos(1°)=0.999848,tan(1°)=0.017455 sin(2°)=0.034899,cos(2°)=0.999391,tan(2°)=0.034921 sin(3°)=0.052336,cos(3°)=0.998630,tan(3°)=0.052408 sin(4°)=0.069756,cos(4°)=0.997564,tan(4°)=0.069927 sin(5°)=0.087156,cos(5°)=0.996195,tan(5°)=0.087489 sin(6°)=0.104528,cos(6°)=0.994522,tan(6°)=0.105104 sin(7°)=0.121869,cos(7°)=0.992546,tan(7°)=0.122785 sin(8°)=0.139173,cos(8°)=0.990268,tan(8°)=0.140541 sin(9°)=0.156434,cos(9°)=0.987688,tan(9°)=0.158384 sin(10°)=0.173648,cos(10°)=0.984808,tan(10°)=0.176327 sin(11°)=0.190809,cos(11°)=0.981627,tan(11°)=0.194380sin(12°)=0.207912,cos(12°)=0.978148,tan(12°)=0.212557 sin(13°)=0.224951,cos(13°)=0.974370,tan(13°)=0.230868 sin(14°)=0.241922,cos(14°)=0.970296,tan(14°)=0.249328 sin(15°)=0.258819,cos(15°)=0.965926,tan(15°)=0.267949 sin(16°)=0.275637,cos(16°)=0.961262,tan(16°)=0.286745 sin(17°)=0.292372,cos(17°)=0.956305,tan(17°)=0.305731 sin(18°)=0.309017,cos(18°)=0.951057,tan(18°)=0.324920 sin(19°)=0.325568,cos(19°)=0.945519,tan(19°)=0.344328 sin(20°)=0.342020,cos(20°)=0.939693,tan(20°)=0.363970 sin(21°)=0.358368,cos(21°)=0.933580,tan(21°)=0.383864 sin(22°)=0.374607,cos(22°)=0.927184,tan(22°)=0.404026 sin(23°)=0.390731,cos(23°)=0.920505,tan(23°)=0.424475 sin(24°)=0.406737,cos(24°)=0.913545,tan(24°)=0.445229sin(25°)=0.422618,cos(25°)=0.906308,tan(25°)=0.466308 sin(26°)=0.438371,cos(26°)=0.898794,tan(26°)=0.487733 sin(27°)=0.453990,cos(27°)=0.891007,tan(27°)=0.509525 sin(28°)=0.469472,cos(28°)=0.882948,tan(28°)=0.531709 sin(29°)=0.484810,cos(29°)=0.874620,tan(29°)=0.554309 sin(30°)=0.500000,cos(30°)=0.866025,tan(30°)=0.577350 sin(31°)=0.515038,cos(31°)=0.857167,tan(31°)=0.600861 sin(32°)=0.529919,cos(32°)=0.848048,tan(32°)=0.624869 sin(33°)=0.544639,cos(33°)=0.838671,tan(33°)=0.649408 sin(34°)=0.559193,cos(34°)=0.829038,tan(34°)=0.674509 sin(35°)=0.573576,cos(35°)=0.819152,tan(35°)=0.700208 sin(36°)=0.587785,cos(36°)=0.809017,tan(36°)=0.726543 sin(37°)=0.601815,cos(37°)=0.798636,tan(37°)=0.753554sin(38°)=0.615661,cos(38°)=0.788011,tan(38°)=0.781286 sin(39°)=0.629320,cos(39°)=0.777146,tan(39°)=0.809784 sin(40°)=0.642788,cos(40°)=0.766044,tan(40°)=0.839100 sin(41°)=0.656059,cos(41°)=0.754710,tan(41°)=0.869287 sin(42°)=0.669131,cos(42°)=0.743145,tan(42°)=0.900404 sin(43°)=0.681998,cos(43°)=0.731354,tan(43°)=0.932515 sin(44°)=0.694658,cos(44°)=0.719340,tan(44°)=0.965689 sin(45°)=0.707107,cos(45°)=0.707107,tan(45°)=1.000000 sin(46°)=0.719340,cos(46°)=0.694658,tan(46°)=1.035530 sin(47°)=0.731354,cos(47°)=0.681998,tan(47°)=1.072369 sin(48°)=0.743145,cos(48°)=0.669131,tan(48°)=1.110613 sin(49°)=0.754710,cos(49°)=0.656059,tan(49°)=1.150368 sin(50°)=0.766044,cos(50°)=0.642788,tan(50°)=1.191754sin(51°)=0.777146,cos(51°)=0.629320,tan(51°)=1.234897 sin(52°)=0.788011,cos(52°)=0.615661,tan(52°)=1.279942 sin(53°)=0.798636,cos(53°)=0.601815,tan(53°)=1.327045 sin(54°)=0.809017,cos(54°)=0.587785,tan(54°)=1.376382 sin(55°)=0.819152,cos(55°)=0.573576,tan(55°)=1.428148 sin(56°)=0.829038,cos(56°)=0.559193,tan(56°)=1.482561 sin(57°)=0.838671,cos(57°)=0.544639,tan(57°)=1.539865 sin(58°)=0.848048,cos(58°)=0.529919,tan(58°)=1.600335 sin(59°)=0.857167,cos(59°)=0.515038,tan(59°)=1.664279 sin(60°)=0.866025,cos(60°)=0.500000,tan(60°)=1.732051 sin(61°)=0.874620,cos(61°)=0.484810,tan(61°)=1.804048 sin(62°)=0.882948,cos(62°)=0.469472,tan(62°)=1.880726 sin(63°)=0.891007,cos(63°)=0.453990,tan(63°)=1.962611sin(64°)=0.898794,cos(64°)=0.438371,tan(64°)=2.050304 sin(65°)=0.906308,cos(65°)=0.422618,tan(65°)=2.144507 sin(66°)=0.913545,cos(66°)=0.406737,tan(66°)=2.246037 sin(67°)=0.920505,cos(67°)=0.390731,tan(67°)=2.355852 sin(68°)=0.927184,cos(68°)=0.374607,tan(68°)=2.475087 sin(69°)=0.933580,cos(69°)=0.358368,tan(69°)=2.605089 sin(70°)=0.939693,cos(70°)=0.342020,tan(70°)=2.747477 sin(71°)=0.945519,cos(71°)=0.325568,tan(71°)=2.904211 sin(72°)=0.951057,cos(72°)=0.309017,tan(72°)=3.077684 sin(73°)=0.956305,cos(73°)=0.292372,tan(73°)=3.270853 sin(74°)=0.961262,cos(74°)=0.275637,tan(74°)=3.487414 sin(75°)=0.965926,cos(75°)=0.258819,tan(75°)=3.732051 sin(76°)=0.970296,cos(76°)=0.241922,tan(76°)=4.010781sin(77°)=0.974370,cos(77°)=0.224951,tan(77°)=4.331476 sin(78°)=0.978148,cos(78°)=0.207912,tan(78°)=4.704630 sin(79°)=0.981627,cos(79°)=0.190809,tan(79°)=5.144554 sin(80°)=0.984808,cos(80°)=0.173648,tan(80°)=5.671282 sin(81°)=0.987688,cos(81°)=0.156434,tan(81°)=6.313752 sin(82°)=0.990268,cos(82°)=0.139173,tan(82°)=7.115370 sin(83°)=0.992546,cos(83°)=0.121869,tan(83°)=8.144346 sin(84°)=0.994522,cos(84°)=0.104528,tan(84°)=9.514364 sin(85°)=0.996195,cos(85°)=0.087156,tan(85°)=11.430052 sin(86°)=0.997564,cos(86°)=0.069756,tan(86°)=14.300666 sin(87°)=0.998630,cos(87°)=0.052336,tan(87°)=19.081137 sin(88°)=0.999391,cos(88°)=0.034899,tan(88°)=28.636253 sin(89°)=0.999848,cos(89°)=0.017452,tan(89°)=57.289962sin(90°)=1.000000,cos(90°)=0.000000,tan(90°)=无意义sin(91°)=0.999848,cos(91°)=-0.017452,tan(91°)=-57.289962 sin(92°)=0.999391,cos(92°)=-0.034899,tan(92°)=-28.636253 sin(93°)=0.998630,cos(93°)=-0.052336,tan(93°)=-19.081137 sin(94°)=0.997564,cos(94°)=-0.069756,tan(94°)=-14.300666 sin(95°)=0.996195,cos(95°)=-0.087156,tan(95°)=-11.430052 sin(96°)=0.994522,cos(96°)=-0.104528,tan(96°)=-9.514364 sin(97°)=0.992546,cos(97°)=-0.121869,tan(97°)=-8.144346 sin(98°)=0.990268,cos(98°)=-0.139173,tan(98°)=-7.115370 sin(99°)=0.987688,cos(99°)=-0.156434,tan(99°)=-6.313752 sin(100°)=0.984808,cos(100°)=-0.173648,tan(100°)=-5.671282 sin(101°)=0.981627,cos(101°)=-0.190809,tan(101°)=-5.144554 sin(102°)=0.978148,cos(102°)=-0.207912,tan(102°)=-4.704630sin(103°)=0.974370,cos(103°)=-0.224951,tan(103°)=-4.331476 sin(104°)=0.970296,cos(104°)=-0.241922,tan(104°)=-4.010781 sin(105°)=0.965926,cos(105°)=-0.258819,tan(105°)=-3.732051 sin(106°)=0.961262,cos(106°)=-0.275637,tan(106°)=-3.487414 sin(107°)=0.956305,cos(107°)=-0.292372,tan(107°)=-3.270853 sin(108°)=0.951057,cos(108°)=-0.309017,tan(108°)=-3.077684 sin(109°)=0.945519,cos(109°)=-0.325568,tan(109°)=-2.904211 sin(110°)=0.939693,cos(110°)=-0.342020,tan(110°)=-2.747477 sin(111°)=0.933580,cos(111°)=-0.358368,tan(111°)=-2.605089 sin(112°)=0.927184,cos(112°)=-0.374607,tan(112°)=-2.475087 sin(113°)=0.920505,cos(113°)=-0.390731,tan(113°)=-2.355852 sin(114°)=0.913545,cos(114°)=-0.406737,tan(114°)=-2.246037 sin(115°)=0.906308,cos(115°)=-0.422618,tan(115°)=-2.144507sin(116°)=0.898794,cos(116°)=-0.438371,tan(116°)=-2.050304 sin(117°)=0.891007,cos(117°)=-0.453990,tan(117°)=-1.962611 sin(118°)=0.882948,cos(118°)=-0.469472,tan(118°)=-1.880726 sin(119°)=0.874620,cos(119°)=-0.484810,tan(119°)=-1.804048 sin(120°)=0.866025,cos(120°)=-0.500000,tan(120°)=-1.732051 sin(121°)=0.857167,cos(121°)=-0.515038,tan(121°)=-1.664279 sin(122°)=0.848048,cos(122°)=-0.529919,tan(122°)=-1.600335 sin(123°)=0.838671,cos(123°)=-0.544639,tan(123°)=-1.539865 sin(124°)=0.829038,cos(124°)=-0.559193,tan(124°)=-1.482561 sin(125°)=0.819152,cos(125°)=-0.573576,tan(125°)=-1.428148 sin(126°)=0.809017,cos(126°)=-0.587785,tan(126°)=-1.376382 sin(127°)=0.798636,cos(127°)=-0.601815,tan(127°)=-1.327045 sin(128°)=0.788011,cos(128°)=-0.615661,tan(128°)=-1.279942sin(129°)=0.777146,cos(129°)=-0.629320,tan(129°)=-1.234897 sin(130°)=0.766044,cos(130°)=-0.642788,tan(130°)=-1.191754 sin(131°)=0.754710,cos(131°)=-0.656059,tan(131°)=-1.150368 sin(132°)=0.743145,cos(132°)=-0.669131,tan(132°)=-1.110613 sin(133°)=0.731354,cos(133°)=-0.681998,tan(133°)=-1.072369 sin(134°)=0.719340,cos(134°)=-0.694658,tan(134°)=-1.035530 sin(135°)=0.707107,cos(135°)=-0.707107,tan(135°)=-1.000000 sin(136°)=0.694658,cos(136°)=-0.719340,tan(136°)=-0.965689 sin(137°)=0.681998,cos(137°)=-0.731354,tan(137°)=-0.932515 sin(138°)=0.669131,cos(138°)=-0.743145,tan(138°)=-0.900404 sin(139°)=0.656059,cos(139°)=-0.754710,tan(139°)=-0.869287 sin(140°)=0.642788,cos(140°)=-0.766044,tan(140°)=-0.839100 sin(141°)=0.629320,cos(141°)=-0.777146,tan(141°)=-0.809784sin(142°)=0.615661,cos(142°)=-0.788011,tan(142°)=-0.781286 sin(143°)=0.601815,cos(143°)=-0.798636,tan(143°)=-0.753554 sin(144°)=0.587785,cos(144°)=-0.809017,tan(144°)=-0.726543 sin(145°)=0.573576,cos(145°)=-0.819152,tan(145°)=-0.700208 sin(146°)=0.559193,cos(146°)=-0.829038,tan(146°)=-0.674509 sin(147°)=0.544639,cos(147°)=-0.838671,tan(147°)=-0.649408 sin(148°)=0.529919,cos(148°)=-0.848048,tan(148°)=-0.624869 sin(149°)=0.515038,cos(149°)=-0.857167,tan(149°)=-0.600861 sin(150°)=0.500000,cos(150°)=-0.866025,tan(150°)=-0.577350 sin(151°)=0.484810,cos(151°)=-0.874620,tan(151°)=-0.554309 sin(152°)=0.469472,cos(152°)=-0.882948,tan(152°)=-0.531709 sin(153°)=0.453990,cos(153°)=-0.891007,tan(153°)=-0.509525 sin(154°)=0.438371,cos(154°)=-0.898794,tan(154°)=-0.487733sin(155°)=0.422618,cos(155°)=-0.906308,tan(155°)=-0.466308 sin(156°)=0.406737,cos(156°)=-0.913545,tan(156°)=-0.445229 sin(157°)=0.390731,cos(157°)=-0.920505,tan(157°)=-0.424475 sin(158°)=0.374607,cos(158°)=-0.927184,tan(158°)=-0.404026 sin(159°)=0.358368,cos(159°)=-0.933580,tan(159°)=-0.383864 sin(160°)=0.342020,cos(160°)=-0.939693,tan(160°)=-0.363970 sin(161°)=0.325568,cos(161°)=-0.945519,tan(161°)=-0.344328 sin(162°)=0.309017,cos(162°)=-0.951057,tan(162°)=-0.324920 sin(163°)=0.292372,cos(163°)=-0.956305,tan(163°)=-0.305731 sin(164°)=0.275637,cos(164°)=-0.961262,tan(164°)=-0.286745 sin(165°)=0.258819,cos(165°)=-0.965926,tan(165°)=-0.267949 sin(166°)=0.241922,cos(166°)=-0.970296,tan(166°)=-0.249328 sin(167°)=0.224951,cos(167°)=-0.974370,tan(167°)=-0.230868sin(169°)=0.190809,cos(169°)=-0.981627,tan(169°)=-0.194380 sin(170°)=0.173648,cos(170°)=-0.984808,tan(170°)=-0.176327 sin(171°)=0.156434,cos(171°)=-0.987688,tan(171°)=-0.158384 sin(172°)=0.139173,cos(172°)=-0.990268,tan(172°)=-0.140541 sin(173°)=0.121869,cos(173°)=-0.992546,tan(173°)=-0.122785 sin(174°)=0.104528,cos(174°)=-0.994522,tan(174°)=-0.105104 sin(175°)=0.087156,cos(175°)=-0.996195,tan(175°)=-0.087489 sin(176°)=0.069756,cos(176°)=-0.997564,tan(176°)=-0.069927 sin(177°)=0.052336,cos(177°)=-0.998630,tan(177°)=-0.052408 sin(178°)=0.034899,cos(178°)=-0.999391,tan(178°)=-0.034921 sin(179°)=0.017452,cos(179°)=-0.999848,tan(179°)=-0.017455 sin(180°)=0.000000,cos(180°)=-1.000000,tan(180°)=-0.000000sin(182°)=-0.034899,cos(182°)=-0.999391,tan(182°)=0.034921 sin(183°)=-0.052336,cos(183°)=-0.998630,tan(183°)=0.052408 sin(184°)=-0.069756,cos(184°)=-0.997564,tan(184°)=0.069927 sin(185°)=-0.087156,cos(185°)=-0.996195,tan(185°)=0.087489 sin(186°)=-0.104528,cos(186°)=-0.994522,tan(186°)=0.105104 sin(187°)=-0.121869,cos(187°)=-0.992546,tan(187°)=0.122785 sin(188°)=-0.139173,cos(188°)=-0.990268,tan(188°)=0.140541 sin(189°)=-0.156434,cos(189°)=-0.987688,tan(189°)=0.158384 sin(190°)=-0.173648,cos(190°)=-0.984808,tan(190°)=0.176327 sin(191°)=-0.190809,cos(191°)=-0.981627,tan(191°)=0.194380 sin(192°)=-0.207912,cos(192°)=-0.978148,tan(192°)=0.212557 sin(193°)=-0.224951,cos(193°)=-0.974370,tan(193°)=0.230868sin(194°)=-0.241922,cos(194°)=-0.970296,tan(194°)=0.249328 sin(195°)=-0.258819,cos(195°)=-0.965926,tan(195°)=0.267949 sin(196°)=-0.275637,cos(196°)=-0.961262,tan(196°)=0.286745 sin(197°)=-0.292372,cos(197°)=-0.956305,tan(197°)=0.305731 sin(198°)=-0.309017,cos(198°)=-0.951057,tan(198°)=0.324920 sin(199°)=-0.325568,cos(199°)=-0.945519,tan(199°)=0.344328 sin(200°)=-0.342020,cos(200°)=-0.939693,tan(200°)=0.363970 sin(201°)=-0.358368,cos(201°)=-0.933580,tan(201°)=0.383864 sin(202°)=-0.374607,cos(202°)=-0.927184,tan(202°)=0.404026 sin(203°)=-0.390731,cos(203°)=-0.920505,tan(203°)=0.424475 sin(204°)=-0.406737,cos(204°)=-0.913545,tan(204°)=0.445229 sin(205°)=-0.422618,cos(205°)=-0.906308,tan(205°)=0.466308 sin(206°)=-0.438371,cos(206°)=-0.898794,tan(206°)=0.487733sin(207°)=-0.453990,cos(207°)=-0.891007,tan(207°)=0.509525 sin(208°)=-0.469472,cos(208°)=-0.882948,tan(208°)=0.531709 sin(209°)=-0.484810,cos(209°)=-0.874620,tan(209°)=0.554309 sin(210°)=-0.500000,cos(210°)=-0.866025,tan(210°)=0.577350 sin(211°)=-0.515038,cos(211°)=-0.857167,tan(211°)=0.600861 sin(212°)=-0.529919,cos(212°)=-0.848048,tan(212°)=0.624869 sin(213°)=-0.544639,cos(213°)=-0.838671,tan(213°)=0.649408 sin(214°)=-0.559193,cos(214°)=-0.829038,tan(214°)=0.674509 sin(215°)=-0.573576,cos(215°)=-0.819152,tan(215°)=0.700208 sin(216°)=-0.587785,cos(216°)=-0.809017,tan(216°)=0.726543 sin(217°)=-0.601815,cos(217°)=-0.798636,tan(217°)=0.753554 sin(218°)=-0.615661,cos(218°)=-0.788011,tan(218°)=0.781286 sin(219°)=-0.629320,cos(219°)=-0.777146,tan(219°)=0.809784sin(220°)=-0.642788,cos(220°)=-0.766044,tan(220°)=0.839100 sin(221°)=-0.656059,cos(221°)=-0.754710,tan(221°)=0.869287 sin(222°)=-0.669131,cos(222°)=-0.743145,tan(222°)=0.900404 sin(223°)=-0.681998,cos(223°)=-0.731354,tan(223°)=0.932515 sin(224°)=-0.694658,cos(224°)=-0.719340,tan(224°)=0.965689 sin(225°)=-0.707107,cos(225°)=-0.707107,tan(225°)=1.000000 sin(226°)=-0.719340,cos(226°)=-0.694658,tan(226°)=1.035530 sin(227°)=-0.731354,cos(227°)=-0.681998,tan(227°)=1.072369 sin(228°)=-0.743145,cos(228°)=-0.669131,tan(228°)=1.110613 sin(229°)=-0.754710,cos(229°)=-0.656059,tan(229°)=1.150368 sin(230°)=-0.766044,cos(230°)=-0.642788,tan(230°)=1.191754 sin(231°)=-0.777146,cos(231°)=-0.629320,tan(231°)=1.234897 sin(232°)=-0.788011,cos(232°)=-0.615661,tan(232°)=1.279942sin(233°)=-0.798636,cos(233°)=-0.601815,tan(233°)=1.327045 sin(234°)=-0.809017,cos(234°)=-0.587785,tan(234°)=1.376382 sin(235°)=-0.819152,cos(235°)=-0.573576,tan(235°)=1.428148 sin(236°)=-0.829038,cos(236°)=-0.559193,tan(236°)=1.482561 sin(237°)=-0.838671,cos(237°)=-0.544639,tan(237°)=1.539865 sin(238°)=-0.848048,cos(238°)=-0.529919,tan(238°)=1.600335 sin(239°)=-0.857167,cos(239°)=-0.515038,tan(239°)=1.664279 sin(240°)=-0.866025,cos(240°)=-0.500000,tan(240°)=1.732051 sin(241°)=-0.874620,cos(241°)=-0.484810,tan(241°)=1.804048 sin(242°)=-0.882948,cos(242°)=-0.469472,tan(242°)=1.880726 sin(243°)=-0.891007,cos(243°)=-0.453990,tan(243°)=1.962611 sin(244°)=-0.898794,cos(244°)=-0.438371,tan(244°)=2.050304 sin(245°)=-0.906308,cos(245°)=-0.422618,tan(245°)=2.144507sin(246°)=-0.913545,cos(246°)=-0.406737,tan(246°)=2.246037 sin(247°)=-0.920505,cos(247°)=-0.390731,tan(247°)=2.355852 sin(248°)=-0.927184,cos(248°)=-0.374607,tan(248°)=2.475087 sin(249°)=-0.933580,cos(249°)=-0.358368,tan(249°)=2.605089 sin(250°)=-0.939693,cos(250°)=-0.342020,tan(250°)=2.747477 sin(251°)=-0.945519,cos(251°)=-0.325568,tan(251°)=2.904211 sin(252°)=-0.951057,cos(252°)=-0.309017,tan(252°)=3.077684 sin(253°)=-0.956305,cos(253°)=-0.292372,tan(253°)=3.270853 sin(254°)=-0.961262,cos(254°)=-0.275637,tan(254°)=3.487414 sin(255°)=-0.965926,cos(255°)=-0.258819,tan(255°)=3.732051 sin(256°)=-0.970296,cos(256°)=-0.241922,tan(256°)=4.010781 sin(257°)=-0.974370,cos(257°)=-0.224951,tan(257°)=4.331476 sin(258°)=-0.978148,cos(258°)=-0.207912,tan(258°)=4.704630sin(259°)=-0.981627,cos(259°)=-0.190809,tan(259°)=5.144554 sin(260°)=-0.984808,cos(260°)=-0.173648,tan(260°)=5.671282 sin(261°)=-0.987688,cos(261°)=-0.156434,tan(261°)=6.313752 sin(262°)=-0.990268,cos(262°)=-0.139173,tan(262°)=7.115370 sin(263°)=-0.992546,cos(263°)=-0.121869,tan(263°)=8.144346 sin(264°)=-0.994522,cos(264°)=-0.104528,tan(264°)=9.514364 sin(265°)=-0.996195,cos(265°)=-0.087156,tan(265°)=11.430052 sin(266°)=-0.997564,cos(266°)=-0.069756,tan(266°)=14.300666 sin(267°)=-0.998630,cos(267°)=-0.052336,tan(267°)=19.081137 sin(268°)=-0.999391,cos(268°)=-0.034899,tan(268°)=28.636253 sin(269°)=-0.999848,cos(269°)=-0.017452,tan(269°)=57.289962 sin(270°)=-1.000000,cos(270°)=-0.000000,tan(270°)=无意义sin(271°)=-0.999848,cos(271°)=0.017452,tan(271°)=-57.289962sin(272°)=-0.999391,cos(272°)=0.034899,tan(272°)=-28.636253 sin(273°)=-0.998630,cos(273°)=0.052336,tan(273°)=-19.081137 sin(274°)=-0.997564,cos(274°)=0.069756,tan(274°)=-14.300666 sin(275°)=-0.996195,cos(275°)=0.087156,tan(275°)=-11.430052 sin(276°)=-0.994522,cos(276°)=0.104528,tan(276°)=-9.514364 sin(277°)=-0.992546,cos(277°)=0.121869,tan(277°)=-8.144346 sin(278°)=-0.990268,cos(278°)=0.139173,tan(278°)=-7.115370 sin(279°)=-0.987688,cos(279°)=0.156434,tan(279°)=-6.313752 sin(280°)=-0.984808,cos(280°)=0.173648,tan(280°)=-5.671282 sin(281°)=-0.981627,cos(281°)=0.190809,tan(281°)=-5.144554 sin(282°)=-0.978148,cos(282°)=0.207912,tan(282°)=-4.704630 sin(283°)=-0.974370,cos(283°)=0.224951,tan(283°)=-4.331476 sin(284°)=-0.970296,cos(284°)=0.241922,tan(284°)=-4.010781sin(285°)=-0.965926,cos(285°)=0.258819,tan(285°)=-3.732051 sin(286°)=-0.961262,cos(286°)=0.275637,tan(286°)=-3.487414 sin(287°)=-0.956305,cos(287°)=0.292372,tan(287°)=-3.270853 sin(288°)=-0.951057,cos(288°)=0.309017,tan(288°)=-3.077684 sin(289°)=-0.945519,cos(289°)=0.325568,tan(289°)=-2.904211 sin(290°)=-0.939693,cos(290°)=0.342020,tan(290°)=-2.747477 sin(291°)=-0.933580,cos(291°)=0.358368,tan(291°)=-2.605089 sin(292°)=-0.927184,cos(292°)=0.374607,tan(292°)=-2.475087 sin(293°)=-0.920505,cos(293°)=0.390731,tan(293°)=-2.355852 sin(294°)=-0.913545,cos(294°)=0.406737,tan(294°)=-2.246037 sin(295°)=-0.906308,cos(295°)=0.422618,tan(295°)=-2.144507 sin(296°)=-0.898794,cos(296°)=0.438371,tan(296°)=-2.050304 sin(297°)=-0.891007,cos(297°)=0.453990,tan(297°)=-1.962611sin(298°)=-0.882948,cos(298°)=0.469472,tan(298°)=-1.880726 sin(299°)=-0.874620,cos(299°)=0.484810,tan(299°)=-1.804048 sin(300°)=-0.866025,cos(300°)=0.500000,tan(300°)=-1.732051 sin(301°)=-0.857167,cos(301°)=0.515038,tan(301°)=-1.664279 sin(302°)=-0.848048,cos(302°)=0.529919,tan(302°)=-1.600335 sin(303°)=-0.838671,cos(303°)=0.544639,tan(303°)=-1.539865 sin(304°)=-0.829038,cos(304°)=0.559193,tan(304°)=-1.482561 sin(305°)=-0.819152,cos(305°)=0.573576,tan(305°)=-1.428148 sin(306°)=-0.809017,cos(306°)=0.587785,tan(306°)=-1.376382 sin(307°)=-0.798636,cos(307°)=0.601815,tan(307°)=-1.327045 sin(308°)=-0.788011,cos(308°)=0.615661,tan(308°)=-1.279942 sin(309°)=-0.777146,cos(309°)=0.629320,tan(309°)=-1.234897 sin(310°)=-0.766044,cos(310°)=0.642788,tan(310°)=-1.191754sin(311°)=-0.754710,cos(311°)=0.656059,tan(311°)=-1.150368 sin(312°)=-0.743145,cos(312°)=0.669131,tan(312°)=-1.110613 sin(313°)=-0.731354,cos(313°)=0.681998,tan(313°)=-1.072369 sin(314°)=-0.719340,cos(314°)=0.694658,tan(314°)=-1.035530 sin(315°)=-0.707107,cos(315°)=0.707107,tan(315°)=-1.000000 sin(316°)=-0.694658,cos(316°)=0.719340,tan(316°)=-0.965689 sin(317°)=-0.681998,cos(317°)=0.731354,tan(317°)=-0.932515 sin(318°)=-0.669131,cos(318°)=0.743145,tan(318°)=-0.900404 sin(319°)=-0.656059,cos(319°)=0.754710,tan(319°)=-0.869287 sin(320°)=-0.642788,cos(320°)=0.766044,tan(320°)=-0.839100 sin(321°)=-0.629320,cos(321°)=0.777146,tan(321°)=-0.809784 sin(322°)=-0.615661,cos(322°)=0.788011,tan(322°)=-0.781286 sin(323°)=-0.601815,cos(323°)=0.798636,tan(323°)=-0.753554sin(324°)=-0.587785,cos(324°)=0.809017,tan(324°)=-0.726543 sin(325°)=-0.573576,cos(325°)=0.819152,tan(325°)=-0.700208 sin(326°)=-0.559193,cos(326°)=0.829038,tan(326°)=-0.674509 sin(327°)=-0.544639,cos(327°)=0.838671,tan(327°)=-0.649408 sin(328°)=-0.529919,cos(328°)=0.848048,tan(328°)=-0.624869 sin(329°)=-0.515038,cos(329°)=0.857167,tan(329°)=-0.600861 sin(330°)=-0.500000,cos(330°)=0.866025,tan(330°)=-0.577350 sin(331°)=-0.484810,cos(331°)=0.874620,tan(331°)=-0.554309 sin(332°)=-0.469472,cos(332°)=0.882948,tan(332°)=-0.531709 sin(333°)=-0.453990,cos(333°)=0.891007,tan(333°)=-0.509525 sin(334°)=-0.438371,cos(334°)=0.898794,tan(334°)=-0.487733 sin(335°)=-0.422618,cos(335°)=0.906308,tan(335°)=-0.466308 sin(336°)=-0.406737,cos(336°)=0.913545,tan(336°)=-0.445229sin(337°)=-0.390731,cos(337°)=0.920505,tan(337°)=-0.424475 sin(338°)=-0.374607,cos(338°)=0.927184,tan(338°)=-0.404026 sin(339°)=-0.358368,cos(339°)=0.933580,tan(339°)=-0.383864 sin(340°)=-0.342020,cos(340°)=0.939693,tan(340°)=-0.363970 sin(341°)=-0.325568,cos(341°)=0.945519,tan(341°)=-0.344328 sin(342°)=-0.309017,cos(342°)=0.951057,tan(342°)=-0.324920 sin(343°)=-0.292372,cos(343°)=0.956305,tan(343°)=-0.305731 sin(344°)=-0.275637,cos(344°)=0.961262,tan(344°)=-0.286745 sin(345°)=-0.258819,cos(345°)=0.965926,tan(345°)=-0.267949 sin(346°)=-0.241922,cos(346°)=0.970296,tan(346°)=-0.249328 sin(347°)=-0.224951,cos(347°)=0.974370,tan(347°)=-0.230868 sin(348°)=-0.207912,cos(348°)=0.978148,tan(348°)=-0.212557 sin(349°)=-0.190809,cos(349°)=0.981627,tan(349°)=-0.194380sin(350°)=-0.173648,cos(350°)=0.984808,tan(350°)=-0.176327 sin(351°)=-0.156434,cos(351°)=0.987688,tan(351°)=-0.158384 sin(352°)=-0.139173,cos(352°)=0.990268,tan(352°)=-0.140541 sin(353°)=-0.121869,cos(353°)=0.992546,tan(353°)=-0.122785 sin(354°)=-0.104528,cos(354°)=0.994522,tan(354°)=-0.105104 sin(355°)=-0.087156,cos(355°)=0.996195,tan(355°)=-0.087489 sin(356°)=-0.069756,cos(356°)=0.997564,tan(356°)=-0.069927 sin(357°)=-0.052336,cos(357°)=0.998630,tan(357°)=-0.052408 sin(358°)=-0.034899,cos(358°)=0.999391,tan(358°)=-0.034921 sin(359°)=-0.017452,cos(359°)=0.999848,tan(359°)=-0.017455 sin(360°)=-0.000000,cos(360°)=1.000000,tan(360°)=-0.000000。
三角函数值表
三角函数值表一常用三角函数值:二反三角函数值同角三角函数的基本关系式1,倒数关系:sinx•escx二1cosx•secx二1tanx•cotx二12,商数关系:sinxtanx=cosxcosxcotx=sinx3,平方关系sin2x+cos2x=11+tan2x=sec2x1+cot2x=csc2x倍角公式:cos2x€cos2x一sin2x2x12x cosx€cos-sin-22€2cos?丄-12€1一2sin22tanx tan2x€1一tan2x2tan—tanx€22x 1一tan-2sin2x€2sinxcosx sinx €2sin xx cos—22 半角公式:.x,1一cosx sin€,22 sin2x€1一cos2x2x;1+cosx cos€,22 cos2x€1+cos2x2x,l1一cosx1一cosxtan€,€_21+cosxsinxsinx 1+cosx万能公式:sinx€2tan2€2COS2x一1 €1一2sin2x2x1-tan-22tan —tanx ,22x 1-tan-2奉送直线有关1,斜截式斜率K 和在Y 轴的截距是b y ,kx €b3,两点式点P(—,y …和戶(—,y1112224,截距式在x 轴上截距是a -€兰,1ab在y 轴上截距是b两条直线平行的充要条件:k ,k12两条直线垂直的充要条件:k •k ,-112圆:圆心在圆点,半径为r 的圆的方程是:x 2+y 2,r 22点截式点P (—,y …和斜率k111cosx , y —y —-xi ,1y —yx -x2121圆心在点C(a,b…,半径为r的圆的方程是:(—-a I€(y-b I,r2n经过圆x 2+y 2€r2上一点p 5,y 0)的切线方程是:xx +y 0y €r 2等差数列与等比数列等差数列:从第2项起,每一项与他的前一项的差都等于同一个常数的数列通项公式:a €a +(n 一1)dn1n (a +a )1n —2 n (n -1)7=na +d12等比数列:从第2项起,每一项与他的前一项的比都等于同一个常数的数列a,aq,aq 2,111通项公式:a €aq n (1)n1排列组合:P m €n C —1)C —2)C n —m —1)nP n €n (n -1)C -2)3...2 (1)nP m €.^!)nv n -m )p n €n!前n 项和的公式:叮丰”ca 一a q S €—1n-n1一q前n 项和的公式:SP m n\n——m—1丿C m=n—=n P m m!mn!m!(n-m丿排列组合应用题:1,不带限制条件的排列或组合题:可直接根据有关公式求得结果2,带限制条件的排列或组合题:通常有1,直接计算法,把符合条件的排列或组合种数直接计算出来.2,间接计算法,先算出无限制条件的所有排列组合种数,在从中减去全部不符合条件的排列或组合种数. 2,排列组合的综合题:通常先考虑组合,再考虑排列.关键:1,明确是排列问题还是组合问题,排列与元素排列顺序有关,组合与元素排列顺序无关.2,正确使用加法原理和乘法原理.加法与分类有关,乘法与分步有关.3,考察被考虑的排列,组合是否恰是符合要求的所有不同答案,即不要重复也不要遗漏.数,式,方程和方程组幕的运算法则:a m・a n=a m+na m-n(a丰0,m>n)a n=a mnC ab丿n=a n b n常用乘法公式:(a土b丿2=a2±2ab+b2C…b)C-b)=a2_b2(a…b)C2€ab…b2^=a3…b3C3…b3)=a3±3a2b…3ab3…b3二次根式运算:fa•、.:b=ab(a>0,b>0)巴='-(a>0,b>0)vbVb定义域:分母丰0,.「>0,ln>0,y=1(x丰0)C®0)6,+Jxy=sinx,(-g,+8),以2兀为周期的奇函数,关于原点对称,图形在直线y=1,y=-1之间,|sinx|<1 y=cosx,(-g,+8),以2兀为周期的偶函数,关于Y轴对称,图形在直线y=1,y=-1之叫cosx|<1y=tanx,(x丰(2k+1)|),以兀为周期的奇函数在(-夕,|)内是增函数y=cotx,(x丰kx),以兀为周期的奇函数,在(0,兀内是减函数y=arcsinx l,1,1]单调增加的奇函数,值域:-殳<y<—22y=arccosx,L1,1]单调减少,值域:0<y<—y=arctanx,(,°+"单调增加的奇函数,值域:,—<y<—y=arccotx,v,s,+丿,单调减少,值域:0<y<—指数和对数:1, 正整数指数幕:a n =a •a •a (n G N,n €1)a i =a2, 零指数幕:a o =1(a …0) 3, 负整数指数幕:a -n =丄(a …0,n G N ) a n 4, N 为奇数时:n a n =a N 为偶数时:总=W =a (a -0)=-a(a <0)对数运算法则: 1,log (MN )=log M +logN(M ,N €0)aaa 2,log M =logM -logN(M,N €0)a Naa 3,logM n =nlogM(€0)aa 4, log n M =IlogM(M €0)a n a5, loga =1,x =a log a x ,特别x =€lnxa 三角形面积: S =—absinC =—acsinB =—bcsinA 222平行四边形面积:S =absina梯形面积:S =2(a €b )h2正方形体积:V 边长*边长*高 圆柱体体积:V =,r 2h S 侧=2,rh =底x 高S 全=2,rh +2,r 2圆锥体积:V =f ,r 2hS 狈9=,r\r 2€h 2=,rlS 全=,r\r 2€h 2€r球体积:V =-,r 33球面积: 侧面扇形的e =学=36。
