基于Matlab的图像曲线数据提取方法_付昆昆
如何用MATLAB实现图片曲线数字化?(附代码)
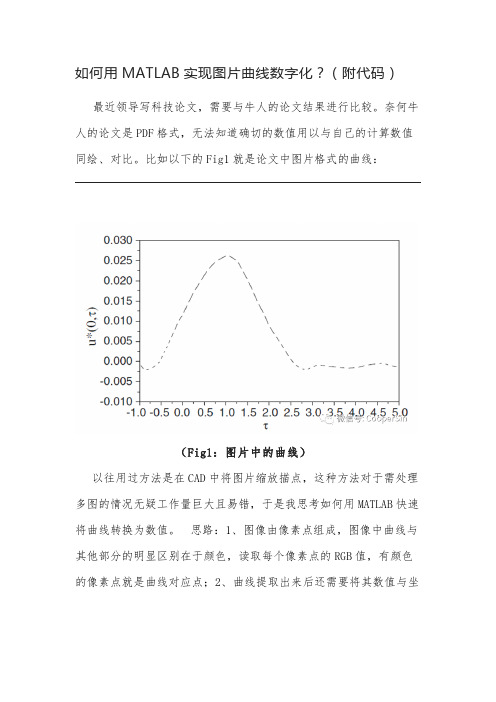
如何用MATLAB实现图片曲线数字化?(附代码)最近领导写科技论文,需要与牛人的论文结果进行比较。
奈何牛人的论文是PDF格式,无法知道确切的数值用以与自己的计算数值同绘、对比。
比如以下的Fig1就是论文中图片格式的曲线:(Fig1:图片中的曲线)以往用过方法是在CAD中将图片缩放描点,这种方法对于需处理多图的情况无疑工作量巨大且易错,于是我思考如何用MATLAB快速将曲线转换为数值。
思路:1、图像由像素点组成,图像中曲线与其他部分的明显区别在于颜色,读取每个像素点的RGB值,有颜色的像素点就是曲线对应点;2、曲线提取出来后还需要将其数值与坐标轴数值相对应,可以采用像素点坐标与曲线实际坐标的转换取得。
以下是实现此功能的MATLAB代码%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%clear;clc;%Step1:将论文PDF中图像截图保存为img_data.jpg,读取并显示图像fip=imread('img_data.jpg');imshow(fip)%Step2:手动输入x、y坐标轴交点值和箭头处值;N为采样点数x_sj0=-1.0;x_sjmax=5.0;y_sj0=-0.01;y_sjmax=0.03;N=100; %Step3:依次手工点取x轴箭头处上方以及右侧框线左边一丢丢;%y轴箭头处下侧及左侧框线右边一丢丢;以避免读取坐标轴像素点。
[x0,y0] = ginput(2);%Step4:存储曲线点(黑色像素点)x、y坐标%x_xs0、y_xs0存储图形原点像素x、y坐标;x_xs0=ceil(min(x0));x_xsmax=floor(max(x0));%x_xsmax、y_xsmax存储图形坐标轴最大点像素x、y坐标;y_xs0=ceil(max(y0));y_xsmax=floor(min(y0));x1=[];y1=[];for i=x_xs0:x_xsmaxfor j=y_xsmax:y_xs0if mean(fip(j,i,:))<=100x1=[x1 i];y1=[y1j];endendend%Step5:曲线像素点坐标与实际坐标(数值)的转换x2=(x_sjmax-x_sj0)/(x_xsmax-x_xs0)*(x1-x_xs0)+x_sj0;y2=(y_sjmax-y_sj0)/(y_xsmax-y_xs0)*(y1-y_xs0)+y_sj0;x2=x2(1:(length(x2))/N:end);y2=y2(1:(length(y2))/N:end); save img_data.mat x2 y2plot(x2,y2)程序运行之后绘制的图像,可以看出与图片中曲线吻合度很好。
在Matlab中进行数字图像处理与特征提取

在Matlab中进行数字图像处理与特征提取数字图像处理是一种通过使用计算机算法对图像进行处理和分析的技术。
在现代科学和技术中,数字图像处理具有广泛的应用,包括医学影像、遥感图像、计算机视觉等。
Matlab是一个功能强大且广泛使用的数值计算和绘图环境,也是数字图像处理和特征提取的理想工具。
Matlab提供了丰富的函数和工具箱,可用于各种图像处理任务,例如滤波、边缘检测、图像增强、图像分割等。
在数字图像处理中,最基本的操作之一是图像滤波。
滤波可以通过不同的滤波器来增强或降低图像的某些特征。
在Matlab中,可以使用imfilter函数来实现各种滤波器,例如高斯滤波器、中值滤波器等。
这些滤波器可以消除噪声、平滑图像或者突出图像的某些细节。
边缘检测是数字图像处理的另一个重要任务。
边缘检测可以帮助我们找到图像中的物体边界或者纹理变化。
在Matlab中,常用的边缘检测算法有Sobel算子、Canny算子等。
这些算法可以根据图像的梯度变化来检测边缘,并生成二值化的边缘图像。
除了滤波和边缘检测,图像增强也是数字图像处理领域的一个重要任务。
图像增强可以通过增加图像的对比度、调整亮度或者变化色彩来改善图像的视觉效果。
在Matlab中,我们可以使用imadjust函数来进行图像增强。
该函数可以通过调整图像的灰度级别来增加图像的对比度,并改善图像的细节。
图像分割是数字图像处理中的一个挑战性任务。
图像分割可以将图像分成若干个子区域,每个子区域代表不同的对象或者纹理。
在Matlab中,常用的图像分割算法有阈值法、区域生长法、基于边缘的分割等。
这些算法可以根据图像的灰度级别、像素关系或者纹理特征来将图像分割成不同的区域。
除了数字图像处理,特征提取也是图像处理中的一个重要任务。
特征提取可以从图像中提取出有用的信息,用于分类、识别或者分析任务。
在Matlab中,可以使用各种特征提取算法,例如局部二值模式(LBP)、灰度共生矩阵(GLCM)、主成分分析(PCA)等。
Matlab中的图像特征提取与匹配技术

Matlab中的图像特征提取与匹配技术引言图像特征提取与匹配技术是计算机视觉领域中一项重要的技术,它广泛应用于图像处理、物体识别、目标跟踪等领域。
而在Matlab中,也提供了许多强大的函数和工具箱来支持图像特征提取与匹配。
本文将介绍Matlab中的一些常用的图像特征提取与匹配技术及其应用。
一、图像特征提取1. 颜色特征提取颜色是图像中最直观的视觉特征之一,对于图像分类和目标识别起着重要的作用。
在Matlab中,我们可以通过颜色直方图、颜色矩等统计方法来提取图像的颜色特征。
2. 纹理特征提取纹理是图像中的重要特征之一,可以用来描述物体的表面细节。
Matlab提供了丰富的纹理特征提取函数,比如灰度共生矩阵(GLCM)、局部二值模式(LBP)等。
这些函数可以帮助我们从图像中提取出不同尺度和方向的纹理特征。
3. 形状特征提取形状是图像中物体的几何外形,是图像特征中最常用的特征之一。
Matlab中可以使用边缘检测算法(如Canny边缘检测)来提取图像中的边缘信息,然后通过边缘描述子(如形状上下文)来提取图像的形状特征。
4. 尺度不变特征提取尺度不变特征是一种具有尺度不变性的图像特征,可以有效应对图像中物体的尺度变化。
在Matlab中,我们可以使用尺度不变特征变换(SIFT)算法来提取图像的尺度不变特征。
SIFT算法通过检测关键点和计算局部特征描述子,能够在不同尺度下对图像进行特征提取。
二、图像特征匹配1. 特征点匹配特征点匹配是图像特征匹配的一种常用方法,通过寻找两幅图像中相同或相似的特征点,来实现图像匹配和目标检测。
在Matlab中,我们可以使用SURF(加速稳健特征)算法或者基于特征距离的匹配算法(如欧氏距离、汉明距离等)来进行特征点的匹配。
2. 相似性度量相似性度量是图像特征匹配中另一种常见的方法,它通过计算两幅图像特征之间的相似度来实现图像匹配。
在Matlab中,我们可以使用余弦相似度、欧氏距离等数学公式来度量图像特征的相似性。
在Matlab中进行数据拟合和曲线拟合的方法

在Matlab中进行数据拟合和曲线拟合的方法在科学研究或工程应用中,数据拟合和曲线拟合是常见的计算任务之一。
Matlab作为一种强大的数值计算软件,提供了丰富的工具和函数,方便我们进行数据拟合和曲线拟合的操作。
本文将介绍在Matlab中进行数据拟合和曲线拟合的几种方法。
一、线性回归线性回归是最简单的数据拟合方法之一,常用于建立变量之间的线性关系模型。
在Matlab中,可以使用polyfit函数进行线性回归拟合。
该函数可以根据输入数据点的横纵坐标,拟合出一条直线,并返回直线的斜率和截距。
例如,以下代码演示了如何使用polyfit函数进行线性回归拟合:```matlabx = [1, 2, 3, 4, 5];y = [2, 3, 4, 5, 6];coefficients = polyfit(x, y, 1);slope = coefficients(1);intercept = coefficients(2);```在上述代码中,数组x和y分别表示数据点的横纵坐标。
polyfit函数的第三个参数1表示拟合的直线为一阶多项式。
函数返回的coefficients是一个包含斜率和截距的数组,可以通过coefficients(1)和coefficients(2)获取。
二、多项式拟合在实际应用中,线性模型并不适用于所有情况。
有时,数据点之间的关系可能更复杂,需要使用更高阶的多项式模型来拟合。
Matlab中的polyfit函数同样支持多项式拟合。
我们可以通过调整多项式的阶数来拟合不同次数的曲线。
以下代码展示了如何使用polyfit函数进行二次多项式拟合:```matlabx = [1, 2, 3, 4, 5];y = [2, 6, 10, 16, 24];coefficients = polyfit(x, y, 2);a = coefficients(1);b = coefficients(2);c = coefficients(3);```在上述代码中,polyfit的第三个参数2表示拟合的多项式为二阶。
matlab曲线点输出方法

matlab曲线点输出方法
在MATLAB中,你可以使用plot函数来绘制曲线。
该函数支持多种输入格式来表示曲线上的点。
一种常用的方法是通过向plot函数传递两个向量x和y来指定曲线上的点。
其中x表示横坐标,y表示纵坐标。
例如,下面的代码将绘制一个连接点(1, 2)和点(3, 4)的直线:
```matlab
x = [1, 3];
y = [2, 4];
plot(x, y);
```
如果你只有一个向量,它将被认为是纵坐标,而横坐标将被自动生成。
例如,下面的代码将绘制一个以索引作为纵坐标的点序列:```matlab
y = [2, 4, 5, 3, 6];
plot(y);
```
你还可以使用plot函数传递一系列的横坐标和纵坐标来绘制多条曲线。
每个横坐标和纵坐标序列对应于一条曲线。
例如,下面的代码将绘制两条曲线,其中第一条曲线连接点(1, 2)和点(3, 4),第二条曲线连接点(1, 5)和点(3, 6):
```matlab
x = [1, 3];
y1 = [2, 4];
y2 = [5, 6];
plot(x, y1, x, y2);
```
这些只是一些常用的方法,plot函数还有许多其他的输入格式,
可以根据具体需求进行调整。
你可以查阅MATLAB文档来获取更详细的说明。
MATLAB图像特征提取与匹配技术

MATLAB图像特征提取与匹配技术概述:近年来,随着计算机视觉和图像处理技术的快速发展,图像特征提取与匹配技术在各个领域得到广泛应用。
MATLAB作为一种先进的科学计算软件,在图像处理和分析方面发挥着巨大作用。
本文将介绍MATLAB在图像特征提取和匹配技术方面的应用。
一、图像特征提取技术1.1 边缘检测边缘是图像中明显变化的区域,边缘检测可以帮助我们捕捉到图像中的边缘信息。
MATLAB提供了各种边缘检测算法,如Sobel、Prewitt和Canny等算法。
这些算法可以通过一些简单的函数调用实现。
边缘检测技术在目标检测、物体跟踪和图像分割等领域有广泛的应用。
1.2 目标检测目标检测是图像处理中的一个重要任务,其目的是在图像中自动识别和定位感兴趣的目标。
MATLAB提供了一些经典的目标检测算法,如HOG(Histogram of Oriented Gradients)和SURF(Speeded Up Robust Features)。
这些算法可以用于人脸检测、车辆检测和物体识别等应用。
1.3 图像特征描述图像特征描述是将图像中的特征转换为数值描述的过程。
常用的图像特征描述方法有SIFT(Scale-Invariant Feature Transform)和ORB(Oriented FAST and Rotated BRIEF)等。
这些方法在图像匹配、图像拼接和目标识别等方面具有重要作用。
MATLAB提供了相应的函数和工具箱,可以方便地提取和描述图像特征。
二、图像特征匹配技术2.1 特征匹配方法图像特征匹配是指在两幅或多幅图像中找到相对应的特征点或特征区域的过程。
常用的图像特征匹配方法有基于距离的匹配和基于几何关系的匹配。
在MATLAB 中,我们可以使用函数vl_ubcmatch和matchFeatures等来实现特征匹配。
2.2 特征匹配的应用图像特征匹配技术在许多领域都有广泛的应用,如图像拼接、三维重建和目标跟踪等。
X线特征图像边缘曲线提取的MATLAB实现
总第252期2010年第10期计算机与数字工程Computer&D igital EngineeringVol.38No.10137牙X线特征图像边缘曲线提取的M AT LAB实现3马 旭(辽宁大学计算中心 沈阳 110036)摘 要 以X口腔线龋齿边缘图像为例,给出其边缘描述及曲线平滑处理的MAT LAB函数。
在边缘图像边沿平滑处理后,采用了简单的点扫描方式描述边缘函数t ocurve(g,h,w),其中引入了边缘线宽度约定参数w,以保证生成函数f比较准确;采用了适当改进的移动均值法,编制的平滑函数s mooth_r(x,s pan,n)在对原函数头尾数据截断处理后,再按指定循环次数,进行了循环平滑处理。
通过实验可知,采用上述函数处理医疗牙X线特征图像算法简洁,实用性强。
关键词 X线特征图像;边缘描述函数;曲线平滑函数;MAT LAB中图分类号 TP317.4E d ge E x trac tion of Too th X2rayF ea tu re Im agean d itπs M A TLAB Im p lem en ta tionM a Xu(Computer Center of L iaoning University,Shenyang 110036)A b s t ra c t Taking the t ooth X_ray i m age f or examp le,this paper gives the MAT LAB functi ons of edge descri p ti on and the s mooth treat m ent.The s pot scanning functi on t ocurve(g,h,w)leads in the width para meter w in order t o assure the accuracy of the generating functi on.By way of i m p r oving the method of moving averages.The s mooth functi on s mooth_r(x,s pan,n)app licates the cycling treat m ents.The test result shows that these functi ons are si m p le and useful.Ke y W o rd s X2ray feature i m age,edge descri p ti on functi on,curve s moothing functi on,MAT LABC la s s N um b e r TP317.41 引言特征区域边缘分析是医疗图像分析的重点、难点,特征图像边缘函数的合理描述是边缘特征分析的基础[5]。
Matlab中的特征提取与选择方法
Matlab中的特征提取与选择方法概述:特征提取与选择是机器学习和模式识别中非常重要的环节,它们涉及到从原始数据中提取有用的信息,并选择最具代表性的特征。
在Matlab中,提供了丰富的工具和函数来实现这些任务。
本文将介绍一些常用的特征提取和选择方法,并通过实例展示它们在实际应用中的效果。
一、特征提取方法1. 基于频域的特征提取频域特征提取通过将信号从时域转换到频域来获取更多的特征信息。
Matlab中的fft函数可以实现信号的傅里叶变换,得到频谱和相位信息。
常用的频域特征包括功率谱密度、频率峰值等。
例如,我们可以使用Matlab中的fft函数对音频信号进行频域特征提取,得到不同频率区间的能量值,从而实现音频的声音识别或分类任务。
2. 基于时域的特征提取时域特征提取是在时序数据中提取特征。
Matlab中的一些函数,如mean、var 等,可以计算时域特征,如均值、方差等。
例如,在心电图数据中,我们可以使用Matlab中的mean函数计算心率的平均值,通过比较不同人群的平均心率,可以判断身体健康状况。
3. 基于图像的特征提取图像特征提取是在图像数据中提取特征。
Matlab中提供了丰富的图像处理函数和工具箱,可以实现图像的边缘检测、纹理分析等。
例如,在图像分类任务中,我们可以使用Matlab中的SIFT(尺度不变特征变换)算法提取关键点和描述子,从而实现图像匹配和识别。
二、特征选择方法1. 过滤式特征选择过滤式特征选择是在特征提取之后,通过一些评价指标对特征进行筛选,选择最有代表性的特征。
Matlab中的corrcoef函数可以计算特征之间的相关性,并根据相关性来选择特征。
例如,在某个肿瘤分类任务中,我们可以使用Matlab中的corrcoef函数计算各个特征与肿瘤类型之间的相关性,选择与肿瘤类型相关性最高的特征进行分类。
2. 包裹式特征选择包裹式特征选择是通过构建一个评估器,将特征选入或排除出模型,使用模型的性能来评估特征的重要性。
MATLAB简介+图像轮廓线提取+图像分割技术
MATLAB 软件使用简介MATLAB 是一个功能强大的数学软件, 它不但可以解决数学中的数值计算问题, 还可以解决符号演算问题, 并且能够方便地绘出各种函数图形。
MATLAB自1984年由美国的MathWorks公司推向市场,现已成为国际最优秀的科技应用软件之一。
一、MATLAB 的工作界面启动MATLAB后, 出现MATLAB命令窗口,空白区域是MATLAB 的工作区, 在此可输入和执行命令。
二、 MATLAB 操作的须知事项●在工作区输入MATLAB命令后, 按下Enter键才能执行命令。
●MATLAB 是区分字母大小写的。
●如果不想显示结果,只要在所输入命令的后面加上一个分号“;〞即可。
如:x= 2 + 3↙ x=5x = 2 + 3 ; ↙不显示结果5●如果一个表达式一行写不下,可以在行尾键入“...〞来换行。
如:q=5^6+sin(pi)+exp(3)+(1+2+3+4+5) ...-5+1/2-567●命令行与M文件中的百分号“%〞标明注释。
三、MATLAB的变量与表达式●MATLAB的变量名MATLAB的变量名是用一个字母打头,后面最多跟19个字母或数字。
应该注意不要用MATLAB中的内部函数或命令名作为变量名。
列出当前工作空间中的变量命令为:who 将内存中的当前变量以简单形式列出;whos 列出当前内存变量的名称、大小、类型等信息;clear 去除内存中的所有变量与函数。
● MATLAB 常用的预定义变量ans :保存计算结果的缺省变量;Inf 或inf :无穷大; i 或jpi :圆周率π。
● MATLAB 的运算符数学运算符:+,-,*, \〔左除〕, / (右除), ^ (乘幂) 关系运算符:<, >, <=, >=, = =(等于), ~= (不等于) 逻辑运算符:&(逻辑与), |( 逻辑或), ~( 逻辑非)● MATLAB 的表达式与语句表达式由运算符、函数、变量名和数字组成的式子。
基于Matlab平台的瑞雷波频散曲线提取
基于Matlab平台的瑞雷波频散曲线提取作者:吴少奇刘雪峰甘立烽柳承成来源:《科技视界》2016年第26期【摘要】拉东变换算法是目前从瑞雷波中提取频散曲线的较常用和较好的方法。
由于拉东变换算法复杂,给提取频散曲线带来不便;为了提高提取效率和优化提取效果,本文利用Matlab软件平台对该算法进行可视化的实现,为利用频散曲线进行相关研究提供便捷。
【关键词】瑞雷波;频散曲线;拉东变换;Matlab【Abstract】The arithmetic of Radon Transform is a common and relatively well used measure in extracting dispersion curve from Rayleigh wave.It is inconvenient to picking up the dispersion curve,Because of complicacy of this arithmetic.In order to improve efficiency and effects,in this thesis, using Matlab to realize the visualization of arithmetic and easy to do related post researches for dispersion curve.【Key words】Rayleigh wave;Dispersion curve;Radon Transform;Matlab0 引言瑞雷波是沿地表传播的一种弹性波,形式为面波。
在用于用于研究地质结构时,主要是通过提取频散曲线来反分析和反演地质结构。
简单说来,利用瑞雷波分为两步,面波信号及其频散曲线的提取和频散曲线的反演。
其中最为关键的是频散曲线提取,目前比较常见的频散曲线提取算法有相位差法[1],倾斜叠加算法[2],时频分析法[3],拉东变换法[4]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通过 Matlab 软件实现. 首先用滤波器去除图片噪声, 并确定用于灰度图转化为二值黑白图的阈
值, 然后通过搜索坐标框在灰度矩阵中的位置来确定真实坐标与灰度矩阵坐标的比例因子, 最后
获取曲线各像素点在灰度矩阵的坐标, 并乘以比例因子得到曲线各点的坐标值. 对曲线图像进行
处理的结果表明, 这种方法提取的数据准确, 相对误差在- 0.7% ~ + 1.2%范围内, 精度取决于原图
付昆昆 1, 郑百林 2, 李 鑫 3
(1. 哈尔滨第 703 研究所, 黑龙江 哈尔滨 150036; 2. 同济大学航空航天与力学学院, 上海 200092; 3. 哈尔滨理工大学测控技术与通信工程学院, 黑龙江 哈尔滨 150080)
摘 要: 对于文献中图的曲线数据的提取, 提出一种通过采集像素点来识别曲线坐标的方法, 并
未经处理的原始图像都存在着一定程度的噪声干扰, 使图像质量变差, 甚至淹没 了特征. 消除图像噪声的工作可以称为图像平滑或滤波, 目的是改善图像质量和抽出对 象特征[4] , 主要方法有均值滤波法, 中值滤波法, 维纳滤波法和小波变换法等 . [5-6]
2 曲线识别基本原理
本文方法基本原理是将曲线转换为二值黑白图, 通过搜索坐标框在图像矩阵中的 位置, 与真实坐标框大小相比较来确定比例因子, 将除曲线外所有特征如坐标框、 标 尺、 标注及图片噪声等都设为背景色(白色), 进而搜索到曲线的像素点在灰度矩阵的 坐标, 乘以比例因子就得到曲线各点的真实坐标值. 对于有多 Y 值的像素点, 对 Y 值进行均值处理, 得到曲线各点的坐标值.
参考文献:
[1] 司三平. 原图扫描屏幕矢量化技术在水电建设中的应用[J]. 西北水电, 2009(4): 73-77. [2] 王晓丹, 吴崇明. 基于 MATLAB 的系统分析与设计— ——图像处理 [M]. 西安: 西安电子科技大学出
版社, 2000: 21-22. [3] 王磊, 段会川. Otsu 方法在多阈值图像分割中的应用[J]. 计算机工程与设计, 2008(29): 2 844-2 845. [4] 夏德深, 傅德胜. 现代图像处理技术与应用 [M]. 南京: 东南大学出版社, 1997: 49-54. [5] 高克芳, 郭建钢. 一种基于噪声点检测的自适应中值 滤 波 方 法[J] . 福 建 农 林 大 学 学 报 , 2009(38):
长度 l/mm
400 350 300 250
200
150
0
2
4
6
8 10
时间 t/s
(a) 原始曲线和局部放大图
长度 l/mm
400 350 300 250 200 150
0
2
4
6
8
10
时间 t/s
(b) 最终曲线
长度 l/mm
235
0.015
230
225
220
。 像素点
最终曲线 215
相对误差 σ/%
4结语
对于文献中图的曲线数据的提取, 可以按如下方法进行. 1) 通过 Matlab 软件将带有噪声的图片转化为灰度图后进行二维滤波, 初步去除 噪声. 2) 因为大部分图线的背景色为白色且占据非常大的面积, 设定合适的阈值即可 分开成二值黑白图像, 而对于一些背景色灰度值较低且曲线占据图像面积较大的图 片, 需要通过大津法找到最优的阈值来处理. 3) 通过确定坐标框或轴位置的方法来确定比例因子, 并通过搜索, 将除曲线外 的坐标像素点全部设为背景色, 可方便准确地提取曲线像素点, 对于多 Y 值的像素 点则需要作均值处理. 4) 通过本文方法得到的图像曲线与原始曲线相比, 数据非常吻合, 相对误差 在- 0.7% ~ + 1.2%范围内, 其精度取决于像素点的数目. 本方法具有一定的实际应用 意义.
将 曲 线 图 像 (一 般 是 RGB 图 像 )以 图 片 的 格 式 导 入 到 Mat lab 软 件 中 , 用 函 数 rgb2gray 转化 为灰度图 像. 再用 Matlab 中的中 值滤波器 进行 滤 波 , 初 步 去 掉 一 些 噪 声, 此时图像的像素具有不同灰度等级. 为了删去一些不必要的特征, 如图上的水印 等, 可以通过设定一个阈值, 将灰度图转化为二值黑白图像. 由于水印等的灰度值与 背景色(大多为白色)和曲线的灰度值有差异, 一般把阈值设为低于水印灰度值即可消 除水印, 但一些背景色灰度值较低且曲线占据图像面积较大的图片, 因为难以找到水 印灰度值的范围, 需要用大津法找到合适的阈值来进行图片的转换.
比例因子是通过搜索坐标框来定的. 通过编程, 搜索出坐标框各角点在灰度矩阵 的位置, 与实际坐标相比, 可以定出比例因子. 为了精确, 需要考虑坐标框的宽度. 在图片中对矩阵的每行每列进行搜索, 若每行或每列三分之二的元素值累加仍然不大 于一定的灰度值(通常为零), 那么可以认为该列或该行为坐标框. 得到坐标框的精确
为了验证本文方法的准确性, 取函数关系为 y = sin x + 25cos (5x) + ex/ 2 + 200 的曲 线图像如图 2(a)所示, 用本文方法进行曲线提取, 从局部图可以看到图像是由一系 列像素点组成. 运行程序, 得到曲线坐标图如图 2(b)所示, 与原图吻合. 取其横坐 标为 3.5 ~ 4, 纵坐标为 210 ~ 235 的图像放大, 观察像素坐标点和本文方 法得到 的曲 线, 如图 2(c)所示. 在这些多 Y 值的像素点处取均值, 结果说明像素点数目越多, 曲线的表征就越完整.
灰度阈值化方法是最常用的图像分割方法, 只要选取一个适当的阈值, 并与每个 像素灰度值比较, 像素灰度值超过阈值则重新分配为最大灰度, 低于阈值分配为最小 灰度, 分配完成就组成一个新的二值图像, 从而把目标物体从背景中分离出来. 大津 法[3]是求取阈值最简单有效的方法, 适用于图像的二值化, 其基本思想是根据图像的 灰度直方图将原图像分为两部分, 背景和目标物体, 使得两部分的类间方差最大. 1.3 图像滤波去噪声
误差 d / μm
误差 d / μm
0
0
-1.6
-1.6
0
1
2
3
4
0
1
2
3
4
时间 t/s
时间 t/s
(a) 加入噪声的原始曲线图
(b) 二维滤波后曲线图
累加灰度强度 I
× 104 2.5
2 1.5
1 0.5
0 0 50 100 150 200 250
灰度值 m (c) 图像累加灰度直方图
1.6
1.6
本文提出一种通过搜索坐标框和采集像素点来识别图片中曲线坐标的方法, 避免 了手工标记的复杂和误差, 获取的曲线数据具有较高的精度.
收稿日期: 2009 - 11 - 03 作者简介: 付昆昆(1984- ), 男, 黑龙江同江人, 硕士研究生. 研究方向: 船舶动力机械传动设计及其振动理论.
E-mail: stone_fkk@
第2期
付昆昆等: 基于 Matlab 的图像曲线数据提取方法
53
位置后, 为了提取曲线坐标, 可将坐标框和框外的区域设为背景色(白色), 再以框的 内边为搜索起点, 找到标尺位置, 将其也设为背景色. 这样, 图片中就只剩下曲线像 素点, 即像素灰度值为 0 的点, 于是就得到了曲线在矩阵中的位置. 根据比例因子, 就得到曲线上各像素点的实际坐标. 若同一横轴上的像素点由于曲线较粗, 可能存在 同一 X 值对应多 Y 值的现象, 本方法对此类点取其计算值的均值处理. 由于本方法 是基于像素点的捕捉, 只要曲线图像精度高, 即像素点数目多, 能够准确地表征其曲 线特征, 则提取的数据就非常准确.
像像素点的数目.
关键词: 曲线数据提取; 像素; 阈值; 二值图
中图分类号: TP 391.41
文献标识码: A
0引言
在阅读文献过程中, 读者为了更好地理解研究者的研究思路和成果, 经常需要查 取文献中一些以曲线图给出的研究数据, 而通过观察曲线图不能准确地得到其坐标 值. 为了准确提取图中曲线的坐标值, 需要对文献中的曲线图进行数据处理.
0.01 0.005
0 -0.005
0.01
210 3.5 3.6 3.7 3.8 3.9 4 时间 t/s
(c) 曲线与像素点比较
-0.015 0
2
4
6
8
10
时间 t/s
(d) 相对误差曲线
图 2 提取的曲线数据准确度和误差分析
事先知道函数的关系, 通过相对误差可以判断该方法与实际值的相似程度, 也就
误差 d / μm
误差 d / μm
0
0
-1.6
-1.6
0
1
2
3
4
01234时间 t/s
时间 t/s
(d) 二值黑白图
(e) 最终曲线
图 1 图像的曲线数据提取
54
汕头大学学报(自然科学版)
第 25 卷
乎全被过滤掉, 如图 1(b)所示. 计算灰度矩阵的灰度直方图, 如图 1(c)所示, 发现大 部分背景色是灰度值为 255 的白色, 此时用大津法求取阈值为 253, 结果不能够分离 出水印及一些残余噪声. 观察图 1(c), 发现在 245 处累加值已经降为很小, 此时可认 为水印、 噪点等的灰度值在 245 以上, 但为了避免一些特殊情况, 例如只有个别的噪 点存在, 此时会比 245 稍小, 故选取灰度值为 200 作为阈值, 得到二值黑白图像如图 1(d)所示, 发现选取的阈值将剩余的噪声去除了. 运行整个程序, 最终得到曲线的 XY 坐标并作图, 如图 1(e)所示, 提取出了原图像质量较差且波动频繁的曲线数据. 3.2 实例 2
3 实例分析
3.1 实例 1 根据上节方法编制程序. 为了体现该方法比手工标记数据法适应性广, 选取波动
