初中八年级数学 11.2与三角形有关的角习题课学案附答案
人教版八年级上11.2.2三角形的外角学案附答案
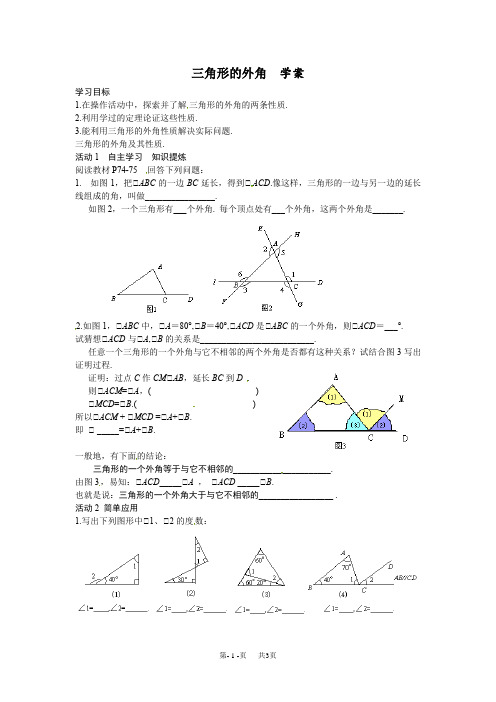
三角形的外角学案学习目标1.在操作活动中,探索并了解三角形的外角的两条性质.2.利用学过的定理论证这些性质.3.能利用三角形的外角性质解决实际问题.三角形的外角及其性质.活动1自主学习知识提炼阅读教材P74-75回答下列问题:1.如图1,把△ABC的一边BC延长,得到△ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做________________.如图2,一个三角形有___个外角. 每个顶点处有___个外角,这两个外角是_______.2.如图1,△ABC中,△A=80°,△B=40°,△ACD是△ABC的一个外角,则△ACD=___°.试猜想△ACD与△A,△B的关系是__________________________.任意一个三角形的一个外角与它不相邻的两个外角是否都有这种关系?试结合图3写出证明过程.证明:过点C作CM△AB,延长BC到D .则△ACM=△A,( )△MCD=△B.( )所以△ACM + △MCD =△A+△B.即△ _____=△A+△B.一般地,有下面的结论:三角形的一个外角等于与它不相邻的______________________.由图3,易知:△ACD_____△A,△ACD _____△B.也就是说:三角形的一个外角大于与它不相邻的_________________ .活动2 简单应用1.写出下列图形中△1、△2的度数:归纳:三角形的外角和等于_______.(每个顶点处取一个外角)活动3 课堂小结这节课我的收获是:活动4 课堂练习1.如图,P是△ABC内一点,延长BP交AC于点D,用“<”表示△1,△2,△A之间的关系为__________________ .2.如图,D是AB上一点,E是AC上一点,BE,CD相交于点F,△A=62°,△ACD=35°,△ABE=20°,则△BDC=_______,△BFD=_______ .3.如图,AB△CD,△A=45°,△C=△E,求△C.4.如图,D是△ABC的BC边上一点,且△1=△2,△3=△4,△BAC=63°,求△DAC的度数.拓展延伸1.图中△A+△B+△C+△D+△E的度数等于______ .2.如图,在△ABC中,BP平分△ABC,CP平分△ACD,试探究△A与△BPC之间的关系.活动1 1. 三角形的外角. 6,2,对顶角. 2. 120,△ACD=△A+△B.两直线平行,内错角相等.两直线平行,同位角相等. ACD. 两个内角的和. > ,>. 任何一个内角.活动2 1. 50°,140°;60°,30°;80°,40°;70°,40°. 2. 360°.活动4 1. △1>△2>△A. 2. 97°,63°. 3. 22.5°.4. 24°.拓展延伸1. 180°2. △A=2△BPC.。
八年级上册数学11.2与三角形有关的角练习题(含答案)

11.2与三角形有关的角练习题姓名:_______________班级:_______________考号:______________一、选择题1、在中,,则的度数为(???)A.?????B.??????C.??????D.2、如图,已知直线AB∥CD,∠C=115°,∠A=25°,则∠E=(??)A.70°?????B.80°??????C.90°?????D.100°3、如图8,AB=BC=CD,且∠A=15°,则∠ECD=(????)A.30°??????B.45°??????C.60°???????D.75°4、如图,在ΔABC中,AC=DC=DB,∠ACD=100°,则∠B等于(??)A.50°??????B.40°??????C.25°????D.20°第4题第5题5、如图,△ABC中,,点D、E分别在AB、AC上,则的大小为(????)??A、??????B、??????C、?????D、第6题第7题第9题6、如图,已知,∠1=130o,∠2=30o,则∠C=??????.7、如下图所示,已知:∠AEC的度数为110°,则∠A+∠B+∠C+∠D的度数为(??)A.110°?????B.130°?????C.220°???D.180°8、已知等腰三角形的一个角为75°,则其顶角为(?)A.30°???B.75°???C.105°????D.30°或75°9、如图,已知,若,,则C等于(???)A.20°????B.35°??????C.45°????D.55°10、如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为()第10题第11题第12题11、如图,已知△ABC的两条高BE、CF相交于点O,,则的度数为(??)A.95o???B.130o??????C.140o???D.150o12、如图,已知与相交于点,,如果,,则的大小为(???)A.??????B.?????C.???????D.13、如图,在△ABC中,∠C=90o,∠B=40o,AD是角平分线,则∠ADC等于A.25o?????B.50o???????C.65o??????D.70o第13题第14题14、如图,直线a∥b,直角三角形如图放置,∠DCB=90°.若∠1+∠B=70°,则∠2的度数为()A.?20°????B.40°??????C.30°????D.25°15、如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是(????)A.45°?????B.54°?????C.40°?????D.50°第15题第16题第18题16、如图7-7,C在AB的延长线上,CE⊥AF于E,交FB于D,若∠F=40°,∠C=20°,则∠FBA 的度数为(?????).?A.50°??B.60°??C.70°??D.80°17、适合条件的三角形ABC是(????)A.锐角三角形??B.直角三角形C.钝角三角形?D.等边三角形???????????18、如图1,若∠1=110°,∠2=135°,则∠3等于A.55°????B.65°????C.75°????D.85°19、如图,在△AB C中,∠A=60°,∠ABC=50°,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是(?)①∠ACB=70°;??????②∠BFC=115°;③∠BDF=130°;?④∠CFE=40°;A.①②?????B.③④?????C.①③????D.①②③第19题第20题20、如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DE;③∠DBE=∠DCE.其中正确结论的个数为( )A.0??????B.1??????C.2??????D.3二、填空题21、如图,∠l=20°,∠2=25°,∠A=35°,则∠BDC=???????????.第21题第22题第23题22、如下图,?∠A=27°,?∠CBE=96°,?∠C=30°,?则∠ADE的度数是________度.?23、如图,∠1,∠2,∠3的大小关系是??????.24、如图,∠A=50°,∠ACD=38°,∠ABE=32°,则∠BFC= _________ .第24题第25题第26题25、如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=50°,则∠ACD的度数为.26、如图,已知△ABC中,AD是BC边上的高,AE是∠BAC的平分线,若∠B=42°,∠C=70°,则∠DAE=????°.27、△ABC中,∠A∶∠B∶∠C=1∶2∶3,则△ABC是??????三角形.28、如图,⊿ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=????????度。
人教版八年级数学上册与三角形有关的角复习及习题11.2解析答案教案

人教版八年级数学11.2复习及习题11.2教案备课人:备课日期:年月日四、习题指导复习巩固1.求下列图形中x的值:【解析】利用三角形的内角和定理列出方程求解。
2.(1)一个三角形最多有几个直角,为什么?(2)一个三角形最多有几个钝角,为什么?(3)直角三角形的外角可以是锐角吗?为什么?【解析】一个三角形只能有一个直角或一个钝角,因为有两个直角或钝角时,三个内角的和就超过了180°。
因为三角形的一个顶点处的外角和相邻的内角互为补角,而直角三角形的内角是一个直角和两个锐角,所以它的外角就只能是直角或钝角,不可以是锐角。
3.△ABC中,∠B=∠A+ 10°,∠C=∠B+10°。
求△ABC各角的度数。
【解析】可设∠A为x°,根据内角和定理列方程解答。
4.如图,AD⊥BC,∠1=∠2,∠C=65°。
求∠BAC的度数。
【解析】根据锐角三角形两个内角互余,分别求出∠1和∠DAC,求其和即得∠BAC的度数。
综合运用5.如图,AB∥CD,∠A=40°,∠D=45°.求∠1和∠2的度数.【解析】根据平行线的性质得∠2=∠A=40°。
根据三角形的外角等于与它不相邻的两个内角的和,得∠1=∠D+∠2=85°.【答案】∠2=40°,∠1=85°.6.如图,AB∥CD,∠A=45°,∠C=∠E,求∠C的度数.【解析】记AE与CD的交点为F。
∵AB∥CD,∴∠DFE=∠A=45°.F∵∠DFE是△CEF的外角,∠C=∠E,∴ 2∠C=∠DFE=45°.∴∠C==22.5°.7.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB的度数.【解析】根据方位角和平行线的性质,得∠ABC=80°-45°=35°,∠BAC=45°+15°=60°。
初二数学上册(人教版)第十一章三角形11.2知识点总结含同步练习及答案

描述:初二数学上册(人教版)知识点总结含同步练习题及答案第十一章 三角形 11.2 与三角形有关的角一、学习任务1. 掌握三角形的内角和和外角和定理,并会熟练运用内外角和定理解决相关的角的问题.2. 会证明三角形内角和和外角和定理.3. 掌握直角三角形中角的性质和判定.二、知识清单三角形的内外角和三、知识讲解1.三角形的内外角和三角形内角与外角在三角形中,相邻两边组成的角,叫做三角形的内角,简称三角形的角.三角形的一边与其邻边的延长线组成的角,叫做三角形的外角.三角形内角和定理三角形三个内角的和等于 .三角形外角和定理三角形的外角等于与它不相邻的两个内角的和.三角形内角和定理的推论直角三角形两个锐角互余.两锐角互余的三角形是直角三角形.飞镖模型及“8”字模型三角形角平分线与内角和180∘例题:在 ,,则 ______.解:.△ABC ∠A :∠B :∠C =2:1:3∠A =60∘一个三角形三个外角之比为 ,三个内角的度数分别是______.解:,,.三角形外角和是,再根据比例分别求出三个外角,即可求出对应的内角.2:3:4100∘60∘20∘360∘如图,三角板的直角顶点在直线 上,若 ,则 的度数是______.解:.l ∠1=40∘∠250∘如图所示,已知 ,,,求 的度数.解:方法一:延长 交 于 ,所以 .∠A =70∘∠B =40∘∠C =20∘∠BOC BO AC D ∠BOC =∠1+∠C =∠A +∠B +∠C=130∘方法二:连接 ,因为 ,所以 .因为 ,所以 .方法三:连接 并延长到点 ,因为 ,,所以.BC ∠1+∠2+∠A +∠B +∠C =180∘∠1+∠2=50∘∠1+∠2+∠BOC =180∘∠BOC =130∘AO D ∠3+∠B =∠1∠4+∠C =∠2∠3+∠B +∠4+∠C =∠1+∠2=130∘已知如图1,线段 、 相交于点 ,连接 、,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下, 和 的平分线 和 相交于点 ,并且与 、 分别相交于 、.试解答下列问题:(1)在图1中,请直接写出 ,,, 之间的数量关系:__________________;(2)仔细观察,在图2中“8字形”的个数:_____个;(3)在图2中,若 ,,试求 的度数.分析:(1)根据三角形内角和定理即可得出 ;(2)根据“8字形”的定义,仔细观察图形即可得出“8字形”共有 个;(3)现根据“8字形”中的角的规律,可得 ,,再根据角平分线的定义,得出 ,,可得 ,进而求出 的度数.解:(1);(2)① 线段 , 相交于点 ,形成“8字形”;② 线段 , 相交于点 ,形成“8字形”;③ 线段 , 相交于点 ,形成“8字形”;④ 线段 , 相交于点 ,形成“8字形”;⑤ 线段 , 相交于点 ,形成“8字形”;AB CD O AD CB ∠DAB ∠BCD AP CP P CD AB M N ∠A ∠B ∠C ∠D ∠D =40∘∠B =36∘∠P ∠A +∠D =∠C +∠B 6∠DAP +∠D =∠P +∠DCP ∠P CB +∠B =∠P AB +∠P ∠DAP =∠P AB ∠DCP =∠P CB 2∠P =∠D +∠B ∠P ∠A +∠D =∠C +∠B AB CD O AN CM O AB CP N AB CM O APCD M AN∠E=30高考不提分,赔付1万元,关注快乐学了解详情。
人教版八年级上册数学与三角形有关的角含答案

11.2与三角形有关的角专题一利用三角形的内角和求角度1.如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=()A.15° B.20° C.25° D.30°2.如图,已知:在直角△ABC中,∠C=90°,BD平分∠ABC且交AC于D. 若AP平分∠BAC且交BD于P,求∠BPA的度数.3.已知:如图1,线段AB、CD相交于点O,连接AD、CB,如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:__________;(2)在图2中,若∠D=40°,∠B=30°,试求∠P的度数;(写出解答过程)(3)如果图2中∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间的数量关系.(直接写出结论即可)专题二利用三角形外角的性质解决问题4.如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为()A.15°B.20° C.25° D.30°5.如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠A=40°,∠B=72°.(1)求∠DCE的度数;(2)试写出∠DCE与∠A、∠B的之间的关系式.(不必证明)6.如图:(1)求证:∠BDC=∠A+∠B+∠C;(2)如果点D与点A分别在线段BC的两侧,猜想∠BDC、∠A、∠ABD、∠ACD这4个角之间有怎样的关系,并证明你的结论.状元笔记【知识要点】1.三角形内角和定理三角形三个内角的和等于180°.2.直角三角形的性质及判定性质:直角三角形的两个锐角互余.判定:有两个角互余的三角形是直角三角形.3.三角形的外角及性质外角:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.性质:三角形的外角等于与它不相邻的两个内角的和.【温馨提示】1.三角形的外角是一边与另一边的延长线组成的角,而不是两边延长线组成的角.2.三角形的外角的性质中的内角一定是与外角不相邻的内角.【方法技巧】1.在直角三角形中已知一个锐角求另一个锐角时,可直接使用“直角三角形的两个锐角互余”.2.由三角形的外角的性质可得出:三角形的外角大于任何一个与它不相邻的内角.参考答案:1.C 解析:∵∠ABC的平分线与∠ACB的外角平分线相交于点D,∴∠1=12∠ACE,∠2=12∠ABC.又∵∠D=∠1-∠2,∠A=∠ACE-∠ABC,∴∠D=12∠A=25°.故选C.2.解:(法1)因为∠C=90°,所以∠BAC+∠ABC=90°,所以12(∠BAC+∠ABC)=45°.因为BD平分∠ABC,AP平分∠BAC ,∠BAP=12∠BAC,∠ABP=12∠ABC ,即∠BAP+∠ABP=45°,所以∠APB=180°-45°=135°. (法2)因为∠C=90°,所以∠BAC+∠ABC=90°,所以12(∠BAC+∠ABC)=45°,因为BD平分∠ABC,AP平分∠BAC,∠DBC=12∠ABC,∠PAC=12∠BAC ,所以∠DBC+∠PAD=45°. 所以∠APB=∠PDA+∠PAD =∠DBC+∠C+∠PAD=∠DBC+∠PAD+∠C =45°+90°=135°.3.解:(1)∠A+∠D=∠B+∠C;(2)由(1)得,∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,∴∠1-∠3=∠P-∠D,∠2-∠4=∠B-∠P,又∵AP、CP分别平分∠DAB和∠BCD,∴∠1=∠2,∠3=∠4,∴∠P-∠D=∠B-∠P,即2∠P=∠B+∠D,∴∠P=(40°+30°)÷2=35°.(3)2∠P=∠B+∠D.4.B 解析:延长DC,与AB交于点E.根据三角形的外角等于不相邻的两内角和,可得∠ACD=50°+∠AEC=50°+∠ABD+10°,整理得∠ACD-∠ABD=60°.设AC与BP相交于点O,则∠AOB=∠POC,∴∠P+12∠ACD=∠A+12∠ABD,即∠P=50°-12(∠ACD-∠ABD)=20°.故选B.5.解:(1)∵∠A=40°,∠B=72°,∴∠ACB=68°.∵CD平分∠ACB,∴∠DCB=1∠ACB=34°.2∵CE是AB边上的高,∴∠ECB=90°-∠B=90°-72°=18°.∴∠DCE=34°-18°=16°.(∠B-∠A).(2)∠DCE=126.(1)证明:延长BD交AC于点E,∵∠BEC是△ABE的外角,∴∠BEC=∠A+∠B.∵∠BDC是△CED的外角,∴∠BDC=∠C+∠DEC=∠C+∠A+∠B.(2)猜想:∠BDC+∠ACD+∠A+∠ABD=360°.证明:∠BDC+∠ACD+∠A+∠ABD=∠3+∠2+∠6+∠5+∠4+∠1=(∠3+∠2+∠1)+(∠6+∠5+∠4)=180°+180°=360°.别浪费一分一秒——如何利用零散时间学人们常说,时间是公平的,每个人的一天只有24个小时,所以应该珍惜时间去充实自己。
初中数学人教版八年级上册第十一章《三角形》练习册(含答案)11.2 与三角形有关的角
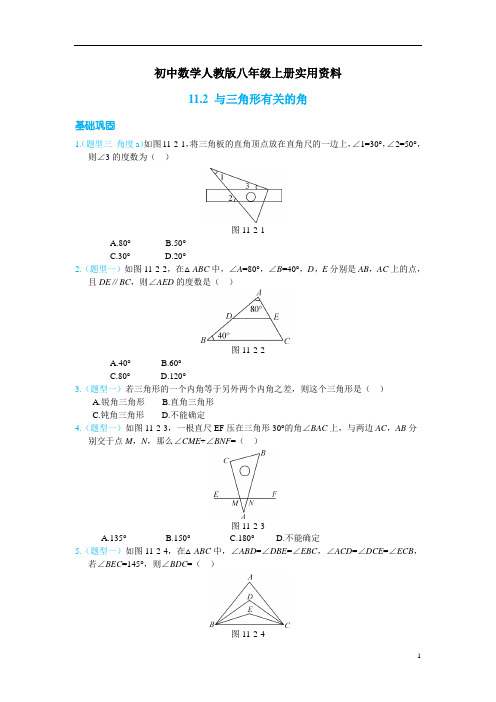
初中数学人教版八年级上册实用资料11.2 与三角形有关的角基础巩固1.(题型三角度a)如图11-2-1,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为()图11-2-1A.80°B.50°C.30°D.20°2.(题型一)如图11-2-2,在△ABC中,∠A=80°,∠B=40°,D,E分别是AB,AC上的点,且DE∥BC,则∠AED的度数是()图11-2-2A.40°B.60°C.80°D.120°3.(题型一)若三角形的一个内角等于另外两个内角之差,则这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定4.(题型一)如图11-2-3,一根直尺EF压在三角形30°的角∠BAC上,与两边AC,AB分别交于点M,N,那么∠CME+∠BNF=()图11-2-3A.135°B.150°C.180°D.不能确定5.(题型一)如图11-2-4,在△ABC中,∠ABD=∠DBE=∠EBC,∠ACD=∠DCE=∠ECB,若∠BEC=145°,则∠BDC=()图11-2-4A.100°B.105°C.110°D.115°6.(题型三角度a)将一副直角三角板,按图11-2-5叠放在一起,则图中α的度数是.图11-2-57.(题型一)如图11-2-6,EF∥BC,AC平分∠BAF,∠B=80°,则∠C的度数是.图11-2-68.(知识点2)如图11-2-7,在Rt△ACB中,∠ACB=90°,CD⊥AB,则图中互余的角有对.图11-2-79.(知识点3)如图11-2-8,已知在△ABC中,∠A=40°,剪去∠A后成四边形,∠1+∠2= °.图11-2-810.(知识点2)如图11-2-9,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=40°,∠C=60°.求∠DAE的度数.图11-2-911.(题型二角度b)如图11-2-10,∠1,∠2,∠3的大小关系是.图11-2-1012.(题型一)(1)如图11-2-11(1),有一块直角三角板XYZ放置在△ABC下,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C.在△ABC中,∠A=30°,则∠ABC+∠ACB=度,∠XBC+∠XCB=度.(2)如图11-2-11(2),改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否发生变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.(1)(2)图11-2-1113.(题型一、二)(1)如图11-2-12,在△ABC中,AD⊥BC于点D,AE平分∠BAC,且∠C大于∠B.求证:∠EAD=12(∠C-∠B).(2)若把问题(1)中的“AD⊥BC于点D”改为“点F为EA上一点且FD⊥BC于点D”,画出新的图形,并说明∠EFD=12(∠C-∠B).(3)若把问题(2)中的“F为EA上一点”改为“F为AE延长线上的一点”,则问题(2)中的结论成立吗?说明你的理由.图11-2-1214.(题型一)如图11-2-13,在Rt△ABC中,∠C=90°,点D,E分别是△ABC边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=α.(注:四边形的内角和是360°)(1)若点P在线段AB上,如图11-2-13(1),且α=50°,则∠1+∠2= .(2)若点P在边AB上运动,如图11-2-13(2),则α,∠1,∠2之间的关系为 .(1)(2)(3)(4)图11-2-13(3)若点P运动到边AB的延长线上,图11-2-13(3),则α,∠1,∠2之间有何关系?请写出你的猜想,并说明理由.(4)若点P运动到△ABC外,如图11-2-13(4),则α,∠1,∠2之间的关系为.答案基础巩固1. D 解析:如图D11-2-1,∵BC∥DE,∴∠CBD=∠2=50°.又∵∠CB D为△ABC的外角,∴∠CBD=∠1+∠3,即∠3=∠CBD-∠1=50°-30°=20°.故选D.图D11-2-12. B 解析:∵DE∥BC,∠B=40°,∴∠A DE=∠B=40°.又∵∠A=80°,∴在△ADE中,∠AED=180°-∠A-∠A DE=180°-80°-40°=60°(三角形的内角和定理).故选B.3. B 解析:设此三角形的三个内角分别是∠1,∠2,∠3(其中∠3最大),根据题意,得∠1=∠3-∠2,∴∠1+∠2=∠3.又∵∠1+∠2+∠3=180°,∴2∠3=180°,∴∠3=90°,∴这个三角形是直角三角形.故选B.4. B 解析:∵∠A+∠AMN+∠ANM=180°,∠A=30°,∴∠AMN+∠ANM=180°-∠A=180°-30°=150°.∵∠AMN=∠CME,∠ANM=∠BNF,∴∠CME+∠BNF=∠AMN+∠ANM=150°.故选B.5. C 解析:在△BCE中,∵∠BEC=145°,∴∠EBC+∠ECB=180°-145°=35°.∵∠DBE=∠EBC,∠DCE=∠ECB,∴∠DBC+∠DCB=2(∠EBC+∠ECB)=2×35°=70°.在△BCD中,∠BDC=180°-(∠DBC+∠DCB)=180°-70°=110°.故选C. 6. 75°解析:如图D11-2-2,∠1=90°-60°=30°,所以α=45°+∠1=45°+30°=75°.图D11-2-2 图D11-2-37. 50°解析:∵EF∥BC,∴∠BAF=180°-∠B=100°.∵AC平分∠BAF,∴∠CAB=12∠BAF=50°.∴∠C=180°-∠B-∠CAB=50°.8. 4 解析:由直角三角形的两个锐角互余,得∠ACD+∠A=90°,∠BCD+∠B=∠90°,∠A+∠B=90°.∵∠ACB=90°,∴∠BCD+∠ACD=90°.∴互余的角有4对.9. 220解析:如图D11-2-3,∠1+∠2=(∠A+∠4)+(∠A+∠3)=∠A+(∠A+∠3+∠4)=∠A+180°.∵∠A=40°,∴∠1+∠2=40°+180°=220°.10. 解:在△ABC中,∠B=40°,∠C=60°,∴∠BAC=80°.∵AE平分∠BAC,∴∠BAE=40°.又∵AD⊥BC,∠B=40°,∴∠BAD=90°-40°=50°.∴∠DAE=∠BAD-∠BAE=50°-40°=10°.能力提升11. ∠3>∠1>∠2 解析:如图D11-2-4,∵∠3=∠1+∠5,∴∠3>∠1.∵∠1=∠2+∠4,∴∠1>∠2.∴∠3>∠1>∠2.图D11-2-412. 解:(1)∵∠A=30°,∴∠ABC+∠ACB=180°-∠A=150°.∵∠X=90°,∴∠XBC+∠XCB=90°.(2)不变化.∵∠A=30°,∴∠ABC+∠ACB=150°.∵∠X=90°,∴∠XBC+∠XCB=90°.∴∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.13.(1)证明:在Rt△ADE中,∵∠AED+∠DAE=90°,∴∠DAE=90°-∠AED.∵∠AED=180°-∠C-∠CAE,且AE平分∠BAC,∴∠CAE=12∠BAC=12(180°-∠C-∠B).∴∠EAD=90°-180°-∠C-1/2(180°-∠C-∠B)=12(∠C-∠B).(2)解:如图D11-2-5(1),由三角形的内角和定理的推论,得∠FED=∠B+12∠BAC,故∠B+12∠BAC+∠EFD=90°①.在△ABC中,由三角形的内角和定理,得∠B+∠BAC+∠C=180°,即12∠C+12∠B+12∠BAC=90°②.②-①,得∠EFD=12(∠C-∠B).(3)解:成立.理由:如图D11-2-5(2),由三角形的内角和定理的推论,得∠FED=∠AEC=∠B+12∠BAC,故∠B+12∠BAC+∠EFD=90°①.在△ABC中,由三角形的内角和定理,得∠B+∠BAC+∠C=180°,即12∠C+12∠B+12∠BAC=90°②.②-①,得∠EFD=1(∠C-∠B).2(1)(2)图D11-2-514. 解:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+α.∵∠C=90°,α=50°,∴∠1+∠2=140°.(2)由(1)得α+∠C=∠1+∠2,∴∠1+∠2=90°+α.(3)∠1=90°+∠2+α.理由如下:如图D11-2-6(1),∵∠2+α=∠DME,∠DME+∠C=∠1,∴∠1=∠C+∠2+α=90°+∠2+α.(4)如图D11-2-6(2),∵∠PFC=∠DFE,∴α+180°-∠1=∠C+180°-∠2,∴∠2=90°+∠1-α.(1)(2)图D11-2-6。
人教版八年级数学11.2 与三角形有关的角 同步练习及答案
第11章《三角形》同步练习(§11.2 与三角形有关的角)班级学号姓名得分1.填空:(1)三角形的内角和性质是____________________________________________________.(2)三角形的内角和性质是利用平行线的______与______的定义,通过推理得到的.它的推理过程如下:已知:△ABC,求证:∠BAC+∠ABC+∠ACB=______.证明:过A点作______∥______,则∠EAB=______,∠F AC=______.(___________,___________)∵∠EAF是平角,∴∠EAB+______+______=180°.( )∴∠ABC+∠BAC+∠ACB=∠EAB+∠______+∠______.( )即∠ABC+∠BAC+∠ACB=______.2.填空:(1)三角形的一边与_________________________________________叫做三角形的外角.因此,三角形的任意一个外角与和它相邻的三角形的一个内角互为______.(2)利用“三角形内角和”性质,可以得到三角形的外角性质?如图,∵∠ACD是△ABC的外角,∴∠ACD与∠ACB互为______,即∠ACD=180°-∠ACB.①又∵∠A+∠B+∠ACB=______,∴∠A+∠B=______.②由①、②,得∠ACD=______+______.∴∠ACD>∠A,∠ACD>∠B由上述(2)的说理,可以得到三角形外角的性质如下:三角形的一个外角等于____________________________________________________.三角形的一个外角大于____________________________________________________. 3.(1)已知:如图,∠1、∠2、∠3分别是△ABC的外角,求:∠1+∠2+∠3.(2)结论:三角形的外角和等于______.4.已知:如图,BE与CF相交于A点,试确定∠B+∠C与∠E+∠F之间的大小关系,并说明你的理由.5.已知:如图,CE⊥AB于E,AD⊥BC于D,∠A=30°,求∠C的度数.6.依据题设,写出结论,想一想,为什么?已知:如图,△ABC中,∠ACB=90°,则:(1)∠A+∠B=______.即∠A与∠B互为______;(2)若作CD⊥AB于点D,可得∠BCD=∠______,∠ACD=∠______.7.填空:(1)△ABC中,若∠A+∠C=2∠B,则∠B=______.(2)△ABC中,若∠A∶∠B∶∠C=2∶3∶5,则∠A=______,∠B=______,∠C=______.(3)△ABC中,若∠A∶∠B∶∠C=1∶2∶3,则它们的相应邻补角的比为______.(4)如图,直线a∥b,则∠A=______度.(5)已知:如图,DE⊥AB,∠A=25°,∠D=45°,则∠ACB=______.(6)已知:如图,∠DAC=∠B,∠ADC=115°,则∠BAC=______.(7)已知:如图,△ABC中,∠ABC=∠C=∠BDC,∠A=∠ABD,则∠A=______(8)在△ABC中,若∠B-∠A=15°,∠C-∠B=60°,则∠A=______,∠B=______,∠C=______.8.已知:如图,一轮船在海上往东行驶,在A处测得灯塔C位于北偏东60°,在B处测得灯塔C位于北偏东25°,求∠ACB.9.已知:如图,在△ABC中,AD、AE分别是△ABC的高和角平分线.(1)若∠B=30°,∠C=50°,求∠DAE的度数.(2)试问∠DAE与∠C-∠B有怎样的数量关系?说明理由.10.已知:如图,O是△ABC内一点,且OB、OC分别平分∠ABC、∠ACB.(1)若∠A=46°,求∠BOC;(2)若∠A=n°,求∠BOC;(3)若∠BOC=148°,利用第(2)题的结论求∠A.11.已知:如图,O是△ABC的内角∠ABC和外角∠ACE的平分线的交点.(1)若∠A=46°,求∠BOC;(2)若∠A=n°,用n的代数式表示∠BOC的度数.12.类比第10、11题,若O是△ABC外一点,OB、OC分别平分△ABC的外角∠CBE、∠BCF,若∠A=n°,画出图形并用n的代数表示∠BOC.13.如图,点M是△ABC两个内角平分线的交点,点N是△ABC两个外角平分线的交点,如果∠CMB;∠CNB=3∶2求∠CAB的度数.14.如图,已知线段AD、BC相交于点Q,DM平分∠ADC,BM平分∠ABC,且∠A=27°,∠M=33°,求∠C的度数.参考答案1.(1)三角形的内角和等于180°,(2)性质、平角,说理过程(略) 2.略.3.∠1+∠2+∠3=360°,360°.4.∠B +∠C =∠E +∠F .(此图中的结论为常用结论) 5.30° 6.(1)90°,余角,(2)∠A ,∠B7.(1)60°.(2)36°,54°,90°.(3)5∶4∶3.(4)39°.(5)110°. (6)115°.(7)36°.(8)30°,45°,105°. 8.35°. 9.(1)10°;(2)).(21B C DAE ∠-∠=∠ 10.(1)113°,(2),2190o n + (3)116°.11.(1)23°.(2).21 n BOC =∠ 证明:∵OB 平分∠ABC ,OC 平分∠ACE , ∴.21,21ABC OBC ACE OCE ∠=∠∠=∠ ∴.2121)(21 n A ABC ACE OBC OCF BOC =∠=∠-∠=∠-∠=∠ 12.)(21180)32(180FCB EBC BOC ∠+∠-=∠+∠-=∠)]()[(21180o ABC A ACB A ∠+∠+∠+∠-=)180(21180o o A ∠+-=A ∠-=2190.2190o n -=13.36°. 14.39°.由本练习中第4题结论可知: ∠C +∠CDM =∠M +∠MBC , 即①.2121ABC M ADC C ∠+∠=∠+∠同理,②.2121ABC A ADC M ∠+∠=∠+∠由①、②得),(21C A M ∠+∠=∠因此∠C =39°.。
人教版数学八年级上册11.2与三角形有关的角习题课优秀教学案例
(三)小组合作
1.合理划分学习小组,培养学生合作学习的习惯;
2.设计具有挑战性和综合性的任务,激发学生的合作兴趣;
3.引导学生进行互动交流,培养他们的沟通能力和团队协作精神;
4.关注小组合作过程,及时给予反馈和指导,提高学生的合作效果。
在教学过程中,我会合理划分学习小组,培养学生合作学习的习惯。我会设计具有挑战性和综合性的任务,激发学生的合作兴趣。例如,我可以让学生分组讨论三角形分类的规律,并总结出各自的结论。在小组合作过程中,我会引导学生进行互动交流,培养他们的沟通能力和团队协作精神。同时,我会关注小组合作过程,及时给予反馈和指导,提高学生的合作效果。
(三)情感态度与价值观
1.培养学生对数学的兴趣和热情,使他们愿意主动参与数学学习;
2.培养学生勇于探究、积极思考的学习精神,提高他们的自主学习能力;
3.培养学生合作意识,使他们认识到团队协作的重要性;
4.培养学生面对困难不退缩,勇于克服的精神,增强他们的自信心。
在教学过程中,我将关注学生的情感需求,以生动有趣的教学手段,激发学生对数学的兴趣。同时,我会鼓励学生积极思考、勇于探究,培养他们自主学习的能力。在小组合作过程中,我会引导学生互相尊重、互相帮助,培养他们的合作意识。在面对困难时,我会鼓励学生勇敢面对,帮助他们克服困难,增强他们的自信心。通过本节课的学习,使学生形成积极向上的情感态度,树立正确的价值观。
人教版 八年级 上册 11.2与三角形有关的角 同步练习(带答案)
与三角形有关的角同步练习一、选择题1.若一个三角形的三个内角的度数之比为2:8:5,则这个三角形是().A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形2.在不等边三角形中,最小的角可以是().A. 80°B. 66°C. 70°D. 57°3.在锐角三角形中,最大角的取值范围是().A. 0°<α<90°B. 60°<α<180°C. 60°<α<90°D. 60°≤α<90°4.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A等于().A. 35°B. 95°C. 85°D. 75°5.下列说法正确的是()A. 三角形的内角中最多有一个锐角B. 三角形的内角中最多有两个锐角C. 三角形的内角中最多有一个直角D. 三角形的三个内角都大于60°6.如图,在△ABC中,∠C=70°,沿图中虚线截去∠C,则∠1+∠2的度数为()A. 140°B. 180°C. 250°D. 360°7.如图,AB//CD,∠A=50°,∠C=30°,则∠AEC等于()A. 20°B. 50°C. 80°D. 100°8.如图,△ABC中,∠A=60°,∠B=40°,则∠C等于()A. 100°B. 80°C. 60°D. 40°9.在三角形的三个外角中,钝角的个数最少有().A. 1个B. 2个C. 3个D. 4个10.如图,在△ABC中,点D在AB上,点E在AC上,DE//BC.若∠A=62°,∠AED=54°,则∠B的大小为()A. 54°B. 62°C. 64°D. 74°11.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数为()A. 120°B. 80°C. 60°D. 40°二、填空题12.如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,则∠DBC=_________.13.在△ABC中,AE为边BC上的高线,若∠ABC=50°,∠CAE=20°,则∠ACB=_________.14.如果一个三角形的两个不同的外角之和为270°,那么这个三角形是________三角形(填“锐角”“直角”或“钝角”).15.根据如图所示的图形直接写出∠α的度数.(1)如图①,∠α=________;(2)如图②,∠α=________;(3)如图③,∠α=________.三、解答题16.如图,已知∠BCD=92°,∠A=27°,∠BED=44°.求:(1)∠B的度数.(2)∠BFD的度数.17.如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=75°,∠C=45°,求∠DAE与∠AEC的度数.答案和解析1.C解:设其三个内角度数分别是2k,8k,5k.根据三角形的内角和定理,得:2k+8k+5k=180,解得:k=12,∴8k=96,∴这个三角形是钝角三角形.2.D解:在不等边三角形中,最小的角要小于60°,否则三内角的和大于180°.3.D解:三角形中最大的角不能小于60°,如果小于60°,则三角形的内角和将小于180°,又该三角形是锐角三角形,则最大角必须小于90°,故最大角的取值范围是60°≤α< 90°.4.C解:∵CE是△ABC的外角∠ACD的平分线,∠ACE=60°,∴∠ACD=120°,又∵∠ACD=∠A+∠B,∴∠A=∠ACD−∠B=120°−35°=85°.故选C.5.C解:A、直角三角形中有两个锐角,故本选项错误;B、等边三角形的三个角都是锐角,故本选项错误;C、三角形的内角中最多有一个直角,故本选项正确;D、若三角形的内角都大于60°,则三个内角的和大于180°,这样的三角形不存在,故本选项错误.6C解:作∠3、∠4如上图,∵∠C=70°,∴∠3+∠4=180°−70°=110°,∴∠1+∠2=(180°−∠3)+(180°−∠4)=360°−(∠3+∠4)=250°.7.C解:∵AB//CD,∠A=50°,∴∠ADC=∠A=50°,∵∠AEC=∠C+∠ADC∴∠AEC=30°+50°=80°8.B解:由三角形内角和定理得,∠C=180°−∠A−∠B=80°,9.B解:∵三角形的外角与它相邻的内角互补,在一个三角形中最多有一个钝角,∴它的外角至少有两个钝角.故选B.10.C解:∵DE//BC,∴∠C=∠AED=54°,∵∠A=62°,∴∠B=180°−∠A−∠C=64°,故选:C.11.C解:∵△ABC中∠A:∠B:∠C=2:3:4,∴设∠A=2x,∠B=3x,∠C=4x.∵∠A+∠B+∠C=180°,∴2x+3x+4x=180°,解得x=20°,∴∠B=3x=60°.故选C.12.18°解:∵∠C=∠ABC=2∠A,∴∠A+∠ABC+∠C=5∠A=180°,解得∠A=36°,∴∠C=2×36°=72°,∵BD是AC边上的高,∴∠DBC=90°−∠C=90°−72°=18°.故答案为18°.13.70°或110°解:∵AE⊥BC,∴∠BAE+∠ABC=90°,∴∠BAE=90°−50°=40°,当∠ACB为锐角时,如图1,在△AEC中,∠ACB+∠CAE=90°,∴∠ACB=90°−20°=70°,当∠ACB为钝角时,如图2,,则∠ACB=∠CAE+∠AEC=20°+90°=110°.故答案为70°或110°14.直角解:∵一个三角形的两个不同的外角之和为270°,∴第三个外角是90°,∴与90°的外角相邻的内角是90°,∴这个三角形一定是直角三角形.故答案为直角.15.(1)60°;(2)30°;(3)70°.解:(1)如图①,∠1=180°−140°=40°,∵100°=∠1+∠α,∴∠α=100°−∠1=100°−40°=60°.故答案为60°.(2)如图②,∵∠2+60°+20°=180°,∴∠2=100°,又∵∠2=70°+∠α,∴∠α=∠2−70°=100°−70°=30°.故答案为30°.(3)如图③,∵∠3+45°=135°,∴∠3=90°,又∵∠3=20°+∠α,∴∠α=∠3−20°=90°−20°=70°.故答案为70°.16.解:(1)在△ABC中,∵∠BCD=∠A+∠B,∠BCD=92°,∠A=27°,∴∠B=∠BCD−∠A=92°−27°=65°;(2)在△BEF中,∵∠BFD=∠B+∠BED,∠BED=44°,∠B=65°,∴∠BFD=44°+65°=109°.17.解:∵∠B+∠C+∠BAC=180°,∠B=75°,∠C=45°,∴∠BAC=60°,∵AE平分∠BAC,∴∠BAE=∠CAE=12∠BAC=12×60°=30°,∵AD是BC上的高,∴∠B+∠BAD=90°,∴∠BAD=90°−∠B=90°−75°=15°,∴∠DAE=∠BAE−∠BAD=30°−15°=15°,在△AEC中,∠AEC=180°−∠C−∠CAE=180°−45°−30°=105°.。
八年级数学上册11.2与三角形有关的角习题课学案新人教版
与三角形有关的角习题课学习目标1. 进一步理解掌握三角形的内角和定理、内外角关系定理及应用;2. 体会转化思想、整体思想等知识与方法,提高探究的能力及说理能力.重点三角形的内角和定理、内外角关系定理的应用活动1 三角形的基本知识 三角形是最基本的几何图形,许多几何问题都可以转化为三角形问题来解。
三角形内角和定理、内外角关系定理是三角形重要的基本定理.在解答三角形问题时,经常用到分类讨论、整体考虑、转化等知识与方法。
熟悉以下重要基本图形、基本结论:1. 三角形内角和定理:在△ABC 中,∠A +∠B +∠C =180°。
2. 三角形内外角关系:⑴ ⎧⎪⎨⎪⎩1,2______,3_______.αβ∠=∠+∠∠=+∠=+ ⑵ ⎧⎪⎨⎪⎩1,1;2___,2___;3___,3____.αβ∠>∠∠>∠∠>∠>∠>∠>⑶ 1180,2180,3___180.γα∠+∠=∠+∠=∠+=3. 三角形外角和:123______.∠+∠+∠=4. 对顶三角形 12______.∠+∠=+5. P 点为△ABC 的角平分线的交点,则190___.2BPC ∠=+∠活动2 简单应用 体会整体考虑、转化思想等知识与方法1.图⑴中∠A+∠B+∠C+∠D+∠E的度数等于______ .(组内交流,说说你的思路)变化练习:图⑵中∠A+∠B+∠C+∠D+∠E的度数等于______ 。
图⑶中∠A+∠B+∠C+∠D+∠E的度数等于______ .图⑷中∠A+∠B+∠C+∠D+∠E+∠F的度数等于______ .2.如图⑴,P点为△ABC的角平分线的交点,求证:190.2 BPC A ∠=+∠证明:∵P点为△ABC的角平分线的交点,∴111,2.22ABC ACB∠=∠∠=∠( )∴180(12)BPC∠=-∠+∠( )=1180(____)2ABC-∠+∠=1180(180)2A--∠=190.2A+∠变化练习:图⑵中,点P是△ABC 外角平分线的交点,试探究∠BPC与∠A的关系.图⑶中,点P 是△ABC 内角平分线BP 与外角平分线CP 的交点,试探究∠BPC 与∠A 的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与三角形有关的角习题课 学案
学习目标
1. 进一步理解掌握三角形的内角和定理、内外角关系定理及应用;
2. 体会转化思想、整体思想等知识与方法,提高探究的能力及说理能力.
重点
三角形的内角和定理、内外角关系定理的应用
活动1 三角形的基本知识
三角形是最基本的几何图形,许多几何问题都可以转化为三角形问题来解.三角形内角和定理、内外角关系定理是三角形重要的基本定理.在解答三角形问题时,经常用到分类讨论、整体考虑、转化等知识与方法.
熟悉以下重要基本图形、基本结论:
1. 三角形内角和定理:在△ABC 中,△A +△B +△C =180°.
2. 三角形内外角关系:
△ △ △
3. 三角形外角和:
4. 对顶三角形
5. P 点为△ABC 的角平分线的交点,则 活动2 简单应用 体会整体考虑、转化思想等知识与方法
1. 图△中△A +△B +△C +△D +△E 的度数等于______ .(组内交流,说说你的思路)
图△中△A +△B +△C +△D +△E 的度数等于______ .
图△中△A +△B +△C +△D +△E 的度数等于______ .
⎧⎪⎨⎪⎩
1,2______,3_______.αβ∠=∠+∠∠=+∠=+⎧⎪⎨⎪⎩
1,1;2___,2___;3___,3____.αβ∠>∠∠>∠∠>∠>∠>∠>1180,2180,3___180.γα∠+∠=∠+∠=∠+=123______.∠+∠+∠=12______.∠+∠=+190
___.2BPC ∠=+∠
图△中△A +△B +△C +△D +△E +△F 的度数等于______ .
2. 如图△,P 点为△ABC 的角平分线的交点,求证: 证明:△P 点为△ABC 的角平分线的交点,
△( ) △ ( )
===
变化练习:
图△中,点P 是△ABC 外角平分线的交点,试探究△BPC 与△A 的关系.
图△中,点P 是△ABC 内角平分线BP 与外角平分线CP 的交点,试探究△BPC 与△A 的关系.
活动3 课堂练习
1. △ABC 中,,则
2. 如图,在△ABC 中,△A =50°,点D 、E 分别在AB 、AC 上,
则
△1+△2的大小为( )
A .130°
B .230°
C .180°
D .310°
190.2BPC A ∠=+∠111,2.22
ABC ACB ∠=∠∠=∠180(12)BPC ∠=-∠+∠1180(____)2ABC -∠+∠1180(180)2A --∠190.2
A +∠2
B
C A ∠=∠=∠___,___,___.A B C ∠=∠=∠=
3. 如图,AD 、AE 分别是△ABC 的角平分线和高,△B =25°,△C =75°,求△DAE 的度数.
活动1
2.△ ,.△ ,.△
3.360°
4.△3 △4.
5.A. 活动2
1.180°,180°,180°,
360°.2.角平分线定义 三角形内角和定理 ACB . △BPC =
△BPC =. 活动3
1.36,72,7
2. 2.B.
3.25°.
β∠γ∠α∠γ∠β∠γ∠α∠γ∠β∠190.2A -∠12A ∠。
