内心、外心、重心、垂心的区分
内心、外心、重心、垂心定义及性质总结

内心、外心、重心、垂心1、内心(1)定义:三角形的内心是三角形三条角平分线的交点(或内切圆的圆心)。
(2)三角形的内心的性质①三角形的三条角平分线交于一点,该点即为三角形的内心②三角形的内心到三边的距离相等,都等于内切圆半径r③s= (r是内切圆半径)2④在Rt△ ABC中,/ C=90 , r=(a+b-c)/2 .⑤/BOC = 90 +Z A/2 / BOA = 90+/C/2 / AOC = 90+/B/22、外心(1)定义:三角形的外心是三角形三条垂直平分线的交点(或三角形外接圆的圆心)。
(2)三角形的外心的性质①三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.②三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合。
③锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合④OA=OB=OC=R⑤/ B0C=2 BAC / AOB=Z ACB / C0A=2 CBA⑥S A ABC二abc/4R 3、重心(1)三角形的三条边的中线交于一点。
该点叫做三角形的重心。
(2)三角形的重心的性质①重心到顶点的距离与重心到对边中点的距离之比为2:1。
②重心和三角形 3 个顶点组成的 3 个三角形面积相等。
③重心到三角形 3 个顶点距离的平方和最小。
④在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3) ;空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:( Z1+Z2+Z3) /3 ⑤重心和三角形 3 个顶点的连线的任意一条连线将三角形面积平分。
⑥重心是三角形内到三边距离之积最大的点。
4、垂心(1)定义:三角形的垂心是三角形三边上的高的交点(通常用H表示)。
(2)三角形的垂心的性质①锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外②三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心③垂心0关于三边的对称点,均在△ ABC的外接圆上④厶ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,且AO- OD=BOOE=COOF⑤H A B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
内心、外心、重心、垂心定义及性质总结

内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4垂心:三条高所在直线的交点。
5重心:三条中线定相交,交点位置真奇巧,
交点命名为“重心”,重心性质要明了,
重心分割中线段,数段之比听分晓;
长短之比二比一,灵活运用掌握好.
6垂心:三角形上作三高,三高必于垂心交.
高线分割三角形,出现直角三对整,
直角三角形有十二,构成六对相似形,
四点共圆图中有,细心分析可找清.
7内心:三角对应三顶点,角角都有平分线,
三线相交定共点,叫做“内心”有根源;
8外心点至三边均等距,可作三角形内切圆,此圆圆心称“内心”如此定义理当然.
三角形有六元素,三个内角有三边.
作三边的中垂线,三线相交共一点.
此点定义为“外心”,用它可作外接圆.
“内心”“外心”莫记混,“内切”“外接”是关键.:。
三角形的内心,外心,重心,垂心,旁心及性质分别是指什么?
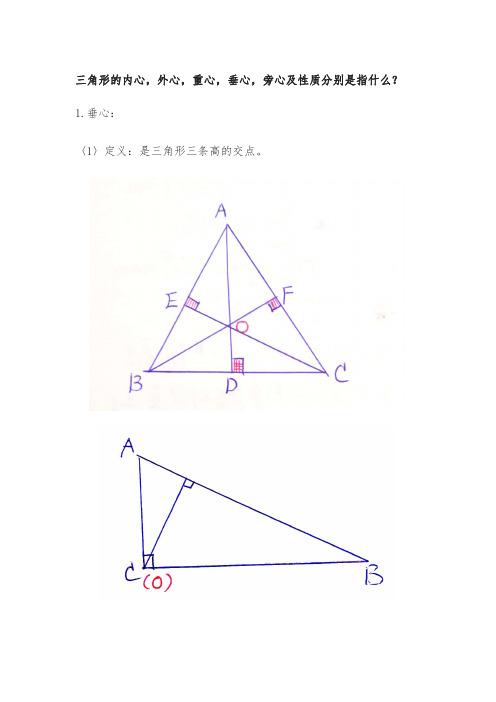
三角形的内心,外心,重心,垂心,旁心及性质分别是指什么?1.垂心:〈1〉定义:是三角形三条高的交点。
〈2〉性质:[性质1]锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。
[性质2]三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心。
[性质3]垂心O关于三边的对称点,均在△ABC的外接圆圆上。
[性质4]△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,。
[性质5]O、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为--垂心组)。
[性质6]△ABC,△ABO,△BCO,△ACO的外接圆是等圆。
[性质7]三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。
[性质8]设O、H分别为△ABC的外心和垂心,则∠BAO=∠HAC,∠ABH=∠OBC,∠BCO=∠HCA.[性质9]锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍,即AH+BH+CH=2(r+R)。
[性质10]锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形(顶点在原三角形的边上)中,以垂足三角形的周长最短。
[性质11]设H为非直角三角形的垂心,且D、E、F分别为H在BC,CA,AB.上的射影,H1,H2,H3分别为△AEF,△BDF,△CDE的垂心,则△DEF≌△H1H2H3.[性质12]三角形垂心H的垂足三角形的三边,分别平行于原三角形外接圆在各顶点的切线。
2.内心〈1〉定义:是三角形三条内角平分线的交点即内接圆的圆心。
交于点O,点O即为△ABC的内心。
〈2〉性质:[性质1]三角形的内心到三边的距离相等,都等于内切圆半径r. [性质2]∠BOC=90°+∠BAC/2。
[性质3]在Rt△ABC中,∠A=90°,三角形内切圆切BC于D,则S△ABC=BDxCD3.重心:〈1〉重心的定义:重心是三角形三条中线的交点。
三角形的重心、垂心、内心、外心

三角形的重心,外心,垂心,内心和旁心称之为三角形的五心。
三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理,旁心定理的总称。
一、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2︰1。
2、重心和三角形任意两个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
二、三角形外心定理三角形外接圆的圆心,叫做三角形的外心。
外心的性质:1、三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、外心到三顶点的距离相等三、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG︰GH=1︰2。
(此直线称为三角形的欧拉线(Euler line))3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
4、垂心分每条高线的两部分乘积相等。
定理证明已知:ΔABC中,AD、BE是两条高,AD、BE交于点O,连接CO并延长交AB于点F ,求证:CF⊥AB证明:连接DE ∵∠ADB=∠AEB=90度∴A、B、D、E四点共圆∴∠ADE=∠ABE ∵∠EAO=∠DAC ∠AEO=∠ADC ∴ΔAEO∽ΔADC ∴AE/AO=AD/AC ∴ΔEAD∽ΔOAC ∴∠ACF=∠ADE=∠ABE 又∵∠ABE+∠BAC=90度∴∠ACF+∠BAC=90度∴CF⊥AB 因此,垂心定理成立!四、三角形内心定理三角形内切圆的圆心,叫做三角形的内心。
数学中的四个“心”

数学中的四个“心”
在数学中几何等等题目中经常出现外心,内心,重心,垂心,这些名词在我们的题目中出现的频率很高,所以我们有必要把这四个“心”单独列出来,彻底的弄清楚。
.外心:指三角形三条边的垂直平分线的相交点。
用这个点做圆心可以画三角形的外接圆。
性质:到外心到三角形的三个顶点距离相等
内心:内心是三角形三条内角平分线的交点,即内切圆的圆心。
性质:内心到三边的距离相等。
重心:重心是三角形三边中线的交点。
性质:1.重心到顶点的距离与重心到对边中点的距离之比为2:1。
2.重心和三角形3个顶点组成的3个三角形面积相等。
垂心:三角形的三条高线的交点叫做三角形的垂心。
性质:1、锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外.
2、垂心H关于三边的对称点,均在△ABC的外接圆上。
三角形中的内心外心垂心与重心

三角形中的内心外心垂心与重心三角形是几何学中最基本的图形之一,它有很多有趣和重要的性质。
其中,内心、外心、垂心和重心是与三角形密切相关的四个特殊点。
本文将探讨这四个点的定义、性质及其在三角形中的应用。
一、内心内心是指三角形内部与三边各自相切的圆的圆心,记为I。
对于任意三角形ABC,I的定义如下:1. 点I到三角形的每条边的距离相等,即IA=IB=IC。
2. 点I恰好在三边的内部。
3. 内切圆的半径为r,称为三角形的内切圆半径。
内心有很多重要的性质:1. 内心到三边的距离分别是三边长度的函数,可以通过海伦公式计算。
2. 内心是三角形的垂心和重心的共轭点,也是三角形的唯一一个同时与三边相切的圆心。
3. 对于等边三角形,内心、重心和外心重合于同一个点。
4. 内心是三角形三条角平分线的交点。
二、外心外心是指三角形外接圆的圆心,记为O。
对于任意三角形ABC,O 的定义如下:1. 三角形的三条边的中垂线相交于一点,该点就是外心。
2. 外接圆半径为R,称为三角形的外接圆半径。
外心也有一些重要的性质:1. 外心到三个顶点的距离相等,即OA=OB=OC=R。
2. 外心是垂心和内心的共轭点,也是三角形的唯一一个同时与三边相切的圆心。
3. 对于钝角三角形,外心在三角形外部;对于直角三角形,外心在三角形斜边上;对于锐角三角形,外心在三角形内部。
4. 外心是三角形三个垂直平分线的交点。
三、垂心垂心是指三角形三条高或垂直平分线的交点,记为H。
对任意三角形ABC,H的定义如下:1. 三角形的三条高或垂直平分线相交于一点,该点就是垂心。
垂心有以下重要性质:1. 垂心到三边距离之积为定值,等于三角形面积的两倍。
2. 垂心是内心和外心的共轭点,也是三角形的唯一一个同时与三边相切的圆心。
3. 对于锐角三角形,垂心在三角形内部;对于直角三角形,垂心在斜边上;对于钝角三角形,垂心在三角形外部。
4. 垂心是三角形三个中线的交点。
四、重心重心是指三角形三条中线的交点,记为G。
内心、外心、重心、垂心定义及性质总结

此文档收集于网络,如有侵权请联系网站删除
内心、外心、重心、垂心定义及性质总结
1. 内
心:(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2 外
心:1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重
心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍
4 垂心:三条高所在直线的交点
5 重心: 三条中线定相交,交点位置真奇巧,交点命名为“重心”,重心性质要明了,重心分割中线段,数段之比听分晓;长短之比二比一,灵活运用掌握好.
6 垂心: 三角形上作三高,三高必于垂心交.高线分割三角形,出现直角三对整,直
角三角形有十二,构成六对相似形,四点共圆图中有,细心分析可找清.
7 内心: 三角对应三顶点,角角都有平分线,三线相交定共点,叫做“内心”有根
源;点至三边均等距,可作三角形内切圆,此圆圆心称“内心”如此定
义理当然.
8 外心: 三角形有六元素,三个内角有三边.作三边的中垂线,三线相交共一点.此点定义为“外心” ,用它可作外接圆.“内心”“外心”莫记混,“内切”“外接”是关键.。
内心、外心、重心、垂心定义及性质总结

内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂心:三条高所在直线的交点。
5 重心: 三条中线定相交,交点位置真奇巧,
交点命名为“重心”,重心性质要明了,
重心分割中线段,数段之比听分晓;
长短之比二比一,灵活运用掌握好.
6 垂心: 三角形上作三高,三高必于垂心交.
高线分割三角形,出现直角三对整,直角三角形有十二,构成六对相似形,四点共圆图中有,细心分析可找清.
7内心: 三角对应三顶点,角角都有平分线,
三线相交定共点,叫做“内心”有根源;
点至三边均等距,可作三角形内切圆,
此圆圆心称“内心”如此定义理当然.
8外心: 三角形有六元素,三个内角有三边.
作三边的中垂线,三线相交共一点.
此点定义为“外心”,用它可作外接圆.
“内心”“外心”莫记混,“内切”“外接”是关键.如有侵权请联系告知删除,感谢你们的配合!
如有侵权请联系告知删除,感谢你们的配合!。
