人教版初三数学二次函数知识点及难点总结
人教版九年级上册 第22章 二次函数复习知识点总结和题型讲解
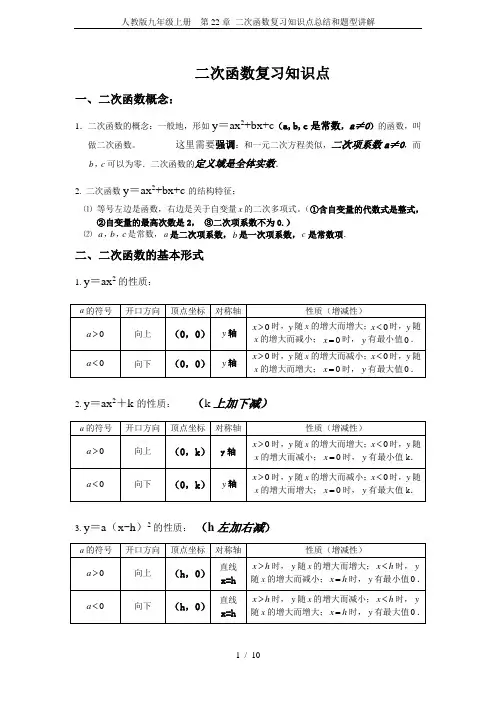
二次函数复习知识点一、二次函数概念:1.二次函数的概念:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数a≠0,而b c,可以为零.二次函数的定义域是全体实数.2. 二次函数y=ax2+bx+c的结构特征:⑴等号左边是函数,右边是关于自变量x的二次多项式。
(①含自变量的代数式是整式,②自变量的最高次数是2,③二次项系数不为0.)⑵a b c,,是常数,a是二次项系数,b是一次项系数,c是常数项.二、二次函数的基本形式1. y=ax2的性质:2. y=ax2+k的性质:(k上加下减)3. y=a(x-h)2的性质:(h左加右减)4. y =a (x -h)2+k 的性质:5. y =ax2+bx+c 的性质:三、二次函数的图象与各项系数之间的关系1. 二次项系数a.(a 决定了抛物线开口的大小和方向)二次函数2y ax bx c =++中,a 作为二次项系数,显然a ≠0 ① 当0a >时,抛物线开口向上,当0a <时,抛物线开口向下;②a 的绝对值越大,开口越小,反之a 的绝对值越小,开口越大。
总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小.2. 一次项系数b (a 和b 共同决定抛物线对称轴的位置).抛物线c bx ax y ++=2的对称轴是直线abx 2-=,故:①0=b 时,对称轴为y 轴;② (即a 、b 同号)时,对称轴在y 轴左侧;③ (即a 、b 异号)时,对称轴在y 轴右侧.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异”3. 常数项c(c 决定了抛物线与y 轴交点的位置)⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置.总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的. 四、二次函数图象的平移1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,;⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”.方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿x 轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)五、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,. 六、二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点). 画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.七、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达1. 关于x 轴对称2y a x b x c =++关于x 轴对称后,得到的解析式是2y ax bx c =---; ()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---;2. 关于y 轴对称2y a x b x c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+; ()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称2y a x b x c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-; 根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.八、二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠),适用条件:已知抛物线上三点的坐标,一般选用一般式;2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠),适用条件:已知图像上点两坐标,且其中一点为抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 交点式(两根式):12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标), 适用条件:已知图像上三点坐标,其中两点为抛物线与x 轴的两个交点(1x ,0),(2x ,0),一般选用交点式;九、二次函数的最值如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当abx 2-=时,a b ac y 442-=最值。
人教版数学九年级上册 第二十二章《二次函数》章节知识点归纳复习总结

人教版数学九年级上学期《二次函数》章节知识点归纳总结一、二次函数概念:1.二次函数的概念:(1)一般地,形如2y ax bx c =++(a b c ,,是常数,a ≠0)的函数,叫做二次函数。
(2)这里需要强调:和一元二次方程类似,二次项系数a ≠0,而b c ,可以为零.二次函数的定义域(x)是全体实数.2. 二次函数 2y ax bx c =++ 的结构特征:(1)等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. (2)a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项.3. 二次函数解析式的几种形式(1)一般式:y=ax 2+bx+c (a ,b ,c 为常数,a ≠0) (2)顶点式:y=a(x-h)2+k [抛物线的顶点P ( h ,k )](3)交点式:y=a(x-x 1)(x-x 2)[仅限于与x 轴有交点A (x 1,0)和 B (x 2,0)的抛物线]其中x 1,x 2是抛物线与x 轴的交点的横坐标,即一元二次方程ax 2+bx+c =0的两个根,a ≠0. x 1,x 2 = (-b ±ac 4b 2-)/2a在三种形式的互相转化中,有如下关系:h= -b / 2a ; k=(4ac-b 2) / 4a ; x 1,x 2 = (-b ±ac 4b 2-) / 2a说明:(1)任何一个二次函数通过配方都可以化为顶点式y=a(x-h)2+k,抛物线的顶点坐标是(h,k);(2) 当h=0时,抛物线y=ax2+k的顶点在y轴上;当k=0时,抛物线a(x-h)2的顶点在x轴上;当h=0且k=0时,抛物线y=ax2的顶点在原点;(3) 如果图像经过原点,并且对称轴是y轴,则设y=ax2;如果对称轴是y轴,但不过原点,则设y=ax2+k4.抛物线的性质(1).抛物线是轴对称图形。
对称轴为直线 x = -b/2a。
对称轴与抛物线唯一的交点为抛物线的顶点P。
(完整word版)人教版初三数学二次函数知识点及难点总结

初三数学二次函数知识点总结二次项系数a决定二次函数图像的开口方向和大小.当a>0时,二次函数图像向上开口;当a<0时,抛物线向下开口.|a|越大,则二次函数图像的开口越小.1、决定对称轴位置的因素一次项系数b和二次项系数a共同决定对称轴的位置.当a与b同号时(即ab>0),对称轴在y轴左;因为对称轴在左边则对称轴小于0,也就是- b/2a0,所以b/2a要小于0,所以a、b要异号可简单记忆为左同右异,即当a与b同号时(即ab>0),对称轴在y轴左;当a与b 异号时(即ab<0 ),对称轴在y轴右.事实上,b有其自身的几何意义:二次函数图像与y轴的交点处的该二次函数图像切线的函数解析式(一次函数)的斜率k的值.可通过对二次函数求导得到.2、决定二次函数图像与y轴交点的因素常数项c决定二次函数图像与y轴交点.二次函数图像与y轴交于(0,c)一、二次函数概念:1.二次函数的概念:一般地,形如2=++(a b cy ax bx c,,是常数,0a≠)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数0a≠,而b c,可以为零.二次函数的定义域是全体实数.2. 二次函数2=++的结构特征:y ax bx c⑴等号左边是函数,右边是关于自变量x的二次式,x的最高次数是2.⑵a b c,,是常数,a是二次项系数,b是一次项系数,c是常数项.二、二次函数的基本形式1. 二次函数基本形式:2=的性质:y axa 的绝对值越大,抛物线的开口越小。
Array 2. 2=+的性质:上加下减。
y ax c3. ()2=-的性质:左加右减。
y a x h Array 4. ()2=-+的性质:y a x h k三、二次函数图象的平移 1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭,其中2424b ac b h k a a-=-=,.五、二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,. 当2bx a <-时,y 随x 的增大而减小;当2b x a>-时,y 随x 的增大而增大; 当2bx a=-时,y 有最小值244ac b a -.2. 当0a <时,抛物线开口向下,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,. 当2bx a <-时,y 随x 的增大而增大;当2b x a>-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a -.七、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化. 八、二次函数的图象与各项系数之间的关系1. 二次项系数a 二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小.2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02ba-<,即抛物线的对称轴在y 轴左侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba->,即抛物线对称轴在y 轴的右侧. ⑵ 在0a <的前提下,结论刚好与上述相反,即 当0b >时,02ba->,即抛物线的对称轴在y 轴右侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧. 总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异” 总结: 3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置.总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的. 二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x 轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式. 九、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k=-+关于x 轴对称后,得到的解析式是()2y a x h k =---;2. 关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k=-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称 2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-;()2y a x h k=-+关于原点对称后,得到的解析式是()2y a x h k =-+-;4. 关于顶点对称(即:抛物线绕顶点旋转180°)2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k=-+关于顶点对称后,得到的解析式是()2y a x h k =--+.5. 关于点()m n ,对称()2y a x h k=-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.十、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的距离21AB x x =-.② 当0∆=时,图象与x 轴只有一个交点; ③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2'当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;3. 二次函数常用解题方法总结:⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a ,b ,c的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式,二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数;下面以0a >时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:二次函数图像参考:2-32y=3(x+4)22y=3x 2十一、函数的应用二次函数应用⎧⎪⎨⎪⎩刹车距离何时获得最大利润最大面积是多少二次函数考查重点与常见题型1、考查二次函数的定义、性质,有关试题常出现在选择题中,如:已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点, 则m 的值是 2、综合考查正比例、反比例、一次函数、二次函数的图像,习题的特点是在同一直角坐标系内考查两个函数的图像,试题类型为选择题,如:如图,如果函数b kx y +=的图像在第一、二、三象限内,那么函数12-+=bx kx y 的图像大致是( )y 0 0 -1 x D1、考查用待定系数法求二次函数的解析式,有关习题出现的频率很高,习题类型有中档解答题和选拔性的综合题,如:已知一条抛物线经过(0,3),(4,6)两点,对称轴为35=x ,求这条抛物线的解析式。
人教版九年级数学《二次函数》知识点梳理与总结(超经典)

《二次函数》单元知识梳理与总结一、二次函数的概念1、定义:一般地,如果c b a c bx ax y ,,(2++=是常数,)0≠a ,那么y 叫做x 的二次函数.2、注意点:(1)二次函数是关于自变量x 的二次式,二次项系数a 必须为非零实数,即a ≠0,而b 、c 为任意实数。
(2)当b=c=0时,二次函数2ax y =是最简单的二次函数。
(3)二次函数c b a c bx ax y ,,(2++=是常数,)0≠a 自变量的取值为全体实数 (c bx ax ++2为整式)3、三种函数解析式:(1)一般式: y=ax 2+bx+c (a ≠0),对称轴:直线x=ab2- 顶点坐标:( a b ac a b 4422--, ) (2)顶点式:()k h x a y +-=2(a ≠0),对称轴:直线x=h 顶点坐标为(h ,k )(3)交点式:y=a (x-x 1)(x-x 2)(a ≠0), 对称轴:直线x=22x1x + (其中x 1、x 2是二次函数与x 轴的两个交点的横坐标).二、二次函数的图象1、二次函数 c bx ax y ++=2的图像是对称轴平行于(包括重合)y 轴的抛物线.2、二次函数由特殊到一般,可分为以下几种形式:①2ax y =;②k ax y +=2;③()2h x a y -=;④()k h x a y +-=2;⑤c bx ax y ++=2.注:二次函数的图象可以通过抛物线的平移得到 3、二次函数c bx ax y ++=2的图像的画法因为二次函数的图像是抛物线,是轴对称图形,所以作图时常用简化的描点法和五点法,其步骤是:(1)先找出顶点坐标,画出对称轴;(2)找出抛物线上关于对称轴的四个点(如与坐标轴的交点等); (3)把上述五个点按从左到右的顺序用平滑曲线连结起来.1、增减性:当a>0时,在对称轴左侧,y 随着x 的增大而减少;在对称轴右侧,y 随着x 的增大而增大; 当a<0时,在对称轴左侧,y 随着x 的增大而增大;在对称轴右侧,y 随着x 的增大而减少; 2、最大或最小值:当a>0时,函数有最小值,并且当x=a b2- , y 最小 =a b ac 442-当a<0时,函数有最大值,并且当x=ab2- , y 最大 =a b ac 442-四、.抛物线的三要素:开口方向、对称轴、顶点坐标。
(完整版)九年级上册数学二次函数知识点汇总

标相等,设纵坐标为 k ,则横坐标是 ax 2 bx c k 的两个实数根.
(5)一次函数 y kx nk 0的图像 l 与二次函数 y ax2 bx ca 0的图像
y kx n
G
的交点,由方程组
(1)当二次函数的图象与 x 轴有两个交点,这时
,则方程有两个不相等实根;
(2)当二次函数的图象与 x 轴有且只有一个交点,这时
,则方程有两个相等实
根;(3)当二次函数的图象与 x 轴没有交点,这时
,则方程没有实根.
通过下面表格可以直观地观察到二次函数图象和一元二次方程的关系:
5
hing at a time and All things in their being are good for somethin
利用题中存在的公式、内含的规律等相等关系,建立函数关系式,再利用函数的图象及性 质去研究问题.在研究实际问题时要注意自变量的取值范围应具有实际意义. 利用二次函数解决实际问题的一般步骤是: (1)建立适当的平面直角坐标系; (2)把实际问题中的一些数据与点的坐标联系起来; (3)用待定系数法求出抛物线的关系式;
③运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直 平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.
(5)抛物线 y ax 2 bx c 中, a,b, c 的作用
① a 决定开口方向及开口大小,这与 y ax 2 中的 a 完全一样. ② b 和 a 共同决定抛物线对称轴的位置 由于抛物线 y ax 2 bx c 的对称轴是直线 x b ,故
的图象
的解
第二十二章《二次函数》知识点总结人教版数学九年级上册

《二次函数》知识点总结【知识点1 二次函数的表达式】1. 一般式: . 顶点坐标: . 对称轴: .2. 顶点式: .顶点坐标: . 对称轴: . 【知识点2 二次函数的图象与性质】 1. 二次项系数a 决定抛物线的 开口方向 ;①当0>a 时,抛物线的 ; ②当0<a 时,抛物线的 ; ③ ||a 越大,抛物线的开口 .3.常数项c 决定抛物线 与y 轴 交点的位置 . ①当0=c ,抛物线与y 轴交于 ; ②当0>c ,抛物线与y 轴交于 ; ③当0<c ,抛物线与y 轴交于 .5.根据a 、b 、c 的符号,画出二次函数的草图:①已知 a <0、b <0、c <0 ②已知 a>0、b <0、c >0 6.描述下面二次函数c bx ax y ++=2的增减性: 【知识点3 抛物线与坐标轴的交点】 1. 抛物线c bx ax y ++=2与x 轴的交点个数,即02=++c bx ax . ①当 ,抛物线与x 轴有两个交点; ②当 ,抛物线与x 轴有1个交点; ③当 ,抛物线与x 轴有没有交点;2.求抛物线c bx ax y ++=2与x 轴的交点的过程: 3.求抛物线c bx ax y ++=2与y 轴的交点的过程:4.函数 y = ax 2 + bx + c 的图象如图,那么 ①方程 ax 2 + bx + c =2 的根是 ______________;2.系数a 和b 共同决定抛物线 对称轴的位置 . ①a 和b 同号,对称轴在原点的 ; ②a 和b 异号, .4.根据图象判断出a 、b 、c 的符号:方法总结:第一步:求出对称轴;第二步:用箭头在对称轴两侧标出上升和下降;第三步:描述增减性.①当 时,随的增大而减小; ②当 时, 随的增大而增大;∵轴上的点, 为零,∴ . ∵轴上的点, 为零,∴ .②不等式 ax 2 + bx + c >0 的解集是 ___________; ③不等式 ax 2 + bx + c <2 的解集是 _________.④ a + b + c 0 ,4a 2 b + c 0 , 9a +3 b + c 0 .【知识点4 抛物线的平移】二次函数 y = ax 2 + bx + c 的平移口诀:“上下平移, ;左右平移, .” 【 * *知识点5 抛物线的对称 ** 】抛物线c bx ax y ++=2关于x 轴对称的解析式为 . 抛物线c bx ax y ++=2关于y 轴对称的解析式为 . 【 * *知识点6 二次函数图象的画法 ** 】 画出二次函数3-2-2x x y =的的图象.【典型例题 】1.m2+1+2x −是二次函数,则m 的值为( )C. −1D. 1或−12.【求顶点坐标 】抛物线y =2(x −3)4的顶点坐标是( ) A. (3,4)B. (−3,4)C. (3,−4)D. (2,4)3.【与坐标轴的交点 】抛物线y =−x 2+4x −4与坐标轴的交点个数为( ) A. 0B. 1C. 2D. 34.【平移】将函数y =x 2的图象用下列方法平移后,所得的图象不经过点A(1,4)的方法是( ) A. 向左平移1个单位 B. 向右平移3个单位C. 向上平移3个单位D. 向下平移1个单位5.【平移】抛物线y =x 2+6x +7可由抛物线y =x 2如何平移得到的( )A. 先向左平移3个单位,再向下平移2个单位B. 先向左平移6个单位,再向上平移7个单位C. 先向上平移2个单位,再向左平移3个单位D. 先向右平移3个单位,再向上平移2个单位 6.【图象与性质】对于抛物线y =−3(x +1)2−2,下列说法正确的是( ) A. 抛物线开口向上 B. 当x >−1时,y 随x 的增大而减小 C. 函数最小值为−2D. 顶点坐标为(1,−2)7.【增减性】已知(−3,y 1),(−1,y 2),(2,y 3)是抛物线y =−3x 2+6x +m 上的三个点.则( ) A. y 1<y 3<y 2B. y 3<y 2<y 1C. y 1<y 2<y 3D. y 2<y 1<y 38.【最值】已知二次函数y=x2−4x+2,关于该函数在−1≤x≤3的取值范围内,下列说法正确的是( )A. 有最大值−1,有最小值−2B. 有最大值0,有最小值−1C. 有最大值7,有最小值−1D. 有最大值7,有最小值−29.【系数与图象】二次函数y=ax2+bx+c(a≠0)与一次函数y=ax+c在同一坐标系中的图象大致为( )A. B. C. D.10.【求解析式】如图所示,已知二次函数y=ax2+bx+c的图象,求二次函数的解析式.11.如图,已知二次函数y=ax2−4x+c的图象经过点A(−1,−1)和点B(3,−9).(1)求该二次函数的解析式、对称轴及顶点坐标;(2)点C是抛物线与x轴的一个交点,点D是抛物线与y轴的交点,求三角形ACD 的面积;(3)已知点M(x1,y1)和N(1+x1,y2)在抛物线对称轴的右侧,判段y1和y2的大小.12.在运动会比赛时,九年级的一名男同学推铅球,已知铅球经过的路线是某二次函数图象的一部分(如图所示),如果这名男同学的出手处A点的坐标为(0,2),铅球路线的最高处B点的坐标为(6,5).(1)求出这个二次函数的解析式;(2)请求出这名男同学比赛时的成绩?13.如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.(1)建立平面直角坐标系,求抛物线的解析式;(2)如果水面下降1m,则水面宽度是多少米?14.某商场一种商品的进价为每件30元,售价为每件50元.每天可以销售48件,为尽快减少库存,商场决定降价促销.(1)若该商品连续两次下调相同的百分率后售价降至每件40.5元,求两次下降的百分率;(2)经调查,若该商品每降价2元,每天可多销售16件,那么每天要想获得最大利润,每件售价应多少元?最大利润是多少?。
九年级上册数学二次函数知识点汇总
新人教版九年级上二次函数知识点总结知识点一:二次函数的定义1.二次函数的定义:一般地,形如2=++(a b cy ax bx c,,是常数,0a≠)的函数,叫做二次函数.其中a是二次项系数,b是一次项系数,c是常数项.知识点二:二次函数的图象与性质⇒2. 二次函数()2=-+的图象与性质y a x h k(1)二次函数基本形式2=的图象与性质:a的绝对值越大,抛物线的开口越小y ax(2)2=+的图象与性质:上加下减y ax c(3)()2y a x h =-的图象与性质:左加右减(4)二次函数()2y a x h k =-+的图象与性质3. 二次函数c bx ax y ++=2的图像与性质(1)当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2bx a=-时,y 有最小值244ac b a-. (2)当0a <时,抛物线开口向下,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a-.4. 二次函数常见方法指导(1)二次函数2y ax bx c =++图象的画法 ①画精确图 五点绘图法(列表-描点-连线)利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.②画草图 抓住以下几点:开口方向,对称轴,与y 轴的交点,顶点. (2)二次函数图象的平移 平移步骤:① 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ② 可以由抛物线2ax 经过适当的平移得到具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位平移规律:概括成八个字“左加右减,上加下减”. (3)用待定系数法求二次函数的解析式 ①一般式:.已知图象上三点或三对、的值,通常选择一般式.②顶点式:.已知图象的顶点或对称轴,通常选择顶点式.③交点式:.已知图象与轴的交点坐标、,通常选择交点式.(4)求抛物线的顶点、对称轴的方法①公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=,∴顶点是),(a b ac a b 4422--,对称轴是直线abx 2-=. ②配方法:运用配方的方法,将抛物线的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是直线h x =.③运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点. (5)抛物线c bx ax y ++=2中,c b a ,,的作用①a 决定开口方向及开口大小,这与2ax y =中的a 完全一样. ②b 和a 共同决定抛物线对称轴的位置由于抛物线c bx ax y ++=2的对称轴是直线abx 2-=,故 如果0=b 时,对称轴为y 轴;如果0>a b(即a 、b 同号)时,对称轴在y 轴左侧; 如果0<ab(即a 、b 异号)时,对称轴在y 轴右侧.③c 的大小决定抛物线c bx ax y ++=2与y 轴交点的位置当0=x 时,c y =,所以抛物线c bx ax y ++=2与y 轴有且只有一个交点(0,c ),故 如果0=c ,抛物线经过原点; 如果0>c ,与y 轴交于正半轴; 如果0<c ,与y 轴交于负半轴.知识点三:二次函数与一元二次方程的关系5.函数c bx ax y ++=2,当0y =时,得到一元二次方程20ax bx c ++=,那么一元二次方程的解就是二次函数的图象与x 轴交点的横坐标,因此二次函数图象与x 轴的交点情况决定一元二次方程根的情况.(1)当二次函数的图象与x 轴有两个交点,这时,则方程有两个不相等实根;(2)当二次函数的图象与x 轴有且只有一个交点,这时,则方程有两个相等实根;(3)当二次函数的图象与x 轴没有交点,这时,则方程没有实根.通过下面表格可以直观地观察到二次函数图象和一元二次方程的关系:6.拓展:关于直线与抛物线的交点知识(1)y 轴与抛物线c bx ax y ++=2得交点为(0,)c .(2)与y 轴平行的直线h x =与抛物线c bx ax y ++=2有且只有一个交点(h ,c bh ah++2).(3)抛物线与x 轴的交点二次函数c bx ax y ++=2的图像与x 轴的两个交点的横坐标1x 、2x ,是对应一元二次方程02=++c bx ax 的两个实数根.抛物线与x 轴的交点情况可以由对应的一元二次方程的根的判别式判定:①有两个交点⇔0>∆⇔抛物线与x 轴相交;②有一个交点(顶点在x 轴上)⇔0=∆⇔抛物线与x 轴相切; ③没有交点⇔0<∆⇔抛物线与x 轴相离. (4)平行于x 轴的直线与抛物线的交点同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为k ,则横坐标是k c bx ax =++2的两个实数根.(5)一次函数()0≠+=k n kx y 的图像l 与二次函数()02≠++=a c bx ax y 的图像G 的交点,由方程组2y kx n y ax bx c=+⎧⎨=++⎩的解的数目来确定:①方程组有两组不同的解时⇔l 与G 有两个交点;②方程组只有一组解时⇔l 与G 只有一个交点; ③方程组无解时⇔l 与G 没有交点.(6)抛物线与x 轴两交点之间的距离:若抛物线c bx ax y ++=2与x 轴两交点为()()0021,,,x B x A ,由于1x 、2x 是方程02=++c bx ax 的两个根,故acx x a b x x =⋅-=+2121,()()a a acb ac a b x x x x x x x x AB ∆=-=-⎪⎭⎫ ⎝⎛-=-+=-=-=444222122122121知识点四:利用二次函数解决实际问题7.利用二次函数解决实际问题,要建立数学模型,即把实际问题转化为二次函数问题,利用题中存在的公式、内含的规律等相等关系,建立函数关系式,再利用函数的图象及性质去研究问题.在研究实际问题时要注意自变量的取值范围应具有实际意义. 利用二次函数解决实际问题的一般步骤是: (1)建立适当的平面直角坐标系;(2)把实际问题中的一些数据与点的坐标联系起来; (3)用待定系数法求出抛物线的关系式;(4)利用二次函数的图象及其性质去分析问题、解决问题.。
人教版初中数学九年级上册二次函数重点知识归纳
人教版初中数学九年级上册二次函数重点知识归纳知识点1 二次函数的概念和一般形式1.概念:一般地,形如y=ax2+bx+c(a ,b ,c 是常数,a≠0)的函数,叫做二次函数。
其中, x 是自变量,a,b,c 分别是函数解析式的二次项系数、一次项系数和常数项。
【注意】(1)自变量x的最高次数是2,a≠0,b,c可以为0;(2)含自变量x 的代数式是整式而不是分式或根式。
2.一般式:y=ax2+bx+c(a ,b ,c 是常数,a≠0)知识点2 二次函数的图像和性质1.二次函数的图像:是一条平滑的曲线叫做抛物线。
2.二次函数图像的画法:①列表;②描点;③连线。
3.二次函数的解析式(4种形式)(1)y = ax 2(a≠0)(2)y = ax 2+k(a,k是常数,a≠0)(3)y = a(x-h)2(a,h是常数,a≠0)(4)y = a(x-h)2+k(a,k,h是常数,a≠04.二次函数的图像和性质:分别从五种图像(4种特殊+1个一般式)和7个性质(顶点特点、开口方向、顶点坐标、对称轴、最值、增减性、形状和大小等7个方面研究)。
如下图:二次函数的图像与性质a <05.图像平移后的解析式:y = a(x-h)2+k(a,k,h是常数,a≠0)平移规则:左加右减,上加下减。
知识点3 用待定系数法求二次函数的解析式:一般式、顶点式、交点式。
(1)已知抛物线上普通的3点的坐标,一般选用一般式;(2)顶点在原点,可设y = ax 2(3)顶点在x轴上,若抛物线与x轴有一个交点,可设y = a(x-h)2;若抛物线与x轴有两个交点,可设y=a(x-x1)(x-x2);(4)顶点在y轴上(或对称轴在y轴上),可设y = ax 2+k;(5)已知顶点(h,k),可设顶点式y = a(x-h)2+k知识点4 二次函数与一元二次方程的关系1. 二次函数与一元二次方程的关系二次函数y=ax2+bx+c(a≠0)的图像与x轴(直线y=0)交点的横坐标就是一元二次方程ax2+bx+c=0的解。
九年级上册数学二次函数知识点汇总
新人教版九年级上二次函数知识点总结知识点一:二次函数的定义 1.二次函数的定义:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数. 其中a 是二次项系数,b 是一次项系数,c 是常数项.知识点二:二次函数的图象与性质⇒⇒抛物线的三要素:开口、对称轴、顶点2. 二次函数()2y a x h k =-+的图象与性质(1)二次函数基本形式2y ax =的图象与性质:a 的绝对值越大,抛物线的开口越小(2)2y ax c =+的图象与性质:上加下减(3)()2y a x h=-的图象与性质:左加右减(4)二次函数()2y a x h k =-+的图象与性质3. 二次函数c bx ax y ++=2的图像与性质(1)当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,. 当2bx a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2b x a=-时,y 有最小值244ac b a-.(2)当0a <时,抛物线开口向下,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,. 当2bx a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2b x a=-时,y 有最大值244ac b a-.4. 二次函数常见方法指导(1)二次函数2y ax bx c =++图象的画法 ①画精确图 五点绘图法(列表-描点-连线)利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.②画草图 抓住以下几点:开口方向,对称轴,与y 轴的交点,顶点. (2)二次函数图象的平移 平移步骤:① 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ② 可以由抛物线2ax 经过适当的平移得到具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位平移规律:概括成八个字“左加右减,上加下减”. (3)用待定系数法求二次函数的解析式 ①一般式:.已知图象上三点或三对、的值,通常选择一般式. ②顶点式:.已知图象的顶点或对称轴,通常选择顶点式.③交点式:.已知图象与轴的交点坐标、,通常选择交点式.(4)求抛物线的顶点、对称轴的方法①公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=,∴顶点是),(a b ac a b 4422--,对称轴是直线abx 2-=. ②配方法:运用配方的方法,将抛物线的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是直线h x =.③运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点. (5)抛物线c bx ax y ++=2中,c b a ,,的作用①a 决定开口方向及开口大小,这与2ax y =中的a 完全一样. ②b 和a 共同决定抛物线对称轴的位置 由于抛物线c bx ax y ++=2的对称轴是直线abx 2-=,故 如果0=b 时,对称轴为y 轴;如果0>ab (即a 、b 同号)时,对称轴在y 轴左侧; 如果0<a b(即a 、b 异号)时,对称轴在y 轴右侧. ③c 的大小决定抛物线c bx ax y ++=2与y 轴交点的位置当0=x 时,c y =,所以抛物线c bx ax y ++=2与y 轴有且只有一个交点(0,c ),故 如果0=c ,抛物线经过原点; 如果0>c ,与y 轴交于正半轴; 如果0<c ,与y 轴交于负半轴.知识点三:二次函数与一元二次方程的关系5.函数c bx ax y ++=2,当0y =时,得到一元二次方程20ax bx c ++=,那么一元二次方程的解就是二次函数的图象与x 轴交点的横坐标,因此二次函数图象与x 轴的交点情况决定一元二次方程根的情况.(1)当二次函数的图象与x 轴有两个交点,这时,则方程有两个不相等实根;(2)当二次函数的图象与x 轴有且只有一个交点,这时,则方程有两个相等实根;(3)当二次函数的图象与x 轴没有交点,这时,则方程没有实根.通过下面表格可以直观地观察到二次函数图象和一元二次方程的关系:的解6.拓展:关于直线与抛物线的交点知识 (1)y 轴与抛物线c bx ax y ++=2得交点为(0,)c .(2)与y 轴平行的直线h x =与抛物线c bx ax y ++=2有且只有一个交点(h ,c bh ah ++2). (3)抛物线与x 轴的交点二次函数c bx ax y ++=2的图像与x 轴的两个交点的横坐标1x 、2x ,是对应一元二次方程02=++c bx ax 的两个实数根.抛物线与x 轴的交点情况可以由对应的一元二次方程的根的判别式判定: ①有两个交点⇔0>∆⇔抛物线与x 轴相交;②有一个交点(顶点在x 轴上)⇔0=∆⇔抛物线与x 轴相切; ③没有交点⇔0<∆⇔抛物线与x 轴相离. (4)平行于x 轴的直线与抛物线的交点同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为k ,则横坐标是k c bx ax =++2的两个实数根.(5)一次函数()0≠+=k n kx y 的图像l 与二次函数()02≠++=a c bx ax y 的图像G的交点,由方程组2y kx ny ax bx c=+⎧⎨=++⎩的解的数目来确定: ①方程组有两组不同的解时⇔l 与G 有两个交点; ②方程组只有一组解时⇔l 与G 只有一个交点; ③方程组无解时⇔l 与G 没有交点.(6)抛物线与x 轴两交点之间的距离:若抛物线c bx ax y ++=2与x 轴两交点为()()0021,,,x B x A ,由于1x 、2x 是方程02=++c bx ax 的两个根,故 acx x a b x x =⋅-=+2121,()()a a acb ac a b x x x x x x x x AB ∆=-=-⎪⎭⎫ ⎝⎛-=-+=-=-=444222122122121知识点四:利用二次函数解决实际问题7.利用二次函数解决实际问题,要建立数学模型,即把实际问题转化为二次函数问题,利用题中存在的公式、内含的规律等相等关系,建立函数关系式,再利用函数的图象及性质去研究问题.在研究实际问题时要注意自变量的取值范围应具有实际意义.利用二次函数解决实际问题的一般步骤是: (1)建立适当的平面直角坐标系;(2)把实际问题中的一些数据与点的坐标联系起来; (3)用待定系数法求出抛物线的关系式;(4)利用二次函数的图象及其性质去分析问题、解决问题.。
人教版初三数学二次函数知识点总结
初三數學二次函數知識點總結一、二次函數概念:1.二次函數的概念:一般地,形如2=++(a b cy ax bx ca≠)的函數,,,是常數,0叫做二次函數。
這裡需要強調:和一元二次方程類似,二次項係數a≠,而b c,可以為零.二次函數的定義域是全體實數.2. 二次函數2=++的結構特徵:y ax bx c⑴等號左邊是函數,右邊是關於引數x的二次式,x的最高次數是2.⑵a b c,,是常數,a是二次項係數,b是一次項係數,c是常數項.二、二次函數的基本形式1. 二次函數基本形式:2=的性質:y axa 的絕對值越大,抛物線的開口越小。
Array2.2y ax c=+的性質:上加下減。
3.()2y a x h =-的性質:左加右減。
4.()2y a x h k=-+的性質:三、二次函數圖像的平移 1. 平移步驟:方法一:⑴ 將抛物線解析式轉化成頂點式()2y a x h k =-+,確定其頂點座標()h k ,;⑵ 保持抛物線2y ax =的形狀不變,將其頂點平移到()h k ,處,具體平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移規律在原有函數的基礎上“h 值正右移,負左移;k 值正上移,負下移”. 概括成八個字“左加右減,上加下減”. 方法二:⑴c bx ax y ++=2沿y 軸平移:向上(下)平移m 個單位,c bx ax y ++=2變成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿軸平移:向左(右)平移m 個單位,c bx ax y ++=2變成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)四、二次函數()2y a x h k =-+與2y ax bx c =++的比較從解析式上看,()2y a x h k =-+與2y ax bx c =++是兩種不同的表達形式,後者通過配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭,其中2424b ac b h k a a-=-=,.五、二次函數2y ax bx c =++圖像的畫法五點繪圖法:利用配方法將二次函數2y ax bx c =++化為頂點式2()y a x h k =-+,確定其開口方向、對稱軸及頂點座標,然後在對稱軸兩側,左右對稱地描點畫圖.一般我們選取的五點為:頂點、與y 軸的交點()0c ,、以及()0c ,關於對稱軸對稱的點()2h c ,、與x 軸的交點()10x ,,()20x ,(若與x 軸沒有交點,則取兩組關於對稱軸對稱的點).畫草圖時應抓住以下幾點:開口方向,對稱軸,頂點,與x 軸的交點,與y 軸的交點.六、二次函數2y ax bx c =++的性質1. 當0a >時,抛物線開口向上,對稱軸為2bx a =-,頂點座標為2424b ac b a a ⎛⎫-- ⎪⎝⎭,. 當2bx a <-時,y 隨x 的增大而減小;當2b x a >-時,y 隨x 的增大而增大;當2b x a=-時,y 有最小值244ac b a-.2. 當0a <時,抛物線開口向下,對稱軸為2bx a =-,頂點座標為2424b ac b a a ⎛⎫-- ⎪⎝⎭,.當2bx a <-時,y 隨x 的增大而增大;當2b x a >-時,y 隨x 的增大而減小;當2b x a=-時,y 有最大值244ac b a-.七、二次函數解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 為常數,0a ≠);2. 頂點式:2()y a x h k =-+(a ,h ,k 為常數,0a ≠);3. 兩根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物線與x 軸兩交點的橫坐標). 注意:任何二次函數的解析式都可以化成一般式或頂點式,但並非所有的二次函數都可以寫成交點式,只有抛物線與x 軸有交點,即240b ac -≥時,抛物線的解析式才可以用交點式表示.二次函數解析式的這三種形式可以互化.八、二次函數的圖像與各項係數之間的關係 1. 二次項係數a二次函數2y ax bx c =++中,a 作為二次項係數,顯然0a ≠.⑴ 當0a >時,抛物線開口向上,a 的值越大,開口越小,反之a 的值越小,開口越大;⑵ 當0a <時,抛物線開口向下,a 的值越小,開口越小,反之a 的值越大,開口越大.總結起來,a 決定了抛物線開口的大小和方向,a 的正負決定開口方向,a的大小決定開口的大小. 2. 一次項係數b在二次項係數a 確定的前提下,b 決定了抛物線的對稱軸. ⑴ 在0a >的前提下,當0b >時,02ba-<,即抛物線的對稱軸在y 軸左側; 當0b =時,02ba-=,即抛物線的對稱軸就是y 軸; 當0b <時,02ba->,即抛物線對稱軸在y 軸的右側. ⑵ 在0a <的前提下,結論剛好與上述相反,即當0b >時,02ba->,即抛物線的對稱軸在y 軸右側; 當0b =時,02ba-=,即抛物線的對稱軸就是y 軸; 當0b <時,02ba-<,即抛物線對稱軸在y 軸的左側. 總結起來,在a 確定的前提下,b 決定了抛物線對稱軸的位置.ab 的符號的判定:對稱軸abx 2-=在y 軸左邊則0>ab ,在y 軸的右側則0<ab ,概括的說就是“左同右異”總結: 3. 常數項c⑴ 當0c >時,抛物線與y 軸的交點在x 軸上方,即抛物線與y 軸交點的縱坐標為正;⑵ 當0c =時,抛物線與y 軸的交點為座標原點,即抛物線與y 軸交點的縱坐標為0;⑶ 當0c <時,抛物線與y 軸的交點在x 軸下方,即抛物線與y 軸交點的縱坐標為負.總結起來,c 決定了抛物線與y 軸交點的位置.總之,只要a b c ,,都確定,那麼這條抛物線就是唯一確定的.二次函數解析式的確定:根據已知條件確定二次函數解析式,通常利用待定係數法.用待定係數法求二次函數的解析式必須根據題目的特點,選擇適當的形式,才能使解題簡便.一般來說,有如下幾種情況:1. 已知抛物線上三點的座標,一般選用一般式;2. 已知抛物線頂點或對稱軸或最大(小)值,一般選用頂點式;3. 已知抛物線與x 軸的兩個交點的橫坐標,一般選用兩根式;4. 已知抛物線上縱坐標相同的兩點,常選用頂點式.九、二次函數圖像的對稱二次函數圖像的對稱一般有五種情況,可以用一般式或頂點式表達 1. 關於x 軸對稱2y ax bx c =++關於x 軸對稱後,得到的解析式是2y ax bx c =---; ()2y a x h k=-+關於x 軸對稱後,得到的解析式是()2y a x h k =---;2. 關於y 軸對稱2y ax bx c =++關於y 軸對稱後,得到的解析式是2y ax bx c =-+; ()2y a x h k =-+關於y 軸對稱後,得到的解析式是()2y a x h k =++;3. 關於原點對稱 2y ax bx c =++關於原點對稱後,得到的解析式是2y ax bx c =-+-;()2y a x h k =-+關於原點對稱後,得到的解析式是()2y a x h k=-+-;4. 關於頂點對稱(即:抛物線繞頂點旋轉180°)2y ax bx c =++關於頂點對稱後,得到的解析式是222b y ax bx c a=--+-;()2y a x h k=-+關於頂點對稱後,得到的解析式是()2y a x h k =--+.5. 關於點()m n ,對稱()2y a x h k=-+關於點()m n ,對稱後,得到的解析式是()222y a x h m n k =-+-+-根據對稱的性質,顯然無論作何種對稱變換,抛物線的形狀一定不會發生變化,因此a 永遠不變.求抛物線的對稱抛物線的運算式時,可以依據題意或方便運算的原則,選擇合適的形式,習慣上是先確定原抛物線(或運算式已知的抛物線)的頂點座標及開口方向,再確定其對稱抛物線的頂點座標及開口方向,然後再寫出其對稱抛物線的運算式.十、二次函數與一元二次方程:1. 二次函數與一元二次方程的關係(二次函數與x 軸交點情況):一元二次方程20ax bx c ++=是二次函數2y ax bx c =++當函數值0y =時的特殊情況. 圖像與x 軸的交點個數:① 當240b ac ∆=->時,圖像與x 軸交於兩點()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的兩根.這兩點間的距離21AB x x =-=.② 當0∆=時,圖像與x 軸只有一個交點; ③ 當0∆<時,圖像與x 軸沒有交點.1' 當0a >時,圖像落在x 軸的上方,無論x 為任何實數,都有0y >; 2' 當0a <時,圖像落在x 軸的下方,無論x 為任何實數,都有0y <.2. 抛物線2y ax bx c =++的圖像與y 軸一定相交,交點座標為(0,)c ;3. 二次函數常用解題方法總結:⑴ 求二次函數的圖像與x 軸的交點座標,需轉化為一元二次方程; ⑵ 求二次函數的最大(小)值需要利用配方法將二次函數由一般式轉化為頂點式;⑶ 根據圖像的位置判斷二次函數2y ax bx c =++中a ,b ,c 的符號,或由二次函數中a ,b ,c 的符號判斷圖像的位置,要數形結合;⑷ 二次函數的圖像關於對稱軸對稱,可利用這一性質,求和已知一點對稱的點座標,或已知與x 軸的一個交點座標,可由對稱性求出另一個交點座標.⑸ 與二次函數有關的還有二次三項式,二次三項式2(0)ax bx c a ++≠本身就是所含字母x 的二次函數;下麵以0a >時為例,揭示二次函數、二次三項式和一元二次方程之間的內在聯繫:二次函數圖像參考:y=3(x+4)22y=3x 2十一、函數的應用二次函數應用⎧⎪⎨⎪⎩刹车距离何时获得最大利润最大面积是多少二次函數考查重點與常見題型1. 考查二次函數的定義、性質,有關試題常出現在選擇題中,如:已知以x 為引數的二次函數2)2(22--+-=m m x m y 的圖像經過原點, 則m 的值是2. 綜合考查正比例、反比例、一次函數、二次函數的圖像,習題的特點是在同一直角坐標系內考查兩個函數的圖像,試題類型為選擇題,如: 如圖,如果函數b kx y +=的圖像在第一、二、三象限內,那麼函數12-+=bx kx y 的圖像大致是( )y y y 0 x o-1 x 0 0 -1 x A B C D3. 考查用待定係數法求二次函數的解析式,有關習題出現的頻率很高,習題類型有中檔解答題和選拔性的綜合題,如:已知一條抛物線經過(0,3),(4,6)兩點,對稱軸為35=x ,求這條抛物線的解析式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学二次函数知识点总结二次项系数a决定二次函数图像的开口方向和大小.当a>0时,二次函数图像向上开口;当a<0时,抛物线向下开口.|a|越大,则二次函数图像的开口越小.1、决定对称轴位置的因素一次项系数b和二次项系数a共同决定对称轴的位置.当a与b同号时(即ab>0),对称轴在y轴左;因为对称轴在左边则对称轴小于0,也就是- b/2a0,所以b/2a要小于0,所以a、b要异号?可简单记忆为左同右异,即当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab< 0 ),对称轴在y轴右.事实上,b有其自身的几何意义:二次函数图像与y轴的交点处的该二次函数图像切线的函数解析式(一次函数)的斜率k的值.可通过对二次函数求导得到.2、决定二次函数图像与y轴交点的因素常数项c决定二次函数图像与y轴交点.二次函数图像与y轴交于(0,c)一、二次函数概念:1.二次函数的概念:一般地,形如2=++(a b cy ax bx c,,是常数,0a≠)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数a≠,而b c,可以为零.二次函数的定义域是全体实数.2. 二次函数2=++的结构特征:y ax bx c⑴等号左边是函数,右边是关于自变量x的二次式,x的最高次数是2.⑵a b c,,是常数,a是二次项系数,b是一次项系数,c是常数项.二、二次函数的基本形式1. 二次函数基本形式:2=的性质:y axa 的绝对Array值越大,抛物线的开口越小。
2.2y ax c=+的性质:上加下减。
)2h-4.()2y a x h k=-+的性质:三、二次函数图象的平移 1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,;⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭,其中2424b ac b h k a a-=-=,.五、二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,. 当2bx a <-时,y 随x 的增大而减小;当2b x a>-时,y 随x 的增大而增大; 当2bx a=-时,y 有最小值244ac b a -.2. 当0a <时,抛物线开口向下,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,. 当2bx a <-时,y 随x 的增大而增大;当2b x a>-时,y 随x 的增大而减小; 当2bx a=-时,y 有最大值244ac b a -.七、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a 二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小.2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02ba-<,即抛物线的对称轴在y 轴左侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba->,即抛物线对称轴在y 轴的右侧. ⑵ 在0a <的前提下,结论刚好与上述相反,即 当0b >时,02ba->,即抛物线的对称轴在y 轴右侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧. 总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异”总结: 3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0;⑶当0c<时,抛物线与y轴的交点在x轴下方,即抛物线与y轴交点的纵坐标为负.总结起来,c决定了抛物线与y轴交点的位置.总之,只要a b c,,都确定,那么这条抛物线就是唯一确定的.二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式.九、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达1. 关于x轴对称2=---;y ax bx cy ax bx c=++关于x轴对称后,得到的解析式是2()2=---;y a x h ky a x h k=-+关于x轴对称后,得到的解析式是()22. 关于y轴对称2=-+;y ax bx cy ax bx c=++关于y轴对称后,得到的解析式是2()2y a x h k=++;y a x h k=-+关于y轴对称后,得到的解析式是()23. 关于原点对称2=-+-;y ax bx cy ax bx c=++关于原点对称后,得到的解析式是2()2=-+-;y a x h ky a x h k=-+关于原点对称后,得到的解析式是()24. 关于顶点对称(即:抛物线绕顶点旋转180°)2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k=-+关于顶点对称后,得到的解析式是()2y a x h k =--+.5. 关于点()m n ,对称()2y a x h k=-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式. 十、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的距离21AB x x =-=.② 当0∆=时,图象与x 轴只有一个交点; ③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2'当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;3. 二次函数常用解题方法总结:⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a ,b ,c 的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式,二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数;下面以0a >时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:二次函数图像参考:十一、函数的应用二次函数应用⎧⎪⎨⎪⎩刹车距离何时获得最大利润最大面积是多少二次函数考查重点与常见题型1、考查二次函数的定义、性质,有关试题常出现在选择题中,如:2-32y=-2x 2y=-2(x-3)已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点, 则m 的值是2、综合考查正比例、反比例、一次函数、二次函数的图像,习题的特点是在同一直角坐标系内考查两个函数的图像,试题类型为选择题,如:如图,如果函数b kx y +=的图像在第一、二、三象限内,那么函数12-+=bx kx y 的图像大致是( )1、考查用待定系数法求二次函数的解析式,有关习题出现的频率很高,习题类型有中档解答题和选拔性的综合题,如:已知一条抛物线经过(0,3),(4,6)两点,对称轴为35=x ,求这条抛物线的解析式。
