正弦电磁场复数表示法解读
合集下载
电工基础 第三节 正弦量的复数表示法

复习巩固
则为
设 Z1= a + jb =|Z1|/ ,Z2 = c + jd = |Z2|/ ,复数的运算规
1.加减法 2.乘法 3.除法 4.乘方
Z1 Z2 = (a c) + j(b d) Z1 · Z2 = |Z1| · |Z2|/ +
Z1 Z1 / Z2 Z2
初相 u = 30,所以它的相量为
= U/u = 220/30 V U
(2) 正弦电流 I 的有效值为 I = 0.7071 4.24 = 3 A,初相 i = 45,所以它的相量为 = I/ = 3/45 A I
i
例2: 将 u1、u2 用相量表示
u1 220 2 sin(ω t 20 ) V
④相量的两种表示形式
Ue jψ U ψ U ( cos ψ jsinψ) 相量式: U 相量图: 把相量表示在复平面的图形
可不画坐标轴
I
U
⑤相量的书写方式 、 I 模用最大值表示 ,则用符号:U m m
பைடு நூலகம்
、 I 实际应用中,模多采用有效值,符号:U
u2 110 2 sin(ω t 45) V
解: (1) 相量式
+j
U 2
U 1
+1
220 20V U 1 110 45 V U 2
(2) 相量图
落后于U U 2 1
U 2
45 20
超前 落后 U 1 ?
【例3】 把下列正弦相量用三角函数的瞬时值表达示,设角频
n Z1 Z1 n
/n
新课教学
第三节 正弦量的复数表示法
则为
设 Z1= a + jb =|Z1|/ ,Z2 = c + jd = |Z2|/ ,复数的运算规
1.加减法 2.乘法 3.除法 4.乘方
Z1 Z2 = (a c) + j(b d) Z1 · Z2 = |Z1| · |Z2|/ +
Z1 Z1 / Z2 Z2
初相 u = 30,所以它的相量为
= U/u = 220/30 V U
(2) 正弦电流 I 的有效值为 I = 0.7071 4.24 = 3 A,初相 i = 45,所以它的相量为 = I/ = 3/45 A I
i
例2: 将 u1、u2 用相量表示
u1 220 2 sin(ω t 20 ) V
④相量的两种表示形式
Ue jψ U ψ U ( cos ψ jsinψ) 相量式: U 相量图: 把相量表示在复平面的图形
可不画坐标轴
I
U
⑤相量的书写方式 、 I 模用最大值表示 ,则用符号:U m m
பைடு நூலகம்
、 I 实际应用中,模多采用有效值,符号:U
u2 110 2 sin(ω t 45) V
解: (1) 相量式
+j
U 2
U 1
+1
220 20V U 1 110 45 V U 2
(2) 相量图
落后于U U 2 1
U 2
45 20
超前 落后 U 1 ?
【例3】 把下列正弦相量用三角函数的瞬时值表达示,设角频
n Z1 Z1 n
/n
新课教学
第三节 正弦量的复数表示法
正弦电磁场复数表示法

j Dv&e jt
0
Re
Hv& Jv&
j
Dv&
e
jt
0
故当t为任意时 Hv& Jv& jDv&
5
麦氏方程组微分形式
麦氏方程组复数形式
v H
v E v
v J
v D
vt
B
t
B 0
v D
Hv& Jv& j Dv&
Ev&
j
Bv&
Bv&
0
Dv&
&
vv v
H J j D
Re
v S
复坡印廷矢量定义:复功率流密度矢量。其实部为平
均功率流密度(有功功率密度),虚部为无功功率
v S
1
v E
v H*
2
注意:式中的电磁场强度是复振幅值而不是有效值 9
同理可得:
e (t)
m (t)
1
v D(t
)
2பைடு நூலகம்
1
v B(t
)
2
v E(t)
1 4
Re
v E
v D*
v H(t)
1 4
E t
v
Re
j
Ev&e
j t
Re v
B t
&e jt
Re
j
Bv&e
j t
以瞬时形式
v H
v J
D
为例,推导其复数形式
t
Re
Hv&e
j t
Re
Jv&e
j t
正弦电磁场

1 正弦电磁场的复数形式; 2 坡印亭定理的复数形式; 3 达朗贝尔方程及特解的复数形式.
dV
e jR —表示场点变化滞后于源点变化的相位差为 R 。
三、 达朗贝尔方程及其解的复数形式
在正弦电磁场,电场 E 、磁场 B 与动态位A 、 的关系
B A
A
E t
A
t
0
B A
E j A
j A ( A) j
A j 0
即只要求出 A ,就可计算出电场和磁场。
重要知识点
正弦电磁场
电工基础教研室 周学
➢ 本节的研究目的
了解正弦电磁场、坡印亭定理、达朗贝尔 方程及其特解的复数形式。
➢ 本节的研究内容
一、正弦电磁场的复数形式 二、坡印亭定理的复数形式
三、达朗贝尔方程及其特解的复数形式
一、 正弦电磁场的复数形式
以一定频率做正弦变化的场,称为正弦电磁场。
研究时变电磁场的意义: 一般情况下,非正弦变化的时变场可以应用傅里叶
正弦变化的电场强度对时间的微分可表示为:
E(x, y, z;t) Re[ jE(x, y, z) 2ejt ]
t
H
E
JC
B t
D t
B
0
D f
H J jD
E
C
jB
B
D
0
f
二、 坡印亭定理的复数形式
坡印亭定理复数形式
E
H*
H*
E
HE*(J(C*jjB)D*
级数将它分解成稳态场和频率分量各不相同的正弦电 磁 场,来分别加以研究。
在直角坐标系中,正弦变化的电场强度的一般形式为
E(x, y, z;t) Exm (x, y, z) cos(t x )ex Eym (x, y, z) cos(t y )ey Ezm (x, y, z) cos(t z )ez
dV
e jR —表示场点变化滞后于源点变化的相位差为 R 。
三、 达朗贝尔方程及其解的复数形式
在正弦电磁场,电场 E 、磁场 B 与动态位A 、 的关系
B A
A
E t
A
t
0
B A
E j A
j A ( A) j
A j 0
即只要求出 A ,就可计算出电场和磁场。
重要知识点
正弦电磁场
电工基础教研室 周学
➢ 本节的研究目的
了解正弦电磁场、坡印亭定理、达朗贝尔 方程及其特解的复数形式。
➢ 本节的研究内容
一、正弦电磁场的复数形式 二、坡印亭定理的复数形式
三、达朗贝尔方程及其特解的复数形式
一、 正弦电磁场的复数形式
以一定频率做正弦变化的场,称为正弦电磁场。
研究时变电磁场的意义: 一般情况下,非正弦变化的时变场可以应用傅里叶
正弦变化的电场强度对时间的微分可表示为:
E(x, y, z;t) Re[ jE(x, y, z) 2ejt ]
t
H
E
JC
B t
D t
B
0
D f
H J jD
E
C
jB
B
D
0
f
二、 坡印亭定理的复数形式
坡印亭定理复数形式
E
H*
H*
E
HE*(J(C*jjB)D*
级数将它分解成稳态场和频率分量各不相同的正弦电 磁 场,来分别加以研究。
在直角坐标系中,正弦变化的电场强度的一般形式为
E(x, y, z;t) Exm (x, y, z) cos(t x )ex Eym (x, y, z) cos(t y )ey Ezm (x, y, z) cos(t z )ez
电工电子技术基础知识点详解2-1-正弦量的相量表示法(1)
电压的有效值相量
注意:
(1) 相量只是表示正弦量,而不等于正弦量,两者只有对应关系。
? i Imsin(ωt ψ) = Imejψ Im ψ
正弦量是时间的函数,而相量仅仅是表示正弦量的复数,两者不 能划等号!
(2) 只有正弦周期量才能用相量表示,非正弦量不能用相量表示。 因此,只有表示正弦量的复数才能称之为相量。
三角式
r a2 b2b ψ arctan
复数的模 复数的辐角
a
A r cos ψ j r sin ψ r (cos ψ jsin ψ)
2. 正弦量的相量表示 实质:用复数表示正弦量。
+j
b
A
r
(1) 复数表示形式
O
a +1
由欧拉公式:
ej ψ ej ψ
cos ψ
,
2
可得: ej ψ cosψ jsin ψ
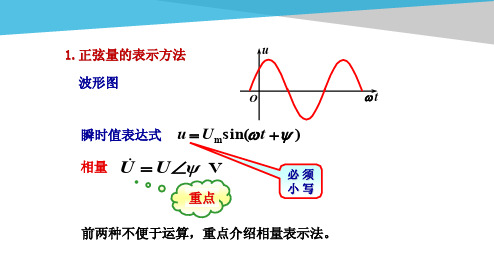
1.正弦量的表示方法
u
波形图
O
t
瞬时值表达式 u Umsin( t )
相量 U Uψ V
必须
重点
小写
前两种不便于运算,重点介绍相量表示法。
正弦量的相量表示法
2. 正弦量的相量表示 实质:用复数表示正弦量 (1) 复数表示形式
设A为复数
代数式 A =a + jb
+j b
r
O
A a +1
式中: a r cos ψ b r sinψ
正弦量的相量表示法
3. 相量的两种表示形式
相量式: U Uejψ Uψ U(cos ψ jsin ψ)
相量图: 把相量在复平面中用有向线段表示出来
U1 220 20V U2 110 45V
正弦量的复数表示法

新课讲授
教后记
教学程序
教学内容
教学方法与
教学手段
一、正弦量的复数表示法
正弦交流电的解析式和复数之间的对应关系可表示为 Nhomakorabea1、电压
u= Usin(ωt+φu0)
=U∠φu0
2、电流
i= Isin(ωt+φi0)
=I∠φi0
例如:
u=220 sin(ωt+30°)V,i=5 sin(ωt-60°)A
将它们表示成有效值的相量式为
二、复数形式的欧姆定律
1、复数形式的欧姆定律
2、电阻、感抗和容抗的复数表示
教学程序
教学内容
教学方法与
教学手段
Ⅰ
Ⅱ
Ⅲ
课前复习
(作业讲评)
新课导入
由于正弦量可以用矢量表示,而复数也可以用矢量表示。因此正弦量也可以用复数表示。确切地说,正弦量和复数之间存在着对应关系,应用这种对应关系,就可以用复数的模表示正弦电压或电流的有效值,用辐角表示正弦电压或电流的初相角。这种与正弦电压(或电流)相对应的复数电压(或电流)称为相量。电压相量和电流相量分别以和表示。
所以,电阻R的复数仍为R,感抗的复数表示为jXL,容抗的复数表示为-jXC。
课堂小结
复阻抗是阻抗的一种新的表达形式,它既能把电压和电流间的相位关系表示出来,又能把电路参数R、XL和XC表示出来。引人复阻抗的概念,得到复数形式的欧姆定律,它既表示出电压和电流有效值间的关系,又给出了它们之间的相位关系。
布置作业
教后记
举例讲解
板书作图
例题1
教后记
教学程序
教学内容
教学方法与
教学手段
解:i1和i2分别用相量表示为
教后记
教学程序
教学内容
教学方法与
教学手段
一、正弦量的复数表示法
正弦交流电的解析式和复数之间的对应关系可表示为 Nhomakorabea1、电压
u= Usin(ωt+φu0)
=U∠φu0
2、电流
i= Isin(ωt+φi0)
=I∠φi0
例如:
u=220 sin(ωt+30°)V,i=5 sin(ωt-60°)A
将它们表示成有效值的相量式为
二、复数形式的欧姆定律
1、复数形式的欧姆定律
2、电阻、感抗和容抗的复数表示
教学程序
教学内容
教学方法与
教学手段
Ⅰ
Ⅱ
Ⅲ
课前复习
(作业讲评)
新课导入
由于正弦量可以用矢量表示,而复数也可以用矢量表示。因此正弦量也可以用复数表示。确切地说,正弦量和复数之间存在着对应关系,应用这种对应关系,就可以用复数的模表示正弦电压或电流的有效值,用辐角表示正弦电压或电流的初相角。这种与正弦电压(或电流)相对应的复数电压(或电流)称为相量。电压相量和电流相量分别以和表示。
所以,电阻R的复数仍为R,感抗的复数表示为jXL,容抗的复数表示为-jXC。
课堂小结
复阻抗是阻抗的一种新的表达形式,它既能把电压和电流间的相位关系表示出来,又能把电路参数R、XL和XC表示出来。引人复阻抗的概念,得到复数形式的欧姆定律,它既表示出电压和电流有效值间的关系,又给出了它们之间的相位关系。
布置作业
教后记
举例讲解
板书作图
例题1
教后记
教学程序
教学内容
教学方法与
教学手段
解:i1和i2分别用相量表示为
正弦量的相量表示法

小结:
❖ 正弦量能够用相量表达,正弦量也能够用复数 表达。
❖ 正弦量旳相量旳幅角等于正弦量旳初相角, 相 量旳模等于正弦量旳最大值或有效值。
❖ 为了使计算成果能直接表达正弦量旳有效值, 一般使相量旳模等于正弦量旳有效值,即能够 表达为: U Ue j U
❖ 将几种同频率旳正弦量用相应旳相量表达并画 在同一种坐标平面上,这么旳图叫做相量图。
❖ 在同一量图中,以t=0时刻旳相量表达正弦量。
作业:
❖ 课后复习本节内容。 ❖ 预习下一节“交流电路基本元件”。
谢谢,再见!
2023年9月
( 4 ) 正弦量旳瞬时值=相量虚部
u U
例1: 已知 i1 10 2sin t 30A
+j
试i2 写 5出I21s和inI2旳t 体 6现0式A,并
画出其向量图。
I1 解: i1 和 i2 相应旳电流向量
30
体现式分别为
0 -60
+1
I1 1030 A
I2
I2 5 60A
I1旳长度是I2旳二倍。
例2:
已知 A1 10 j5,A2 3 j4
求
A1 A2 和
A1 A2
。
解: A1 10 j5 11.1826.57
A2 3 j4 553.13
A1 A2 11.1826.57 553.13
55.9079.70
A1 A2
11.1826.57 553.13
2.236 26.56
这么,表达正弦电压 u Umsin t
旳相量为
U m Ume j Um
为了使计算成果能直接表达正弦量旳有 效值,一般使相量旳模等于正弦量旳有效 值,即能够表达为:
正弦电磁场复数表示法

jt jt jt R e H e R e J e R e D e t
j t j t j t 由 E R e E e D R e D e H R e H e
麦克斯韦方程的复数形式
1 * 1 j 2 t S ( t ) R e E H R e E H e 2 2
1 * 1 j 2 t S ( t ) R e E H R e E H e 2 2
坡印廷矢量即瞬时电磁功率流密度,未指 定电场强度和磁场强度随时间的变化规律
j t j t j t R e H e R e J e R e j D e 故当t为任意时 jt jt jt R e H e J e jD e 0 HJ j D jt R e H JjD e 0
B E t B 0 D
均匀无耗媒质中无源区域波动方程的推导:
B E t
E ( H ) t 2 E 2 ( E ) E 2 t
D t
2 E 2 ( E ) E 2 t 2 无源区电场 E 2 E 2 0 波动方程 t
时变电磁场中的位函数
静态场中:
A B A 0
库仑规范
洛仑兹规范
位函数的 波动方程
2 A J 0
磁矢位的泊松方程
时变场中,复数形式:
2 2
k 2A k2A J
A B Aj
由电流连续性方程,可得
j t j t j t 由 E R e E e D R e D e H R e H e
麦克斯韦方程的复数形式
1 * 1 j 2 t S ( t ) R e E H R e E H e 2 2
1 * 1 j 2 t S ( t ) R e E H R e E H e 2 2
坡印廷矢量即瞬时电磁功率流密度,未指 定电场强度和磁场强度随时间的变化规律
j t j t j t R e H e R e J e R e j D e 故当t为任意时 jt jt jt R e H e J e jD e 0 HJ j D jt R e H JjD e 0
B E t B 0 D
均匀无耗媒质中无源区域波动方程的推导:
B E t
E ( H ) t 2 E 2 ( E ) E 2 t
D t
2 E 2 ( E ) E 2 t 2 无源区电场 E 2 E 2 0 波动方程 t
时变电磁场中的位函数
静态场中:
A B A 0
库仑规范
洛仑兹规范
位函数的 波动方程
2 A J 0
磁矢位的泊松方程
时变场中,复数形式:
2 2
k 2A k2A J
A B Aj
由电流连续性方程,可得
复数三角公式

复数三角公式是复数在三角函数中的应用,主要包括以下几种:
1. 欧拉公式:e^(ix) = cosx + isinx。
这个公式将复数、指数、三角函数联系在一起,是复数理论的基础。
2. 复数的正弦和余弦:sin(z) = (e^(iz) - e^(-iz)) / (2i),cos(z) = (e^(iz) + e^(-iz)) / 2。
这两个公式将复数与三角函数联系起来,使得复数可以表示为极坐标形式。
3. 复数的正切和余切:tan(z) = sin(z) / cos(z),cot(z) = 1 / tan(z)。
这两个公式将复数与三角函数的倒数联系起来。
4. 复数的正割和余割:sec(z) = 1 / cos(z),csc(z) = 1 / sin(z)。
这两个公式将复数与三角函数的倒数联系起来。
5. 复数的反正弦和反余弦:asin(z) = sin(z) / sqrt(1 - sin^2(z)),acos(z) = cos(z) / sqrt(1 - cos^2(z))。
这两个公式将复数与三角函数的反函数联系起来。
6. 复数的反余弦和反正弦:acosh(z) = (e^z + e^-z) / 2,acosh(z) = (e^z - e^-z) / 2。
这两个公式将复数与双曲三角函数的反函数联系起来。
