晶体学基础 3
合集下载
晶体学基础第三章-晶体的定向和晶体学符号

晶体定向的几个基本概念:
(1)结晶轴:晶体坐标系中的坐标轴,需满足晶体对称性 特征。用x轴、y轴、z轴或X轴、Y轴、Z轴表示。 (2)轴角:两个结晶轴正向之夹角。用a,b,g 表示。
(3)轴单位:晶体坐标系中结晶轴的长度单位。是相应 晶体点阵中平行于晶轴的行列上相邻节点间距。用a, b, c分 别表示x轴位之连比。用a:b:c 表示。
(5)晶体几何常数:轴率a:b:c和轴角a,b,g的合称。表 示晶体坐标系特征的一组参数,用以区分不同的晶系。
第三章 晶体的定向和晶体学符号
➢ 晶体学坐标系 ➢ 各晶系的定向方法 ➢ 晶胞与原子坐标 ➢ 晶面指数 ➢ 晶向指数 ➢ 晶带指数
3.1 晶体学坐标系
晶体定向的目的:
建立坐标系,简单明确地描述晶体中晶面、晶列的 空间方位。为研究晶体的结构特性提供定量标记。
晶体的定向:
在晶体中设置符合晶体对称特征或与晶体点阵参数 一致的坐标系,并将晶体按相应的空间取向关系进行安 置。
《结晶学基础》
在离子晶体结构中,每个正离子周围都形成 一个负离子配位多面体;正负离子间距离取决 于离子半径之和,正离子配位数取决于正负离 子半径之比,与离子电价无关。
.
2.鲍林第二规则---静电价规则
在一个稳定的晶体结构中,从所有相邻接的阳离 子到达一个阴离子的静电键的总强度,等于阴离子 的电荷数。
静电键强度
S= Z+ CN+
• 在离子晶体中,配位数指的是最紧邻的异号离子数,所以正、 负离子的配位数不一定是相等的。阳离子一般处于阴离子紧密堆 积阳的离空子隙还中可,能其出配现位其数 它一 的般 配为 位数4或。6. 。如果阴离子不作紧密堆积,
配位数
阴离子作正八 面体堆积,正、 负离子彼此都能 相互接触的必要
条件为r+/r=0.414。
凸几何多面体倾向。
❖ 4.对称性--晶体的物理化学性质能够在不同方
向或位置上有规律地出现,也称周期性 .
晶体的性质
❖ 5.均匀性(均一性)--一个晶体的各个部分性
质都是一样的。 这里注意:均匀性与各向异性不同,前者是指晶
体的位置,后者是指观察晶体的方向。
❖ 6. 固定熔点 ❖ 7.晶面角守恒定律--晶面(或晶棱)间的夹角
宏观晶体中对称性只有32种,根据对称型中是否存在 高次轴及数目对晶体分类
❖ 存在高次轴(n>2)且多于一个―――高级晶族 ――包括:等轴(立方)晶系
❖ 存在高次轴(n>2)且只有一个―――中级晶族 ――包括:三方、四方、六方晶系
❖ 不存在高次轴(n>2)―――低级晶族――包括: 三斜、单斜、正交晶系
第一章 结晶学基础
.
1-1 晶体的基本概念与性质
一、晶体的基本概念
➢ 人们对晶体的认识,是从石英开始的。 ➢ 人们把外形上具有规则的几何多面体形态的
.
2.鲍林第二规则---静电价规则
在一个稳定的晶体结构中,从所有相邻接的阳离 子到达一个阴离子的静电键的总强度,等于阴离子 的电荷数。
静电键强度
S= Z+ CN+
• 在离子晶体中,配位数指的是最紧邻的异号离子数,所以正、 负离子的配位数不一定是相等的。阳离子一般处于阴离子紧密堆 积阳的离空子隙还中可,能其出配现位其数 它一 的般 配为 位数4或。6. 。如果阴离子不作紧密堆积,
配位数
阴离子作正八 面体堆积,正、 负离子彼此都能 相互接触的必要
条件为r+/r=0.414。
凸几何多面体倾向。
❖ 4.对称性--晶体的物理化学性质能够在不同方
向或位置上有规律地出现,也称周期性 .
晶体的性质
❖ 5.均匀性(均一性)--一个晶体的各个部分性
质都是一样的。 这里注意:均匀性与各向异性不同,前者是指晶
体的位置,后者是指观察晶体的方向。
❖ 6. 固定熔点 ❖ 7.晶面角守恒定律--晶面(或晶棱)间的夹角
宏观晶体中对称性只有32种,根据对称型中是否存在 高次轴及数目对晶体分类
❖ 存在高次轴(n>2)且多于一个―――高级晶族 ――包括:等轴(立方)晶系
❖ 存在高次轴(n>2)且只有一个―――中级晶族 ――包括:三方、四方、六方晶系
❖ 不存在高次轴(n>2)―――低级晶族――包括: 三斜、单斜、正交晶系
第一章 结晶学基础
.
1-1 晶体的基本概念与性质
一、晶体的基本概念
➢ 人们对晶体的认识,是从石英开始的。 ➢ 人们把外形上具有规则的几何多面体形态的
(完整版)1《材料科学基础》第一章晶体学基础

一、晶向指数 二、晶面指数 三、六方晶系的晶向指数和晶面指数 四、晶带 五、晶面间距
晶向、晶
钯的PDF卡片-----Pd 89-4897
crystal system,space
图 2 CdS纳米棒的TEM照片(左)和 HRTEM照片(右)
图2 选区电子衍射图
图1. La(Sr)3SrMnO7的低 温电子衍射图
晶向、晶面、晶面间距
晶向:空间点阵中行列的方向代表晶体中原子排 列的方向,称为晶向。
晶面:通过空间点阵中任意一组结点的平面代表 晶体中的原子平面,称为晶面。
L M
P点坐标?
(2,2,2)或222
N
一、晶向指数
1、晶向指数:表示晶体中点阵方向的指数,由晶向上结点的 坐标值决定。
2、求法 1)建立坐标系。 以晶胞中待定晶向上的某一阵点O为原点,
联系:一般情况下,晶胞的几何形状、大小与对应的单胞是 一致的,可由同一组晶格常数来表示。
不区分 图示
晶 胞
空间点阵
单
胞
•NaCl晶体的晶胞,对应的是立方面心格子 •晶格常数a=b=c=0.5628nm,α=β=γ=90°
大晶胞
大晶胞:是相对 于单位晶胞而言 的
例:六方原始格子形式的晶胞就是常见的大晶胞
① 所选取的平行六面体应能反映整个空间点阵的对称性; ② 在上述前提下,平行六面体棱与棱之间的直角应最多; ③ 在遵循上两个条件的前提下,平行六面体的体积应最小。
具有L44P的平面点阵
单胞表
3、单胞的表征
原点:单胞角上的某一阵点 坐标轴:单胞上过原点的三个棱边 x,y,z 点阵参数:a,b,c,α,β,γ
准晶
是一种介于晶体和非晶体之间的固体。准晶具有长程定向有 序,然而又不具有晶体所应有的平移对称性,因而可以具有 晶体所不允许的宏观对称性。
晶向、晶
钯的PDF卡片-----Pd 89-4897
crystal system,space
图 2 CdS纳米棒的TEM照片(左)和 HRTEM照片(右)
图2 选区电子衍射图
图1. La(Sr)3SrMnO7的低 温电子衍射图
晶向、晶面、晶面间距
晶向:空间点阵中行列的方向代表晶体中原子排 列的方向,称为晶向。
晶面:通过空间点阵中任意一组结点的平面代表 晶体中的原子平面,称为晶面。
L M
P点坐标?
(2,2,2)或222
N
一、晶向指数
1、晶向指数:表示晶体中点阵方向的指数,由晶向上结点的 坐标值决定。
2、求法 1)建立坐标系。 以晶胞中待定晶向上的某一阵点O为原点,
联系:一般情况下,晶胞的几何形状、大小与对应的单胞是 一致的,可由同一组晶格常数来表示。
不区分 图示
晶 胞
空间点阵
单
胞
•NaCl晶体的晶胞,对应的是立方面心格子 •晶格常数a=b=c=0.5628nm,α=β=γ=90°
大晶胞
大晶胞:是相对 于单位晶胞而言 的
例:六方原始格子形式的晶胞就是常见的大晶胞
① 所选取的平行六面体应能反映整个空间点阵的对称性; ② 在上述前提下,平行六面体棱与棱之间的直角应最多; ③ 在遵循上两个条件的前提下,平行六面体的体积应最小。
具有L44P的平面点阵
单胞表
3、单胞的表征
原点:单胞角上的某一阵点 坐标轴:单胞上过原点的三个棱边 x,y,z 点阵参数:a,b,c,α,β,γ
准晶
是一种介于晶体和非晶体之间的固体。准晶具有长程定向有 序,然而又不具有晶体所应有的平移对称性,因而可以具有 晶体所不允许的宏观对称性。
2-1晶体学基础--西安交大材料科学基础

1
13
c
c1
(463)
O a a1
b1
b
图2-6 晶面指数的确定 1 Oa1=1/2a Ob1=1/2b Oc1=1/2c
14
在确定密勒指数时,还需规定几点: 在确定密勒指数时,还需规定几点: (1)该晶面不能通过原点,因为这时截距为零,其倒数 )该晶面不能通过原点,因为这时截距为零, 是无意义的, 是无意义的,这时应选择与该晶面平行但不过原点的面来 确定晶面指数或把坐标原点移到该面之外; 确定晶面指数或把坐标原点移到该面之外; (2)当晶面与某晶轴平行时,规定其截距为 ,则截距 )当晶面与某晶轴平行时,规定其截距为∞, 的倒数为零; 的倒数为零; ( 3)当晶面与坐标轴的负方向相交时,截距为负,该指数 当晶面与坐标轴的负方向相交时, 当晶面与坐标轴的负方向相交时 截距为负, 的负号最后标在数字的上方。 的负号最后标在数字的上方。 (4)由于任一晶面平移一个位置后仍然是等同的晶面, )由于任一晶面平移一个位置后仍然是等同的晶面, 因此指数相同而符号相反的晶面指数是可以通用的。 因此指数相同而符号相反的晶面指数是可以通用的。
相同,还要看晶面的面间距和原子密度是否相等 如果它们 相同 还要看晶面的面间距和原子密度是否相等.如果它们 还要看晶面的面间距和原子密度是否相等 不相等,尽管晶面指数的数字相等 尽管晶面指数的数字相等,也不是性质相同的等同 不相等 尽管晶面指数的数字相等 也不是性质相同的等同 晶面,而不属于同族晶面 而不属于同族晶面。 晶面 而不属于同族晶面。
1
9
●确定晶向指数时,坐标原点不一定非选在晶向上,若 确定晶向指数时,坐标原点不一定非选在晶向上, 原点不在待标晶向上, 原点不在待标晶向上,那就需要找出该晶向上 ( x 1 , y 1 , z 1 )和 ( x 2 , y 2 , z 2 ) 两点的坐标 标 (x 1 − x 2 ) ( y 1 − y 2 ) (z 1 − z 2 ) 并使之满足: 质整数 uvw ,并使之满足: ,然后将三个数化成互 然后将三个数化成互
晶体学基础

2020/3/3
3
1.1 晶体及其基本性质
晶体结构 = 点阵 + 结构基元
2020/3/3
4
空间点阵的四要素
1. 阵点: 空间点阵中的点; 2. 阵列: 结点在直线上的排列; 3. 阵面: 阵点在平面上的分布。
2020/3/3
5
空间点阵的四要素
4. 阵胞: 结点在三维空间形成的平行六面体。
原胞:最小的平行六面体,只考虑周期性,不考虑对称性; 晶胞:通常满足对称性的前提下,选取体积最小的平行六面体。
ur b/k
P
a/h A
v
a
2020/3/3
25
倒易点阵的应用
uur dhkl 1/ r *hkl
1、计算面间距
1
d2 hkl
r rhkl
r .rhkl
h
k
av*
l
r bcv**
av*
r b*
h
cv*
k
l
h
h
k
l
G
*
k
2020/3/3
3
c
28
倒易点阵的应用
2、计算晶面夹角
• 两晶面之间的夹角,可以用各自法线之间的夹角来表示, 或用它们的倒易矢量的夹角来表示:
c((ohhs21kk12ll12)c)osrvrv(hh2rv1kk2h1l1l21k1l1 ,hhrv21hav2avk*2*l+2+)kk21bvbv*rvv*+h+1kl12ll11cvcv*vrv*h2k2l2
4. 若已知两个晶带面,则晶带轴;
5. 已知两个不平行的晶向,可以求出过这两个晶向的晶面;
2-3晶体学基础

• • • • 对照片中各对弧对进行编号、标注。 测量有效周长(半周长L)。 测量并计算各弧对的间距(S/2)。 S 90 1 计算 和 d。 d
2 L
2 sin i
• 指数标定,计算晶胞参数。
a d ( HKL ) H 2 K 2 L2
2 sin
Fhkl = fa e2i(h0+k0+l0) = fa [cos2(0)+isin2(0)] = fa
讨论点阵消光的时候,只考虑每个 点阵点对应一个原子的最简单情况。 讨论结构消光的时候,考虑到一个 点阵点对应多个原子的情况。
欧拉公式: e+ix = cos(x) +isin(x) e-ix = cos(x) -isin(x).
4
面心点阵
(相同)
cos2n+isin2n = 1
cos(2n+1)+isin(2n+1) =-1
结论:在面心点阵情况下,hkl 为全奇或全偶时,都 能产生衍射。奇偶混合时出现消光。
5
• 底心点阵
– 每个晶胞中有2个同类原子,其坐标分别为0,0,0 和1/2,1/2,0。 – 在底心点阵中,h + k 为奇数时出现消光。
H 2 K 2 L2
33
f. •
•
34
衍射角为 7.5
35
2. 聚焦法
利用发散度较大的入射 X 射线束,照射试样上较大区域,由多晶体试 样中某一组 (hkl) 晶面族所发生的衍射线束在照相底片上仍然聚焦到一 点 (或一条细线) 的衍射方法,称为聚焦法。该方法比德拜-谢乐法具有 更高的灵敏度。
不对称装片法计算 时,不需要相机半径 数据,可减少误差来源。
2 L
2 sin i
• 指数标定,计算晶胞参数。
a d ( HKL ) H 2 K 2 L2
2 sin
Fhkl = fa e2i(h0+k0+l0) = fa [cos2(0)+isin2(0)] = fa
讨论点阵消光的时候,只考虑每个 点阵点对应一个原子的最简单情况。 讨论结构消光的时候,考虑到一个 点阵点对应多个原子的情况。
欧拉公式: e+ix = cos(x) +isin(x) e-ix = cos(x) -isin(x).
4
面心点阵
(相同)
cos2n+isin2n = 1
cos(2n+1)+isin(2n+1) =-1
结论:在面心点阵情况下,hkl 为全奇或全偶时,都 能产生衍射。奇偶混合时出现消光。
5
• 底心点阵
– 每个晶胞中有2个同类原子,其坐标分别为0,0,0 和1/2,1/2,0。 – 在底心点阵中,h + k 为奇数时出现消光。
H 2 K 2 L2
33
f. •
•
34
衍射角为 7.5
35
2. 聚焦法
利用发散度较大的入射 X 射线束,照射试样上较大区域,由多晶体试 样中某一组 (hkl) 晶面族所发生的衍射线束在照相底片上仍然聚焦到一 点 (或一条细线) 的衍射方法,称为聚焦法。该方法比德拜-谢乐法具有 更高的灵敏度。
不对称装片法计算 时,不需要相机半径 数据,可减少误差来源。
材料科学导论-第一章 晶体学基础3
3、六方晶系晶面指数标定
根据六方晶系的对称特点,对六方晶系采用a1,a2,a3 及c四个晶轴,a1,a2,a3之间的夹角均为120度,这样, 其晶面指数就以(h k i l)四个指数来表示。 根据几何学可知,三维空间独立的坐标轴最多不超过三 个。前三个指数中只有两个是独立的,它们之间存在以 下关系:i =- ( h + k ) 。
三轴晶面指数(h k l) 四轴晶面指数(h k i l) i=- ( h + k )
立方晶系:
d hkl
a h k l
2 2 2
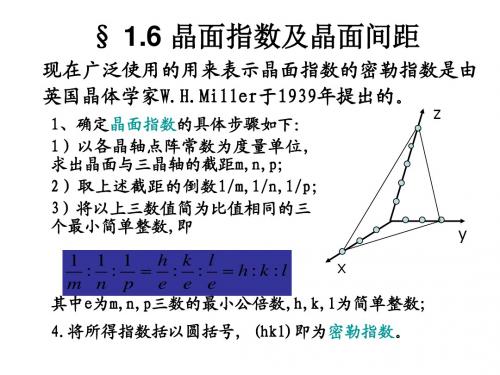
§ 1.6 晶面指数及晶面间距 范例:
m/l
c
a
m/k
b
m/h
画出晶面 (100),(110),(111),(201),(211),(321)
பைடு நூலகம்
c a
(100)
b
画出晶面 (100),(110),(111),(201),(211),(321)
d V [h b c sin k a c sin l a b sin
2 2 2 2 2 2 2 2 2 2 2 2
2hkabc (cos cos cos )
2
2kla bc(cos cos cos )
2
2hlab c(cos cos cos )]
2
2 2 2
1
2
1 2
V abc(1 cos cos cos 2cos cos cos )
单斜晶系:d=sinβ(h2/a2+k2sin2β/b2+l2/c2-2hlcosβ/ac)-1/2 正交晶系:d=[h2/a2+k2/b2+l2/c2]-1/2 四方晶系:d=[(h2+k2)/a2+l2/c2]-1/2 六方晶系:d=[4(h2+hk+k2)/3a2+l2/c2]-1/2
晶体学基础 3

η=nv/V
n:晶胞原子数 v:每个原子所占的体积 V:晶胞的体积
一个晶胞内的原子数n
• 这可从晶胞图中直观看出。但要注意,位于晶胞顶点的原子 是相邻的8个晶胞共有的,故属于一个晶胞的原子数是1/8。 位于晶胞的棱上原子是相邻的4个晶胞共有的,故属于一个 晶胞的原子数是1/4。位于晶胞外表面上的原子是两个晶胞 共有的,故属于一个晶胞的原子数是1/2。
• 填在四面体间隙的最大间隙原子是和4个顶 点的原子同时相切,故二者半径之和为:
密排六方间隙
八面体间隙
• hcp 晶体的八面体间隙如图所示。其形状与fcc 晶胞的八面体间隙完全相似,而间隙的位置不同 。从图看出,在一个hcp 晶胞内有6个八面体间隙 ,故八面体间隙数与原子数之比为6∶6 = 1∶1。
和
D2 是晶体学上的等
价方向,但其晶向指 数却分别是[100]和 [110]。
• 由于等价晶面或晶向不具有类似的指数, 人们就无法从指数判断其等价性,也无法 由晶面族或晶向族指数写出它们所包括的 各种等价晶面或晶向,这就给晶体研究带 来很大的不便。为了克服这一缺点,或者 说,为了使晶体学上等价的晶面或晶向具 有类似的指数,对六方晶体来说,就得放 弃三指数表示,而采用四指数表示。
共3个等价面(Ⅱ型棱柱面)。 •而{0001}只包括(0001) 一个晶面,称为基面。六 方晶体中比较重要的晶面 族还有 ,请读者写 出其全部等价面。
四指数表示晶向指数
• 用四个轴分量来表示一个空间矢量的方法有无穷多种,现在 行走法的方法的困难来自共面的三个轴。 • 看OA矢量,两轴的唯一表示是[-2,-1]。但三轴则有无限多种 • [-1,0,1],[0,1,2],[-2,-1,0],[1,2,3]等。 • 看OB矢量,两轴的唯 • 一表示是[-4,-3],但三 • 轴则有[-1,0,3],[-4,-3,0] • 一定要附加一个约束 • 条件,才能是指数唯 • 一。因 • a1 + a2 + a3 = 0 • 所以约束条件是: • u+ v + t = 0 • 这样,正确的指数是 • OA是 [1 0-1] , • OB是[-5-2 7]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
2
6
间
隙
• 从晶体原子排列的刚球模型可以看到,在原子球与原子球 之间存在着不同形貌的间隙。主要有两类间隙即:四面体 间隙和八面体间隙。 • 晶体结构中间隙的数量、位置和每个间隙的大小等也是晶 体的一个重要特征,对于了解金属的性能、合金相结构、 扩散、相变等问题很有用处。
面心立方
配位数
CN=12
八面体间隙
体心立方
bcc 晶体的八面体间隙如图所示,其位置和形状不同于 fcc 晶胞的八面 体间隙。间隙的中心位于晶胞的面心和晶胞棱的中点(对 bcc 晶体,这
些都是等同点),一个晶胞中八面体间隙的数量是6(个),故八面体间 隙数与原子数之比为6∶2 = 3∶1。
间隙原子只和相距它为a/2的两个原子相切,既和体心原子相切。 而不和相距为 2 a 的四个原子(顶点原子)相切。
和
D2 是晶体学上的等
价方向,但其晶向指 数却分别是[100]和 [110]。
• 由于等价晶面或晶向不具有类似的指数, 人们就无法从指数判断其等价性,也无法 由晶面族或晶向族指数写出它们所包括的 各种等价晶面或晶向,这就给晶体研究带 来很大的不便。为了克服这一缺点,或者 说,为了使晶体学上等价的晶面或晶向具 有类似的指数,对六方晶体来说,就得放 弃三指数表示,而采用四指数表示。
• 填在四面体间隙的最大间隙原子是和4个顶 点的原子同时相切,故二者半径之和为:
密排六方间隙
八面体间隙
• hcp 晶体的八面体间隙如图所示。其形状与fcc 晶胞的八面体间隙完全相似,而间隙的位置不同 。从图看出,在一个hcp 晶胞内有6个八面体间隙 ,故八面体间隙数与原子数之比为6∶6 = 1∶1。
面心立方致密度
原子直径是a/2<110>的长度,即 面心立方结构的晶胞体积为a3,晶 胞内含4个原子,所以它的致密度η 为
a 2
体心立方
配位数
CN=8
体心立方致密度
• 原子直径是a/2<111>的 长,即 面心立 方结构的晶胞体积为a3 ,晶胞内含2个原子,所 以它的致密度η为
密排六方
配位数 •• • • • • • •• • •• • • • ••
共3个等价面(Ⅱ型棱柱面)。 •而{0001}只包括(0001) 一个晶面,称为基面。六 方晶体中比较重要的晶面 族还有 ,请读者写 出其全部等价面。
四指数表示晶向指数
• 用四个轴分量来表示一个空间矢量的方法有无穷多种,现在 行走法的方法的困难来自共面的三个轴。 • 看OA矢量,两轴的唯一表示是[-2,-1]。但三轴则有无限多种 • [-1,0,1],[0,1,2],[-2,-1,0],[1,2,3]等。 • 看OB矢量,两轴的唯 • 一表示是[-4,-3],但三 • 轴则有[-1,0,3],[-4,-3,0] • 一定要附加一个约束 • 条件,才能是指数唯 • 一。因 • a1 + a2 + a3 = 0 • 所以约束条件是: • u+ v + t = 0 • 这样,正确的指数是 • OA是 [1 0-1] , • OB是[-5-2 7]
• 4)fcc 和 hcp 中的八面体间隙远大于 bcc 中的八面体或 四面体间隙,因而间隙原子在 fcc 和 hcp 中的溶解度往 往比在 bcc 中大得多。 • (5) fcc 和 hcp 晶体中的八面体间隙大小彼此相等,四 面体间隙大小也相等,其原因在于这两种晶体的原子堆垛 方式非常相像。
复
• 复式点阵
习
• 原胞和晶胞区别 • 晶面三指数标定 • 晶向三指数标定 • 晶面族和晶向族
六方晶系指数表示
上面我们用三个指数表示晶面和晶向。这种三 指数表示方法,原则上适用于任意晶系。对六方 晶系,取 a,b,c 为晶轴,而 a 轴与 b 轴的夹 角为120°,c 轴与 a,b 轴相垂直,如图所示。
η=nv/V
n:晶胞原子数 v:每个原子所占的体积 V:晶胞的体积
一个晶胞内的原子数n
• 这可从晶胞图中直观看出。但要注意,位于晶胞顶点的原子 是相邻的8个晶胞共有的,故属于一个晶胞的原子数是1/8。 位于晶胞的棱上原子是相邻的4个晶胞共有的,故属于一个 晶胞的原子数是1/4。位于晶胞外表面上的原子是两个晶胞 共有的,故属于一个晶胞的原子数是1/2。
四轴坐标系中,晶向指数的 确定,首先要求出三轴坐标 系的晶向指数[U V W],然 后利用上述关系,换算成四 轴坐标系中的晶向指数 [u v t w]。
常见晶体结构
一、常见晶体结构在金属晶体中,金属键使原子的排列趋于尽 可能地紧密,构成高度对称性的简单的晶体结构。最常见的金 属晶体结构有以下三类。 面心立方:Al,γ-Fe,Ni,贵金属以及奥氏体不锈钢等。 体心立方:碱金属、难熔金属(V,Nb,Ta,Cr,Mo,W) 、α-Fe 等等。 密排六方 :α-Be, α-Ti, α-Zr等
• 但是,用三指数表示六方晶系的晶面和晶向有一个很大的缺点,
即晶体学上等价的晶面和晶向不具有类似的指数。这一点可以从 图看出。图中六棱柱的两个相邻表面(红面和绿面)是晶体学上
等价的晶面,但其密勒指数(Miller Indices)却分别是
(100)。 •图中夹角为 60°的 两个密排方向 D1 和
• 四指数表示是基于4个坐标轴:a1,a2, a3 和 c 轴,如图所示,其中,a1,a2 和 c 轴就是原胞的 a,b 和c 轴,而 a3 = -(a1+a2)。下面就分别讨论用四指 数表示的晶面及晶向指数。
四指数表示晶面指数
• 六方晶系晶面指数的标定原理和方法同立方晶系中的一样,步 骤如下: • (1)先找出该面在四个坐标轴上的截距长度(以晶胞的点阵 常数 a,c 为单位长); (2)求其倒数并化为最简整数,即得(hkil)指数这样得到的 晶面指数称为 Miller-Bravais 指数。 从图所示的4个轴的几何关系 不难看出,只要晶面在a1和a2 轴上的截距一定,它在a3上的 截距也就随之而定。可见, h,k和i三个指数不是独立的。 事实上,可以证明
此外,以晶胞中部三个原子中的每一个为顶点
,以其上方(顶层)和下方(底层)的三个原
子构成的三角形为底,分别可作一四面体,其 中心就是四面体间隙的中心。这样,一个六方 晶胞内的四面体间隙总数应是 c 轴上的间隙数 、6 条平行于 c 轴的棱上的间隙数以及通过晶 胞中部的三个原子而平行于c 轴的三条竖直线 上的间隙数之和。其值为2+6×2×1/3+2×3
• 相邻的原子相互接触,原子中心就是八面体的各个角顶。
根据几何学关系可以求出间隙能够容纳的最大圆球半径。 假设原子半径为 r,间隙中能容纳的最大圆球半径为 rx ,
则可以算出八面体间隙相对大小rx / r。
四面体间隙
fcc 晶胞的四面体间隙位于 4 个 原子组成的正四面体的中间,如 图 所示。如果用(200),(020)和
2
体心立方四面体间隙
bcc 晶体的四面体间隙如图所示,它是位于由两个相邻晶胞的体心 原子以及它们的公共棱上的两个原子所构成的四面体的中间,图 中的红色三角形表示间隙的中心位置。显然,每个表面({100}面) 上都有 4 个和中心点等同的点,故一个晶胞中的四面体间隙数为 6×4×1/2 (个),四面体间隙数与原子数之比为12∶2 = 6∶1。
0.127nm,按上式求得γ-Fe的四面体和八面体间隙的球半径
分别为0.028nm和0.052nm。由于碳原子半径为0.077nm,氮 原子半径为0.070nm,虽稍大于 -Fe的八面体间隙的球半径, 但只要将铁原子稍微挤开使间隙扩大一点,碳、氮原子即可 进入八面体间隙之中,因此,γ-Fe中能溶入碳、氮原子形成 间隙固溶体。
i=-(h+k)。Fra bibliotek• 六方晶体中常见晶面及其四指数(亦称六方指数)标于图 。从图看出,采用四指数后,同族晶面(即晶体学上等价 的晶面)就具有类似的指数。例如:
1010 1010 1100 0110
• 共3个等价面(Ⅰ型棱柱面)。
1120 1120 1210 2110
几何特征:配位数、一个晶胞原子数、紧密系数和间隙
配位数
配位数是指晶体结构中,与任一原子最近邻并且等距离的原子 数。对纯元素晶体来说,任一原子到最近邻原子的距离必然是 相等的。但是,对于多种元素形成的晶体来说,任一原子到不 同元素的最近邻原子的距离不一定相等,这里,“最近”是就 同种元素的原子相比较而言的,而配位数则是一个原子周围的 各元素的最近邻原子数之和。配位数通常用 CN 表示。
单质晶它是每个原子的最近邻数目,晶体中最大的配位数为12 ,但在一些非单质的晶体中CN可以大于12 。因为金属结构一 般有高的对称性,单质金属的CN没有11、10、9等数值 。 CN 顺序分别为12、8、6、4、2、1。金属结构大部分是密堆的,它 们的CN大多是12或8。
致密度
• 致密度又称堆垛密度或空间填充的效率η,它表示原子排 列的密集程度。它定义为晶体结构中单位体积中原子所占 的体积。假如把金属晶体中的原子看成是有一定直径的刚 球,则紧密系数可以用刚球所占空间的体积百分数来表示 。若以一个晶胞来计算,致密度就等于晶胞中原子所占体 积与晶胞体积之比,即: • 致密度 =晶胞中原子所占体积之和/晶胞的体积。
• 在原子半径相同的条件下,hcp 晶体的八面体间隙大小与fcc 晶胞的八面体间隙大小相同。
四面体间隙
• hcp 晶体的四面体间隙位置如图所示。其形状与 fcc 晶胞的四 面体间隙完全相似,而间隙的位置不同,位于c 轴上有两个四面 体间隙。由于平行于c 轴的6条棱上的原子排列情况是和 c 轴完 全相同的,故在每条棱上与c 轴上间隙对应的位置也有两个四面 体间隙。
=12(个),所以四面体间隙数与原子数的比
为12∶6 = 2∶1。
• •• •• •• •• • • •• • • • • • • • • • • • • • • • •• • •• •• •• • • •• • •• • • •
