安徽省全国示范高中名校2020届高三数学10月联考试题文
2020届高三各地10月和11月英语试卷精选汇编：写作专题含范文
2020届高三各地10月和11月英语试卷精选汇编：写作专题含范文衡阳市八中2020届高三月考试题 (四)书面表达（满分25分）我们学校一年一度的秋季运动会即将进行。
假定你是李华，你的英国朋友Peter 来信询问平常你校学生体育运动情况。
请给他回信，内容包括：（1）学校的体育场馆；（2）主要的运动项目；（3）你喜欢的项目。
注意：（1）词数100左右；（2）可以适当增加细节，以使行文连贯。
书面表达：Dear Peter,How are you doing? You asked me about how our school performs our PE classes in your last letter, so I’m writing to share some details with you.Equipped with two playgrounds as well as a splendid stadium, our school offers us an opportunity to do a variety of sports. Not only do we take volleyball and basketball courses, but our school also holds all kinds of sports competitions. Among all sport s, I’m crazy about volleyball, which contributes to us cooperating with others.Yours,Li Hua武威六中2020届高三一轮复习过关考试（三）书面表达(满分25分)假定你是李华，你的美国笔友Jack给你发来邮件，告诉你他参加美国中西部“汉语桥”比赛（U. S. Midwest Chinese Bridge Speech Contest）获得了一等奖，希望你继续帮他学习中文。
省扬中、省华罗庚中学、省溧中2020┄2021届高三10月联考化学试卷
高三三校联考2021年10月化学试卷注意事项：本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共120分。
考试时间100分钟。
可能用到的原子量：H 1 C 12 O 16 Na 23 S 32第Ⅰ卷（选择题，共56分）一、选择题（本题包括6小题，每小题4分，共24分。
每小题只有一个．．．．选项符合题意）1．探测冥王星（Pluto）的“新地平线（New Horizons）”号具有10.9 kg钚—238（Pu23894）燃料的核电池系统，核电池是由辐射β射线（高速电子流）的放射源，收集这些电子的集电器，以及两者之间的绝缘体三部分组成。
下列有关说法正确的是A．钚电池是将核能转化为电能B．核燃料是可再生能源C．放射源一端为正极，集电器一端为负极D．Pu23894的原子质量是12C原子质量的238倍2．世界著名的科技史专家、英国剑桥大学的李约瑟博士考证说：“中国至少在距今3000年以前，就已经使用玻璃了。
”下列有关玻璃的说法不正确的是A．制普通玻璃的原料主要是纯碱、石灰石和石英 B．玻璃在加热熔化时有固定的熔点C．普通玻璃的成分主要是硅酸钠、硅酸钙和二氧化硅D．盛放烧碱溶液的试剂瓶不能用玻璃塞，是为了防止烧碱跟二氧化硅生成硅酸钠而使瓶塞与瓶口粘在一起3．每年元宵节晚上，人们都要举行盛大的焰火庆祝活动。
焰火绽放出的五颜六色是一些金属离子魅力的展示。
焰火的主要原料是黑火药，还有草酸钠、碳酸铜（发出绿色的光）等发色剂和氯酸钾、镁铝金属粉末等添加剂。
下列说法正确的是A．碳酸铜因为受热分解才发出绿色的光B．氯酸钾的主要用途是产生紫色的焰火C．镁铝在焰火中发出耀眼的白光D．黑火药的主要成分是木炭、硫磺4．2006年11月23日中科院网报道，核磁共振造影增强剂用于疾病的诊断，还可以作为药物载体用于疾病的治疗。
中科院化学研究所在肿瘤鉴别诊断用磁共振造影剂研究方面取得重要进展。
为磁性纳米晶体材料在生物医学领域的应用提供了更广泛的前景。
安徽省2020届高三上学期全国示范高中名校十月联考文科数学参考答案
8.D 解析：∵ DB AB AD ， DB AE ，∴ DB AE 0,Leabharlann 即 ( AB
AD)
( AB
AD)
0
，整理可得
2 AB
(
1) AB
AD
2 AD
0
，
即 9 3( 1) 4 0 ,解得 6 .
x
x
2k, (k
2 2k ,
Z)
且
f
(x)
是偶函数，其图像如图所
示，由图可得 B 正确.
第 1页（共 4页）
1
二、填空题（本大题共 4 小题，每小题 5 分，共 20 分） [
13. 1
14.3
6
15.2
16.(4，6]
13. 1 2
解析：f
(－13)＝f 2
(－1)＝f 2
（2）设 g(x) a x sinx 1 x 3 ，当 a≤1 时，g(x)≤ x sinx 1 x3 ,
6
6
设 h(x)= x sinx 1 x 3, x [0, ) ，则只要证明 h(x)≤0 即可, 6
由 2k x 2k 得2k 2 x 2k 1, k Z ，
2
6
2
3
3
∴f(x)的单调递增区间为[2k 2 , 2k 1], k Z .（7 分） 33
第 2页（共 4页）
2
(2) x [2, a], x [2 , a ],
66
4.B 解析：易知 f(x)为奇函数，且当 0<x<1 时，f(x)>0，当 x>1 时，f(x)<0，故选 B.
2020届安徽省三人行联盟高三上学期10月联考 数学文答案
ln
x1 x1
ln x2
x2
(2x1
x2 )
2
……8 分
2( x1 1)
即证 ln
x1 x2
2( x1 2 x1
x2 ) x2
x2 2 x1
1
x2
令 t x1 1，即证(t) ln t 2(t 1) 0 成立 （*） ……10 分
x2
2t 1
2
3
（2）由 a 2R sin A 2 3 ，且 a2 b2 c2 2bc cos A ，得12 b2 c2 bc 2bc bc bc
∴ SABC
1 2
bc sin
A
3
3. ………………10 分
18．（1）由 1 1 2 知{ 1 }等差数列，公差为 2，首项 1 3
y12 y22
4x1 4x2
y12 y22
4(x1 x2 )
y1 y2 x1 x2
4
1 y1 y2
而 k AB
y2 x2
y1 x1
1
y1 y2 4 ， y中 2, x中 4 ，中点坐标（4，2）
15．4
解： y 2ax 1 . x
(t)
1 t
(2t
6 1)2
4t 2 2t 1 t(2t 1)2
0(t
1)
∴(t) 在 t 1单增，(t) (1) 0 ，（*）成立，得证 ……12 分
2
)] 3
1 [1 1 ] 1 n 9 ， n N ………………12 分 2 3 2n 3 7
安徽省全国示范高中名校2019-2020学年高三上学期10月联考物理试题及答案解析
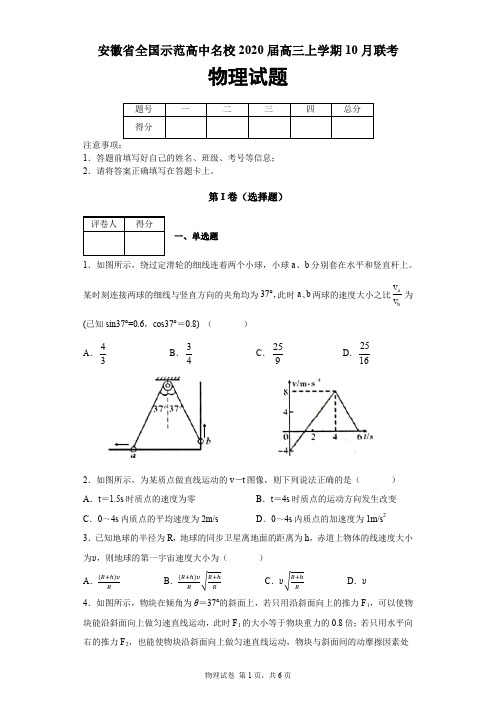
安徽省全国示范高中名校2020届高三上学期10月联考物理试题注意事项：1．答题前填写好自己的姓名、班级、考号等信息； 2．请将答案正确填写在答题卡上。
第I 卷（选择题）一、单选题1．如图所示，绕过定滑轮的细线连着两个小球，小球a 、b 分别套在水平和竖直杆上。
某时刻连接两球的细线与竖直方向的夹角均为37°，此时a 、b 两球的速度大小之比abv v 为(已知sin37°=0.6，cos37°＝0.8) （ ） A ．43B ．34C ．259D ．25162．如图所示，为某质点做直线运动的v －t 图像，则下列说法正确的是（ ） A ．t ＝1.5s 时质点的速度为零 B ．t ＝4s 时质点的运动方向发生改变 C ．0～4s 内质点的平均速度为2m/sD ．0～4s 内质点的加速度为1m/s 23．已知地球的半径为R ，地球的同步卫星离地面的距离为h ，赤道上物体的线速度大小为 ，则地球的第一宇宙速度大小为（ ）A．B ．C ．D ．4．如图所示，物块在倾角为θ＝37°的斜面上，若只用沿斜面向上的推力F 1，可以使物块能沿斜面向上做匀速直线运动，此时F 1的大小等于物块重力的0.8倍；若只用水平向右的推力F 2，也能使物块沿斜面向上做匀速直线运动，物块与斜面间的动摩擦因素处处相同，则12F F 为(已知sin37°=0.6，cos37°＝0.8) （ ）A ．12B ．1320 C ．43D ．535．有甲、乙两只船，它们在静水中航行速度分别为v 1、v 2且21v ，现在两船从同一渡口向河对岸开去，已知甲船用最短时间渡河，乙船以最短航程渡河，结果两船抵达对岸的地点恰好相同。
则甲、乙两船渡河所用时间之比t 1：t 2为（ ） A ．1B1C ．1：3D ．3：16．如图所示，在平直公路上有两辆同向匀速行驶的A 、B 汽车，A 车的速度为10m/s ，B 车的速度为12m/s 。
安徽省2020届高三数学上学期10月联考试题文(最新整理)
安徽省2020届高三数学上学期10月联考试题 文时间:120分钟 满分：150分一、选择题：本大题共12小题,每小题5分，共60分。
每一小题给出的四个选项中只有一项是符合题目要求的。
1.若集合，则A 。
B 。
C. D. 2。
在复平面内，复数对应的点位于A.第一象限 B 。
第二象限 C.第三象限 D 。
第四象限3。
已知，则A 。
a>b>cB 。
b>c 〉aC 。
a 〉c>b D.c>a 〉b 4.已知等差数列｛a n｝的前9项和为45，a 3＝－1，则a 7＝ A.11 B 。
10 C.9 D 。
85.如图所示,在平行四边形ABCD 中，M 为BC 边的中点,N 为线段AM 上靠近M 点的三等分点，则A 。
B 。
C. D 。
6.函数y=log a (x ＋4)＋2（a>0，且a≠1)的图象恒过定点A ，且点A 在角θ的终边上，则cos2θ＝A.－B.C. D 。
7。
己知命题p:在△ABC 中，若A 〉B ，则cosA<cosB ，命题q ：，则下列命题为真命题的是 A.p ∧q B.(p)∧q C。
p∨(q ） D 。
(p)∧（q)8.己知函数f （x)的图像如图所示，则对应的解析式可能是{(2)0},{10}A x x x B x x =->=->AB ={10}x x x ><或{02}x x <<{2}xx >{1}x x >13i+0.21.90.21.9,l o g 1,0.2a b c ===DN =1233A B A D-+1536A B A D-1233A B A D-1334A B A D-5131213-5131213(0,),s i n x xx ∃∈+∞>⌝⌝⌝⌝A 。
y ＝2x －x 2－1 B 。
y ＝2xsinx C 。
D.y ＝(x 2－2x ）e x9.定义在R 上函数f （x ）满足，且当x∈[－1，1)时，，若，则f （5a)＝A. B. C.D.10.己知函数的全部零点构成一个公差为的等差数列，把函数f （x ）的图像沿x 轴向左平移个单位，得到函数g （x)的图像，关于函数g(x)，下列说法正确的是A 。
2020高三数学上学期10月联考试题 文
2020届高三数学上学期10月联考试题 文考生注意：1.本试卷分选择题和非选择题两部分。
满分150分，考试时间120分钟。
2.答题前，考生务必用直径0.5毫米黑色，墨水签字笔将密封线内项目填写清楚。
3.考生作答时，请将答案答在答题卡上。
选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效．．．．．．．．．．．．．．．．．．．．．．．．．．．。
4.本卷命题范围：高考范围。
一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.已知集合A ＝{0，1，2}，B ＝{1，2，3}，则A ∩B ＝ A.{1，2} B.{0，2} C.{0，1} D.{1}2.若i 是虚数单位，则2(3＋i)iA.2＋6iB.2－6iC.－2－6iD.－2＋6i3.若函数222,0()log 2,0x x f x x x ⎧+<=⎨-≥⎩，则f(1)＋f(－1)＝A.0B.1C.－1D.24.若双曲线22221(0)2x y m m m -=>+的离心率为2，则实数m 的值为 A.1 B.13 C.2 D.3 5.若1cos()36πα+=-，且263ππα<<，则7sin()12πα+=A. 12-B.12C.12D.126.在Rt △ABC 中，A ＝90°，AB ＝AC ＝a ，在边BC 上随机取一点D ，则事件“AD>4a ”发生的概率为 A.34 B.23 C.12 D.137.已知某几何体的三视图如图所示，若该几何体的体积为3π＋6，则x 等于A.4B.5C.6D.78.已知点D 是△ABC 所在平面上的一点，且2BD DC AD AB AC λμu u u r u u u r u u u r u u u r u u u r＝－，若＝＋，则λ－µ＝A.6B.－6C.－32D.－3 9.已知函数()sin()(0)6f x x πωω=+>的两个零点之差的绝对值的最小值为2π，将函数f(x)的图象向左平移3π个单位长度得到函数g(x)的图象，则下列说法正确的是 ①函数g(x)的最小正周期为π； ②函数g(x)的图象关于点(712π，0)对称； ③函数g(x)的图象关于直线23x π=对称； ④函数g(x)在[3π，π]上单调递增。
2021届全国新高考仿真模拟试题(二)数学(文)(解析版)
∴CD⊥平面
ABD，∴CD
是三棱锥
C
ABD
的高，∴VC
ABD＝13×12×2×2×sin
60°×2＝2 3， 3
故选 A.
8．答案：C
解析：由射线测厚技术原理公式得I20＝I0e－7.6×0.8μ，∴12＝e－6.08μ，－ln 2＝－6.08μ，μ≈0.114，
故选 C.
9．答案：C
解析：从题图(1)可以看出，该品牌汽车在 1 月份所对应的条形图最高，即销售量最多，
商品销售 25.0 30.0 34.0 37.0 39.0 41.0 42.0 44.0 48.0 y10
额 y/万元
且已知 错误!i＝380.0
(1)求第 10 年的年收入 x10. (2)若该城市居民年收入 x 与该种商品的销售额 y 之间满足线性回归方程y^＝363x＋^a，
254 (ⅰ)求该种商品第 10 年的销售额 y10； (ⅱ)若该城市居民年收入为 40.0 亿元，估计这种商品的销售额是多少？(精确到 0.01) 附：①在线性回归方程y^＝b^x＋^a中，b^＝错误!，^a＝－y －b^－x ；
(1)求轨迹Γ的方程； (2)过点 F 作互相垂直的直线 AB 与 CD，其中直线 AB 与轨迹Γ交于点 A，B，直线 CD 与轨迹Γ交于点 C，D，设点 M，N 分别是 AB 和 CD 的中点，求△FMN 的面积的最小值．
-5-
21．(12 分)[2020·安徽省示范高中名校高三联考]函数 f(x)＝aex＋x2－ln x(e 为自然对数的底数，a 为常 数)，曲线 f(x)在 x＝1 处的切线方程为(e＋1)x－y＝0.
于 8 月份，所以该公司 7 月份汽车的总销售量比 8 月份少，所以选项 C 是错误的；从题图(1)
九师联盟2020届高三10月联考-文数答案
5XY6#)9&)4$/#)4&.9$!¦ZVW35XY§.¨©ª«i0&BC)4%"&PO 4%"!K%#$$%
## $ $ # $ :2;&,$,.!!BC(%%
! &
)&"!7
%:2;&
! &
)&"!7
.!%:2;& &&"!7
.!%&"!+&/%%#&&"!+$%:2;& &&"!+
.!
%&"!8&3%%#4.!$%%#!$%:2;&,!,.!%".!%!!BC3-(-/!
!7!.)!&"$/ .&&($!-%& #$$)%#$$%&&O .%#$$)&/.%#$$.!/%"&PO%#$$%&b%#$$%)!!¬%#$$%
&r&.$/&).$/%&&PO.$/%&b.$/%)!!¬.$/%&r&PO$$ .&&($,¬ .$/%)!r&PO$$ .)!&"$,
¬%#$$%)!r&.$/&) .$/%)!&P!®w&8¯%& #$$)%#$$%&3P°6 .)!&"$/ .&&($!
*槡&(*&%&(槡(!±±±±±±±±±±±±±±±±±±±±±±±±±±
安徽省2020届高三上学期全国示范高中名校十月联考语文参考答案
高三语文参考答案题号12345710111214171819答案A B D D C B A C D C A B D1．A解析：A.“只要常怀感恩之心、砥砺家国情怀，就能自觉把个人前途命运与国家紧密地融合在一起”错，原文为“只有常怀感恩之心、砥砺家国情怀，才能自觉地把个人的前途命运与国家、民族、社会紧密地融合在一起”。
2．B解析：B.文章举大禹治水、戚继光抗倭的例子，证明的是家国情怀体现为一种民族大义。
3.D解析：A.“内化于行、外化于心”错，原文为“内化于心、外化于行”。
B.“不能关注国家为我们做了些什么”错，原文为“对于个体而言，要关注国家为我们做了些什么，更要多问问自己为国家能做什么、做了些什么”。
C.“为了实现个人价值，中国民众”错，应是“对于年轻人来说”。
4.B解析：B.扫码安装手机软件有可能会导致手机中毒。
5.C解析：A.“说明放假时间越长，消费者的日均消费越多”分析错误。
B.“‘中国大妈’成为了使用支付宝支付的主力”错，原文为“‘中国大妈’也开始加入用移动支付消费的主力”。
D.“使得移动支付存在很大的安全隐患”错，材料讨论的是“扫码支付”；且原因分析错误。
6.①中国游客在境外的移动支付再创新高，人均支付接近2500元。
②中国游客境外用卡的目的地更趋分散，跨境用卡场景更加多元。
③中国游客在境外热衷于使用银联“云闪付”等移动支付服务。
（每点2分）7.B解析：B．从小说后面的部分可以看出“麻雀”并没有离开农村。
8.满怀理想时：“麻雀”爱“晶晶”，“晶晶”也爱主人。
“晶晶”是他的伙伴，是他的精神寄托，是他患难与共的伴侣，他们之间达成了不需任何言语就有的默契。
（2分）被招工和进城“闹腾得他周身疲惫”时：“麻雀”对“晶晶”是难舍难分而又无可奈何。
“麻雀”为了达到自己的目的，忍痛把心爱的“晶晶”送给招工的师傅，送到遥远的北方去。
（2分）见到“晶晶”死于自己的枪口下时：理想幻灭的“麻雀”感到了沉痛，进而引起了对生活深邃的思索，“麻雀”的灵魂重获新生，他回到了乡村的怀抱。
小专题-离子方程式的正误判断与书写的答案
B.盐酸的酸性强于亚硫酸， SO2 通入 BaCl2 溶液不反应，故 B 错误；
C. Fe（OH）2 比 NH3·H2O 更难电离，(NH4)2Fe(SO4)2 溶液中加入少量 NaOH 溶液：先发生 Fe2＋+2OH－=Fe（OH）2↓， 故 C 错误；
D. 用 CuCl2 溶液做导电性实验，灯泡发光：CuCl2
本卷由系统自动生成，请仔细校对后使用，答案仅供参考。
离子的物质的量之比与原物质组成比相符。 （2）“多变”就是过量的反应物，其离子的化学计量数根据反应实际需求量来确定，不受化学式中的比例制约， 是可变的。 3．B 【来源】上海交通大学附中 2019-2020 学年高三上学期期中考试化学试题 【解析】 【分析】 还原性 SO32-＞I-，滴加氯水，首先氧化亚硫酸根离子，据此分析解答。 【详解】 A．向 Na2SO3、NaI 的混合溶液中滴加少量氯水，首先氧化亚硫酸根离子，若只氧化亚硫酸根离子，反应的离子 方程式可以为：SO32-+Cl2+H2O═SO42-+2H++2Cl-，故 A 不选； B．向 Na2SO3、NaI 的混合溶液中滴加少量氯水，首先氧化亚硫酸根离子，不可能只发生 2I-+C12=2Cl-+I2，故 B 错误； C．向 Na2SO3、NaI 的混合溶液中滴加少量氯水，首先氧化亚硫酸根离子，若亚硫酸根离子完全反应后，氯气剩 余，可以再氧化碘离子，可能发生 2Cl2+2I-+SO32-+H2O=4Cl-+SO42-+2H++I2，故 C 不选； D．向 Na2SO3、NaI 的混合溶液中滴加少量氯水，首先氧化亚硫酸根离子，若反应后 Na2SO3 过量，则可能发生 Cl2+3SO32-+H2O=2Cl-+SO42-+2HSO3-，故 D 不选； 故选 B。 4．C 【来源】福建省莆田市第十一中学 2019-2020 学年高三上学期期中考试化学试题 【解析】 【详解】 A、次氯酸为弱酸，不能拆分，所以氯气溶于水的离子反应方程式为：Cl2＋H2O=H＋＋Cl－＋HClO，A 错误； B、硝酸具有强氧化性，能将亚硫酸根氧化为硫酸根，所以向稀 HNO3 中滴加 Na2SO3 溶液的离子反应方程式为： 3SO32-＋2H＋+ 2NO3-=3SO42-＋2NO↑+H2O，B 错误； C、酸性溶液中 KIO3 与 KI 反应生成 I2 的离子反应方程式为：IO3-＋5I－＋6H＋=3I2＋3H2O，C 正确； D、向 NaHCO3 溶液中加少量 Ba(OH)2 溶液：2HCO3-＋Ba2＋＋2OH－=BaCO3↓＋2H2O+ CO32-，D 错误； 故选 C。 【点睛】 当离子反应方程式涉及过量和少量时，假设少量的为 1mol，再根据具体反应添加。如 D 选项：Ba(OH)2 溶液少 量，则假设 Ba(OH)2 为 1mol，则含有 2mol OH－和 1mol Ba2＋，2mol OH－能与 2mol HCO3-完全反应同时生成 2molH2O
安徽省2020届高三上学期全国示范高中名校10月联考化学参考答案
化学参考答案选择题（每小题3分，共48分）题号12345678910111213141516选项A C D D B D B D A A A D C C B B1.A解析：A项，芯片的主要成分是Si，错误。
2.C解析：A项，水玻璃是硅酸钠的水溶液，是混合物，错误；B项，二者互为同素异形体，错误；C项，二者不是同一种物质，相互转化过程属于化学变化，正确；D项，磷酸是中强酸，在水中不会完全电离，错误。
3.D解析：有机物一定含有碳元素，所以碳是组成有机物的主要元素，A正确；绿色植物将二氧化碳和水合成葡萄糖和氧气的过程，是把太阳能转化为化学能的过程，B正确；动物有氧呼吸过程中，葡萄糖被氧化为水和二氧化碳，C正确；碳元素在地壳中含量较少，D错误。
4.D解析：具有漂白性或脱水性的溶液不能用pH试纸测定pH，故A错误；无水氯化钙不能干燥NH3，故B错误；试管可以直接加热，故C错误；萃取、过滤都是利用溶解性分离物质，溶解性属于物理性质，故D正确。
5.B解析：实验室用100mL、250mL、500mL、1000mL容量瓶，A项正确；用KSCN溶液只能检测到FeSO4是否被氧化，B项错误；玻璃棒靠在容量瓶刻度线以下，避免损失溶质，C项正确；容量瓶未干燥，不影响配制的浓度，D项正确。
6.D解析：金属铝在空气中不燃烧，A错误；常温下金属铜可以和浓硝酸之间发生反应，金属铁在常温下遇到浓硝酸会钝化，B错误；明矾中的铝离子水解会生成具有净水作用的氢氧化铝胶体，但是该物质能和酸反应生成盐和水，所以不可用于除去酸性废水中的悬浮颗粒，C错误；二氧化硅能与氢氧化钠溶液反应，生成硅酸钠和水，D正确。
7.B解析：A项，图为蒸馏装置，分离互溶但沸点不同的混合物，错误；B项，苯不能隔绝NH3或HCl与水的接触，因此不能防止倒吸，说法正确，正确；C项，NH3、H2的密度比空气小，应用向下排空气法收集，错误；D项，氯化氢为酸性气体，不能用碱石灰干燥，且氯化氢密度比空气的大，收集气体的方式应为长管进短管出，错误。
安徽省示范高中皖北协作区2023届高三联考语文试题及答案解析
安徽省示范高中皖北协作区2023届高三联考语文试题及答案解析考生注意：1.本试卷共150分，考试时间150分钟。
2.请将各题答案填写在答题卡上。
3.本试卷主要考试内容：高考全部内容。
一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，17分）阅读下面的文字，完成1～5题。
材料一：早期中国（秦汉以前）是“一元”还是“多元”，是否存在“一体”，是一个宏大话题。
“元”本义为人首，引申为肇始、本原；“体”本义为肢体，引申为一般事物之体。
因此，“一元”抑或“多元”，实际是早期中国有一个根本还是多个根本的问题；是否存在“一体”，是早期中国是否为一个文化实体的问题。
古史传说中的中华先民，远以伏羲、女娲为祖，近以轩辕黄帝为宗，基本属于“一元”“一体”“一统”。
早在1987年，严文明就提出中国史前文化既有统一性又有多样性，形成了一个“重瓣花朵式”格局，成为统一的多民族的现代中国的史前基础。
其实，1986年张光直还提出，公元前4000年以后中国各地文化相互交流而形成了一个史前的“中国相互作用圈”。
“重瓣花朵式”格局和“中国相互作用圈”都是中华民族早期文化“一体”格局的形象表达，但两人的观点有一定区别：张光直“中国相互作用圈”中的各文化互相“平等”，中原或黄河中游并无特殊地位；而严文明的“重瓣花朵式”格局有主有次，“花心”就是中原文化，“重瓣”就是与中原分层联系的周围文化。
而“多元”说则值得商榷，现在的中华民族共同体有多个民族单位，史前的考古学文化有多个样貌，固然都是事实，但中华民族或中华文化的根本不见得是多个。
“元”既是根本，那么最根本的就应当是能够被长久传承的核心思想观念以及文化基因，而非易变的物质文化。
根据考古发现，我们能够比较清楚地看到，距今8000年左右在中国大部地区已经有了共同的宇宙观、伦理观、历史观等核心思想观念，这些思想观念统合形成了“一元”的“敬天法祖”信仰，又被分解为整体思维、天人合一、诚信仁爱、和合大同等文化基因。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
安徽省全国示范高中名校2020届高三数学10月联考试题文
本试卷共4页。
全卷满分150分，考试时间120分钟。
考试范围：集合与常用逻辑用语，函数与导数约占30%，三角函数、三角恒等变换、解三角形约占60%，平面向量约占10%。
注意事项：
1.答题前，考生务必将自己的姓名，准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其它答案标号。
回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3.考试结束后，将本试卷和答题卡一并交回。
一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
3x≤0}，则B＝{x|x已知集合A＝{x|logx<1}，1.2B?5B A.C.A∩B＝B D.A∪B＝2－
－1∈A B.
＝33?2??2?322??3 A. B. C.
0 2.tan705
D.????)(?0)f(x)?cos(x的最小正周期为已知函数3.π，则该函数图像6??，0)对称A.关于点( B.关于直线x＝对称66??C.关于点(，0)对称 D.关于直线x＝对称333|x| )e的图像大致是f(x)＝2(x－x4.函数
的北偏东，灯塔A在观察站3kmA和B与海洋观察站C的距离分别为，5km5.两座灯塔o B的o20C
距离为A在观察站C的南偏东40方向上，则灯塔与方向上，灯塔B3425km
km C.7km D.A.6km B.3ba31)(mb3)a6.已知向量＝(，在向量＝，方向上的投影为，则与的夹角为- 1 -
120或150 D.60A.30 B.60 C.30222为锐角三，则△ABC，AB，C的对边，命000000或
题p：若a＋b>c7.已知a，b，c分别为△ABC内角。
下列命题为真命题的是角形，命题q：若a>b，则cosA<cosB ﹁p)∨qA.p∧q B.p∨(﹁q) C.(﹁p)∧(﹁q)
D.(?AD?AE?AB0λ，若DB⊥AE，则，且＝8.平行四边形ABCD中，AB3，AD＝2，∠BAD＝60的值为
A.3
B.4
C.5
D.6
9.已知角α的顶点与原点重合，始边与x轴的正半轴重合，终边经过点(2，－1)，则??)??tan(2
24334?? C. D.A. B. 34431倍(纵坐标不变)，再将所10.
将函数y＝sin(x＋φ)的图像上所有点的横坐标缩短到原来的2?个单位后得到的函数图像关
于原点中心对称，则sin2φ＝得图像向左平移123311?? B. C.A.
D.2222011.已知a，b，c均为单位向量，a与b的夹角为60，则(c＋a)·(c－2b)的最大
值为
33 C.2 D.3 A. B.212.设函数f(x)＝|sinx|·cosx，则下列结论正
确的是
??3,[]单调递减 2π B.f(x)在的最小正周期为A.f(x)
44??313),(?个极小值2有且仅有C.y＝f(x)图像的对称轴方程为x＝kπ(k∈Z) D.f(x)在
222点分。
小题，每小题5分，共20二、填空题：本题共4313??x0时，f(x)＝logx，313.若f(x)是R上周期为的偶函数，且当则f(－)＝________。
42214.函数f(x)
＝cos(π＋2x)－sinx的最大值为________。
x?e,x?0?f(x)??x?R，f(x)≥mx，则m的取值范围是已知函数，若________。
16.15.?2x?1,x?0??
m?(tanB?taC,n3)，△ABC别cba已知，，分为内边的C，，A角B对向，量- 2 -
n?(tanBtanC?1,1)，且m//n，a＝2，则△ABC周长的取值范围是________。
三、解答题：共70分。
解答应写出文字说眀、证明过程或演算步骤。
222bcsinAa???17.(10分)已知a，b，c分别为非等腰△ABC内角A，B，C的对边，。
2sinBc(1)证明：C＝2B；
3，求△ABC的面积。
c＝ 2(2)若b＝3，18.(12分)函数f(x)＝sin(ωx＋φ)(ω>0，|φ|<π)
的部分图像如图所示。
(1)求f(x)的解析式及其单调递增区间；
(2)若f(x)在[－2，a]有5个零点，求a的取值范围。
19.(12分)设函数f(x)＝ax－sinx。
(1)若a＝1，求曲线y＝f(x)在点(π，f(π))处的切线方程；
13xx)?f(。
)时，证明： (2)当a≤1，x∈[0，＋∞63sinθ，cosθ)，O(0，，0)C(。
1)
分)设A(－1，2)，B(2，－20.(12??5??AB?BC)sin(2?的值；，求(1)若6mOA?nOB?OC，求5m－n(2)若的最大值。
BA22?bcos?cb?2a2sin。
C的对边，，cb，分别为△ABC内角AB，a21.(12分)已知，22
B(1)求；的取值范围。
6]，求sinC，a∈[2，若(2)c＝612xf?mx,m?Rln)(x?x?。
22.(12分已知函数) 2(1)的单调性；讨论f(x)10?m?，f(x)有两个极值点x，x(x<x)，求f(x若)(2)－f(x)的最小值。
2221113- 3 -
- 4 -- 5 -
- 6 -
- 7 -
- 8 -。