高三数学备考冲刺140分问题34椭圆双曲线抛物线与圆相结合问题含解析

合集下载

第76题椭圆、双曲线、抛物线与圆相结合的问题精品之高中数学(理)黄金100题系列(解析版)

第76题椭圆、双曲线、抛物线与圆相结合的问题I ．题源探究·黄金母题【例1】一动圆与圆05622=+++x y x 外切，同时与圆091622=--+x y x 内切，求动圆圆心的轨迹方程，并说明它是什么曲线．【解析】设圆:1C 05622=+++x y x ，即4)3(22=++y x ，圆心)0,3(1-C ，半径21=r ；设圆:2C 091622=--+x y x ，即100)3(22=+-y x ，圆心)0,3(2C ，半径102=r ，设动圆圆心为),(y x P ，半径为r ，由于动圆P 与圆1C 外切，则21+=r PC ，由于动圆P 与圆2C 内切，则 r PC -=102，所以1221=+PC PC ，而12621<=C C ，因此点P 的轨迹是以21C C 、为焦点的椭圆．设椭圆方程为：)0(12222>>=+b a by a x ，27936,3,6,122222=-=-====c a b c a a ，动圆圆心的轨迹方程为1273622=+y x ，它表示一个焦点在x 轴上的椭圆．精彩解读【试题来源】人教版选修2-1第50页习题2．2B 组第2题【母题评析】本题属于求轨迹问题，采用定义法求轨迹方程．求轨迹问题在近几年高考试题中很常见，采用命题的形式往往是解答题的其中一步．【思路方法】利用两圆外切、内切的条件要求列出式子，经过推到转化为动点需要满足的条件要求，符合定义，最后求出轨迹方程，这是定义法求轨迹．II ．考场精彩·真题回放【例1】【2017新课标III 】已知双曲线C ：()222210,0x y a b a b -=>>的一条渐近线方程为52y x =，且与椭圆221123x y +=有公共焦点，则C 的方程为（） A ．221810x y -= B ．22145x y -=【命题意图】本类题通常主要轨迹方程及求轨迹，考查学生对求轨迹的基本方法的掌握情况及对圆锥曲线的概念的掌握情况．【考试方向】这类试题在考查题型上，通常基本以解答的形式出现，选填题较少，难度持中，一般会出现在解答题中的一步．【难点中心】1．双曲线与椭圆共焦点问题；待定系数法C ．22154x y -= D ．22143x y -= 【答案】B【解析】双曲线C ：()222210,0x y a b a b-=>>的渐近线方程为by x a =±，椭圆中：222212,3,3a b c a b ==∴=-=，椭圆，即双曲线的焦点为()3,0±，据此可得双曲线中的方程组222523b a c a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩，解得224,5a b ==，则双曲线C 的方程为2145x y 2-=，故选B ．【例2】【2017高考新课标II 】若双曲线C :22221x y a b-=（0a >，0b >）的一条渐近线被圆()2224x y -+=所截得的弦长为2，则C 的离心率为（） A ．2 B ．3 C ．2 D ．233【答案】A【解析】由几何关系可得，双曲线()222210,0x y a b a b-=>>的渐近线为：0bx ay ±=，圆心()2,0到渐近线距离为：22213d =-=，不妨考查点()2,0到直线0bx ay +=的距离：222023b a bd c a b+⨯===+，即：()22243c a c -=，整理可得224c a =，双曲线的离心率2242c e a===．故选A ．求双曲线的方程．【名师点睛】求双曲线的标准方程的基本方法是待定系数法．具体过程是先定形，再定量，即先确定双曲线标准方程的形式，然后再根据,,,a b c e 及渐近线之间的关系，求出,a b 的值．如果已知双曲线的渐近线方程，求双曲线的标准方程，可利用有公共渐近线的双曲线方程为()2220x y a bλλ2-=≠，再由条件求出λ的值即可．2．直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系；在解决直线与抛物线的位置关系时，要特别注意直线与抛物线的对称轴平行的特殊情况．中点弦问题，可以利用“点差法”，但不要忘记验证Δ＞0或说明中点在曲线内部．【例3】【2017新课标I 】已知双曲线C ：22221x y a b-=（a>0，b>0）的右顶点为A ，以A 为圆心，b 为半径作圆A ，圆A 与双曲线C 的一条渐近线交于M 、N 两点．若∠MAN=60°，则C 的离心率为________．【答案】233【解析】如图所示，作AP MN ⊥，因为圆A 与双曲线C 的一条渐近线交于M 、N 两点，则MN 为双曲线的渐近线by x a=上的点，且(,0)A a ，AM AN b ==，而AP MN ⊥，30PAN ∴∠=︒，点(,0)A a 到直线by x a =的距离22||1b AP b a=+．在Rt PAN ∆中，cos PAPAN NA=，代入计算得223a b =，即3a b =，由222c a b =+得2c b =，22333c b e a b∴===．【例4】【2017高考新课标III 】已知抛物线C ：y 2=2x ，过点（2，0）的直线l 交C 与A ，B 两点，圆M 是以线段AB 为直径的圆．（1）证明：坐标原点O 在圆M 上；（2）设圆M 过点()4,2P -，求直线l 与圆M 的方程．【答案】(1)证明略；(2)直线l 的方程为20x y --=，圆M 的方程为()()223110x y -+-=，或直线l 的方程为240x y +-=，圆M 的方程为2291854216x y ⎛⎫⎛⎫-++=⎪ ⎪⎝⎭⎝⎭．【解析】试题分析：(1)设出点的坐标，联立直线与圆的方程，由斜率之积为1- 可得OA OB ⊥，即得结论；(2)结合(1)的结论求得实数m 的值，分类讨论即可求得直线l 的方程和圆M 的方程．试题解析：(1)设()()1122,,,A x y B x y ，:2l x my =+ ．由22,2x my y x=+⎧⎨=⎩ 可得2240y my --= ，则124y y = ．又221212,22y y x x == ，故()2121244y y x x == ．因此OA 的斜率与OB 的斜率之积为1212414y y x x -⋅==- ，所以OA OB ⊥ ．故坐标原点O 在圆M 上． (2)由(1)可得()21212122,424y y m x x m y y m +=+=++=+ ．故圆心M 的坐标为()22,m m + ，圆M 的半径()2222r m m =++ ．由于圆M 过点()4,2P - ，因此0AP BP ⋅= ，故()()()()121244220x x y y --+++= ，即()()1212121242200x x x x y y y y ++++++= ．由(1)可得12124,4y y x x =-= ．所以2210m m --= ，解得1m = 或12m =-．当1m = 时，直线l 的方程为20x y --= ，圆心M 的坐标为()3,1 ，圆M 的半径为10 ，圆M 的方程为()()223110x y -+-= ．当12m =-时，直线l 的方程为240x y +-= ，圆心M 的坐标为91,42⎛⎫-⎪⎝⎭，圆M 的半径为854 ，圆M 的方程为2291854216x y ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭．【例5】【2017高考山东卷】在平面直角坐标系xOy 中，椭圆E ：22221x y a b+=()0a b >>的离心率为22，焦距为2．（Ⅰ）求椭圆E 的方程；（Ⅱ）如图，动直线l ：132y k x =-交椭圆E 于,A B 两点，C 是椭圆E 上一点，直线OC 的斜率为2k ，且1224k k =，M 是线段OC 延长线上一点，且:2:3MC AB =，M 的半径为MC ，,OS OT 是M 的两条切线，切点分别为,S T ．求SOT∠的最大值，并求取得最大值时直线l 的斜率．【答案】（I ）2212x y +=．（Ⅱ）SOT ∠的最大值为3π，取得最大值时直线l 的斜率为122k =±．【解析】试题分析：（I ）本小题由22c e a ==，22c =确定,a b 即得．（Ⅱ）通过联立方程组2211,23,2x y y k x ⎧+=⎪⎪⎨⎪=-⎪⎩化简得到一元二次方程后应用韦达定理，应用弦长公式确定||AB 及圆M 的半径r 表达式．进一步求得直线OC 的方程并与椭圆方程联立，确定得到||OC r的表达式，研究其取值范围．这个过程中，可考虑利用换元思想，应用二次函数的性质及基本不等式．试题解析：（I ）由题意知 22c e a ==，22c =，所以 2,1a b ==，因此椭圆E 的方程为2212x y +=．（Ⅱ）设()()1122,,,A x y B x y ，联立方程2211,23,2x y y k x ⎧+=⎪⎪⎨⎪=-⎪⎩得()2211424310k x k x +--=，由题意知0∆>，且()112122211231,21221k x x x x k k +==-++，所以 22112112211181221k k AB kx x k ++=+-=+．由题意可知圆M 的半径r 为22112111822321k k r k ++=+ 由题设知1224k k =，所以2124k k =因此直线OC 的方程为124y x k =．联立方程2211,22,4x y y x k ⎧+=⎪⎪⎨⎪=⎪⎩得2221221181,1414k x y k k ==++，因此 2221211814k OC x y k +=+=+．由题意可知 1sin21SOT rOC r OCr ∠==++，而2121221121181411822321k OC k r k k k ++=+++ 21221112324141k k k +=++，令2112t k =+，则()11,0,1t t >∈，因此2223313112221121119224OC t r t t t t t ===≥+-⎛⎫+---+ ⎪⎝⎭，当且仅当112t =，即2t =时等号成立，此时122k =±，所以1sin 22SOT ∠≤，因此26SOT π∠≤，所以SOT ∠最大值为3π．综上所述：SOT ∠的最大值为3π，取得最大值时直线l 的斜率为122k =±．【例6】【2017高考天津卷】设椭圆22221(0)x y a b a b+=>>的左焦点为F ，右顶点为A ，离心率为12．已知A 是抛物线22(0)y px p =>的焦点，F 到抛物线的准线l 的距离为12．（I ）求椭圆的方程和抛物线的方程；（II ）设l 上两点P ，Q 关于x 轴对称，直线AP 与椭圆相交于点B （B 异于点A ），直线BQ 与x 轴相交于点D ．若APD △的面积为62，求直线AP 的方程．【答案】（1）22413y x +=， 24y x =．（2）3630x y +-=，或3630x y --=．【解析】试题分析：由于A 为抛物线焦点，F 到抛物线的准线l 的距离为12，则12a c -=，又椭圆的离心率为12，求出,,c a b ，得出椭圆的标准方程和抛物线方程；则(1,0)A ，设直线AP 方程为设1(0)x my m =+≠，解出P Q 、两点的坐标，把直线AP 方程和椭圆方程联立解出B 点坐标，写出BQ 所在直线方程，求出点D 的坐标，最后根据APD △的面积为62解方程求出m ，得出直线AP 的方程．试题解析：（Ⅰ）解：设F 的坐标为(,0)c -．依题意，12ca =，2p a =，12a c -=，解得1a =，12c =，2p =，于是22234b a c =-=．所以，椭圆的方程为22413y x +=，抛物线的方程为24y x =．（Ⅱ）解：设直线AP 的方程为1(0)x my m =+≠，与直线l 的方程1x =-联立，可得点2(1,)P m --，故2(1,)Q m-．将1x my =+与22413y x +=联立，消去x ，整理得22(34)60m y my ++=，解得0y =，或2634my m -=+．由点B 异于点A ，可得点222346(,)3434m m B m m -+-++．由2(1,)Q m -，可得直线BQ 的方程为22262342()(1)(1)()03434m m x y m m m m--+-+-+-=++，令0y =，解得222332m x m -=+，故2223(,0)32m D m -+．所以2222236||13232m m AD m m -=-=++．又因为APD △的面积为62，故221626232||2m m m ⨯⨯=+，整理得2326||20m m -+=，解得6||3m =，所以63m =±．所以，直线AP 的方程为3630x y +-=，或3630x y --=．III ．理论基础·解题原理考点一椭圆与圆相结合的问题圆与的结合点有：（1）圆的几何性质与椭圆相联系；（2）利用椭圆的性质判断直线与圆的位置关系．考点二双曲线与圆结合的问题由于双曲线具有渐近线，故渐近线与圆的位置关系便成为命题的常考点．圆本身所具有的几何性质在探索等量关系也经常考查，进而求解双曲线的几何性质，如离心率的求解．圆与双曲线的结合点有：（1）利用圆的性质解决双曲线的相关问题；（2）圆的切线与双曲线相联系；考点三抛物线与圆相结合的问题．圆与抛物线的结合点有：（1）圆的性质与抛物线相结合；（2）抛物线的性质与圆的相联系．IV ．题型攻略·深度挖掘【考试方向】这类试题，可以是选择题、填空题，难度中等，也可以是解答题，这是难度大，为压轴题．【技能方法】灵活运用圆、椭圆、双曲线、抛物线的定义、标准方程及其简单几何性质解决问题．【易错指导】解题过程中最容易出现以下错误：其一是不能正确地运用导数的几何意义求抛物线上点的切线的斜率，进而导致出现错误；其二是不能正确地找出直线与圆的位置关系即切线与过切点的半径垂直的结论，从而导致无法求解．V ．举一反三·触类旁通考向一椭圆与圆相结合的问题【例1】设Q P ,分别为()2622=-+y x 和椭圆11022=+y x 上的点，则Q P ,两点间的最大距离是______________．【答案】26【点评】本题通过圆的性质将Q P ,两点间的最大距离可以转化为圆心到椭圆上的点的最大距离再加上圆的半径进行解决．【例2】【2018湖南师大附中模拟】已知椭圆C 的中心在原点，离心率为22，其右焦点是圆E ：22(1)1x y -+=的圆心．（1）求椭圆C 的标准方程；（2）如图，过椭圆C 上且位于y 轴左侧的一点P 作圆E 的两条切线，分别交y 轴于点M 、N ．试推断是否存在点P ，使14||3MN =？若存在，求出点P 的坐标；若不存在，请说明理由．【分析】(1)由已知条件分别求出,a c 的值，而222b ac =-，代入求出椭圆的方程；(2)假设存在点P 满足题意，设点00(,)P x y （00x <），(0,)M m ，(0,)N n ，利用条件求出直线PM 方程，根据圆心(1,0)E 到直线PM 的距离为1，求出m 与点P 坐标之间的关系，同理求出n 与点P 坐标之间的关系，利用韦达定理求出,m n mn +的表达式，算出MN ，求出P 点坐标．【解析】（1）设椭圆方程22221(0)x y a b a b+=>>，半焦距为c ，因为椭圆的右焦点是圆E 的圆心，则1c =，因为椭圆的离心率为22，则22c a =，即22a c ==，从而2221b a c =-=，故椭圆C 的方程为2212x y +=．由此可知，m ，n 为方程2000(2)20x x y x x -+-=的两个实根，所以0022y m n x +=--，002x mn x =--， 2||||()4MN m n m n mn =-=+-20020044(2)2y x x x =+--220002044(2)x y x x +-=-．因为点00(,)P x y 在椭圆C 上，则220012x y +=，即220012x y =-，则2200022002842(2)4||(2)(2)x x x MN x x -+--==--2042(2)x =--，令204142(2)3x -=-，则20(2)9x -=，因为00x <，则01x =-，220012x y =-12=，即022y =±，故存在点2(1,)2P -±满足题设条件．【点评】(1)处理直线与圆的弦长问题时多用几何法，即弦长的一半、弦心距、半径构成直角三角形． (2)圆的切线问题的处理要抓住圆心到直线的距离等于半径，从而建立关系解决问题．【例3】已知椭圆C ：2224x y +=．（1）求椭圆C 的离心率；（2）设O 为原点，若点A 在椭圆C 上，点B 在直线2y =上，且OA OB ⊥，试判断直线AB 与圆222x y +=的位置关系，并证明你的结论．【分析】（1）把椭圆C ：2224x y +=化为标准方程，确定2a ，2b ，利用ace =求得离心率；（2）设点),(00y x A ，)2,(t B ，其中00≠x ，由OB OA ⊥，即0=∙OB OA ，用0x 、0y 表示t ，当t x =0或t x ≠0分别根据点到直线的距离公式求出圆心到直线的距离，与圆的半径比较，从而判断直线AB 与圆222x y +=的位置关系．（2）直线AB 与圆222=+y x 相切，证明如下：设点),(00y x A ，)2,(t B ，其中00≠x ，因为OB OA ⊥，所以0=∙OB OA ，即0200=+y tx ，解得02x y t -=，当t x =0时，220t y -=，代入椭圆C 的方程得2±=t ，此时直线AB 与圆222=+y x 相切．当t x ≠0时，直线AB 的方程为)(2200t x tx y y ---=-，即02)()2(0000=-+---ty x y t x x y ，圆心到直线AB 的距离为202000)()2(|2|t x y ty x d -+--=，又422020=+y x ，02x y t -=，故22168|4|4|22|202040020202020200200=+++=++-=x x x x x x y y x x y x d ．故此直线AB 与圆222=+y x 相切．【跟踪练习】1．【2018江西吉安模拟】已知椭圆()2222:10x y W a b a b +=>>的离心率为32，其左顶点A 在圆22:16O x y +=上．（Ⅰ）求椭圆W 的方程；（Ⅱ）若点P 为椭圆W 上不同于点A 的点，直线AP 与圆O 的另一个交点为Q ，是否存在点P ，使得3PQ AP=？若存在，求出点P 的坐标；若不存在，说明理由．【答案】（I ）221164x y +=；（II ）不存在，理由见解析．（II ）设点()11,P x y ，()22,Q x y ，设直线AP 的方程为()4y k x =+，与椭圆方程联立得()2241164y k x x y =+⎧⎪⎨+=⎪⎩，化简得到()2222143264160k x k x k +++-=，因为-4为方程的一个根，所以()21232414k x k -+-=+，所以21241614k x k -=+所以228114k AP k +=+因为圆心到直线AP 的距离为2414kd k =+，所以222168216211AQ d k k =-==++．因为1PQ AQ AP AQ APAPAP-==-，代入得到222222228143311*********PQ k k k AP k k kk k ++=-=-==-+++++，显然23331k -≠+，所以不存在直线AP ，使得3PQ AP=．2．已知椭圆()2222+=10x y a b a b >>的左焦点为(),0F c -，离心率为33，点M 在椭圆上且位于第一象限，直线FM 被圆222+4b x y =截得的线段的长为c ，43=3FM ．（1）求直线FM 的斜率；（2）求椭圆的方程；（3）设动点P 在椭圆上，若直线FP 的斜率大于2，求直线OP （O 为原点）的斜率的取值范围．【分析】(1)由椭圆知识先求出,,a b c 的关系，设直线FM 的方程为()y k x c =+，求出圆心到直线的距离，由勾股定理可求斜率k 的值； (2)由(1)设椭圆方程为2222132x y c c+=，直线与椭圆方程联立，求出点M 的坐标，由433FM =可求出c ，从而可求椭圆方程；(3)设出直线FP ：(1)y t x =+，与椭圆方程联立，求得226223(1)x t x -=>+，求出x 的范围，即可求直线OP 的斜率的取值范围．(3)设点P 的坐标为(,)x y ，直线FP 的斜率为t ，得1yt x =+，即(1)y t x =+(1)x ≠-，与椭圆方程联立22(1)132y t x x y =+⎧⎪⎨+=⎪⎩，消去y ，整理得22223(1)6x t x ++=，又由已知，得226223(1)x t x -=>+，解得312x -<<-或10x -<<，设直线OP 的斜率为m ，得y m x =，即(0)y mx x =≠，与椭圆方程联立，整理可得22223m x =-．①当3,12x ⎛⎫∈-- ⎪⎝⎭时，有(1)0y t x =+<，因此0m >，于是2223m x =-，得223,33m ⎛⎫∈ ⎪⎝⎭ ②当()1,0x ∈-时，有(1)0y t x =+>，因此0m <，于是2223m x =--，得23,3m ⎛⎫∈-∞- ⎪⎝⎭综上所述，直线OP 的斜率的取值范围是23223,,333⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭3．【2015福建高考理18】已知椭圆()2222:10x y E a b a b +=>>过点()0,2，且离心率22e =．(1)求椭圆E 的方程；(2)设直线():1l x my m =-∈R 交椭圆E 于A ，B 两点，判断点94G ⎛⎫- ⎪⎝⎭,0与以线段AB 为直径的圆的位置关系，并说明理由．【解析】解法一：（1）由已知得222222b ca abc ⎧=⎪⎪=⎨⎪⎪=+⎩，解得222a b c =⎧⎪=⎨⎪=⎩，所以椭圆E 的方程为22142x y +=．故()22201252514216AB GH my m y y -=+++=()()()22222231525172021622162m m m m m m ++-+=>+++，所以2AB GH >．故点9,04G ⎛⎫-⎪⎝⎭在以AB 为直径的圆外．解法二：（1）同解法一．（2）设点()11,A x y ，()22,B x y ，则119,4GA x y ⎛⎫=+⎪⎝⎭，229,4GB x y ⎛⎫=+ ⎪⎝⎭．由221142x my x y =-⎧⎪⎨+=⎪⎩，得()222230m y my +--=，所以12222m y y m +=+，12232y y m =-+，从而12129944GA GB x x y y ⎛⎫⎛⎫=+++= ⎪⎪⎝⎭⎝⎭12125544my my y y ⎛⎫⎛⎫+++= ⎪⎪⎝⎭⎝⎭()()212125251416m y y m y y ++++=()22225312522216m m m m -+++=++()221720162m m +>+，所以cos ,0GA GB >．又GA ，GB 不共线，所以AGB ∠为锐角．故点9,04G ⎛⎫-⎪⎝⎭在以AB 为直径的圆外． 4．如图所示，已知A 、B 、C 是长轴长为4的椭圆E 上的三点，点A 是长轴的一个端点，BC 过椭圆中心O ，且0AC BC ⋅=，2BC AC =．（1）求椭圆E 的方程；（2）在椭圆E 上是否存点Q ，使得222QB QA -=？若存在，有几个（不必求出Q 点的坐标），若不存在，请说明理由；（3）过椭圆E 上异于其顶点的任一点P ，作圆224:3O x y +=的两条线，切点分别为M 、N ，若直线MN 在x 轴、y 轴上的截距分别为m 、n ，证明：22113m n +为定值．【解析】：（1）依题意知：椭圆的长半轴长2a =，则()2,0A ，解法二：设在椭圆E 上存在点Q ，使得222QB QA -=，设()00,Q x y ，则()()()2222220000001126222QB QA x y x y x y -=+++---=+-=，即00320x y +-=，①又点Q 在椭圆E 上，2200340x y ∴+-=，②由①式得0023y x =-代入②式并整理得：2007920x x -+=，③方程③的根判别式8156250∆=-=>，∴方程③有两个不相等的实数根，即满足条件的点Q 存在，且有两个；解法二：设点()11,P x y 、()22,M x y 、()33,N x y ，则221PM OMx k k y =-=-，直线PM 的方程为()2222x y y x x y -=--，化简得2243x x y y +=，④同理可得直线PN 的方程为3343x x y y +=，⑤把P 点的坐标代入④、⑤得121213134343x x y y x x y y ⎧+=⎪⎪⎨⎪+=⎪⎩，∴直线MN 的方程为1143x x y y +=，令0y =，得143m x =，令0x =得143n y =， 143x m ∴=，143y n =，又点P 在椭圆E 上，22443433m n ⎛⎫⎛⎫∴+= ⎪ ⎪⎝⎭⎝⎭，即2211334m n +=（定值）． 5．【2018河北正定中学月考】已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12，以原点O 为圆心，椭圆的短半轴长为半径的圆与直线60x y -+=相切．（1）求椭圆C 的标准方程；（2）若直线m kx y l +=:与椭圆C 相交于B A ,两点，且22OA OB b k k a⋅=-，判断AOB ∆的面积是否为定值？若为定值，求出定值；若不为定值，说明理由．【答案】（1） 22143y x +=；（2）AOB ∆的面积为定值3．22221212121223(4)()()().34m k y y kx m kx m k x x mk x x m k-⋅=+⋅+=+++=+ 34OA OBk k ⋅=-，121234y y x x =-，121234y y x x =-，222223(4)34(3)34434m k m k k --=-⋅++，22243m k -=，8分 ()()()22222212122248432411413434k m k AB kx x x x kkk-++=++-=+=++21md k =+，()()()()22222222412411113223423411k k m m S AB d k k k k ∆++====++++．6．如图，已知椭圆C:22221(0)x y a b a b+=>>的离心率为32，以椭圆的左顶点T 为圆心作圆T:2222)(0),x y r r ++=>（设圆T 与椭圆C 交于点M 、N ．（Ⅰ）求椭圆C 的方程；（Ⅱ）求TM TN ⋅的最小值，并求此时圆T 的方程；（Ⅲ）设点P 是椭圆C 上异于M ，N 的任意一点，且直线MP ，NP 分别与x 轴交于点R ，S ，O 为坐标原点．试问；是否存在使POSPOR S S ∆∆⋅最大的点P ，若存在求出P 点的坐标，若不存在说明理由．（II ）点M 与点N 关于x 轴对称，设1111(,),(,)M x y N x y -，不妨设10y >，由于点M 在椭圆C 上，∴221114x y =-，由已知),2(),,2),0,2(1111y x TN y x TM T -+=+=-（则， 22111111(2,)(2,)(2)TM TN x y x y x y ∴⋅=++-=+-2221115812)(1)()4455x x x =+--=+-（，由于22,x -<<故当185x =-时，TM TN ⋅取得最小值为15-，当185x =-时135y =，故83(,),55M -又点M 在圆T 上，代入圆的方程得21325r =，故圆T 的方程为：22132)25x y ++=（；7．【2018浙江临海统练】已知抛物线C ：24x y = ，过焦点F 的直线l 与抛物线交于,A B 两点（A 在第一象限）．（1）当2OFA OFB S S ∆∆=时，求直线l 的方程；（2）过点2(2,)A t t 作抛物线C 的切线1l 与圆22(1)1x y ++=交于不同的两点,M N ，设F 到1l 的距离为d ，求MNd的取值范围． XYOABF【答案】（1）214y x =+；（2）3(0,]2（2）由于24x y =，因此'2xy =故切线1l 的方程为2(2)y t t x t -=-，化简得20tx y t --=则圆心（0，-1）到1l 的距离为212|1|1t d t -=+，且11d <，故203t <<，则21||21MN d=-2232||1t t t -=+，则点F 到1l 距离21d t =+，则24423221MN t t d t t -=++，今2424242235125112121816t t t m z t t t t m m -+==-+=-+++++++ 251(1,16)m t =+∈ 则2591(0,]16168z m m=-+∈++，故3(0,]2MN d ∈． 8．如图所示，已知A 、B 、C 是长轴长为4的椭圆E 上的三点，点A 是长轴的一个端点，BC 过椭圆中心O ，且0AC BC ⋅=，2BC AC =．（1）求椭圆E 的方程；（2）在椭圆E 上是否存点Q ，使得222QB QA -=？若存在，有几个（不必求出Q 点的坐标），若不存在，请说明理由；（3）过椭圆E 上异于其顶点的任一点P ，作圆224:3O x y +=的两条线，切点分别为M 、N ，若直线MN 在x 轴、y 轴上的截距分别为m 、n ，证明：22113m n +为定值．（2）解法一：设在椭圆E 上存在点Q ，使得222QB QA -=，设()00,Q x y ，则()()()2222220000001126222QB QA x y x y x y -=+++---=+-=，即点Q 在直线320x y +-=上，∴点Q 即直线320x y +-=与椭圆E 的交点，直线320x y +-=过点2,03⎛⎫⎪⎝⎭，而点椭圆2,03⎛⎫⎪⎝⎭在椭圆E 的内部， ∴满足条件的点Q 存在，且有两个；解法二：设在椭圆E 上存在点Q ，使得222QB QA -=，设()00,Q x y ，则()()()2222220000001126222QB QA x y x y x y -=+++---=+-=，即00320x y +-=，①又点Q 在椭圆E 上，2200340x y ∴+-=，②由①式得0023y x =-代入②式并整理得：2007920x x -+=，③ 方程③的根判别式8156250∆=-=>，∴方程③有两个不相等的实数根，即满足条件的点Q 存在，且有两个；（3）解法一：设点()11,P x y ，由M 、N 是圆O 的切点知，OM MP ⊥，ON NP ⊥，O ∴、M 、P 、N 四点在同一圆上，且圆的直径为OP ，则圆心为11,22x y ⎛⎫⎪⎝⎭，其方程为22221111224x y x y x y +⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭，即22110x y x x y y +--=，④即点M 、N 满足方程④，又点M 、N 都在圆O 上，M ∴、N 坐标也满足圆O 的方程2243x y +=，⑤ ⑤-④得直线MN 的方程为1143x x y y +=，令0y =，得143m x =，令0x =得143n y =， 143x m ∴=，143y n =，又点P 在椭圆E 上，22443433m n ⎛⎫⎛⎫∴+= ⎪ ⎪⎝⎭⎝⎭，即2211334m n +=（定值）；考向二双曲线与圆相结合的问题【例4】已知点(,0)(0)F c c ->是双曲线22221x y a b-=的左焦点，离心率为e ，过F 且平行于双曲线渐近线的直线与圆222x y c +=交于点P ，且点P 在抛物线24y cx =上，则e 2 =（） A ．352+ B ．5 C ．512- D ．152+ 【答案】D【点评】本题将双曲线的渐近线与圆的位置关系联系到一起，从而确定点P 的坐标，进而建立等量关系求解双曲线的离心率．【例5】已知双曲线12222=-by a x 的左右焦点分别为12F F 、，O 为双曲线的中心，P 是双曲线右支上的点，21F PF ∆的内切圆的圆心为I ，且圆I 与x 轴相切于点A ，过2F 作直线PI 的垂线，垂足为B ，若e 为双曲线的离心率，则( )A ．||||OA e OB = B ．||||OB e OA =C ．||||OA OB =D ．||OA 与||OB 关系不确定【答案】C【例6】已知双曲线12222=-by a x 的左右焦点分别为12F F 、，O 为双曲线的中心，P 是双曲线右支上的点，21F PF ∆的内切圆的圆心为I ，且圆I 与x 轴相切于点A ，过2F 作直线PI 的垂线，垂足为B ，若e 为双曲线的离心率，则( )A ．||||OA e OB = B ．||||OB e OA =C ．||||OA OB =D ．||OA 与||OB 关系不确定【答案】C【跟踪练习】1．【2017河北定州市上学期期中】过双曲线22115y x -=的右支上一点P ，分别向圆1C ：22(+4)+4x y =和圆2C ：22(4)1x y -+=作切线，切点分别为M ，N ，则22||||PM PN -的最小值为（） A ．10 B ．13 C ．16 D ．19 【答案】B【解析】由题可知，)1|(|)4|(|||||222122---=-PC PC PN PM ，因此=--=-3||||||||222122PC PC PN PM 121212(||||)2(||||)32||3PC PC PC PC C C -=+-≥-13=．故选B ．2．【2017届湖南长沙一中高三月考五】已知双曲线22221(a 0,b 0)x y a b-=>>的左、右焦点分别为1F 、2F ，过1F 作圆222x y a +=的切线分别交双曲线的左、右两支于点B 、C ，若2|BC ||CF |=，则双曲线的渐近线方程为（）A ．3y x =±B ．22y x =±C ．(31)y x =±+D ．(31)y x =±- 【答案】C3．【2018河北武邑调研】已知双曲线()2222:10,0x y C a b a b==>>的右顶点为A ，O 为坐标原点，以A 为圆心的圆与双曲线C 的某渐近线交于两点P ，Q ．若60PAQ ∠=︒，且3OQ OP =，则双曲线C 的离心率为_________．【答案】724．双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为(,0)F c ，以原点为圆心，c 为半径的圆与双曲线在第二象限的交点为A ，若此圆在A 点处的切线的斜率为33，则双曲线C 的离心率为_________．【答案】31+【解析】设切点A 为00(,)x y ，则22200222200003,344x y c c c x y y x ⎧+=⎪⇒==⎨=-⎪⎩，代入22221x y a b -=，化简得：4224840c a c a -+=22(423)(31)31cc a c a a⇒=+⇒=+⇒=+． 5．已知点1F 、2F 为双曲线C ：()01222>=-b by x 的左、右焦点，过2F 作垂直于x 轴的直线，在x 轴上方交双曲线C 于点M ，且︒=∠3021F MF ．圆O 的方程是222b y x =+．（1）求双曲线C 的方程；（2）过双曲线C 上任意一点P 作该双曲线两条渐近线的垂线，垂足分别为1P 、2P ，求21PP PP ⋅的值；（3）过圆O 上任意一点()00y ,x Q 作圆O 的切线l 交双曲线C 于A 、B 两点，AB 中点为M ，求证：2AB OM =．解：（1）设2,F M 的坐标分别为220(1,0),(1,)b b y ++因为点M 在双曲线C 上，所以220211y b b+-=，即20y b =±，所以22MF b =在21Rt MF F ∆中，01230MF F ∠=，22MF b =，所以212MF b = ……2分由双曲线的定义可知：2122MF MF b -==故双曲线C 的方程为：2212y x -= ……4分（3）由题意，即证：OA OB ⊥．设1122(,),(,)A x y B x y ，切线l 的方程为：002x x y y += ……11分 ①当00y ≠时，切线l 的方程代入双曲线C 中，化简得：22220000(2)4(24)0y x x x x y -+-+=所以：2001212222200004(24),(2)(2)x y x x x x y x y x ++=-=--- 又22010201201201222200000(2)(2)82142()2x x x x x y y x x x x x x y y y y x ---⎡⎤=⋅=-++=⎣⎦-……13分所以……15分②当00y =时，易知上述结论也成立．所以……16分综上，OA OB ⊥，所以．6．圆224x y +=的切线与x 轴正半轴，y 轴正半轴围成一个三角形，当该三角形面积最小时，切点为P（如图），双曲线22122:1x y C a b-=过点P 且离心率为3．（1）求1C 的方程；（2）椭圆2C 过点P 且与1C 有相同的焦点，直线l 过2C 的右焦点且与2C 交于A ，B 两点，若以线段AB 为直径的圆心过点P ，求l 的方程．【解析】（Ⅱ）由（Ⅰ）知2C 的焦点坐标为(3,0),(3,0)-，由此2C 的方程为22221113x y b b +=+，其中10b >．由(2,2)P 在2C 上，得22112213b b +=+，显然，l 不是直线y =0．设l 的方程为x =my +3，点1122(,),(,)A x y B x y由223163x my x y ⎧=+⎪⎨+=⎪⎩ 得22(2)2330m y my ++-=，又12,y y 是方程的根，因此12212223232my y m y y m ⎧+=-⎪⎪+⎨-⎪=⎪+⎩①②，考向三抛物线与圆相结合的问题【例7】一个酒杯的轴截面是开口向上的抛物线的一段弧，它的口宽是的 4 10，杯深20，在杯内放一玻璃球，当玻璃球的半径r 最大取时，才能使玻璃球触及杯底．【答案】1【解析】建立如图所示的直角坐标系，酒杯所在抛物线的方程设为22(0)x py p =>，因为过点(210,20)，所以2(210)220,1p p =⨯=，即22(020)x y y =≤≤．玻璃球触及杯底，就是小球的截面圆222()x y r r +-=与抛物线22x y =有且仅有一个交点，即原点．由222()x y r r +-=与22x y =消去x 得：0y =或2 2.y r =-因为有且仅有一个交点，即原点，所以220,1,r r -≤≤即半径r 最大取1．【例8】【2018重庆模拟】已知椭圆()2212210x y C a b a b +=>>：离心率为63，焦距为22，抛物线()22:20C x py p =>的焦点F 是椭圆1C 的顶点．（Ⅰ）求1C 与2C 的标准方程；（Ⅱ）设过点F 的直线l 交2C 于,P Q 两点，若1C 的右顶点A 在以PQ 为直径的圆内，求直线l 的斜率的取值范围．【分析】（Ⅰ）椭圆1C 的焦距为222=c ，36=a c ，得椭圆的标准方程，得到抛物线焦点，可得抛物线方程；（Ⅱ）联立直线与抛物线的方程结合韦达定理得k x x 421=+，421-=⋅x x ，A 在以PQ 为直径的圆内⇔0<⋅AQ AP ，得结果．（Ⅱ）由题意可设直线的方程为：1y kx =+，设点()11,P x y ，()22,Q x y ，联立214y kx x y =+⎧⎨=⎩得2440x kx --=，由韦达定理得124x x k +=，124x x =-．A 在以PQ 为直径的圆内()1212120330AP AQ x x x x y y ⇔<⇔-+++<()2212121216163480x x x x x x ⇔-+++<，641634481600k k --⨯++<⇒>．【例9】已知抛物线2:2(0)E y px p =>的准线与x 轴交于点M ，过点M 作圆22:(2)1C x y -+=的两条切线，切点为A 、B ，42||3AB =．（1）求抛物线E 的方程；（2）过抛物线E 上的点N 作圆C 的两条切线，切点分别为P 、Q ，若P ，Q ，O （O 为原点）三点共线，求点N 的坐标．【解析】：（Ⅰ）由已知得M (－ p2，0)，C (2，0)．设AB 与x 轴交于点R ，由圆的对称性可知，|AR |＝223．于是|CR |＝|AC |2－|AR |2＝ 1 3，所以|CM |＝|AC |sin ∠AMC ＝|AC |sin ∠CAR＝3，即2＋ p2＝3，p ＝2．故抛物线E 的方程为y 2＝4x ．R BAMC yxOPQ NCyxO【跟踪练习】1．【2018四川双流模拟】已知P 为抛物线x y 42=上一个动点，Q 为圆1)4(22=-+y x 上一个动点，当点P 到点Q 的距离与点P 到抛物线的准线的距离之和最小时，点P 的横坐标为（）A ．8179- B ．89C ．817D ．17【答案】A2．【2018河南郑州模拟】已知抛物线28y x =，点Q 是圆22:28130C x y x y ++-+=上任意一点，记抛物线上任意一点到直线2x =-的距离为d ，则PQ d +的最小值为（） A ．5 B ．4 C ．3 D ．2 【答案】C3．【2018吉林长春模拟】已知点A 是抛物线()2:20C x px p =>上一点，O 为坐标原点，若,A B 是以点()0,10M 为圆心，OA 的长为半径的圆与抛物线C 的两个公共点，且ABO ∆为等边三角形，则p 的值是．【答案】564．已知圆222:()()C x a y b r -+-=的圆心为抛物线24x y =-的焦点，直线1x y +=与圆C 相切，则该圆的方程为___________________．【答案】22(1)2x y ++=5．如图，抛物线E ： 22(0)y px p =>与圆O ： 228x y +=相交于A ， B 两点，且点A 的横坐标为2．过劣弧AB 上动点()00,P x y 作圆O 的切线交抛物线E 于C ， D 两点，分别以C ， D 为切点作抛物线E 的切线1l ， 2l ， 1l 与2l 相交于点M ．（Ⅰ）求p 的值；（Ⅱ）求动点M 的轨迹方程．【注意问题】求出轨迹方程后注意范围，不符合的点．6．已知抛物线C ：22(0)y px p =>的焦点为F ，直线4y =与y 轴的交点为P ，与C 的交点为Q ，且5||||4QF PQ =．（I ）求C 的方程；（II ）过F 的直线l 与C 相交于A ，B 两点，若AB 的垂直平分线l '与C 相较于M ，N 两点，且A ，M ，B ，N 四点在同一圆上，求l 的方程．【解析】：（I ）设()0,4Q x ，代入22y px =，得00888,,.22p p x PQ QF x p p p=\==+=+．由题设得85824p p p+=?，解得2p =-（舍去）或2p =，∴C 的方程为24y x =；（II ）由题设知l 与坐标轴不垂直，故可设l 的方程为()10x my m =+?，代入24y x =得2440y my --=．设()()1122,,,,Ax y Bx y 则124,y y m +=124y y =-．故AB 的中点为()()2221221,2,141D m m AB m y y m +=+-=+．又l ¢的斜率为,m l ¢-\的方程为2123x y m m =-++．将上式代入24y x =，并整理得()2244230y y m m+-+=．设()()3344,,,,M x y B x y 则()234344,423y y y y m m+=-=-+．故MN 的中点为()22234222412122123,,1m m E m MN y y m m m m ++骣÷ç++-=+-=÷ç÷ç桫．由于MN 垂直平分线AB ，故,,,A M B N四点在同一圆上等价于12AE BE MN ==，从而22211,44AB DE MN +=即()()()2222222244121224122m m m m m m m++骣骣鼢珑+++++=鼢珑鼢珑桫桫，化简得210m -=，解得1m =或1m =-．所求直线l 的方程为10x y --=或10x y +-=．7．已知抛物线C ：22(0)y px p =>的焦点为F ，直线4y =与y 轴的交点为P ，与C 的交点为Q ，且5||||4QF PQ =．（I ）求C 的方程；（II ）过F 的直线l 与C 相交于A ，B 两点，若AB 的垂直平分线l '与C 相较于M ，N 两点，且A ，M ，B ，N 四点在同一圆上，求l 的方程．为2123x y m m =-++．将上式代入24y x =，并整理得()2244230y y m m+-+=．设()()3344,,,,M x y B x y 则()234344,423y y y y m m+=-=-+．故MN 的中点为()22234222412122123,,1m m E m MN y y m m m m ++骣÷ç++-=+-=÷ç÷ç桫．由于MN 垂直平分线AB ，故,,,A M B N 四点在同一圆上等价于12AE BE MN ==，从而22211,44AB DE MN +=即()()()2222222244121224122m m m m m m m++骣骣鼢珑+++++=鼢珑鼢珑桫桫，化简得210m -=，解得1m =或1m =-．所求直线l 的方程为10x y --=或10x y +-=．考向四椭圆、双曲线、抛物线与圆相结合的问题【例10】【2018安徽合肥一中、马鞍山二中等六校教育研究会高三上学期第一次联考】椭圆1C ：()22210x y a b a b +=>>的离心率为32，椭圆1C 截直线y x =所得的弦长为4105．过椭圆1C 的左顶点A 作直线l 与椭圆交于另一点M ，直线l 与圆2C ： ()()22240x y r r -+=>相切于点N ．（Ⅰ）求椭圆1C 的方程；（Ⅱ）若43AN MN =，求直线l 的方程和圆2C 的半径r ．【答案】(1) 2214x y +=；(2) :525100,25l x y r ±+==．（Ⅰ）由题意知， 32c a =，即22234a b a -=，∴224a b =，∵由椭圆1C 截直线y x =所得的弦长为4105，∴弦在第一象限的端点的坐标为2525,55⎛⎫ ⎪ ⎪⎝⎭，∴2244155a b +=，将224a b =代入上式，解得2,1a b ==．∴椭圆1C 的方程为2214x y +=．【例11】已知点()1,0F ，直线:1l x =-，直线l '垂直l 于点P ，线段PF 的垂直平分线交l '于点Q ．（1）求点Q 的轨迹C 的方程；（2）已知点()1,2H ，过F 且与x 轴不垂直的直线交C 于,A B 两点，直线,AH BH 分别交l 于点,M N ，求证：以MN 为直径的圆必过定点．（2）由题意可设直线():10AB x my m =+≠，代入24y x =，得2440y m y --=，设221212,,,44y y A y B y ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，则12124,4y y m y y +==-；又()1,2H ，设直线,AH BH 的斜率分别为12,k k ，则12122212122244,221144y y k k y y y y --====++--，设()()1,,1,M N M y N y --，令1x =-，得()111228222M y y y y -=-=++，同理，得()222228222N y y y y -=-=++，从而()()()()()121212121212424222244244·422244244M N y y y y y y m y y y y y y y y m ⎡⎤-++----⨯+⎣⎦====-+++++-+⨯+；12882222M N y y y y ⎛⎫⎛⎫+=-+- ⎪ ⎪++⎝⎭⎝⎭12114822y y ⎛⎫=-+ ⎪++⎝⎭()()12121284424y y y y y y ⎡⎤++⎣⎦=-+++()84444244m m +=--+⨯+4m=-．又以MN 为直径的圆的方程为： ()()()210M N x y y y y ++--=，即()()22·10M N M N y y y y y y x -++++=，即224230x x y y m +-++=，令220{230y x x y =+-+=，解得3x =-或1x =，从而以MN 为直径的圆恒过定点()3,0-和()1,0．【跟踪练习】1．【2018河南郑州模拟】如图，已知椭圆111:221=+y x C ，双曲线)0,0(1:22222>>=-b a by a x C ，若以1C 的长轴为直径的圆与2C 的一条渐近线交于A 、B 两点，且1C 与该渐近线的两交点将线段AB 三等分，则2C 的离心率为（）A ．5B ．5C ．17D ．7142【答案】A2．【2017届湖南师大附中高三上学期月考三】如图，抛物线21:8C y x =与双曲线()22222:10,0x y C a b a b-=>>有公共焦点2F ，点A 是曲线12,C C 在第一象限的交点，且25AF =．（Ⅰ）求双曲线2C 的方程；（Ⅱ）以1F 为圆心的圆M 与双曲线的一条渐近线相切，圆()22:21N x y -+=．已知点()1,3P ，过点P 作互相垂直且分别与圆M 、圆N 相交的直线1l 和2l ，设被圆M 截得的弦长为s ，2l 被圆N 截得的弦长为t ．试探索ts 是否为定值？请说明理由．【答案】（Ⅰ）2213y x -=；（Ⅱ）s t 为定值3．∴2083y =⨯，∴026y =±． ()()22132267AF =++±=又∵点A 在双曲线上，由双曲线定义得，2752a =-=，∴1a =． ∴双曲线的方程为：2213y x -=．（Ⅱ）s t为定值．下面给出说明：设圆M 的方程为：()2222x y r ++=，双曲线的渐近线方程为：3y x =±．∵圆M 与渐近线3y x =±相切，∴圆M 的半径为()223313r ==+．故圆()22:23M x y ++=．依题意12l l 、的斜率存在且均不为零，设1l 的方程为()31y k x -=-，即30kx y k -+-=，设2l 的方程为()131y x k -=--，即310x k y k +--=，∴点M 到直线1l 的距离为12331k d k-=+，点N 到直线2l 的距离为22311k d k -=+，∴直线1l 被圆M 截得的弦长22223363623211k k k s k k ⎛⎫--=-= ⎪ ⎪++⎝⎭，直线2l 被圆N 截得的弦长22223123221211k k k t k k ⎛⎫--=-= ⎪ ⎪++⎝⎭， ∴()()222263636323223k k s k k t k k k k --===--，故s t为定值3．。

高中数学高考试卷考点之椭圆双曲线抛物线和圆锥曲线的综合应用知识汇总,带参考答案共五十六页

数学高考试卷椭圆双曲线抛物线和圆锥曲线的综合应用，带参考答案本文收集整理了高中数学高考试卷椭圆、双曲线、抛物线和圆锥曲线的综合应用知识知识，并配上详细参考答案，内容全共五十六页。

同学们认真完成这些练习，并对过答案，对学习高中椭圆、双曲线、抛物线和圆锥曲线的综合应用知识知识，一定有很大的帮助，希望大家喜欢这份文档。

一、椭圆知识1．（2018全国Ⅱ，12）已知F 1，F 2是椭圆C ： x 2a +y 2b =1 (a >b >0)的左，右焦点，A是C 的左顶点，点P 在过A 且斜率为√36的直线上，△PF 1F 2为等腰三角形，∠F 1F 2P =120°，则C 的离心率为( )A ．23 B ．12 C ．13 D ．141.答案：D 因为△PF 1F 2为等腰三角形，∠F 1F 2P =120°，所以PF 2=F 1F 2=2c,由AP 斜率为√36得，tan∠PAF 2=√36,∴sin∠PAF 2=√13cos∠PAF 2=√12√13，由正弦定理得PF 2AF 2=sin∠PAF 2sin∠APF 2,所以2c a+c =1√13sin(π3−∠PAF 2)1√13√32⋅√12√13−12⋅1√1325∴a =4c,e =14，选D.2.（2017•新课标Ⅲ,10）已知椭圆C ： =1（a ＞b ＞0）的左、右顶点分别为A 1 ， A 2 ，且以线段A 1A 2为直径的圆与直线bx ﹣ay+2ab=0相切，则C 的离心率为（）A. B. C. D.2. 答案：A 以线段A 1A 2为直径的圆与直线bx ﹣ay+2ab=0相切， ∴原点到直线的距离=a ，化为：a 2=3b 2 ． ∴椭圆C 的离心率e= = = ．故选A ．3.（2017•浙江,）椭圆+=1的离心率是（）A. B. C. D.3. 答案：B 椭圆+=1，可得a=3，b=2，则c==，所以椭圆的离心率为： =．故选B ．4.(2016·浙江，7)已知椭圆C 1：x 2m 2＋y 2＝1(m ＞1)与双曲线C 2：x 2n2－y 2＝1(n ＞0)的焦点重合，e 1，e 2分别为C 1，C 2的离心率，则( )A.m ＞n 且e 1e 2＞1B.m ＞n 且e 1e 2＜1C.m ＜n 且e 1e 2＞1D.m ＜n 且e 1e 2＜14.答案： A [由题意可得：m 2－1＝n 2＋1，即m 2＝n 2＋2，又∵m ＞0，n ＞0，故m ＞n . 又∵e 21·e 22＝m 2－1m 2·n 2＋1n 2＝n 2＋1n 2＋2·n 2＋1n 2＝n 4＋2n 2＋1n 4＋2n 2＝1＋1n 4＋2n 2＞1，∴e 1·e 2＞1.] 5.(2016·全国Ⅲ，11)已知O 为坐标原点，F 是椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左焦点，A ，B分别为C 的左，右顶点.P 为C 上一点，且PF ⊥x 轴.过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E .若直线BM 经过OE 的中点，则C 的离心率为( ) A.13 B.12 C.23 D.345.A [设M (－c ，m )，则E ⎝⎛⎭⎫0，am a －c ，OE 的中点为D ，则D ⎝⎛⎭⎫0，am2（a －c ），又B ，D ，M 三点共线，所以m 2（a －c ）＝m a ＋c，a ＝3c ，e ＝13.]6.(2014·大纲全国，6)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点为F 1、F 2，离心率为33，过F 2的直线l 交C 于A 、B 两点.若△AF 1B 的周长为43，则C 的方程为( ) A.x 23＋y 22＝1 B.x 23＋y 2＝1 C.x 212＋y 28＝1 D.x 212＋y 24＝1 6.A [由椭圆的性质知|AF 1|＋|AF 2|＝2a ，|BF 1|＋|BF 2|＝2a ， ∴△AF 1B 的周长＝|AF 1|＋|AF 2|＋|BF 1|＋|BF 2|＝43，∴a ＝ 3.又e ＝33，∴c ＝1.∴b 2＝a 2－c 2＝2，∴椭圆的方程为x 23＋y 22＝1，故选A.]7．（2018浙江，17）已知点P (0，1)，椭圆x24+y 2=m (m >1)上两点A ，B 满足AP⃑⃑⃑⃑⃑ =2PB ⃑⃑⃑⃑⃑ ，则当m =___________时，点B 横坐标的绝对值最大．7.5 设A(x 1,y 1),B(x 2,y 2)，由AP ⃑⃑⃑⃑⃑ =2PB ⃑⃑⃑⃑⃑ 得−x 1=2x 2,1−y 1=2(y 2−1),∴−y 1=2y 2−3, 因为A ,B 在椭圆上,所以x 124+y 12=m,x 224+y 22=m, ∴4x 224+(2y 2−3)2=m,∴x 224+(y 2−32)2=m4，与x 224+y 22=m 对应相减得y 2=3+m 4,x 22=−14(m 2−10m +9)≤4，当且仅当m =5时取最大值.8.(2016·江苏，10)如图，在平面直角坐标系xOy 中，F 是椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的右焦点，直线y ＝b2与椭圆交于B ，C 两点，且∠BFC ＝90°，则该椭圆的离心率是________.8.63 [联立方程组⎩⎨⎧x 2a 2＋y 2b 2＝1，y ＝b2，解得B 、C 两点坐标为B ⎝⎛⎭⎫－32a ，b 2,C ⎝⎛⎭⎫32a ，b2,又F (c ,0),则FB →＝⎝⎛⎭⎫－32a －c ，b 2，FC →＝⎝⎛⎭⎫3a 2－c ，b 2，又由∠BFC ＝90°，可得FB →·FC →＝0，代入坐标可得：c 2－34a 2＋b 24＝0①，又因为b 2＝a 2－c 2.代入①式可化简为c 2a 2＝23，则椭圆离心率为e ＝ca＝23＝63. 9.(2014·辽宁，15)已知椭圆C ：x 29＋y 24＝1，点M 与C 的焦点不重合.若M 关于C 的焦点的对称点分别为A ，B ，线段MN 的中点在C 上，则|AN |＋|BN |＝________.9.12 [设MN 交椭圆于点P ，连接F 1P 和F 2P (其中F 1、F 2是椭圆C 的左、右焦点)，利用中位线定理可得|AN |＋|BN |＝2|F 1P |＋2|F 2P |＝2×2a ＝4a ＝12.] 10.(2014·安徽，14)设F 1，F 2分别是椭圆E ：x 2＋y 2b 2＝1(0<b <1)的左、右焦点，过点F 1的直线交椭圆E 于A ，B 两点.若|AF 1|＝3|F 1B |，AF 2⊥x 轴，则椭圆E 的方程为________. 10.x 2＋3y 22＝1 [设点A 在点B 上方，F 1(－c ，0)，F 2(c ，0)，其中c ＝1－b 2，则可设A (c ，b 2)，B (x 0，y 0)，由|AF 1|＝3|F 1B |，可得AF 1→＝3F 1B →，故⎩⎪⎨⎪⎧－2c ＝3（x 0＋c ），－b 2＝3y 0，即⎩⎨⎧x 0＝－53c ，y 0＝－13b 2，代入椭圆方程可得25（1－b 2）9＋19b 2＝1，得b 2＝23，故椭圆方程为x 2＋3y 22＝1.] 11.(2014·江西，15)过点M (1,1)作斜率为－12的直线与椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)相交于A ，B两点，若M 是线段AB 的中点，则椭圆C 的离心率等于________. 11.22 [设A (x 1，y 1)，B (x 2，y 2)，分别代入椭圆方程相减得（x 1－x 2）（x 1＋x 2）a 2＋（y 1－y 2）（y 1＋y 2）b 2＝0，根据题意有x 1＋x 2＝2×1＝2，y 1＋y 2＝2×1＝2，且y 1－y 2x 1－x 2＝－12，所以2a 2＋2b 2×⎝⎛⎭⎫－12＝0，得a 2＝2b 2，所以a 2＝2(a 2－c 2)，整理得a 2＝2c 2得c a ＝22，所以e ＝22.] 12．（2018全国Ⅲ，20）已知斜率为k 的直线l 与椭圆C ： x 24+y 23=1交于A ，B 两点，线段AB的中点为M(1 ， m)(m >0)．（1）证明：k <−12；（2）设F 为C 的右焦点，P 为C 上一点,且FP ⃑⃑⃑⃑⃑ +FA ⃑⃑⃑⃑⃑ +FB ⃑⃑⃑⃑⃑ =0．证明：|FA ⃑⃑⃑⃑⃑ |，|FP ⃑⃑⃑⃑⃑ |，|FB ⃑⃑⃑⃑⃑ |成等差数列，并求该数列的公差． 12.（1）设A(x 1,y 1),B(x 2,y 2)，则x 124+y 123=1,x 224+y 223=1.两式相减，并由y 1−y2x 1−x 2=k 得x 1+x 24+y 1+y 23⋅k =0. 由题设知x 1+x 22=1,y 1+y 22=m ，于是k =−34m .①由题设得0<m <32，故k <−12. （2）由题意得F(1,0)，设P(x 3,y 3)，则 (x 3−1,y 3)+(x 1−1,y 1)+(x 2−1,y 2)=(0,0).由（1）及题设得x 3=3−(x 1+x 2)=1,y 3=−(y 1+y 2)=−2m <0. 又点P 在C 上，所以m =34，从而P(1,−32)，|FP ⃑⃑⃑⃑⃑ |=32. 于是|FA⃑⃑⃑⃑⃑ |=√(x 1−1)2+y 12=√(x 1−1)2+3(1−x 124)=2−x 12. 同理|FB⃑⃑⃑⃑⃑ |=2−x 22.所以|FA⃑⃑⃑⃑⃑ |+|FB ⃑⃑⃑⃑⃑ |=4−12(x 1+x 2)=3. 故2|FP⃑⃑⃑⃑⃑ |=|FA ⃑⃑⃑⃑⃑ |+|FB ⃑⃑⃑⃑⃑ |，即|FA ⃑⃑⃑⃑⃑ |,|FP ⃑⃑⃑⃑⃑ |,|FB ⃑⃑⃑⃑⃑ |成等差数列. 设该数列的公差为d ，则2|d|=||FB⃑⃑⃑⃑⃑ |−|FA ⃑⃑⃑⃑⃑ ||=12|x 1−x 2|=12√(x 1+x 2)2−4x 1x 2.② 将m =34代入①得k =−1.所以l 的方程为y =−x +74，代入C 的方程，并整理得7x 2−14x +14=0.故x 1+x 2=2,x 1x 2=128，代入②解得|d|=3√2128. 所以该数列的公差为3√2128或−3√2128. 13．（2018天津，19）设椭圆22221x x a b+= (a >b >0)的左焦点为F ，上顶点为B . 已知椭圆的点A 的坐标为(),0b，且FB AB ⋅=（I ）求椭圆的方程；（II ）设直线l ： (0)y kx k =>与椭圆在第一象限的交点为P ，且l 与直线AB 交于点Q .若sin 4AQ AOQ PQ=∠ (O 为原点) ，求k 的值. 13.（Ⅰ）设椭圆的焦距为2c ，由已知有2259c a =，又由a 2=b 2+c 2，可得2a =3b ．由已知可得， FB a =，AB =，由FB AB ⋅=ab =6，从而a =3，b =2．所以，椭圆的方程为22194x y +=．（Ⅱ）设点P 的坐标为（x 1，y 1），点Q 的坐标为（x 2，y 2）．由已知有y 1>y 2>0，故12PQ sin AOQ y y ∠=-．又因为2y AQ sin OAB =∠，而∠OAB =π4，故2AQ =．由4AQ sin AOQ PQ=∠，可得5y 1=9y 2．由方程组22{ 194y kx x y =+=，，消去x，可得1y =．易知直线AB 的方程为x +y –2=0，由方程组{20y kx x y =+-=，，消去x ，可得221ky k =+．由5y 1=9y 2，可得5（k +1）= 两边平方，整理得25650110k k -+=，解得12k =，或1128k =．所以，k 的值为12或1128．14.（2017•江苏,17）如图，在平面直角坐标系xOy 中，椭圆E ： =1（a ＞b ＞0）的左、右焦点分别为F 1 ， F 2 ，离心率为，两准线之间的距离为8．点P 在椭圆E 上，且位于第一象限，过点F 1作直线PF 1的垂线l 1 ，过点F 2作直线PF 2的垂线l 2 ．（Ⅰ）求椭圆E 的标准方程；（Ⅱ）若直线l 1 ， l 2的交点Q 在椭圆E 上，求点P 的坐标．14.（1）设椭圆的半焦距为c .因为椭圆E 的离心率为12，两准线之间的距离为8，所以12c a =， 228a c =，解得2,1a c ==，于是b ==因此椭圆E 的标准方程是22143x y +=. （2）由（1）知， ()11,0F -， ()21,0F . 设()00,P x y ，因为点P 为第一象限的点，故000,0x y >>. 当01x =时， 2l 与1l 相交于1F ，与题设不符. 当01x ≠时，直线1PF 的斜率为001y x +，直线2PF 的斜率为001y x -.因为11l PF ⊥， 22l PF ⊥，所以直线1l 的斜率为001x y -+，直线2l 的斜率为001x y --，从而直线1l 的方程： ()0011x y x y +=-+， ① 直线2l 的方程： ()0011x y x y -=--. ② 由①②，解得2001,x x x y y -=-=，所以20001,x Q x y ⎛⎫-- ⎪⎝⎭.因为点Q 在椭圆上，由对称性，得20001x y y -=±，即2201x y -=或22001x y +=. 又P 在椭圆E 上，故2200143x y +=. 由22002201{ 143x y x y-=+=，解得00x y ==； 220022001{ 143x y x y +=+=，无解.因此点P的坐标为⎝⎭15.(2016·全国Ⅱ，20)已知椭圆E ：x 2t ＋y 23＝1的焦点在x 轴上，A 是E 的左顶点，斜率为k (k >0)的直线交E 于A ，M 两点，点N 在E 上，MA ⊥NA . (1)当t ＝4，|AM |＝|AN |时，求△AMN 的面积； (2)当2|AM |＝|AN |时，求k 的取值范围.15.解 (1)设M (x 1，y 1)，则由题意知y 1>0.当t ＝4时，E 的方程为x 24＋y 23＝1,A (-2,0).由|AM |＝|AN |及椭圆的对称性知，直线AM 的倾斜角为π4.因此直线AM 的方程为y ＝x ＋2.将x ＝y －2代入x 24＋y 23＝1得7y 2－12y ＝0，解得y ＝0或y ＝127，所以y 1＝127.因此△AMN 的面积S △AMN ＝2×12×127×127＝14449.(2)由题意t >3，k >0，A (－t ，0)，将直线AM 的方程y ＝k (x ＋t )代入x 2t ＋y 23＝1得(3＋tk 2)x 2＋2t ·tk 2x ＋t 2k 2－3t ＝0.由x 1·(－t )＝t 2k 2－3t 3＋tk 2得x 1＝t （3－tk 2）3＋tk 2，故|AM |＝|x 1＋t |1＋k 2＝6t （1＋k 2）3＋tk 2.由题设，直线AN 的方程为y ＝－1k (x ＋t )，故同理可得|AN |＝6k t （1＋k 2）3k 2＋t .由2|AM |＝|AN |得23＋tk 2＝k3k 2＋t ，即(k 3－2)t ＝3k (2k －1)，当k ＝32时上式不成立，因此t ＝3k （2k －1）k 3－2.t >3等价于k 3－2k 2＋k －2k 3－2＝（k －2）（k 2＋1）k 3－2<0，即k －2k 3－2<0.由此得⎩⎪⎨⎪⎧k －2>0，k 3－2<0，或⎩⎪⎨⎪⎧k －2<0，k 3－2>0，解得32<k <2.因此k 的取值范围是(32，2).16.(2016·四川，20)已知椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线l ：y ＝－x ＋3与椭圆E 有且只有一个公共点T . (1)求椭圆E 的方程及点T 的坐标；(2)设O 是坐标原点，直线l ′平行于OT ，与椭圆E 交于不同的两点A 、B ，且与直线l 交于点P .证明：存在常数λ，使得|PT |2＝λ|P A |·|PB |，并求λ的值. 16.(1)解由已知，a ＝2b ，则椭圆E 的方程为x 22b 2＋y 2b 2＝1.由方程组⎩⎪⎨⎪⎧x 22b 2＋y 2b 2＝1，y ＝－x ＋3，得3x 2－12x ＋(18－2b 2)＝0.①方程①的判别式为Δ＝24(b 2－3)，由Δ＝0，得b 2＝3，此时方程①的解为x ＝2，所以椭圆E 的方程为x 26＋y 23＝1.点T 的坐标为(2，1).(2)证明由已知可设直线l ′的方程为y ＝12x ＋m (m ≠0)，由方程组⎩⎪⎨⎪⎧y ＝12x ＋m ，y ＝－x ＋3，可得⎩⎨⎧x ＝2－2m3，y ＝1＋2m 3.所以P 点坐标为⎝⎛⎭⎫2－2m 3，1＋2m 3.|PT |2＝89m 2. 设点A ，B 的坐标分别为A (x 1，y 1)，B (x 2，y 2).由方程组⎩⎨⎧x 26＋y 23＝1，y ＝12x ＋m ，可得3x 2＋4mx ＋(4m 2－12)＝0.②方程②的判别式为Δ＝16(9－2m 2)，由Δ>0，解得－322<m <322.由②得x 1＋x 2＝－4m3，x 1x 2＝4m 2－123.所以|P A |＝⎝⎛⎭⎫2－2m 3－x 12＋⎝⎛⎭⎫1＋2m 3－y 12＝52⎪⎪⎪⎪2－2m 3－x 1，同理|PB |＝52⎪⎪⎪⎪2－2m 3－x 2.所以|P A |·|PB |＝54⎪⎪⎪⎪⎝⎛⎭⎫2－2m3－x 1⎝⎛⎭⎫2－2m 3－x 2 ＝54⎪⎪⎪⎪⎪⎪⎝⎛⎭⎫2－2m 32－⎝⎛⎭⎫2－2m 3（x 1＋x 2）＋x 1x 2 ＝54⎪⎪⎪⎪⎪⎪⎝⎛⎭⎫2－2m 32－⎝⎛⎭⎫2－2m 3⎝⎛⎭⎫－4m 3＋4m 2－123＝109m 2. 故存在常数λ＝45，使得|PT |2＝λ|P A |·|PB |.17.(2015·重庆，21)如图，椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点分别为F 1，F 2，过F 2的直线交椭圆于P 、Q 两点，且PQ ⊥PF 1.(1)若|PF 1|＝2＋2，|PF 2|＝2－2，求椭圆的标准方程； (2)若|PF 1|＝|PQ |，求椭圆的离心率e .17.解 (1)由椭圆的定义，2a ＝|PF 1|＋|PF 2|＝(2＋2)＋(2－2)＝4，故a ＝2. 设椭圆的半焦距为c ，由已知PF 1⊥PF 2，因此2c ＝|F 1F 2|＝|PF 1|2＋|PF 2|2＝（2＋2）2＋（2－2）2＝23，即c ＝3，即c ＝3，从而b ＝a 2－c 2＝1. 故所求椭圆的标准方程为x 24＋y 2＝1.(2)法一如图设点P (x 0，y 0)在椭圆上，且PF 1⊥PF 2，则x 20a 2＋y 20b2＝1，x 20＋y 20＝c 2，求得x 0＝±a c a 2－2b 2，y 0＝±b 2c .由|PF 1|＝|PQ |＞|PF 2|得x 0＞0，从而 |PF 1|2＝⎝ ⎛⎭⎪⎫a a 2－2b 2c ＋c 2＋b 4c 2＝2(a 2－b 2)＋2a a 2－2b 2＝(a ＋a 2－2b 2)2. 由椭圆的定义,|PF 1|＋|PF 2|＝2a ,|QF 1|＋|QF 2|＝2a , 从而由|PF 1|＝|PQ |＝|PF 2|＋|QF 2|,有|QF 1|＝4a －2|PF 1|. 又由PF 1⊥PF 2，|PF 1|＝|PQ |，知|QF 1|＝2|PF 1|，因此，(2＋2)|PF 1|＝4a ，即(2＋2)(a ＋a 2－2b 2)＝4a ，于是(2＋2)(1＋2e 2－1)＝4，解得e ＝12⎣⎢⎡⎦⎥⎤1＋⎝ ⎛⎭⎪⎫42＋2－12＝6－ 3. 法二如图，由椭圆的定义，|PF 1|＋|PF 2|＝2a ，|QF 1|＋|QF 2|＝2a .从而由|PF 1|＝|PQ |＝|PF 2|＋|QF 2|，有|QF 1|＝4a －2|PF 1|.又由PF 1⊥PQ ，|PF 1|＝|PQ |，知|QF 1|＝2|PF 1|，因此，4a －2|PF 1|＝2|PF 1|，得|PF 1|＝2(2－2)a ，从而|PF 2|＝2a －|PF 1|＝2a －2(2－2)a ＝2(2－1)a . 由PF 1⊥PF 2，知|PF 1|2＋|PF 2|2＝|F 1F 2|2＝(2c )2，因此e ＝ca ＝|PF 1|2＋|PF 2|22a ＝（2－2）2＋（2－1）2＝9－62＝6－ 3. 18.(2015·福建，18)已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)过点(0，2)，且离心率e ＝22.(1)求椭圆E 的方程；(2)设直线l ：x ＝my －1(m ∈R )交椭圆E 于A ，B 两点，判断点G ⎝⎛⎭⎫－94，0与以线段AB 为直径的圆的位置关系，并说明理由.18.解法一 (1)由已知得，⎩⎪⎨⎪⎧b ＝2，c a ＝22，a 2＝b 2＋c 2.解得⎩⎨⎧a ＝2，b＝2，c ＝ 2.所以椭圆E 的方程为x 24＋y 22＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，AB 的中点为H (x 0，y 0).⎩⎪⎨⎪⎧x ＝my －1，x 24＋y 22＝1得(m 2＋2)y 2－2my －3＝0.所以y 1＋y 2＝2m m 2＋2，y 1y 2＝－3m 2＋2，从而y 0＝mm 2＋2.所以|GH |2＝⎝⎛⎭⎫x 0＋942＋y 20＝⎝⎛⎭⎫my 0＋542＋y 20＝(m 2＋1)y 20＋52my 0＋2516. |AB |24＝（x 1－x 2）2＋（y 1－y 2）24 ＝（1＋m 2）（y 1－y 2）24＝（1＋m 2）[（y 1＋y 2）2－4y 1y 2]4＝(1＋m 2)(y 20－y 1y 2)，故|GH |2－|AB |24＝52my 0＋(1＋m 2)y 1y 2＋2516＝5m 22（m 2＋2）－3（1＋m 2）m 2＋2＋2516＝17m 2＋216（m 2＋2）＞0，所以|GH |＞|AB |2.故点G ⎝⎛⎭⎫－94，0在以AB 为直径的圆外. 法二 (1)同法一.(2)设点A (x 1，y 1)，B (x 2，y 2)，则GA →＝⎝⎛⎭⎫x 1＋94，y 1，GB →＝⎝⎛⎭⎫x 2＋94，y 2.由⎩⎪⎨⎪⎧x ＝my －1，x 24＋y 22＝1得(m 2＋2)y 2－2my －3＝0，所以y 1＋y 2＝2m m 2＋2，y 1y 2＝－3m 2＋2，从而GA →·GB →＝⎝⎛⎭⎫x 1＋94⎝⎛⎭⎫x 2＋94＋y 1y 2＝⎝⎛⎭⎫my 1＋54⎝⎛⎭⎫my 2＋54＋y 1y 2 ＝(m 2＋1)y 1y 2＋54m (y 1＋y 2)＋2516＝－3（m 2＋1）m 2＋2＋52m2m 2＋2＋2516＝17m 2＋216（m 2＋2）＞0，所以cos 〈GA →，GB →〉＞0.又GA →，GB →不共线，所以∠AGB 为锐角. 故点G ⎝⎛⎭⎫－94，0在以AB 为直径的圆外. 19.(2015·陕西，20)已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的半焦距为c ，原点O 到经过两点(c,0)，(0，b )的直线的距离为12c .(1)求椭圆E 的离心率；(2)如图，AB 是圆M ：(x ＋2)2＋(y －1)2＝52的一条直径，若椭圆E 经过A ，B 两点，求椭圆E的方程.19.解 (1)过点(c ，0)，(0，b )的直线方程为bx ＋cy －bc ＝0，则原点O 到该直线的距离d ＝bc b 2＋c 2＝bc a,由d ＝12c ,得a ＝2b ＝2a 2－c 2,解得离心率c a ＝32.(2)法一由(1)知，椭圆E 的方程为x 2＋4y 2＝4b 2.① 依题意，圆心M (－2，1)是线段AB 的中点，且|AB |＝10，易知,AB 与x 轴不垂直,设其方程为y ＝k (x ＋2)＋1,代入①得(1＋4k 2)x 2＋8k (2k ＋1)x ＋4(2k ＋1)2－4b 2＝0，设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－8k （2k ＋1）1＋4k 2，x 1x 2＝4（2k ＋1）2－4b 21＋4k 2，由x 1＋x 2＝－4，得－8k （2k ＋1）1＋4k 2＝－4，解得k ＝12，从而x 1x 2＝8－2b 2，于是|AB |＝1＋⎝⎛⎭⎫122|x 1－x 2|＝52（x 1＋x 2）2－4x 1x 2＝10（b 2－2），由|AB |＝10，得10（b 2－2）＝10，解得b 2＝3，故椭圆E 的方程为x 212＋y 23＝1.法二由(1)知，椭圆E 的方程为x 2＋4y 2＝4b 2，②依题意，点A ，B 关于圆心M (－2，1)对称，且|AB |＝10，设A (x 1，y 1)，B (x 2，y 2)，则x 21＋4y 21＝4b 2，x 22＋4y 22＝4b 2，两式相减并结合x 1＋x 2＝－4，y 1＋y 2＝2，得－4(x 1－x 2)＋8(y 1－y 2)＝0，易知AB 与x 轴不垂直，则x 1≠x 2，所以AB 的斜率k AB ＝y 1－y 2x 1－x 2＝12，因此直线AB 的方程为y ＝12(x ＋2)＋1，代入②得x 2＋4x ＋8－2b 2＝0，所以x 1＋x 2＝－4，x 1x 2＝8－2b 2，于是|AB |＝1＋⎝⎛⎭⎫122|x 1－x 2|＝52（x 1＋x 2）2－4x 1x 2＝10（b 2－2）.由|AB |＝10，得10（b 2－2）＝10，解得b 2＝3，故椭圆E 的方程为x 212＋y 23＝1.20.(2015·北京，19)已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为22，点P (0,1)和点A (m ，n )(m ≠0)都在椭圆C 上，直线P A 交x 轴于点M .(1)求椭圆C 的方程，并求点M 的坐标(用m ，n 表示)；(2)设O 为原点，点B 与点A 关于x 轴对称，直线PB 交x 轴于点N .问：y 轴上是否存在点Q ，使得∠OQM ＝∠ONQ ？若存在，求点Q 的坐标；若不存在，说明理由.20.解 (1)由题意得⎩⎪⎨⎪⎧b ＝1，c a ＝22，a 2＝b 2＋c2解得a 2＝2，故椭圆C 的方程为x22＋y 2＝1.设M (x M ，0).因为m ≠0，所以－1＜n ＜1.直线P A 的方程为y －1＝n －1m x .所以x M ＝m 1－n，即M ⎝⎛⎭⎫m 1－n ，0. (2)因为点B 与点A 关于x 轴对称，所以B (m ，－n ). 设N (x N ，0)，则x N ＝m1＋n.“存在点Q (0，y Q )使得∠OQM ＝∠ONQ ”，等价于“存在点Q (0，y Q )使得|OM ||OQ |＝|OQ ||ON |”，即y Q 满足y 2Q ＝|x M ||x N |.因为x M ＝m 1－n ，x N ＝m 1＋n ，m 22＋n 2＝1.所以y 2Q ＝|x M ||x N |＝m 21－n 2＝2.所以y Q ＝2或y Q ＝－ 2.故在y 轴上存在点Q ，使得∠OQM ＝∠ONQ ，点Q 的坐标为(0，2)或(0，－2). 21.(2015·江苏,18)如图,在平面直角坐标系xOy 中,已知椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为22,且右焦点F 到左准线l 的距离为3. (1)求椭圆的标准方程；(2)过F 的直线与椭圆交于A ,B 两点,线段AB 的垂直平分线分别交直线l 和AB 于点P ,C ,若PC ＝2AB ,求直线AB 的方程. 21.解 (1)由题意,得c a ＝22且c ＋a 2c＝3,解得a ＝2,c ＝1,则b ＝1,所以椭圆的标准方程为x 22＋y 2＝1.(2)当AB ⊥x 轴时,AB ＝2,又CP ＝3,不合题意.当AB 与x 轴不垂直时,设直线AB 的方程为y ＝k (x －1),A (x 1,y 1),B (x 2,y 2), 将AB 的方程代入椭圆方程,得(1＋2k 2)x 2－4k 2x ＋2(k 2－1)＝0, 则x 1,2＝2k 2±2（1＋k 2）1＋2k 2,C 的坐标为⎝ ⎛⎭⎪⎫2k 21＋2k 2，－k 1＋2k 2,且 AB ＝（x 2－x 1）2＋（y 2－y 1）2＝（1＋k 2）（x 2－x 1）2＝22（1＋k 2）1＋2k 2.若k ＝0,则线段AB 的垂直平分线为y 轴,与左准线平行,不合题意. 从而k ≠0,故直线PC 的方程为y ＋k 1＋2k 2＝－1k ⎝⎛⎭⎫x －2k 21＋2k 2,则P 点的坐标为⎝ ⎛⎭⎪⎫－2，5k 2＋2k （1＋2k 2）,从而PC ＝2（3k 2＋1）1＋k 2|k |（1＋2k 2）.因为PC ＝2AB ,所以2（3k 2＋1）1＋k 2|k |（1＋2k 2）＝42（1＋k 2）1＋2k 2,解得k ＝±1.此时直线AB 的方程为y ＝x －1或y ＝－x ＋1.二、双曲线知识1．（2018浙江，2）双曲线x 23−y 2=1的焦点坐标是( ) A ．(−√2，0)，(√2，0) B ．(−2，0)，(2，0) C ．(0，−√2)，(0，√2) D ．(0，−2)，(0，2)1.B 因为双曲线方程为x 23−y 2=1，所以焦点坐标可设为(±c,0)，因为c 2=a 2+b 2=3+1=4,c =2，所以焦点坐标为(±2,0)，选B. 2．（2018全国Ⅰ，11）已知双曲线C ：x 23−y 2=1，O 为坐标原点，F 为C 的右焦点，过F的直线与C 的两条渐近线的交点分别为M 、N .若△OMN 为直角三角形，则|MN |=( ) A ．32 B ．3 C ．2√3 D ．42.B 根据题意，可知其渐近线的斜率为±√33，且右焦点为F(2,0)，从而得到∠FON =30°，所以直线MN 的倾斜角为60°或120°，根据双曲线的对称性，设其倾斜角为60°，可以得出直线MN 的方程为y =√3(x −2)，分别与两条渐近线y =√33x 和y =−√33x 联立，求得M(3,√3),N(32,−√32)，所以|MN |=2)√2)=3，故选B.3．（2018全国Ⅱ，5）双曲线x 2a 2−y 2b 2=1 (a >0, b >0)的离心率为√3，则其渐近线方程为( )A ．y =±√2xB ．y =±√3xC ．y =±√22x D ．y =±√32x 3.A ∵e =ca =√3,∴b 2a 2=c 2−a 2a 2=e 2−1=3−1=2,∴ba =√2,因为渐近线方程为y =±ba x ，所以渐近线方程为y =±√2x ，选A. 4．（2018全国Ⅲ，11）设F 1,F 2是双曲线C:x 2a 2−y 2b 2=1（）的左、右焦点，O 是坐标原点．过F 2作C 的一条渐近线的垂线，垂足为P ．若|PF 1|=√6|OP |，则C 的离心率为( ) A ．√5 B ．√3 C ．2 D ．√24.B 由题可知|PF 2|=b,|OF 2|=c ,∴|PO |=a ,在Rt △POF 2中，cos∠PF 2O =|PF 2||OF 2|=bc, ∵在△PF 1F 2中,cos∠PF 2O =|PF 2|2+|F 1F 2|2−|PF 1|22|PF 2||F 1F 2|=bc ,∴b 2+4c 2−(√6a)22b∙2c=bc ⇒c 2=3a 2,∴e =√3.故选C.5．（2018天津，7）已知双曲线22221(0,0)x y a b a b-=>>的离心率为2，过右焦点且垂直于x 轴的直线与双曲线交于A ，B 两点. 设A ，B 到双曲线的同一条渐近线的距离分别为1d 和2d ，且126d d +=，则双曲线的方程为( )A ．221412x y -= B ．221124x y -= C ．22139x y -= D ．22193x y -=5.C 设双曲线的右焦点坐标为(),0F c （c >0），则A B x x c ==，由22221c y a b-=可得：2b y a =±，不妨设： 22,,,b b Ac B c a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭，双曲线的一条渐近线方程为： 0bx ay -=，据此可得：21bc b d c -==，22bc b d c +==，则12226bcd d b c+===，则23,9b b ==，双曲线的离心率：2c e a ====，据此可得： 23a =，则双曲线的方程为22139x y -=. 本题选择C 选项.6.（2017•新课标Ⅱ,9）若双曲线C ： ﹣ =1（a ＞0，b ＞0）的一条渐近线被圆（x ﹣2）2+y 2=4所截得的弦长为2，则C 的离心率为（）A.2B.C.D.6. A 双曲线C ： ﹣=1（a ＞0，b ＞0）的一条渐近线不妨为：bx+ay=0，圆（x ﹣2）2+y 2=4的圆心（2，0），半径为：2，双曲线C ： ﹣=1（a ＞0，b ＞0）的一条渐近线被圆（x ﹣2）2+y 2=4所截得的弦长为2，可得圆心到直线的距离为： = ，解得：，可得e 2=4，即e=2．故选A ．7.（2017•新课标Ⅲ,5）已知双曲线C ：﹣ =1 （a ＞0，b ＞0）的一条渐近线方程为y= x ，且与椭圆 + =1有公共焦点，则C 的方程为（）A.﹣ =1B.﹣ =1C.﹣=1 D.﹣=17. B 椭圆 +=1的焦点坐标（±3，0），则双曲线的焦点坐标为（±3，0），可得c=3，双曲线C ：﹣ =1 （a ＞0，b ＞0）的一条渐近线方程为y=x ，可得，即，可得 = ，解得a=2，b= ，所求的双曲线方程为： ﹣ =1．故选B ．8.（2017·天津,5）已知双曲线 ﹣ =1（a ＞0，b ＞0）的左焦点为F ，离心率为．若经过F 和P （0，4）两点的直线平行于双曲线的一条渐近线，则双曲线的方程为（） A.=1 B.=1 C.=1 D.=18. B 设双曲线的左焦点F （﹣c ，0），离心率e= =，c=a ，则双曲线为等轴双曲线，即a=b ，双曲线的渐近线方程为y=±x=±x ，则经过F 和P （0，4）两点的直线的斜率k= =，则=1，c=4，则a=b=2，∴双曲线的标准方程：；故选B ．9.(2016·全国Ⅰ，5)已知方程x 2m 2＋n －y 23m 2－n ＝1表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是( )A.(－1，3)B.(－1，3)C.(0，3)D.(0，3)9.A [∵方程x 2m 2＋n －y 23m 2－n ＝1表示双曲线，∴(m 2＋n )·(3m 2－n )>0，解得－m 2<n <3m 2，由双曲线性质，知c 2＝(m 2＋n )＋(3m 2－n )＝4m 2(其中c 是半焦距)，∴焦距2c ＝2×2|m |＝4，解得|m |＝1，∴－1<n <3，故选A.]10.(2016·全国Ⅱ，11)已知F 1，F 2是双曲线E ：x 2a 2－y 2b 2＝1的左，右焦点，点M 在E 上，MF 1与x 轴垂直，sin ∠MF 2F 1＝13，则E 的离心率为( )A.2B.32C.3D.210.A [离心率e ＝F 1F 2MF 2－MF 1，由正弦定理得e ＝F 1F 2MF 2－MF 1＝sin Msin F 1－sin F 2＝2231－13＝ 2.故选A.]11.(2015·福建，3)若双曲线E ：x 29－y 216＝1的左、右焦点分别为F 1，F 2，点P 在双曲线E 上，且|PF 1|＝3，则|PF 2|等于( )A.11B.9C.5D.311.B [由双曲线定义||PF 2|－|PF 1||＝2a ,∵|PF 1|＝3,∴P 在左支上,∵a ＝3,∴|PF 2|－|PF 1|＝6，∴|PF 2|＝9，故选B.]12.(2015·安徽，4)下列双曲线中，焦点在y 轴上且渐近线方程为y ＝±2x 的是( ) A.x 2－y 24＝1 B.x 24－y 2＝1 C.y 24－x 2＝1 D.y 2－x 24＝112.C [由双曲线性质知A 、B 项双曲线焦点在x 轴上，不合题意；C 、D 项双曲线焦点均在y 轴上，但D 项渐近线为y ＝±12x ，只有C 符合，故选C.]13.(2015·广东，7)已知双曲线C ：x 2a 2－y 2b 2＝1的离心率e ＝54，且其右焦点为F 2(5,0)，则双曲线C 的方程为( )A.x 24－y 23＝1B.x 216－y 29＝1C.x 29－y 216＝1D.x 23－y 24＝1 13.B [因为所求双曲线的右焦点为F 2(5，0)且离心率为e ＝c a ＝54，所以c ＝5，a ＝4，b 2＝c 2－a 2＝9，所以所求双曲线方程为x 216－y 29＝1，故选B.] 14.(2015·四川，5)过双曲线x 2－y 23＝1的右焦点且与x 轴垂直的直线，交该双曲线的两条渐近线于A ，B 两点，则|AB |＝( ) A.433B.2 3C.6D.4 314.D [焦点F (2，0)，过F 与x 轴垂直的直线为x ＝2，渐近线方程为x 2－y 23＝0，将x ＝2代入渐近线方程得y 2＝12，y ＝±23，∴|AB |＝23－(－23)＝4 3.选D.]15.(2015·新课标全国Ⅱ，11)已知A ，B 为双曲线E 的左，右顶点，点M 在E 上，△ABM 为等腰三角形，且顶角为120°，则E 的离心率为( ) A. 5 B.2 C. 3 D. 2 15.D [如图，设双曲线E 的方程为x 2a 2－y 2b 2＝1(a ＞0，b ＞0),则|AB |＝2a ,由双曲线的对称性,可设点M (x 1，y 1)在第一象限内,过M 作MN ⊥x 轴于点N (x 1，0)，∵△ABM 为等腰三角形，且∠ABM ＝120°，∴|BM |＝|AB |＝2a ，∠MBN ＝60°，∴y 1＝|MN |＝|BM |sin ∠MBN ＝2a sin 60°＝3a ，x 1＝|OB |＋|BN |＝a ＋2a cos 60°＝2a .将点M (x 1，y 1)的坐标代入x 2a 2－y 2b 2＝1，可得a 2＝b 2，∴e ＝ca ＝a 2＋b 2a 2＝2，选D.] 16.(2015·新课标全国Ⅰ，5)已知M (x 0，y 0)是双曲线C ：x 22－y 2＝1上的一点，F 1，F 2是C 的两个焦点，若MF 1→·MF 2→<0，则y 0的取值范围是( ) A.⎝⎛⎭⎫－33，33 B.⎝⎛⎭⎫－36，36 C.⎝⎛⎭⎫－223，223 D.⎝⎛⎭⎫－233，233 16.A [由题意知M 在双曲线C ：x 22－y 2＝1上，又在x 2＋y 2＝3内部，由⎩⎪⎨⎪⎧x 22－y 2＝1，x 2＋y 2＝3，得y ＝±33，所以－33<y 0<33.] 17.(2014·天津，5)已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的一条渐近线平行于直线l ：y ＝2x ＋10，双曲线的一个焦点在直线l 上，则双曲线的方程为( ) A.x 25－y 220＝1 B.x 220－y 25＝1 C.3x 225－3y 2100＝1 D.3x 2100－3y 225＝1 17.A [由题意可知，双曲线的其中一条渐近线y ＝b a x 与直线y ＝2x ＋10平行，所以ba ＝2且左焦点为(-5,0),所以a 2＋b 2＝c 2＝25,解得a 2＝5,b 2＝20,故双曲线方程为x 25－y 220＝1.选A.]18.(2014·广东，4)若实数k 满足0<k <9，则曲线x 225－y 29－k ＝1与曲线x 225－k －y 29＝1的( )A.离心率相等B.实半轴长相等C.虚半轴长相等D.焦距相等18.D [由0<k <9，易知两曲线均为双曲线且焦点都在x 轴上，由25＋9－k ＝25－k ＋9，得两双曲线的焦距相等，选D.]19.(2014·新课标全国Ⅰ，4)已知F 为双曲线C ：x 2－my 2＝3m (m >0)的一个焦点，则点F 到C 的一条渐近线的距离为( ) A. 3 B.3 C.3m D.3m19.A [∵双曲线的方程为x 23m －y 23＝1，∴焦点F 到一条渐近线的距离为 3.]20.(2014·重庆，8)设F 1，F 2分别为双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左、右焦点，双曲线上存在一点P 使得|PF 1|＋|PF 2|＝3b ，|PF 1|·|PF 2|＝94ab ，则该双曲线的离心率为( )A.43B.53C.94D.3 20.B [由双曲线的定义得||PF 1|-|PF 2||＝2a ,又|PF 1|＋|PF 2|＝3b ,所以(|PF 1|＋|PF 2|)2－(|PF 1|-|PF 2|)2＝9b 2-4a 2,即4|PF 1|·|PF 2|＝9b 2－4a 2，又4|PF 1|·|PF 2|＝9ab ，因此9b 2－4a 2＝9ab ，即9⎝⎛⎭⎫b a 2-9b a －4＝0,则⎝⎛⎭⎫3b a ＋1⎝⎛⎭⎫3b a －4＝0，解得b a ＝43⎝⎛⎭⎫b a ＝－13舍去，则双曲线的离心率e ＝1＋⎝⎛⎭⎫b a 2＝53.]21.(2014·山东，10)已知a >b >0，椭圆C 1的方程为x 2a 2＋y 2b 2＝1，双曲线C 2的方程为x 2a 2－y 2b 2＝1，C 1与C 2的离心率之积为32，则C 2的渐近线方程为( ) A.x ±2y ＝0 B.2x ±y ＝0 C.x ±2y ＝0 D.2x ±y ＝021.A [椭圆C 1的离心率为a 2－b 2a ,双曲线C 2的离心率为a 2＋b 2a ，所以a 2－b 2a ·a 2＋b 2a ＝32，所以a 4－b 4＝34a 4，即a 4＝4b 4，所以a ＝2b ，所以双曲线C 2的渐近线方程是y ＝±12x ，即x ±2y ＝0.]22.(2014·大纲全国，9)已知双曲线C 的离心率为2，焦点为F 1、F 2，点A 在C 上.若|F 1A |＝2|F 2A |，则cos ∠AF 2F 1＝( ) A.14 B.13 C.24 D.2322.A [由双曲线的定义知|AF 1|－|AF 2|＝2a ，又|AF 1|＝2|AF 2|，∴|AF 1|＝4a ，|AF 2|＝2a . ∵e ＝ca ＝2，∴c ＝2a ，∴|F 1F 2|＝4a .∴cos ∠AF 2F 1＝|AF 2|2＋|F 1F 2|2－|AF 1|22|AF 2|·|F 1F 2|＝（2a ）2＋（4a ）2－（4a ）22×2a ×4a＝14，故选A.]23．（2018江苏，8）在平面直角坐标系xOy 中，若双曲线x 2a −y 2b =1(a >0,b >0)的右焦点F(c,0)到一条渐近线的距离为√32c ，则其离心率的值是________．23.2 因为双曲线的焦点F(c,0)到渐近线y =±ba x,即bx ±ay =0的距离为√a 2+b2=bc c=b,所以b =√32c ，因此a 2=c 2−b 2=c 2−34c 2=14c 2, a =12c,e =2.24.（2017•山东,14）在平面直角坐标系xOy 中，双曲线=1（a ＞0，b ＞0）的右支与焦点为F 的抛物线x 2=2py （p ＞0）交于A ，B 两点，若|AF|+|BF|=4|OF|，则该双曲线的渐近线方程为________．24. y=± x 把x 2=2py （p ＞0）代入双曲线=1（a ＞0，b ＞0），可得：a 2y2﹣2pb 2y+a 2b 2=0，∴y A +y B =，∵|AF|+|BF|=4|OF|，∴y A +y B +2× =4× ，∴ =p ，∴ = ．∴该双曲线的渐近线方程为：y=± x ．故答案为：y=± x ．25.（2017•北京,9）若双曲线x 2﹣=1的离心率为，则实数m=________．25.2 双曲线x 2﹣=1（m ＞0）的离心率为，可得：，解得m=2．故答案为：2．26.（2017•江苏,8）在平面直角坐标系xOy 中，双曲线﹣y 2=1的右准线与它的两条渐近线分别交于点P ，Q ，其焦点是F 1 ， F 2 ，则四边形F 1PF 2Q 的面积是________． 26.2双曲线﹣y 2=1的右准线：x=，双曲线渐近线方程为：y= x ，所以P （，），Q （，﹣ ），F 1（﹣2，0）．F 2（2，0）．则四边形F 1PF 2Q 的面积是： =2．故答案为：2．27.(2016·山东，13)已知双曲线E ：x 2a 2－y 2b 2＝1(a >0，b >0)，若矩形ABCD 的四个顶点在E 上，AB ，CD 的中点为E 的两个焦点，且2|AB |＝3|BC |，则E 的离心率是________.27.2 [由已知得|AB |＝2b 2a ,|BC |＝2c ,∴2×2b 2a ＝3×2c ,又∵b 2＝c 2-a 2,整理得：2c 2-3ac -2a 2=0，两边同除以a 2得2⎝⎛⎭⎫c a 2－3c a－2＝0，即2e 2－3e －2＝0，解得e ＝2或e ＝－1(舍去).] 28.(2015·浙江，9)双曲线x 22－y 2＝1的焦距是______，渐近线方程是______.28.23 y ＝±22x [由双曲线方程得a 2＝2，b 2＝1，∴c 2＝3，∴焦距为23，渐近线方程为y ＝±22x .]29.(2015·北京，10)已知双曲线x 2a 2－y 2＝1(a ＞0)的一条渐近线为3x ＋y ＝0，则a ＝________.29.33 [双曲线渐近线方程为y ＝±b a x ，∴b a ＝3，又b ＝1，∴a ＝33.] 30.(2015·湖南，13)设F 是双曲线C ：x 2a 2－y 2b 2＝1的一个焦点，若C 上存在点P ，使线段PF的中点恰为其虚轴的一个端点，则C 的离心率为________.30.5 [不妨设F (c ，0)，则由条件知P (－c ，±2b )，代入x 2a 2－y 2b 2＝1得c 2a 2＝5，∴e ＝ 5.]31.(2015·江苏，12)在平面直角坐标系xOy 中，P 为双曲线x 2－y 2＝1右支上的一个动点.若点P 到直线x －y ＋1＝0的距离大于c 恒成立，则实数c 的最大值为________. 31.22[双曲线x 2－y 2＝1的渐近线为x ±y ＝0，直线x －y ＋1＝0与渐近线x －y ＝0平行，故两平行线的距离d ＝|1－0|12＋12＝22.由点P 到直线x －y ＋1＝0的距离大于c 恒成立，得c ≤22，故c 的最大值为22.] 32.(2014·浙江，16)设直线x －3y ＋m ＝0(m ≠0)与双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的两条渐近线分别交于点A ，B .若点P (m,0)满足|P A |＝|PB |，则该双曲线的离心率是________. 32.52 [联立直线方程与双曲线渐近线方程y ＝±bax 可解得交点为 ⎝⎛⎭⎫am 3b －a ，bm 3b －a ，⎝ ⎛⎭⎪⎫－am 3b ＋a ，bm 3b ＋a ，而k AB ＝13，由|P A |＝|PB |，可得AB 的中点与点P 连线的斜率为－3，即bm 3b －a ＋bm3b ＋a2－0am3b －a ＋－am 3b ＋a2－m＝－3，化简得4b 2＝a 2，所以e ＝52.]33.(2014·江西，20)如图，已知双曲线C ：x 2a 2－y 2＝1(a >0)的右焦点为F ，点A ，B 分别在C的两条渐近线上，AF ⊥x 轴，AB ⊥OB ，BF ∥OA (O 为坐标原点). (1)求双曲线C 的方程；(2)过C 上一点P (x 0，y 0)(y 0≠0)的直线l ：x 0x a 2－y 0y ＝1与直线AF 相交于点M ，与直线x ＝32相交于点N .证明：当点P 在C 上移动时，|MF ||NF |恒为定值，并求此定值.33.(1)解设F (c ，0)，因为b ＝1，所以c ＝a 2＋1，直线OB 的方程为y ＝－1a x ，直线BF 的方程为y ＝1a (x －c )，解得B ⎝⎛⎭⎫c 2，－c 2a . 又直线OA 的方程为y ＝1a x ，则A ⎝⎛⎭⎫c ，c a ，k AB ＝c a －⎝⎛⎭⎫－c 2a c －c 2＝3a.又因为AB ⊥OB ，所以3a ·⎝⎛⎭⎫－1a ＝－1，解得a 2＝3，故双曲线C 的方程为x 23－y 2＝1.(2)证明由(1)知a ＝3，则直线l 的方程为x 0x3－y 0y ＝1(y 0≠0)，即y ＝x 0x －33y 0.因为直线AF 的方程为x ＝2，所以直线l 与AF 的交点为M ⎝⎛⎭⎫2，2x 0－33y 0；直线l 与直线x ＝32的交点为N ⎝ ⎛⎭⎪⎫32，32x 0－33y 0. 则|MF |2|NF |2＝（2x 0－3）2（3y 0）214＋⎝⎛⎭⎫32x 0－32（3y 0）2＝（2x 0－3）29y 204＋94（x 0－2）2＝43·（2x 0－3）23y 20＋3（x 0－2）2，因为P (x 0，y 0)是C 上一点，则x 203－y 20＝1，代入上式得 |MF |2|NF |2＝43·（2x 0－3）2x 20－3＋3（x 0－2）2＝43·（2x 0－3）24x 20－12x 0＋9＝43，所求定值为|MF ||NF |＝23＝233.三、抛物线1．（2018全国Ⅰ，8）设抛物线C ：y 2=4x 的焦点为F ，过点（–2，0）且斜率为23的直线与C 交于M ，N 两点，则FM ⃑⃑⃑⃑⃑⃑ ⋅FN ⃑⃑⃑⃑⃑ =( ) A ．5 B ．6 C ．7 D ．81.D 根据题意，过点（–2，0）且斜率为23的直线方程为y =23(x +2)，与抛物线方程联立{y =23(x +2)y 2=4x ，消元整理得：y 2−6y +8=0，解得M(1,2),N(4,4)，又F(1,0)，所以FM ⃑⃑⃑⃑⃑⃑ =(0,2),FN ⃑⃑⃑⃑⃑ =(3,4)，从而可以求得FM⃑⃑⃑⃑⃑⃑ ⋅FN ⃑⃑⃑⃑⃑ =0×3+2×4=8，故选D. 2.(2016·全国Ⅰ，10)以抛物线C 的顶点为圆心的圆交C 于A ，B 两点，交C 的准线于D ，E 两点.已知|AB |＝42，|DE |＝25，则C 的焦点到准线的距离为( ) A.2 B.4 C.6 D.82.B [不妨设抛物线C ：y 2＝2px (p >0)，则圆的方程可设为x 2＋y 2＝r 2(r >0),如图，又可设A (x 0，22)，D ⎝⎛⎭⎫－p2，5，点A (x 0，22)在抛物线y 2＝2px 上，∴8＝2px 0，① 点A (x 0，22)在圆x 2＋y 2＝r 2上，∴x 20＋8＝r 2，② 点D ⎝⎛⎭⎫－p 2，5在圆x 2＋y 2＝r 2上，∴5＋⎝⎛⎭⎫p22＝r 2，③ 联立①②③，解得p ＝4，即C 的焦点到准线的距离为p ＝4，故选B.]3.(2015·天津，6)已知双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的一条渐近线过点(2，3) ，且双曲线的一个焦点在抛物线y 2＝47x 的准线上，则双曲线的方程为( ) A.x 221－y 228＝1 B.x 228－y 221＝1 C.x 23－y 24＝1 D.x 24－y 23＝1 3.D [双曲线x 2a 2－y 2b 2＝1的渐近线方程为y ＝±b a x ，又渐近线过点(2，3)，所以2ba ＝3，即2b ＝3a ，①抛物线y 2＝47x 的准线方程为x ＝－7，由已知，得a 2＋b 2＝7，即a 2＋b 2＝7②，联立①②解得a 2＝4，b 2＝3，所求双曲线的方程为x 24－y 23＝1，选D.] 4.(2015·浙江，5)如图，设抛物线y 2＝4x 的焦点为F ，不经过焦点的直线上有三个不同的点A ，B ，C ，其中点A ，B 在抛物线上，点C 在y 轴上，则△BCF 与△ACF 的面积之比是( )A.|BF |－1|AF |－1B.|BF |2－1|AF |2－1C.|BF |＋1|AF |＋1D.|BF |2＋1|AF |2＋14.A [由图象知S △BCF S △ACF ＝|BC ||AC |＝x B x A ，由抛物线的性质知|BF |＝x B ＋1，|AF |＝x A ＋1，∴x B ＝|BF |-1，x A ＝|AF |－1，∴S △BCF S △ACF ＝|BF |－1|AF |－1.故选A.]5．（2018全国Ⅲ，16）已知点M(−1 ， 1)和抛物线C ： y 2=4x ，过C 的焦点且斜率为k 的直线与C 交于A ，B 两点．若∠AMB =90°，则k =________．5.2 设A (x 1,y 1),B(x 2,y 2),则{y 12=4x 1y 22=4x2,所以y 12−y 22=4x 1−4x 2,所以k =y 1−y 2x 1−x 2=4y 1+y 2.取AB 中点M′(x 0，y 0),分别过点A,B 作准线x =−1的垂线，垂足分别为A ′,B′,因为∠AMB =90°,∴|MM ′|=12|AB |=12(|AF |+|BF |)=12(|AA ′|+|BB′|),因为M’为AB 中点，所以MM’平行于x 轴,因为M(-1,1),所以y 0=1，则y 1+y 2=2即k =2.6.（2017•新课标Ⅱ,16）已知F 是抛物线C ：y 2=8x 的焦点，M 是C 上一点，FM 的延长线交y 轴于点N ．若M 为FN 的中点，则|FN|=________．6. 6 抛物线C ：y 2=8x 的焦点F （2，0），M 是C 上一点，FM 的延长线交y 轴于点N ．若M 为FN 的中点，可知M 的横坐标为：1，则M 的纵坐标为：，|FN|=2|FM|=2 =6．故答案为：6．7.(2016·浙江，9)若抛物线y 2＝4x 上的点M 到焦点的距离为10，则M 到y 轴的距离是________. 7.9 [抛物线y 2＝4x 的焦点F (1,0).准线为x ＝-1,由M 到焦点的距离为10,可知M 到准线x ＝-1的距离也为10,故M 的横坐标满足x M ＋1＝10,解得x M ＝9,所以点M 到y 轴的距离为9.] 8.(2015·陕西，14)若抛物线y 2＝2px (p ＞0)的准线经过双曲线x 2－y 2＝1的一个焦点，则p ＝________.8.22 [由于双曲线x 2－y 2＝1的焦点为(±2，0)，故应有p2＝2，p ＝2 2.]9.(2014·湖南，15)如图，正方形ABCD 和正方形DEFG 的边长分别为a ， b (a <b )，原点O 为AD 的中点，抛物线y 2＝2px (p >0)经过C ，F 两点，则b a ＝________.9.1＋2 [由正方形的定义可知BC ＝CD ，结合抛物线的定义得点D 为抛物线的焦点，所以|AD |＝p ＝a ，D ⎝⎛⎭⎫p 2，0，F ⎝⎛⎭⎫p2＋b ，b ，将点F 的坐标代入抛物线的方程得b 2＝2p⎝⎛⎭⎫p 2＋b ＝a 2＋2ab ，变形得⎝⎛⎭⎫b a 2－2b a －1＝0，解得b a ＝1＋2或b a＝1－2(舍去)，所以ba ＝1＋ 2.]10.(2014·上海，3)若抛物线y 2＝2px的焦点与椭圆x 29＋y 25＝1的右焦点重合，则该抛物线的准线方程为______________. 10.x ＝-2[∵c 2＝9-5＝4,∴c ＝2.∴椭圆x 29＋y 25＝1的右焦点为(2，0),∴p2＝2,即p ＝4. ∴抛物线的准线方程为x ＝-2.]。

高中数学高考几何解析(椭圆双曲线抛物线)课本知识讲解及练习(含答案)

高中数学高考几何解析（椭圆双曲线抛物线）课本知识讲解及练习（含答案）第五节椭圆一、必记3个知识点1．椭圆的定义(1)设椭圆x2a2＋y2b2＝1(a>b>0)上任意一点P(x，y)，则当x＝0时，|OP|有最小值b，这时，P在短轴端点处；当x＝±a时，|OP|有最大值a，这时，P在长轴端点处．(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形，其中a是斜边长，a2＝b2＋c2.(3)已知过焦点F1的弦AB，则△ABF2的周长为4a.(4)若P为椭圆上任一点，F为其焦点，则a－c≤|PF|≤a＋c.二、必明3个易误点1．椭圆的定义中易忽视2a>|F1F2|这一条件，当2a＝|F1F2|其轨迹为线段F1F2，当2a<|F1F2|不存在轨迹．2．求椭圆的标准方程时易忽视判断焦点的位置，而直接设方程为x2a2＋y2b2＝1(a>b>0)．3．注意椭圆的范围，在设椭圆x2a2＋y2b2＝1(a>b>0)上点的坐标为P(x，y)时，则|x|≤a，这往往在求与点P有关的最值问题中特别有用，也是容易被忽略而导致求最值错误的原因．三、技法1.求椭圆标准方程的2种常用方法(1)直接求出a，c来求解e.通过已知条件列方程组，解出a，c的值．(2)构造a，c的齐次式，解出e.由已知条件得出关于a，c的二元齐次方程，然后转化为关于离心率e的一元二次方程求解．(3)通过取特殊值或特殊位置，求出离心率．提醒：在解关于离心率e的二次方程时，要注意利用椭圆的离心率e∈(0,1)进行根的取舍，否则将产生增根.3.求解最值、取值范围问题的技巧(1)与椭圆几何性质有关的问题要结合图形进行分析，即使画不出图形，思考时也要联想到一个图形．(2)椭圆的范围或最值问题常常涉及一些不等式．例如，－a≤x≤a，－b≤y≤b,0<e<1，在求椭圆的相关量的范围时，要注意应用这些不等关系．(3)最值问题，将所求列出表达式，构造基本不等式或利用函数单调性求解.4.判断直线与椭圆位置关系的四个步骤第一步：确定直线与椭圆的方程．第二步：联立直线方程与椭圆方程．第三步：消元得出关于x(或y)的一元二次方程．第四步：当Δ>0时，直线与椭圆相交；当Δ＝0时，直线与椭圆相切；当Δ<0时，直线与椭圆相离．5．直线被椭圆截得的弦长公式设直线与椭圆的交点坐标为A(x1，y1)，B(x2，y2)，则|AB|＝(1＋k2)[(x1＋x2)2－4x1x2])＝(y1＋y2)2－4y1y2])(k为直线斜率).参考答案①F1，F2②|F1F2|③x轴，y轴④坐标原点⑤(－a,0)⑥(a,0)⑦(0，－b)⑧(0，b)⑨(0，－a)⑩(0，a)⑪(－b,0)⑫(b,0)⑬2a⑭2b⑮2c⑯(0,1)⑰c2＝a2－b2第六节双曲线一、必记3个知识点1．双曲线的定义(1)平面内与两个定点F1、F2(|F1F2|＝2c>0)的距离①________________为非零常数2a(2a<2c)的点的轨迹叫做双曲线．这两个定点叫做双曲线的②________，两焦点间的距离叫做③________.(2)集合P＝{M|||MF1|－|MF2||＝2a}，|F1F2|＝2c，其中a，c为常数且a>0，c>0.(ⅰ)当④________________时，M点的轨迹是双曲线；(ⅱ)当⑤________________时，M点的轨迹是两条射线；(ⅲ)当⑥________________时，M点不存在．2．双曲线的标准方程和几何性质⑧________x ∈对称轴：⑪________对称中心：⑫________顶点坐标：A 1⑮______，A 2⑯________⑱____________c ＝⑳________|＝21________；线段________；a 叫做双曲线的虚半轴长＞b ＞0)(1)双曲线为等轴双曲线⇔双曲线的离心率e ＝2⇔双曲线的两条渐近线互相垂直．(2)渐近线的斜率与双曲线的焦点位置的关系：当焦点在x 轴上时，渐近线斜率为±ba，当焦点在y 轴上时，渐近线斜率为±ab.(3)渐近线与离心率．x2a2－y2b2＝1(a >0，b >0)的一条渐近线的斜率为ba＝e2－1.(4)若P 为双曲线上一点，F 为其对应焦点，则|PF |≥c －a .二、必明4个易误点1．双曲线的定义中易忽视2a <|F 1F 2|这一条件．若2a ＝|F 1F 2|，则轨迹是以F 1，F 2为端点的两条射线，若2a >|F 1F 2|则轨迹不存在．2．双曲线的标准方程中对a ，b 的要求只是a >0，b >0，易误认为与椭圆标准方程中a ，b 的要求相同．若a >b >0，则双曲线的离心率e ∈(1，2)；若a ＝b >0，则双曲线的离心率e ＝2；若0<a <b ，则双曲线的离心率e >2.3．注意区分双曲线中的a ，b ，c 大小关系与椭圆a ，b ，c 关系，在椭圆中a 2＝b 2＋c 2，而在双曲线中c2＝a2＋b2.4．易忽视渐近线的斜率与双曲线的焦点位置关系．当焦点在x轴上，渐近线斜率为±ba，当焦点在y轴上，渐近线斜率为±ab.三、技法1.双曲线定义的应用(1)判定满足某条件的平面内动点的轨迹是否为双曲线，进而根据要求可求出曲线方程；(2)在“焦点三角形”中，常利用正弦定理、余弦定理，经常结合||PF1|－|PF2||＝2a，运用平方的方法，建立|PF1|与|PF2|的关系．[注意]在应用双曲线定义时，要注意定义中的条件，搞清所求轨迹是双曲线，还是双曲线的一支，若是双曲线的一支，则需确定是哪一支.2.求双曲线标准方程的一般方法(1)待定系数法：设出双曲线方程的标准形式，根据已知条件，列出参数a，b，c的方程并求出a，b，c的值．与双曲线x2a2－y2b2＝1有相同渐近线时，可设所求双曲线方程为：x2a2－y2b2＝λ(λ≠0)．(2)定义法：依定义得出距离之差的等量关系式，求出a的值，由定点位置确定c的值.3.求双曲线离心率或其范围的方法(1)求a，b，c的值，由c2a2＝a2＋b2a2＝1＋b2a2直接求e.(2)列出含有a，b，c的齐次方程(或不等式)，借助于b2＝c2－a2消去b，然后转化成关于e的方程(或不等式)求解．4．求双曲线的渐近线方程的方法求双曲线x2a2－y2b2＝1(a>0，b>0)的渐近线的方法是令x2a2－y2b2＝0，即得两渐近线方程为：xa±yb＝0.参考答案①之差的绝对值②焦点③焦距④2a<|F1F2|⑤2a＝|F1F2|⑥2a>|F1F2|⑦x≥a或x≤－a⑧y≥a或y≤－a⑨x轴，y轴⑩坐标原点⑪x轴，y轴⑫坐标原点⑬(－a,0)⑭(a,0)⑮(0，－a)⑯(0，a)⑰y＝±ba x⑱y＝±ab x⑲ca⑳a2＋b2212a222b23a2＋b2第七节抛物线一、必记2个知识点1．抛物线定义、标准方程及几何性质x轴⑤________y轴⑥________O(0,0)O(0,0)O(0,0)O(0,0)F⑦________⑧________⑨________设AB是过抛物线y2＝2px(p>0)的焦点F的弦，若A(x1，y1)，B(x2，y2)，则(1)x1x2＝p24，y1y2＝－p2.(2)弦长|AB|＝x1＋x2＋p＝2psin2α(α为弦AB的倾斜角)．(3)以弦AB为直径的圆与准线相切．(4)通径：过焦点且垂直于对称轴的弦，长等于2p.二、必明2个易误点1．抛物线的定义中易忽视“定点不在定直线上”这一条件，当定点在定直线上时，动点的轨迹是过定点且与直线垂直的直线．2．抛物线标准方程中参数p易忽视，只有p>0，才能证明其几何意义是焦点F到准线l 的距离，否则无几何意义．三、技法1.应用抛物线定义的2个关键点(1)由抛物线定义，把抛物线上点到焦点距离与到准线距离相互转化．(2)注意灵活运用抛物线上一点P(x，y)到焦点F的距离|PF|＝|x|＋p2或|PF|＝|y|＋p2.2.求抛物线的标准方程的方法(1)求抛物线的标准方程常用待定系数法，因为未知数只有p，所以只需一个条件确定p值即可．(2)因为抛物线方程有四种标准形式，因此求抛物线方程时，需先定位，再定量．3．确定及应用抛物线性质的技巧(1)利用抛物线方程确定及应用其焦点、准线等性质时，关键是将抛物线方程化为标准方程．(2)要结合图形分析，灵活运用平面几何的性质以图助解.4.解决直线与抛物线位置关系问题的常用方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系．(2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB|＝x1＋x2＋p，若不过焦点，则必须用一般弦长公式．(3)涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”“整体代入”等解法．提醒：涉及弦的中点、斜率时，一般用“点差法”求解.参考答案①相等②y2＝－2px(p＞0)③x2＝－2py(p＞0)④x2＝2py(p＞0)⑤x轴⑥y轴⑦F(－p2，0)⑧F(0，－p2)⑨F(0，p2)⑩e＝1⑪x＝－p2⑫y＝－p2⑬－y0＋p2⑭y0＋p2⑮y≤0⑯y≥0。

高三数学双曲线试题答案及解析

高三数学双曲线试题答案及解析1.已知双曲线，分别是它的左、右焦点，是其左顶点，且双曲线的离心率为.设过右焦点的直线与双曲线C的右支交于两点，其中点位于第一象限内.（1）求双曲线的方程；（2）若直线分别与直线交于两点，求证：；（3）是否存在常数，使得恒成立？若存在，求出的值，若不存在，请说明理由。

【答案】（1）；（2）见解析；（3）存在，，理由祥见解析．【解析】（1）由已知首先得到，再由离心率为２可求得的值，最后利用双曲线中基本量的关系求出值，从而就可写出所求双曲线的标准方程；（2）设直线的方程为：，与双曲线方程联立，消去得到关于的一个一元二次方程；再设，则由韦达定理就可用的式子表示出，再用点Ｐ，Ｑ的坐标表示出直线ＡＰ及ＡＱ的方程，再令就可写出点Ｍ，Ｎ的坐标，进而就可写出向量的坐标，再计算得，即证明得；（3）先取直线的斜率不存在的特列情形，研究出对应的的值，然后再对斜率存在的情形给予一般性的证明：不难获得，从而假设存在使得恒成立，然后证明即可．试题解析：（1）由题可知： 1分2分∴双曲线C的方程为： 3分（2）设直线的方程为：，另设：4分5分又直线AP的方程为，代入 6分同理，直线AQ的方程为，代入 7分9分（3）当直线的方程为时，解得. 易知此时为等腰直角三角形，其中，即，也即：. 10分下证：对直线存在斜率的情形也成立.11分12分13分∴结合正切函数在上的图像可知， 14分【考点】1．双曲线的标准方程；2．直线与双曲线的位置关系；３．探索性问题．2.已知双曲线C：(a＞0，b＞0)的一条渐近线与直线l：垂直，C的一个焦点到l的距离为1，则C的方程为__________________.【答案】x2－＝1【解析】由已知，一条渐近线方程为，即又，故c＝2，即a2＋b2＝4，解得a＝1，b＝3双曲线方程为x2－＝1考点:双曲线的渐近线，直线与直线的垂直关系，点到直线距离公式3.若点P在曲线C1：－＝1上，点Q在曲线C2：(x－5)2＋y2＝1上，点R在曲线C3：(x＋5)2＋y2＝1上，则|PQ|－|PR|的最大值是________．【答案】10【解析】依题意得，点F1(－5,0)，F2(5,0)分别为双曲线C1的左、右焦点，因此有|PQ|－|PR|≤|(|PF2|＋1)－(|PF1|－1)|≤||PF2|－|PF1||＋2＝2×4＋2＝10，故|PQ|－|PR|的最大值是10．4.（本小题满分13分）已知双曲线的两条渐近线分别为.（1）求双曲线的离心率；（2）如图，为坐标原点，动直线分别交直线于两点（分别在第一，四象限），且的面积恒为8，试探究：是否存在总与直线有且只有一个公共点的双曲线？若存在，求出双曲线的方程；若不存在，说明理由.【答案】(1) ;(2)存在【解析】(1) 已知双曲线的两条渐近线分别为,所以根据即可求得结论.(2)首先分类讨论直线的位置.由直线垂直于x轴可得到一个结论.再讨论直线不垂直于x轴,由的面积恒为8,则转化为.由直线与双曲线方程联立以及韦达定理,即可得到直线有且只有一个公共点.试题解析：(1)因为双曲线E的渐近线分别为和.所以,从而双曲线E的离心率.(2)由(1)知,双曲线E的方程为.设直线与x轴相交于点C.当轴时,若直线与双曲线E有且只有一个公共点,则,又因为的面积为8,所以.此时双曲线E的方程为.若存在满足条件的双曲线E,则E的方程只能为.以下证明:当直线不与x轴垂直时，双曲线E：也满足条件.设直线的方程为,依题意,得k>2或k<-2.则，记.由,得,同理得.由得, 即. 由得, .因为,所以,又因为.所以,即与双曲线E有且只有一个公共点.因此,存在总与有且只有一个公共点的双曲线E,且E的方程为.【考点】1.双曲线的性质.2.直线与双曲线的位置关系.3. 三角形的面积的表示.5.设的离心率为,则的最小值为( )A．B．C．D．【答案】B【解析】由题意得，所以.【考点】双曲线及重要不等式.6.设圆锥曲线I’的两个焦点分别为F1，F2，若曲线I’上存在点P满足：：= 4:3:2，则曲线I’的离心率等于( )A．B．C．D．【答案】A【解析】由：：= 4:3:2，可设,,,若圆锥曲线为椭圆,则,,;若圆锥曲线为双曲线,则,,,故选A.7.已知点F是双曲线的左焦点，点E是该双曲线的右焦点，过点F且垂直于x轴的直线与双曲线交于A，B两点，△ABE是锐角三角形，则该双曲线的离心率e的取值范围是() A．(1，＋∞)B．(1,2)C．D．【答案】B【解析】由AB⊥x轴，可知△ABE为等腰三角形，又△ABE是锐角三角形，所以∠AEB为锐角，即∠AEF<45°，于是|AF|<|EF|，，即，解得，又双曲线的离心率大于1，从而，故选B。

高考数学专题复习：双曲线(含解析)

高考数学专题复习：双曲线(含解析)本文存在大量的格式错误和段落问题，需要进行修正和删减。

修正后的文章如下：研究目标：1.理解双曲线的定义、几何图形、标准方程以及简单几何性质。

2.理解数形结合的思想。

3.了解双曲线的实际背景及其简单应用。

一、单选题1.设 $F_1,F_2$ 分别是双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ 的左右焦点，点 $P$ 在双曲线 $C$ 的右支上，且 $F_1P=F_2P=c$，则 $\frac{c^2}{a^2-b^2}$ 的值为：A。

$1$B。

$\frac{1}{2}$C。

$\frac{1}{3}$D。

$\frac{1}{4}$答案】B解析】根据双曲线的性质求出 $c$ 的值，结合向量垂直和向量和的几何意义进行转化求解即可。

点睛】本题主要考查双曲线性质的意义，根据向量垂直和向量和的几何意义是解决本题的关键。

2.设 $F_1(-1,0),F_2(1,0)$ 是双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ 的左右焦点，$A(0,b)$ 为左顶点，点$P$ 为双曲线右支上一点，且 $AP=\frac{a}{2}$，则$\frac{b^2}{a^2}$ 的值为：A。

$1$B。

$\frac{1}{2}$C。

$\frac{1}{3}$D。

$\frac{1}{4}$答案】D解析】先求出双曲线的方程为 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$，再求出点 $P$ 的坐标，最后求$\frac{b^2}{a^2}$。

点睛】本题主要考查双曲线的几何性质和向量的数量积运算，考查双曲线方程的求法，意在考查学生对这些知识的掌握水平和分析推理计算能力。

双曲线的通径为 $2a$。

3.已知直线$l$ 的倾斜角为$\theta$，且$l: y=x\tan\theta$，直线 $l$ 与双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ 的左、右两支分别交于 $A,B$ 两点，$OA\perp$轴，$OB\perp$轴（其中 $O$、$F_1,F_2$ 分别为双曲线的坐标原点、左、右焦点），则该双曲线的离心率为：A。

高三数学二轮专题复习椭圆双曲线抛物线01含答案

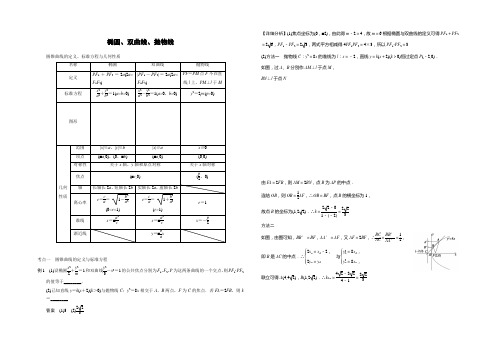
椭圆、双曲线、抛物线圆锥曲线的定义、标准方程与几何性质名称椭圆双曲线抛物线定义 PF 1＋PF 2＝2a (2a > F 1F 2)|PF 1－PF 2|＝2a (2a < F 1F 2)PF ＝PM 点F 不在直线l 上，PM ⊥l 于M标准方程x 2a 2＋y 2b 2＝1(a >b >0) x 2a 2－y 2b 2＝1(a >0，b >0) y 2＝2px (p >0)图形几何性质范围 |x |≤a ，|y |≤b |x |≥a x ≥0 顶点 (±a,0)，(0，±b )(±a,0)(0,0) 对称性关于x 轴，y 轴和原点对称关于x 轴对称焦点(±c,0)(p2，0) 轴长轴长2a ，短轴长2b 实轴长2a ，虚轴长2b离心率 e ＝ca＝ 1－b 2a 2(0<e <1)e ＝c a＝ 1＋b 2a 2(e >1) e ＝1 准线 x ＝±a 2cx ＝±a 2cx ＝－p 2渐近线y ＝±b ax考点一圆锥曲线的定义与标准方程例1 (1)设椭圆x 22＋y 2m ＝1和双曲线y 23－x 2＝1的公共焦点分别为F 1、F 2，P 为这两条曲线的一个交点，则PF 1·PF 2的值等于________．(2)已知直线y ＝k (x ＋2)(k ＞0)与抛物线C ：y 2＝8x 相交于A 、B 两点，F 为C 的焦点．若F A ＝2FB ，则k ＝________. 答案 (1)3 (2)223【详细分析】(1)焦点坐标为(0，±2)，由此得m －2＝4，故m ＝6.根据椭圆与双曲线的定义可得PF 1＋PF 2＝26，PF 1－PF 2＝23，两式平方相减得4PF 1PF 2＝4×3，所以PF 1·PF 2＝3.(2)方法一抛物线C ：y 2＝8x 的准线为l ：x ＝－2，直线y ＝k (x ＋2)(k ＞0)恒过定点P (－2,0)．如图，过A 、B 分别作AM ⊥l 于点M ， BN ⊥l 于点N .由F A ＝2FB ，则AM ＝2BN ，点B 为AP 的中点．连结OB ，则OB ＝12AF ，∴OB ＝BF ，点B 的横坐标为1，故点B 的坐标为(1,22)．∴k ＝22－01－(－2)＝223.方法二如图，由图可知，BB ′＝BF ，AA ′＝AF ，又AF ＝2BF ，∴BC AC ＝BB ′AA ′＝12，即B 是AC 的中点．∴⎩⎪⎨⎪⎧ 2x B ＝x A －2，2y B ＝y A 与⎩⎪⎨⎪⎧y 2A ＝8x A ，y 2B ＝8x B ，联立可得A (4,42)，B (1,22)．∴k AB ＝42－224－1＝223.(1)对于圆锥曲线的定义不仅要熟记，还要深入理解细节部分：比如椭圆的定义中要求PF 1＋PF 2＞F 1F 2，双曲线的定义中要求PF 1－PF 2＜F 1F 2，抛物线上的点到焦点的距离与到准线的距离相等的转化． (2)注意数形结合，提倡画出合理草图．(1)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32.双曲线x 2－y 2＝1的渐近线与椭圆C 有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C 的方程为________．(2)如图，过抛物线y 2＝2px (p >0)的焦点F 的直线交抛物线于点A ，B ，交其准线l 于点C ，若BC ＝2BF ，且AF ＝3，则此抛物线的方程为 ________．答案 (1)x 220＋y 25＝1 (2)y 2＝3x【详细分析】(1)∵椭圆的离心率为32，∴ca ＝a 2－b 2a ＝32， ∴a ＝2b .∴椭圆方程为x 2＋4y 2＝4b 2.∵双曲线x 2－y 2＝1的渐近线方程为x ±y ＝0，∴渐近线x ±y ＝0与椭圆x 2＋4y 2＝4b 2在第一象限的交点为⎝⎛⎭⎫255b ，255b ，∴由圆锥曲线的对称性得四边形在第一象限部分的面积为255b ×255b ＝4，∴b 2＝5，∴a 2＝4b 2＝20.∴椭圆C 的方程为x 220＋y 25＝1.(2)如图，分别过A ，B 作AA 1⊥l 于A 1，BB 1⊥l 于B 1，由抛物线的定义知，AF ＝AA 1，BF ＝BB 1，∵BC ＝2BF ，∴BC ＝2BB 1，∴∠BCB 1＝30°，∴∠AFx ＝60°.连结A 1F ，则△AA 1F 为等边三角形，过F 作FF 1⊥AA 1于F 1，则F 1为AA 1的中点，设l 交x 轴于N ，则NF ＝A 1F 1＝12AA 1＝12AF ，即p ＝32，∴抛物线方程为y 2＝3x .考点二圆锥曲线的几何性质例2 (1)已知椭圆C ：x 2a 2＋y 2b2＝1(a ＞b ＞0)的左焦点为F ，C 与过原点的直线相交于A ，B 两点，连结AF ，BF .若AB ＝10，BF ＝8，cos ∠ABF ＝45，则C 的离心率为________．(2)(2013·江苏)在平面直角坐标系xOy 中，椭圆C 的标准方程为x 2a 2＋y 2b 2＝1(a >b >0)，右焦点为F ，右准线为l ，短轴的一个端点为B ，设原点到直线BF 的距离为d 1，F 到l 的距离为d 2.若d 2＝6d 1，则椭圆C 的离心率为________．答案 (1)57 (2)33【详细分析】(1)在△ABF 中，由余弦定理得 AF 2＝AB 2＋BF 2－2AB ·BF cos ∠ABF ， ∴AF 2＝100＋64－128＝36，∴AF ＝6，从而AB 2＝AF 2＋BF 2，则AF ⊥BF . ∴c ＝OF ＝12AB ＝5，利用椭圆的对称性，设F ′为右焦点，则BF ′＝AF ＝6，∴2a ＝BF ＋BF ′＝14，a ＝7. 因此椭圆的离心率e ＝c a ＝57.(2)如图，F (c,0)，B (0，b )，则直线BF 的方程为x c ＋yb ＝1，即bx ＋cy－bc ＝0，d 1＝bcb 2＋c 2＝bc a d 2＝a 2c －c ＝b 2c ，由已知条件d 2＝6d 1 即b 2c ＝6bca ，整理得：6b 2＋ab －6a 2＝0解得b a ＝26，∴e ＝c 2a 2＝ 1－b 2a 2＝33. 解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于a ，b ，c 的方程或不等式，再根据a ，b ，c 的关系消掉b 得到a ，c 的关系式．建立关于a ，b ，c 的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等．(1)已知F 是椭圆C 的一个焦点，B 是短轴的一个端点，线段BF 的延长线交C 于点D ，且B F →＝2 F D →，则C 的离心率为________．(2)过双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左焦点F 作圆x 2＋y 2＝a 24的切线，切点为E ，延长FE 交双曲线右支于点P ，若E 为PF 的中点，则双曲线的离心率为________．答案 (1)33 (2)102【详细分析】(1)设椭圆C 的焦点在x 轴上，如图，B (0，b )，F (c,0)，D (x D ，y D )，则B F →＝(c ，－b )，F D →＝(x D －c ，y D )，∵B F →＝2F D →，∴⎩⎪⎨⎪⎧c ＝2(x D －c )，－b ＝2y D ，∴⎩⎨⎧x D ＝3c2，y D＝－b2.又∵点D 在椭圆C 上，∴⎝⎛⎭⎫3c 22a 2＋⎝⎛⎭⎫－b 22b 2＝1，即e 2＝13.∴e ＝33.(2)设c ＝a 2＋b 2，双曲线的右焦点为F ′.则PF －PF ′＝2a ，FF ′＝2c .∵E 为PF 的中点，O 为FF ′的中点，∴OE ∥PF ′，且PF ′＝2OE . ∵OE ⊥PF ，OE ＝a2，∴PF ⊥PF ′，PF ′＝a ，∴PF ＝PF ′＋2a ＝3a . ∵PF 2＋PF ′2＝FF ′2，即9a 2＋a 2＝4c 2，∴c a ＝102.∴双曲线的离心率为102.考点三圆锥曲线的综合问题例3 已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率e ＝22，点F 为椭圆的右焦点，点A 、B 分别为椭圆的左、右顶点，点M 为椭圆的上顶点，且满足MF →·FB →＝2－1. (1)求椭圆C 的方程；(2)是否存在直线l ，当直线l 交椭圆于P 、Q 两点时，使点F 恰为△PQM 的垂心？若存在，求出直线l 的方程；若不存在，请说明理由．解 (1)根据题意得，F (c,0)(c >0)，A (－a,0)，B (a,0)，M (0，b )， ∴MF →＝(c ，－b )，FB →＝(a －c,0)，∴MF →·FB →＝ac －c 2＝2－1.又e ＝c a ＝22，∴a ＝2c ，∴2c 2－c 2＝2－1，∴c 2＝1，a 2＝2，b 2＝1，∴椭圆C 的方程为x 22＋y 2＝1.(2)假设存在满足条件的直线l .∵k MF ＝－1，且MF ⊥l ，∴k l ＝1.设直线l 的方程为y ＝x ＋m ，P (x 1，y 1)，Q (x 2，y 2)，由⎩⎪⎨⎪⎧y ＝x ＋m ，x 22＋y 2＝1消去y 得3x 2＋4mx ＋2m 2－2＝0，则有Δ＝16m 2－12(2m 2－2)>0，即m 2<3，又x 1＋x 2＝－4m3，x 1x 2＝2m 2－23，∴y 1y 2＝(x 1＋m )(x 2＋m )＝x 1x 2＋m (x 1＋x 2)＋m 2＝2m 2－23－4m 23＋m 2＝m 2－23.又F 为△MPQ 的垂心，连结PF ，则PF ⊥MQ ，∴PF →·MQ →＝0，又PF →＝(1－x 1，－y 1)，MQ →＝(x 2，y 2－1)，∴PF →·MQ →＝x 2＋y 1－x 1x 2－y 1y 2＝x 2＋x 1＋m －x 1x 2－y 1y 2 ＝－43m ＋m －2m 2－23－m 2－23＝－m 2－m 3＋43＝－13(3m 2＋m －4)＝－13(3m ＋4)(m －1)＝0，∴m ＝－43或m ＝1(舍去)，经检验m ＝－43符合条件，∴存在满足条件的直线l ，其方程为3x －3y －4＝0.(1)对于弦中点问题常用“根与系数的关系”或“点差法”求解，在使用根与系数的关系时，要注意使用条件Δ≥0，在用“点差法”时，要检验直线与圆锥曲线是否相交．(2)涉及弦长的问题中，应熟练地利用根与系数关系、设而不求法计算弦长；涉及垂直关系时也往往利用根与系数关系、设而不求法简化运算；涉及过焦点的弦的问题，可考虑用圆锥曲线的定义求解．已知A ，B ，C 是椭圆W ：x 24＋y 2＝1上的三个点，O 是坐标原点．(1)当点B 是W 的右顶点，且四边形OABC 为菱形时，求此菱形的面积； (2)当点B 不是W 的顶点时，判断四边形OABC 是否可能为菱形，并说明理由．解 (1)由椭圆W ：x 24＋y 2＝1，知B (2,0)∴线段OB 的垂直平分线x ＝1.在菱形OABC 中，AC ⊥OB ，将x ＝1代入x 24＋y 2＝1，得y ＝±32.∴AC ＝|y 2－y 1|＝ 3.因此菱形的面积S ＝12OB ·AC ＝12×2×3＝ 3.(2)假设四边形OABC 为菱形．因点B 不是W 的顶点，且直线AC 不过原点，所以可设AC 的方程为y ＝kx ＋m (k ≠0，m ≠0)．由⎩⎪⎨⎪⎧x 2＋4y 2＝4，y ＝kx ＋m 消y 并整理得(1＋4k 2)x 2＋8kmx ＋4m 2－4＝0. 设A (x 1，y 1)，C (x 2，y 2)，则x 1＋x 22＝－4km 1＋4k 2，y 1＋y 22＝k ·x 1＋x 22＋m ＝m1＋4k 2. ∴线段AC 中点M ⎝ ⎛⎭⎪⎫－4km 1＋4k 2，m 1＋4k 2，∵M 为AC 和OB 交点，∴k OB ＝－14k .又k ·⎝⎛⎭⎫－14k ＝－14≠－1，∴AC 与OB 不垂直．故OABC 不是菱形，这与假设矛盾．综上，四边形OABC 不是菱形．1．对涉及圆锥曲线上点到焦点距离或焦点弦问题，恰当选用定义解题，会效果明显，定义中的定值是标准方程的基础．2．椭圆、双曲线的方程形式上可统一为Ax 2＋By 2＝1，其中A 、B 是不等的常数，A >B >0时，表示焦点在y轴上的椭圆；B >A >0时，表示焦点在x 轴上的椭圆；AB <0时表示双曲线．3．求双曲线、椭圆的离心率的方法：方法一：直接求出a ，c ，计算e ＝ca；方法二：根据已知条件确定a ，b ，c 的等量关系，然后把b 用a ，c 代换，求ca.4．通径：过双曲线、椭圆、抛物线的焦点垂直于对称轴的弦称为通径，双曲线、椭圆的通径长为2b 2a ，过椭圆焦点的弦中通径最短；抛物线通径长是2p ，过抛物线焦点的弦中通径最短．椭圆上点到焦点的最长距离为a ＋c ，最短距离为a －c . 5．抛物线焦点弦性质：已知AB 是抛物线y 2＝2px (p >0)的焦点弦，F 为抛物线的焦点，A (x 1，y 1)、B (x 2，y 2)．(1)y 1y 2＝－p 2，x 1x 2＝p 24；(2)AB ＝x 1＋x 2＋p ＝2psin 2α(α为弦AB 的倾斜角)；(3)S △AOB ＝p 22sin α；(4)1F A ＋1FB 为定值2p； (5)以AB 为直径的圆与抛物线的准线相切.1．已知点F 是双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左焦点，点E 是该双曲线的右顶点，过点F 且垂直于x 轴的直线与双曲线交于A ，B 两点，△ABE 是锐角三角形，则该双曲线的离心率e 的取值范围是________．答案 (1,2)【详细分析】由AB ⊥x 轴，可知△ABE 为等腰三角形，又△ABE 是锐角三角形，所以∠AEB 为锐角，即∠AEF <45°，于是AF <EF ，b 2a<a ＋c ，于是c 2－a 2<a 2＋ac ，即e 2－e －2<0，解得－1<e <2.又双曲线的离心率e >1，从而1<e <2.2．设椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率为e ＝12，右焦点为F (c,0)，方程ax 2＋bx －c ＝0的两个实根分别为x 1和x 2，则点P (x 1，x 2)必在圆x 2＋y 2＝2________.(填“内”“外”“上”) 答案内【详细分析】∵x 1＋x 2＝－b a ，x 1x 2＝－c a .∴x 21＋x 22＝(x 1＋x 2)2－2x 1x 2＝b 2a 2＋2c a ＝b 2＋2ac a 2. ∵e ＝c a ＝12，∴c ＝12a ，∴b 2＝a 2－c 2＝a 2－⎝⎛⎭⎫12a 2＝34a 2. ∴x 21＋x 22＝34a 2＋2a ×12a a 2＝74<2.∴P (x 1，x 2)在圆x 2＋y 2＝2内． 3．过抛物线y 2＝2px (p >0)的对称轴上一点A (a,0)(a >0)的直线与抛物线相交于M 、N 两点，自M 、N 向直线l ：x ＝－a 作垂线，垂足分别为M 1、N 1. (1)当a ＝p2时，求证：AM 1⊥AN 1；(2)记△AMM 1、△AM 1N 1、△ANN 1的面积分别为S 1、S 2、S 3.是否存在λ，使得对任意的a >0，都有S 22＝λS 1S 3成立？若存在，求出λ的值；若不存在，说明理由．(1)证明当a ＝p 2时，A (p2，0)为该抛物线的焦点，而l ：x ＝－a 为准线，由抛物线的定义知MA ＝MM 1，NA ＝NN 1，则∠NN 1A ＝∠NAN 1，∠MM 1A ＝∠MAM 1. 又∠NN 1A ＝∠BAN 1，∠MM 1A ＝∠BAM 1，则∠BAN 1＋∠BAM 1＝∠NAN 1＋∠MAM 1，而∠BAN 1＋∠BAM 1＋∠NAN 1＋∠MAM 1＝180°，则∠N 1AM 1＝∠BAN 1＋∠BAM 1＝90°，所以AM 1⊥AN 1.(2)解可设直线MN 的方程为x ＝my ＋a ，由⎩⎪⎨⎪⎧x ＝my ＋a ，y 2＝2px 得y 2－2pmy －2pa ＝0.设M (x 1，y 1)，N (x 2，y 2)，则y 1＋y 2＝2pm ，y 1y 2＝－2pa . S 1＝12(x 1＋a )|y 1|，S 2＝12(2a )|y 1－y 2|，S 3＝12(x 2＋a )|y 2|，由已知S 22＝λS 1S 3恒成立，则4a 2(y 1－y 2)2＝λ(x 1＋a )(x 2＋a )|y 1y 2|.(y 1－y 2)2＝(y 1＋y 2)2－4y 1y 2＝4p 2m 2＋8pa ，(x 1＋a )(x 2＋a )＝(my 1＋2a )(my 2＋2a )＝m 2y 1y 2＋2ma (y 1＋y 2)＋4a 2 ＝m 2(－2pa )＋2ma ×2pm ＋4a 2＝4a 2＋2pam 2.则得4a 2(4p 2m 2＋8pa )＝2pa λ(4a 2＋2pam 2)，解得λ＝4，即当λ＝4时，对任意的a >0，都有S 22＝λS 1S 3成立．(推荐时间：70分钟)一、填空题1．设抛物线C ：y 2＝2px (p >0)的焦点为F ，点M 在C 上，|MF |＝5，若以MF 为直径的圆过点(0,2)，则C 的方程为________________．答案 y 2＝4x 或y 2＝16x【详细分析】由题意知：F ⎝⎛⎭⎫p 2，0，抛物线的准线方程为x ＝－p 2，则由抛物线的定义知，x M ＝5－p2，设以MF 为直径的圆的圆心为⎝⎛⎭⎫52，y M 2，所以圆的方程为⎝⎛⎭⎫x －522＋⎝⎛⎭⎫y －y M 22＝254，又因为圆过点(0,2)，所以y M ＝4，又因为点M 在C 上，所以16＝2p ⎝⎛⎭⎫5－p2，解得p ＝2或p ＝8，所以抛物线C 的方程为y 2＝4x 或y 2＝16x .2．与椭圆x 212＋y 216＝1共焦点，离心率互为倒数的双曲线方程是____________．答案y 2－x 23＝1 【详细分析】椭圆x 212＋y 216＝1的离心率为16－1216＝12，且焦点为(0，±2)，所以所求双曲线的焦点为(0，±2)且离心率为2，所以c ＝2，2a ＝2得a ＝1，b 2＝c 2－a 2＝3，故所求双曲线方程是y 2－x 23＝1.3．已知点A (2,0)，抛物线C ：x 2＝4y 的焦点为F ，射线F A 与抛物线C 相交于点M ，与其准线相交于点N ，则FM ∶MN ＝________. 答案 1∶ 5【详细分析】由抛物线定义知M 到F 的距离等于M 到准线l 的距离MH . 即FM ∶MN ＝MH ∶MN ＝FO ∶AF ＝1∶ 5.4．过双曲线x 2a 2－y 2b2＝1(a >0，b >0)的右焦点F ，作圆x 2＋y 2＝a 2的切线FM 交y 轴于点P ，切圆于点M,2OM →＝OF →＋OP →，则双曲线的离心率是________．答案2【详细分析】由已知条件知，点M 为直三角形OFP 斜边PF 的中点，故OF ＝2OM ，即c ＝2a ，所以双曲线的离心率为 2.5．抛物线C 1：y ＝12p x 2(p >0)的焦点与双曲线C 2：x 23－y 2＝1的右焦点的连线交C 1于第一象限的点M .若C 1在点M 处的切线平行于C 2的一条渐近线，则p 等于________．答案433【详细分析】抛物线C 1的标准方程为x 2＝2py ，其焦点F 为⎝⎛⎭⎫0，p2，双曲线C 2的右焦点F ′为(2,0)，渐近线方程为y ＝±33x .由y ′＝1p x ＝33得x ＝33p ，故M ⎝⎛⎭⎫33p ，p6.由F 、F ′、M 三点共线得p ＝433.6．在平面直角坐标系xOy 中，若双曲线x 2m －y 2m 2＋4＝1的离心率为5，则m 的值为________．答案 2【详细分析】建立关于m 的方程求解．∵c 2＝m ＋m 2＋4，∴e 2＝c 2a 2＝m ＋m 2＋4m＝5，∴m 2－4m ＋4＝0，∴m ＝2.7．椭圆M ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1、F 2，P 为椭圆M 上任一点，且PF →1·PF →2的最大值的取值范围是[c 2,3c 2]，其中c ＝a 2－b 2，则椭圆M 的离心率e 的取值范围是________．答案 [12，22]【详细分析】设P (x ，y )，F 1(－c,0)，F 2(c,0)，则PF →1＝(－c －x ，－y )，PF →2＝(c －x ，－y )，PF →1·PF →2＝x 2＋y 2－c 2. 又x 2＋y 2可看作P (x ，y )到原点的距离的平方，所以(x 2＋y 2)max ＝a 2，所以(PF 1→·PF 2→)max ＝b 2，所以c 2≤b 2＝a 2－c 2≤3c 2，即14≤e 2≤12，所以12≤e ≤22.8．椭圆Г：x 2a 2＋y 2b2＝1(a >b >0)的左，右焦点分别为F 1，F 2，焦距为2c .若直线y ＝3(x ＋c )与椭圆Г的一个交点M 满足∠MF 1F 2＝2∠MF 2F 1，则该椭圆的离心率等于________．答案3－1 【详细分析】由直线方程为y ＝3(x ＋c )，知∠MF 1F 2＝60°，又∠MF 1F 2＝2∠MF 2F 1，所以∠MF 2F 1＝30°， MF 1⊥MF 2，所以MF 1＝c ，MF 2＝3c ，所以MF 1＋MF 2＝c ＋3c ＝2a .即e ＝ca＝3－1.9．已知F 为双曲线C ：x 29－y 216＝1的左焦点，P ，Q 为C 上的点．若PQ 的长等于虚轴长的2倍，点A (5,0)在线段PQ 上，则△PQF 的周长为________．答案 44【详细分析】由双曲线C 的方程，知a ＝3，b ＝4，c ＝5， ∴点A (5,0)是双曲线C 的右焦点，且PQ ＝QA ＋P A ＝4b ＝16，由双曲线定义，PF －P A ＝6，QF －QA ＝6.∴PF ＋QF ＝12＋P A ＋QA ＝28，因此△PQF 的周长为PF ＋QF ＋PQ ＝28＋16＝44.10．已知P 为椭圆x 225＋y 216＝1上的一点，M ，N 分别为圆(x ＋3)2＋y 2＝1和圆(x －3)2＋y 2＝4上的点，则PM ＋PN 的最小值为________．答案 7【详细分析】由题意知椭圆的两个焦点F 1，F 2分别是两圆的圆心，且PF 1＋PF 2＝10，从而PM ＋PN 的最小值为PF 1＋PF 2－1－2＝7. 二、解答题11．平面直角坐标系xOy 中，过椭圆M ：x 2a 2＋y 2b2＝1(a >b >0)右焦点的直线x ＋y －3＝0交M 于A ，B 两点，P为AB 的中点，且OP 的斜率为12.(1)求M 的方程；(2)C ，D 为M 上的两点，若四边形ACBD 的对角线CD ⊥AB ，求四边形ACBD 面积的最大值．解 (1)设A (x 1，y 1)，B (x 2，y 2)，则x 21a 2＋y 21b 2＝1①x 22a 2＋y 22b2＝1②①－②，得(x 1－x 2)(x 1＋x 2)a 2＋(y 1－y 2)(y 1＋y 2)b 2＝0.因为y 1－y 2x 1－x 2＝－1，设P (x 0，y 0)，因为P 为AB 的中点，且OP 的斜率为12，所以y 0＝12x 0，即y 1＋y 2＝12(x 1＋x 2)．所以可以解得a 2＝2b 2，即a 2＝2(a 2－c 2)，即a 2＝2c 2，又因为c ＝3，所以a 2＝6，所以M 的方程为x 26＋y 23＝1.(2)因为CD ⊥AB ，直线AB 方程为x ＋y －3＝0，所以设直线CD 方程为y ＝x ＋m ，将x ＋y －3＝0代入x 26＋y 23＝1得：3x 2－43x ＝0，即A (0，3)，B ⎝⎛⎭⎫433，－33，所以可得AB ＝463；将y ＝x ＋m 代入x 26＋y 23＝1得：3x 2＋4mx ＋2m 2－6＝0，设C (x 3，y 3)，D (x 4，y 4)，则CD ＝2(x 3＋x 4)2－4x 3x 4＝22318－2m 2，又因为Δ＝16m 2－12(2m 2－6)>0，即－3<m <3，所以当m ＝0时，CD 取得最大值4，所以四边形ACBD 面积的最大值为12AB ·CD ＝863.12．如图，椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)经过点P ⎝⎛⎭⎫1，32，离心率e ＝12，直线l 的方程为x ＝4.(1)求椭圆C 的方程；(2)AB 是经过右焦点F 的任一弦(不经过点P )，设直线AB 与直线l 相交于点M ，记P A 、PB 、PM 的斜率分别为k 1、k 2、k 3.问：是否存在常数λ，使得k 1＋k 2＝λk 3？若存在，求λ的值；若不存在，说明理由．解 (1)由P ⎝⎛⎭⎫1，32在椭圆x 2a 2＋y 2b 2＝1上，得1a 2＋94b2＝1，① 又e ＝c a ＝12，得a 2＝4c 2，b 2＝3c 2，②②代入①得，c 2＝1，a 2＝4，b 2＝3. 故椭圆方程为x 24＋y 23＝1.(2)设直线AB 的方程为y ＝k (x －1)，A (x 1，y 1)，B (x 2，y 2)．由⎩⎪⎨⎪⎧y ＝k (x －1)x 24＋y 23＝1得，(4k 2＋3)x 2－8k 2x ＋4k 2－12＝0， x 1＋x 2＝8k 24k 2＋3，x 1x 2＝4k 2－124k 2＋3.k 1＋k 2＝y 1－32x 1－1＋y 2－32x 2－1＝k (x 1－1)－32x 1－1＋k (x 2－1)－32x 2－1＝2k －32⎝ ⎛⎭⎪⎫1x 1－1＋1x 2－1＝2k －32·x 1＋x 2－2x 1x 2－(x 1＋x 2)＋1＝2k －32·8k 24k 2＋3－24k 2－124k 2＋3－8k24k 2＋3＋1＝2k －1.又将x ＝4代入y ＝k (x －1)得M (4,3k )， ∴k 3＝3k －323＝k －12，∴k 1＋k 2＝2k 3.故存在常数λ＝2符合题意．13．已知中心在原点，焦点在x 轴上的椭圆C 的离心率为12，其一个顶点的抛物线x 2＝－43y 的焦点．(1)求椭圆C 的标准方程；(2)若过点P (2,1)的直线l 与椭圆C 在第一象限相切于点M ，求直线l 的方程和点M 的坐标；(3)是否存在过点P (2,1)的直线l 1与椭圆C 相交于不同的两点A ，B ，且满足P A →·PB →＝PM →2？若存在，求出直线l 1的方程；若不存在，请说明理由．解 (1)设椭圆C 的方程为x 2a 2＋y 2b 2＝1 (a >b >0)，由题意得b ＝3，c a ＝12，解得a ＝2，c ＝1.故椭圆C 的标准方程为x 24＋y 23＝1.(2)因为过点P (2,1)的直线l 与椭圆C 在第一象限相切，所以直线l 的斜率存在，故可设直线l 的方程为y ＝k (x －2)＋1 (k ≠0)．由⎩⎪⎨⎪⎧x 24＋y 23＝1y ＝k (x －2)＋1得(3＋4k 2)x 2－8k (2k －1)x ＋16k 2－16k －8＝0. ①因为直线l 与椭圆C 相切，所以Δ＝[－8k (2k －1)]2－4(3＋4k 2)(16k 2－16k －8)＝0. 整理，得32(6k ＋3)＝0，解得k ＝－12.所以直线l 的方程为y ＝－12(x －2)＋1＝－12x ＋2.将k ＝－12代入①式，可以解得M 点的横坐标为1，故切点M 的坐标为⎝⎛⎭⎫1，32. (3)若存在直线l 1满足条件，则直线l 1的斜率存在，设其方程为y ＝k 1(x －2)＋1，代入椭圆C 的方程得(3＋4k 21)x 2－8k 1(2k 1－1)x ＋16k 21－16k 1－8＝0.设A (x 1，y 1)，B (x 2，y 2)，因为直线l 1与椭圆C 相交于不同的两点A ，B ，所以Δ＝[－8k 1(2k 1－1)]2－4(3＋4k 21)(16k 21－16k 1－8)＝32(6k 1＋3)>0.所以k 1>－12. x 1＋x 2＝8k 1(2k 1－1)3＋4k 21，x 1x 2＝16k 21－16k 1－83＋4k 21. 因为P A →·PB →＝PM →2，即(x 1－2)(x 2－2)＋(y 1－1)(y 2－1)＝54，所以(x 1－2)(x 2－2)(1＋k 21)＝54，即[x 1x 2－2(x 1＋x 2)＋4](1＋k 21)＝54. 所以⎣⎢⎡⎦⎥⎤16k 21－16k 1－83＋4k 21－2·8k 1(2k 1－1)3＋4k 21＋4(1＋k 21)＝4＋4k 213＋4k 21＝54，解得k 1＝±12.因为A ，B 为不同的两点，所以k 1＝12.于是存在直线l 1满足条件，其方程为y ＝12x .。

高三数学备考冲刺140分问题实际应用中的统计解答题含解析1

问题42实际应用中的统计解答题一、考情分析概率统计在高考中扮演着很重要的角色,概率统计解答题是全国卷及多数省市高考数学必考内容,内容主要涉及古典概型、相互独立事件的概率、条件概率、二项分布、正态分布、频率分布直方图、回归分析、离散型随机变量的分布列、期望与方差的实际应用等.回顾近几年的高考试题,可以看出概率统计解答题,大多紧密结合社会实际,以现实生活为背景设置试题,注重知识的综合应用与实际应用,作为考查实践能力的重要载体,命题者要求考生会收集、整理、分析数据,能从大量数据中抽取对研究问题有用的信息,建立数学模型,再应用数学原理和数学工具解决实际问题.该类问题阅读量一般比较大,但难度多为中等或中等偏易. 二、经验分享(1)明确频率分布直方图的意义，即图中的每一个小矩形的面积是数据落在该区间上的频率，所有小矩形的面积和为1. 利用分布列中各概率之和为1可求参数的值，此时要注意检验，以保证每个概率值均为非负数．对于统计图表类题目，最重要的是认真观察图表，从中提炼有用的信息和数据．(2)随机变量的均值反映了随机变量取值的平均水平，方差反映了随机变量稳定于均值的程度，它们从整体和全局上刻画了随机变量，是生产实际中用于方案取舍的重要理论依据．一般先比较均值，若均值相同，再用方差来决定．(3)解决正态分布问题有三个关键点：(1)对称轴x ＝μ；(2)标准差σ；(3)分布区间．利用对称性可求指定范围内的概率值；由μ，σ，分布区间的特征进行转化，使分布区间转化为3σ特殊区间，从而求出所求概率．注意只有在标准正态分布下对称轴才为x ＝0. (4)判定两个变量正、负相关性的方法①画散点图：点的分布从左下角到右上角，两个变量正相关；点的分布从左上角到右下角，两个变量负相关．②相关系数：r >0时，正相关；r <0时，负相关．③线性回归方程中：b ^>0时，正相关；b ^<0时，负相关．(5) 回归分析是处理变量相关关系的一种数学方法．主要解决：①确定特定量之间是否有相关关系，如果有就找出它们之间贴近的数学表达式；② 根据一组观测值，预测变量的取值及判断变量取值的变化趋势；③ 求出线性回归方程．线性回归分析问题的类型及解题方法 ①求线性回归方程利用公式，求出回归系数b ^，或待定系数法：利用回归直线过样本点的中心求系数．②利用回归方程进行预测，把线性回归方程看作一次函数，求函数值．③利用回归直线判断正、负相关；决定正相关还是负相关的是系数b ^.(6)回归方程的拟合效果，可以利用相关系数判断，当|r |越趋近于1时，两变量的线性相关性越强． (7)比较几个分类变量有关联的可能性大小的方法①通过计算K 2的大小判断：K 2越大，两变量有关联的可能性越大．②通过计算|ad －bc |的大小判断：|ad －bc |越大，两变量有关联的可能性越大． (8)独立性检验的一般步骤 ①根据样本数据制成2×2列联表． ②根据公式计算K 2的观测值k .③比较k 与临界值的大小关系，作统计推断．三、知识拓展四、题型分析(一) 期望与方差的应用数学期望反应的是随机变量取值的平均水平，而方差则是反应随机变量取值在其平均值附近的离散程度.现代实际生活中，越来越多的决策需要应用数学期望与方差这思想来对事件发生大小的可能性进行评估，通过计算分析可以比较科学地得出各个方案的预期效果及出现偏差的大小，从而决定要选择的最佳方案.品种的优劣、仪器的好坏、预报的准确与否等很多问题都与这两个特征两量有关.(1)若我们希望实际的平均水平较理想,则先求随机变量12ξξ，的期望,当12E E ξξ=时,不应认为它们一定一样好,需要用12,D D ξξ来比较这两个随机变量的方差,确定它们的偏离程度. (2)若我们希望比较稳定性,应先考虑方差,再考虑均值是否相等或接近.【例1】例3.7（2018新课标I 卷理20）某工厂的某种产品成箱包装，每箱200件，每一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品．检验时，先从这箱产品中任取20件作检验，再根据检验结果决定是否对余下的所有产品作检验，设每件产品为不合格品的概率都为，且各件产品是否为不合格品相互独立．（1）记20件产品中恰有2件不合格品的概率为,求的最大值点．（2）现对一箱产品检验了20件，结果恰有2件不合格品，以（1）中确定的作为的值．已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用．（i ）若不对该箱余下的产品作检验，这一箱产品的检验费用与赔偿费用的和记为，求;（ii）以检验费用与赔偿费用和的期望值为决策依据，是否该对这箱余下的所有产品作检验？【分析】利用独立重复实验成功次数对应的概率，求得，之后对其求导，利用导数确定其单调性，再求最大值点，注意；(2)先根据第一问的条件，确定出，在解（i）的时候,先求件数对应的期望，之后应用变量之间的关系，求得赔偿费用的期望；在解（ii）的时候，就通过比较两个期望的大小，得到结果.【解析】（1）20件产品中恰有2件不合格品的概率为.因此.令，得.当时，；当时，.所以的最大值点为.（2）由（1）知，.（i）令表示余下的180件产品中的不合格品件数，依题意知，，即.所以.（ii）如果对余下的产品作检验，则这一箱产品所需要的检验费为400元.由于，故应该对余下的产品作检验.【点评】随机变量的均值反映了随机变量取值的平均水平，方差反映了随机变量稳定于均值的程度，它们从整体和全局上刻画了随机变量，是生产实际中用于方案取舍的重要理论依据．一般先比较均值，若均值相同，再用方差来决定．【小试牛刀】【广东省江门市2019届第一次模拟】甲、乙两家外卖公司，其送餐员的日工资方案如下：甲公司的底薪元，每单提成元；乙公司无底薪，单以内（含单）的部分每单提成元，大于单的部分每单提成元，假设同一公司送餐员一天的送餐单数相同，现从两家公司各随机抽取一名送餐员，并分别记录其天的送餐单数，得到如下频数表：甲公司送餐员送餐单数频数表乙公司送餐员送餐单数频数表（1）若将大于单的工作日称为“繁忙日”，根据以上频数表能否在犯错误的概率不超过的前提下认为“繁忙日”与公司有关？（2）若将频率视为概率，回答下列两个问题：①记乙公司送餐员日工资为（单位：元），求的分布列和数学期望；②小王打算到甲、乙两家公司中的一家应聘，你会推荐小王去哪家？为什么？参考公式和数据：【解析】（1）依题意得，公司与“繁忙日”列联表,，所以，能在犯错误的概率不超过的前提下认为“繁忙日”与公司有关 .（2）①设乙公司送餐员送餐单数为，则当时，，当时，，当时，，当时，，当时， . 所以，的所有可能取值为、、、、，的分布列为：.②依题意，甲公司送餐员日平均送餐单数为,所以甲公司送餐员日平均工资为（元）,因为，故从更高收入角度考虑推荐小王去乙公司应聘；因为乙公司比甲公司繁忙，故从工作闲适角度考虑推荐小王去甲公司应聘． (二)正态分布的应用正态分布随处可见，处处显现着他神秘的身影.对于某一件事或者某个要达到的目标，很多很多的个体发挥出来的水平大致上服从正态分布.也就是说，对于大量个体的发挥统计，常常能看到正态分布“冥冥之中”束缚着整体的状态. 对于某个单独的单位，一般来说，对于“发挥出来的水平”这件事，也往往有波动的效果，不管是机器、工具还是我们人本身：有的时候，超水平发挥了；有的时候正常发挥；有的时候又会发挥失常.这种东西应该也可以抽象为围绕期望水平的正态分布. 而对于若干数据，包括发挥水平、排位情况，但是没有整体数据的时候，如果能推测是正态分布的情形，就可以近似计算出分布函数来，然后去估计其他的分布情况.这是反向推导的过程. 生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述.例如，在生产条件不变的情况下，产品的强力、抗压强度、口径、长度等指标；同一种生物体的身长、体重等指标；同一种种子的重量；测量同一物体的误差；弹着点沿某一方向的偏差；某个地区的年降水量；以及理想气体分子的速度分量，等等.【例2】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸（单位：cm ）．根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布()2,N μσ．（1）假设生产状态正常,记X 表示一天内抽取的16个零件中其尺寸在()–3,3μσμσ+之外的零件数,求()1P X …及X 的数学期望；（2）一天内抽检零件中,如果出现了尺寸在()–3,3μσμσ+之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查．（ⅰ）试说明上述监控生产过程方法的合理性；（ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：9.95 10.12 9.969.96 10.01 9.929.98 10.0410.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95经计算得16119.9716i i x x ===∑,0.212s ===,其中i x 为抽取的第i 个零件的尺寸,1216i =⋯，，，．用样本平均数x 作为μ的估计值ˆμ,用样本标准差s 作为σ的估计值ˆσ,利用估计值判断是否需对当天的生产过程进行检查？剔除()ˆˆˆˆ3,3μσμσ-+之外的数据,用剩下的数据估计μ和σ（精确到0.01）．附：若随机变量Z服从正态分布()2,N μσ,则()–330.9974P Z μσμσ<<+=,160.99740.9592≈0.09≈．【分析】 (1)先确定()~160.0026X B ，,再利用EX np =求期望；（2）（i ）判断监控生产过程的方法是否合理,可通过一天内抽取的16个零件中,尺寸落()33μσμσ-+，之外概率的大小判断,（ii ）剔除异常数据,在利用公式求μ和σ.【解析】（1）由题可知尺寸落在()33μσμσ-+，之内的概率为0.9974,落在()33μσμσ-+，之外的概率为0.0026．()()016160C 10.99740.99740.9592P X ==-≈,()()11010.95920.0408P X P X =-=≈-=…,由题可知()~160.0026X B ，,所以()160.00260.0416E X =⨯=. （2）（i ）尺寸落在()33μσμσ-+，之外的概率为0.0026,由正态分布知尺寸落()33μσμσ-+，之外为小概率事件,因此上述监控生产过程的方法合理．（ii ）39.9730.2129.334μσ-=-⨯=,39.9730.21210.606μσ+=+⨯=,()()339.33410.606μσμσ-+=，，,因为()9.229.33410.606∉，, 所以需对当天的生产过程检查．因此剔除9.22,剔除数据之后：9.97169.2210.0215μ⨯-==．()()()()()222222[9.9510.0210.1210.029.9610.029.9610.0210.0110.02σ=-+-+-+-+-+()()()()()222229.9210.029.9810.0210.0410.0210.2610.029.9110.02-+-+-+-+-+()()()()()22222110.1310.0210.0210.0210.0410.0210.0510.029.9510.02]0.00815-+-+-+-+-⨯≈.所以0.09σ=.【点评】正态分布是概率统计中相对较独立的一个考点,且已经从冷点转化为热点,求解此类问题,一般从,μσ入手,对于应用问题,要注意从较大的阅读量中提取有用的信息.以下两类问题是正态分布中的基本问题：(1)利用正态分布密度曲线的对称性研究相关概率问题,涉及的知识主要是正态曲线关于直线x＝μ对称,及曲线与x轴之间的面积为1.(2)利用3σ原则求概率问题时,要注意把给出的区间或范围与正态变量的μ,σ进行对比联系,确定它们属于(μ－σ,μ＋σ),(μ－2σ,μ＋2σ),(μ－3σ,μ＋3σ)中的哪一个.【小试牛刀】【山东省济宁市2019届高三第一次模拟】某学校为了了解全校学生的体重情况，从全校学生中随机抽取了100人的体重数据，结果这100人的体重全部介于45公斤到75公斤之间，现将结果按如下方式分为6组：第一组[45，50)，第二组[50，55)，…，第六组[70，75)，得到如下图(1)所示的频率分布直方图，并发现这100人中，其体重低于55公斤的有15人，这15人体重数据的茎叶图如图(2)所示，以样本的频率作为总体的概率．(I)求频率分布直方图中的值；(II)从全校学生中随机抽取3名学生，记X为体重在[55，65)的人数，求X的概率分布列和数学期望；(III)由频率分布直方图可以认为，该校学生的体重近似服从正态分布，其中若，则认为该校学生的体重是正常的．试判断该校学生的体重是否正常?并说明理由．【解析】解：(Ⅰ)由图（2）知，100名样本中体重低于50公斤的有2人，用样本的频率估计总体的概率，可得体重低于50公斤的概率为，则，在上有13人，该组的频率为0.13，则，所以，即c=0.07.(Ⅱ)用样本的频率估计总体的概率，可知从全体学生中随机抽取一人，体重在的概率为0.07×10=0.7，随机抽取3人，相当于三次独立重复试验，随机变量X服从二项分布，则，，，，所以，X的概率分布列为：X 0 1 2 3P 0.027 0.189 0.441 0.343E(X)=3×0.7=2.1(Ⅲ)由N(60,25)得由图（2）知.所以可以认为该校学生的体重是正常的.(三) 用样本估计总体频率分布直方图是高考考查的热点，考查频率很高，题型有选择题、填空题，也有解答题，难度为低中档．用样本频率分布来估计总体分布的重点是频率分布表和频率分布直方图的绘制及用样本频率分布估计总体分布；难点是频率分布表和频率分布直方图的理解及应用．在计数和计算时一定要准确，在绘制小矩形时，宽窄要一致．通过频率分布表和频率分布直方图可以对总体作出估计．频率分布直方图的纵坐标为频率/组距，每一个小长方形的面积表示样本个体落在该区间内的频率；条形图的纵坐标为频数或频率，把直方图视为条形图是常见的错误．【例3】2018年9月的台风“山竹”对我国多个省市的财产造成重大损害，据统计直接经济损失达亿元.某青年志愿者组织调查了某地区的个农户在该次台风中造成的直接经济损失，将收集的损失数据分成五组：，，，，（单位：元），得到如图所示的频率分布直方图.（1）试根据频率分布直方图估计该地区每个农户的损失（同一组中的数据用该区间的中点值代表）；（2）台风后该青年志愿者与当地政府向社会发出倡议，为该地区的农户捐款帮扶，现从这户损失超过元的农户中随机抽取户进行重点帮扶，设抽出损失超过元的农户数为，求的分布列和数学期望. 【分析】（1）根据频率分布直方图计算每个农户的平均损失；（2）根据频率分布直方图计算随机变量X的可能取值，再求X的分布列和数学期望值．【解析】（1）记每个农户的平均损失为元，则；（2）由频率分布直方图，可得损失超过1000元的农户共有（0.00009+0.00003+0.00003）×2000×50＝15（户），损失超过8000元的农户共有0.00003×2000×50＝3（户），随机抽取2户，则X的可能取值为0，1，2；计算P（X＝0）＝＝，P（X＝1）＝＝，P（X＝2）＝＝，所以X的分布列为；X 0 1 2P数学期望为E（X）＝0×+1×+2×＝．【点评】用样本估计总体是统计的基本思想，而利用频率分布表和频率分布直方图来估计总体则是用样本的频率分布去估计总体分布的两种主要方法．分布表在数量表示上比较准确，直方图比较直观．【小试牛刀】中国农业银行开始为全国农行ATM机安装刷脸取款系统.某农行营业点为调查居民对刷脸取款知识的了解情况,制作了刷脸取款知识有奖调查问卷,发放给2018年度该行的所有客户,并从参与调查且年龄(单位:岁)在[25,55]内的客户中随机抽取100名给予物质奖励,再从中选出一名客户参加幸运大抽奖.调查结果按年龄分成6组,制作成如下的频数分布表和女客户的年龄茎叶图,其中a∶b∶c=2∶4∶5.年龄/岁[25,30) [30,35) [35,40) [40,45) [45,50) [50,55]频数/人5 a b c 15 25女客户的年龄茎叶图幸运大抽奖方案如下:客户最多有两次抽奖机会,每次抽奖的中奖率均为,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则客户获得5000元奖金,不进行第二次抽奖;若正面朝上,客户需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金10000元,如果未中奖,则所获得的奖金为0元.(1)求a,b,c的值,若分别从男、女客户中随机选取1人,求这2人的年龄均在[40,45)内的概率;(2)若参加幸运大抽奖的客户所获奖金(单位:元)用X表示,求X的分布列与数学期望E(X).【解析】(1)由频数分布表知,a+b+c=100-45=55.因为a∶b∶c=2∶4∶5,所以a=×55=10,b=×55=20,c=×55=25,由茎叶图可知年龄在[25,30)内的女客户有2人,年龄在[30,35)内的女客户有4人,年龄在[35,40)内的女客户有8人,年龄在[40,45)内的女客户有10人,年龄在[45,50)内的女客户有6人,年龄在[50,55]内的女客户有10人,故年龄在[40,45)内的男客户有15人,在100名客户中,男客户有60人,女客户有40人,所以从男客户中随机选取1人,年龄恰在[40,45)内的概率P 1=,从女客户中随机选取1人,年龄恰在[40,45)内的概率P 2=,则分别从男、女客户中随机选取1人,这2人的年龄均在[40,45)内的概率P =P 1×P 2=.(2)由题意可知,X 的所有可能取值为0,5000,10000,则P (X =0)=,P (X =5000)=,P (X =10000)=.X 的分布列为 X5 00010 000PE (X )=0×+5000×+10000×=5200(元).(四) 回归分析回归分析是对具有相关关系的两个变量进行统计分析的方法，只有在散点图大致呈线性时，求出的回归直线方程才有实际意义，否则无意义．根据回归方程进行的估计仅是一个预测值，而不是真实发生的值．用最小二乘法求回归方程，关键在于正确求出系数a ^，b ^，由于a ^，b ^的计算量较大，计算应仔细小心．【例4】【湖北省黄冈市2019届模拟】某基地蔬菜大棚采用无土栽培方式种植各类蔬菜.根据过去50周的资料显示，该基地周光照量（小时）都在30小时以上，其中不足50小时的有5周，不低于50小时且不超过70小时的有35周，超过70小时的有10周.根据统计，该基地的西红柿增加量（千克）与使用某种液体肥料的质量（千克）之间的关系如图所示.（1）依据上图，是否可用线性回归模型拟合与的关系？请计算相关系数并加以说明（精确到0.01）.（若，则线性相关程度很高，可用线性回归模型拟合）（2）蔬菜大棚对光照要求较大，某光照控制仪商家为该基地提供了部分光照控制仪，但每周光照控制仪运行台数受周光照量限制，并有如下关系：周光照量（单位：小时）光照控制仪运行台数 3 2 1若某台光照控制仪运行，则该台光照控制仪周利润为3000元；若某台光照控制仪未运行，则该台光照控制仪周亏损1000元.以频率作为概率，商家欲使周总利润的均值达到最大，应安装光照控制仪多少台？附：相关系数公式，参考数据：，.【分析】(1)根据公式得到相关系数的值，通过比较得到判断；（2）分别求出安装一台，两台，三台时的利润均值，得到结果.【解析】（1）由已知数据可得，.∵，，.∴相关系数.∵，∴可用线性回归模型拟合与的关系.（2）记商家周总利润为元，由条件可知至少需安装1台，最多安装3台光照控制仪.①安装1台光照控制仪可获得周总利润3000元.②安装2台光照控制仪的情形：当时，只有1台光照控制仪运行，此时周总利润（元），，当时，2台光照控制仪都运行，此时周总利润（元），，故的分布列为2000 60000.2 0.8∴（元）.③安装3台光照控制仪的情形：当时，只有1台光照控制仪运行，此时周总利润（元），，当时，有2台光照控制仪运行，此时周总利润（元），，当时，3台光照控制仪都运行，周总利润（元），，故的分布列为1000 5000 90000.2 0.7 0.1∴（元）.综上可知，为使商家周总利润的均值达到最大，应该安装2台光照控制仪.【点评】判断两个变量是否具有相关关系的常用方法：(1)利用散点图进行判断；(2)利用相关系数r进行判断．【小试牛刀】【江西省临川第一中学等九校2019届高三3月联考】某商场营销人员进行某商品市场营销调查发现，每回馈消费者一定的点数，该商品每天的销量就会发生一定的变化，经过试点统计得到以下表：反馈点数 1 2 3 4 5销量（百件）/天0.5 0.6 1 1.4 1.7（1）经分析发现，可用线性回归模型拟合当地该商品销量（千件）与返还点数之间的相关关系.请用最小二乘法求关于的线性回归方程，并预测若返回6个点时该商品当天销量；（2）若节日期间营销部对商品进行新一轮调整.已知某地拟购买该商品的消费群体十分庞大，经营销调研机构对其中的200名消费者的返点数额的心理预期值进行了一个抽样调查，得到如下一份频数表：返还点数预期值区间（百分比）频数20 60 60 30 20 10（i）求这200位拟购买该商品的消费者对返点点数的心理预期值的样本平均数及中位数的估计值（同一区间的预期值可用该区间的中点值代替；估计值精确到0.1）；（ii）将对返点点数的心理预期值在和的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者，现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名，再从这6人中随机抽取3名进行跟踪调查，设抽出的3人中“欲望膨胀型”消费者的人数为随机变量，求的分布列及数学期望.参考公式及数据：①，；②.【解析】（1）易知，，，，.则关于的线性回归方程为，当时，，即返回6个点时该商品每天销量约为2百件.（2）（i）根据题意，这200位拟购买该商品的消费者对返回点数的心里预期值的平均值，及中位数的估计值分别为：，中位数的估计值为.（ii）抽取6名消费者中“欲望紧缩型”消费者人数为，“欲望膨胀型”消费者人数为.，，，故随机变量的分布列为1 2 3.(五) 独立性检验独立性检验的一般步骤(1)假设两个分类变量x与y没有关系；(2)计算出K2的观测值，其中K2＝n（ad－bc）2（a＋b）（c＋d）（a＋c）（b＋d）；(3)把K2的值与临界值比较，作出合理的判断．【例5】【福建省莆田市2019届高三下学期教学质量检测】为推进“千村百镇计划”，年月某新能源公司开展“电动莆田绿色出行”活动，首批投放台型新能源车到莆田多个村镇，供当地村民免费试用三个月。

【高三】2021届高考数学备考复习：椭圆双曲线抛物线(含轨迹问题)

【高三】2021届高考数学备考复习：椭圆双曲线抛物线（含轨迹问题）【高三】2021届高考数学备考复习：椭圆、双曲线、抛物线（含轨迹问题）主题五：解析几何第二讲椭圆、双曲线、抛物线（含轨迹问题）【最新考试大纲分析】1．圆锥曲线（1）了解圆锥曲线的实际背景，以及圆锥曲线在描绘现实世界和解决实际问题中的作用。

（2）掌握椭圆、抛物线的定义、几何图形、标准方程及简单性质。

（3）了解双曲线的定义、几何和标准方程，了解其简单的几何性质。

（4）了解圆锥曲线的简单应用。

（5）理解数字和形式结合的概念。

2．曲线与方程了解方程的曲线与方程的对应关系。

【核心要点突破】重点测试方向1：圆锥曲线的定义、几何特性和标准方程考情聚焦：1．圆锥曲线的定义、几何性质及标准方程是每年必考内容，虽然大纲降低了对双曲线的要求，但在选择题中仍然考查双曲线。

2.可以单独检查，也可以结合向量、序列、不等式等知识进行检查。

3．既可以以小题的形式考查（属中、低档题），也可以以解答题形式考查（属于中、高档题）。

考虑到圆锥曲线的重点，我们首先要考虑使用圆锥曲线的定义来解决它。

2.2．求圆锥曲线方程常用的方法有定义法、待定系数法、轨迹方程法。

3.计算椭圆和双曲线的偏心率，关键是根据已知条件确定等效关系，然后用a和C代替B来计算B值。

4．在双曲线中由于，故双曲线的渐近线与离心率密切相关。

例1：（2022？安徽高考科学？T19）已知椭圆通过该点，对称轴是坐标轴，焦点在轴上，偏心率。

(1)求椭圆的方程；（2）求角平分线所在直线的方程；(3)在椭圆上是否存在关于直线对称的相异两点？若存在，请找出；若不存在，说明理由。

【命题意图】本题主要考查椭圆的定义和标准方程、椭圆的简单性质、直线点的对称性等知识，考查考生在解析几何的基本思想和方法、探索意识、，创新意识和综合运营解决能力【思路点拨】（1）设出椭圆的标准方程，再根据题设条件构建方程（组）求解；（2）根据角平分线的性质，求出直线的斜率或直线上一点的坐标，进而得到直线方程；（3）先假设椭圆上存在关于直线对称的相异两点，在此基础之上进行推理运算，求解此两点，根据推理结果做出判断。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

问题34 椭圆、双曲线、抛物线与圆相结合问题一、考情分析通过近几年各地高考试题可以发现,对圆的考查在逐渐加深,并与圆锥曲线相结合在一起命题,成为一个新的动向.与圆相关几何性质、最值问题、轨迹问题等都能与椭圆、双曲线和抛物线想结合可以呈现别具一格的新颖试题.二、经验分享1.对于圆与圆锥曲线的相交问题，设出交点，由交点(或韦达定理)结合条件解决问题，在求解过程中、数形结合是常用的打开思路的方式、形是引路、数是依据、二者联手，解决问题就易如反掌、设面不求、灵活消参是常用的策略。

2. 垂直问题的呈现有多种形式，处理重直问题最好的方法是应用向量的坐标形式转化，常规的思路是:联立方程组消去成y,得到一个二次方程，设交点，韦达定理代人垂直的数量积坐标公式整理求解。

3.涉及弦长要注意圆的几何性质的应用。

三、知识拓展以MN为直径的圆经过点P，则，可转化为四、题型分析(一) 圆与椭圆的结合点1.1圆的几何性质与椭圆相联系【例1】【2017届湖南师大附中高三上学期月考四】已知椭圆的中心在原点,离心率为,其右焦点是圆：的圆心．（1）求椭圆的标准方程；（2）如图,过椭圆上且位于轴左侧的一点作圆的两条切线,分别交轴于点、．试推断是否存在点,使？若存在,求出点的坐标；若不存在,请说明理由．【分析】(1)由已知条件分别求出的值,而,代入求出椭圆的方程；(2)假设存在点满足题意,设点（）, , ,利用条件求出直线方程,根据圆心到直线的距离为,求出与点坐标之间的关系,同理求出与点坐标之间的关系,利用韦达定理求出的表达式,算出,求出点坐标.【解析】（1）设椭圆方程,半焦距为,因为椭圆的右焦点是圆的圆心,则,因为椭圆的离心率为,则,即,从而,故椭圆的方程为．（2）设点（）, , ,则直线的方程为,即,因为圆心到直线的距离为1,即,即,即,同理．由此可知, ,为方程的两个实根,所以, ,．因为点在椭圆上,则,即,则,令,则,因为,则, ,即,故存在点满足题设条件．【点评】(1)处理直线与圆的弦长问题时多用几何法,即弦长的一半、弦心距、半径构成直角三角形．(2)圆的切线问题的处理要抓住圆心到直线的距离等于半径,从而建立关系解决问题．【小试牛刀】已知椭圆的离心率为,其左顶点在圆上.（Ⅰ）求椭圆的方程；（Ⅱ）若点为椭圆上不同于点的点,直线与圆的另一个交点为,是否存在点,使得？若存在,求出点的坐标；若不存在,说明理由.【答案】（I）；（II）不存在,理由见解析.【解析】（I）因为椭圆的左顶点在圆上,令,得,所以.又离心率为,所以,所以,所以.所以的方程为.（II）设点, ,设直线的方程为,与椭圆方程联立得,化简得到,因为-4为方程的一个根,所以,所以因为圆心到直线的距离为,所以.因为,代入得到,显然,所以不存在直线,使得.1.2 利用椭圆的性质判断直线与圆的位置关系【例2】已知椭圆：.（1）求椭圆的离心率；（2）设为原点,若点在椭圆上,点在直线上,且,试判断直线与圆的位置关系,并证明你的结论.【分析】（1）把椭圆：化为标准方程,确定, ,利用求得离心率；（2）设点, ,其中,由,即,用、表示,当或分别根据点到直线的距离公式求出圆心到直线的距离,与圆的半径比较,从而判断直线与圆的位置关系.【解析】（1）由题意椭圆的标准方程为,所以, ,从而,所以.（2）直线与圆相切,证明如下：设点, ,其中,因为,所以,即,解得,当时, ,代入椭圆的方程得,此时直线与圆相切.当时,直线的方程为,即,圆心到直线的距离为,又, ,故.故此直线与圆相切.【小试牛刀】已知椭圆过点,且离心率．(1)求椭圆的方程；(2)设直线交椭圆于,两点,判断点与以线段为直径的圆的位置关系,并说明理由．【解析】解法一：（1）由已知得,解得,所以椭圆的方程为．（2）设点, ,的中点为．由,得,所以, ,从而,,故,所以．故点在以为直径的圆外．解法二：（1）同解法一．（2）设点, ,则,．由,得,所以, ,从而,所以．又,不共线,所以为锐角．故点在以为直径的圆外．(二) 圆与双曲线的结合点2.1 利用圆的性质解决双曲线的相关问题由于双曲线具有渐近线,故渐近线与圆的位置关系便成为命题的常考点.圆本身所具有的几何性质在探索等量关系也经常考查,进而求解双曲线的几何性质,如离心率的求解.【例3】【黑龙江省齐齐哈尔市2019届高三第一次模拟】已知半圆：，、分别为半圆与轴的左、右交点，直线过点且与轴垂直，点在直线上，纵坐标为，若在半圆上存在点使，则的取值范围是（）A．B．C．D．【答案】A【分析】根据题意，设PQ与x轴交于点T，分析可得在Rt△PBT中，|BT||PB||t|，分p在x轴上方、下方和x轴上三种情况讨论，分析|BT|的最值，即可得t的范围，综合可得答案．【解析】根据题意，设PQ与x轴交于点T，则|PB|＝|t|，由于BP与x轴垂直，且∠BPQ，则在Rt△PBT中，|BT||PB||t|，当P在x轴上方时，PT与半圆有公共点Q，PT与半圆相切时，|BT|有最大值3，此时t有最大值，当P在x轴下方时，当Q与A重合时，|BT|有最大值2，|t|有最大值，则t取得最小值，t＝0时，P与B重合，不符合题意，则t的取值范围为[，0）]；故选：A．【小试牛刀】【福建省厦门市2019届高中毕业班第一次（3月)质量检查】已知双曲线的一个焦点为，点是的一条渐近线上关于原点对称的两点，以为直径的圆过且交的左支于两点，若，的面积为8，则的渐近线方程为（）A．B．C．D．【答案】B【解析】设双曲线的另一个焦点为，由双曲线的对称性，四边形是矩形，所以，即，由，得：，所以，所以，所以，，所以，的渐近线方程为.故选B2.2 圆的切线与双曲线相联系【例4】已知双曲线的左右焦点分别为,为双曲线的中心,是双曲线右支上的点,的内切圆的圆心为,且圆与轴相切于点,过作直线的垂线,垂足为,若为双曲线的离心率,则( )A. B. C. D.与关系不确定【答案】C【解析】设内切圆在上的切点为,上的切点为,上的切点为,的坐标为,∴,即,延长交于,∵是角平分线和垂线,∴是的中点,是的中点,是中位线, ,∴,∴.【小试牛刀】已知点、为双曲线：的左、右焦点,过作垂直于轴的直线,在轴上方交双曲线于点,且．圆的方程是．（1）求双曲线的方程；（2）过双曲线上任意一点作该双曲线两条渐近线的垂线,垂足分别为、,求的值；（3）过圆上任意一点作圆的切线交双曲线于、两点,中点为,求证：．【解析】（1）设的坐标分别为因为点在双曲线上,所以,即,所以在中, , ,所以由双曲线的定义可知：故双曲线的方程为：（2）由条件可知：两条渐近线分别为设双曲线上的点,设两渐近线的夹角为,则则点到两条渐近线的距离分别为因为在双曲线：上,所以又,所以（3）由题意,即证：.设,切线的方程为：①当时,切线的方程代入双曲线中,化简得：所以：又所以②当时,易知上述结论也成立．所以综上, ,所以．(三) 圆与抛物线的结合点3.1圆的性质与抛物线相结合【例5】一个酒杯的轴截面是开口向上的抛物线的一段弧,它的口宽是的4,杯深20,在杯内放一玻璃球,当玻璃球的半径r最大取时,才能使玻璃球触及杯底．【答案】1【解析】建立如图所示的直角坐标系,酒杯所在抛物线的方程设为,因为过点,所以,即.玻璃球触及杯底,就是小球的截面圆与抛物线有且仅有一个交点,即原点.由与消去得：或因为有且仅有一个交点,即原点,所以即半径r最大取1.【小试牛刀】【广东省2019届天河区普通高中毕业班综合测试（二)】已知抛物线C：的焦点为F，准线l 与x轴的交点为A，M是抛物线C上的点，且轴，若以AF为直径的圆截直线AM所得的弦长为2，则 ( ) A．2 B． C．4 D．【答案】B【解析】把代入可得，不妨设M在第一象限，则，又，直线AM的方程为，即，原点O到直线AP的距离，以AF为直径的圆截直线AM所得的弦长为2，，解得．故选：B．3.2 抛物线的性质与圆的相联系【例6】已知椭圆离心率为,焦距为,抛物线的焦点是椭圆的顶点.（Ⅰ）求与的标准方程；（Ⅱ）设过点的直线交于两点,若的右顶点在以为直径的圆内,求直线的斜率的取值范围.【分析】（Ⅰ）椭圆的焦距为, ,得椭圆的标准方程,得到抛物线焦点,可得抛物线方程；（Ⅱ）联立直线与抛物线的方程结合韦达定理得, ,在以为直径的圆内,得结果.【解析】（Ⅰ）设椭圆的焦距为,依题意有, ,解得, ,故椭圆的标准方程为,又抛物线开口向上,故是椭圆的上顶点, ,,故抛物线的标准方程为.（Ⅱ）由题意可设直线的方程为：,设点, ,联立得,由韦达定理得,.在以为直径的圆内.【小试牛刀】已知抛物线C：的焦点为F,直线与y轴的交点为P,与C的交点为Q,且.（I）求C的方程；（II）过F的直线与C相交于A,B两点,若AB的垂直平分线与C相较于M,N两点,且A,M,B,N四点在同一圆上,求的方程.【解析】（I）设,代入,得．由题设得,解得（舍去）或,∴C的方程为；（II）由题设知与坐标轴不垂直,故可设的方程为,代入得．设则．故的中点为．又的斜率为的方程为．将上式代入,并整理得．设则．故的中点为．由于垂直平分线,故四点在同一圆上等价于,从而即,化简得,解得或．所求直线的方程为或．四、迁移运用1．【江西省南昌市2019届高三第一次模拟】过双曲线的左焦点作圆的切线交双曲线的右支于点，且切点为，已知为坐标原点，为线段的中点（点在切点的右侧），若的周长为，则双曲线的渐近线的方程为( ) A．B．C．D．【答案】B【解析】解：连OT，则OT⊥F1T，在直角三角形OTF1中，|F1T|b．连PF2，M为线段F1P的中点，O为坐标原点∴OMPF2，∴|MO|﹣|MT|PF2﹣（PF1﹣F1T）（PF2﹣PF1）+bb﹣a．又|MO|+|MT|+|TO|=，即|MO|+|MT|=3a故|MO|=, |MT|=,由勾股定理可得：，即∴渐近线方程为：故选：B2．【山东省淄博市2018-2019学年度高三3月模拟】已知直线与双曲线交于两点，以为直径的圆恰好经过双曲线的右焦点，若的面积为，则双曲线的离心率为A． B． C．2 D．【答案】D【解析】由题意可得图像如下图所示：为双曲线的左焦点为圆的直径根据双曲线、圆的对称性可知：四边形为矩形又，可得：本题正确选项：3．【河南省濮阳市2019届高三下学期摸底】双曲线的两顶点为，，虚轴两端点为，，两焦点为，，若以为直径的圆内切于菱形，则双曲线的离心率是（）A． B． C． D．【答案】C【解析】由题意可得，，，，，，且，菱形的边长为，由以为直径的圆内切于菱形，切点分别为A，B，C，D．由面积相等，可得，即为，即有，由，可得，解得，可得，或 (舍去)故选：C．4．【广东省潮州市2019届高三上学期期末】已知双曲线C：的左、右焦点分别为、，且双曲线C与圆在第一象限相交于点A，且，则双曲线C的离心率是A． B． C． D．【答案】A【解析】双曲线C与圆在第一象限相交于点A，可得，由，可得，，由，可得，即为，即有，即有．故选：A．5.【安徽省合肥一中、马鞍山二中等六校教育研究会2019届高三第二次联考】已知抛物线上一点到焦点的距离为，分别为抛物线与圆上的动点，则的最小值为（）A． B． C． D．【答案】D【解析】由抛物线焦点在轴上，准线方程，则点到焦点的距离为，则，所以抛物线方程：，设，圆，圆心为，半径为1，则，当时，取得最小值，最小值为，故选D.6．【辽宁省沈阳市郊联体2019届高三上学期期末】已知椭圆的右焦点为，离心率为e，过原点斜率为k的直线与椭圆交于A、B两点，M、N分别为线段AF、BF的中点，以MN为直径的圆过原点O，若，则e的取值范围是A． B． C． D．【答案】D【解析】记线段MN与x轴交点为C．的中点为M，BF的中点为N，，，、B为椭圆上关于原点对称的两点，．原点O在以线段MN为直径的圆上，．．，，．设，，易得．由，可得得，．直线AB斜率为，，，由于，离心率e的取值范围为故选：D．7．【山东省临沂市2019届高三2月教学质量检测】是双曲线的左、右焦点，直线l为双曲线C的一条渐近线，关于直线l的对称点为，且点在以F2为圆心、以半虚轴长b为半径的圆上，则双曲线C的离心率为A． B． C．2 D．【答案】B【解析】因为直线l为双曲线C的一条渐近线，则直线因为是双曲线的左、右焦点所以（-c，0），（c，0）因为关于直线l的对称点为，设为（x，y）则解得所以为（）因为是以为圆心，以半虚轴长b为半径的圆，则圆的方程为将以的（）代入圆的方程得化简整理得，所以所以选B8．【河南省中原名校（即豫南九校)2018届高三第六次质量考评】已知抛物线的焦点为，过点且斜率为1的直线与抛物线交于点，以线段为直径的圆上存在点，使得以为直径的圆过点，则实数的取值范围为（）A． B．C． D．【答案】D【解析】由题得直线AB的方程为即y=x-1,设A，联立所以，|AB|=所以AB为直径的圆E的圆心为（3,2），半径为4.所以该圆E的方程为.所以点D恒在圆E外，圆E上存在点P,Q，使得以PQ为直径的圆过点D(-2,t)，即圆E上存在点P,Q，使得DP⊥DQ，显然当DP,DQ与圆E相切时，∠PDQ最大，此时应满足∠PDQ，所以，整理得.解之得，故选D.9．【河北省石家庄市2018届高三下学期一模】已知，分别为双曲线的左焦点和右焦点，过的直线与双曲线的右支交于，两点，的内切圆半径为，的内切圆半径为，若，则直线的斜率为（）A. 1B.C. 2D.【答案】D【解析】设的内切圆圆心为，的内切圆圆心为，边上的切点分别为易见横坐标相等，则由即得即，记的横坐标为，则，于是，得同理内心的横坐标也为则有轴，设直线的倾斜角为，则则故选D.10．【河南省郑州市2018届高三毕业年级第二次质量预测】如图，已知抛物线的顶点在坐标原点，焦点在轴上，且过点，圆,过圆心的直线与抛物线和圆分别交于,则的最小值为( )A. 23B. 42C. 12D. 52【答案】A【解析】由题意抛物线过定点（2，4），得抛物线方程，焦点为F(2,0).圆的标准方程为，所以圆心为（2，0），半径r=1.由于直线过焦点，所以有，又=，当且仅当时等号成立。